Skip to main content
LibreTexts - Ukrayinska

6.4E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59591

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Фактор Ідеальні квадратні триноми

    У наступних вправах фактор повністю використовуючи ідеальний квадратний тріноми візерунок.

    1. \(16y^2+24y+9\)

    Відповідь

    \((4y+3)^2\)

    2. \(25v^2+20v+4\)

    3. \(36s^2+84s+49\)

    Відповідь

    \((6s+7)^2\)

    4. \(49s^2+154s+121\)

    5. \(100x^2−20x+1\)

    Відповідь

    \((10x−1)^2\)

    6. \(64z^2−16z+1\)

    7. \(25n^2−120n+144\)

    Відповідь

    \((5n−12)^2\)

    8. \(4p^2−52p+169\)

    9. \(49x^2+28xy+4y^2\)

    Відповідь

    \((7x+2y)^2\)

    10. \(25r^2+60rs+36s^2\)

    11. \(100y^2−52y+1\)

    Відповідь

    \((50y−1)(2y−1)\)

    12. \(64m^2−34m+1\)

    13. \(10jk^2+80jk+160j\)

    Відповідь

    \(10j(k+4)^2\)

    14. \(64x^2y−96xy+36y\)

    15. \(75u^4−30u^3v+3u^2v^2\)

    Відповідь

    \(3u^2(5u−v)^2\)

    16. \(90p^4+300p^4q+250p^2q^2\)

    Факторні відмінності квадратів

    У наступних вправах, фактор повністю використовуючи різницю квадратів візерунка, якщо це можливо.

    17. \(25v^2−1\)

    Відповідь

    \((5v−1)(5v+1)\)

    18. \(169q^2−1\)

    19. \(4−49x^2\)

    Відповідь

    \((7x−2)(7x+2)\)

    20. \(121−25s^2\)

    21. \(6p^2q^2−54p^2\)

    Відповідь

    \(6p^2(q−3)(q+3)\)

    22. \(98r^3−72r\)

    23. \(24p^2+54\)

    Відповідь

    \(6(4p^2+9)\)

    24. \(20b^2+140\)

    25. \(121x^2−144y^2\)

    Відповідь

    \((11x−12y)(11x+12y)\)

    26. \(49x^2−81y^2\)

    27. \(169c^2−36d^2\)

    Відповідь

    \((13c−6d)(13c+6d)\)

    28. \(36p^2−49q^2\)

    29. \(16z^4−1\)

    Відповідь

    \((2z−1)(2z+1)(4z^2+1)\)

    30. \(m^4−n^4\)

    31. \(162a^4b^2−32b^2\)

    Відповідь

    \(2b^2(3a−2)(3a+2)(9a^2+4)\)

    32. \(48m^4n^2−243n^2\)

    33. \(x^2−16x+64−y^2\)

    Відповідь

    \((x−8−y)(x−8+y)\)

    34. \(p^2+14p+49−q^2\)

    35. \(a^2+6a+9−9b^2\)

    Відповідь

    \((a+3−3b)(a+3+3b)\)

    36. \(m^2−6m+9−16n^2\)

    Факторні суми та відмінності кубів

    У наступних вправах, коефіцієнт повністю використовуючи суми і відмінності кубиків візерунка, якщо це можливо.

    37. \(x^3+125\)

    Відповідь

    \((x+5)(x^2−5x+25)\)

    38. \(n^6+512\)

    39. \(z^6−27\)

    Відповідь

    \((z^2−3)(z^4+3z^2+9)\)

    40. \(v^3−216\)

    41. \(8−343t^3\)

    Відповідь

    \((2−7t)(4+14t+49t^2)\)

    42. \(125−27w^3\)

    43. \(8y^3−125z^3\)

    Відповідь

    \((2y−5z)(4y^2+10yz+25z^2)\)

    44. \(27x^3−64y^3\)

    45. \(216a^3+125b^3\)

    Відповідь

    \((6a+5b)(36a^2−30ab+25b^2)\)

    46. \(27y^3+8z^3\)

    47. \(7k^3+56\)

    Відповідь

    \(7(k+2)(k^2−2k+4)\)

    48. \(6x^3−48y^3\)

    49. \(2x^2−16x^2y^3\)

    Відповідь

    \(2x^2(1−2y)(1+2y+4y^2)\)

    50. \(−2x^3y^2−16y^5\)

    51. \((x+3)^3+8x^3\)

    Відповідь

    \(9(x+1)(x^2+3)\)

    52. \((x+4)^3−27x^3\)

    53. \((y−5)^3−64y^3\)

    Відповідь

    \(−(3y+5)(21y^2−30y+25)\)

    54. \((y−5)^3+125y^3\)

    Змішана практика

    У наступних вправах фактор повністю.

    55. \(64a^2−25\)

    Відповідь

    \((8a−5)(8a+5)\)

    56. \(121x^2−144\)

    57. \(27q^2−3\)

    Відповідь

    \(3(3q−1)(3q+1)\)

    58. \(4p^2−100\)

    59. \(16x^2−72x+81\)

    Відповідь

    \((4x−9)^2\)

    60. \(36y^2+12y+1\)

    61. \(8p^2+2\)

    Відповідь

    \(2(4p^2+1)\)

    62. \(81x^2+169\)

    63. \(125−8y^3\)

    Відповідь

    \((5−2y)(25+10y+4y^2)\)

    64. \(27u^3+1000\)

    65. \(45n^2+60n+20\)

    Відповідь

    \(5(3n+2)^2\)

    66. \(48q^3−24q^2+3q\)

    67. \(x^2−10x+25−y^2\)

    Відповідь

    \((x+y−5)(x−y−5)\)

    68. \(x^2+12x+36−y^2\)

    69. \((x+1)^3+8x^3\)

    Відповідь

    \((3x+1)(3x^2+1)\)

    70. \((y−3)^3−64y^3\)

    Письмові вправи

    71. Чому важливо було практикувати використання шаблону біноміальних квадратів у розділі про множення многочленів?

    Відповідь

    Відповіді будуть відрізнятися.

    72. Як ви розпізнаєте візерунок біноміальних квадратів?

    73. Поясніть чому\(n^2+25\neq (n+5)^2\). Використовуйте алгебру, слова або картинки.

    Відповідь

    Відповіді будуть відрізнятися.

    74. Марібель зарахував\(y^2−30y+81\) як\((y−9)^2\). Вона була права чи не права? Звідки ти знаєш?

    Самостійна перевірка

    а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

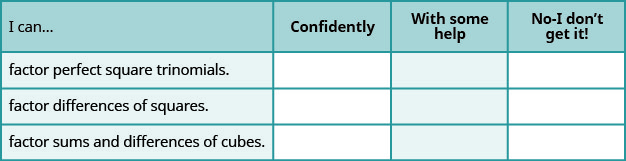
    Ця таблиця має 4 стовпці, 3 рядки та рядок заголовка. Рядок заголовка позначає кожен стовпець, який я можу, впевнено, з деякою допомогою і ні, я не розумію. Перший стовпець має такі твердження: коефіцієнт досконалих квадратних триноміалів, факторні відмінності квадратів, коефіцієнтні суми та відмінності кубів. Решта стовпці порожні.

    б Що говорить вам цей контрольний список про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?