6.3: Факторні термінали
- Page ID
- 59541
До кінця цього розділу ви зможете:
- Факторні триміали форми\(x^2+bx+c\)
- Факторні тріноми форми з\(ax^2+bx+c\) використанням проб і помилок
- Факторні тріноми форми з\(ax^2+bx+c\) використанням методу\(ac\) ''
- Фактор, що використовує заміщення
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Знайти всі фактори 72.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Знайдіть товар:\((3y+4)(2y+5)\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Спростити:\(−9(6);\space −9(−6)\).
Якщо ви пропустили цю проблему, перегляньте [посилання].
Факторні триміали форми\(x^2+bx+c\)
Ви вже дізналися, як множити біноміали за допомогою FOIL. Тепер вам потрібно буде «скасувати» це множення. Фактор тріноміал означає почати з продукту, а закінчити з факторами.
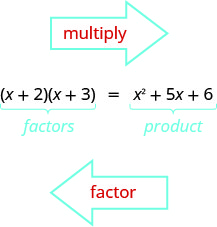
Щоб з'ясувати, як ми б фактор триноміалу форми\(x^2+bx+c\), наприклад,\(x^2+5x+6\) і фактор його\((x+2)(x+3)\), давайте почнемо з двох загальних біноміалів форми\((x+m)\) і\((x+n)\).
| \((x+m)(x+n)\) | |
| Фольга, щоб знайти продукт. | \(x^{2}+m x+n x+m n\) |
| Фактор GCF з середніх термінів. | \(x^{2}+(m+n) x+m n\) |
| Наш триноміал має форму\(x^2+bx+c\). | \(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\) |
Це говорить нам про те, що для множника триноміалу форми\(x^2+bx+c\) нам потрібні два множники\((x+m)\) і\((x+n)\) де два числа\(m\) і\(n\) помножити\(c\) і додати до\(b\).
Фактор:\(x^2+11x+24\).
- Відповідь
-




Фактор:\(q^2+10q+24\).
- Відповідь
-
\((q+4)(q+6)\)
Фактор:\(t^2+14t+24\).
- Відповідь
-
\((t+2)(t+12)\)
Давайте підсумуємо кроки, які ми використовували для пошуку факторів.
- Запишіть множники як два біноміали з першими долями x. \(\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} \)
- Знайти два числа\(m\) і\(n\) що
- помножити на\(c\),\(m·n=c\)
- додати в\(b\),\(m+n=b\)
- Використовують\(m\) і в\(n\) якості останніх термінів чинники. \(\quad (x+m)(x+n)\)
- Перевірте, множивши коефіцієнти.
У першому прикладі всі терміни в триноміале були позитивними. Що відбувається, коли є негативні терміни? Ну, це залежить, який термін негативний. Давайте спочатку розглянемо триноми з лише середнім терміном негативним.
Як отримати позитивний твір і негативну суму? Використовуємо два від'ємних числа.
Фактор:\(y^2−11y+28\).
- Відповідь
-
Знову ж таки, з позитивним останнім терміном\(28\), і негативним середнім терміном\(−11y\), нам потрібні два негативні фактори. Знайти два числа, які множаться\(28\) і додати до\(−11\).
\(\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}\)Фактори\(28\) Сума множників \ (28\)» перевірка даних = «верх">\(−1,\space −28\)
\(−2,\space −14\)
\(−4,\space −7\)\(−1+(−28)=−29\)
\(−2+(−14)=−16\)
\(−4+(−7)=−11^∗\)\(\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} \)
Фактор:\(u^2−9u+18\).
- Відповідь
-
\((u−3)(u−6)\)
Фактор:\(y^2−16y+63\).
- Відповідь
-
\((y−7)(y−9)\)
Тепер, що робити, якщо останній термін у триноміалі негативний? Подумайте про ФОЛЬГУ. Останній термін є добутком останніх членів у двох біноміалах. Негативний твір є результатом множення двох чисел з протилежними знаками. Ви повинні бути дуже обережними, щоб вибрати фактори, щоб переконатися, що ви отримаєте правильний знак для середнього терміну, теж.
Як отримати негативний продукт і позитивну суму? Використовуємо одне позитивне і одне негативне число.
Коли ми враховуємо триноми, ми повинні мати терміни, написані в порядку спадання - для того, щоб від найвищого ступеня до найнижчого ступеня.
Фактор:\(2x+x^2−48\).
- Відповідь
-
\(\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} \)
Фактори −48−48 Сума множників \(−1,\space 48\)
\(−2,\space 24\)
\(−3,\space 16\)
\(−4,\space 12\)
\(−6,\space 8\)\(−1+48=47\)
\(−2+24=22\)
\(−3+16=13\)
\(−4+12=8\)
\(−6+8=2^∗\)\(\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} \)
Фактор:\(9m+m^2+18\).
- Відповідь
-
\((m+3)(m+6)\)
Фактор:\(−7n+12+n^2\).
- Відповідь
-
\((n−3)(n−4)\)
Іноді вам потрібно буде враховувати тріноми форми\(x^2+bxy+cy^2\) з двома змінними, наприклад\(x^2+12xy+36y^2\). Перший термін,\(x^2\), є добутком перших членів біноміальних факторів,\(x·x\). \(y^2\)Останній термін означає, що другі члени біноміальних факторів повинні містити кожен\(y\). Щоб отримати коефіцієнти\(b\) і\(c\), ви використовуєте той самий процес, узагальнений в How To Factor trinomials.
Фактор:\(r^2−8rs−9s^2\).
- Відповідь
-
Нам потрібно\(r\) в першому семестрі кожного двочлена і\(s\) в другому. Останній термін триноміала негативний, тому фактори повинні мати протилежні ознаки.
\(\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}\)Фактори\(−9\) Сума множників \ (−9\)» перевірка даних ="верх">\(1,\space −9\) \(−1+9=8\) \ (−9\)» перевірка даних ="верх">\(−1,\space 9\) \(1+(−9)=−8^∗\) \ (−9\)» перевірка даних ="верх">\(3,\space −3\) \(3+(−3)=0\) \(\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} \)
Фактор:\(a^2−11ab+10b^2\).
- Відповідь
-
\((a−b)(a−10b)\)
Фактор:\(m^2−13mn+12n^2\).
- Відповідь
-
\((m−n)(m−12n)\)
Деякі триноміали є простими. Єдиний спосіб бути впевненим, що триноміал є простим - це перерахувати всі можливості і показати, що жодна з них не працює.
Фактор:\(u^2−9uv−12v^2\).
- Відповідь
-
Нам потрібно\(u\) в першому семестрі кожного двочлена і\(v\) в другому. Останній термін триноміала негативний, тому фактори повинні мати протилежні ознаки.
\(\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} \)Фактори\(−12\) Сума множників \ (−12\)» перевірка даних="верх">\(1,−12\)
\(−1,12\)
\(2,−6\)
\(−2,6\)
\(3,−4\)
\(−3,4\)\(1+(−12)=−11\)
\(−1+12=11\)
\(2+(−6)=−4\)
\(−2+6=4\)
\(3+(−4)=−1\)
\(−3+4=1\)Зверніть увагу, що немає пар факторів, які дають нам\(−9\) як суму. Триноміал є простим.
Фактор:\(x^2−7xy−10y^2\).
- Відповідь
-
прем'єр
Фактор:\(p^2+15pq+20q^2\).
- Відповідь
-
прем'єр
Давайте підсумуємо метод, який ми тільки що розробили для фактора триноміалів форми\(x^2+bx+c\).
Коли ми фактуємо триноміал, ми спочатку дивимося на ознаки його термінів, щоб визначити ознаки біноміальних факторів.
| \( x^{2}+b x+c \) | ||
| \( (x+m)(x+n) \) | ||
| Коли\( c \) позитивний,\( m \) і\( n \) мають однаковий знак. | ||
| \( b \)позитивний | \( b \)негативний | |
| \( m,n \)позитивний | \( m,n \)негативний | |
| \( x^{2}+5 x+6 \) | \( x^{2}-6 x+8 \) | |
| \( (x+2)(x+3) \) | \( (x-4)(x-2) \) | |
| ті ж ознаки | ті ж ознаки | |
| Коли\( c \) негативний,\( m \) і\( n \) мають протилежний знак. | ||
| \( x^{2}+x-12 \) | \( x^{2}-2 x-15 \) | |
| \( (x+4)(x-3) \) | \( (x-5)(x+3) \) | |
| протилежні ознаки | протилежні ознаки | |
Зверніть увагу, що в разі, коли\(m\) і\(n\) мають протилежні знаки, знак того, що має більшу абсолютну величину, відповідає знаку\(b\).
Фактор Тримінали виду ax 2 + bx + c використанням методу проб і помилок
Наступним нашим кроком є множник тріномів, провідний коефіцієнт яких не дорівнює 1, триноміали форми\(ax^2+bx+c\).
Пам'ятайте, що завжди спочатку перевіряйте наявність GCF! Іноді, після того, як ви фактор GCF, провідний коефіцієнт триноміалу стає,\(1\) і ви можете зарахувати його методами, які ми використовували досі. Давайте зробимо приклад, щоб побачити, як це працює.
Фактор повністю:\(4x^3+16x^2−20x\).
- Відповідь
-
\(\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} \)
Фактори\(−5\) Сума множників \ (−5\)» перевірка даних ="верх">\(−1,5\)
\(1,−5\)\(−1+5=4^∗\)
\(1+(−5)=−4\)\(\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} \)
Фактор повністю:\(5x^3+15x^2−20x\).
- Відповідь
-
\(5x(x−1)(x+4)\)
Фактор повністю:\(6y^3+18y^2−60y\).
- Відповідь
-
\(6y(y−2)(y+5)\)
Що відбувається, коли провідного\(1\) коефіцієнта немає і немає ГКФ? Існує кілька методів, які можуть бути використані для фактора цих триноміалів. Для початку скористаємося методом проб і помилок.
Давайте врахуємо тріноміал\(3x^2+5x+2\).
З нашої попередньої роботи ми очікуємо, що це буде коефіцієнт на два біноміали.
\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]
Ми знаємо, що перші члени біноміальних факторів будуть множитися, щоб дати нам\(3x^2\). Єдиними факторами\(3x^2\) є\(1x,\space 3x\). Ми можемо розмістити їх у двочленах.
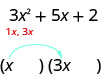
Перевірте: Чи є\(1x·3x=3x^2\)?
Ми знаємо, що останні члени біноміалів будуть множитися на\(2\). Оскільки цей триноміал має всі позитивні моменти, потрібно лише враховувати позитивні фактори. Єдиними факторами\(2\) є\(1\) і\(2\). Але тепер у нас є два випадки, щоб розглянути, як це буде мати значення, якщо ми пишемо\(1\),\(2\) або\(2\),\(1\).

Які чинники правильні? Щоб вирішити, що, множимо внутрішній і зовнішній члени.
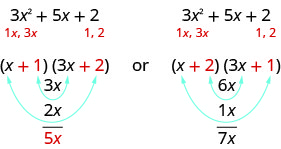
Так як середній термін триноміала є\(5x\), то фактори в першому випадку спрацюють. Давайте використовувати FOIL для перевірки.
\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]
Нашим результатом факторингу є:
\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]
Фактор повністю за допомогою проб і помилок:\(3y^2+22y+7\).
- Відповідь
-






Фактор повністю за допомогою проб і помилок:\(2a^2+5a+3\).
- Відповідь
-
\((a+1)(2a+3)\)
Фактор повністю за допомогою проб і помилок:\(4b^2+5b+1\).
- Відповідь
-
\((b+1)(4b+1)\)
- Напишіть триноміал у порядку спадання градусів за потребою.
- Фактор будь-якого GCF.
- Знайти всі пари коефіцієнтів першого члена.
- Знайти всі пари множників третього члена.
- Перевірте всі можливі комбінації факторів, поки не буде знайдений правильний продукт.
- Перевірка шляхом множення.
Пам'ятайте, коли середній термін негативний, а останній - позитивний, ознаки в біноміалах повинні бути негативними.
Фактор повністю за допомогою проб і помилок:\(6b^2−13b+5\).
- Відповідь
-
Триноміал знаходиться вже в порядку спадання. 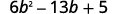
Знайдіть фактори першого терміну. 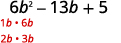
Знайдіть фактори останнього терміну. Розглянемо прикмети.
Оскільки останній термін, є позитивним\(5\), його фактори повинні бути як
позитивними, так і негативними. Коефіцієнт
середньострокового негативний, тому використовуємо негативні фактори.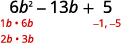
Розглянемо всі комбінації факторів.
\(6b^2−13b+5\) Можливі фактори Продукт \ (6b^2−13b+5\) Можливі фактори» data-valign="top">\((b−1)(6b−5)\) \ (6b^2−13b+5\) Продукт» перевірка даних = «верх">\(6b^2−11b+5\) \ (6b^2−13b+5\) Можливі фактори» data-valign="top">\((b−5)(6b−1)\) \ (6b^2−13b+5\) Продукт» перевірка даних = «верх">\(6b^2−31b+5\) \ (6b^2−13b+5\) Можливі фактори» data-valign="top">\((2b−1)(3b−5)\) \ (6b^2−13b+5\) Продукт» перевірка даних = «середина» >\(6b^2−13b+5^∗\) \ (6b^2−13b+5\) Можливі фактори» data-valign="top">\((2b−5)(3b−1)\) \ (6b^2−13b+5\) Продукт» перевірка даних = «середина» >\(6b^2−17b+5\) \(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} \)
Фактор повністю за допомогою проб і помилок:\(8x^2−14x+3\).
- Відповідь
-
\((2x−3)(4x−1)\)
Фактор повністю за допомогою проб і помилок:\(10y^2−37y+7\).
- Відповідь
-
\((2y−7)(5y−1)\)
Коли ми враховуємо вираз, ми завжди спочатку шукаємо найбільший загальний фактор. Якщо вираз не має найбільшого спільного фактора, у його факторах теж не може бути такого. Це може допомогти нам усунути деякі можливі комбінації факторів.
Фактор повністю за допомогою проб і помилок:\(18x^2−37xy+15y^2\).
- Відповідь
-
Триноміал знаходиться вже в порядку спадання. 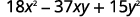
Знайдіть фактори першого терміну. 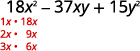
Знайдіть фактори останнього терміну. Розглянемо прикмети.
Оскільки 15 позитивний, а коефіцієнт
середньострокового негативний, використовуємо негативні фактори.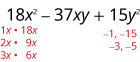
Розглянемо всі комбінації факторів.

\(\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} \)
Фактор повністю за допомогою проб і помилок\(18x^2−3xy−10y^2\).
- Відповідь
-
\((3x+2y)(6x−5y)\)
Фактор повністю за допомогою проб і помилок:\(30x^2−53xy−21y^2\).
- Відповідь
-
\((3x+y)(10x−21y)\)
Не забудьте спочатку шукати GCF і згадати, чи провідний коефіцієнт негативний, так само як і GCF.
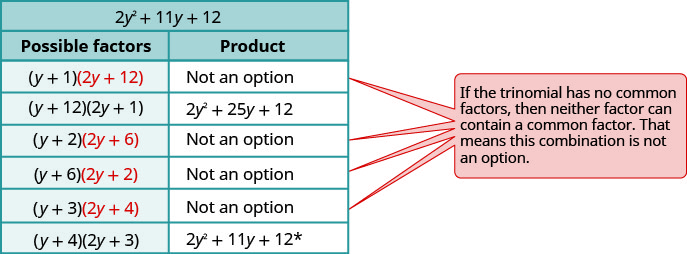
Фактор повністю за допомогою проб і помилок:\(−10y^4−55y^3−60y^2\).
- Відповідь
-
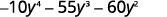
Зверніть увагу на найбільший загальний фактор, тому спочатку вважайте його. 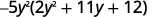
Фактор триноміалу. 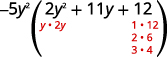
Розглянемо всі комбінації.
-
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} \)
Фактор повністю за допомогою проб і помилок:\(15n^3−85n^2+100n\).
- Відповідь
-
\(5n(n−4)(3n−5)\)
Фактор повністю за допомогою проб і помилок:\(56q^3+320q^2−96q\).
- Відповідь
-
\(8q(q+6)(7q−2)\)
Факторні триноміали форми\(ax^2+bx+c\) методом «\(ac\)»
Ще одним способом фактора триномів форми\(ax^2+bx+c\) є метод «\(ac\)». (Метод «\(ac\)» іноді називають методом групування.) Метод «\(ac\)» насправді є розширенням методів, які ви використовували в останньому розділі, до факторних тріномів з провідним коефіцієнтом один. Цей метод дуже структурований (тобто покроковий), і він завжди працює!
Фактор за допомогою методу «\(ac\)»:\(6x^2+7x+2\).
- Відповідь
-






Фактор за допомогою методу «\(ac\)»:\(6x^2+13x+2\).
- Відповідь
-
\((x+2)(6x+1)\)
Фактор за допомогою методу «\(ac\)»:\(4y^2+8y+3\).
- Відповідь
-
\((2y+1)(2y+3)\)
Метод «\(ac\)» підсумований тут.
- Фактор будь-якого GCF.
- Знайдіть товар\(ac\).
- Знайдіть два числа\(m\) і\(n\) що:
\(\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} \) - Розділіть середній термін, використовуючи\(m\) і\(n\). \(ax^2+mx+nx+c\)
- Фактор за групуванням.
- Перевірте, множивши коефіцієнти.
Не забувайте шукати загальний фактор!
Фактор за допомогою методу «\(ac\)»:\(10y^2−55y+70\).
- Відповідь
-
Чи існує найбільший загальний фактор? Так. GCF є\(5\). 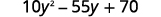
Фактор його. 
Триноміал всередині дужок має
провідний коефіцієнт, який не є\(1\).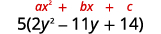
Знайдіть товар\(ac\). \(ac=28\) Знайти два числа, які множаться на\(ac\) \((−4)(−7)=28\) і додати в\(b\). \(−4(−7)=−11\) Розділіть середньостроковий термін. 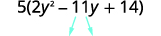
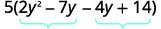
Фактор тріноміалу шляхом групування. 
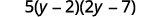
Перевірте, перемноживши всі три коефіцієнти.
\(\hspace{50mm} 5(y−2)(2y−7)\)\(\hspace{45mm} 5(2y^2−7y−4y+14)\)
\(\hspace{48mm} 5(2y^2−11y+14)\)
\(\hspace{49mm} 10y^2−55y+70\checkmark\)
Фактор за допомогою методу «\(ac\)»:\(16x^2−32x+12\).
- Відповідь
-
\(4(2x−3)(2x−1)\)
Фактор за допомогою методу «\(ac\)»:\(18w^2−39w+18\).
- Відповідь
-
\(3(3w−2)(2w−3)\)
Фактор, що використовує підстановку
Іноді триноміал виявляється не в\(ax^2+bx+c\) формі. Однак ми часто можемо зробити продуману заміну, яка дозволить нам зробити її під\(ax^2+bx+c\) форму. Це називається факторингом шляхом заміни. Стандартно використовувати\(u\) для заміни.
У\(ax^2+bx+c\), середній член має змінну\(x\), а його квадрат\(x^2\), є змінною частиною першого члена. Шукайте ці відносини, намагаючись знайти підміну.
Коефіцієнт шляхом заміщення:\(x^4−4x^2−5\).
- Відповідь
-
Змінна частина середнього члена є\(x^2\) і його квадрат\(x^4\),, є змінною частиною першого члена. (Ми знаємо\((x^2)^2=x^4)\). Якщо ми дозволимо\(u=x^2\), ми можемо поставити наш триноміал у\(ax^2+bx+c\) формі, яку нам потрібно враховувати.
\(x^4−4x^2−5\) Перепишіть триноміал, щоб підготуватися до заміни. \((x^2)^2−4(x^2)-5\) Нехай\(u=x^2\) і підставляємо. \((u)^2−4(u)-5\) Фактор триноміалу. \((u+1)(u-5)\) \(u\)Замінити на\(x^2\). \((x^2+1)(x^2-5)\) Перевірка:
\(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)
Коефіцієнт шляхом заміщення:\(h^4+4h^2−12\).
- Відповідь
-
\((h^2−2)(h^2+6)\)
Коефіцієнт шляхом заміщення:\(y^4−y^2−20\).
- Відповідь
-
\((y^2+4)(y^2−5)\)
Іноді підставляється вираз не є мономіальним.
Коефіцієнт заміщення:\((x−2)^2+7(x−2)+12\)
- Відповідь
-
Біноміал в середньому семестрі,\((x−2)\) знаходиться в квадраті в першому семестрі. Якщо ми дозволимо\(u=x−2\) і підставимо, наш триноміал буде за\(ax^2+bx+c\) формою.
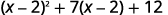
Перепишіть триноміал, щоб підготуватися до заміни. 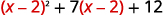
Нехай\(u=x−2\) і підставляємо. 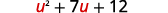
Фактор триноміалу. 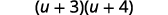
\(u\)Замінити на\(x−2\). 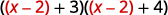
Спростити всередині дужок. 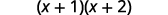
Це також може бути враховано спочатку множенням, а потім об'єднанням подібних термінів, а потім факторингом.\((x−2)^2\)\(7(x−2)\) Більшість студентів віддають перевагу методу заміщення.
Коефіцієнт шляхом заміщення:\((x−5)^2+6(x−5)+8\).
- Відповідь
-
\((x−3)(x−1)\)
Коефіцієнт шляхом заміщення:\((y−4)^2+8(y−4)+15\).
- Відповідь
-
\((y−1)(y+1)\)
Перегляньте це відео для додаткової інструкції та практики з факторингом.
Ключові концепції
- Як враховувати триноми форми\(x^2+bx+c\).
- Запишіть множники як два біноміали з першими долями x. \(\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}\)
- Знайти два числа\(m\) і\(n\) що
\(\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}\) - Використовують\(m\) і в\(n\) якості останніх термінів чинники. \(\qquad (x+m)(x+n)\)
- Перевірте, множивши коефіцієнти.
- Стратегія факторингу триноміалів форми\(x^2+bx+c\): Коли ми фактуємо триноміал, ми спочатку розглядаємо ознаки його термінів, щоб визначити ознаки біноміальних факторів.
Для тріномів форми:\(x^2+bx+c = (x+m)(x+n)\)
Коли\(c\) позитивний,\(m\) і\(n\) повинен мати однаковий знак (і це буде ознака\(b\) ).
Приклади:\(x^2+5x+6=(x+2)(x+3)\),\(x^2−6x+8 = (x−4)(x−2)\)
Коли\(c\) негативний,\(m\) і\(n\) мають протилежні ознаки. Більший з\(m\) і\(n\) буде мати знак\(b\).
Приклади:\(x^2+x−12=(x+4)(x−3)\),\(x^2−2x−15=(x−5)(x+3)\)
Зверніть увагу, що в разі, коли\(m\) і\(n\) мають протилежні знаки, знак того, що має більшу абсолютну величину, відповідає знаку\(b\). - Як зарахувати триноми форми за\(ax^2+bx+c\) допомогою проб і помилок.
- Напишіть триноміал у порядку спадання градусів за потребою.
- Фактор будь-якого GCF.
- Знайти всі пари коефіцієнтів першого члена.
- Знайти всі пари множників третього члена.
- Перевірте всі можливі комбінації факторів, поки не буде знайдений правильний продукт.
- Перевірка шляхом множення.
- Як зарахувати триноми форми за\(ax^2+bx+c\) допомогою методу «\(ac\)».
- Фактор будь-якого GCF.
- Знайдіть товар\(ac\).
- Знайдіть два числа\(m\) і\(n\) що:
\(\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}\) - Розділіть середній термін, використовуючи\(m\) і\(n\). \(\quad ax^2+mx+nx+c\)
- Фактор за групуванням.
- Перевірте, множивши коефіцієнти.
