Глава 3 Огляд вправ

Last updated
Save as PDF

Page ID: 59416

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Розділ Огляд Вправи

Графік лінійних рівнянь у двох змінних

Графік точок у прямокутній системі координат

У наступних вправах побудуйте кожну точку в прямокутній системі координат.

1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

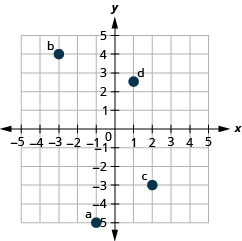
Відповідь: $На цьому малюнку показані точки, нанесені на координатній площині x y. Осі x і y проходять від негативних 5 до 5. Точка, позначена а, становить 1 одиницю ліворуч від початку та 5 одиниць нижче початку та розташована в III квадранті. Точка, позначена b, - це 3 одиниці зліва від початку та 4 одиниці вище початку та розташована у II квадранті. Точка, позначена c, становить 2 одиниці праворуч від початку і 3 одиниці нижче початку і розташована в четвертому квадранті. Точка з маркуванням d становить 1 одиницю праворуч від початку і 2,5 одиниці вище початку і знаходиться в квадранті I.$

2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

У наступних вправах визначте, які впорядковані пари є розв'язками заданих рівнянь.

3. $5x+y=10$;

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

Відповідь: ⓑ, ⓒ

4. $y=6x−2$;

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

Графік лінійного рівняння шляхом побудови точок

У наступних вправах граф за допомогою побудови точок.

5. $y=4x−3$

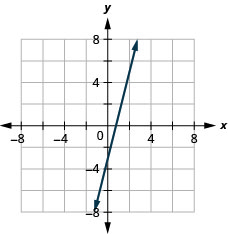
Відповідь: $На цьому малюнку показана пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємний 1, від'ємний 7), (0, негативний 3), (1, негативний 1), і (2, 3).$

6. $y=−3x$

7. $y=\frac{1}{2}x+3$

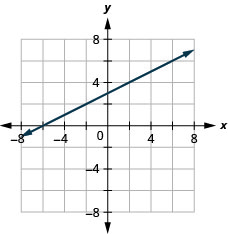
Відповідь: $На цьому малюнку показана пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 8 до 8. Лінія проходить через точки (від'ємні 6, 0), (0, 3), (2, 4) і (4, 5).$

8. $y=−\frac{4}{5}|x−1$

9. $x−y=6$

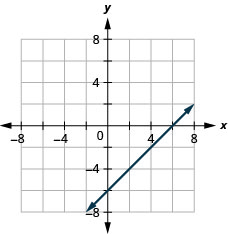
Відповідь: $На цьому малюнку показана пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємний 1, від'ємний 7), (0, від'ємний 6), (3, негативний 3), і (6, 0).$

10. $2x+y=7$

11. $3x−2y=6$

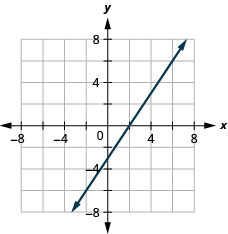
Відповідь: $На цьому малюнку показана пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємний 2, від'ємний 6), (0, негативний 3), (2, 0), і (4, 3).$

Графік Вертикальні та Горизонтальні лінії

У наступних вправах проведіть графік кожного рівняння.

12. $y=−2$

13. $x=3$

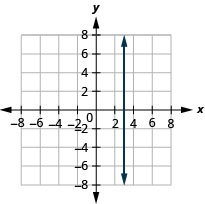
Відповідь: $На цьому малюнку показана вертикальна пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 8 до 8. Лінія проходить через точки (3, від'ємний 1), (3, 0) і (3, 1).$

У наступних вправах графік кожної пари рівнянь в одній і тій же прямокутній системі координат.

14. $y=−2x$і$y=−2$

15. $y=\frac{4}{3}x$і$y=\frac{4}{3}$

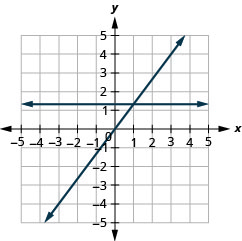
Відповідь: $На малюнку показані графіки прямої горизонтальної лінії і прямої похилій лінії на тій же x y координатної площині. Осі x і y проходять від негативних 5 до 5. Горизонтальна лінія проходить через точки (0, 4 поділені на 3), (1, 4 поділені на 3), і (2, 4 поділені на 3). Коса лінія проходить через точки (0, 0), (1, 4 ділиться на 3), і (2, 8 ділиться на 3).$

Знайти x- і y- перехоплення

У наступних вправах знайдіть x - і y -перехоплення.

16.
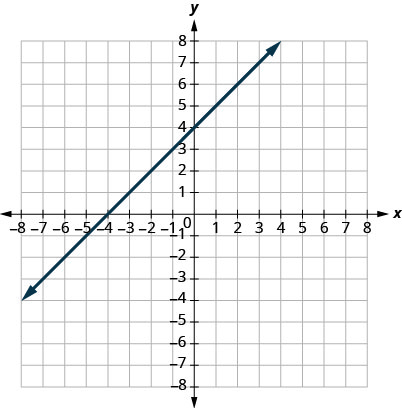
$На малюнку показана пряма лінія, зображена на координатній площині x y. Осі x і y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємний 6, від'ємний 2), (негативний 4, 0), (негативний 2, 2), (0, 4), (2, 6) і (4, 8).$

17.
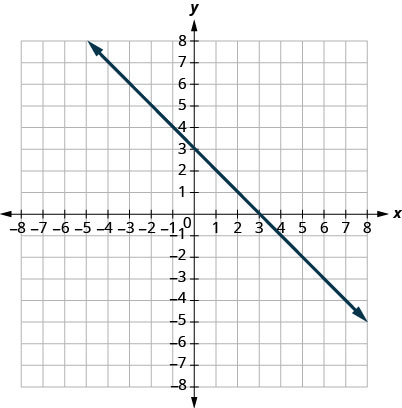
$На малюнку показана пряма лінія, зображена на координатній площині x y. Осі x і y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємний 2, 5), (негативний 1, 4), (0, 3), (3, 0), і (6, негативний 3).$

Відповідь: $(0,3)(3,0)$

У наступних вправах знайдіть перехоплення кожного рівняння.

18. $x−y=−1$

19. $x+2y=6$

Відповідь: $(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Відповідь: $(16,0),\space (0,−12)$

22. $y=3x$

Графік лінії за допомогою перехоплення

У наступних вправах граф з використанням перехоплень.

23. $−x+3y=3$

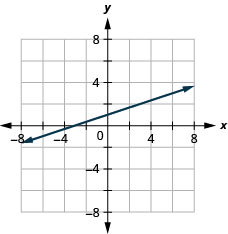
Відповідь: $На малюнку показана пряма лінія, зображена на координатній площині x y. Осі x і y проходять від негативних 8 до 8. Лінія проходить через точки (від'ємні 3, 0), (0, 1), (3, 2) і (6, 3).$

24. $x−y=4$

25. $2x−y=5$

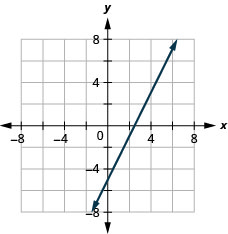
Відповідь: $На малюнку показана пряма лінія, зображена на координатній площині x y. Осі x і y проходять від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 5), (1, негативний 3), (2, негативний 1), і (3, 1).$

26. $2x−4y=8$

27. $y=4x$

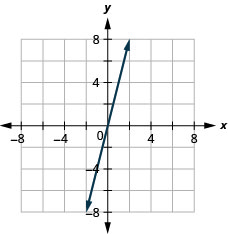
Відповідь: $На малюнку показана пряма лінія, зображена на координатній площині x y. Осі x і y проходять від негативних 8 до 8. Рядок проходить через точки (від'ємні 1, 4), (0, 0) і (1, негативні 4).$

Нахил лінії

Знайти нахил лінії

У наступних вправах знайдіть нахил кожної показаної лінії.

28.
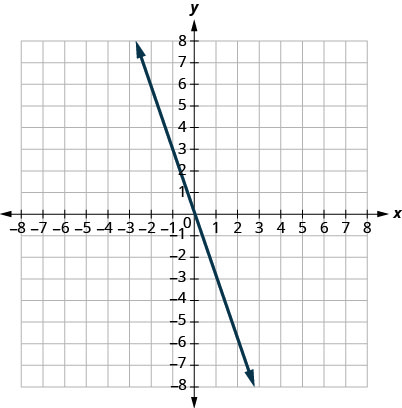
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (0, 0) і (1, негативні 3).$

29.
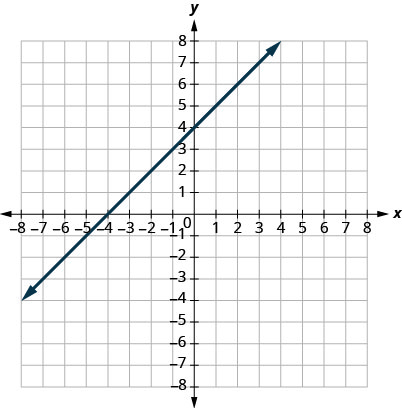
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (від'ємні 4, 0) і (0, 4).$

Відповідь: 1

30.
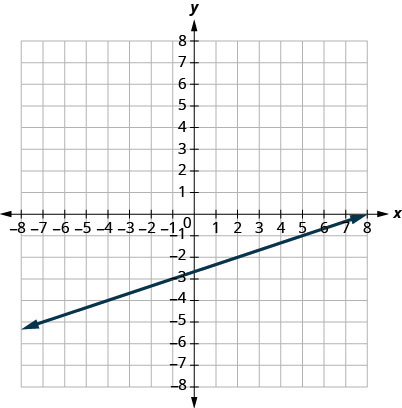
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (від'ємний 4, негативний 4) і (2, негативний 2).$

31.
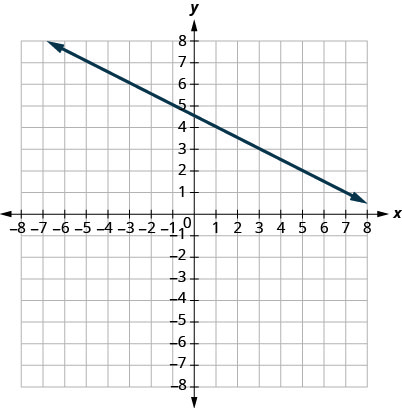
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (1, 4) і (5, 2).$

Відповідь: $−12$

У наступних вправах знайдіть нахил кожної лінії.

32. $y=2$

33. $x=5$

Відповідь: невизначений

34. $x=−3$

35. $y=−1$

Відповідь: 0

Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Відповідь: $−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

Відповідь: $52$

Графік лінії з заданою точкою та нахилом

У наступних вправах графік кожної лінії з заданою точкою і нахилом.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

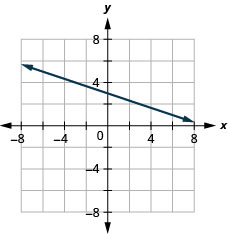
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (від'ємні 3, 4) і (0, 3).$

42. $x$-перехопити$−4; m=3$

43. $y$-перехопити$1; m=−34$

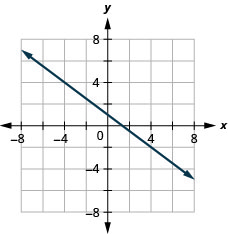
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, 1) і (4, негативні 2).$

Графік лінії, використовуючи її нахил і перехоплення

У наступних вправах визначте нахил і$y$ -перехоплення кожної лінії.

44. $y=−4x+9$

45. $y=53x−6$

Відповідь: $m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Відповідь: $m=\frac{4}{5};\space (0,−\frac{8}{5})$

У наступних вправах графік лінії кожного рівняння, використовуючи його нахил і y -перехоплення.

48. $y=2x+3$

49. $y=−x−1$

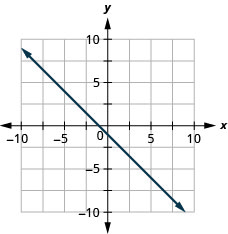
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 1) і (1, від'ємний 2).$

50. $y=−25x+3$

51. $4x−3y=12$

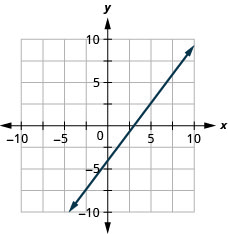
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 4) і (3, 0).$

У наступних вправах визначте найбільш зручний метод для графіка кожного рядка.

52. $x=5$

53. $y=−3$

Відповідь: горизонтальна лінія

54. $2x+y=5$

55. $x−y=2$

Відповідь: перехоплює

56. $y=22x+2$

57. $y=34x−1$

Відповідь: побудова точок

Графік та інтерпретація застосувань перехоплення нахилу

58. Кетрін - приватний шеф-кухар. Рівняння$C=6.5m+42$ моделює співвідношення між її тижневою вартістю, С, у доларах та кількістю прийомів їжі, м, яку вона обслуговує.

ⓐ Знайдіть вартість Кетрін на тиждень, коли вона не подає їжі.
ⓑ Знайти вартість за тиждень, коли вона подає 14 прийомів їжі.
ⓒ Інтерпретувати нахил і C -перехоплення рівняння.
ⓓ Графік рівняння.

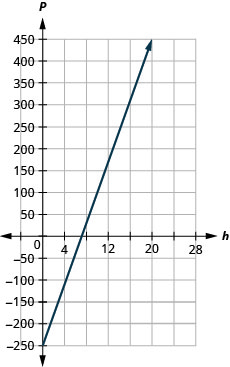
59. Марджорі викладає фортепіано. Рівняння$P=35h−250$ моделює співвідношення між її тижневим прибутком, P, у доларах та кількістю учнівських уроків, з, які вона викладає.

ⓐ Знайдіть прибуток Марджорі за тиждень, коли вона не викладає жодних учнівських уроків.
ⓑ Знайдіть прибуток за тиждень, коли вона викладає 20 учнівських уроків.
ⓒ Інтерпретувати нахил і P -перехоплення рівняння.
ⓓ Графік рівняння.

Відповідь

ⓐ$−$250$
ⓑ$$450$
ⓒ Схил, 35, означає, що щотижневий прибуток Марджорі, P, збільшується на 35 доларів за кожен додатковий урок учня, який вона викладає.
P -перехоплення означає, що коли кількість уроків дорівнює 0, Марджорі втрачає 250 доларів.
ⓓ

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 4 до 28. Вісь Y працює від негативних 250 до 450. Лінія проходить через точки (0, від'ємні 250) і (20, 450).$

Використання нахилів для визначення паралельних і перпендикулярних ліній

У наступних вправах використовуйте нахили та$y$ -перехоплення, щоб визначити, чи є лінії паралельними, перпендикулярними чи ні.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Відповідь: ні

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Відповідь: не паралельно

Знайти рівняння прямої

Знайти рівняння прямої з заданим нахилом та y -перехопленням

У наступних вправах знайдіть рівняння прямої з заданим нахилом і y-перехопленням. Запишіть рівняння у формі нахилу—перехоплення.

64. Ухил$\frac{1}{3}$ і$y$ -перехоплення$(0,−6)$

65. Ухил$−5$ і$y$ -перехоплення$(0,−3)$

Відповідь: $y=−5x−3$

66. Ухил$0$ і$y$ -перехоплення$(0,4)$

67. Ухил$−2$ і$y$ -перехоплення$(0,0)$

Відповідь: $y=−2x$

У наступних вправах знайдіть рівняння лінії, показане на кожному графіку. Запишіть рівняння у формі нахилу—перехоплення.

68.
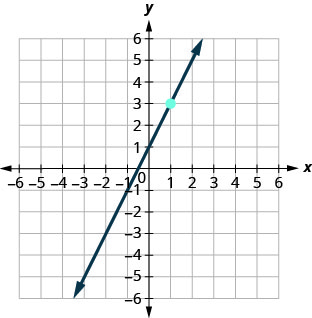
$Ця фігура має графік прямої лінії на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, 1), (1, 3) і (2, 5).$

69.
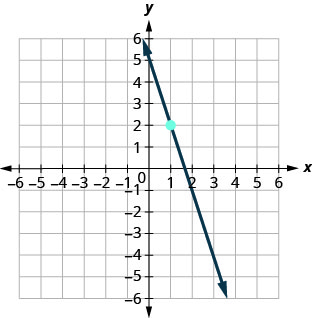
$Ця фігура має графік прямої лінії на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, 5), (1, 2) і (2, негативні 1).$

Відповідь: $y=−3x+5$

70.
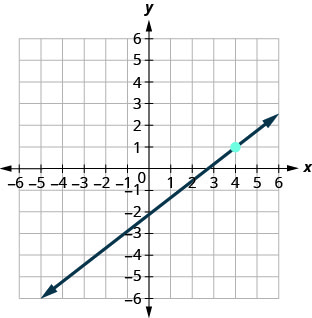
$Ця фігура має графік прямої лінії на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 2), (4, 1) і (8, 4).$

71.
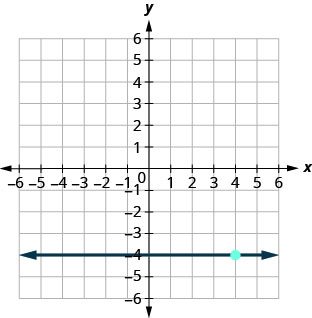
$Ця фігура має графік горизонтальної прямої на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Рядок проходить через точки (0, від'ємний 4), (1, від'ємний 4), і (2, негативний 4).$

Відповідь: $y=−4$

Знайти рівняння прямої з заданим нахилом і точкою

У наступних вправах знайдіть рівняння прямої з заданим нахилом і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

72. $m=−\frac{1}{4}$, точка$(−8,3)$

73. $m=\frac{3}{5}$, точка$(10,6)$

Відповідь: $y=\frac{3}{5}x$

74. Горизонтальна лінія, що містить$(−2,7)$

75. $m=−2$, точка$(−1,−3)$

Відповідь: $y=−2x−5$

Знайти рівняння прямої за двома точками

У наступних вправах знайдіть рівняння рядка, що містить задані точки. Запишіть рівняння у формі нахилу—перехоплення.

76. $(2,10)$і$(−2,−2)$

77. $(7,1)$і$(5,0)$

Відповідь: $y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$і$(3,−4)$

79. $(5,2)$і$(−1,2)$

Відповідь: $y=2$

Знайти рівняння прямої, паралельної заданій прямій

У наступних вправах знайдіть рівняння прямої, паралельної заданій лінії і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

80. лінія$y=−3x+6$, точка$(1,−5)$

81. лінія$2x+5y=−10$, точка$(10,4)$

Відповідь: $y=−\frac{2}{5}x+8$

82. лінія$x=4$, точка$(−2,−1)$

83. лінія$y=−5$, точка$(−4,3)$

Відповідь: $y=3$

Знайти рівняння прямої, перпендикулярної заданій прямій

У наступних вправах знайдіть рівняння прямої, перпендикулярної заданій лінії і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

84. лінія$y=−\frac{4}{5}x+2$, точка$(8,9)$

85. лінія$2x−3y=9$, точка$(−4,0)$

Відповідь: $y=−\frac{3}{2}x−6$

86. лінія$y=3$, точка$(−1,−3)$

87.$x=−5$ точка лінії$(2,1)$

Відповідь: $y=1$

Лінійні нерівності графа у двох змінних

Перевірка рішень нерівності в двох змінних

У наступних вправах визначте, чи є кожна впорядкована пара розв'язком заданої нерівності.

88. Визначте, чи є кожна впорядкована пара розв'язком нерівності$y<x−3$:

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89. Визначте, чи є кожна впорядкована пара розв'язком нерівності$x+y>4$:

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

Відповідь: ⓐ так ⓑ ні ⓒ так ⓓ так; ⓔ ном

Визнати зв'язок між розв'язками нерівності та її графіком

У наступних вправах напишіть нерівність, показану затіненою областю.

90. Запишіть нерівність, показану графіком, з граничною лінією$y=−x+2.$

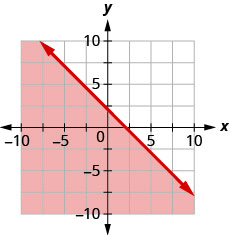
$Ця цифра має графік прямої лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Через точки (0, 2), (1, 1) і (2, 0) проводиться лінія. Лінія ділить площину координат x y на дві половини. Лінія та нижня ліва половина затінені червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

91. Запишіть нерівність, показану графіком, з граничною лінією$y=\frac{2}{3}x−3$.

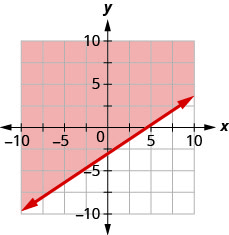
$Ця цифра має графік прямої лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Через точки (0, від'ємний 3), (3, від'ємний 1), і (6, 1) проводиться лінія. Лінія ділить площину координат x y на дві половини. Лінія та верхня ліва половина затінені червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

Відповідь: $y>\frac{2}{3}x−3$

92. Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією$x+y=−4$.

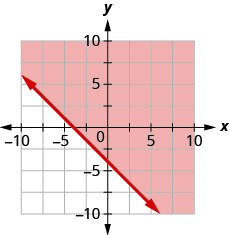
$Ця цифра має графік прямої лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Через точки (0, від'ємний 4), (від'ємний 2, від'ємний 2), і (негативний 4, 0). Лінія ділить площину координат x y на дві половини. Лінія та верхня права половина затінені червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

93. Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією$x−2y=6$.

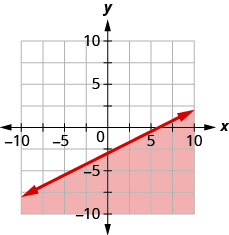
$Ця цифра має графік прямої лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Через точки (0, від'ємний 3), (2, від'ємний 2), і (6, 0) проводиться лінія. Лінія ділить площину координат x y на дві половини. Лінія та нижня права половина затінені червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

Відповідь: $x−2y\geq 6$

Лінійні нерівності графа у двох змінних

У наступних вправах проведіть графік кожної лінійної нерівності.

94. Графік лінійної нерівності$y>\frac{2}{5}x−4$.

95. Графік лінійної нерівності$y\leq −\frac{1}{4}x+3$.

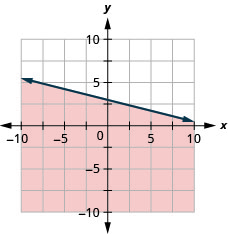
Відповідь: $Ця фігура має графік прямої пунктирної лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Пряма пунктирна лінія проводиться через точки (0, 3), (4, 2), і (8, 1). Лінія ділить площину координат x y на дві половини. Нижня ліва половина затінена червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

96. Графік лінійної нерівності$x−y\leq 5$.

97. Графік лінійної нерівності$3x+2y>10.$

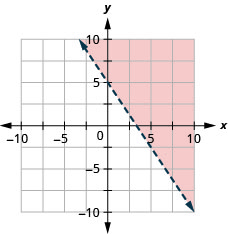
Відповідь: $Ця фігура має графік прямої пунктирної лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Пряма пунктирна лінія проводиться через точки (0, 5), (2, 2) і (4, негативний 1). Лінія ділить площину координат x y на дві половини. Верхня права половина затінена червоним кольором, щоб вказати, що саме тут знаходяться рішення нерівності.$

98. Графік лінійної нерівності$y\leq −3x$.

99. Графік лінійної нерівності$y<6.$

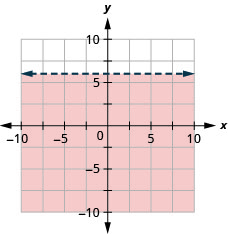
Відповідь: $Ця фігура має графік прямої горизонтальної пунктирної лінії на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Пряма пунктирна лінія проводиться через точки (0, 6), (1, 6), і (2, 6). Лінія ділить площину координат x y на дві половини. Нижня половина затінена червоним кольором, щоб вказати, що саме тут знаходяться розв'язки нерівності.$

Розв'язуйте програми за допомогою лінійних нерівностей у двох змінних

100. Шанті потрібно заробляти щонайменше 500 доларів на тиждень під час літньої перерви, щоб заплатити за коледж. Вона працює на двох роботах. Один як інструктор з плавання, який платить $10 годину, а інший як стажер в адвокатському бюро за $25 годину. Скільки годин Шанті потрібно працювати на кожній роботі, щоб заробити щонайменше 500 доларів на тиждень?

ⓐ Нехай x - кількість годин, які вона працює, навчаючи плаванню, і нехай y - кількість годин, які вона працює в якості стажера. Напишіть нерівність, яка б моделювала цю ситуацію.
ⓑ Графік нерівності.
ⓒ Знайдіть три впорядковані пари$(x,y)$, які були б розв'язками нерівності. Потім поясніть, що це означає для Шанті.

101. Ацуші йому потрібно вправлятися достатньо, щоб щодня спалювати$600$ калорії. Він вважає за краще бігати або їздити на велосипеді і спалює$20$ калорії в хвилину під час бігу і$15$ калорій хвилину під час їзди на велосипеді.

ⓐ Якщо x - це кількість хвилин, які працює Atsushi, а y - кількість хвилин, які він велосипедів, знайдіть нерівність, яка моделює ситуацію.
ⓑ Графік нерівності.
ⓒ Перерахуйте три рішення нерівності. Які варіанти надає рішення Atsushi?

Відповідь

ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

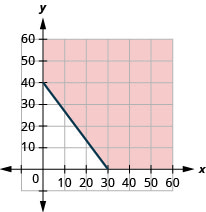
$Фігура має пряму лінію, розміщену на координатній площині x y. Вісь x працює від 0 до 50. Вісь Y працює від 0 до 50. Лінія проходить через точки (0, 40) і (30, 0). Лінія ділить координатну площину на дві половини. Верхня права половина і лінія пофарбовані в червоний колір, щоб вказати, що це набір рішення.$

Відносини та функції

Пошук домену та діапазону зв'язку

У наступних вправах для кожного відношення ⓐ знайдіть область відношення ⓑ знайдіть діапазон відношення.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

Відповідь: ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

У наступній вправі скористайтеся відображенням відношення до ⓐ переліку впорядкованих пар відношення ⓑ знайдіть область відношення ⓒ знайдіть діапазон відношення.

104. Наведене нижче відображення показує середню вагу дитини відповідно до віку.

$На цьому малюнку показані дві таблиці, кожна з яких має один стовпець. Таблиця зліва має заголовок «Вік (yrs)» і містить цифри 1, 2, 3, 4, 5, 6 і 7. Таблиця праворуч має заголовок «Вага (фунти)» і перераховані цифри 20, 35, 30, 45, 40, 25 і 50. У таблиці віків є стрілки, що починаються з цифр і вказують на цифри в таблиці ваги. Перша стрілка йде від 1 до 20. Друга стрілка йде від 2 до 25. Третя стрілка йде від 3 до 30. Четверта стрілка йде від 4 до 35. П'ята стрілка йде від 5 до 40. Шоста стрілка йде від 6 до 45. Сьома стрілка йде від 7 до 50.$

У наступній вправі скористайтеся графіком відношення до ⓐ перерахуйте впорядковані пари відношення ⓑ знайдіть область відношення ⓒ знайдіть діапазон відношення.

105.
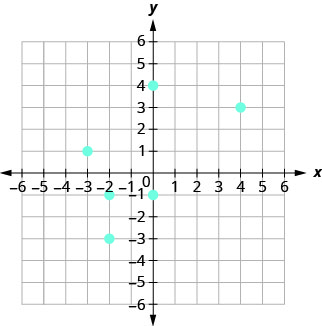
$На малюнку показаний графік деяких точок на координатній площині x y. Осі x та y проходять від негативних 6 до 6. Точки (негативні 3, 1), (негативні 2, негативні 1), (негативні 2, негативні 3), (0, негативні 1), (0, 4), і (4, 3).$

Відповідь: ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

Визначте, чи є Relation функцією

У наступних вправах використовуйте набір впорядкованих пар, щоб ⓐ визначити, чи є відношення функцією ⓑ знайти область відношення ⓒ знайти діапазон відношення.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

Відповідь: ⓐ так ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

У наступних вправах використовуйте відображення, щоб ⓐ визначити, чи є відношення функцією ⓑ знайти область функції ⓒ знайти діапазон функції.

108.
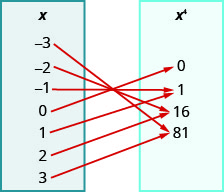
$На цьому малюнку показані дві таблиці, кожна з яких має один стовпець. Таблиця зліва має заголовок «x» і містить числа від'ємні 3, від'ємні 2, від'ємні 1, 0, 1, 2 та 3. Таблиця праворуч має заголовок «х до четвертої степені» і перераховані цифри 0, 1, 16 і 81. Є стрілки, що починаються з цифр в таблиці x і вказують на цифри в х до четвертої таблиці потужності. Перша стрілка йде від негативних 3 до 81. Друга стрілка йде від негативних 2 до 16. Третя стрілка йде від негативного 1 до 1. Четверта стрілка йде від 0 до 0. П'ята стрілка йде від 1 до 1. Шоста стрілка йде від 2 до 16. Сьома стрілка йде від 3 до 81.$

109.
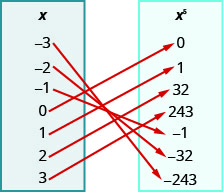
$На цьому малюнку показані дві таблиці, кожна з яких має один стовпець. Таблиця зліва має заголовок «x» і містить числа від'ємні 3, від'ємні 2, від'ємні 1, 0, 1, 2 та 3. Таблиця праворуч має заголовок «х до п'ятої степені» і перераховує числа 0, 1, 32, 243, негативний 1, негативний 32 та негативний 243. Є стрілки, що починаються з цифр в таблиці x і вказують на цифри в х до п'ятої таблиці потужності. Перша стрілка переходить від негативних 3 до негативних 243. Друга стрілка йде від негативних 2 до негативних 32. Третя стрілка йде від негативного 1 до 1. Четверта стрілка йде від 0 до 0. П'ята стрілка йде від 1 до 1. Шоста стрілка йде від 2 до 32. Сьома стрілка йде від 3 до 243.$

Відповідь: ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

У наступних вправах визначте, чи є кожне рівняння функцією.

110. $2x+y=−3$

111. $y=x^2$

Відповідь: так

112. $y=3x−5$

113. $y=x^3$

Відповідь: так

114. $2x+y2=4$

Знайти значення функції

У наступних вправах оцініть функцію:

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$.

115. $f(x)=3x−4$

Відповідь: ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

Відповідь: ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

У наступних вправах оцініть функцію.

119. $g(x)=3x2−5x;\space g(2)$

Відповідь: $2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

Відповідь: $18$

122. $f(x)=x+2x−1;\space f(3)$

Графіки функцій

Використовуйте тест вертикальної лінії

У наступних вправах визначте, чи є кожен графік графіком функції.

123.
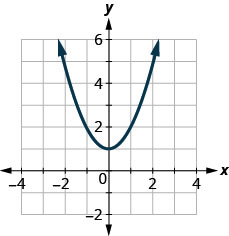
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 2, 5), (негативні 1, 2), (0, 1), (1, 2) і (2, 5). Найнижча точка на графіку - (0, 1).$

Відповідь: так

124.
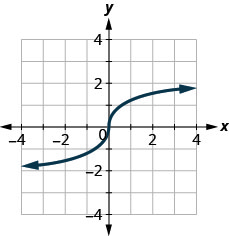
$Фігура має s-подібну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Крива проходить через точки (від'ємний 1, негативний 1), (0, 0) і (1, 1).$

125.
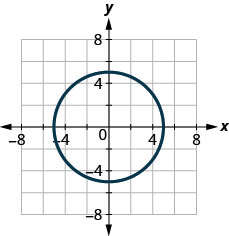
$Фігура має коло, розміщене на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Коло проходить через точки (негативні 5, 0), (5, 0), (0, негативні 5), і (0, 5).$

Відповідь: ні

126.
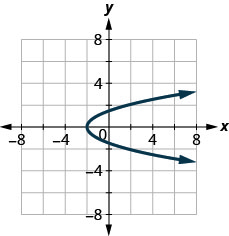
$Фігура має параболу, що відкривається праворуч на графіку на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативний 2, 0), (негативний 1, 1), (негативний 1, негативний 1), (2, 2) і (2, негативний 2). Найлівіша точка на графіку - (від'ємна 2, 0).$

127.
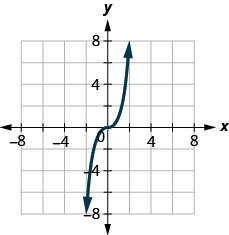
$Фігура має функцію куба, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (від'ємний 1, негативний 1), (0, 0) і (1, 1).$

Відповідь: так

128.
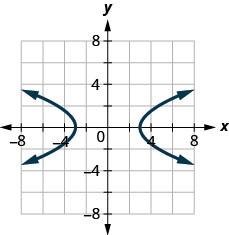
$Фігура має дві криві лінії, зображені на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія зліва проходить через точки (негативні 3, 0), (негативні 4, 2), і (негативні 4, негативні 2). Вигнута лінія справа проходить через точки (3, 0), (4, 2) і (4, негативні 2).$

129.
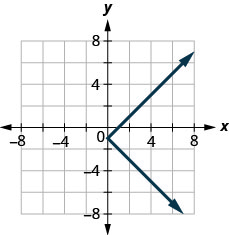
$Фігура має бічну функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія згинається в точці (0, негативна 1) і йде вправо. Лінія проходить через точки (1, 0), (1, від'ємний 2), (2, 1) і (2, негативний 3).$

Відповідь: ні

Визначте графіки основних функцій

У наступних вправах ⓐ графік кожної функції ⓑ вказати свою область та діапазон. Запишіть домен і діапазон в інтервальному позначенні.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

Відповідь

ⓐ

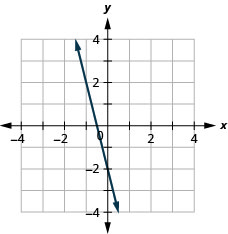
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Рядок проходить через точки (від'ємний 2, 6), (негативний 1, 2), і (0, негативний 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

Відповідь

ⓐ

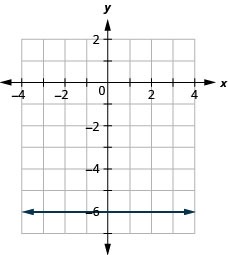
$Фігура має постійну функцію, зображену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 8 до 4. Лінія проходить через точки (0, від'ємний 6), (1, від'ємний 6), і (2, негативний 6).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

Відповідь

ⓐ

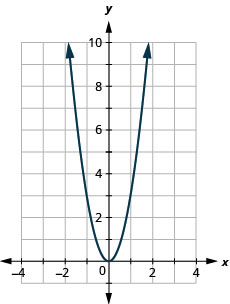
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 1, 3), (0, 0) і (1, 3). Найнижча точка на графіку - (0, 0).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

Відповідь

ⓐ

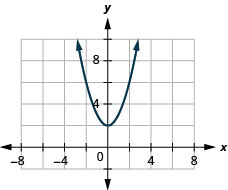
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Парабола проходить через точки (негативні 2, 6), (негативні 1, 3), (0, 2), (1, 3) і (2, 6). Найнижча точка на графіку - (0, 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138. $f(x)=x^3−2$

139. $f(x)=\sqrt{x+2}$

Відповідь

ⓐ

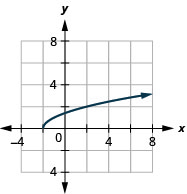
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 8. Вісь Y проходить від негативних 2 до 10. Півлінія починається в точці (від'ємна 2, 0) і проходить через точки (негативні 1, 1) і (2, 2).$

ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

140. $f(x)=−|x|$

141. $f(x)=|x|+1$

Відповідь

ⓐ

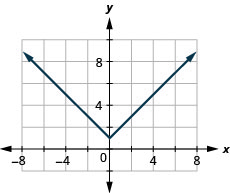
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Вершина знаходиться в точці (0, 1). Лінія проходить через точки (від'ємні 1, 2) і (1, 2).$

ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

Читання інформації з графіка функції

У наступних вправах використовуйте графік функції, щоб знайти її область і діапазон. Запишіть домен і діапазон в інтервальному позначенні

142.
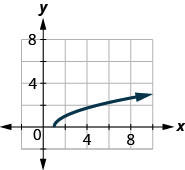
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь x працює від 0 до 10. Вісь Y працює від 0 до 10. Півлінія починається в точці (1, 0) і проходить через точки (2, 1) і (5, 2).$

143.
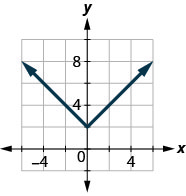
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Вершина знаходиться в точці (0, 2). Лінія проходить через точки (від'ємні 1, 3) і (1, 3).$

Відповідь: $D: (-\inf ,\inf ), R: [2,\inf )$

144.
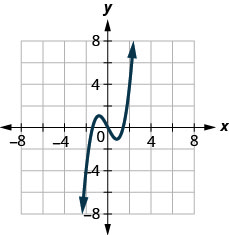
$Фігура має кубічну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (від'ємний 2, негативний 4), (0, 0), і (2, 4).$

У наступних вправах використовуйте графік функції, щоб знайти зазначені значення.

145.
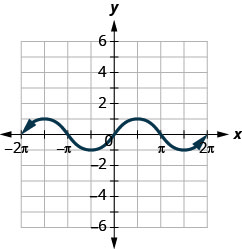
$Ця фігура має хвилясту вигнуту лінію, розміщену на координатній площині x y. Вісь x проходить від негативного 2 рази pi до 2 разів pi. Вісь Y проходить від негативних 6 до 6. Вигнутий відрізок лінії проходить через точки (негативний 2 рази пі, 0), (негативний 3 ділиться на 2 рази пі, 1), (негативний пі, 0), (негативний 1 ділиться на 2 рази пі, негативний 1), (0, 0), (1 ділиться на 2 рази пі, 1), (пі, 0), (3 ділиться на 2 рази пі, 0), і (2 рази пі, 0). Точки (від'ємні 3, поділені на 2 рази пі, 1) і (1 поділена на 2 рази пі, 1) є найвищими точками на графіку. Точки (від'ємний 1 поділений на 2 рази пі, від'ємний 1) і (3 поділений на 2 рази пі, від'ємний 1) є найнижчими точками на графіку. Візерунок поширюється нескінченно вліво і вправо.$

ⓐ Знайти$f(0)$.
ⓑ Знайти$f(12\pi )$.
ⓒ Знайти$f(−32\pi )$.
ⓓ Знайдіть значення для$x$ коли$f(x)=0$.
ⓔ Знайдіть$x$ -перехоплення.
ⓕ Знайти$y$ -перехоплення (и).
ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

Відповідь: ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ$f(x)=0$ за$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146.
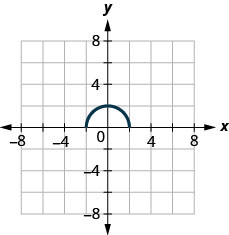
$Фігура має півколо, зображене на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Відрізок кривої лінії починається в точці (мінус 2, 0). Лінія проходить через точку (0, 2) і закінчується в точці (2, 0). Точка (0, 2) - найвища точка на графіку.$

ⓐ Знайти$f(0)$.
ⓑ Знайдіть значення для$x$ коли$f(x)=0$.
ⓒ Знайдіть$x$ -перехоплення.
ⓓ Знайти$y$ -перехоплення (и).
ⓔ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓕ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

Практичний тест

1. Покладіть кожну точку в прямокутній системі координат.

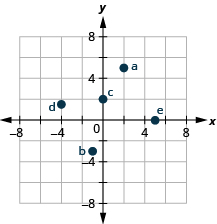
Відповідь: $На цьому малюнку показані точки, нанесені на координатній площині x y. Осі x і y проходять від негативних 10 до 10. Точка, позначена a, - це 2 одиниці праворуч від початку та 5 одиниць вище початку та розташована в квадранті I. Точка, позначена b, є 1 одиницею ліворуч від початку та 3 одиниць нижче початку та розташована в квадранті III. Точка, позначена c, знаходиться на 2 одиниці вище початку і розташована на осі y. Точка, позначена d, становить 4 одиниці зліва від початку і на 1,5 одиниці вище початку і розташована в II квадранті. Точка, позначена e, знаходиться на 5 одиницях праворуч від початку і розташована на осі х.$

2. Які з заданих впорядкованих пар є розв'язками рівняння$3x−y=6$?

3. Знайдіть нахил кожної показаної лінії.

ⓐ

ⓑ

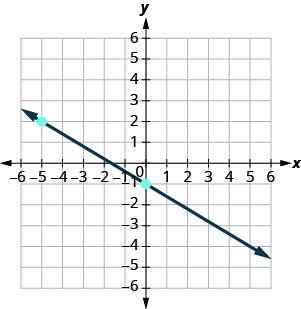
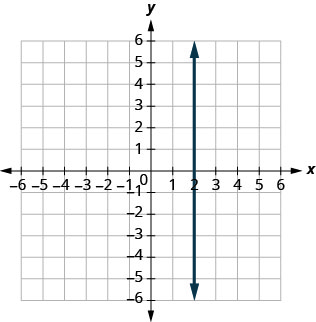
$Фігура має пряму вертикальну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (2, 0) (2, від'ємні 1), і (2, 1).$

Відповідь: ⓐ$−\frac{3}{5}$ ⓑ невизначений

4. Знайдіть нахил лінії між точками$(5,2)$ і$(−1,−4)$.

5. Графік лінії з нахилом$\frac{1}{2}$, що містить точку$(−3,−4)$.

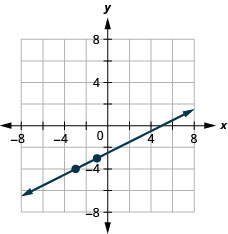
Відповідь: $Фігура має пряму лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Рядок проходить через точки (від'ємний 3, негативний 4) (негативний 1, негативний 3), і (1, негативний 2).$

6. Знайдіть перехоплення$4x+2y=−8$ і графік.

Графік лінії для кожного з наступних рівнянь.

7. $y=\frac{5}{3}x−1$

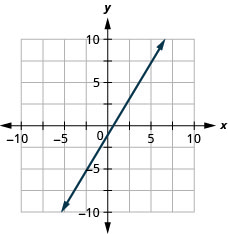
Відповідь: $Фігура має пряму лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Рядок проходить через точки (від'ємний 3, від'ємний 6) (0, негативний 1), і (3, 4).$

8. $y=−x$

9. $y=2$

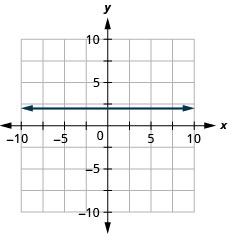
Відповідь: $Фігура має пряму горизонтальну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (від'ємні 1, 2) (0, 2), і (1, 2).$

Знайдіть рівняння кожного рядка. Запишіть рівняння у вигляді ухил-перехоплення.

10. нахил$−\frac{3}{4}$ і$y$ -перехоплення$(0,−2)$

11. $m=2$, точка$(−3,−1)$

Відповідь: $y=2x+5$

12. містять$(10,1)$ і$(6,−1)$

13. перпендикулярно$y=\frac{5}{4}x+2$ прямій, що містить точку$(−10,3)$

Відповідь: $y=−\frac{4}{5}x−5$

14. Запишіть нерівність, показану графіком, з граничною лінією$y=−x−3$.

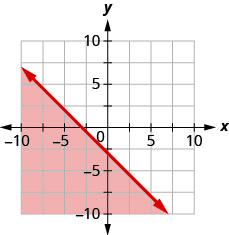
$Фігура має пряму лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Рядок проходить через точки (від'ємний 3, 0), (0, від'ємний 3), і (1, негативний 4). Лінія ділить координатну площину на дві половини. Нижня ліва половина і лінія пофарбовані в червоний колір, щоб вказати, що це набір рішення.$

Графік кожної лінійної нерівності.

15. $y>\frac{3}{2}x+5$

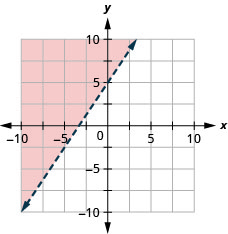
Відповідь: $Фігура має пряму пунктирну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (від'ємні 2, 2), (0, 5) і (2, 8). Лінія ділить координатну площину на дві половини. Верхня ліва половина пофарбована в червоний колір, щоб вказати, що це набір рішень.$

16. $x−y\geq −4$

17. $y\leq −5x$

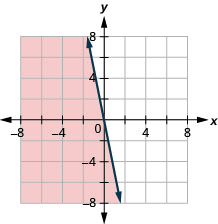
Відповідь: $Фігура має пряму лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Рядок проходить через точки (від'ємні 1, 5), (0, 0) і (1, негативні 5). Лінія ділить координатну площину на дві половини. Нижня ліва половина і лінія пофарбовані в червоний колір, щоб вказати, що це набір рішення.$

18. Хіро працює на двох роботах неповний робочий день, щоб заробити достатньо грошей, щоб виконати свої зобов'язання щонайменше 450 доларів на тиждень. Її робота в торговому центрі платить 10 доларів на годину, а її адміністративна робота помічника в кампусі платить 15 доларів на годину. Скільки годин потрібно Хіро працювати на кожній роботі, щоб заробити не менше 450 доларів?

ⓐ Нехай x - кількість годин, які вона працює в торговому центрі, і нехай y - кількість годин, які вона працює адміністративним помічником. Напишіть нерівність, яка б моделювала цю ситуацію.
ⓑ Графік нерівності.
ⓒ Знайдіть три впорядковані пари$(x,y)$, які були б розв'язками нерівності. Потім поясніть, що це означає для Хіро.

19. Використовуйте набір впорядкованих пар, щоб ⓐ визначити, чи є відношення функцією, ⓑ знайти область відношення і ⓒ знайти діапазон відношення.

\ ({\ {(−3,27), (−2,8), (−1,1), (0,0),
(1,1), (2,8), (3,27)}\}\)

$f(x)=4x^2−2x−3$

21. Для$h(y)=3|y−1|−3$, оцініть$h(−4)$.

Відповідь: $12$

22. Визначте, чи є графік графіком функції. Поясніть свою відповідь.

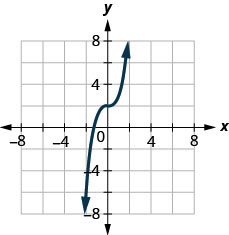
$Фігура має функцію куба, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (негативні 1, 1), (0, 2), і (1, 3).$

У наступних вправах ⓐ графік кожної функції ⓑ вказати свою область та діапазон.
Запишіть домен і діапазон в інтервальному позначенні.

23. $f(x)=x^2+1$

Відповідь

ⓐ

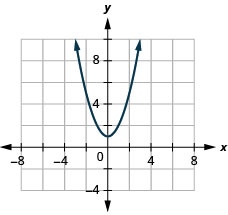
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 2, 5), (негативні 1, 2), (0, 1), (1, 2) і (2, 5). Найнижча точка на графіку - (0, 1).$

ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

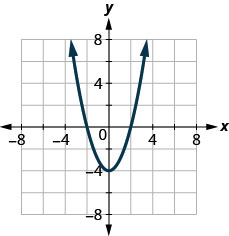
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Парабола проходить через точки (негативний 2, 0), (негативний 1, негативний 3), (0, негативний 4), (1, негативний 3), і (2, 0). Найнижча точка на графіку - (0, від'ємна 4).$

ⓑ Знайдіть$y$ -перехоплення.
ⓒ Знайти$f(−1)$.
ⓓ Знайти$f(1)$.
ⓔ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓕ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.