3.3: Нахил лінії

Last updated
Save as PDF

Page ID: 59434

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Знайти нахил лінії
Графік лінії з заданою точкою і нахилом
Графік лінії, використовуючи її нахил і перехоплення
Виберіть найбільш зручний метод для побудови графіка лінії
Графік та інтерпретація застосувань перехоплення нахилу
Використовуйте ухили для визначення паралельних і перпендикулярних ліній

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Спростити:$\frac{(1–4)}{(8−2)}$.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Розділити:$\frac{0}{4}$,$\frac{4}{0}$.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Спростити:$\frac{15}{-3}$,$\frac{-15}{3}$,$\frac{-15}{-3}$.
Якщо ви пропустили цю проблему, перегляньте [посилання].

Знайти нахил лінії

Коли ви графуєте лінійні рівняння, ви можете помітити, що деякі лінії нахиляються вгору, коли вони йдуть зліва направо, а деякі лінії нахиляються вниз. Деякі лінії дуже круті, а деякі лінії більш плоскі.

У математиці міра крутизни прямої називається нахилом лінії.

Поняття схилу має багато застосувань у реальному світі. У будівництві крок даху, нахил сантехнічних труб та крутизна сходів - це все застосування схилу. і коли ви катаєтесь на лижах або бігаєте по пагорбу, ви точно відчуваєте схил.

Ми можемо призначити числове значення нахилу лінії, знайшовши співвідношення підйому та пробігу. Підйом - це сума, на яку змінюється вертикальна відстань, поки пробіг вимірює зміну горизонталі, як показано на цій ілюстрації. Ухил - це швидкість зміни. Див. Малюнок.

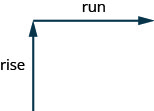
Ця цифра має схему з двох стрілок. Перша стрілка вертикальна і спрямована вгору і позначена «підйом». Друга стрілка починається в кінці першої. Друга стрілка горизонтальна і спрямована вправо і позначена «бігти». — Малюнок$\PageIndex{1}$.

НАХИЛ ЛІНІЇ

Нахил лінії є$m=\frac{\text{rise}}{\text{run}}$.

Підйом вимірює вертикальну зміну, а пробіг вимірює зміну горизонталі.

Щоб знайти нахил прямої, ми знаходимо дві точки на лінії, координати яких цілі числа. Потім ми намалюємо прямокутний трикутник, де дві точки є вершинами і одна сторона горизонтальна, а одна сторона вертикальна.

Щоб знайти нахил лінії, заміряємо відстань по вертикальній і горизонтальній сторонам трикутника. Вертикальна відстань називається підйомом, а горизонтальна відстань називається пробігом,

ЗНАЙТИ НАХИЛ ЛІНІЇ З ЇЇ ГРАФІКА ЗА ДОПОМОГОЮ$m=\frac{\text{rise}}{\text{run}}$

Знайдіть дві точки на лінії, координати яких є цілими числами.
Починаючи з однієї точки, накидайте прямокутний трикутник, що йде від першої точки до другої точки.
Підрахуйте підйом і біг на ніжках трикутника.
Візьміть співвідношення підйому до бігу, щоб знайти нахил:$m=\frac{\text{rise}}{\text{run}}$.

Приклад$\PageIndex{1}$

Знайдіть нахил показаної лінії.

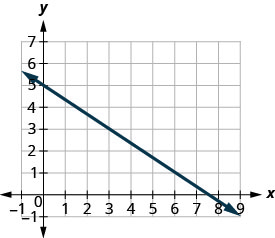
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативного 1 до 9. Вісь Y проходить від негативного 1 до 7. Лінія проходить через точки (0, 5), (3, 3) і (6, 1).$

Відповідь

Знайдіть дві точки на графіку, координати яких є цілими числами.	$(0,5)$і$(3,3)$
Починаючи з$(0,5)$, намалюйте прямокутний трикутник $(3,3)$, як показано на цьому графіку.	$.$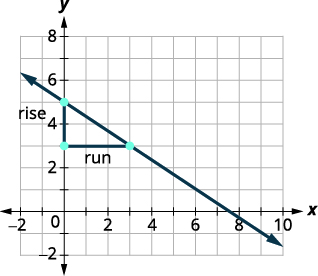
Підрахуйте rise— так як він йде вниз, це негативно.	Підйом є$−2$.
Підрахуйте пробіг.	Пробіг дорівнює 3.
Скористайтеся формулою нахилу.	$m=\frac{\text{rise}}{\text{run}}$
Підставляємо значення підйому і бігу.	$m=−23$
Спростити.	$m=−23$
	Ухил лінії дорівнює$−23$.
	Таким чином, y зменшується на 2 одиниці, оскільки x збільшується на 3 одиниці.

Приклад$\PageIndex{2}$

Знайдіть нахил показаної лінії.

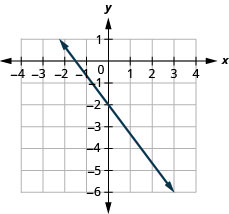
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативного 1 до 5. Вісь Y проходить від негативних 6 до 1. Лінія проходить через точки (0, від'ємний 2) і (3, негативний 6).$

Відповідь: $-\frac{4}{3}$

Приклад$\PageIndex{3}$

Знайдіть нахил показаної лінії.

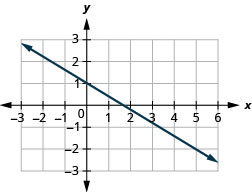
$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 3 до 6. Вісь Y проходить від негативних 3 до 2. Лінія проходить через точки (0, 1) і (5, негативні 2).$

Відповідь: $-\frac{3}{5}$

Як ми знаходимо нахил горизонтальних і вертикальних ліній? Щоб знайти нахил горизонтальної лінії$y=4$, ми могли б намалювати лінію, знайти дві точки на ній і порахувати підйом і пробіг. Давайте подивимося, що відбувається, коли ми це зробимо, як показано на графіку нижче.

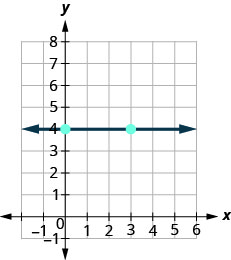
$Потім на малюнку показано графік прямої лінії на координатній площині x y. Вісь X проходить від негативного 1 до 6. Вісь Y проходить від негативного 1 до 8. Лінія проходить через точки (0, 4) і (3, 4). Що таке підйом? Підйом дорівнює 0. Що таке пробіг? Пробіг дорівнює 3. Що таке ухил? m дорівнює підйом, розділений на пробіг. m дорівнює 0 ділиться на 3. m дорівнює 0. Нахил горизонтальної лінії y дорівнює 4 дорівнює 0.$

$ \begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{0}{3}} \\ {} &{m=0} \\{}&{\text{The slope of the horizontal line } y=4 \text{ is }0.} \\ \end{array} \nonumber$

Розглянемо також вертикальну лінію, лінію$x=3$, як показано на графіку.

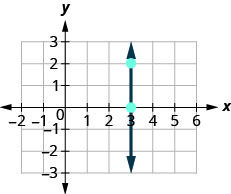
$Потім на малюнку показано графік прямої лінії на координатній площині x y. Вісь X проходить від негативних 2 до 6. Вісь Y проходить від негативних 3 до 3. Лінія проходить через точки (3, 0) і (3, 2). Що таке підйом? Підйом дорівнює 2. Що таке пробіг? Прогін дорівнює 0. Що таке ухил? m дорівнює підйому, розділеному на пробіг. m дорівнює 2 ділиться на 0.$

Нахил не визначено, оскільки поділ на нуль не визначено. Так ми говоримо, що нахил вертикальної лінії$x=3$ невизначений.

Всі горизонтальні лінії мають нахил 0. Коли y -координати однакові, підйом дорівнює 0.

Нахил будь-якої вертикальної лінії не визначено. Коли x -координати рядка однакові, прогін дорівнює 0.

НАХИЛ ГОРИЗОНТАЛЬНОЇ І ВЕРТИКАЛЬНОЇ ЛІНІЇ

Ухил горизонтальної лінії$y=b$, дорівнює 0.

Нахил вертикальної лінії$x=a$, не визначено.

Приклад$\PageIndex{4}$

Знайдіть нахил кожної лінії: ⓐ$x=8$ ⓑ $y=−5$.

Відповідь: ⓐ$x=8$
Це вертикальна лінія. Його нахил невизначений.
ⓑ$y=−5$
Це горизонтальна лінія. Він має нахил 0.

Приклад$\PageIndex{5}$

Знайдіть ухил лінії:$x=−4$.

Відповідь: невизначений

Приклад$\PageIndex{6}$

Знайдіть ухил лінії:$y=7$.

Відповідь: 0

КОРОТКИЙ ПОСІБНИК ПО УХИЛАХ ЛІНІЙ

$На зображенні зображені чотири стрілки. Перша стрілка похила і спрямована вгору і вправо і має позначення «позитивна». Друга стрілка похила і спрямована вниз і вправо і позначена «негативною». Третя стрілка горизонтальна і позначена «нуль». Четверта стрілка вертикальна і позначена «undefined».$

Іноді нам потрібно знайти нахил лінії між двома точками, коли у нас немає графіка, щоб відрахувати підйом і пробіг. Ми могли б побудувати точки на папері сітки, потім підрахувати підйом і пробіг, але, як ми побачимо, є спосіб знайти схил без графіки. Перш ніж ми дістанемося до нього, нам потрібно ввести деякі алгебраїчні позначення.

Ми бачили, що впорядкована пара (x, y) (x, y) дає координати точки. Але коли ми працюємо з ухилами, ми використовуємо два пункти. Як можна використовувати один і той же символ (x, y) (x, y) для представлення двох різних точок? Математики використовують індекси для розрізнення точок.

$ \begin{array} {ll} {(x_1, y_1)} &{\text{read “} x \text{ sub } 1, \space y \text{ sub } 1 \text{”}} \\ {(x_2, y_2)} &{\text{read “} x \text{ sub } 2, \space y \text{ sub } 2 \text{”}} \\ \end{array} \nonumber$

Ми будемо використовувати$(x_1,y_1)$ для виявлення першої точки і$(x_2,y_2)$ для ідентифікації другої точки.

Якби у нас було більше двох точок, ми могли б використовувати$(x_3,y_3)$$(x_4,y_4)$, і так далі.

Давайте подивимося, як підйом і пробіг співвідносяться з координатами двох точок, по-іншому поглянемо на нахил лінії між точками$(2,3)$ і$(7,6)$, як показано на цьому графіку.

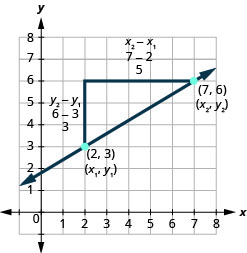
$На малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативного 1 до 7. Вісь Y проходить від негативного 1 до 7. Лінія проходить через точки (2, 3) і (7, 6). Прямокутний трикутник малюється шляхом з'єднання трьох точок (2, 3), (2, 6) і (7, 6). Точка (2, 3) позначається (x 1, y 1). Точка (7, 6) позначається (х 2, у 2). Вертикальна сторона трикутника має мітки y 2 мінус y 1, 6 мінус 3 і 3. Горизонтальна сторона трикутника має мітки х 2 мінус х 1, 7 мінус 2 і 5.$

\( \begin{array} {ll} {\text{Since we have two points, we will use subscript notation.}} &{ \begin{pmatrix} x_1, & y_1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ 6 & 6 \end{pmatrix}} \\ {} &{m=\frac{\text{rise}}{\text{run}}} \\ {\text{On the graph, we counted the rise of 3 and the run of 5.}} &{m=\frac{3}{5}} \\ {\text{Notice that the rise of 3 can be found by subtracting the}} &{} \\ {y\text{-coordinates, 6 and 3, and the run of 5 can be found by}} &{} \\ {\text{subtracting the x-coordinates 7 and 2.}} &{} \\ {\text{We rewrite the rise and run by putting in the coordinates.}} &{m=\frac{6-3}{7-2}} \\ {} &{} \\ {\text{But 6 is } y_2 \text{, the y-coordinate of the second point and 3 is }y_1 \text{, the y-coordinate}} &{} \\ {\text{of the first point. So we can rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{7-2}} \\ {\text{Also 7 is the x-coordinate of the second point and 2 is the x-coordinate}} &{} \\ {\text{of the first point. So again we rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ \end{array} \nonumber\)

Ми показали, що$m=\frac{y_2−y_1}{x_2−x_1}$ це дійсно інша версія$m=\frac{\text{rise}}{\text{run}}$. Ми можемо використовувати цю формулу, щоб знайти нахил прямої, коли у нас є дві точки на лінії.

НАХИЛ ЛІНІЇ МІЖ ДВОМА ТОЧКАМИ

Нахил лінії між двома точками$(x_1,y_1)$ і$(x_2,y_2)$ становить:

$m=\frac{y_2−y_1}{x_2−x_1}$.

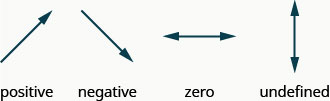
Ухил буває:

\[y\text{ of the second point minus }y\text{ of the first point} \nonumber\]\[\text{over} \nonumber\]\[x\text{ of the second point minus }x\text{ of the first point} \nonumber\]

Приклад$\PageIndex{7}$

Використовуйте формулу нахилу, щоб знайти нахил лінії через точки$(−2,−3)$ and $(-7,4)$.

Відповідь

$ \begin{array} {ll} {\text{We’ll call (−2,−3) point #1and (−7,4) point #2.}} &{ \begin{pmatrix} x_1, & y_1 \\ -2 & -3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ -7 & 4 \end{pmatrix}} \\ {\text{Use the slope formula.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{} \\ {\text{x of the second point minus x of the first point}} &{m=\frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify}}&{m=\frac{7}{-5}} \\ {} &{m=\frac{-7}{5}} \\ \end{array} \nonumber$

Давайте перевіримо цей нахил на показаному графіку.

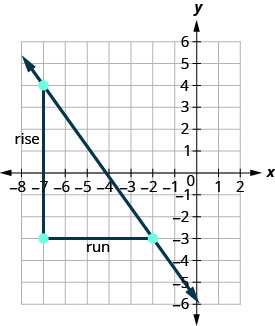
$На малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 2. Вісь Y проходить від негативних 6 до 6. Лінія йде через точки (від'ємний 7, 4) і (негативний 2, негативний 3). Прямокутний трикутник малюється з'єднанням трьох точок (негативний 7, 4), (негативний 7, негативний 3), і (негативний 2, негативний 3). Вертикальна сторона трикутника позначена «підйом». Горизонтальна сторона трикутника позначена «бігти».$

\[m=\frac{\text{rise}}{\text{run}} \nonumber\]\[m=\frac{7}{−5} \nonumber\]\[m=\frac{−7}{5} \nonumber\]

Використовуйте формулу нахилу, щоб знайти нахил прямої через пару точок:$(−3,4)$ і$(2,−1)$.

Відповідь: $-1$

Приклад$\PageIndex{9}$

Використовуйте формулу нахилу, щоб знайти нахил прямої через пару точок:$(−2,6)$ і$(−3,−4)$.

Відповідь: 10

Графік лінії з заданою точкою та нахилом

До цих пір в цьому розділі ми графували лінії шляхом побудови точок, використовуючи перехоплення та розпізнаючи горизонтальні та вертикальні лінії.

Ми також можемо графікувати лінію, коли ми знаємо одну точку та нахил лінії. Ми почнемо з побудови точки, а потім використаємо визначення нахилу, щоб намалювати графік лінії.

Приклад$\PageIndex{10}$: How to graph a Line Given a Point and the Slope

Графік лінії, що проходить через точку$(1,−1)$, нахил якої дорівнює$m=\frac{3}{4}$.

Відповідь

$Крок 1 полягає в тому, щоб намітити задану точку. Сюжет (1, негативний 1). Потім на малюнку показано графік точки на координатній площині x y. Вісь X проходить від негативних 2 до 6. Вісь Y проходить від негативних 2 до 4. Точка (1, від'ємна 1) наноситься і позначена її координатами.$ $Крок 2 полягає у використанні формули нахилу m дорівнює підйому, розділеному на пробіг, щоб визначити підйом і пробіг. Визначте підйом і забіг. m дорівнює 3 розділити на 4. Підйом розділений на пробіг дорівнює 3 розділеним на 4. Підйом дорівнює 3. Виконати дорівнює 4.$ $Крок 3 полягає в тому, щоб почати в заданій точці і відрахувати підйом і бігти, щоб відзначити другу точку. Почніть з (1, негативний 1) і порахуйте підйом і біг. Вгору 3 одиниці, праворуч 4 одиниці. Потім на малюнку показано графік трьох точок, з'єднаних двома прямими відрізками на координатній площині x y. Вісь X проходить від негативних 2 до 6. Вісь Y проходить від негативних 2 до 4. Намальовані точки (1, від'ємний 1), (1, 2) і (5, 2). Відрізок вертикальної лінії з'єднується (1, негативний 1) з (1, 2) і маркується 3. Відрізок горизонтальної лінії з'єднується (1, 2) з (5, 2) і маркується 4.$ $Крок 4 полягає в з'єднанні точок лінією. З'єднайте дві точки лінією. Потім на малюнку показано графік прямої лінії, трьох точок та двох відрізків лінії на координатній площині x y. Вісь X проходить від негативних 2 до 6. Вісь Y проходить від негативних 2 до 4. Намальовані точки (1, від'ємний 1), (1, 2) і (5, 2). Вертикальний відрізок лінії з'єднує (1, негативний 1) до (1, 2). Відрізок горизонтальної лінії з'єднується (1, 2) з (5, 2) і маркується 4. Через точки (1, негативний 1) і (5, 2) проводять пряму лінію зі стрілками на обох кінцях.$

Перевірити свою роботу можна, знайшовши третій пункт. Оскільки нахил є$m=34$, його також можна записати як$m=\frac{−3}{−4}$ (негативний розділений на негативний позитивний!). Поверніться назад$(1,−1)$ і відраховуйте підйом$−3$, і біг,$−4$.

Приклад$\PageIndex{11}$

Графік лінії, що проходить через точку$(2,−2$ з нахилом$m=\frac{4}{3}$.

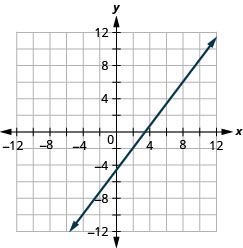
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (2, від'ємні 2) і (5, 2).$

Приклад$\PageIndex{12}$

Графік лінії, що проходить через точку$(−2,3)$ with the slope $m=\frac{1}{4}$.

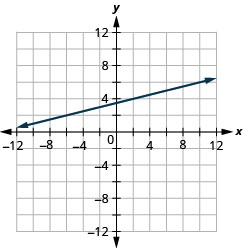
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (від'ємні 2, 3) і (2, 4).$

ГРАФІК ЛІНІЇ ЗАДАНО ТОЧКУ І НАХИЛ.

Побудуйте задану точку.
Використовуйте формулу нахилу$m=\frac{\text{rise}}{\text{run}}$, щоб визначити підйом і пробіг.
Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку.
З'єднайте точки лінією.

Графік лінії з використанням її нахилу та перехоплення

Ми намалювали лінійні рівняння шляхом побудови точок, використовуючи перехоплення, розпізнаючи горизонтальні та вертикальні лінії та використовуючи одну точку та нахил лінії. Як тільки ми побачимо, як рівняння у формі перехоплення нахилу та його графік пов'язані, ми матимемо ще один метод, який ми можемо використовувати для графіків ліній.

Див. Малюнок. Давайте подивимося на графік рівняння$y=12x+3$ і знайдемо його нахил і y -перехоплення.

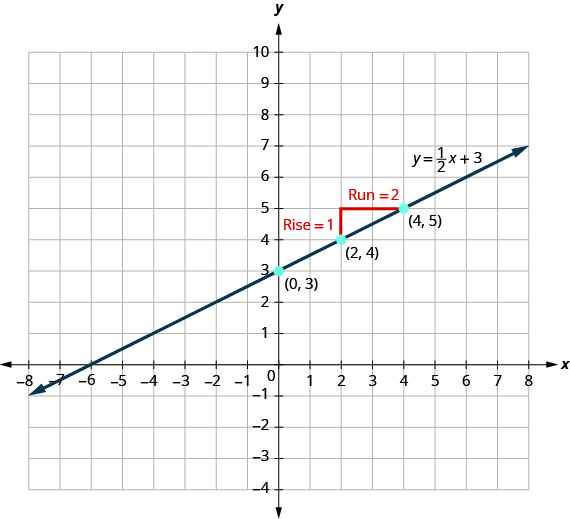
На малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, 3), (2, 4), і (4, 5). Прямокутний трикутник малюється шляхом з'єднання трьох точок (2, 4), (2, 5) і (4, 5). Вертикальна сторона трикутника позначена «Підйом дорівнює 1». Горизонтальна сторона трикутника позначена «Виконати дорівнює 2». Рядок позначений y дорівнює 1 ділиться на 2 х плюс 3. — Малюнок$\PageIndex{2}$

Червоні лінії на графіку показують нам підйом дорівнює 1, а пробіг - 2. Підставляємо в ухил формулу:

\[m=\frac{\text{rise}}{\text{run}} \nonumber\]\[m=\frac{1}{2} \nonumber\]

Y -перехоплення є$(0,3)$.

Подивіться на рівняння цієї лінії.

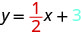
$На малюнку показано рівняння y дорівнює 1 поділеному на 2 х плюс 3. 1, розділене на 2, підкреслено червоним кольором. 3 підкреслено синім кольором.$

Подивіться на схил і у -перехоплення.

$Ухил m дорівнює 1 поділеному на 2 і y-перехоплення (0, 3). 1, розділене на 2, підкреслено червоним кольором. 3 підкреслено синім кольором.$

Коли лінійне рівняння вирішується для y, коефіцієнт члена x - нахил, а постійний член - y -координата y -перехоплення. Ми говоримо, що рівняння$y=12x+3$ знаходиться у формі нахилу - перехоплення. Іноді форма перехоплення нахилу називається «y -форма».

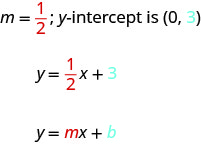
$m дорівнює 1 поділеному на 2; y-перехоплення дорівнює (0, 3). y дорівнює 1 поділений на 2 х плюс 3. у дорівнює m x плюс b. m і 1, розділені на 2, підкреслюються червоним кольором. B і 3 підкреслені синім кольором.$

ФОРМА ПЕРЕХОПЛЕННЯ НАХИЛУ РІВНЯННЯ ПРЯМОЇ

Форма нахилу—перехоплення рівняння прямої з нахилом m та y -перехоплення,$(0,b)$ є$y=mx+b$.

Давайте потренуємося знаходити значення нахилу і y -перехоплення з рівняння прямої.

Приклад$\PageIndex{13}$

Визначте нахил і y -перехоплення прямої з рівняння:

ⓐ$y=−\frac{4}{7}x−2$ ⓑ$x+3y=9$

Відповідь

ⓐ Порівнюємо наше рівняння з формою ухил-перехоплення рівняння.

Запишіть форму ухил-перехоплення рівняння прямої.	$.$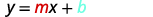
Запишіть рівняння прямої.	$.$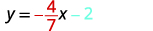
Визначте ухил.	$.$
Визначте y -перехоплення.	$.$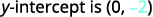

ⓑ Коли рівняння прямої не задано у формі нахилу - перехоплення, нашим першим кроком буде розв'язання рівняння для y.

Вирішити для y.	х+3р=9х+3р=9
Відніміть x з кожного боку.	$.$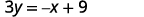
Розділіть обидві сторони на 3.	$.$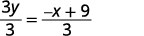
Спростити.	$.$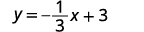
Запишіть форму ухил-перехоплення рівняння прямої.	$.$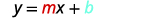
Запишіть рівняння прямої.	$.$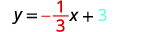
Визначте ухил.	$.$
Визначте y -перехоплення.	$.$

Приклад$\PageIndex{14}$

Визначте ухил і y -перехоплення з рівняння прямої.

ⓐ$y=\frac{2}{5}x−1$ ⓑ$x+4y=8$

Відповідь: ⓐ$m=\frac{2}{5}$;$(0,−1)$
ⓑ$m=−\frac{1}{4}$;$(0,2)$

Приклад$\PageIndex{15}$

Визначте ухил і y -перехоплення з рівняння прямої.

ⓐ$y=−\frac{4}{3} x+1$ ⓑ$3x+2y=12$

Відповідь: ⓐ$m=−\frac{4}{3}$;$(0,1)$
ⓑ$m=−\frac{3}{2}$;$(0,6)$

Ми накреслили лінію, використовуючи нахил і точку. Тепер, коли ми знаємо, як знайти нахил і y -перехоплення прямої з її рівняння, ми можемо використовувати y -перехоплення як точку, а потім відрахувати нахил звідти.

Приклад$\PageIndex{16}$

Графік лінії рівняння$y=−x+4$ using its slope and y -перехоплення.

Відповідь

	$y=mx+b$
Рівняння знаходиться у формі нахилу-перехоплення.	$y=−x+4$
Визначте ухил і y -перехоплення.	$m=−1$ y -перехоплення є$(0,4)$
Ділянка y -перехоплення.	Див. Графік.
Визначте підйом над бігом.	$m=−11$
Відраховуйте підйом і біжіть, щоб відзначити другу точку.	підйом$-1$, біг$1$ $.$

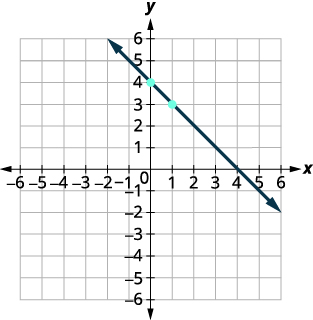
Намалюйте лінію, як показано на графіку.

Приклад$\PageIndex{17}$

Графік лінії рівняння,$y=−x−3$ використовуючи його нахил і y -перехоплення.

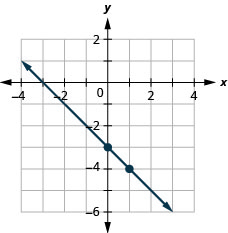
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 3) і (1, негативний 4).$

Приклад$\PageIndex{18}$

Графік лінії рівняння,$y=−x−1$ використовуючи його нахил і y -перехоплення.

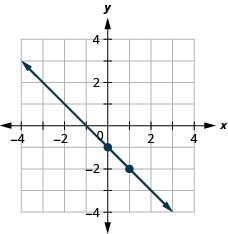
Відповідь: $На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 1) і (1, від'ємний 2).$

Тепер, коли у нас є графічні лінії за допомогою нахилу та y -перехоплення, давайте підсумуємо всі методи, які ми використовували для графіків ліній.

$Таблиця має рядок заголовка, який читає «Методи до ліній графіка». Нижче це чотири стовпчики. Перший стовпець містить наступне: Точкова побудова графіків. Порожня таблиця з двома стовпцями і чотирма рядками. Перший рядок є рядком заголовка з заголовками «x» і «y». Знайдіть три точки. Намалюйте точки, переконайтеся, що вони шикуються, ними проведіть лінію. Другий стовпець містить: Ухил-Перехоплення. Y дорівнює m x плюс b Знайдіть нахил і y-перехоплення, а потім порахуйте нахил, щоб отримати другу точку. Третя колонка: Перехоплення. Таблиця з двома стовпцями і чотирма рядками. Перший рядок є рядком заголовка з заголовками «x» і «y». У першому рядку є 0 у стовпці x. У другому рядку є 0 у стовпці y. Решта пробілів пусті. Четверта колонка. Розпізнавати вертикальні і горизонтальні лінії. Рівняння має тільки одну змінну. X дорівнює вертикалі. Y дорівнює b по горизонталі.$

Виберіть найбільш зручний метод для побудови графіка лінії

Тепер, коли ми побачили кілька методів, які ми можемо використовувати для графіків ліній, як ми знаємо, який метод використовувати для даного рівняння?

Хоча ми могли б побудувати точки, використовувати форму нахилу - перехоплення або знайти перехоплення для будь-якого рівняння, якщо ми визнаємо найзручніший спосіб побудови графіка певного типу рівняння, наша робота буде простішою.

Як правило, побудова точок не є найефективнішим способом графіка лінії. Давайте розглянемо деякі закономірності, які допоможуть визначити найбільш зручний метод побудови графіка лінії.

Ось п'ять рівнянь, які ми намалювали в цьому розділі, і метод, який ми використовували для графіка кожного з них.

\[ \begin{array} {lll} {} &{\textbf{Equation}} &{\textbf{Method}} \\ {\text{#1}} &{x=2} &{\text{Vertical line}} \\ {\text{#2}} &{y=−1} &{\text{Horizontal line}} \\ {\text{#3}} &{−x+2y=6} &{\text{Intercepts}} \\ {\text{#4}} &{4x−3y=12} &{\text{Intercepts}} \\ {\text{#5}} &{y=−x+4} &{\text{Slope–intercept}} \\ \end{array} \nonumber\]

Рівняння #1 та #2 мають лише одну змінну. Пам'ятайте, в рівняннях такої форми значення цієї однієї змінної є постійним; воно не залежить від значення іншої змінної. Рівняння такого виду мають графіки, які представляють собою вертикальні або горизонтальні лінії.

У рівняннях #3 і #4 обидва x і y знаходяться на одній стороні рівняння. Ці два рівняння мають вигляд Ax+By=C.Ax+By=C Ми підставили y=0y=0, щоб знайти x - перехоплення і x = 0x=0, щоб знайти y -перехоплення, а потім знайшли третю точку, вибравши інше значення для x або y.

Рівняння #5 записано у формі нахилу - перехоплення. Після ідентифікації нахилу і y- перехоплення з рівняння ми використовували їх для побудови графіка прямої.

Це призводить до наступної стратегії.

СТРАТЕГІЯ ВИБОРУ НАЙБІЛЬШ ЗРУЧНОГО МЕТОДУ ГРАФУ ЛІНІЇ

Розглянемо форму рівняння.

Якщо він має лише одну змінну, це вертикальна або горизонтальна лінія.
- $x=a$вертикальна лінія, що проходить через вісь x на a.
- $y=b$горизонтальна лінія, що проходить через вісь y в b.
Якщо y ізольовано на одній стороні рівняння, то у вигляді$y=mx+b$ графа за допомогою нахилу і y -перехоплення.
- Визначте нахил і y -перехоплення, а потім графік.
Якщо рівняння має вигляд$Ax+By=C$, знайдіть перехоплення.
- Знайдіть x - і y -перехоплення, третю точку, а потім графік.

Приклад$\PageIndex{19}$

Визначте найбільш зручний метод для графіка кожного рядка:

ⓐ$y=5$ ⓑ$4x−5y=20$ ⓒ$x=−3$ ⓓ$y=−\frac{5}{9}x+8$

Відповідь: ⓐ$y=5$
Це рівняння має лише одну змінну, y. Його графік являє собою горизонтальну лінію, що перетинає вісь y в$5$.
ⓑ$4x−5y=20$
Це рівняння має вигляд$Ax+By=C$. Найпростішим способом графіка буде знайти перехоплення і ще одну точку.
ⓒ$x=−3$
Існує лише одна змінна, x. Графік являє собою вертикальну лінію, що перетинає вісь x в$−3$.
ⓓ$y=−\frac{5}{9}x+8$
Оскільки це рівняння має$y=mx+b$ форму, найпростіше буде графікувати цю лінію за допомогою нахилу та y -перехоплення.

Приклад$\PageIndex{20}$

Визначте найбільш зручний метод для графіка кожного рядка:

ⓐ$3x+2y=12$ ⓑ$y=4$ ⓒ$y=\frac{1}{5}x−4$ ⓓ$x=−7$.

Відповідь: ⓐ перехоплює ⓑ горизонтальну лінію ⓒ схил-перехоплення ⓓ вертикальна лінія

Приклад$\PageIndex{21}$

Визначте найбільш зручний метод для графіка кожного рядка:

ⓐ$x=6$ ⓑ$y=−\frac{3}{4}x+1$ ⓒ$y=−8$ ⓓ$4x−3y=−1$.

Відповідь: ⓐ вертикальна лінія ⓑ схил-перехоплення ⓒ горизонтальна лінія
ⓓ перехоплює

Графік та інтерпретація застосувань перехоплення нахилу

Багато реальних додатків моделюються лінійними рівняннями. Ми розглянемо кілька додатків тут, щоб ви могли побачити, як рівняння, написані у формі перехоплення нахилу, відносяться до реальних ситуацій.

Зазвичай, коли лінійні моделі рівнянь використовують реальні дані, для змінних використовуються різні літери, замість того, щоб використовувати лише x та y. Імена змінних нагадують нам про те, які величини вимірюються.

Крім того, нам часто потрібно буде розширити осі в нашій прямокутній системі координат до більших позитивних і негативних чисел, щоб розмістити дані в додатку.

Приклад$\PageIndex{22}$

Рівняння$F=\frac{9}{5}C+32$ використовується для перетворення температур, С, за шкалою Цельсія в температури, F, за шкалою Фаренгейта.

ⓐ Знайдіть температуру за Фаренгейтом для температури за Цельсієм 0.

ⓑ Знайдіть температуру за Фаренгейтом для температури за Цельсієм 20.

ⓓ Графік рівняння.

Відповідь

ⓐ

$ \begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 0.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=0.}} &{F=\frac{9}{5}(0)+32} \\ {\text{Simplify.}} &{F=32} \\ \end{array} \nonumber$

ⓑ

$ \begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 20.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=20.}} &{F=\frac{9}{5}(20)+32} \\ {\text{Simplify.}} &{F=36+32} \\ {\text{Simplify.}} &{F=68} \\ \end{array} \nonumber$

ⓒ
Інтерпретувати нахил і F -перехоплення рівняння.
Незважаючи на те, що це рівняння використовує F і C, воно все ще знаходиться у формі перехоплення нахилу.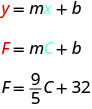

$y дорівнює м х плюс б F дорівнює m C плюс b. y і F підкреслені червоним кольором. X і C підкреслені синім кольором. F дорівнює 9 ділиться на 5 C плюс 32.$

Нахил$\frac{9}{5}$, означає, що температура за Фаренгейтом (F) збільшується на 9 градусів, коли температура Цельсія (C) збільшується на 5 градусів.
F -перехоплення означає, що коли температура знаходиться$0°$ за шкалою Цельсія, вона знаходиться$32°$ за шкалою Фаренгейта.
ⓓ Графік рівняння.
Нам потрібно буде використовувати більший масштаб, ніж наш звичайний. Почніть з F -перехоплення$(0,32)$, а потім відрахуйте підйом 9 і пробіг 5, щоб отримати другу точку, як показано на графіку.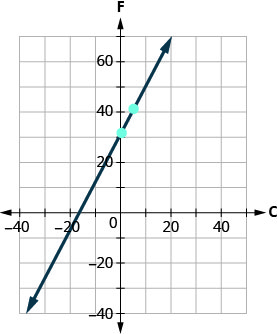

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативних 40 до 80. Вісь Y проходить від негативних 40 до 80. Лінія проходить через точки (0, 32) і (5, 41).$

Приклад$\PageIndex{23}$

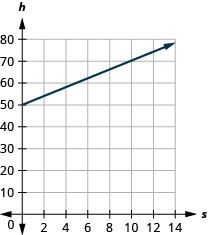
Рівняння$h=2s+50$ is used to estimate a woman’s height in inches, h, виходячи з її розміру взуття, s.

ⓐ Оцініть зріст дитини, яка носить жіноче взуття розміру 0.

ⓑ Оцініть зріст жінки з розміром взуття 8.

ⓓ Графік рівняння.

Відповідь

ⓐ 50 дюймів
ⓑ 66 дюймів
ⓒ Нахил, 2, означає, що висота, h, збільшується на 2 дюйми, коли розмір взуття, s, збільшується на 1. h -intercept означає, що коли розмір взуття дорівнює 0, висота становить 50 дюймів.
ⓓ

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативного 1 до 14. Вісь Y проходить від негативного 1 до 80. Лінія проходить через точки (0, 50) і (10, 70).$

Приклад$\PageIndex{24}$

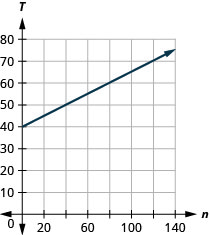
Рівняння$T=\frac{1}{4}n+40$ is used to estimate the temperature in degrees Fahrenheit, T, засноване на кількості цвіркунів цвіркуна, n, за одну хвилину.

ⓐ Оцініть температуру, коли немає щебекання.

ⓑ Оцініть температуру, коли кількість щебетів за одну хвилину становить 100.

ⓓ Графік рівняння.

Відповідь

ⓐ 40 градусів
ⓑ 65 градусів
ⓒ Нахил$\frac{1}{4}$, означає, що температура за Фаренгейтом (F) збільшується на 1 градус, коли кількість щебетів, n, збільшується на 4. T -перехоплення означає, що коли кількість щебетів дорівнює 0, температура дорівнює 40°.
ⓓ

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативного 1 до 140. Вісь Y проходить від негативного 1 до 80. Лінія проходить через точки (0, 40) і (40, 50).$

Вартість ведення деяких видів бізнесу має дві складові - фіксовану вартість та змінну вартість. Фіксована вартість завжди однакова незалежно від того, скільки одиниць вироблено. Це витрати на оренду, страховку, обладнання, рекламу та інші предмети, які необхідно оплачувати регулярно. Змінна вартість залежить від кількості вироблених одиниць. Це для матеріалу та праці, необхідних для виготовлення кожного предмета.

Приклад$\PageIndex{25}$

Сем керує фургоном доставки. Рівняння$C=0.5m+60$ моделює співвідношення між його тижневою вартістю, C, у доларах та кількістю миль, м, що він їздить.

ⓐ Знайдіть вартість Сема за тиждень, коли він проїжджає 0 миль.

ⓑ Знайти вартість за тиждень, коли він проїде 250 миль.

ⓓ Графік рівняння.

Відповідь

ⓐ
$ \begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 0 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=0.}} &{C=0.5(0)+60} \\ {\text{Simplify.}} &{C=60} \\ {} &{\text{Sam’s costs are }$\text{60 when he drives 0 miles.}} \\ \end{array} \nonumber $
ⓑ
$ \begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 250 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=250.}} &{C=0.5(250)+60} \\ {\text{Simplify.}} &{C=185} \\ {} &{\text{Sam’s costs are }$\text{185 when he drives 250 miles.}} \\ \end{array} \nonumber $
ⓒ Інтерпретувати нахил і C -перехоплення рівняння.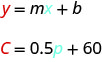

$у дорівнює м х плюс б С дорівнює 0,5 р плюс 60. У і С підкреслені червоним кольором. X і p підкреслені синім кольором.$

Нахил, 0,5, означає, що тижнева вартість, C, збільшується на 0,50 долара, коли кількість пройдених миль, n, збільшується на 1.
C -intercept означає, що коли кількість пройдених миль дорівнює 0, тижнева вартість становить 60 доларів.
ⓓ Графік рівняння.
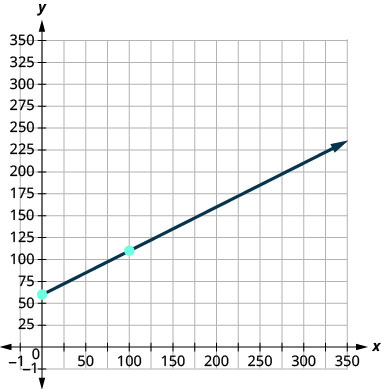
Нам потрібно буде використовувати більший масштаб, ніж наш звичайний. Почніть з перехоплення C$(0,60)$.

Щоб відрахувати нахил$m= 0.5$, ми переписуємо його як еквівалентний дріб, який полегшить нашу графіку.

$ \begin{array} {ll} {} &{m=0.5} \\ {\text{Rewrite as a fraction.}} &{m=\frac{0.5}{1}} \\ {\text{Multiply numerator and}} &{} \\ {\text{denominator by 100}} &{m=\frac{0.5(100)}{1(100)}} \\ {\text{Simplify.}} &{m=\frac{50}{100}} \\ \end{array} \nonumber $

Таким чином, щоб графік наступної точки піднімаємося вгору 50 від перехоплення 60, а потім вправо 100. Другим пунктом буде$(100, 110)$.

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативного 1 до 350. Вісь Y проходить від негативного 1 до 350. Лінія проходить через точки (0, 60) і (200, 160).$

Приклад$\PageIndex{26}$

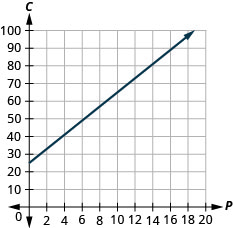
Стелла має домашній бізнес з продажу піци для гурманів. Рівняння$C=4p+25$ моделює співвідношення між її тижневою вартістю, C, у доларах та кількістю піци, р, яку вона продає.

ⓐ Знайдіть вартість Стелли на тиждень, коли вона не продає піци.

ⓑ Знайти вартість за тиждень, коли вона продасть 15 піц.

ⓓ Графік рівняння.

Відповідь

ⓐ $25
ⓑ $85
ⓒ Схил, 4, означає, що тижнева вартість, C, збільшується на 4 долари, коли кількість проданих піц, р, збільшується на 1. C -intercept означає, що коли кількість проданих піц дорівнює 0, тижнева вартість становить 25 доларів.
ⓓ

$На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 2 до 20. Вісь Y працює від негативних 10 до `00. Лінія проходить через точки (0, 25) і (1, 29).$

Приклад$\PageIndex{27}$

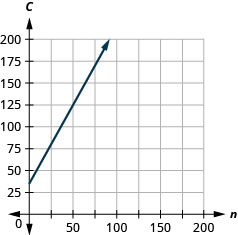
Лорен має каліграфічний бізнес. Рівняння$C=1.8n+35$ моделює співвідношення між її тижневою вартістю, C, у доларах та кількістю весільних запрошень, n, що вона пише.

ⓐ Знайдіть вартість Лорен на тиждень, коли вона не пише запрошень.

ⓑ Знайти вартість за тиждень, коли вона напише 75 запрошень.

ⓓ Графік рівняння.

Відповідь

ⓐ $35
ⓑ $170
ⓒ Схил$1.8$, означає, що тижнева вартість, C, збільшується на те,$$1.80$ коли кількість запрошень, n, збільшується на 1.
C -intercept означає, що коли кількість запрошень дорівнює 0, тижнева вартість становить 35 доларів.
ⓓ

Використання нахилів для визначення паралельних і перпендикулярних ліній

Дві лінії, які мають однаковий нахил, називаються паралельними лініями. Паралельні лінії мають однакову крутизну і ніколи не перетинаються.

Ми говоримо про це більш формально з точки зору прямокутної системи координат. Дві лінії, які мають однаковий нахил і різні y -перехоплення, називаються паралельними лініями. Див. Малюнок.

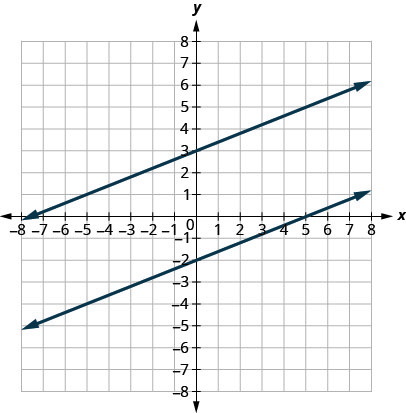
На цьому малюнку показаний графік двох прямих ліній на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Перша лінія проходить через точки (0, 3) і (5, 5). Другий рядок проходить через точки (0, від'ємний 2) і (5, 0). Лінії паралельні, тобто вони завжди будуть на однаковій відстані один від одного і ніколи не перетинаються. Вони похилі під однаковим кутом. — Малюнок$\PageIndex{3}$

Переконайтеся, що обидві лінії мають однаковий нахил$m=\frac{2}{5}$, і різні y -перехоплення.

А як щодо вертикальних ліній? Нахил вертикальної лінії не визначено, тому вертикальні лінії не відповідають визначенню вище. Ми говоримо, що вертикальні лінії, які мають різні x -перехоплення, паралельні, як і лінії, показані на цьому графіку.

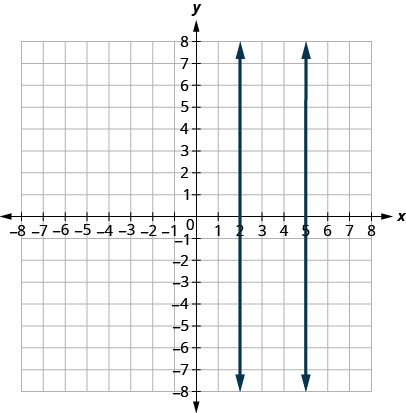
На цьому малюнку показаний графік двох прямих вертикальних ліній на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Перша лінія проходить через точки (2, 0) і (2, 1). Друга лінія проходить через точки (5, 0) і (5, 1). Лінії паралельні, тобто вони завжди будуть на однаковій відстані один від одного і ніколи не перетинаються. — Малюнок$\PageIndex{4}$

ПАРАЛЕЛЬНІ ЛІНІЇ

Паралельні лінії - це лінії в одній площині, які не перетинаються.

Паралельні лінії мають однаковий нахил і різні y -перехоплення.
Якщо m1m1 і m2m2 - це ухили двох паралельних ліній, то m1=m2.m1 = м2.
Паралельні вертикальні лінії мають різні x -перехоплення

Оскільки паралельні лінії мають однаковий нахил і різні y -перехоплення, тепер ми можемо просто подивитися на нахил - перехоплення форми рівнянь ліній і вирішити, чи є лінії паралельними.

Приклад$\PageIndex{28}$

Використовуйте нахили та y -перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$3x−2y=6$ і$y=\frac{3}{2}x+1$ ⓑ$y=2x−3$ і$−6x+3y=−9$.

Відповідь: ⓐ
$ \begin{array} {llll} {} &{3x−2y=6} &{\text{and}} &{y=\frac{3}{2}x+1} \\ {} &{−2y=−3x+6} &{} &{} \\ {\text{Solve the first equation for y.}} &{\frac{-2y}{-2}=\frac{-3x+6}{-2}} &{} &{} \\ {\text{The equation is now in slope–intercept form.}} &{y=\frac{3}{2}x−3} &{} &{} \\ {\text{The equation of the second line is already}} &{} &{} &{} \\ {\text{in slope–intercept form.}} &{} &{} &{y=\frac{3}{2}x+1} \\ {} &{} &{} &{} \\ {} &{y=\frac{3}{2}x−3} &{} &{y=\frac{3}{2}x+1} \\ {Identify the slope andy-intercept of both lines.} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=\frac{3}{2}} &{} &{y=\frac{3}{2}} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,1)} \\ \end{array} \nonumber$
Лінії мають однаковий нахил і різні y -перехоплення, і тому вони паралельні.
Можливо, ви захочете скласти графік ліній, щоб підтвердити, чи є вони паралельними.

ⓑ
$ \begin{array} {llll} {} &{y=2x−3} &{\text{and}} &{−6x+3y=−9} \\ {\text{The first equation is already in slope–intercept form.}} &{y=2x−3} &{} &{} \\ {} &{} &{} &{−6x+3y=−9} \\ {} &{} &{} &{3y=6x−9} \\ {\text{Solve the second equation for y.}} &{} &{} &{\frac{3y}{3}=\frac{6x−9}{3}} \\ {} &{} &{} &{y=2x−3} \\ {\text{The second equation is now in slope–intercept form.}} &{} &{} &{y=2x−3} \\ {} &{} &{} &{} \\ {} &{y=2x−3} &{} &{y=2x−3} \\ {\text{Identify the slope andy-intercept of both lines.}} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=2} &{} &{m=2} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,-3)} \\ \end{array} \nonumber$
Лінії мають однаковий нахил, але вони також мають однакові y -перехоплення. Їх рівняння представляють одну і ту ж лінію, і ми говоримо, що лінії збігаються. Вони не паралельні, вони є однією лінією.

Приклад$\PageIndex{29}$

Використовуйте нахили і y- перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$2x+5y=5$ і$y=−\frac{2}{5}x−4$ ⓑ$y=−\frac{1}{2}x−1$ і$x+2y=−2$.

Відповідь: ⓐ паралельно ⓑ не паралельно; та ж лінія

Приклад$\PageIndex{30}$

Використовуйте нахили і y- перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$4x−3y=6$ і$y=\frac{4}{3}x−1$ ⓑ$y=\frac{3}{4}x−3$ і$3x−4y=12$.

Відповідь: ⓐ паралельно ⓑ не паралельно; та ж лінія

Приклад$\PageIndex{31}$

Використовуйте нахили і y- перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$y=−4$ і$y=3$ ⓑ$x=−2$ і$x=−5$.

Відповідь

ⓐ$y=−4$ і$y=3$

Ми відразу визнаємо від рівнянь, що це горизонтальні лінії, і тому ми знаємо, що їх нахили обидва 0.
Оскільки горизонтальні лінії перетинають вісь y при y = −4y=−4 та y=3, y=3, ми знаємо, що y -перехоплення є (0, −4) (0, −4) та (0,3). (0,3).
Лінії мають однаковий нахил і різні y -перехоплення і тому вони паралельні.

ⓑ$x=−2$ і$x=−5$

Ми відразу визнаємо з рівнянь, що це вертикальні лінії, і тому ми знаємо, що їх нахили не визначені.
Оскільки вертикальні лінії перетинають вісь x в$x=−2$ і$x=−5$, ми знаємо y -перехоплення є$(−2,0)$ і$(−5,0)$.
Лінії вертикальні і мають різні x -перехоплення і тому вони паралельні.

Приклад$\PageIndex{32}$

Використовуйте нахили і y- перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$y=8$ і$y=−6$ ⓑ$x=1$ і$x=−5$.

Відповідь: ⓐ паралельно ⓑ паралельно

Приклад$\PageIndex{33}$

Використовуйте нахили і y- перехоплення, щоб визначити, чи паралельні лінії:

ⓐ$y=1$ і$y=−5$ ⓑ$x=8$ і$x=−6$.

Відповідь: ⓐ паралельно ⓑ паралельно

Давайте розглянемо лінії, рівняння яких$y=\frac{1}{4}x−1$ і$y=−4x+2$, показані на малюнку.

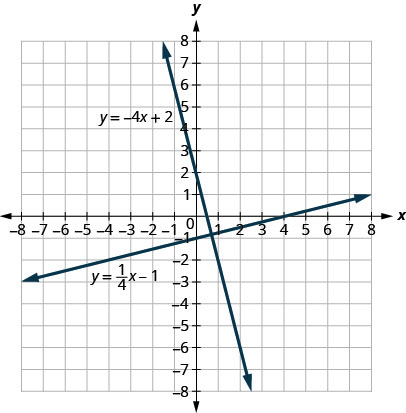
На цьому малюнку показаний графік двох перпендикулярних прямих на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Перший рядок проходить через точки (0, від'ємний 1) і (4, 0). Перший рядок позначено y дорівнює 1 ділиться на 4 x мінус 1. Другий рядок проходить через точки (0, 2) і (1, від'ємна 2). Другий рядок позначений y дорівнює від'ємним 4 х плюс 2. Лінії перпендикулярні, тобто вони утворюють прямий кут, де вони перетинаються. — Малюнок$\PageIndex{5}$

Ці лінії лежать в одній площині і перетинаються в прямих кутах. Ми називаємо ці лінії перпендикулярними.

Якщо подивитися на нахил першої лінії$m_1=\frac{1}{4}$, і нахил другої лінії, то можна побачити$m_2=−4$, що вони негативні взаємні один одному. Якщо ми їх помножимо, то їх продукт є$−1$.

\[\begin{array} {l} {m_1·m_2} \\ {14(−4)} \\ {−1} \\ \end{array} \nonumber\]

Це завжди вірно для перпендикулярних ліній і призводить нас до цього визначення.

ПЕРПЕНДИКУЛЯРНІ

Перпендикулярні лінії - це лінії в одній площині, які утворюють прямий кут.

Якщо$m_1$ і$m_2$ є ухилами двох перпендикулярних ліній, то:
- їх нахили негативні взаємні один одному,$m_1=−\frac{1}{m_2}$.
- твором їх укосів є$−1$,$m_1·m_2=−1$.
Вертикальна лінія і горизонтальна лінія завжди перпендикулярні один одному

Ми змогли подивитися на форму лінійних рівнянь похило-перехоплення і визначити, чи були лінії паралельними. Ми можемо зробити те ж саме для перпендикулярних ліній.

Ми знаходимо форму ухил-перехоплення рівняння, а потім бачимо, чи нахили протилежні взаємно. Якщо твір укосів є$−1$, лінії розташовують перпендикулярно.

Приклад$\PageIndex{34}$

Використовуйте ухили, щоб визначити, чи є лінії перпендикулярними:

ⓐ$y=−5x−4$ і$x−5y=5$ ⓑ$7x+2y=3$ і$2x+7y=5$

Відповідь: ⓐ
Перше рівняння знаходиться у формі нахилу - перехоплення. Розв'яжіть друге рівняння для.Визначте нахил кожної лініїY=−5x−4YM1=−5x−4=mx+B=−5Y−5Y−5Y−5Y=5−x+5−5=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15x+B=15 перше рівняння знаходиться у формі нахилу - перехоплення.Y = −5x−4Розв'яжіть друге рівняння для.x−5y=5−5y=−x+5−5y−5y=−x+5 −5y=15x−1Визначте нахил кожної лінії y=−5x−4y=mx+bm1=−5y=15x−1y=mx+bm2=15
Нахили є від'ємними взаємними один одному, тому лінії перпендикулярні. Перевіряємо множенням нахилів, оскільки −5 (15) =−1, −5 (15) =−1, він перевіряє.

ⓑ
Розв'яжіть рівняння для.Визначте нахил кожної лінії7x+2Y2Y2Y2Y=−7x+3=−7x+32=−72YM1=MX+B=−722x+7Y7Y7Y7Y=−2x+5=−2x+57=27x+57YM1=MX+B=27−Вирішити рівняння для.7х+2Y = 32y=−7х+32Y2=−7х+32Y = −72x+322x+7Y = −2x+57Y7=−2x+57Y=−2x+57Y = −27х+57 ідентифікувати нахил кожної лініїy=mx+bm1=−72y=mx+bm1=−27
Нахили взаємні один одному, але мають однаковий знак. Оскільки вони не негативні зворотні, лінії не перпендикулярні.

Приклад$\PageIndex{3}$

Використовуйте ухили, щоб визначити, чи є лінії перпендикулярними:

ⓐ$y=−3x+2$ і$x−3y=4$ ⓑ$5x+4y=1$ і$4x+5y=3$.

Відповідь: ⓐ перпендикулярно ⓑ не перпенди

Приклад$\PageIndex{3}$

Використовуйте ухили, щоб визначити, чи є лінії перпендикулярними:

ⓐ$y=2x−5$ і$x+2y=−6$ ⓑ$2x−9y=3$ і$9x−2y=1$.

Відповідь: ⓐ перпендикулярно ⓑ не перпенди

Ключові концепції

Нахил лінії
- Нахил лінії є$m=\frac{\text{rise}}{\text{run}}$.
- Підйом вимірює вертикальну зміну, а пробіг вимірює зміну горизонталі.
Як знайти нахил прямої з її графіка за допомогою$m=\frac{\text{rise}}{\text{run}}$.
1. Знайдіть дві точки на лінії, координати яких є цілими числами.
2. Починаючи з однієї точки, накидайте прямокутний трикутник, що йде від першої точки до другої точки.
3. Підрахуйте підйом і біг на ніжках трикутника.
4. Візьміть співвідношення підйому до бігу, щоб знайти нахил:$m=\frac{\text{rise}}{\text{run}}$.

Нахил лінії між двома точками.
- Нахил лінії між двома точками$(x_1,y_1)$ і$(x_2,y_2)$ становить:
  \[m=\frac{y_2−y_1}{x_2−x_1} \nonumber\].
Як побудувати графік лінії з заданою точкою і нахилом.
1. Побудуйте задану точку.
2. Використовуйте формулу нахилу$m=\frac{\text{rise}}{\text{run}}$, щоб визначити підйом і пробіг.
3. Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку.
4. З'єднайте точки лінією.
Форма перехоплення нахилу рівняння прямої
- Форма нахилу—перехоплення рівняння прямої з нахилом m та y -перехоплення,$(0,b)$ є$y=mx+b$
- $Таблиця має рядок заголовка, який читає «Методи до ліній графіка». Нижче це чотири стовпчики. Перший стовпець містить наступне: Точкова побудова графіків. Порожня таблиця з двома стовпцями і чотирма рядками. Перший рядок є рядком заголовка з заголовками «x» і «y». Знайдіть три точки. Намалюйте точки, переконайтеся, що вони шикуються, ними проведіть лінію. Другий стовпець містить: Ухил-Перехоплення. Y дорівнює m x плюс b Знайдіть нахил і y-перехоплення, а потім порахуйте нахил, щоб отримати другу точку. Третя колонка: Перехоплення. Таблиця з двома стовпцями і чотирма рядками. Перший рядок є рядком заголовка з заголовками «x» і «y». У першому рядку є 0 у стовпці x. У другому рядку є 0 у стовпці y. Решта пробілів пусті. Четверта колонка. Розпізнавати вертикальні і горизонтальні лінії. Рівняння має тільки одну змінну. X дорівнює вертикалі. Y дорівнює b по горизонталі.$
Паралельні лінії
- Паралельні лінії - це лінії в одній площині, які не перетинаються.
  Паралельні лінії мають однаковий нахил і різні y -перехоплення.
  Якщо$m_1$ і$m_2$ є нахилами двох паралельних ліній, то$m_1=m_2$.
  Паралельні вертикальні лінії мають різні x -перехоплення.
Перпендикулярні лінії
- Перпендикулярні лінії - це лінії в одній площині, які утворюють прямий кут.
- Якщо$m_1$ і$m_2$ є нахилами двох перпендикулярних ліній, то:
  їх нахили негативні взаємні один одному,$m_1=−\frac{1}{m_2}$.
  твором їх укосів є$−1$,$m_1·m_2=−1$.
- Вертикальна лінія і горизонтальна лінія завжди перпендикулярні один одному.

Глосарій

паралельні лінії: Паралельні лінії - це лінії в одній площині, які не перетинаються.

перпендикулярні лінії: Перпендикулярні лінії - це лінії в одній площині, які утворюють прямий кут.

Знайдіть дві точки на графіку, координати яких є цілими числами.	\((0,5)\)і\((3,3)\)
Починаючи з\((0,5)\), намалюйте прямокутний трикутник \((3,3)\), як показано на цьому графіку.	$.$
Підрахуйте rise— так як він йде вниз, це негативно.	Підйом є\(−2\).
Підрахуйте пробіг.	Пробіг дорівнює 3.
Скористайтеся формулою нахилу.	\(m=\frac{\text{rise}}{\text{run}}\)
Підставляємо значення підйому і бігу.	\(m=−23\)
Спростити.	\(m=−23\)
	Ухил лінії дорівнює\(−23\).
	Таким чином, y зменшується на 2 одиниці, оскільки x збільшується на 3 одиниці.

	\(y=mx+b\)
Рівняння знаходиться у формі нахилу-перехоплення.	\(y=−x+4\)
Визначте ухил і y -перехоплення.	\(m=−1\) y -перехоплення є\((0,4)\)
Ділянка y -перехоплення.	Див. Графік.
Визначте підйом над бігом.	\(m=−11\)
Відраховуйте підйом і біжіть, щоб відзначити другу точку.	підйом\(-1\), біг\(1\) $.$

Цілі навчання

Знайти нахил лінії

НАХИЛ ЛІНІЇ

ЗНАЙТИ НАХИЛ ЛІНІЇ З ЇЇ ГРАФІКА ЗА ДОПОМОГОЮ\(m=\frac{\text{rise}}{\text{run}}\)

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

НАХИЛ ГОРИЗОНТАЛЬНОЇ І ВЕРТИКАЛЬНОЇ ЛІНІЇ

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\)

КОРОТКИЙ ПОСІБНИК ПО УХИЛАХ ЛІНІЙ

НАХИЛ ЛІНІЇ МІЖ ДВОМА ТОЧКАМИ

Приклад\(\PageIndex{7}\)

Приклад\(\PageIndex{9}\)

Графік лінії з заданою точкою та нахилом

Приклад\(\PageIndex{10}\): How to graph a Line Given a Point and the Slope

Приклад\(\PageIndex{11}\)

Приклад\(\PageIndex{12}\)

ГРАФІК ЛІНІЇ ЗАДАНО ТОЧКУ І НАХИЛ.

Графік лінії з використанням її нахилу та перехоплення

ФОРМА ПЕРЕХОПЛЕННЯ НАХИЛУ РІВНЯННЯ ПРЯМОЇ

Приклад\(\PageIndex{13}\)

Приклад\(\PageIndex{14}\)

Приклад\(\PageIndex{15}\)

Приклад\(\PageIndex{16}\)

Приклад\(\PageIndex{17}\)

Приклад\(\PageIndex{18}\)

Виберіть найбільш зручний метод для побудови графіка лінії

СТРАТЕГІЯ ВИБОРУ НАЙБІЛЬШ ЗРУЧНОГО МЕТОДУ ГРАФУ ЛІНІЇ

Приклад\(\PageIndex{19}\)

Приклад\(\PageIndex{20}\)

Приклад\(\PageIndex{21}\)

Графік та інтерпретація застосувань перехоплення нахилу

Приклад\(\PageIndex{22}\)

Приклад\(\PageIndex{23}\)

Приклад\(\PageIndex{24}\)

Приклад\(\PageIndex{25}\)

Приклад\(\PageIndex{26}\)

Приклад\(\PageIndex{27}\)

Використання нахилів для визначення паралельних і перпендикулярних ліній

ПАРАЛЕЛЬНІ ЛІНІЇ

Приклад\(\PageIndex{28}\)

Приклад\(\PageIndex{29}\)

Приклад\(\PageIndex{30}\)

Приклад\(\PageIndex{31}\)

Приклад\(\PageIndex{32}\)

Приклад\(\PageIndex{33}\)

ПЕРПЕНДИКУЛЯРНІ

Приклад\(\PageIndex{34}\)

Приклад\(\PageIndex{3}\)

Приклад\(\PageIndex{3}\)

Ключові концепції

Глосарій