3.7E: Вправи

Last updated
Save as PDF

Page ID: 59469

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Використовуйте тест вертикальної лінії

У наступних вправах визначте, чи є кожен графік графіком функції.

1. ⓐ

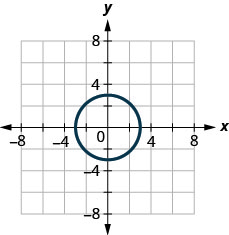
$Фігура має коло, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Коло проходить через точки (негативні 3, 0), (3, 0), (0, негативні 3) і (0, 3).$

ⓑ

$Фігура має параболу, що відкриває діаграму на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Парабола проходить через точки (негативні 2, 6), (1, 3), (0, 2), (1, 3) і (2, 6).$

Відповідь: ⓐ ні ⓑ так

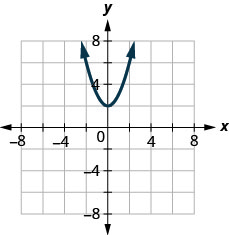
2. ⓐ

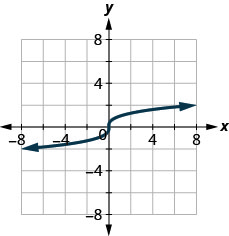
$Фігура має S-подібну вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. S-подібна крива лінія проходить через точки (негативні 1, 1), (0, 0) і (1, 1).$

ⓑ

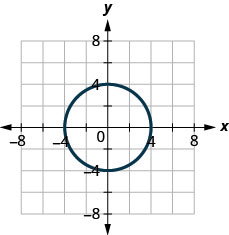
$Фігура має коло, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Коло проходить через точки (негативні 4, 0), (4, 0), (0, негативні 4) і (0, 4).$

3. ⓐ

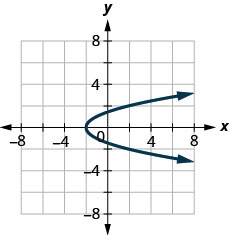
$Фігура має параболу, що відкривається праворуч, зображена на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Парабола проходить через точки (негативний 2, 0), (негативний 1, 1), (негативний 1, негативний 1), (негативний 2, 2) і (2, 2).$

ⓑ

$Фігура має функцію куба, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (від'ємний 1, негативний 1), (0, 0) і (1, 1).$

Відповідь: ⓐ ні ⓑ так

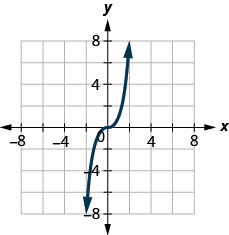
4. ⓐ

$Фігура має дві криві лінії, зображені на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія зліва проходить через точки (негативні 2, 0), (негативні 4, 5), і (негативні 4, негативні 5). Вигнута лінія справа проходить через точки (2, 0), (4, 5) і (4, негативні 5).$

ⓑ

$Фігура має бічну функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія згинається в точці (0, 2) і йде вправо. Лінія проходить через точки (1, 3), (2, 4), (1, 1) і (2, 0).$

Визначте графіки основних функцій

У наступних вправах ⓐ графік кожної функції ⓑ вказати свою область та діапазон. Запишіть домен і діапазон в інтервальному позначенні.

5. $f(x)=3x+4$

Відповідь

ⓐ

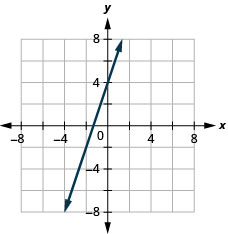
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Рядок проходить через точки (від'ємний 2, від'ємний 2), (негативний 1, 1), і (0, 4).$

ⓑ$ D:(-\inf ,\inf ),\space R:(-\inf ,\inf ) $

6. $f(x)=2x+5$

7. $f(x)=−x−2$

Відповідь

ⓐ

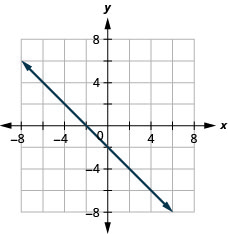
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Рядок проходить через точки (від'ємний 2, 0), (0, від'ємний 2), і (2, негативний 4).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

8. $f(x)=−4x−3$

9. $f(x)=−2x+2$

Відповідь

ⓐ

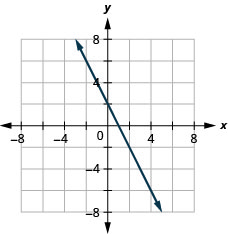
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Рядок проходить через точки (від'ємний 2, 2), (негативний 1, 0), і (0, негативний 2).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

10. $f(x)=−3x+3$

11. $f(x)=\frac{1}{2}x+1$

Відповідь

ⓐ

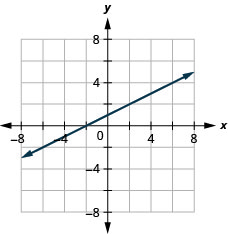
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (від'ємні 2, 0), (0, 1) і (2, 2).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

12. $f(x)=\frac{2}{3}x−2$

13. $f(x)=5$

Відповідь

ⓐ

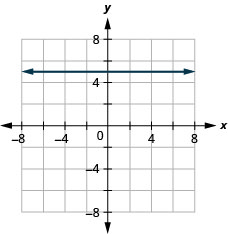
$Фігура має постійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (від'ємні 2, 5), (від'ємні 1, 5), і (0, 5).$

ⓑ$D:(-\inf ,\inf ), R:{5}$

14. $f(x)=2$

15. $f(x)=−3$

Відповідь

ⓐ

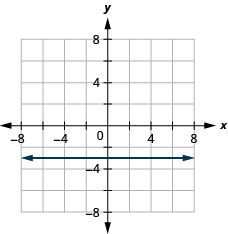
$Фігура має постійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Лінія проходить через точки (0, від'ємний 3), (1, негативний 3), і (2, негативний 3).$

ⓑ$D:(-\inf ,\inf ),\space R: {−3}$

16. $f(x)=−1$

17. $f(x)=2x$

Відповідь

ⓐ

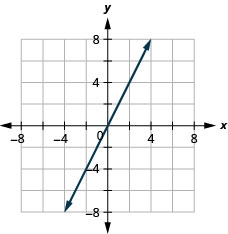
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, 0), (2, 4), і (негативні 2, негативні 4).$

ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

18. $f(x)=3x$

19. $f(x)=−2x$

Відповідь

ⓐ

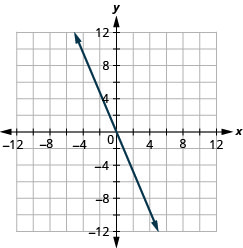
$Фігура має лінійну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (0, 0), (1, від'ємний 2), і (від'ємний 1, 2).$

ⓑ$D:(-\inf ,\inf ), R:(-\inf ,\inf )$

20. $f(x)=−3x$

21. $f(x)=3x^2$

Відповідь

ⓐ

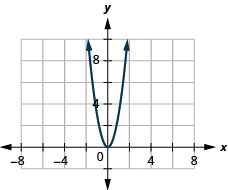
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 1, 3), (0, 0) і (1, 3). Найнижча точка на графіку - (0, 0).$

ⓑ$D:(-\inf ,\inf ),\space R:[0,\inf )$

22. $f(x)=2x^2$

23. $f(x)=−3x^2$

Відповідь

ⓐ

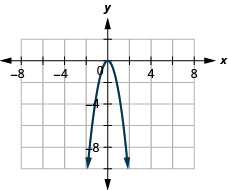
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 10 до 2. Парабола проходить через точки (негативний 1, негативний 3), (0, 0) і (1, негативний 3). Найвища точка на графіку - (0, 0).$

ⓑ$ D: (-\inf ,\inf ),\space R:(-\inf ,0]$

24. $f(x)=−2x^2$

25. $f(x)=12x^2$

Відповідь

ⓐ

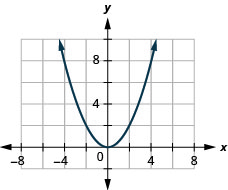
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 4, 8), (негативні 2, 2), (0, 0), (2, 2) і (4, 8). Найнижча точка на графіку - (0, 0).$

ⓑ$D: (-\inf ,\inf ),\space R:[-\inf ,0)$

26. $f(x)=\frac{1}{3}x^2$

27. $f(x)=x^2−1$

Відповідь

ⓐ

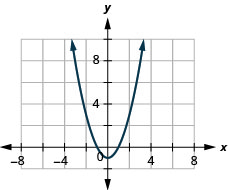
$Фігура має квадратну функцію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (негативні 2, 3), (негативні 1, 0), (0, негативні 1), (1, 0) і (2, 3). Найнижча точка на графіку - (0, від'ємна 1).$

ⓑ$D: (-\inf ,\inf ),\space R:[−1, \inf )$

28. $f(x)=x^2+1$

29. $f(x)=−2x^3$

Відповідь

ⓐ

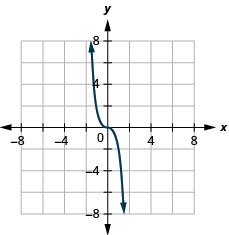
ⓑ$D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

30. $f(x)=2x^3$

31. $f(x)=x^3+2$

Відповідь

ⓐ

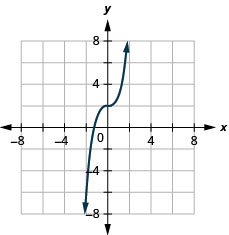
ⓑ$D:(-\inf ,\inf ), R:(-\inf ,\inf )$

32. $f(x)=x^3−2$

33. $f(x)=2\sqrt{x}$

Відповідь

ⓐ

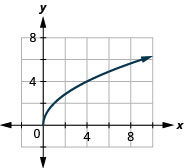
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь x працює від 0 до 10. Вісь Y працює від 0 до 10. Півлінія починається в точці (0, 0) і проходить через точки (1, 2) і (4, 4).$

ⓑ$D:[0,\inf ), R:[0,\inf )$

34. $f(x)=−2\sqrt{x}$

35. $f(x)=\sqrt{x-1}$

Відповідь

ⓐ

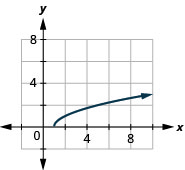
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь x працює від 0 до 10. Вісь Y працює від 0 до 10. Півлінія починається в точці (1, 0) і проходить через точки (2, 1) і (5, 2).$

ⓑ$D:[1,\inf ), R:[0,\inf )$

36. $f(x)=\sqrt{x+1}$

37. $f(x)=3|x|$

Відповідь

ⓐ

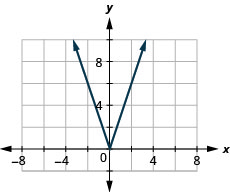
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Вершина знаходиться в точці (0, 0). Лінія проходить через точки (від'ємні 1, 3) і (1, 3).$

ⓑ$D:[ −1,−1, \inf ), R:[−\inf ,\inf )$

38. $f(x)=−2|x|$

39. $f(x)=|x|+1$

Відповідь

ⓐ

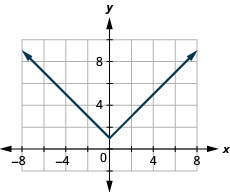
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Вершина знаходиться в точці (0, 1). Лінія проходить через точки (від'ємні 1, 2) і (1, 2).$

ⓑ$D:(-\inf ,\inf ), R:[1,\inf )$

40. $f(x)=|x|−1$

Читання інформації з графіка функції

У наступних вправах використовуйте графік функції, щоб знайти її область і діапазон. Запишіть домен і діапазон в інтервальному позначенні.

41.
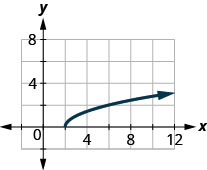
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь X проходить від негативних 2 до 8. Вісь Y проходить від негативних 2 до 8. Півлінія починається в точці (2, 0) і проходить через точки (3, 1) і (6, 2).$

Відповідь: $D: [2,\inf ),\space R: [0,\inf )$

42.
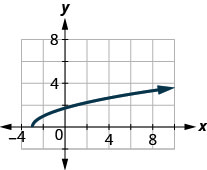
$Фігура має функцію квадратного кореня, розміщену на координатній площині x y. Вісь X проходить від негативних 2 до 8. Вісь Y проходить від негативних 2 до 10. Півлінія починається в точці (від'ємна 3, 0) і проходить через точки (негативні 2, 1) і (1, 2).$

43.
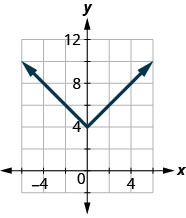
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y працює від 0 до 12. Вершина знаходиться в точці (0, 4). Лінія проходить через точки (від'ємні 2, 6) і (2, 6).$

Відповідь: $D: (-\inf ,\inf ),\space R: [4,\inf )$

44.
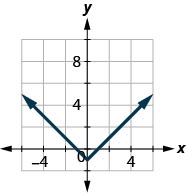
$Фігура має функцію абсолютного значення, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Вершина знаходиться в точці (0, від'ємна 1). Лінія проходить через точки (від'ємні 1, 0) і (1, 0).$

45.
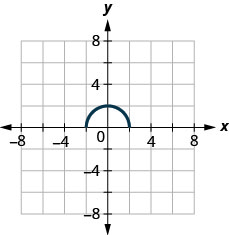
$Фігура має півколо, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Відрізок кривої лінії починається в точці (мінус 2, 0). Лінія проходить через точку (0, 2) і закінчується в точці (2, 0).$

Відповідь: $D: [−2,2],\space R: [0, 2]$

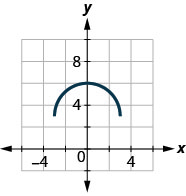
46.
$Фігура має півколо, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Вигнутий відрізок лінії починається в точці (негативний 3, 3). Лінія проходить через точку (0, 6) і закінчується в точці (3, 3).$

У наступних вправах використовуйте графік функції, щоб знайти зазначені значення.

47.
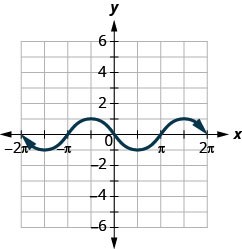
$Ця фігура має хвилясту вигнуту лінію, розміщену на координатній площині x y. Вісь x проходить від негативного 2 рази pi до 2 разів pi. Вісь Y проходить від негативних 6 до 6. Вигнутий відрізок лінії проходить через точки (негативний 2 рази пі, 0), (негативний 3 ділиться на 2 рази пі, негативний 1), (негативний пі, 0), (негативний 1 ділиться на 2 рази пі, 1), (0, 0), (1 ділиться на 2 рази пі, від'ємний 1), (пі, 0), (3 ділиться на 2 рази пі, 1) і (2 рази пі, 0). Точки (від'ємні 3, поділені на 2 рази пі, від'ємні 1) і (1 поділені на 2 рази пі, від'ємні 1) є найнижчими точками на графіку. Точки (від'ємний 1 поділений на 2 рази пі, 1) і (3 поділений на 2 рази пі, 1) є найвищими точками на графіку. Візерунок поширюється нескінченно вліво і вправо.$

ⓐ Знайти:$f(0)$.
ⓑ Знайти:$f(12\pi)$.
ⓒ Знайти:$f(−32\pi)$.
ⓓ Знайдіть значення для$x$ коли$f(x)=0$.
ⓔ Знайдіть$x$ -перехоплення.
ⓕ Знайдіть$y$ -перехоплення.
ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

Відповідь: ⓐ$f(0)=0$ ⓑ$(\pi/2)=−1$
ⓒ$f(−3\pi/2)=−1$ ⓓ$f(x)=0$ за$x=−2\pi,-\pi,0,\pi,2\pi$
ⓔ$(−2\pi,0),(−\pi,0),$$(0,0),(\pi,0),(2\pi,0)$$(f)(0,0)$
ⓖ$[−2\pi,2\pi]$ ⓗ$[−1,1]$

48.
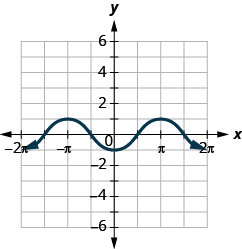
$Int_Alg_Section03_07_Exercise_48.jpeg$

ⓐ Знайти:$f(0)$.
ⓑ Знайти:$f(\pi)$.
ⓒ Знайти:$f(−\pi)$.
ⓓ Знайдіть значення для$x$ коли$f(x)=0$.
ⓔ Знайдіть$x$ -перехоплення.
ⓕ Знайдіть$y$ -перехоплення.
ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓗ Знайдіть асортимент. Запишіть його в інтервальне позначення

49.
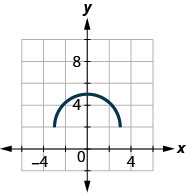
$Фігура має верхню половину кола, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Вигнутий відрізок лінії починається в точці (негативний 3, 2). Лінія проходить через точку (0, 5) і закінчується в точці (3, 2). Точка (0, 5) - найвища точка на графіку. Точки (від'ємні 3, 2) і (3, 2) є найнижчими точками на графіку.$

ⓐ Знайти:$f(0)$.
ⓑ Знайти:$f(−3)$.
ⓒ Знайти:$f(3)$.
ⓓ Знайдіть значення для$x$ коли$f(x)=0$.
ⓔ Знайдіть$x$ -перехоплення.
ⓕ Знайдіть$y$ -перехоплення.
ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

50.
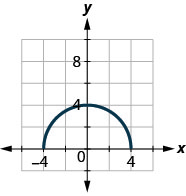
$Фігура має верхню половину кола, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Відрізок кривої лінії починається в точці (мінус 4, 0). Лінія проходить через точку (0, 4) і закінчується в точці (4, 0). Точка (0, 4) - найвища точка на графіку. Точки (від'ємні 4, 0) і (4, 0) є найнижчими точками на графіку.$

ⓐ Знайти:$f(0)$.
ⓑ Знайдіть значення для$x$ коли$f(x)=0$.
ⓒ Знайдіть$x$ -перехоплення.
ⓓ Знайдіть$y$ -перехоплення.
ⓔ Знайти домен. Запишіть його в інтервальних позначеннях.
ⓕ Знайдіть асортимент. Запишіть його в інтервальне позначення

Письмові вправи

51. Поясніть своїми словами, як знайти домен з графіка.

52. Поясніть своїми словами, як знайти діапазон з графіка.

53. Поясніть своїми словами, як використовувати тест вертикальної лінії.

54. Намалюйте ескіз функцій квадрата та куба. Які подібності та відмінності в графіках?

Самостійна перевірка

ⓐ Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

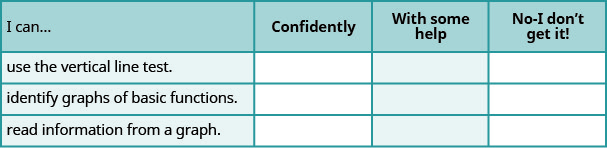
$На малюнку представлена таблиця з чотирма рядками і чотирма стовпцями. Перший рядок є рядком заголовка, і він позначає кожен стовпець. Перший заголовок стовпця - «Я можу...», другий - «впевнено», третій - «з деякою допомогою», «без мінуса я не отримую!». Під першою колонкою знаходяться фрази «використовувати тест вертикальної лінії», «визначити графіки основних функцій» і «читати інформацію з графіка». Під другим, третім, четвертим стовпцями є порожні пробіли, де учень може перевірити, якого рівня майстерності вони досягли.$

ⓑ Ознайомившись з цим контрольним списком, що ви робите, щоб стати впевненими у всіх цілях?