Skip to main content
LibreTexts - Ukrayinska

3.7: Графіки функцій

  1. Last updated
  2. Save as PDF
  • Page ID
    59458

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Використовуйте тест вертикальної лінії
    • Визначте графіки основних функцій
    • Зчитування інформації з графіка функції

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Оцініть: ⓐ\(2^3\) ⓑ\(3^2\).
      Якщо ви пропустили цю проблему, перегляньте [посилання].
    2. Оцініть: ⓐ\(|7|\) ⓑ\(|−3|\).
      Якщо ви пропустили цю проблему, перегляньте [посилання].
    3. Оцініть: ⓐ\(\sqrt{4}\) ⓑ\(\sqrt{16}\).
      Якщо ви пропустили цю проблему, перегляньте [посилання].

    Використовуйте тест вертикальної лінії

    В останньому розділі ми дізналися, як визначити, чи є відношення функцією. Відносини, які ми розглядали, були виражені у вигляді набору впорядкованих пар, відображення або рівняння. Зараз ми розглянемо, як визначити, чи є графік функції.

    Впорядкована пара\((x,y)\) - це рішення лінійного рівняння, якщо рівняння є істинним твердженням, коли x - і y -значення впорядкованої пари підставляються в рівняння.

    Графік лінійного рівняння - це пряма лінія, де кожна точка на лінії є розв'язком рівняння, і кожне рішення цього рівняння є точкою на цій лінії.

    На малюнку ми бачимо, що на графіку\(y=2x−3\) рівняння для кожного x -значення існує лише одне y -значення, як показано в супровідній таблиці.

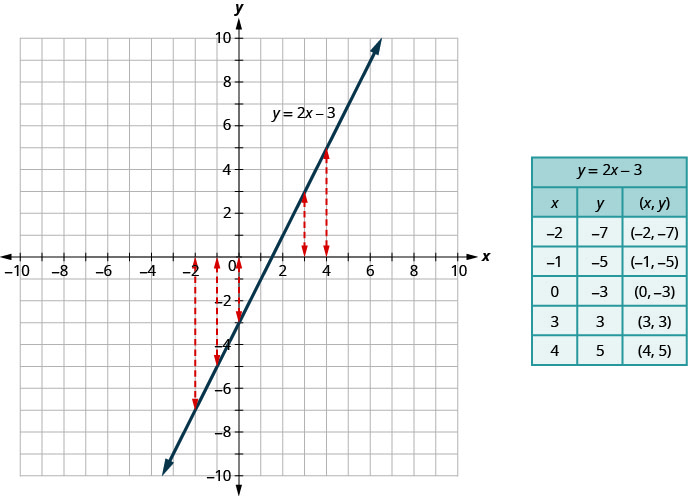
    літак. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 3), (1, від'ємний 1), і (2, 1). Рядок маркується y рівно2 х мінус 3. Існує кілька вертикальних стрілок, які пов'язують значення на осі x з точками на лінії. Перша стрілка відносить х рівнонегативного 2 на осі х до точки (негативна 2, негативна 7) на прямій. Друга стрілка відносить х рівнонегативний 1 на осі х до точки (негативна 1, негативна 5) на прямій. Наступна стрілка пов'язує x рівно0 на осі x до точки (0, від'ємна 3) на прямій. Наступна стрілка пов'язує x рівні3 на осі x до точки (3, 3) на лінії. Остання стрілка пов'язує x рівно4 на осі x до точки (4, 5) на лінії. Таблиця має 7 рядків і 3 стовпців. Перший рядок - це рядок заголовка з міткою y рівно2 х мінус 3. Другий рядок — рядок заголовка із заголовками x, y та (x, y). Третій ряд має координати від'ємні 2, від'ємні 7 і (від'ємні 2, від'ємні 7). Четвертий ряд має координати від'ємні 1, від'ємні 5 і (від'ємні 1, негативні 5). П'ятий рядок має координати 0, від'ємний 3 і (0, від'ємний 3). Шостий ряд має координати 3, 3 і (3, 3). Сьомий ряд має координати 4, 5 і (4, 5).
    Малюнок\(\PageIndex{1}\)

    Відношення - це функція, якщо кожен елемент домену має рівно одне значення в діапазоні. Таким чином, відношення, визначене рівнянням\(y=2x−3\), є функцією.

    Якщо ми подивимося на графік, кожна вертикальна пунктирна лінія перетинає лише лінію в одній точці. Це має сенс, як у функції, для кожного x -значення існує лише одне y -значення.

    Якщо вертикальна лінія двічі потрапить на графік, значення x буде зіставлено на два y -значення, і тому графік не буде представляти функцію.

    Це призводить нас до тесту вертикальної лінії. Набір точок прямокутної системи координат - це графік функції, якщо кожна вертикальна лінія перетинає графік не більше ніж в одній точці. Якщо будь-яка вертикальна лінія перетинає графік у більш ніж одній точці, графік не представляє функції.

    ТЕСТ ВЕРТИКАЛЬНОЇ ЛІНІЇ

    Набір точок прямокутної системи координат - це графік функції, якщо кожна вертикальна лінія перетинає графік не більше ніж в одній точці.

    Якщо будь-яка вертикальна лінія перетинає графік у більш ніж одній точці, графік не представляє функції.

    Приклад\(\PageIndex{1}\)

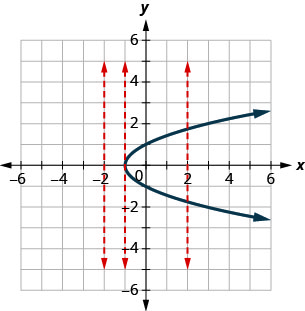
    Визначте, чи є кожен графік графіком функції.

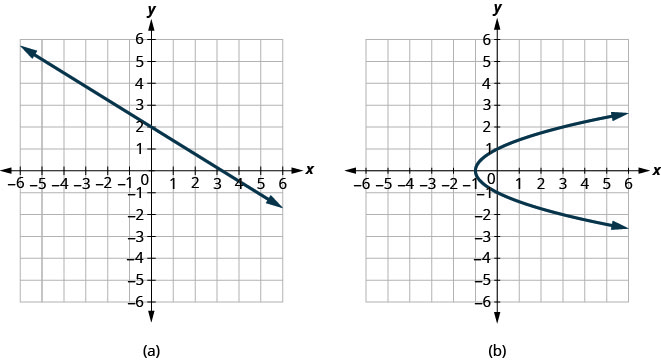
    Цифра має два графіки. У графі a є пряма лінія, зображена на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, 2), (3, 0) і (6, негативні 2). У графі b є парабола, що відкривається праворуч, зображена на координатній площині x y. Осі x та y проходять від негативних 6 до 6. Парабола проходить через точки (негативний 1, 0), (0, 1), (0, негативний 1), (3, 2) і (3, негативний 2).

    Відповідь

    ⓐ Оскільки будь-яка вертикальна лінія перетинає графік максимум в одній точці, графік є графіком функції.

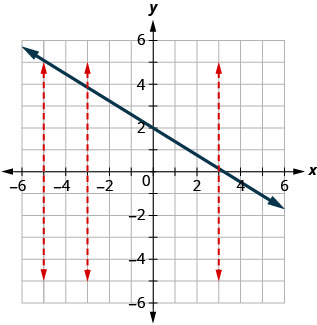
    Фігура має пряму лінію, розміщену на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, 2), (3, 0) і (6, негативні 2). Три пунктирні вертикальні прямі лінії малюються при x рівновід'ємному 5, х дорівнює негативному 3, а x дорівнює 3. Кожна лінія перетинає похилу лінію рівно в одній точці.

    ⓑ Одна з вертикальних ліній, показаних на графіку, перетинає її в двох точках. Цей графік не представляє функцію.

    Фігура має параболу, що відкривається праворуч на графіку на координатній площині x y. Осі x та y проходять від негативних 6 до 6. Парабола проходить через точки (негативний 1, 0), (0, 1), (0, негативний 1), (3, 2) і (3, негативний 2). Три пунктирні вертикальні прямі лінії малюються при x рівновід'ємному 2, х дорівнює негативному 1, а x дорівнює 2. Вертикальна лінія x — від'ємна 2 не перетинає параболу. Вертикальна лінія x рівнонегативному 1 перетинає параболу рівно в одній точці. Вертикальна лінія x дорівнює 3 перетинає параболу в двох окремих точках.

    Приклад\(\PageIndex{2}\)

    Визначте, чи є кожен графік графіком функції.

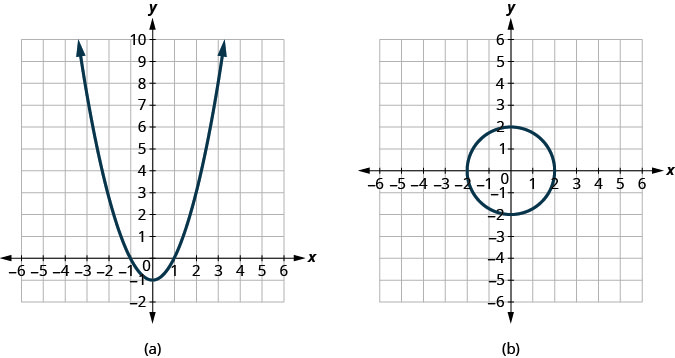
    Цифра має два графіки. У графі a є парабола, що відкривається на графіку на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. Парабола проходить через точки (0, негативний 1), (негативний 1, 0), (1, 0), (негативний 2, 3) і (2, 3). У графі b є коло, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Коло проходить через точки (негативні 2, 0), (2, 0), (0, негативні 2), і (0, 2).

    Відповідь

    ⓐ так ⓑ ні

    Приклад\(\PageIndex{3}\)

    Визначте, чи є кожен графік графіком функції.

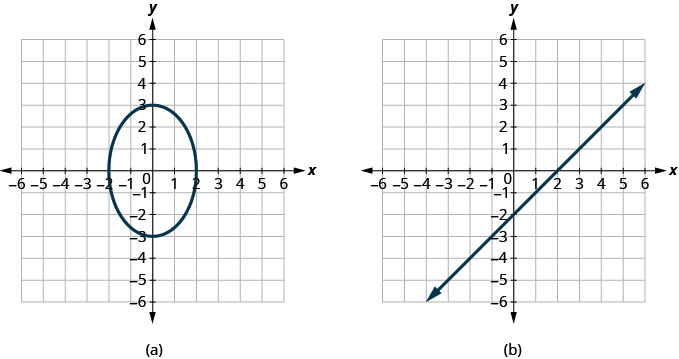
    Цифра має два графіки. У графі a є еліпс, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Еліпс проходить через точки (0, від'ємний 3), (негативний 2, 0), (2, 0) і (0, 3). У графі b є пряма лінія, зображена на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (0, від'ємний 2), (2, 0) і (4, 2).

    Відповідь

    ⓐ ні ⓑ так

    Визначте графіки основних функцій

    Ми використовували рівняння\(y=2x−3\) та його графік під час розробки тесту вертикальної лінії. Ми сказали, що відношення, визначене рівнянням\(y=2x−3\), є функцією.

    Ми можемо написати це як у функції позначення як\(f(x)=2x−3\). Це все ще означає те ж саме. Графік функції - це графік всіх впорядкованих пар\((x,y)\) де\(y=f(x)\). Таким чином, ми можемо написати впорядковані пари як\((x,f(x))\). Виглядає по-іншому, але графік буде однаковим.

    Порівняйте графік\(y=2x−3\) раніше показаного на малюнку з графіком,\(f(x)=2x−3\) показаним на малюнку. Нічого не змінилося, крім позначення.

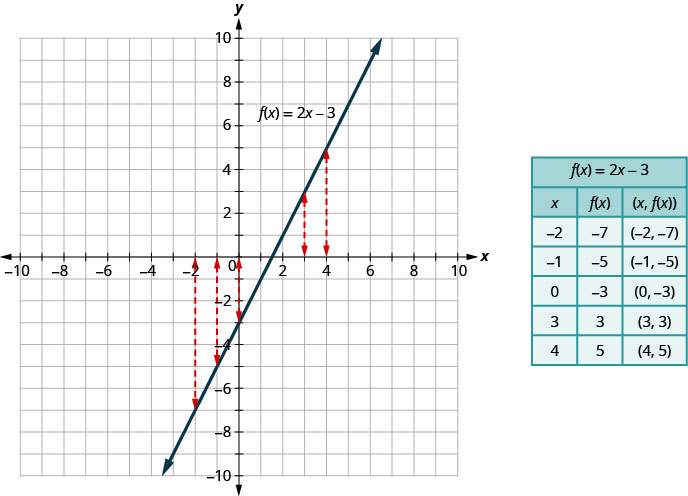
    Ця цифра має графік поруч з таблицею. Графік має пряму лінію на координатній площині x y. Осі x та y проходять від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 3), (1, від'ємний 1), і (2, 1). Рядок позначається f з x рівно2 х мінус 3. Існує кілька вертикальних стрілок, які пов'язують значення на осі x з точками на лінії. Перша стрілка відносить х рівнонегативного 2 на осі х до точки (негативна 2, негативна 7) на прямій. Друга стрілка відносить х рівнонегативний 1 на осі х до точки (негативна 1, негативна 5) на прямій. Наступна стрілка пов'язує x рівно0 на осі x до точки (0, від'ємна 3) на прямій. Наступна стрілка пов'язує x рівні3 на осі x до точки (3, 3) на лінії. Остання стрілка пов'язує x рівно4 на осі x до точки (4, 5) на лінії. Таблиця має 7 рядків і 3 стовпців. Перший рядок - це рядок заголовка з міткою f x дорівнює 2 x мінус 3. Другий рядок є рядком заголовка з заголовками x, f або x, і (x, f з x). Третій ряд має координати від'ємні 2, від'ємні 7 і (від'ємні 2, від'ємні 7). Четвертий ряд має координати від'ємні 1, від'ємні 5 і (від'ємні 1, негативні 5). П'ятий рядок має координати 0, від'ємний 3 і (0, від'ємний 3). Шостий ряд має координати 3, 3 і (3, 3). Сьомий ряд має координати 4, 5 і (4, 5).
    Малюнок\(\PageIndex{2}\)
    ГРАФІК ФУНКЦІЇ

    Графік функції - це графік усіх її впорядкованих пар (x, y) (x, y) або з використанням позначення функції, (x, f (x)) (x, f (x)) де y=f (x) .y=f (x).

    \[\begin{array} {ll} {f} &{\text{name of function}} \\ {x} &{\text{x-coordinate of the ordered pair}} \\ {f(x)} &{\text{y-coordinate of the ordered pair}} \\ \nonumber \end{array}\]

    Коли ми рухаємось вперед у нашому дослідженні, корисно ознайомитися з графіками декількох основних функцій та вміти їх ідентифікувати.

    Завдяки нашій більш ранній роботі ми знайомі з графіками лінійних рівнянь. Процес, який ми використовували, щоб вирішити, чи\(y=2x−3\) є функція, буде застосовуватися до всіх лінійних рівнянь. Всі невертикальні лінійні рівняння є функціями. Вертикальні лінії не є функціями, оскільки значення x має нескінченно багато y -значень.

    Ми писали лінійні рівняння в декількох формах, але нам тут буде корисним використовувати форму перехоплення нахилу лінійного рівняння. Форма ухил-перехоплення лінійного рівняння є\(y=mx+b\). У позначенні функції ця лінійна функція стає\(f(x)=mx+b\) там, де m - нахил прямої, а b - y -перехоплення.

    Домен - це набір всіх дійсних чисел, а діапазон - це також набір всіх дійсних чисел.

    ЛІНІЙНА ФУНКЦІЯ

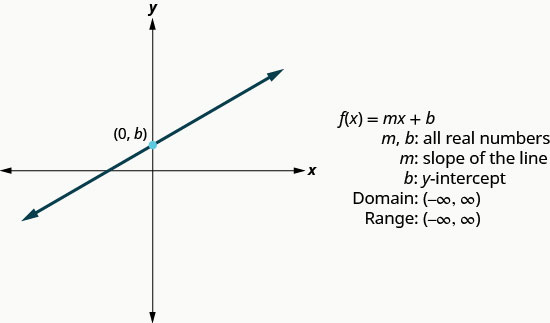
    Ця фігура має графік прямої на координатній площині x y. Лінія йде через точку (0, б). Поруч з графіком розташовані такі: «f x рівних x плюс b», «m, b: всі дійсні числа», «m: нахил прямої», «b: y-перехоплення», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: (негативна нескінченність, нескінченність)».

    Ми будемо використовувати методи графіки, які ми використовували раніше, щоб графікувати основні функції.

    Приклад\(\PageIndex{4}\)

    Графік:\(f(x)=−2x−4\).

    Відповідь
      \(f(x)=−2x−4\)
    Ми визнаємо це як лінійну функцію.  
    Знайдіть нахил і y -перехоплення. \(m=−2\)
    \(b=−4\)
    Графік за допомогою перехоплення нахилу. .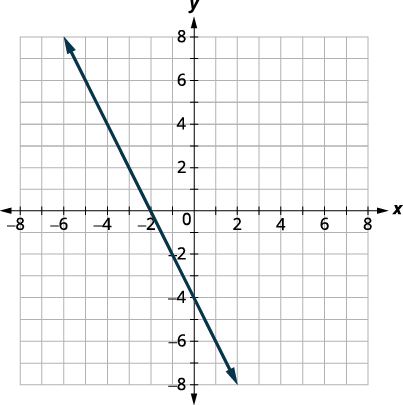
    Приклад\(\PageIndex{5}\)

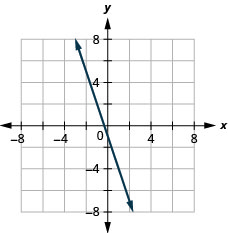
    Графік:\(f(x)=−3x−1\)

    Відповідь

    Фігура має графік лінійної функції на координатній площині x y. Осі x та y проходять від негативних 6 до 6. Лінія проходить через точки (1, від'ємний 4), (0, від'ємний 1), і (від'ємний 1, 2).

    Приклад\(\PageIndex{6}\)

    Графік:\(f(x)=−4x−5\)

    Відповідь

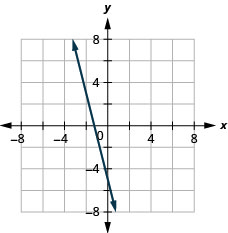
    Фігура має графік лінійної функції на координатній площині x y. Осі x та y проходять від негативних 6 до 6. Рядок проходить через точки (від'ємний 2, 3), (0, негативний 5), і (негативний 1, негативний 1).

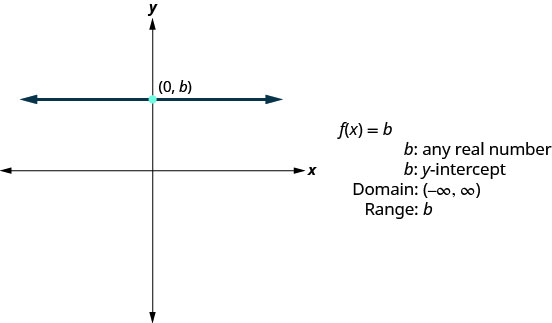
    Наступна функція, графік якої ми розглянемо, називається постійною функцією і її рівняння має вигляд\(f(x)=b\), де b - будь-яке дійсне число. Якщо ми замінимо на\(f(x)\) y, ми отримаємо\(y=b\). Ми визнаємо це як горизонтальну лінію, у якої y -перехоплення дорівнює b. Графік функції\(f(x)=b\), також є горизонтальною лінією, у якої y -перехоплення дорівнює b.

    Зверніть увагу, що для будь-якого дійсного числа ми ставимо в функцію, значення функції буде b. Це говорить нам, що діапазон має лише одне значення, b.

    ПОСТІЙНА ФУНКЦІЯ

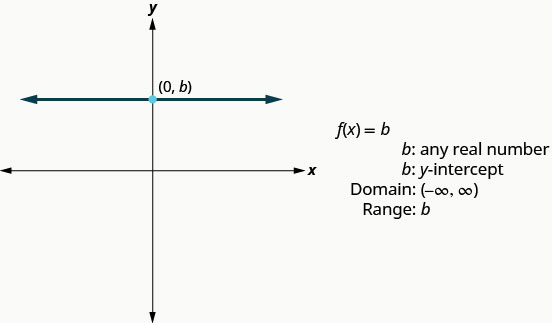
    Ця фігура має графік прямої горизонтальної лінії на координатній площині x y. Лінія йде через точку (0, б). Поруч з графіком розташовані такі: «f з x рівнівb», «b: будь-яке дійсне число», «b: y-перехоплення», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: b».

    Приклад\(\PageIndex{7}\)

    Графік:\(f(x)=4\).

    Відповідь
      \(f(x)=4\)
    Ми визнаємо це як постійну функцію.  
    Графік буде горизонтальною лінією наскрізь\((0,4)\). .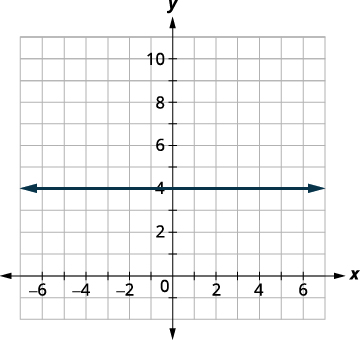
    Приклад\(\PageIndex{8}\)

    Графік:\(f(x)=−2\).

    Відповідь

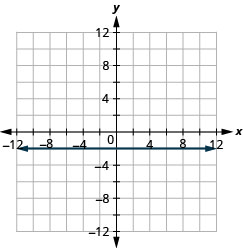
    Фігура має графік постійної функції на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Рядок проходить через точки (0, від'ємний 2), (1, від'ємний 2), і (2, негативний 2).

    Приклад\(\PageIndex{9}\)

    Графік:\(f(x)=3\).

    Відповідь

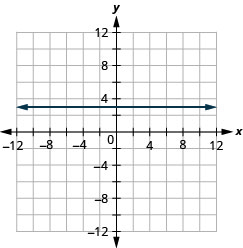
    Фігура має графік постійної функції на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (0, 3), (1, 3) і (2, 3).

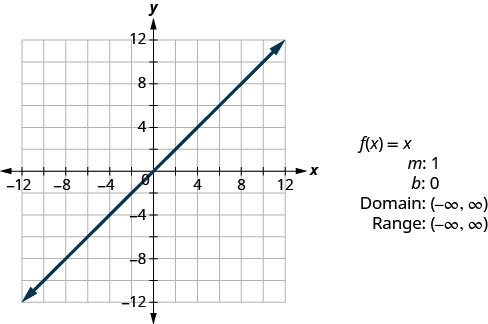
    Функція ідентичності,\(f(x)=x\) є окремим випадком лінійної функції. Якщо ми запишемо його у формі лінійної функції\(f(x)=1x+0\), ми бачимо нахил 1, а y -перехоплення дорівнює 0.

    ФУНКЦІЯ ІДЕНТИЧНОСТІ

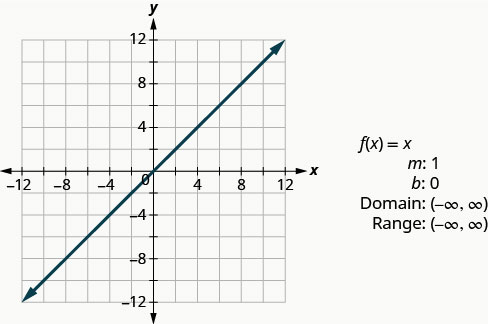
    Ця фігура має графік прямої на координатній площині x y. Лінія проходить через точки (0, 0), (1, 1) і (2, 2). Поруч з графіком розташовані такі: «f x рівноx», «m: 1», «b: 0», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: (негативна нескінченність, нескінченність)».

    Наступна функція, яку ми розглянемо, - це не лінійна функція. Так що графік не буде лінією. Єдиний метод, який ми повинні графувати цю функцію, - це точкове побудова. Оскільки це незнайома функція, ми переконуємося вибрати кілька позитивних і негативних значень, а також 0 для наших значень x.

    Графік:\(f(x)=x^2\).

    Відповідь

    Вибираємо х -значення. Ми підставляємо їх, а потім створюємо діаграму, як показано на малюнку.

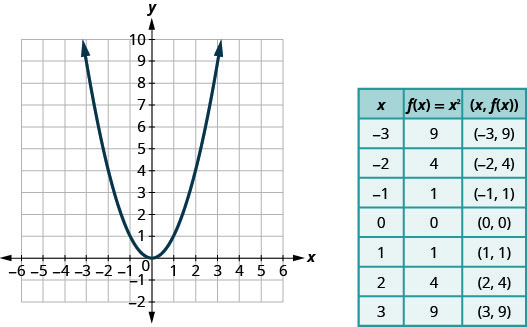
    Ця цифра має графік поруч з таблицею. На графіку є парабола, що відкривається на графіку на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 2 до 6. Парабола проходить через точки (негативні 3, 9), (негативні 2, 4), (негативні 1, 1), (0, 0), (1, 1), (2, 4) і (3, 9). Таблиця має 8 рядків і 3 стовпці. Перший рядок є рядком заголовка з заголовками x, f x дорівнює x в квадраті, і (x, f або x). Другий ряд має від'ємні координати 3, 9 і (негативні 3, 9). Третій ряд має від'ємні координати 2, 4 і (від'ємні 2, 4). Четвертий ряд має від'ємні координати 1, 1 і (від'ємні 1, 1). П'ятий рядок має координати 0, 0 та (0, 0). Шостий ряд має координати 1, 1 і (1, 1). Сьомий ряд має координати 2, 4 і (2, 4). Сьомий ряд має координати 3, 9 і (3, 9).

    Приклад\(\PageIndex{11}\)

    Графік:\(f(x)=x^2\).

    Відповідь

    Ця цифра має графік поруч з таблицею. На графіку є парабола, що відкривається на графіку на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Парабола проходить через точки (негативні 2, 4), (негативні 1, 1), (0, 0), (1, 1) і (2, 4).

    Приклад\(\PageIndex{12}\)

    \(f(x)=−x^2\)

    Відповідь

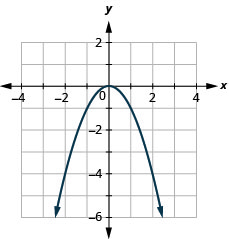
    Ця цифра має графік поруч з таблицею. На графіку є парабола, що відкривається на графіку на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 4 до 8. Парабола проходить через точки (негативний 2, негативний 4), (негативний 1, негативний 1), (0, 0), (1, негативний 1) і (2, негативний 4).

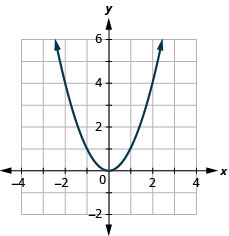
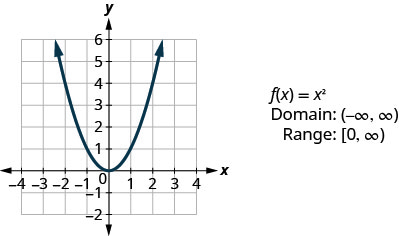
    Дивлячись на результат у прикладі, ми можемо узагальнити особливості квадратної функції. Ми називаємо цей графік параболою. Коли ми розглядаємо домен, зверніть увагу, що будь-яке дійсне число може бути використано як значення x. Домен - це всі дійсні числа.

    Діапазон - це не всі дійсні числа. Зверніть увагу, що графік складається з значень y ніколи не опускаються нижче нуля. Це має сенс, оскільки квадрат будь-якого числа не може бути від'ємним. Отже, діапазон квадратної функції - це все невід'ємні дійсні числа.

    КВАДРАТНА ФУНКЦІЯ

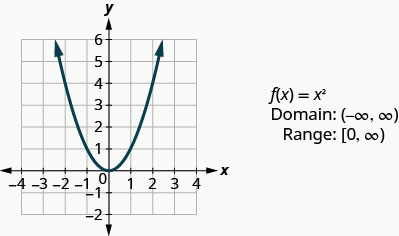
    Ця фігура має графік параболи, що відкривається, графічний на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 2 до 6. Парабола проходить через точки (негативні 2, 4), (негативні 1, 1), (0, 0), (1, 1) і (2, 4). Поруч з графіком розташовані такі: «f x дорівнює x у квадраті», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: [0, нескінченність)».

    Наступна функція, яку ми розглянемо, також не є лінійною функцією, тому графік не буде лінією. Знову ми будемо використовувати точкові побудови, і переконайтеся, що вибрати кілька позитивних і негативних значень, а також 0 для наших х -values.

    Графік:\(f(x)=x^3\).

    Відповідь

    Вибираємо х -значення. Ми підставляємо їх, а потім створюємо діаграму.

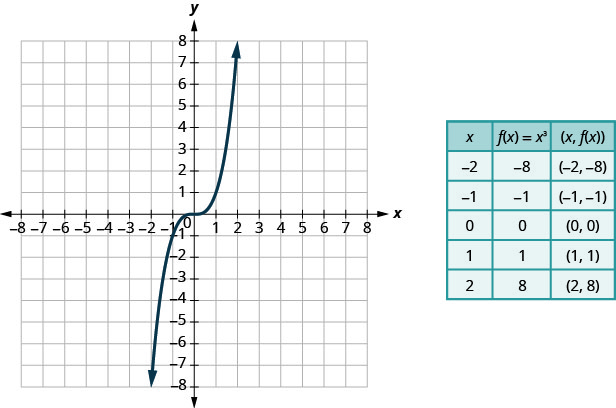
    Ця фігура має вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 4 до 4. Вигнута лінія проходить через точки (від'ємний 2, негативний 8), (негативний 1, негативний 1), (0, 0), (1, 1) і (2, 8). Поруч з графіком знаходиться таблиця. Таблиця має 6 рядків і 3 стовпців. Перший рядок є рядком заголовка з заголовками x, f x дорівнює x в кубі, і (x, f або x). Другий рядок має координати від'ємні 2, від'ємні 8 і (від'ємні 2, від'ємні 8). Третій рядок має координати від'ємні 1, від'ємні 1 і (від'ємні 1, від'ємні 1). Четвертий рядок має координати 0, 0 та (0, 0). П'ятий ряд має координати 1, 1 і (1, 1). Шостий ряд має координати 2, 8 і (2, 8).

    Приклад\(\PageIndex{14}\)

    Графік:\(f(x)=x^3\).

    Відповідь

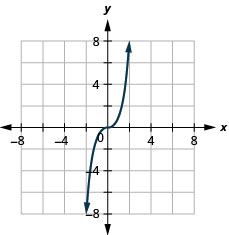
    Ця фігура має вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (від'ємний 2, негативний 8), (негативний 1, негативний 1), (0, 0), (1, 1) і (2, 8).

    Приклад\(\PageIndex{15}\)

    Графік:\(f(x)=−x^3\).

    Відповідь

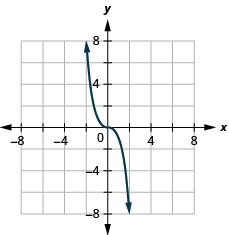
    Ця фігура має вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнута лінія проходить через точки (негативний 2, 8), (негативний 1, 1), (0, 0), (1, негативний 1), і (2, негативний 8).

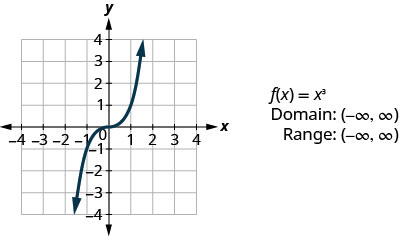
    Дивлячись на результат у прикладі, ми можемо узагальнити особливості функції куба. Коли ми розглядаємо домен, зверніть увагу, що будь-яке дійсне число може бути використано як значення x. Домен - це всі дійсні числа.

    Діапазон - це всі дійсні числа. Це має сенс, оскільки куб будь-якого ненульового числа може бути позитивним або негативним. Отже, діапазон функції куба - це всі дійсні числа.

    ФУНКЦІЯ КУБА

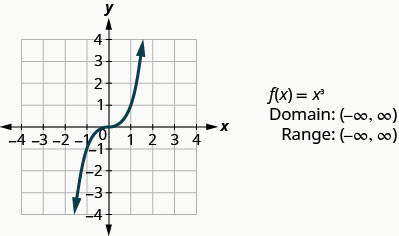
    Ця фігура має вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 4 до 4. Вигнута лінія проходить через точки (від'ємний 2, негативний 8), (негативний 1, негативний 1), (0, 0), (1, 1) і (2, 8).). Поруч з графіком розташовані такі: «f x рівноx в кубі», «Домен: (негативна нескінченність, нескінченність)» і «Діапазон: (негативна нескінченність, нескінченність)».

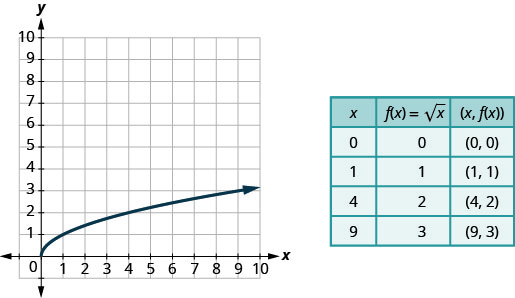
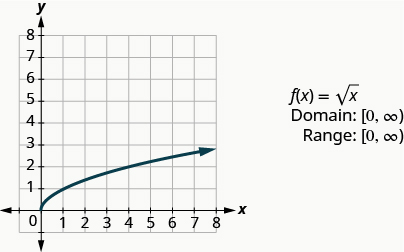
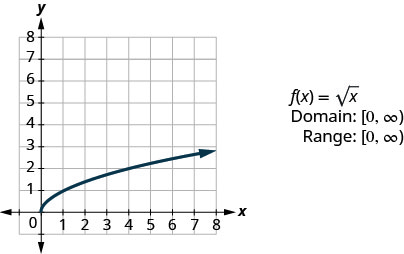
    Наступна функція, яку ми розглянемо, не квадрат або куб вхідних значень, а скоріше приймає квадратний корінь цих значень.

    Давайте проведемо графік функції,\(f(x)=\sqrt{x}\) а потім підсумуємо особливості функції. Пам'ятайте, що ми можемо взяти тільки квадратний корінь невід'ємних дійсних чисел, тому наш домен буде невід'ємними дійсними числами.

    Приклад\(\PageIndex{16}\)

    \(f(x)=\sqrt{x}\)

    Відповідь

    Вибираємо х -значення. Оскільки ми будемо брати квадратний корінь, ми вибираємо числа, які є ідеальними квадратами, щоб полегшити нашу роботу. Ми підставляємо їх, а потім створюємо діаграму.

    Ця фігура має вигнуту півлінію, розміщену на координатній площині x y. Вісь x працює від 0 до 8. Вісь Y працює від 0 до 8. Вигнута напівлінія починається в точці (0, 0), а потім йде вгору і вправо. Вигнута напівлінія проходить через точки (1, 1) і (4, 2). Поруч з графіком знаходиться таблиця. Таблиця має 5 рядків і 3 стовпці. Перший рядок є рядком заголовка з заголовками x, f x дорівнює квадратному кореню x, і (x, f або x). Другий рядок має координати 0, 0 та (0, 0). Третій ряд має координати 1, 1 і (1, 1). Четвертий ряд має координати 4, 2 і (4, 2). П'ятий ряд має координати 9, 3 і (9, 3).

    Приклад\(\PageIndex{17}\)

    Графік:\(f(x)=x\).

    Відповідь

    Ця фігура має вигнуту півлінію, розміщену на координатній площині x y. Вісь x працює від 0 до 10. Вісь Y працює від 0 до 10. Вигнута напівлінія починається в точці (0, 0), а потім йде вгору і вправо. Вигнута половина лінії проходить через точки (1, 1), (4, 2), і (9, 3).

    Приклад\(\PageIndex{18}\)

    Графік:\(f(x)=−\sqrt{x}\).

    Відповідь

    Ця фігура має вигнуту півлінію, розміщену на координатній площині x y. Вісь x працює від 0 до 10. Вісь Y працює від від'ємного 10 до 0. Вигнута напівлінія починається в точці (0, 0), а потім йде вниз і вправо. Вигнута половина лінії проходить через точки (1, негативний 1), (4, негативний 2), і (9, негативний 3).

    ФУНКЦІЯ КВАДРАТНОГО КОРЕНЯ

    Ця фігура має вигнуту півлінію, розміщену на координатній площині x y. Вісь x працює від 0 до 8. Вісь Y працює від 0 до 8. Вигнута напівлінія починається в точці (0, 0), а потім йде вгору і вправо. Вигнута напівлінія проходить через точки (1, 1) і (4, 2). Поруч з графіком розташовані такі: «f з x рівноквадратний корінь x», «Домен: [0, нескінченність)» і «Діапазон: [0, нескінченність)».

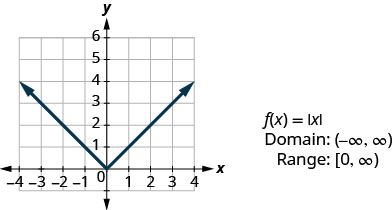
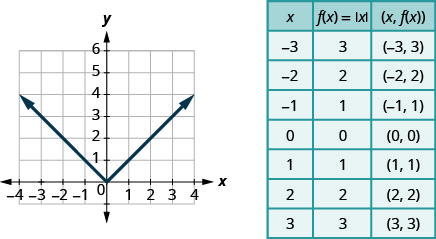
    Наша остання основна функція - це функція абсолютного значення,\(f(x)=|x|\). Майте на увазі, що абсолютне значення числа - це його відстань від нуля. Оскільки ми ніколи не вимірюємо відстань як від'ємне число, ми ніколи не отримаємо негативне число в діапазоні.

    Графік:\(f(x)=|x|\).

    Відповідь

    Вибираємо х -значення. Ми підставляємо їх, а потім створюємо діаграму.

    Ця фігура має v-подібну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативного 1 до 6. V-подібна лінія проходить через точки (негативні 3, 3), (від'ємні 2, 2), (негативні 1, 1), (0, 0), (1, 1), (2, 2) і (3, 3). Поруч з графіком знаходиться таблиця. Таблиця має 8 рядків і 3 стовпці. Перший рядок є рядком заголовка з заголовками x, f x дорівнює абсолютному значенню x, а (x, f x). Другий ряд має від'ємні координати 3, 3 і (від'ємні 3, 3). Третій ряд має від'ємні координати 2, 2 і (від'ємні 2, 2). Четвертий ряд має від'ємні координати 1, 1 і (від'ємні 1, 1). П'ятий рядок має координати 0, 0 та (0, 0). Шостий ряд має координати 1, 1 і (1, 1). Сьомий ряд має координати 2, 2 і (2, 2). Восьмий ряд має координати 3, 3 і (3, 3).

    Приклад\(\PageIndex{20}\)

    Графік:\(f(x)=|x|\).

    Відповідь

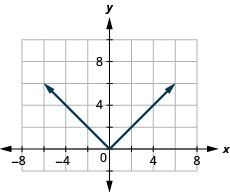
    Ця фігура має v-подібну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 2 до 10. V-подібна лінія проходить через точки (негативні 3, 3), (від'ємні 2, 2), (негативні 1, 1), (0, 0), (1, 1), (2, 2) і (3, 3).

    Приклад\(\PageIndex{21}\)

    Графік:\(f(x)=−|x|\).

    Відповідь

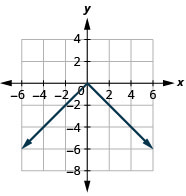
    Ця фігура має v-подібну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 8 до 4. V-подібна лінія проходить через точки (негативний 3, негативний 3), (негативний 2, негативний 2), (негативний 1, негативний 1), (0, 0), (1, негативний 1), (2, негативний 2) і (3, негативний 3).

    ФУНКЦІЯ АБСОЛЮТНОГО ЗНАЧЕННЯ

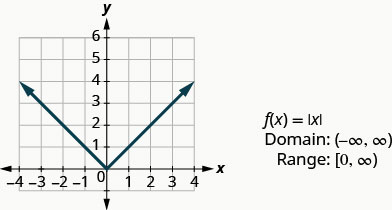
    Ця фігура має v-подібну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативного 1 до 6. V-подібна лінія проходить через точки (негативні 3, 3), (від'ємні 2, 2), (негативні 1, 1), (0, 0), (1, 1), (2, 2) і (3, 3). Точка (0, 0), де лінія змінює нахил, називається вершиною. Поруч з графіком розташовані наступні: «f з x рівняєабсолютному значенню x», «Домен: (негативна нескінченність, нескінченність)» і «Діапазон: [0, нескінченність)».

    Читання інформації з графіка функції

    У науках та бізнесі дані часто збираються, а потім графуються. Графік аналізується, інформація отримується з графіка і потім часто з даних робляться прогнози.

    Ми почнемо з читання домену та діапазону функції з її графіка.

    Пам'ятайте, що домен - це набір всіх x -значень у впорядкованих парах у функції. Щоб знайти домен, ми дивимося на графік і знаходимо всі значення x, які мають відповідне значення на графіку. Дотримуйтесь значення x вгору або вниз по вертикалі. Якщо ви потрапили на графік функції, то x знаходиться в домені.

    Пам'ятайте, що діапазон - це набір всіх y -значень у впорядкованих парах у функції. Щоб знайти діапазон, ми дивимося на графік і знаходимо всі значення y, які мають відповідне значення на графіку. Дотримуйтесь значення y вліво або вправо по горизонталі. Якщо ви потрапили на графік функції, то y знаходиться в діапазоні.

    Приклад\(\PageIndex{22}\)

    Використовуйте графік функції, щоб знайти її область і діапазон. Запишіть домен і діапазон в інтервальному позначенні.

    Ця фігура має вигнутий відрізок лінії, зображений на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 4 до 4. Вигнутий відрізок лінії проходить через точки (негативний 3, негативний 1), (1,5, 3) і (3, 1). На горизонтальній осі відзначається інтервал [негативний 3, 3]. На вертикальній осі відзначається інтервал [негативний 1, 3].

    Відповідь

    Щоб знайти домен, ми дивимося на графік і знаходимо всі значення x, які відповідають точці на графіку. Домен виділений червоним кольором на графіку. Домен є\([−3,3]\).

    Щоб знайти діапазон, ми дивимося на графік і знаходимо всі значення y, які відповідають точці на графіку. Діапазон виділений синім кольором на графіку. Асортимент є\([−1,3]\).

    Приклад\(\PageIndex{23}\)

    Використовуйте графік функції, щоб знайти її область і діапазон. Запишіть домен і діапазон в інтервальному позначенні.

    Ця фігура має вигнутий відрізок лінії, зображений на координатній площині x y. Вісь X проходить від негативних 6 до 6. Вісь Y проходить від негативних 6 до 6. Вигнутий відрізок лінії проходить через точки (негативний 5, негативний 4), (0, негативний 3), і (1, 2). На горизонтальній осі відзначається інтервал [мінус 5, 1]. На вертикальній осі відзначається інтервал [мінус 4, 2].

    Відповідь

    Домен є\([−5,1]\). Асортимент є\([−4,2]\).

    Приклад\(\PageIndex{24}\)

    Використовуйте графік функції, щоб знайти її область і діапазон. Запишіть домен і діапазон в інтервальному позначенні.

    Ця фігура має вигнутий відрізок лінії, зображений на координатній площині x y. Вісь X проходить від негативних 4 до 5. Вісь Y проходить від негативних 6 до 4. Вигнутий відрізок лінії проходить через точки (негативні 2, 1), (0, 3) і (4, негативні 5). На горизонтальній осі відзначається інтервал [мінус 2, 4]. На вертикальній осі відзначається інтервал [мінус 5, 3].

    Відповідь

    Домен є\([−2,4]\). Асортимент є\([−5,3]\).

    Тепер ми збираємося читати інформацію з графіка, яку ви можете побачити в майбутніх класах математики.

    Приклад\(\PageIndex{25}\)

    Використовуйте графік функції, щоб знайти зазначені значення.

    Ця фігура має хвилясту вигнуту лінію, розміщену на координатній площині x y. Вісь x проходить від негативного 2 рази pi до 2 разів pi. Вісь Y проходить від негативних 4 до 4. Вигнутий відрізок лінії проходить через точки (негативний 2 рази пі, 0), (негативний 3 ділиться на 2 рази пі, 1), (негативний пі, 0), (негативний 1 ділиться на 2 рази пі, негативний 1), (0, 0), (1 ділиться на 2 рази пі, 1), (пі, 0), (3 ділиться на 2 рази пі, 0), і (2 рази пі, 0). Точки (від'ємні 3, поділені на 2 рази пі, 1) і (1 поділена на 2 рази пі, 1) є найвищими точками на графіку. Точки (від'ємний 1 поділений на 2 рази пі, від'ємний 1) і (3 поділений на 2 рази пі, від'ємний 1) є найнижчими точками на графіку. Візерунок поширюється нескінченно вліво і вправо.

    ⓐ Знайти:\(f(0)\).
    ⓑ Знайти:\(f(32\pi)\).
    ⓒ Знайти:\(f(−12\pi)\).
    ⓓ Знайдіть значення для x, коли\(f(x)=0\).
    ⓔ Знайдіть x -перехоплення.
    ⓕ Знайдіть y -перехоплення.
    ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
    ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

    Відповідь

    ⓐ Коли\(x=0\) функція перетинає вісь y на 0. Отже,\(f(0)=0\).
    ⓑ Коли\(x=32\pi\), y -значення функції є\(−1\). Отже,\(f(32\pi)=−1\).
    ⓒ Коли\(x=−12\pi\), y -значення функції є\(−1\). Отже,\(f(−12\pi)=−1\).
    ⓓ Функція дорівнює 0 в точках,\((−2\pi,0), (−\pi,0), (0,0),(\pi,0),(2\pi,0)\). Значення x, коли\(f(x)=0\) є\(−2\pi,−\pi,0,\pi,2\pi\).
    ⓔ X -перехоплення відбуваються, коли\(y=0\). Таким чином, x -перехоплення відбуваються, коли\(f(x)=0\). X -перехоплює є\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\).
    ⓕ Y -перехоплення відбуваються, коли x = 0.x = 0. Таким чином, у -перехоплення відбуваються на\(f(0)\). Y -перехоплення є\((0,0)\).
    ⓖ Ця функція має значення, коли x від\(−2\pi\) до\(2\pi\). Тому домен в інтервальному позначенні є\([−2\pi,2\pi]\).
    ⓗ Значення цієї функції, або y -значення переходять від\(−1\) до 1. Тому діапазон, в інтервальних позначеннях, є\([−1,1]\).

    Приклад\(\PageIndex{26}\)

    Використовуйте графік функції, щоб знайти зазначені значення.

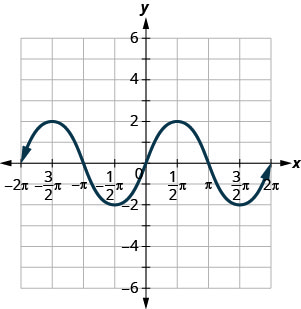
    Ця фігура має хвилясту вигнуту лінію, розміщену на координатній площині x y. Вісь x проходить від негативного 2 рази pi до 2 разів pi. Вісь Y проходить від негативних 6 до 6. Вигнутий відрізок лінії проходить через точки (негативний 2 рази пі, 0), (негативний 3 ділиться на 2 рази пі, 2), (негативний пі, 0), (негативний 1 ділиться на 2 рази пі, від'ємний 2), (0, 0), (1 поділений на 2 рази пі, 2), (пі, 0), (3 ділиться на 2 рази пі, 0), і (2 рази пі, 0). Точки (від'ємні 3, поділені на 2 рази пі, 2) і (1 поділена на 2 рази пі, 2) є найвищими точками на графіку. Точки (від'ємний 1 поділений на 2 рази пі, від'ємний 2) і (3 поділений на 2 рази пі, від'ємний 2) є найнижчими точками на графіку. Лінія тягнеться нескінченно вліво і вправо.

    ⓐ Знайти: f (0) .f (0).
    ⓑ Знайти: f (12\ пі) .f (12\ пі).
    ⓒ Знайти: f (−32\ pi) .f (−32\ pi).
    ⓓ Знайдіть значення для x, коли f (x) = 0.f (x) =0.
    ⓔ Знайдіть x -перехоплення.
    ⓕ Знайдіть y -перехоплення.
    ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
    ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

    Відповідь

    ⓐ\(f(0)=0\) ⓑ\(f=(\pi2)=2\) ⓒ\(f=(−3\pi2)=2\) ⓓ\(f(x)=0\) за\(x=−2\pi,−\pi,0,\pi,2\pi\) ⓔ\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\) ⓕ (0,0) (0,0) ⓖ\([−2\pi,2\pi]\) ⓗ\([−2,2]\)

    Приклад\(\PageIndex{27}\)

    Використовуйте графік функції, щоб знайти зазначені значення.

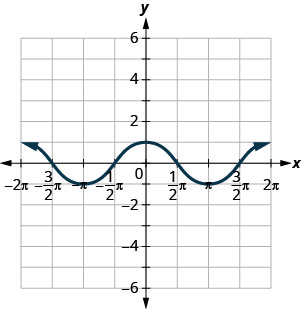
    Ця фігура має хвилясту вигнуту лінію, розміщену на координатній площині x y. Вісь x проходить від негативного 2 рази pi до 2 разів pi. Вісь Y проходить від негативних 6 до 6. Вигнутий відрізок лінії проходить через точки (негативний 2 рази пі, 1), (негативний 3 ділиться на 2 рази пі, 0), (негативний пі, від'ємний 1), (негативний 1 ділиться на 2 рази пі, 0), (0, 1), (1 ділиться на 2 рази пі, 0), (пі, від'ємний 1), (3 ділиться на 2 рази пі, 0) і (2 рази пі, 1). Точки (від'ємні 2 рази pi, 1), (0, 1) і (2 рази pi, 1) є найвищими точками на графіку. Точки (від'ємний пі, від'ємний 1) і (пі, від'ємний 1) є найнижчими точками на графіку. Візерунок поширюється нескінченно вліво і вправо.

    ⓐ Знайти:\(f(0)\).
    ⓑ Знайти:\(f(\pi)\).
    ⓒ Знайти:\(f(−\pi)\).
    ⓓ Знайдіть значення для x, коли\(f(x)=0\).
    ⓔ Знайдіть x -перехоплення.
    ⓕ Знайдіть y -перехоплення.
    ⓖ Знайти домен. Запишіть його в інтервальних позначеннях.
    ⓗ Знайдіть асортимент. Запишіть його в інтервальних позначеннях.

    Відповідь

    ⓐ\(f(0)=1\) ⓑ\(f(\pi)=−1\) ⓒ\(f(−\pi)=−1\) ⓓ\(f(x)=0\) за\(x=−3\pi2,−\pi2,\pi2,3\pi2\) ⓔ\((−2pi,0),(−pi,0),(0,0),(pi,0),(2pi,0)\) ⓕ\((0,1)\) ⓖ\([−2pi,2pi]\) ⓗ\([−1,1]\)

    Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з графіками функцій.

    Ключові концепції

    • Тест вертикальної лінії
      • Набір точок прямокутної системи координат - це графік функції, якщо кожна вертикальна лінія перетинає графік не більше ніж в одній точці.
      • Якщо будь-яка вертикальна лінія перетинає графік у більш ніж одній точці, графік не представляє функції.
    • Графік функції
      • Графік функції - це графік усіх її впорядкованих пар (x, y) (x, y) або з використанням позначення функції, (x, f (x)) (x, f (x)) де y=f (x) .y=f (x).

        fxf (x) назва функції-координата впорядкованої пара-координати впорядкованої pairfname функціїxx-координата впорядкованої пари (x) y-координати впорядкованої пари

    • Лінійна функція
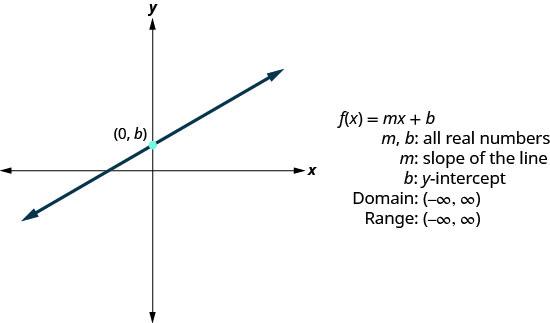
      Ця фігура має графік прямої на координатній площині x y. Лінія йде через точку (0, б). Поруч з графіком розташовані такі: «f x рівних x плюс b», «m, b: всі дійсні числа», «m: нахил прямої», «b: y-перехоплення», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: (негативна нескінченність, нескінченність)».
    • Постійна функція
      Ця фігура має графік прямої горизонтальної лінії на координатній площині x y. Лінія йде через точку (0, б). Поруч з графіком розташовані такі: «f з x рівнівb», «b: будь-яке дійсне число», «b: y-перехоплення», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: b».
    • Функція ідентичності
      Ця фігура має графік прямої на координатній площині x y. Лінія проходить через точки (0, 0), (1, 1) і (2, 2). Поруч з графіком розташовані такі: «f x рівноx», «m: 1», «b: 0», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: (негативна нескінченність, нескінченність)».
    • Квадратна функція
      Ця фігура має графік параболи, що відкривається, графічний на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 2 до 6. Парабола проходить через точки (негативні 2, 4), (негативні 1, 1), (0, 0), (1, 1) і (2, 4). Поруч з графіком розташовані такі: «f x дорівнює x у квадраті», «Домен: (негативна нескінченність, нескінченність)» та «Діапазон: [0, нескінченність)».
    • Функція куба
      Ця фігура має вигнуту лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативних 4 до 4. Вигнута лінія проходить через точки (від'ємний 2, негативний 8), (негативний 1, негативний 1), (0, 0), (1, 1) і (2, 8).). Поруч з графіком розташовані такі: «f x рівноx в кубі», «Домен: (негативна нескінченність, нескінченність)» і «Діапазон: (негативна нескінченність, нескінченність)».
    • Функція квадратного кореня
      Ця фігура має вигнуту півлінію, розміщену на координатній площині x y. Вісь x працює від 0 до 8. Вісь Y працює від 0 до 8. Вигнута напівлінія починається в точці (0, 0), а потім йде вгору і вправо. Вигнута напівлінія проходить через точки (1, 1) і (4, 2). Поруч з графіком розташовані такі: «f з x рівноквадратний корінь x», «Домен: [0, нескінченність)» і «Діапазон: [0, нескінченність)».
    • Функція абсолютного значення
      Ця фігура має v-подібну лінію, розміщену на координатній площині x y. Вісь X проходить від негативних 4 до 4. Вісь Y проходить від негативного 1 до 6. V-подібна лінія проходить через точки (негативні 3, 3), (від'ємні 2, 2), (негативні 1, 1), (0, 0), (1, 1), (2, 2) і (3, 3). Точка (0, 0), де лінія змінює нахил, називається вершиною. Поруч з графіком розташовані наступні: «f з x рівняєабсолютному значенню x», «Домен: (негативна нескінченність, нескінченність)» і «Діапазон: [0, нескінченність)».