Skip to main content
LibreTexts - Ukrayinska

3.3E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59441

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Знайти нахил лінії

    У наступних вправах знайдіть нахил кожної показаної лінії.

    1.
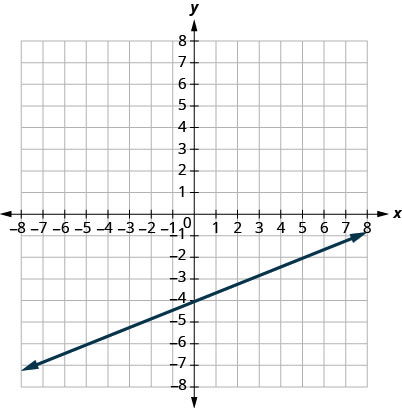
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 4) і (5, від'ємний 2).

    Відповідь

    \(m=\frac{2}{5}\)

    2.
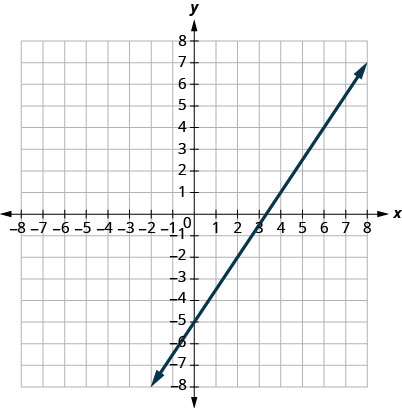
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 5) і (2, від'ємний 2).

    3.
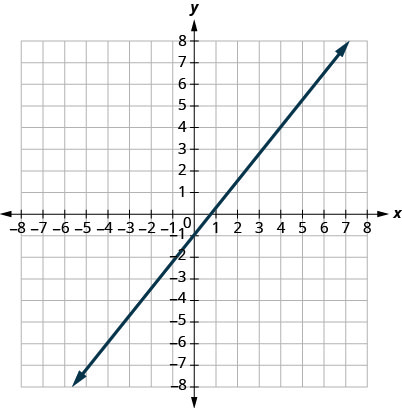
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 1) і (4, 4).

    Відповідь

    \(m=\frac{5}{4}\)

    4.
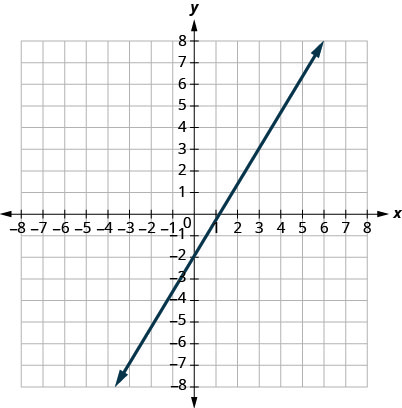
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 2) і (3, 3).

    5.
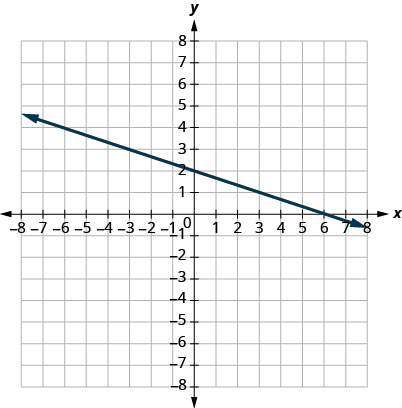
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, 2) і (3, 1).

    Відповідь

    \(m = -\frac{1}{3}\)

    6.
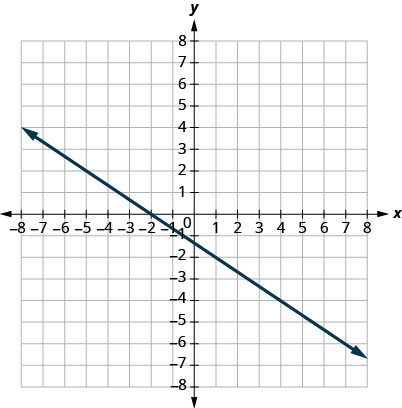
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, від'ємний 1) і (3, негативний 3).

    7.
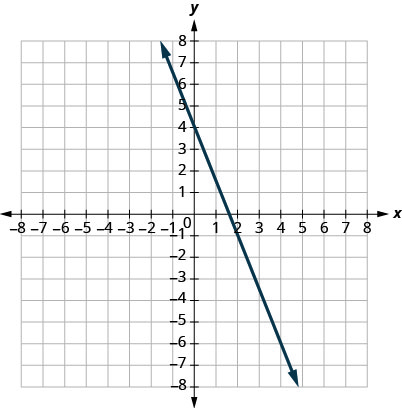
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, 4) і (2, негативні 1).

    Відповідь

    \(m = -\frac{5}{2}\)

    8.
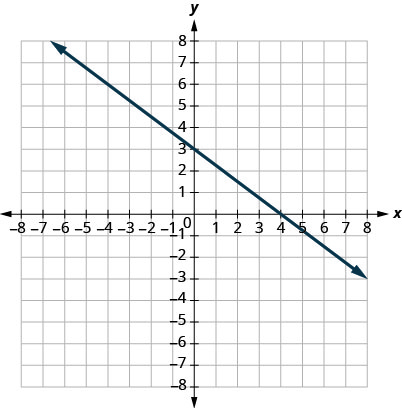
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 8 до 8. Вісь Y проходить від негативних 8 до 8. Лінія проходить через точки (0, 2) і (4, негативні 1).

    У наступних вправах знайдіть нахил кожної лінії.

    9. \(y=3\)

    Відповідь

    \(m = 0\)

    10. \(y=−2\)

    11. \(x=−5\)

    Відповідь

    невизначений

    12. \(x=4\)

    У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

    13. \((2,5),\;(4,0)\)

    Відповідь

    \(m = -\frac{5}{2}\)

    14. \((3,6),\;(8,0)\)

    15. \((−3,3),\;(4,−5)\)

    Відповідь

    \(m = -\frac{8}{7}\)

    16. \((−2,4),\;(3,−1)\)

    17. \((−1,−2),\;(2,5)\)

    Відповідь

    \(m = \frac{7}{3}\)

    18. \((−2,−1),\;(6,5)\)

    19. \((4,−5),\;(1,−2)\)

    Відповідь

    \(m = -1\)

    20. \((3,−6),\;(2,−2)\)

    Графік лінії з заданою точкою та нахилом

    У наступних вправах графік кожної лінії з заданою точкою і нахилом.

    21. \((2,5)\);\(m=−\frac{1}{3}\)

    Відповідь

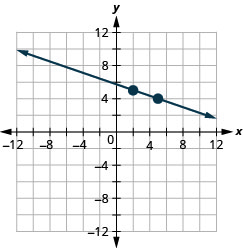
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (2, 5) і (5, 4).

    22. \((1,4)\);\(m=−\frac{1}{2}\)

    23. \((−1,−4)\);\(m=\frac{4}{3}\)

    Відповідь

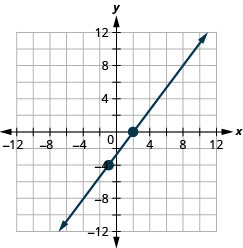
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (від'ємний 1, від'ємний 4) і (2, 0).

    24. \((−3,−5)\);\(m=\frac{3}{2}\)

    25. \(y\)-перехоплення:\((0, 3)\);\(m=−\frac{2}{5}\)

    Відповідь

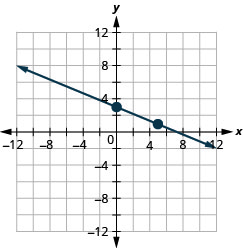
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія проходить через точки (0, 3) і (5, 1).

    26. \(x\)-перехоплення:\((−2,0)\);\(m=\frac{3}{4}\)

    27. \((−4,2)\);\(m=4\)

    Відповідь

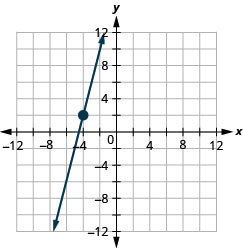
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 12 до 12. Вісь Y проходить від негативних 12 до 12. Лінія йде через точки (негативні 4, 2) і (негативні 3, 6).

    28. \((1,5)\);\(m=−3\)

    Графік лінії, використовуючи її нахил і перехоплення

    У наступних вправах визначте нахил і y -перехоплення кожної лінії.

    29. \(y=−7x+3\)

    Відповідь

    \(m=−7\);\((0,3)\)

    30. \(y=4x−10\)

    31. \(3x+y=5\)

    Відповідь

    \(m=−3\);\((0,5)\)

    32. \(4x+y=8\)

    33. \(6x+4y=12\)

    Відповідь

    \(m=−\frac{3}{2}\);\((0,3)\)

    34. \(8x+3y=12\)

    35. \(5x−2y=6\)

    Відповідь

    \(m=\frac{5}{2}\);\((0,−3)\)

    36. \(7x−3y=9\)

    У наступних вправах графік лінії кожного рівняння, використовуючи його нахил і y -перехоплення.

    37. \(y=3x−1\)

    Відповідь

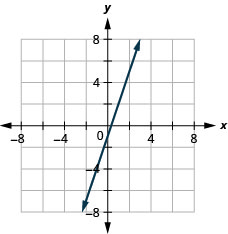
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 1) і (1, 2).

    38. \(y=2x−3\)

    39. \(y=−x+3\)

    Відповідь

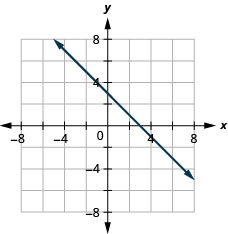
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, 3) і (1, 2).

    40. \(y=−x−4\)

    41. \(y=−\frac{2}{5}x−3\)

    Відповідь

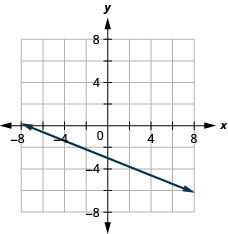
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 3) і (5, негативний 5).

    42. \(y=−\frac{3}{5}x+2\)

    43. \(3x−2y=4\)

    Відповідь

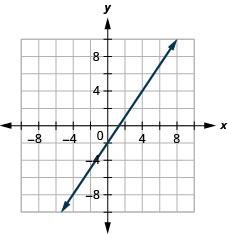
    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь X проходить від негативних 10 до 10. Вісь Y проходить від негативних 10 до 10. Лінія проходить через точки (0, від'ємний 2) і (2, 1).

    44. \(3x−4y=8\)

    Виберіть найбільш зручний метод для побудови графіка лінії

    У наступних вправах визначте найбільш зручний метод графіка кожного рядка.

    45. \(x=2\)

    Відповідь

    вертикальна лінія

    46. \(y=5\)

    47. \(y=−3x+4\)

    Відповідь

    ухил-перехоплення

    48. \(x−y=5\)

    49. \(x−y=1\)

    Відповідь

    перехоплює

    50. \(y=\frac{2}{3}x−1\)

    51. \(3x−2y=−12\)

    Відповідь

    перехоплює

    52. \(2x−5y=−10\)

    Графік та інтерпретація застосувань перехоплення нахилу

    53. Рівняння\(P=31+1.75w\) моделює співвідношення між сумою щомісячної оплати рахунку за воду Туєта\(P\), у доларах, та кількістю одиниць води\(w\), використовуваної.

    a. знайти оплату Tuyet за місяць, коли використовуються\(0\) одиниці води.

    b. знайти оплату Tuyet за місяць, коли використовуються\(12\) одиниці води.

    c Інтерпретувати нахил і\(P\) -перехоплення рівняння.

    d Графік рівняння.

    Відповідь

    а.\($31\)
    б.\($52\)
    c. ухил\(1.75\), означає, що оплата\(P\), збільшується на те,\($1.75\) коли кількість одиниць використовуваної води\(w\), збільшується на\(1\). \(P\)-Перехоплення означає, що коли кількість одиниць води використовується Tuyet є\(0\), оплата є\($31\).
    д.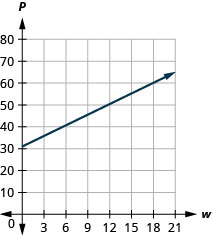

    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативного 1 до 21. Вісь Y проходить від негативного 1 до 80. Лінія проходить через точки (0, 31) і (12, 52).

    54. Рівняння\(P=28+2.54w\) моделює співвідношення між сумою щомісячної оплати рахунків за воду Ренді\(P\), у доларах, та кількістю одиниць води\(w\), використовуваної.

    а. знайти оплату за місяць, коли Ренді використовував\(0\) одиниці води.

    б. знайти оплату за місяць, коли Ренді використовував\(15\) одиниці води.

    c Інтерпретувати нахил і\(P\) -перехоплення рівняння.

    d Графік рівняння.

    55. Брюс їздить на своїй машині для своєї роботи. Рівняння\(R=0.575m+42\) моделює співвідношення між сумою в доларах\(R\), що йому відшкодовується і кількістю миль\(m\), які він проїжджає за один день.

    а. знайти суму Брюсу відшкодовується в день, коли він проїжджає\(0\) милі.

    б. знайти суму Брюсу відшкодовується в день, коли він проїжджає\(220\) милі.

    c Інтерпретувати нахил і\(R\) -перехоплення рівняння.

    d Графік рівняння.

    Відповідь

    а.\($42\)
    б.\($168.50\)
    c. ухил,\(0.575\) означає, що сума, яку йому відшкодовують\(R\), збільшується на те,\($0.575\) коли кількість пройдених миль\(m\), збільшується на\(1\). \(R\)-intercept означає, що коли кількість миль проїхав є\(0\), сума відшкодована є\($42\).
    д.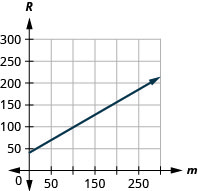

    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативних 50 до 250. Вісь Y проходить від негативних 50 до 300. Лінія проходить через точки (0, 42) і (220, 168,5).

    56. Жанель планує орендувати автомобіль, перебуваючи у відпустці. Рівняння\(C=0.32m+15\) моделює співвідношення між вартістю в доларах\(C\),, за день і кількістю миль\(m\), яку вона проїжджає за один день.

    a. знайти вартість, якщо Janelle їздить на машині\(0\) милі один день.

    б Знайти вартість в день, коли Janelle проїжджає автомобіль\(400\) милі.

    c Інтерпретувати нахил і\(C\) -перехоплення рівняння.

    d Графік рівняння.

    57. Чері працює в роздрібній торгівлі і її щотижнева зарплата включає комісію за суму, яку вона продає. Рівняння\(S=400+0.15c\) моделює співвідношення між її тижневою зарплатою\(S\), у доларах та сумою її продажів\(c\), у доларах.

    a. знайти зарплату Чері за тиждень, коли її продажі були\($0\).

    б. знайти зарплату Чері за тиждень, коли її продажі були\($3,600\).

    c Інтерпретувати нахил і\(S\) -перехоплення рівняння.

    d Графік рівняння.

    Відповідь

    а.\($400\)
    б.\($940\)
    c. нахил\(0.15\), означає, що зарплата Шері, S, збільшується\($0.15\) на кожне\($1\) збільшення її продажів. \(S\)-Перехоплення означає, що коли її продажі є\($0\), її зарплата є\($400\).
    д.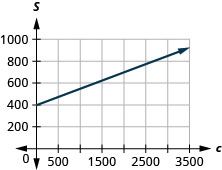

    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативних 500 до 3500. Вісь Y працює від негативних 200 до 1000. Лінія проходить через точки (0, 400) і (3600, 940).

    58. Щотижнева зарплата Пателя включає базову оплату плюс комісію за його продажі. Рівняння\(S=750+0.09c\) моделює співвідношення між його тижневою зарплатою\(S\), у доларах та сумою його продажів\(c\), у доларах.

    a. знайти зарплату Пателя за тиждень, коли його продажі були\(0\).

    б. знайти зарплату Пателя за тиждень, коли його продажі були\(18,540\).

    c Інтерпретувати нахил і\(S\) -перехоплення рівняння.

    d Графік рівняння.

    59. Коста планує обідній банкет. Рівняння\(C=450+28g\) моделює співвідношення між вартістю в доларах\(C\), банкету і кількістю гостей,\(g\).

    a. знайти вартість, якщо кількість гостей є\(40\).

    б. знайти вартість, якщо кількість гостей є\(80\).

    c Інтерпретувати нахил і\(C\) -перехоплення рівняння.

    d Графік рівняння.

    Відповідь

    а.\($1570\)
    б.\($5690\)
    c. ухил дає вартість на одного гостя. Ухил\(28\), означає, що вартість\(C\), збільшується на те,\($28\) коли кількість гостей збільшується на\(1\). \(C\)Перехоплення означає, що якби кількість гостей була\(0\), вартість була б\($450\).
    д.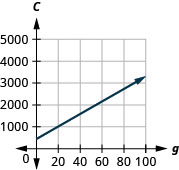

    На цьому малюнку показаний графік прямої на координатній площині x y. Вісь x проходить від негативних 20 до 100. Вісь Y працює від негативних 1000 до 7000. Лінія проходить через точки (0, 450) і (40, 1570).

    60. Марджі планує обідній банкет. Рівняння\(C=750+42g\) моделює співвідношення між вартістю в доларах\(C\), банкету і кількістю гостей,\(g\).

    a. знайти вартість, якщо кількість гостей є\(50\).

    б. знайти вартість, якщо кількість гостей є\(100\).

    c Інтерпретувати нахил і\(C\) -перехоплення рівняння.

    d Графік рівняння.

    Використання нахилів для визначення паралельних і перпендикулярних ліній

    У наступних вправах використовуйте нахили та\(y\) -перехоплення, щоб визначити, чи є лінії паралельними, перпендикулярними чи ні.

    61. \(y=\frac{3}{4}x−3\);\(3x−4y=−2\)

    Відповідь

    паралельний

    62. \(3x−4y=−2\);\(y=\frac{3}{4}x−3\)

    63. \(2x−4y=6\);\(x−2y=3\)

    Відповідь

    ні

    64. \(8x+6y=6\);\(12x+9y=12\)

    65. \(x=5\);\(x=−6\)

    Відповідь

    паралельний

    66. \(x=−3\);\(x=−2\)

    67. \(4x−2y=5\);\(3x+6y=8\)

    Відповідь

    перпендикулярний

    68. \(8x−2y=7\);\(3x+12y=9\)

    69. \(3x−6y=12\);\(6x−3y=3\)

    Відповідь

    ні

    70. \(9x−5y=4\);\(5x+9y=−1\)

    71. \(7x−4y=8\);\(4x+7y=14\)

    Відповідь

    перпендикулярний

    72. \(5x−2y=11\);\(5x−y=7\)

    73. \(3x−2y=8\);\(2x+3y=6\)

    Відповідь

    перпендикулярний

    74. \(2x+3y=5\);\(3x−2y=7\)

    75. \(3x−2y=1\);\(2x−3y=2\)

    Відповідь

    ні

    76. \(2x+4y=3\);\(6x+3y=2\)

    77. \(y=2\);\(y=6\)

    Відповідь

    паралельний

    78. \(y=−1\);\(y=2\)

    Письмові вправи

    79. Чим графік прямої з нахилом\(m=12\) відрізняється від графіка прямої з нахилом\(m=2\)?

    Відповідь

    Відповіді будуть відрізнятися.

    80. Чому нахил вертикальної лінії «невизначений»?

    81. Поясніть, як можна навести графік лінії з заданою точкою та її нахилом.

    Відповідь

    Відповіді будуть відрізнятися.

    82. Поясніть своїми словами, як вирішити, який метод використовувати для графування лінії.

    Самостійна перевірка

    а Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

    Ця таблиця має 7 рядків і 4 стовпців. Перший рядок є рядком заголовка, і він позначає кожен стовпець. Перший заголовок стовпця - «Я можу...», другий - «Впевнено», третій - «З деякою допомогою», а четвертий - «Ні, я не розумію». Під першим стовпцем знаходяться фрази «знайти нахил прямої», «графік лінії з заданою точкою та нахилом», «графік лінії, використовуючи її нахил та перехоплення», «виберіть найбільш зручний метод для побудови графіка лінії», «графік та інтерпретація застосувань перехоплення нахилу» та «використовувати нахили для ідентифікації паралельних та перпендикулярні лінії». Інші стовпці залишаються порожніми, щоб учень міг вказати свій рівень майстерності для кожної теми.

    б Ознайомившись з цим контрольним списком, що ви будете робити, щоб стати впевненими у всіх цілях?