1.5: Десяткові
- Page ID
- 59607
До кінця цього розділу ви зможете:
- Круглі десяткові
- Додавання та віднімання десяткових знаків
- Множення і ділення десяткових знаків
- Перетворення десяткових знаків, дробів та відсотків
- Спростіть вирази за допомогою квадратних коренів
- Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел
- Знайдіть дроби та десяткові дроби на числовому рядку
Більш ретельне ознайомлення з темами, висвітленими в цьому розділі, можна знайти в розділі Елементарна алгебра, Основи.
Круглі десяткові знаки
Десяткові числа - ще один спосіб запису дробів, знаменниками яких є повноваження десяти.
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
Так само, як і в цілих числах, кожна цифра десяткового числа відповідає значенню місця, заснованому на степенях десяти. На малюнку показані назви значень місць зліва і праворуч від десяткової крапки.
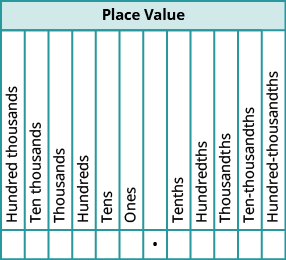
Коли ми працюємо з десятковими знаками, часто доводиться округлити число до найближчого необхідного значення місця. Тут ми підсумовуємо кроки для округлення десяткового числа.
- Знайдіть задане значення місця і позначте його стрілкою.
- Підкресліть цифру праворуч від значення місця.
- Підкреслена цифра більше або дорівнює 5?
- Так: додайте 1 до цифри в даному місці значення.
- Ні: не змінюйте цифру в заданому місці
- Перепишіть число, видаливши всі цифри праворуч від округлення цифри.
\(18.379\)Округлити до найближчого ⓐ сотого ⓑ десятого ⓒ цілого числа.
- Відповідь
-
Круглий\(18.379.\)
ⓐ до найближчої сотої
Знайдіть соті місця за допомогою стрілки. 
Підкресліть цифру праворуч від заданого значення місця. 
Оскільки 9 більше або дорівнює 5, додайте 1 до 7. 
Перепишіть число, видаливши всі цифри праворуч від округлення цифри. 
Зверніть увагу, що видалені цифри НЕ були замінені нулями. 
ⓑ до найближчої десятої
Знайдіть десяте місце за допомогою стрілки. 
Підкресліть цифру праворуч від заданого значення місця. 
Оскільки 7 більше або дорівнює 5, додайте 1 до 3. 
Перепишіть число, видаливши всі цифри праворуч від округлення цифри. 
Зверніть увагу, що видалені цифри НЕ були замінені нулями. 
ⓒ до найближчого цілого числа
Знайдіть ті місця за допомогою стрілки. 
Підкресліть цифру праворуч від заданого значення місця. 
Оскільки 3 не більше або дорівнює 5, не додавайте 1 до 8. 
Перепишіть число, видаливши всі цифри праворуч від округлення цифри. 

\(6.582\)Округлити до найближчого ⓐ сотого ⓑ десятого ⓒ цілого числа.
- Відповідь
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
\(15.2175\)Округлити до найближчої ⓐ тисячної ⓑ сотої ⓒ десятої.
- Відповідь
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
Додавання та віднімання десяткових знаків
Щоб додати або відняти десяткові числа, ми вибудовуємо десяткові крапки. Вибудовуючи десяткові крапки таким чином, ми можемо додати або відняти відповідні значення місця. Потім ми додаємо або віднімаємо числа так, ніби вони були цілими числами, а потім розміщуємо десяткову крапку в сумі.
- Визначте знак суми або різниці.
- Запишіть числа так, щоб десяткові крапки вибудовувалися вертикально.
- Використовуйте нулі як заповнювачі, якщо потрібно.
- Додайте або відніміть числа так, ніби вони були цілими числами. Потім помістіть
десяткову крапку у відповіді під десятковими крапками в заданих числах. - Напишіть суму або різницю відповідним знаком.
Додавання або віднімання: ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- Відповідь
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
Додати або відняти: ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).
- Відповідь
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
Додати або відняти: ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).
- Відповідь
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
Множення та ділення десяткових знаків
Коли ми множимо знакові десяткові числа, спочатку визначаємо знак добутку, а потім множимо так, ніби числа обидва позитивні. Ми множимо числа, тимчасово ігноруючи десяткову крапку, а потім підраховуємо кількість десяткових крапок у множниках, і ця сума повідомляє нам кількість десяткових знаків у добутку. Нарешті, пишемо виріб відповідним знаком.
- Визначте ознаку вироби.
- Пишіть у вертикальному форматі, вишикуючи цифри праворуч. Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки.
- Розставте десяткову крапку. Число десяткових знаків у добутку - це сума кількості
десяткових знаків у множниках. - Напишіть виріб відповідним знаком.
Помножити:\((−3.9)(4.075)\).
- Відповідь
-
\((−3.9)(4.075)\) Прикмети бувають різні. Продукт
буде негативним.Продукт буде негативним. Пишіть у вертикальному форматі, вишикуючи
цифри праворуч.
Помножити. 
Додайте кількість десяткових знаків
у множниках (1 + 3). Поставте десяткову крапку на 4 розряди праворуч.

Ознаки різні, тому продукт негативний. \((−3.9)(4.075)=−15.8925\)
Помножити:\(−4.5(6.107)\).
- Відповідь
-
\(−27.4815\)
Помножити:\(−10.79(8.12)\).
- Відповідь
-
\(−87.6148\)
Часто, особливо в науках, ви будете множити десяткові числа на ступені 10 (10, 100, 1000 і т.д.). Якщо помножити кілька виробів на папері, ви можете помітити закономірність, що стосується кількості нулів у степені 10 до числа десяткових знаків, ми переміщаємо десяткову крапку вправо, щоб отримати твір.
- Перемістіть десяткову крапку вправо на ту ж кількість знаків, що і
кількість нулів в ступені 10. - Додайте нулі в кінці числа за потребою.
Помножте: 5,63 на ⓐ 10 ⓑ 100 ⓒ 1000.
- Відповідь
-
Дивлячись на кількість нулів, кратних десяти, ми бачимо кількість знаків, які нам потрібно перемістити десяткове вправо.
ⓐ
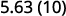
Існує 1 нуль в 10, тому перемістіть десяткову крапку на 1 місце вправо. 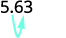
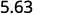
ⓑ
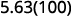
Є 2 нулі в 100, тому перемістіть десяткову крапку на 2 розряди вправо. 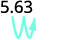

ⓒ
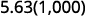
Є 3 нулі в 1000, тому перемістіть десяткову крапку на 3 місце вправо. 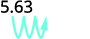
До кінця потрібно додати нуль. 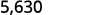
Помножте 2,58 на ⓐ 10 ⓑ 100 ⓒ 1000.
- Відповідь
-
ⓐ 25.8 ⓑ 258 ⓒ 2,580
Помножте 14,2 на ⓐ 10 ⓑ 100 ⓒ 1000.
- Відповідь
-
ⓐ 142 ⓑ 1 420 ⓒ 14 200
Так само, як і при множенні, ділення знакових десяткових знаків дуже схоже на ділення цілих чисел. Ми просто повинні з'ясувати, де десяткова крапка повинна бути розміщена і знак частки. При діленні знакових десяткових знаків спочатку визначте знак частки, а потім діліть так, ніби числа обидва позитивні. Нарешті, напишіть частку відповідним знаком.
Ми переглядаємо позначення та словниковий запас для поділу:

Ми напишемо кроки, які потрібно зробити при діленні десяткових знаків для зручності посилання.
- Визначте ознаку частки.
- Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо. «Перемістіть» десяткову крапку в дивіденді на ту саму кількість місць - додаючи нулі, якщо потрібно.
- Розділити. Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.
- Напишіть частку відповідним знаком.
Розділити:\(−25.65÷(−0.06)\).
- Відповідь
-
Пам'ятайте, що ви можете «перемістити» десяткові числа в дільнику та дивіденді через властивість еквівалентних дробів.
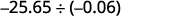
Прикмети ті ж. Коефіцієнт позитивний. Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо. «Перемістити» десяткову крапку в дивіденд на таку ж кількість знаків. 
Розділити. Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді. 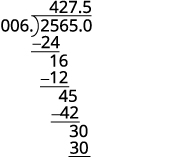
Напишіть частку відповідним знаком. 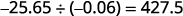
Розділити:\(−23.492÷(−0.04)\).
- Відповідь
-
\(587.3\)
Розділити:\(−4.11÷(−0.12)\).
- Відповідь
-
\(34.25\)
Перетворення десяткових дробів, дробів та відсотків
У нашій роботі часто доводиться міняти форму числа. Можливо, нам доведеться змінити дроби до десяткових знаків або десяткових знаків на відсотки.
Переводимо десяткові дроби в дроби, позначивши місце останньої (найдальшої правої) цифри. У десятковій 0.03. 3 знаходиться на сотому місці, тому 100 - знаменник дробу, еквівалентний 0,03.
\[0.03=\dfrac{3}{100}\]
Кроки, які потрібно зробити для перетворення десяткового дробу, підсумовуються у вікні процедури.
- Щоб перетворити десятковий дріб в правильний дріб, визначте місце кінцевої цифри.
- Запишіть дріб.
- чисельник — «числа» праворуч від десяткової крапки
- знаменник — значення місця, відповідне кінцевій цифрі
- Щоб перетворити дріб в десятковий, розділіть чисельник дробу на знаменник дробу.
Запишіть: ⓐ\(0.374\) як дріб ⓑ у\(−\frac{5}{8}\) вигляді десяткового дробу.
- Відповідь
-
ⓐ
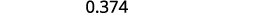
Визначте місце значення кінцевої цифри. 
Напишіть дріб для 0.374: Чисельник 374. Знаменник - 1000. 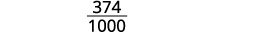
Спростити дріб. 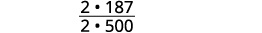
Розділіть загальні фактори. 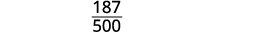
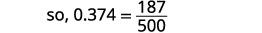
ⓑ Оскільки дробний бар означає ділення, ми починаємо з запису дробу\(\frac{5}{8}\) як\(8\sqrt{5}\). Тепер ділимо.
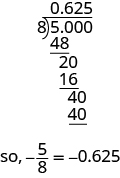
Запишіть: ⓐ\(0.234\) як дріб ⓑ у\(−\frac{7}{8}\) вигляді десяткового дробу.
- Відповідь
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
Запишіть: ⓐ\(0.024\) як дріб ⓑ у\(−\frac{3}{8}\) вигляді десяткового дробу.
- Відповідь
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
Відсоток - це коефіцієнт, знаменник якого дорівнює 100. Відсоток означає на сто. Ми використовуємо символ відсотка,%, щоб показати відсоток. Оскільки відсоток - це співвідношення, його легко можна виразити у вигляді дробу. Відсоток означає на 100, тому знаменник дробу дорівнює 100. Потім ми міняємо дріб на десятковий, діливши чисельник на знаменник. Проробивши це багато разів, ви можете побачити візерунок.
Щоб перетворити процентне число в десяткове число, переміщаємо десяткову крапку на два розряди вліво.
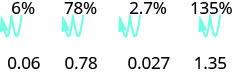
Щоб перетворити десяткове число в відсоток, пам'ятайте, що відсоток означає на сто. Якщо ми змінимо десятковий дріб, знаменник якого дорівнює 100, легко змінити цей дріб на відсоток. Після багатьох конверсій ви можете розпізнати шаблон.
Щоб перетворити десяткове число в відсоток, ми переміщаємо десяткову крапку на два розряди вправо, а потім додаємо знак відсотка.
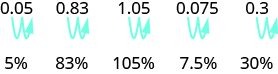
- Щоб перетворити відсоток у десятковий, перемістіть десяткову крапку на два розряди вліво після видалення знака відсотка.
- Щоб перетворити десяткове число у відсоток, перемістіть десяткову крапку на два розряди вправо, а потім додайте знак відсотка.
Перетворити кожен:
ⓐ відсоток до десяткового числа: 62%, 135% і 13,7%.
ⓑ десяткове число до відсотка: 0,51, 1,25 та 0,093.
- Відповідь
-
ⓐ
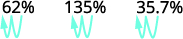
Перемістіть десяткову крапку на два розряди вліво. 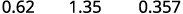
ⓑ
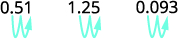
Перемістіть десяткову крапку на два розряди вправо. 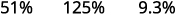
Перетворити кожен:
ⓐ відсоток до десяткового числа: 9%, 87% та 3,9%.
ⓑ десяткове число до відсотка: 0,17, 1,75 та 0,0825.
- Відповідь
-
ⓐ 0.09, 0.87, 0.039 ⓑ 17%, 175%, 8.25%
Перетворити кожен:
ⓐ відсоток до десяткового числа: 3%, 91% та 8,3%.
ⓑ десяткове число до відсотка: 0,41, 2,25 та 0,0925.
- Відповідь
-
ⓐ 0.03, 0.91, 0.083 ⓑ 41%, 225%, 9.25%
Спрощення виразів за допомогою квадратних коренів
Пам'ятайте, що коли число множиться\(n\) саме на себе, ми пишемо\(n^2\) і читаємо його «в\(n\) квадрат». Результат називається квадратом числа n. Наприклад,\(\frac{8}{2}\) читається «8 в квадраті» і 64 називається квадратом 8. Аналогічно, 121 - це квадрат 11, тому що\(11^2\) це 121. Корисно буде навчитися розпізнавати ідеальні квадратні числа.
Якщо\(n^2=m\), то m - квадрат n.
А як щодо квадратів від'ємних чисел? Ми знаємо, що коли знаки двох чисел однакові, їх твір позитивний. Таким чином, квадрат будь-якого негативного числа також позитивний.
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
Тому що\(10^2=100\), ми говоримо, 100 - це квадрат 10. Ми також говоримо, що 10 - це квадратний корінь 100. Число, квадрат якого дорівнює m, називається квадратним коренем числа m.
Якщо\(n^2=m\), то n - квадратний корінь m.
Зауважте\((−10)^2=100\) також, що −10 також є квадратним коренем 100. Тому і 10, і −10 є квадратними коренями 100. Отже, кожне додатне число має два квадратних кореня - один позитивний і один негативний. Радикальний знак,\(\sqrt{m}\), позначає позитивний квадратний корінь. Позитивний квадратний корінь називається основним квадратним коренем. Коли ми використовуємо радикальний знак, який завжди означає, що ми хочемо основний квадратний корінь.
\(\sqrt{m}\)читається «квадратний корінь мм».
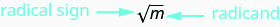
Якщо\(m=n^2\), то\(\sqrt{m}=n\), для\(n≥0\).
Квадратний корінь m\(\sqrt{m}\), - додатне число, квадрат якого дорівнює m.
Ми знаємо, що кожне позитивне число має два квадратних кореня, а знак радикалу вказує на позитивний. Пишемо\(\sqrt{100}=10\). Якщо ми хочемо знайти негативний квадратний корінь числа, ми ставимо негативний перед знаком радикала. Наприклад,\(−\sqrt{100}=−10\). Читаємо\(−\sqrt{100}\) як «протилежність головному квадратному кореню з 10».
Спрощення: ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).
- Відповідь
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
Спрощення: ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- Відповідь
-
ⓐ 6 ⓑ 13 ⓒ −15
Спрощення: ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- Відповідь
-
ⓐ 4 ⓑ 14 ⓒ −10
Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел
Ми вже описували числа як підрахунок чисел s, цілих чисел s та цілих чисел. У чому різниця між цими типами чисел? Різницю можна сплутати з відніманням. Як щодо того, щоб запитати, як ми розрізняємо ці типи чисел?
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
Який тип чисел ми отримаємо, якби ми почали з усіх цілих чисел, а потім включили всі дроби? Числа, які ми мали б, утворюють набір раціональних чисел. Раціональне число - це число, яке можна записати у вигляді співвідношення двох цілих чисел.
Загалом, будь-яке десяткове число, яке закінчується після кількості цифр (наприклад, 7.3 або −1.2684), є раціональним числом. Ми можемо використовувати місце останньої цифри як знаменник при записі десяткового дробу. Десятковий\(\frac{1}{3}\) знак - це число\(0.\overline{3}\). Смуга над 3 вказує на те, що число 3 повторюється нескінченно. Постійно має важливе значення в обчисленні. Число (и) під планкою називається повторюваним блоком і він повторюється безперервно.
Оскільки всі цілі числа можна записати у вигляді дробу, знаменник якого дорівнює 1, цілі числа (а так само лічильні і цілі числа. є раціональними числами.
Кожне раціональне число можна записати як у вигляді співвідношення цілих чисел\(\frac{p}{q}\), де p і q - цілі числа і\(q≠0\), і як десяткове число, яке зупиняється або повторюється.
Раціональне число - це число виду\(\frac{p}{q}\), де p і q - цілі числа і\(q≠0\).
Його десяткова форма зупиняється або повторюється.
Чи є десяткові знаки, які не зупиняються і не повторюються? Так! Число ππ (грецька буква пі, вимовляється «пиріг»), яке дуже важливо при описі кіл, має десяткову форму, яка не зупиняється і не повторюється. Ми використовуємо три точки (...), щоб вказати десяткове число не зупиняється і не повторюється.
\[π=3.141592654...\]
Квадратний корінь числа, яке не є ідеальним квадратом, є десятковим, який не зупиняється і не повторюється.
Числа, десяткова форма яких не зупиняється або повторюється, не можна записати як дріб цілих чисел. Ми називаємо це ірраціональним числом.
Ірраціональне число - це число, яке не можна записати як співвідношення двох цілих чисел.
Його десяткова форма не зупиняється і не повторюється.
Давайте підсумуємо метод, який ми можемо використовувати, щоб визначити, чи є число раціональним чи ірраціональним.
Якщо десяткова форма числа
- повторюється або зупиняється, число - раціональне число.
- не повторюється і не зупиняється, число - ірраціональне число.
Ми бачили, що всі числа підрахунку є цілими числами, всі цілі числа цілі числа, а всі цілі числа - раціональні числа. Ірраціональні числа - це числа, десяткова форма яких не зупиняється і не повторюється. Коли ми збираємо раціональні числа і ірраціональні числа, ми отримуємо безліч дійсних чисел s.
Реальне число - це число, яке є або раціональним, або ірраціональним.
Пізніше в цьому курсі ми введемо числа поза дійсними числами. Малюнок ілюструє, як набори чисел, які ми використовували досі, підходять один до одного.
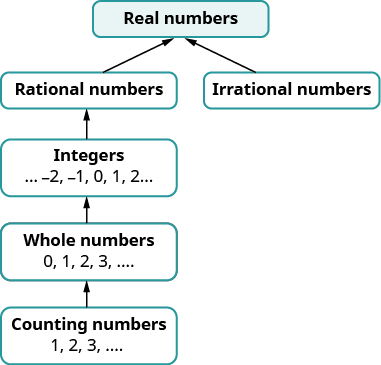
Чи здається вам дивним термін «реальні цифри»? Чи є цифри, які не є «реальними», і якщо так, то якими вони можуть бути? Чи можемо ми спростити\(−\sqrt{25}\)? Чи є число, квадрат якого\(−25\)?
\[()^2=−25?\]
Жодне з чисел, з якими ми мали справу до цих пір, не має квадрата, який є\(−25\). Чому? Будь-яке додатне число в квадраті є позитивним. Будь-яке негативне число в квадраті є позитивним. Таким чином, ми говоримо, що немає реального числа, рівного\(\sqrt{−25}\). Квадратний корінь від'ємного числа не є дійсним числом.
Враховуючи числа\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\), перерахуйте ⓐ цілі числа ⓑ цілі числа ⓒ раціональні числа ⓓ ірраціональні числа ⓔ дійсні числа.
- Відповідь
-
ⓐ Пам'ятайте, цілі числа\(0,1,2,3,…,\) так 8 є єдиним цілим числом.
ⓑ Цілі числа - це цілі числа та їх протилежності (що включає 0). Таким чином, ціле число 8 є цілим числом, а −7 протилежне цілому числу, тому воно теж є цілим числом. Крім того, зверніть увагу, що 64 квадрат 8 так\(−\sqrt{64}=−8\). Таким чином, цілі числа\(−7,8,\) і\(−\sqrt{64}\).
ⓒ Так як всі цілі числа раціональні, то\(−7,8,\) і\(−\sqrt{64}\) є раціональними. Раціональні числа також включають дробові та десяткові дроби, які повторюються або зупиняються, тому\(\frac{14}{5}\) і\(5.9\) є раціональними. Отже, список раціональних чисел - це\(−7,\frac{14}{5},8,5.9,\) і\(−\sqrt{64}\).
ⓓ Пам'ятайте, що 5 - це не ідеальний квадрат,\(\sqrt{5}\) тому нераціонально.
ⓔ Всі перераховані цифри є реальними числами.
Задані числа\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) перераховують ⓐ цілі числа ⓑ цілі числа ⓒ раціональні числа
ⓓ ірраціональні числа ⓔ дійсні числа.
- Відповідь
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
Задані числа\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) перераховують ⓐ цілі числа ⓑ цілі числа ⓒ раціональні числа ⓓ ірраціональні числа ⓔ дійсні числа.
- Відповідь
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
Знайдіть дроби та десяткові дроби на числовому рядку
Тепер ми хочемо включити дроби і десяткові числа на числовому рядку. Давайте почнемо з дробів і знайдіть\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\) і\(\frac{8}{3}\) на числовому рядку.
Ми почнемо з цілих чисел 3 і −5, оскільки їх найпростіше побудувати. Див. Малюнок.
Правильні дроби перераховані\(\frac{1}{5}\) і\(−\frac{4}{5}.\) Ми знаємо, що правильний дріб\(\frac{1}{5}\) має значення менше одиниці і так буде розташовуватися між 0 і 1. Знаменник дорівнює 5, тому ділимо одиницю від 0 до 1 на 5 рівних частин\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). Змова\(\frac{1}{5}\).
Аналогічно,\(−\frac{4}{5}\) знаходиться між 0 і −1. Після поділу одиниці на 5 рівних частин наносимо ділянку\(−\frac{4}{5}\).
Нарешті, подивіться на неправильні дроби\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Розташування цих точок може бути простіше, якщо змінити кожну з них на змішане число.
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
На малюнку показана числова лінія з нанесеними всіма точками.

Знайдіть і позначте на цифровому рядку наступне:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) і\(\frac{7}{3}\).
- Відповідь
-
Знайдіть і побудуйте цілі числа,\(4,−3.\)
\(\frac{3}{4}\)Спочатку знайдіть правильний дріб. Дріб\(\frac{3}{4}\) знаходиться в межах від 0 до 1. Ділимо відстань між 0 і 1 на чотири рівні частини, потім намічаємо\(\frac{3}{4}\). Аналогічно сюжет\(−\frac{1}{4}\).
Тепер знайдіть неправильні\(\frac{6}{5},−\frac{5}{2},\) дроби і\(\frac{7}{3}\). Їх простіше побудувати, якщо ми перетворимо їх у мішані числа, а потім побудуємо їх так, як описано вище:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

Знайдіть і позначте наступне на цифровому рядку:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- Відповідь
-
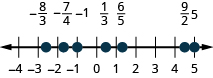
Знайдіть і позначте наступне на цифровому рядку:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- Відповідь
-
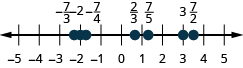
Оскільки десяткові числа є формами дробів, розташування десяткових знаків на числовому рядку аналогічно розташуванню дробів на числовому рядку.
Знайдіть на цифровому рядку: ⓐ 0.4 ⓑ −0.74.
- Відповідь
-
ⓐ Десяткове число 0,4 еквівалентно\(\frac{4}{10}\), правильний дріб, тому 0.4 знаходиться між 0 і 1. На числовому рядку розділіть інтервал між 0 і 1 на 10 рівних частин. Тепер маркуємо деталі 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9, 1,0. Ми пишемо 0 як 0.0 і 1 як 1.0, так що числа послідовно в десятих. Нарешті, позначте 0,4 на цифровому рядку.

ⓑ\(−0.74\) Десяткове значення еквівалентно\(−\frac{74}{100}\), тому воно знаходиться між 0 та .−1. На числовому рядку позначте і позначте соті в інтервалі між 0 і −1.

Знайдіть на цифровому рядку: ⓐ\(0.6\) ⓑ\(−0.25.\)
- Відповідь
-
ⓐ

ⓑ
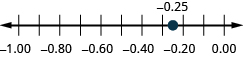
Знайдіть у цифровому рядку: ⓐ 0.90.9 ⓑ −0.75.−0.75.
- Відповідь
-
ⓐ

ⓑ
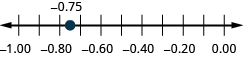
Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з десятковими знаками.
- Основи арифметики: Ділення десяткових знаків
Ключові поняття
- Як округлити десяткові знаки.
- Знайдіть задане значення місця і позначте його стрілкою.
- Підкресліть цифру праворуч від значення місця.
- Підкреслена цифра більше або дорівнює 5?
- Так: додайте 1 до цифри в даному місці значення.
- Ні: не змінюйте цифру в заданому місці
- Перепишіть число, видаливши всі цифри праворуч від округлення цифри.
- Як додати або відняти десяткові знаки.
- Визначте знак суми або різниці.
- Запишіть числа так, щоб десяткові крапки вибудовувалися вертикально.
- Використовуйте нулі як заповнювачі, якщо потрібно.
- Додайте або відніміть числа так, ніби вони були цілими числами. Потім помістіть десяткову крапку у відповіді під десятковими крапками в заданих числах.
- Напишіть суму або різницю відповідним знаком
- Як помножити десяткові знаки.
- Визначте ознаку вироби.
- Пишіть у вертикальному форматі, вишикуючи цифри праворуч. Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки.
- Розставте десяткову крапку. Число десяткових знаків у добутку - це сума кількості десяткових знаків у множниках.
- Напишіть виріб відповідним знаком.
- Як помножити десяткове число на ступінь десять.
- Перемістіть десяткову крапку вправо на ту ж кількість знаків, що і кількість нулів в ступені 10.
- Додайте нулі в кінці числа за потребою.
- Як розділити десяткові знаки.
- Визначте ознаку частки.
- Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо. «Перемістіть» десяткову крапку в дивіденді на ту саму кількість місць - додаючи нулі, якщо потрібно.
- Розділити. Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.
- Напишіть частку відповідним знаком.
- Як перетворити десятковий в правильний дріб і дріб в десятковий.
- Щоб перетворити десятковий дріб в правильний дріб, визначте місце кінцевої цифри.
- Запишіть дріб.
- чисельник — «числа» праворуч від десяткової крапки
- знаменник — значення місця, відповідне кінцевій цифрі
- Щоб перетворити дріб в десятковий, розділіть чисельник дробу на знаменник дробу.
- Як перетворити відсоток в десятковий і десятковий в відсоток.
- Щоб перетворити відсоток у десятковий, перемістіть десяткову крапку на два розряди вліво після видалення знака відсотка.
- Щоб перетворити десяткове число у відсоток, перемістіть десяткову крапку на два розряди вправо, а потім додайте знак відсотка.
- Позначення квадратного кореня\(\sqrt{m}\) читається «квадратний корінь m». Якщо\(m=n^2\), то\(\sqrt{m}=n\), для\(n≥0\). Квадратний корінь m\(\sqrt{m}\), - додатне число, квадрат якого дорівнює m.
- Раціональний або ірраціональний Якщо десяткова форма числа
- повторюється або зупиняється, число - раціональне число.
- не повторюється і не зупиняється, число - ірраціональне число.
- Реальні числа
.jpg)
Малюнок 4.
Глосарій
- ірраціональне число
- Ірраціональне число - це число, яке не можна записати як співвідношення двох цілих чисел. Його десяткова форма не зупиняється і не повторюється.
- відсотків
- Відсоток - це коефіцієнт, знаменник якого дорівнює 100.
- головний квадратний корінь
- Позитивний квадратний корінь називається основним квадратним коренем.
- раціональне число
- Раціональне число - це число виду\(\frac{p}{q}\), де p і q - цілі числа і\(q≠0\). Його десяткова форма зупиняється або повторюється.
- дійсне число
- Реальне число - це число, яке є або раціональним, або ірраціональним.
- квадрат числа
- Якщо\(n^2=m\), то m - квадрат n.
- квадратний корінь числа
- Якщо\(n^2=m\), то n - квадратний корінь m.
