3.4: Додатки
- Page ID
- 61279
Складні відсотки
Переглянути підручник на YouTube
Рівняння зростання інвестиції з безперервним складанням інтересу є диференціальним рівнянням першого порядку. \(S(t)\)Дозволяти значення інвестицій в часі\(t\), і нехай\(r\) буде річна процентна ставка, що складається після кожного часового інтервалу\(∆t\). Ми також можемо включити депозити (або зняття коштів). Нехай\(k\) буде річна сума депозиту, і припустимо, що розстрочка вноситься після кожного часового інтервалу\(∆t\). Вартість інвестицій на той момент потім\(t + ∆t\) задається тим\(∆t\), \[\label{eq:1}S(t+\Delta t)=S(t)+(r\Delta t)S(t)+k\Delta t,\]де в кінці часового інтервалу\(r\Delta tS(t)\) - це сума зарахованих відсотків і\(k∆t\) сума грошей, внесених\((k > 0)\) або знятих\((k < 0)\). Як числовий приклад, якщо\($10,000\) рахунок проводиться вчасно\(t\), і\(r = 6\%\) за рік і на\(k = $12,000\) рік, скажімо, і період складання та депозиту є, то відсотки\(∆t = 1\text{ month} = 1/12\text{ year}\), присуджені через один місяць, є\(r\Delta tS = (0.06/12) × $10,000 = $50\), а сума, що вноситься, є\(k∆t = $1000\).
Переставляючи умови\(\eqref{eq:1}\) виставляти те, що скоро стане похідною, ми маємо\[\frac{S(t+\Delta t)-S(t)}{\Delta t}=rS(t)+k.\nonumber\]
Рівняння для безперервного складання процентних і безперервних депозитів отримують шляхом взяття ліміту\(\Delta t\to 0\). Отримане диференціальне рівняння - це \[\label{eq:2}\frac{dS}{dt}=rS+k,\]яке можна вирішити з початковою умовою\(S(0) = S_0\), де\(S_0\) знаходиться початковий капітал. Ми можемо вирішити або розділяючи змінні, або за допомогою інтегруючого фактора; Я вирішую тут, розділяючи змінні. Інтеграція від\(t = 0\) до кінцевого часу\(t\), \[\begin{align} \int_{S_0}^S \frac{dS}{rS+k}&=\int_0^tdt,\nonumber \\ \frac{1}{r}\ln\left(\frac{rS+k}{rS_0+k}\right)&=t,\nonumber \\ rS+k&=(rS_0+k)e^{rt},\nonumber \\ S&=\frac{rS_0e^{rt}+ke^{rt}-k}{r},\nonumber \\ S&=S_0e^{rt}+\frac{k}{r}e^{rt}(1-e^{-rt}),\label{eq:3} \end{align}\]коли перший термін з правого боку\(\eqref{eq:3}\) походить від початкового вкладеного капіталу, а другий термін походить від депозитів (або зняття коштів). Очевидно, що складання призводить до експоненціального зростання інвестицій.
Як практичний приклад можна проаналізувати простий пенсійний план. Найпростіше припустити, що всі суми і доходи знаходяться в реальних доларах (з поправкою на інфляцію). Припустимо, рік планує відкладати фіксовану суму щороку свого трудового життя, інвестує з реальним прибутком\(6\%\) і виходить на пенсію у віці\(65\).\(25\) Скільки він повинен інвестувати щороку, щоб мати\(\text{HK }$8,000,000\) при виході на пенсію? (Примітка:\(\text{US }$1\approx\text{ HK }$8\).) Нам потрібно вирішити\(\eqref{eq:3}\) для\(k\) використання\(t = 40\text{ years}\),\(S(t) = $8,000,000\)\(S_0 = 0\), і\(r = 0.06\) на рік. У нас є\[\begin{aligned}k&=\frac{rS(t)}{e^{rt}-1}, \\ k&=\frac{0.06\times 8,000,000}{e^{0.06\times 40}-1}, \\ &=$47,889\text{ year}^{-1}.\end{aligned}\]
Щоб заощадити приблизно один мільйон\(\text{US}$\) на пенсії, працівник повинен буде економити приблизно\(\text{HK }$50,000\) на рік протягом свого трудового життя. Зверніть увагу, що сума, зекономлена за життя працівника\(40 × $50,000 = $2,000,000\), приблизно, в той час як сума, зароблена на інвестиції (при передбачуваній\(6\%\) реальній прибутковості) приблизно\($8,000,000 − $2,000,000 = $6,000,000\). Сума, зароблена від інвестицій, становить приблизно\(3×\) збережену суму, навіть при скромній реальній віддачі\(6\%\). Обґрунтоване планування інвестицій варто витрачених зусиль.
Хімічні реакції
Припустимо, що дві хімічні речовини\(A\) і\(B\) реагують на утворення продукту\(C\), який ми пишемо а\[A+B\overset{k}{\to}C,\nonumber\] де\(k\) називається константою швидкості реакції. Для простоти ми будемо використовувати один і той же символ\(C\), скажімо, для позначення як хімічної речовини, так\(C\) і його концентрації. Закон масової дії говорить,\(dC/dt\) що пропорційний добутку концентрацій\(A\) і\(B\), з постійною пропорційністю\(k\); тобто \[\label{eq:4}\frac{dC}{dt}=kAB.\]
Аналогічно закон масової дії дозволяє писати рівняння для похідних за часом концентрацій реагентів\(A\) і\(B\):
\[\label{eq:5}\frac{dA}{dt}=-kAB,\quad\frac{dB}{dt}=-kAB.\]
Ода, надана,\(\eqref{eq:4}\) може бути вирішена аналітично, використовуючи закони збереження. Ми припускаємо, що\(A_0\) і\(B_0\) є початковими концентраціями реагентів, і що жоден продукт спочатку не присутній. Від\(\eqref{eq:4}\) і\(\eqref{eq:5}\),\[\begin{array}{lll} \frac{d}{dt}(A+C)=0&\Longrightarrow &A+C=A_0, \\ \frac{d}{dt}(B+C)=0&\Longrightarrow &B+C=B_0.\end{array}\nonumber\]
Використовуючи ці закони збереження,\(\eqref{eq:4}\) стає,\[\frac{dC}{dt}=k(A_0-C)(B_0-C),\quad C(0)=0,\nonumber\] яке є нелінійним рівнянням, яке може бути інтегровано шляхом поділу змінних. Розділяючи і інтегруючи, отримуємо \[\begin{align}\int_0^C\frac{dC}{(A_0-C)(B_0-C)}&=k\int_0^t dt\nonumber \\ &=kt.\label{eq:6}\end{align}\]
Решта інтеграл можна зробити за допомогою методу часткових дробів. пишемо \[\label{eq:7}\frac{1}{(A_0-C)(B_0-C)}=\frac{a}{A_0-C}+\frac{b}{B_0-C}.\]
Метод приховування є найпростішим методом визначення невідомих коефіцієнтів\(a\) і\(b\). Для визначення\(a\) множимо обидві сторони\(\eqref{eq:7}\) на\(A_0 − C\) і ставимо\(C = A_0\) знайти\[a=\frac{1}{B_0-A_0}.\nonumber\]
Аналогічно, щоб визначити\(b\), ми множимо обидві сторони\(\eqref{eq:7}\) на\(B_0 − C\) і\(C = B_0\) встановити знайти\[b=\frac{1}{A_0-B_0}.\nonumber\]
Тому\[\frac{1}{(A_0-C)(B_0-C)}=\frac{1}{B_0-A_0}\left(\frac{1}{A_0-C}-\frac{1}{B_0-C}\right),\nonumber\] і залишився інтеграл\(\eqref{eq:6}\) стає (використовуючи\(C < A_0,\: B_0\))\[\begin{aligned} \int_0^C\frac{dC}{(A_0-C)(B_0-C)}&=\frac{1}{B_0-A_0}\left(\int_0^C\frac{dC}{A_0-C}-\int_0^C\frac{dC}{B_0-C}\right) \\ &=\frac{1}{B_0-A_0}\left(-\ln\left(\frac{A_0-C}{A_0}\right)+\ln\left(\frac{B_0-C}{B_0}\right)\right) \\ &=\frac{1}{B_0-A_0}\ln\left(\frac{A_0(B_0-C)}{B_0(A_0-C)}\right).\end{aligned}\]
Використовуючи цей інтеграл в\(\eqref{eq:6}\), множивши на\((B_0 − A_0)\) і збільшуючи, отримаємо\[\frac{A_0(B_0-C)}{B_0(A_0-C)}=e^{(B_0-A_0)kt}.\nonumber\]
Вирішуючи для\(C\), ми, нарешті, отримуємо,\[C(t)=A_0B_0\frac{e^{(B_0-A_0)kt}-1}{B_0e^{(B_0-A_0)kt}-A_0},\nonumber\] що здається складним виразом, але має прості межі\[\begin{aligned}\underset{t\to\infty}{\lim}C(t)&=\left\{\begin{array}{ll}A_0,&\text{if }A_0<B_0, \\ B_0,&\text{if }B_0<A_0\end{array}\right. \\ &=\text{min}(A_0,B_0).\end{aligned}\]
Як і слід було очікувати, реакція припиняється після того, як один з реагентів виснажується; і кінцева концентрація продукту дорівнює початковій концентрації виснаженого реагенту.
Швидкість терміналу
Переглянути підручник на YouTube
Використовуючи закон Ньютона, ми моделюємо масу,\(m\) вільну, що падає під гравітацією, але з опором повітря. Припустимо, що сила опору повітря пропорційна швидкості маси і протилежна напрямку руху. Визначаємо\(x\) -вісь, щоб точка у напрямку вгору, протилежна силі тяжіння. Біля поверхні Землі сила тяжіння приблизно постійна і задається\(−mg\), зі звичайним\(g = 9.8\text{m/s}^2\) гравітаційним прискоренням. Сила опору повітря моделюється тим\(−kv\), де\(v\) знаходиться вертикальна швидкість маси і\(k\) є позитивною константою. Коли маса падає,\(v < 0\) а сила опору повітря позитивна, спрямована вгору і протилежна руху. Таким чином, загальна сила на масу задається\(F = −mg − kv\). З\(F = ma\) і\(a = dv/dt\), отримаємо диференціальне рівняння \[\label{eq:8}m\frac{dv}{dt}=-mg-kv.\]
Кінцева швидкість\(v_∞\) маси визначається як асимптотична швидкість після того, як опір повітря врівноважує силу гравітації. Коли маса знаходиться на кінцевій швидкості,\(dv/dt = 0\) так що \[\label{eq:9}v_{\infty}=-\frac{mg}{k}.\]
Наближення до кінцевої швидкості маси спочатку в спокої отримують шляхом розв'язання\(\eqref{eq:8}\) з початковою умовою\(v(0) = 0\). Рівняння є як лінійним, так і роздільним, і я вирішую розділенням змінних:
\[\begin{aligned}m\int_0^v\frac{dv}{mg+kv}&=-\int_0^t dt,\\ \frac{m}{k}\ln\left(\frac{mg+kv}{mg}\right)&=-t, \\ 1+\frac{kv}{mg}&=e^{-kt/m}, \\ v&=-\frac{mg}{k}\left(1-e^{-kt/m}\right).\end{aligned}\]
Тому і\(v\) наближається\(v = v_∞\left( 1 − e^{−kt/m}\right)\),\(v_∞\) як експоненціальний термін розпадається до нуля.
Як приклад, парашутист маси\(m = 100\text{ kg}\) із закритим парашутом може мати кінцеву швидкість\(200\text{ km/hr}\). З\[g=(9.8\text{ m/s}^2)(10^{-3}\text{ km/m})(60\text{ s/min})^2(60\text{ min/hr})^2=127,008\text{ km/hr}^2,\nonumber\] одного виходить від\(\eqref{eq:9}\),\(k = 63, 504\text{ kg/hr}\). Таким чином, половина кінцевої швидкості для вільного падіння (\(100\text{ km/hr}\)) досягається\((1 − e^{−kt/m}) = 1/2\), коли, або\(t = m \ln 2/k\approx 4\text{ sec}\). Приблизно\(95\%\) кінцева швидкість (\(190\text{ km/hr}\)) досягається після\(17\text{ sec}\).
Швидкість втечі
Переглянути підручник на YouTube
Цікава фізична проблема полягає в тому, щоб знайти найменшу початкову швидкість для маси на поверхні Землі для виходу з гравітаційного поля Землі, так званої швидкості втечі. Закон Ньютона про всесвітнє тяжіння стверджує, що гравітаційна сила між двома масивними тілами пропорційна добутку двох мас і обернено пропорційна квадрату відстані між ними. Для маси\(m\) положення\(x\) над поверхнею Землі сила на масу задається тим,\[F=-G\frac{Mm}{(R+x)^2},\nonumber\] де\(M\) і\(R\) є масою і радіусом Землі і\(G\) є гравітаційною константою. Знак мінус означає силу на масу\(m\) точок в сторону зменшення\(x\). Приблизно постійне прискорення\(g\) на поверхні Землі відповідає абсолютному значенню,\(F/m\) коли\(x = 0\):
\[g=\frac{GM}{R^2},\nonumber\]і\(g\approx 9.8\text{ m/s}^2\). Таким чином, закон Ньютона\(F = ma\) для маси\(m\) задається тим, \[\begin{align}\frac{d^2x}{dt^2}&=-\frac{GM}{(R+x)^2}\nonumber \\ &=-\frac{g}{(1+x/R)^2},\label{eq:10}\end{align}\]де радіус Землі, як відомо, є\(R\approx 6350\text{ km}\).
Корисний трюк дозволяє вирішити це диференціальне рівняння другого порядку як рівняння першого порядку. По-перше, зауважте, що\(d^2x/dt^2 = dv/dt\). Якщо ми запишемо\(v(t) = v(x(t))\) - враховуючи швидкість маси\(m\) як функцію її відстані над землею - ми використовуємо правило ланцюга,\[\begin{aligned}\frac{dv}{dt}&=\frac{dv}{dx}\frac{dx}{dt} \\ &=v\frac{dv}{dx},\end{aligned}\] де ми використовували\(v = dx/dt\). Таким чином,\(\eqref{eq:10}\) стає одою першого порядку,\[v\frac{dv}{dx}=-\frac{g}{(1+x/R)^2},\nonumber\] яка може бути вирішена, припускаючи початкову швидкість,\(v(x = 0) = v_0\) коли маса знімається вертикально з поверхні Землі. Відокремлюючи змінні та інтегруючи, отримаємо\[\int_{v_0}^v vdv=-g\int_0^x\frac{dx}{(1+x/R)^2}.\nonumber\]
Лівий інтеграл є\(\frac{1}{2}(v^2 − v_0^2)\), а правий інтеграл може бути виконаний за допомогою підстановки\(u = 1 + x/R\),\(du = dx/R\):
\[\begin{aligned}\int_0^x\frac{dx}{(1+x/R)^2}&=R\int_1^{1+x/R}\frac{du}{u^2} \\ &=-\left.\frac{R}{u}\right]_1^{1+x/R} \\ &=R-\frac{R^2}{x+R} \\ &=\frac{Rx}{x+R}.\end{aligned}\]
Тому,\[\frac{1}{2}(v^2-v_0^2)=-\frac{gRx}{x+R},\nonumber\] яке при множенні на\(m\) є виразом збереження енергії (зміна кінетичної енергії маси дорівнює зміні потенційної енергії). Рішення для\(v^2\),\[v^2=v_0^2-\frac{2gRx}{x+R}.\nonumber\]
Швидкість виходу визначається як мінімальна початкова швидкість,\(v_0\) така, що маса може втекти до нескінченності. Тому,\(v_0 = v_{\text{escape}}\) коли\(v → 0\) як\(x → ∞\). Беручи цю межу, ми маємо\[\begin{aligned}v_{\text{escape}}^2&=\underset{x\to\infty}{\lim}\frac{2gRx}{x+R} \\ &=2gR.\end{aligned}\]
З\(R\approx 6350\text{ km}\) і\(g = 127 008\text{ km/hr}^2\), визначаємося\(v_{\text{escape}} = \sqrt{2gR}\approx 40 000\text{ km/hr}\). Для порівняння, дульна швидкість сучасної високопродуктивної гвинтівки майже на порядок занадто повільна для того\(4300\text{ km/hr}\), щоб куля, вистрілена в небо, втекла від земної гравітації.
RC ланцюг
Переглянути підручник на YouTube
Розглянемо резистор\(R\) і конденсатор,\(C\) з'єднані послідовно, як показано на рис. \(\PageIndex{1}\). Батарея, що забезпечує електрорушійну силу, або ЕРС\(\mathcal{E}\), підключається до цієї ланцюга за допомогою вимикача. Спочатку на конденсаторі немає заряду. Коли перемикач перекидається на а, акумулятор підключається і конденсатор заряджається. Коли перемикач перекидається на\(b\), батарея відключається і конденсатор розряджається, при цьому енергія розсіюється в резисторі. Тут визначаємо падіння напруги на конденсаторі при зарядці і розряді.
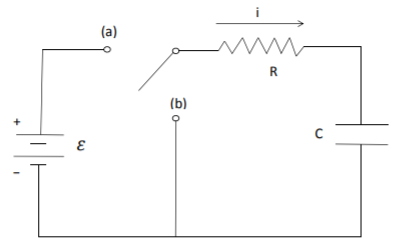
Рівняння для падіння напруги на конденсаторі та резисторі задаються \[\label{eq:11} V_C=q/C,\quad V_R=iR,\]\(C\)тим, де ємність і\(R\) є опір. Заряд\(q\) і струм\(i\) пов'язані \[\label{eq:12}i=\frac{dq}{dt}.\]
Закон напруги Кірхгофа говорить, що ЕРС\(\mathcal{E}\) в будь-якому замкнутому контурі дорівнює сумі падінь напруги в цьому контурі. Застосування закону напруги Кірхгофа, коли перемикач кидається,\(a\) призводить до \[\label{eq:13}V_R+V_C=\mathcal{E}.\]
Використовуючи\(\eqref{eq:11}\) і\(\eqref{eq:12}\), падіння напруги на резистері може бути записано з точки зору падіння напруги на конденсаторі, як\[V_R=RC\frac{dV_C}{dt},\nonumber\] і\(\eqref{eq:13}\) може бути перезаписано, щоб отримати лінійне диференціальне рівняння першого порядку для VC, задане \[\label{eq:14}\frac{dV_C}{dt}+V_C/RC=\mathcal{E}/RC,\]з початковою умовою \(V_C(0)=0.\)
Інтеграційний коефіцієнт для цього рівняння є\[\mu(t)=e^{t/RC},\nonumber\] і\(\eqref{eq:14}\) інтегрується\[V_C(t)=e^{-t/RC}\int_0^t(\mathcal{E}/RC)e^{t/RC}dt,\nonumber\] з розв'язком\[V_C(t)=\mathcal{E}\left(1-e^{-t/RC}\right).\nonumber\]
Напруга починається з нуля і зростає експоненціально до\(\mathcal{E}\), при цьому характерна шкала часу задана\(RC\).
Коли перемикач кидається в\(b\), застосування закону напруги Кірхгофа призводить до\[V_R+V_C=0,\nonumber\] відповідного диференціального рівняння\[\frac{dV_C}{dt}+V_C/RC=0.\nonumber\]
Тут ми припускаємо, що ємність спочатку повністю заряджена так, що\(V_C(0) =\mathcal{E}\). Розчин, то, під час фази розряду, подається\[V_C(t)=\mathcal{E}e^{-t/RC}.\nonumber\]
Напруга починається\(\mathcal{E}\) і спадає експоненціально до нуля, знову ж таки з характерною шкалою часу, заданою\(RC\).
Логістичне рівняння
Переглянути підручник на YouTube
\(N(t)\)Дозволяти кількість особин в популяції на час\(t\), а нехай\(b\) і\(d\) буде середній на душу населення народжуваність і рівень смертності відповідно. За короткий час\(∆t\) кількість пологів у популяції становить\(b\Delta tN\), а кількість смертей -\(d\Delta tN\). Рівняння для\(N\) часу потім\(t + ∆t\) визначається бути\[N(t+\Delta t)=N(t)+b\Delta tN(t)-d\Delta tN(t),\nonumber\] які можуть бути переставлені на\[\frac{N(t+\Delta t)-N(t)}{\Delta t}=(b-d)N(t);\nonumber\] і як\(\Delta t\to 0\), і з\(r=b-d\), ми маємо\[\frac{dN}{dt}=rN.\nonumber\]
Це модель зростання Мальтузіанців (Thomas Malthus, 1766-1834), і це те саме рівняння, що і наша складна модель відсотків.
За мальтузіанською моделлю зростання чисельність населення зростає експоненціально, як і\[N(t)=N_0e^{rt},\nonumber\] де\(N_0\) початкова чисельність населення. Однак, коли приріст населення обмежений обмеженими ресурсами, евристична модифікація мальтузіанської моделі зростання призводить до рівняння Верхулста, \[\label{eq:15}\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right),\]де\(K\) називається несучою здатністю навколишнього середовища. Роблячи\(\eqref{eq:15}\) безрозмірне використання\(\tau = rt\) і\(x = N/K\) призводить до логістичного рівняння,\[\frac{dx}{d\tau}=x(1-x),\nonumber\] де можна припустити початкову умову\(x(0) = x_0 > 0\). Розділення змінних та інтеграція\[\int_{x_0}^x\frac{dx}{x(1-x)}=\int_0^{\tau}d\tau .\nonumber\]
Інтеграл з лівого боку можна зробити за допомогою методу часткових дробів:
\[\frac{1}{x(1-x)}=\frac{a}{x}+\frac{b}{1-x},\nonumber\]і метод прикриття дає\(a = b = 1\). Тому,\[\begin{aligned}\int_{x_0}^x\frac{dx}{x(1-x)}&=\int_{x_0}^x\frac{dx}{x}+\int_{x_0}^x\frac{dx}{(1-x)} \\ &=\ln\frac{x}{x_0}-\ln\frac{1-x}{1-x_0} \\ &=\ln\frac{x(1-x_0)}{x_0(1-x)} \\ &=\tau .\end{aligned}\]
Вирішуючи для\(x\), ми спочатку експонентіруем обидві сторони, а потім виділяємо\(x\):
\[\begin{align}\frac{x(1-x_0)}{x_0(1-x)}&=e^{\tau},\nonumber \\ x(1-x_0)&=x_0e^{\tau}-xx_0e^{\tau},\nonumber \\ x(1-x_0+x_0e^{\tau})&=x_0e^{\tau},\nonumber \\ x&=\frac{x_0}{x_0+(1-x_0)e^{-\tau}}.\label{eq:16}\end{align}\]
Ми спостерігаємо, що для\(x_0 > 0\), у нас\(\lim_{\tau\to\infty} x(\tau ) = 1\), що відповідає\[\underset{t\to\infty}{\lim}N(t)=K.\nonumber\]
Отже, населення збільшується в розмірах, поки не досягне несучої здатності свого середовища.
