5.6: Оптимізація
- Page ID
- 58075
У цьому розділі ми розглянемо науку оптимізації. Припустимо, що ви намагаєтеся знайти пару чисел з фіксованою сумою так, щоб добуток двох чисел був максимальним. Це приклад завдання оптимізації. Однак оптимізація не обмежується пошуком максимуму. Наприклад, розглянемо виробника, який хотів би мінімізувати свої витрати виходячи з певних критеріїв. Це ще один приклад проблеми оптимізації. Як бачите, оптимізація може включати знаходження або максимуму, або мінімуму.
Оптимізація може бути застосована до широкого сімейства різних функцій. Однак у цьому розділі ми зосередимося на пошуку максимумів і мінімумів квадратичних функцій. Існує велика кількість реальних додатків, які можна моделювати квадратичними функціями, тому ми виявимо, що це відмінна точка входу в дослідження оптимізації.
Пошук максимуму або мінімуму квадратичної функції
Розглянемо квадратичну функцію
\[f(x)=-x^{2}+4 x+2 \nonumber\]
Давайте завершимо квадрат, щоб помістити цю квадратичну функцію у формі вершини. По-перше, вирахуйте знак мінус.
\[f(x)=-\left[x^{2}-4 x-2\right] \nonumber\]
Візьмемо половину коефіцієнта\(x\) і квадрат, як в\([(1 / 2)(-4)]^{2}=4\). Додайте і відніміть цю суму, щоб рівняння було збалансованим.
\[f(x)=-\left[x^{2}-4 x+4-4-2\right] \nonumber\]
Фактор досконалий квадратний триноміал, об'єднайте константи в кінці, а потім перерозподіліть знак мінус, щоб помістити квадратичну функцію у вигляді вершини.
\[\begin{array}{l}{f(x)=-\left[(x-2)^{2}-6\right]} \\ {f(x)=-(x-2)^{2}+6}\end{array} \nonumber\]
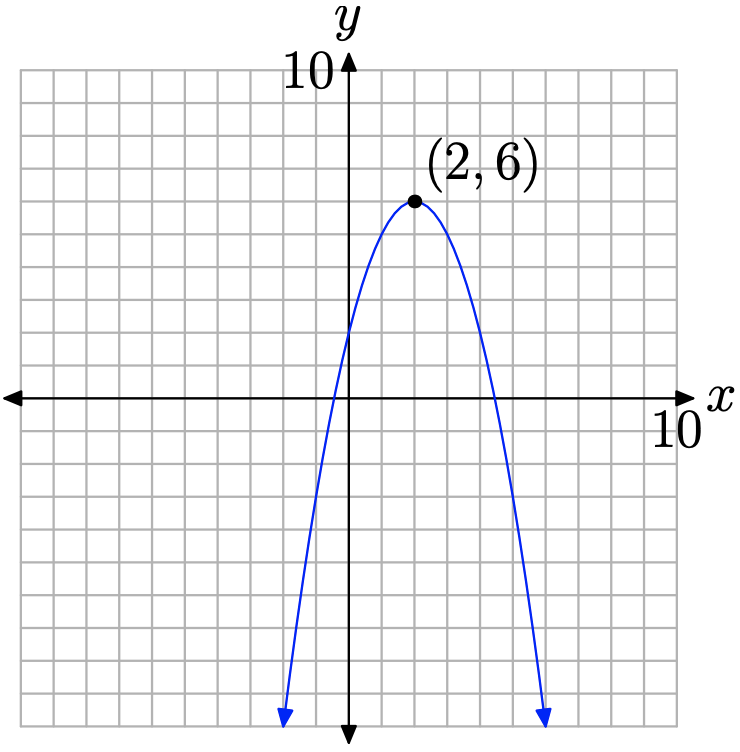
Це парабола, яка відкривається вниз, була зрушена 2 одиниці вправо і 6 одиниць вгору. Це розміщує вершину параболи в (2, 6), як показано на малюнку 1. Зауважте, що максимальне значення функції (y-значення) зустрічається у вершині параболи. Математик сказав би, що функція «досягає максимального значення 6 при\(x\) рівних 2».
Зверніть увагу, що 6 більше або дорівнює будь-якому іншому значенню y (значення функції), яке зустрічається на параболі. Це породжує наступне визначення.
Визначення: Максимальний
\(c\)Дозволяти бути в домені\(f\). \(f\)Функція, як кажуть, досягти максимуму при\(x=c\) якщо\(f(c) \geq f(x)\) для всіх\(x\) в області\(f\).
Далі давайте розглянемо квадратичну функцію, яка досягає мінімуму на своїй області.
Приклад\(\PageIndex{1}\)
Далі давайте розглянемо квадратичну функцію, яка досягає мінімуму на своїй області.
\[f(x)=2 x^{2}+12 x+12\]
Рішення
Фактор з 2. \[f(x)=2\left[x^{2}+6 x+6\right]\]
Візьмемо половину коефіцієнта х і квадрат, як в\([(1 / 2)(6)]^{2}=9\). Додайте і відніміть цю суму, щоб рівняння було збалансованим.
\[f(x)=2\left[x^{2}+6 x+9-9+6\right]\]
Розподіліть тріноміал і об'єднайте константи, а потім перерозподіліть 2 на наступному кроці.
\[\begin{array}{l}{f(x)=2\left[(x+3)^{2}-3\right]} \\ {f(x)=2(x+3)^{2}-6}\end{array}\]
Графік являє собою параболу, яка відкривається вгору, зміщена на 3 одиниці вліво і на 6 одиниць вниз. Це розміщує вершину на (−3, −6), як показано на рисунку\(\PageIndex{2}\). Зауважте, що мінімальне значення функції (y-значення) зустрічається у вершині параболи. Математик скаже, що функція «досягає мінімального значення −6 при x дорівнює −3.
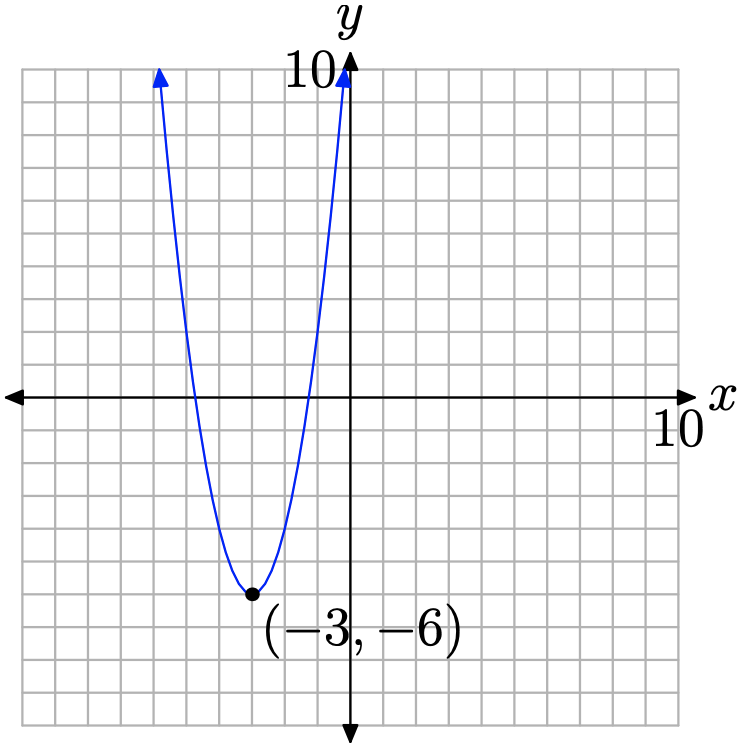
Зауважте, що −6 менше або дорівнює будь-якому іншому значенню y (значенню функції), яке зустрічається на параболі.
Цей останній приклад породжує наступне визначення.
Визначення
Нехай c знаходиться в області f. Функція f, як кажуть, досягає мінімуму при x = c, якщо\(f(c) \leq f(x)\) для всіх х в області f.
Скорочення для вершини
Тепер повинно бути зрозуміло, що вершина параболи відіграє вирішальну роль при оптимізації квадратичної функції. Ми також знаємо, що ми можемо завершити квадрат, щоб знайти координати вершини. Однак було б непогано, якби у нас був більш швидкий спосіб пошуку координат вершини. Давайте розглянемо загальну квадратичну функцію
\[y=a x^{2}+b x+c\]
і завершити квадрат, щоб знайти координати вершини. По-перше, враховуйте a.
\[y=a\left[x^{2}+\frac{b}{a} x+\frac{c}{a}\right]\]
Візьмемо половину коефіцієнта х і квадрат, як в\([(1 / 2)(b / a)]^{2}=[b /(2 a)]^{2}=b^{2} /\left(4 a^{2}\right)\). Додайте і відніміть цю суму, щоб рівняння було збалансованим.
\[y=a\left[x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}-\frac{b^{2}}{4 a^{2}}+\frac{c}{a}\right]\]
Помножте досконалий квадратний триноміал і зробіть еквівалентні дроби для постійних членів із загальним знаменником.
\[\begin{array}{l}{y=a\left[\left(x+\frac{b}{2 a}\right)^{2}-\frac{b^{2}}{4 a^{2}}+\frac{4 a c}{4 a^{2}}\right]} \\ {y=a\left[\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\right]}\end{array}\]
Нарешті, перерозподілити, що a. зверніть увагу, як множення на скасовує один a в знаменнику постійного терміна.
\[y=a\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a}\]
Ось ключова ідея. Результати залежать від значень a, b і c, але повинно бути зрозуміло, що координати вершини
\[\left(-\frac{b}{2 a}, \frac{4 a c-b^{2}}{4 a}\right)\]
Значення y вершини трохи важко запам'ятати, але значення x вершини легко запам'ятати.
Скорочення вершин
Задано параболу, представлену квадратичною функцією\[y=a x^{2}+b x+c\]
координата x вершини задається формулою\[x_{\text { vertex }}=-\frac{b}{2 a}\]
Давайте перевіримо це за допомогою квадратичної функції, наведеної в прикладі\(\PageIndex{1}\).
Приклад\(\PageIndex{2}\)
Використовуйте формулу,\(x_{\text { vertex }}=-b /(2 a)\) щоб знайти координату x вершини параболи, представленої квадратичною функцією у прикладі\(\PageIndex{1}\).
Рішення
У\(\PageIndex{1}\) прикладі квадратична функція була представлена рівнянням\[f(x)=2 x^{2}+12 x+12\]
У формі вершини\[f(x)=2(x+3)^{2}-6\]
координати вершини були легко помітні як (−3, −6) (див.\(\PageIndex{2}\) Рис. Давайте подивимося, що відкриває нова формула для координати x вершини.
Як завжди, порівняйте\(f(x)=2 x^{2}+12 x+12\) з\(f(x)=a x^{2}+b x+c\) і зверніть увагу, що a = 2, b = 12 і c = 12. Таким чином, x-координата вершини задається
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{12}{2(2)}=-3\]
Зверніть увагу, що це узгоджується з попереднім результатом (див. Малюнок\(\PageIndex{2}\)). Ми могли б знайти y-координату вершини з
\[y_{\text { vertex }}=\frac{4 a c-b^{2}}{4 a}=\frac{4(2)(12)-(12)^{2}}{4(2)}=\frac{-48}{8}=-6\]
але ми знаходимо цю формулу для y-координати вершини трохи важко запам'ятати. Нам простіше зробити наступне. Оскільки ми знаємо, що координата x вершини дорівнює x = −3, ми можемо знайти y-координату вершини, просто підставивши x = −3 у рівняння параболи. Тобто, з\(f(x)=2 x^{2}+12 x-12\),
\[f(-3)=2(-3)^{2}+12(-3)+12=-6\]
Давайте виділимо цю останню техніку.
Пошук координати y Вершини
Задано параболу, представлену квадратичною функцією\[f(x)=a x^{2}+b x+c\]
ми бачили, що координата x вершини задається x = −b/ (2a). Щоб знайти y-координату вершини, ймовірно, найпростіше оцінити функцію за адресою x = −b/ (2a). Тобто y-координата вершини задається
\[y_{\text { vertex }}=f\left(-\frac{b}{2 a}\right)\]
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{3}\)
Розглянемо параболу, що має рівняння\[f(x)=-2 x^{2}+3 x-8\]
Знайдіть координати вершини.
Рішення
Спочатку скористайтеся новою формулою, щоб знайти координату x вершини.
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{3}{2(-2)}=\frac{3}{4}\]
Далі підставляємо x = 3/4, щоб знайти відповідну y-координату.
\[\begin{aligned} f\left(\frac{3}{4}\right) &=-2\left(\frac{3}{4}\right)^{2}+3\left(\frac{3}{4}\right)-8 \\ &=-2\left(\frac{9}{16}\right)+\frac{9}{4}-8 \\ &=-\frac{9}{8}+\frac{18}{8}-\frac{64}{8} \\ &=-\frac{55}{8} \end{aligned}\]
Таким чином, координати вершини є (3/4, −55/8).
Додатки
Зараз ми в змозі зробити деякі програми оптимізації. Почнемо з легкого прикладу.
Приклад\(\PageIndex{4}\)
Знайти два дійсних числа x і y, що сума 50 і які мають добуток, який є максимальним.
Рішення
Перш ніж застосувати теорію попередніх прикладів, давайте просто трохи пограємо з цифрами, щоб відчути те, що нас просять зробити. Нам потрібно знайти два числа, які сумують 50, так що давайте почнемо з х = 5 і y = 45. Зрозуміло, що сума цих двох чисел дорівнює 50. З іншого боку, їх твір xy = (5) (45) = 225. Давайте помістимо цей результат в таблицю.
| х | у | xy |
|---|---|---|
| 5 | 45 | 225 |
Для другої здогадки виберіть x = 10 і y = 40. Сума цих двох чисел дорівнює 50 і їх добуток xy = 400. Для третього припущення виберіть x = 20 і y = 30. Сума цих двох чисел дорівнює 50 і їх добуток xy = 600. Давайте додамо ці результати в нашу таблицю.
| х | у | xy |
|---|---|---|
| 5 | 45 | 225 |
| 10 | 40 | 400 |
| 20 | 30 | 600 |
На сьогоднішній день найкращою парою є x = 20 і y = 30, тому що їх твір є максимумом в таблиці вище. Але чи є ще одна пара з більшим продуктом? Пам'ятайте, наша мета - знайти пару з продуктом, який є максимумом. Тобто наша пара повинна мати продукт більше, ніж будь-яка інша пара. Чи можете ви знайти пару, яка має товар більше 600?
Тепер, коли ми відчуваємо те, що нас просять зробити (знайдіть два числа, які становлять 50 і мають продукт, який є максимальним), давайте спробуємо підхід, який є більш абстрактним, ніж підхід «вгадай і перевіряй» наших таблиць. Нашим першим обмеженням є той факт, що сума чисел x і y повинна бути 50. Ми можемо змоделювати це обмеження за допомогою рівняння
\[x+y=50\]
Нас просять максимізувати продукт. Таким чином, ви хочете знайти формулу для продукту. Давайте давайте P представляти добуток x і y і запишемо
\[P=x y\]
Зауважте, що P є функцією двох змінних x і y, проте всі наші функції в цьому курсі досі були функцією однієї змінної. Отже, як ми можемо позбутися від однієї зі змінних? Просте, перше розв'язати рівняння (8) для y.
\[\begin{aligned} x+y &=50 \\ y &=50-x \end{aligned}\]
Тепер підставляємо рівняння (10) у твір рівняння (9).
\[P=x(50-x)\]
або, рівнозначно,
\[P=-x^{2}+50 x\]
Зауважте, що P тепер є функцією однієї змінної x. Зверніть увагу, що функція, визначена рівнянням (11), є квадратичною. Якщо порівнювати\(P=-x^{2}+50 x\) із загальною формою\(P=a x^{2}+b x+c\), зверніть увагу, що a = −1 і b = 50 (у нас немає необхідності того, що c = 0). Тому, якщо ми побудуємо P проти x, графік є параболою, яка відкривається вниз (див. Рис.\(\PageIndex{3}\)), і максимальне значення P буде відбуватися у вершині. X-координата вершини знайдено з
\[x_{\text { vertex }}=-\frac{b}{2 a}=-\frac{50}{2(-1)}=25\]
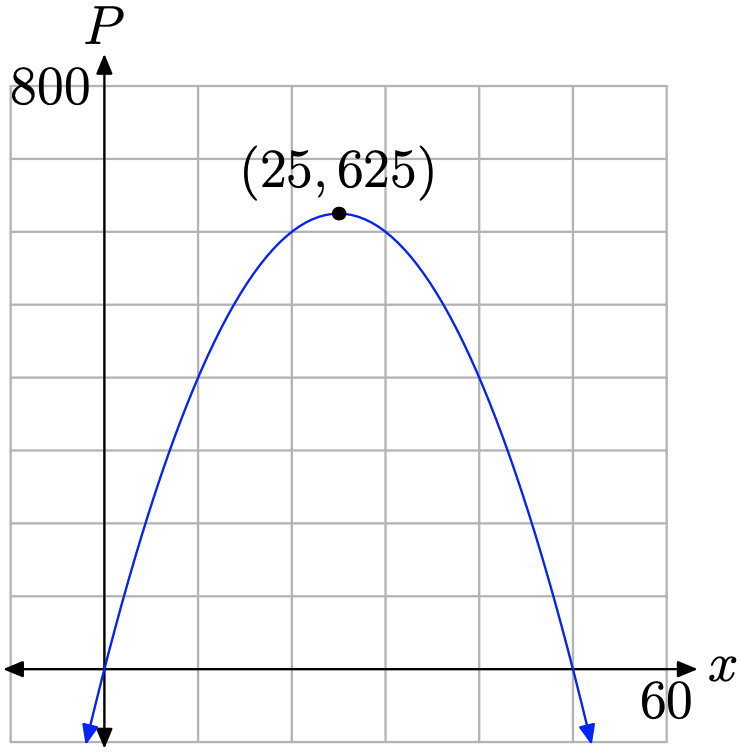
Таким чином, наше перше число - х = 25. Друге число у ми можемо знайти, підставивши x = 25 у рівняння (10).
\[y=50-x=50-25=25\]
Зверніть увагу, що сума x і y дорівнює x + y = 25 + 25 = 50. Є два способи, які ми можемо знайти їх продукт. Оскільки тепер ми знаємо числа x і y, ми можемо помножити, щоб знайти P = xy = (25) (25) = 625. Крім того, ми могли б замінити x = 25 у рівнянні (11), щоб отримати
\[P=-x^{2}+50 x=-(25)^{2}+50(25)=-625+1250=625\]
Коли ви порівнюєте цей результат з нашими експериментальними таблицями, все поєднується. Ми знайшли два числа х і у, що сума 50 з добутком, який є максимальним. Ніякі інші числа, які сумують 50, не мають більшого добутку.
Наша маленька формула\(x_{\text { vertex }}=-b /(2 a)\) виявилася потужним союзником. Спробуємо інший приклад.
Приклад\(\PageIndex{5}\)
Знайдіть два дійсних числа з різницею 8 таких, щоб сума квадратів двох чисел була мінімальною.
Рішення
Давайте почнемо з того, що х і у представляють числа, які ми шукаємо. Далі давайте трохи пограємо, як ми це робили в попередньому прикладі. Спробуйте x = 9 і y = 1. Різниця цих двох чисел, безумовно, 8. Сума квадратів цих двох чисел дорівнює\(S=9^{2}+1^{2}=82\). Поставимо цей результат в табличну форму.
| х | у | \(S=x^{2}+y^{2}\) |
|---|---|---|
| 9 | 1 | \ (S=x^ {2} +y^ {2}\) ">82 |
Для другого припущення виберіть x = 8 і y = 0. Різниця дорівнює x − y = 8 − 0 = 8, але цього разу сума квадратів дорівнює\(S=8^{2}+0^{2}=64\). Для третього припущення спробуйте x = 7 і y = −1. Знову ж таки, різниця дорівнює x − y = 7 − (−1) = 8, але сума квадратів тепер\(S=7^{2}+(-1)^{2}=50\). Давайте додамо ці результати в нашу таблицю.
| х | у | \(S=x^{2}+y^{2}\) |
|---|---|---|
| 9 | 1 | \ (S=x^ {2} +y^ {2}\) ">82 |
| 8 | 0 | \ (S=x^ {2} +y^ {2}\) ">64 |
| 7 | -1 | \ (S=x^ {2} +y^ {2}\) ">50 |
Поки що пара, яка мінімізує суму квадратів, дорівнює x = 7 і y = −1. Однак чи може бути інша пара з різницею 8 і сума квадратів менше 50? Експериментуйте далі, щоб побачити, чи можете ви найкраще поточний мінімум 50.
Спробуємо аналітичний підхід. Наше перше обмеження полягає в тому, що різниця двох чисел повинна дорівнювати 8. Це легко виражається як
\[x-y=8\]
Далі нас просять мінімізувати суму квадратів двох чисел. Для цього потрібно знайти формулу для суми квадратів. Нехай S представляють суму квадратів x і y. таким чином,
\[S=x^{2}+y^{2}\]
Зверніть увагу, що S є функцією двох змінних. Ми можемо усунути одну зі змінних, вирішивши рівняння (13) для x,\[x=y+8\]
потім підставляючи цей результат у рівняння (14).
\[S=(y+8)^{2}+y^{2}\]
Розширюйте і спрощуйте. \[S=2 y^{2}+16 y+64\]
Порівняйте\(S=2 y^{2}+16 y+64\) із загальною квадратикою\(S=a y^{2}+b y+c\) і зверніть увагу, що a = 2 і b = 16. Таким чином, ділянка S проти y буде параболою, яка відкривається вгору (див. Рис.\(\PageIndex{4}\)) і мінімальне значення S буде відбуватися у вершині. Y-координата вершини знайдено з
\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{16}{2(2)}=-4\]
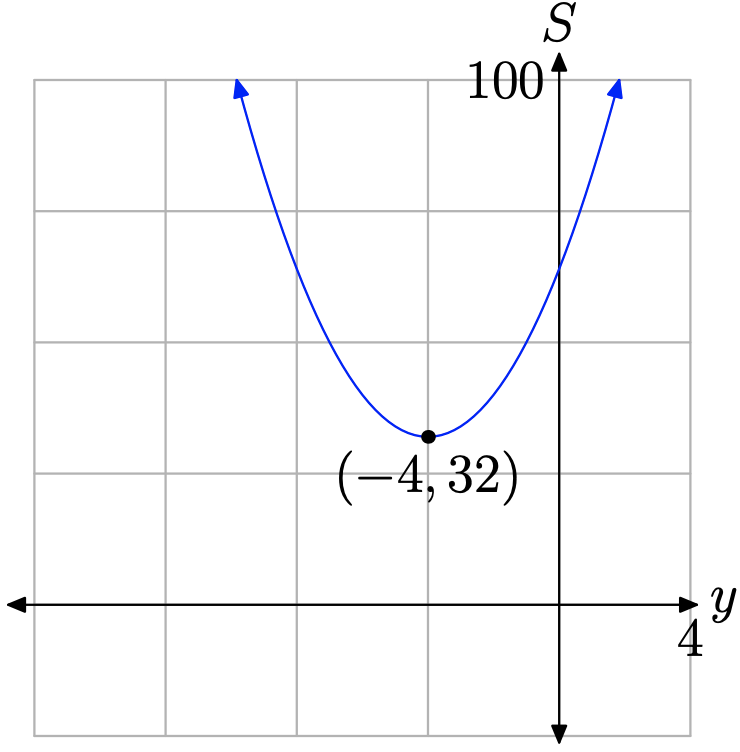
Таким чином, перше число, яке ми шукаємо, є y = −4. Друге число ми можемо знайти, підставивши y = −4 у рівняння (15).
\[x=y+8=(-4)+8=4\]
Отже, числа, які ми шукаємо, є x = 4 та y = −4. Зауважте, що різниця цих двох чисел дорівнює x−y = 4− (−4) = 8, а сума їх квадратів є меншою\(S=(4)^{2}+(-4)^{2}=32\), ніж найкращий результат, знайдений у нашому табличному експерименті вище. Дійсно, наші роботи показують, що це найменша можлива величина S.
Крім того, ви можете знайти S, підставивши y = −4 у рівнянні (16). Ми залишимо це нашим читачам, щоб переконатися, що це також дає мінімальне значення S = 32.
Давайте розглянемо інший додаток.
Приклад\(\PageIndex{6}\)
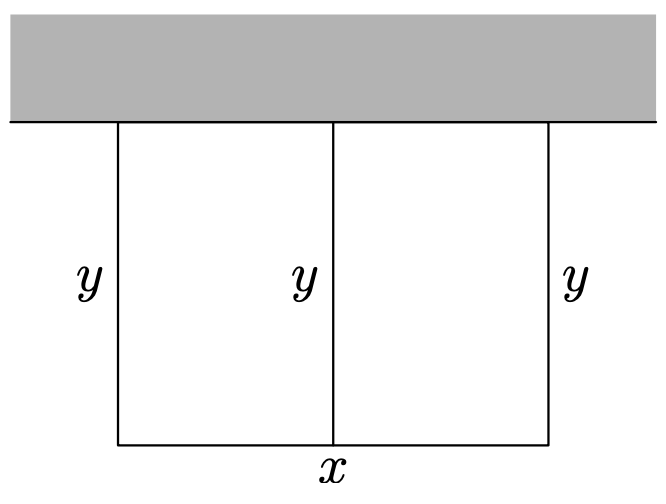
Мері хоче загородити прямокутний сад, щоб тримати оленів від їжі її фрукти і овочі. Одна сторона її саду примикає до її стіни сараю, так що їй не потрібно буде огороджувати цю сторону. Однак вона також хоче використовувати матеріал для поділу прямокутного саду на дві секції (див. Малюнок\(\PageIndex{5}\)). Вона може дозволити собі купити 80 футів огорожі, щоб використовувати для периметра і ділянки, що розділяє прямокутний сад. Які розміри дозволять максимально збільшити загальну площу прямокутного саду?
Рішення
Знову ж таки, перш ніж взяти алгебраїчний підхід, давайте просто поекспериментуємо. Зверніть увагу, що ми позначили ширину буквою x і висоту буквою y на нашому ескізі саду на малюнку\(\PageIndex{5}\).
Існує в цілому 80 футів огорожі матеріалу. Припустимо, що ми пустимо y = 5 футів. Оскільки є три сторони довжини y = 5 футів, ми використовували 15 футів матеріалу. Це залишає 65 футів матеріалу, який буде використаний для огорожі ширини саду. Тобто ширина дорівнює х = 65 футів. Таким чином, розміри саду складають х = 65 футів на y = 5 футів. Площа дорівнює добутку цих двох заходів, так що\(A=325 \mathrm{ft}^{2}\). Покладемо цей результат в таблицю.
| х | у | А = XY |
|---|---|---|
| 65 футів | 5 футів | 325\(\text{ft}^{2}\) |
Припустимо замість цього, що ми дозволяємо висоті бути y = 10 футів. Знову ж таки, є три секції з такою довжиною, тому для цього знадобиться 30 футів матеріалу. Це залишає 50 футів матеріалу, тому ширина х = 50 футів. Площа є продуктом цих двох заходів, так що\(A=500 \mathrm{ft}^{2}\). В якості третього експерименту нехай висота y = 15 футів. Віднімаючи три цих довжини від 80 футів, бачимо, що ширина х = 35 футів. Площа є продуктом цих заходів, так що\(A=525 \mathrm{ft}^{2}\). Давайте додамо ці останні два експерименти з числом до нашої таблиці.
| х | у | А = XY |
|---|---|---|
| 65 футів | 5 футів | 325\(\text{ft}^{2}\) |
| 50 футів | 10 футів | 500\(\text{ft}^{2}\) |
| 35 футів | 15 футів | 525\(\text{ft}^{2}\) |
У цей момент останній набір розмірів дає максимальну площу, але чи можливо, що інший вибір x і y дасть більшу площу? Експериментуйте далі з номерами за вашим вибором, щоб побачити, чи зможете ви знайти розміри, які дадуть площу більше поточного максимуму в таблиці, а саме 525\(\mathrm{ft}^{2}\).
Давайте тепер зателефонуємо про те, що ми дізналися в цьому розділі, щоб атакувати цю модель. По-перше, ми обмежені кількістю матеріалу, який ми маємо для роботи, загалом 80 футів огорожі. Це обмеження вимагає, щоб 3 рази висота саду, додана до ширини городу, дорівнювала наявному кількості огороджувального матеріалу. В символах,
\[x+3 y=80\]
Нас просять максимально збільшити площу, тому ми зосереджуємо свої зусилля на пошуку формули площі прямокутного саду. Оскільки площа А прямокутного саду є твором ширини та висоти,\[A=x y\]
Тепер у нас є формула для площі прямокутного саду, але, на жаль, у нас є площа А як функція двох змінних. Нам потрібно усунути ту чи іншу з цих змінних. Це легко зробити, вирішивши рівняння (18) для x.\[x=80-3 y\]
Далі підставляємо цей результат у рівняння (19), щоб отримати\[A=(80-3 y) y\]
або, рівнозначно,\[A=-3 y^{2}+80 y\]
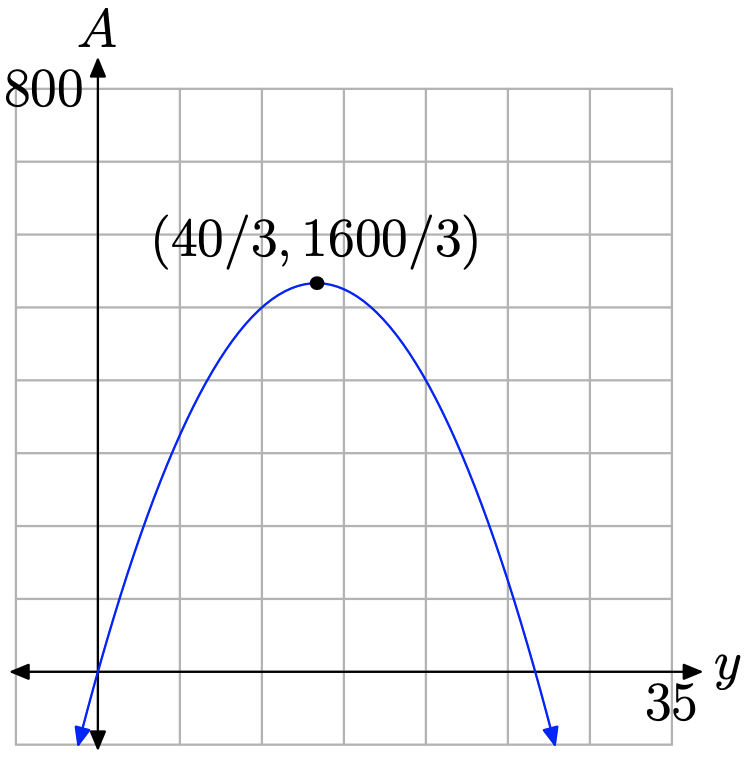
Зауважте, що ми висловили область A як функцію однієї змінної y, а функція, визначена рівнянням (21), є квадратичною. Порівняйте\(A=-3 y^{2}+80 y\) із загальною формою\(A=a y^{2}+b y+c\) і зверніть увагу, що a = −3 і b = 80 (у нас немає необхідності того, що c = 0). Тому, якщо побудувати A проти y, графік є параболою, яка відкривається вниз (див. Рисунок\(\PageIndex{6}\)), тому максимальне значення A буде відбуватися у вершині. Y-координата вершини знайдено з
\[y_{\mathrm{vertex}}=-\frac{b}{2 a}=-\frac{80}{2(-3)}=\frac{80}{6}=\frac{40}{3}\]
Щоб знайти ширину прямокутного саду, підставимо y = 40/3 в рівняння (20) і вирішуємо для x.
\[x=80-3 y=80-3\left(\frac{40}{3}\right)=80-40=40\]
Таким чином, ширина прямокутного саду становить 40 футів. Ми можемо знайти площу саду, помноживши ширину і висоту.
\[A=x y=(40)\left(\frac{40}{3}\right)=\frac{1600}{3}=533 \frac{1}{3}\]
Зверніть увагу, що отримана площа\(A=533 \frac{1}{3} \mathrm{ft}^{2}\), лише трохи більша остання таблична запис, знайдена в наших числових експериментах.
Ви також можете знайти площу прямокутної області, підставивши y = 40/3 в рівняння (21). Ми залишимо це нашим читачам, щоб перевірити, чи це забезпечує ту саму міру для площі. Ви також помітите, що друга координата вершини на малюнку\(\PageIndex{6}\) - це максимальна площа\(A=1600 / 3 \mathrm{ft}^{2}\).
Вправа
Вправа\(\PageIndex{1}\)
Знайти точне максимальне значення функції\(f(x) = −x^2−3x\).
- Відповідь
-
\(\frac{9}{4}\)
Вправа\(\PageIndex{2}\)
Знайти точне максимальне значення функції\(f(x) = −x^2−5x−2\).
Вправа\(\PageIndex{3}\)
Знайти вершину графа функції\(f(x) = −3x^2−x−6\).
- Відповідь
-
\((−\frac{1}{6}, −\frac{71}{12})\)
Вправа\(\PageIndex{4}\)
Знайдіть діапазон функції\(f(x) = −2x^2−9x+2\).
Вправа\(\PageIndex{5}\)
Знайти точне максимальне значення функції\(f(x) = −3x^2−9x−4\).
- Відповідь
-
\(\frac{11}{4}\)
Вправа\(\PageIndex{6}\)
Знайдіть рівняння осі симетрії графіка функції\(f(x) = −x^2−5x−9\).
Вправа\(\PageIndex{7}\)
Знайти вершину графа функції\(f(x) = 3x^2+3x+9\).
- Відповідь
-
\((−\frac{1}{2}, \frac{33}{4})\)
Вправа\(\PageIndex{8}\)
Знайти точне мінімальне значення функції\(f(x) = x^2+x+1\).
Вправа\(\PageIndex{9}\)
Знайти точне мінімальне значення функції\(f(x) = x^2+9x\).
- Відповідь
-
\(−\frac{81}{4}\)
Вправа\(\PageIndex{10}\)
Знайдіть діапазон функції\(f(x) = 5x^2−3x−4\).
Вправа\(\PageIndex{11}\)
Знайдіть діапазон функції\(f(x) = −3x^2+8x−2\).
- Відповідь
-
\((−\infty, \frac{10}{3}]\)= {\(x|x \le \frac{10}{3}\)}
Вправа\(\PageIndex{12}\)
Знайти точне мінімальне значення функції\(f(x) = 2x^2+5x−6\).
Вправа\(\PageIndex{13}\)
Знайдіть діапазон функції\(f(x) = 4x^2+9x−8\).
- Відповідь
-
\([−\frac{209}{16}, \infty)\)= {\(x|x \ge −\frac{209}{16}\)}
Вправа\(\PageIndex{14}\)
Знайти точне максимальне значення функції\(f(x) = −3x^2−8x−1\).
Вправа\(\PageIndex{15}\)
Знайдіть рівняння осі симетрії графіка функції\(f(x) = −4x^2−2x+9\).
- Відповідь
-
\(x = −\frac{1}{4}\)
Вправа\(\PageIndex{16}\)
Знайти точне мінімальне значення функції\(f(x) = 5x^2+2x−3\).
Вправа\(\PageIndex{17}\)
М'яч кидається вгору зі швидкістю 8 футів/с від вершини 182 футів висотою будівлі. Скільки секунд потрібно, щоб м'яч досяг максимальної висоти? Округлите відповідь до сотих часток секунди.
- Відповідь
-
0,25
Вправа\(\PageIndex{18}\)
М'яч кидається вгору зі швидкістю 9 ft/s від вершини 143 футів висотою будівлі. Скільки секунд потрібно, щоб м'яч досяг максимальної висоти? Округлите відповідь до сотих часток секунди.
Вправа\(\PageIndex{19}\)
М'яч кидається вгору зі швидкістю 52 ft/s від вершини 293 футів висотою будівлі. Яка максимальна висота кулі? Округлите відповідь до найближчої сотої частки фута.
- Відповідь
-
335. 25
Вправа\(\PageIndex{20}\)
М'яч кидається вгору зі швидкістю 23 ft/s від вершини 71 фут висотою будівлі. Яка максимальна висота кулі? Округлите відповідь до найближчої сотої частки фута.
Вправа\(\PageIndex{21}\)
Знайдіть два числа, сума яких дорівнює 20 і добуток яких максимальна.
- Відповідь
-
10 і 10
Вправа\(\PageIndex{22}\)
Знайдіть два числа, сума яких дорівнює 36 і добуток яких максимальна.
Вправа\(\PageIndex{23}\)
Знайдіть два числа, різниця яких дорівнює 12 і добуток яких мінімальна.
- Відповідь
-
6 і −6
Вправа\(\PageIndex{24}\)
Знайдіть два числа, різниця яких дорівнює 24 і чиї добуток мінімальна.
Вправа\(\PageIndex{25}\)
Одне число на 3 більше, ніж двічі друге число. Знайдіть два таких числа, щоб їх твір було мінімальним.
- Відповідь
-
\(\frac{3}{2}\)і\(−\frac{3}{4}\)
Вправа\(\PageIndex{26}\)
Одне число в 2 більше, ніж в 5 разів друге число. Знайдіть два таких числа, щоб їх твір було мінімальним.
Вправа\(\PageIndex{27}\)
Серед усіх пар чисел, сума яких дорівнює − 10, знайдіть таку пару, щоб сума їх квадратів була найменшою можливою.
- Відповідь
-
−5, −5
Вправа\(\PageIndex{28}\)
Серед усіх пар чисел, сума яких дорівнює − 24, знайдіть таку пару, щоб сума їх квадратів була найменшою можливою.
Вправа\(\PageIndex{29}\)
Серед всіх пар чисел, сума яких дорівнює 14, знайдіть пару таку, щоб сума їх квадратів була найменшою з можливих.
- Відповідь
-
7, 7
Вправа\(\PageIndex{30}\)
Серед всіх пар чисел, сума яких дорівнює 12, знайдіть пару таку, щоб сума їх квадратів була найменшою з можливих.
Вправа\(\PageIndex{31}\)
Серед усіх прямокутників, що мають периметр 40 футів, знайдіть розміри (довжину і ширину) того, що має найбільшу площу.
- Відповідь
-
10 футів на 10 футів
Вправа\(\PageIndex{32}\)
Серед усіх прямокутників, що мають периметр 100 футів, знайдіть розміри (довжину і ширину) того, що має найбільшу площу.
Вправа\(\PageIndex{33}\)
Фермер з 1700 метрів огорожі хоче обгородити прямокутну ділянку, який межує з річкою. Якщо уздовж річки не потрібно паркан, яка найбільша площа, яку можна огородити?
- Відповідь
-
361250 квадратних метрів
Вправа\(\PageIndex{34}\)
Ранчер з 1500 метрів огорожі хоче обкласти прямокутну ділянку, який межує з річкою. Якщо уздовж річки не потрібно забору, а сторона, паралельна річці, має довжину х метрів, знайдіть значення x, яке дасть найбільшу площу прямокутника.
Вправа\(\PageIndex{35}\)
Парковий рейнджер з 400 метрів огорожі хоче обкласти прямокутну ділянку, який межує з річкою. Якщо уздовж річки не потрібно забору, а сторона, паралельна річці, має довжину х метрів, знайдіть значення x, яке дасть найбільшу площу прямокутника.
- Відповідь
-
200
Вправа\(\PageIndex{36}\)
Ранчер з 1000 метрів огорожі хоче обкласти прямокутну ділянку, який межує з річкою. Якщо уздовж річки не потрібно паркан, яка найбільша площа, яку можна огородити?
Вправа\(\PageIndex{37}\)
Нехай х представляють попит (число, яке публіка буде купувати) на об'єкт і нехай p представляють ціну одиниці об'єкта (у доларах). Припустимо, що ціна одиниці і попит лінійно пов'язані рівнянням\(p = −\frac{1}{3}x + 40\).
- Висловіть дохід R (суму, зароблену продажем об'єктів) як функцію попиту х.
- Знайдіть попит, який дозволить максимізувати дохід.
- Знайдіть ціну за одиницю, яка дозволить максимізувати дохід.
- Який максимальний дохід?
- Відповідь
-
- \(R = −\frac{1}{3}x^2+40x\)
- x = 60 об'єктів
- p = 20 доларів
- Р = $1200
Вправа\(\PageIndex{38}\)
Нехай х представляють попит (число, яке публіка буде купувати) на об'єкт і нехай p представляють ціну одиниці об'єкта (у доларах). Припустимо, що ціна одиниці і попит лінійно пов'язані рівнянням\(p = −\frac{1}{5}x + 200\).
- Висловіть дохід R (суму, зароблену продажем об'єктів) як функцію попиту х.
- Знайдіть попит, який дозволить максимізувати дохід.
- Знайдіть ціну за одиницю, яка дозволить максимізувати дохід.
- Який максимальний дохід?
Вправа\(\PageIndex{39}\)
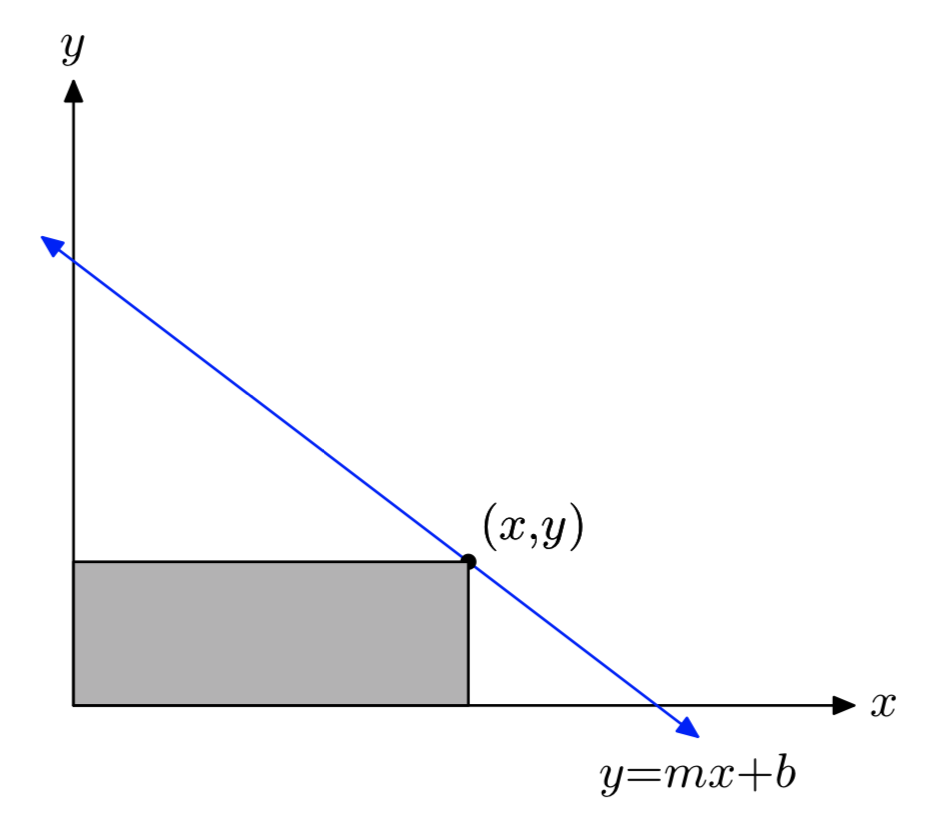
Точка з першого квадранта вибирається на лінії y = mx + b. лінії проводять від цієї точки паралельно осям, щоб утворити прямокутник під лінією в першому квадранті. Серед всіх таких прямокутників знайдіть розміри прямокутника з максимальною площею. Яка максимальна площа? Припустімо m < 0.
- Відповідь
-
\(x = −\frac{b}{2m}\),
\(y = \frac{b}{2}\),
\(A = −\frac{b^2}{4m}\)
Вправа\(\PageIndex{40}\)
Ранчер бажає загородити прямокутну ділянку. Східно-західні сторони прямокутника потребують більш сильної опори через переважаючі східно-західні штормові вітри. Отже, вартість огорожі для східно-західних сторін прямокутної ділянки становить 18 доларів за фут. Вартість огорожі північно-південних сторін прямокутної ділянки становить 12 доларів за фут. Знайдіть розмір максимально можливої прямокутної площі, яку можна обгородити за 7200 доларів.
