8.4: Квадратична формула

Спочатку ми почнемо з визначення квадратного рівняння.

Квадратне рівняння

Поліноміальне рівняння другого ступеня виду$a$, $$ax^2 + bx + c =0 \nonumber$$ де$b$, і$c$ є будь-якими дійсними числами, називається квадратним рівнянням в$x$.

Мета цього розділу - розробити формульний ярлик, який забезпечить точні розв'язки квадратного рівняння ax2+bx+c = 0. Почнемо з переміщення постійного члена на іншу сторону рівняння.

$$\begin{array}{rlrl}{a x^{2}+b x+c} & {=0} & {} & \color{Red} {\text { Quadratic equation. }} \\ {a x^{2}+b x} & {=-c} & {} & \color{Red} {\text { Subtract } c \text { from both sides. }}\end{array} \nonumber$$

Готуючись до завершення квадрата, далі ділимо обидві сторони рівняння на$a$.

$$x^{2}+\dfrac{b}{a} x=-\dfrac{c}{a} \quad \text { Divide both sides by } a \nonumber$$

Тепер завершуємо квадрат. Візьміть половину коефіцієнта$x$, потім вирівняйте результат.

$\dfrac{1}{2} \cdot \dfrac{b}{a}=\dfrac{b}{2 a}$коли в квадраті дає$\left(\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}$

Тепер ми додаємо$\dfrac{b^{2}}{4 a^{2}}$ до обох сторін рівняння.

$$x^{2}+\dfrac{b}{a} x+\dfrac{b^{2}}{4 a^{2}}=-\dfrac{c}{a}+\dfrac{b^{2}}{4 a^{2}} \quad \color {Red} \text { Add } b^{2} /\left(4 a^{2}\right) \text { to both sides. } \nonumber$$

Ліворуч ми враховуємо ідеальний квадратний триноміал. Праворуч робимо еквівалентні дроби із загальним знаменником.

$$\begin{array}{ll}{\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{c}{a} \cdot \dfrac{4 a}{4 a}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { On the left, factor. On the right, }} \\ {} & \color {Red} {\text { create equivalent fractions with }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=-\dfrac{4 a c}{4 a^{2}}+\dfrac{b^{2}}{4 a^{2}}} & \color {Red} {\text { Multiply numerators and denominators. }} \\ {\left(x+\dfrac{b}{2 a}\right)^{2}=\dfrac{b^{2}-4 a c}{4 a^{2}}} & \color {Red} {\text { Add fractions. }}\end{array} \nonumber$$

Коли ми беремо квадратний корінь, є дві відповіді.

$$x+\dfrac{b}{2 a}=\pm \sqrt{\dfrac{b^{2}-4 a c}{4 a^{2}}} \quad \color {Red} \text { Two square roots. } \nonumber$$

Коли ви берете квадратний корінь дробу, ви берете квадратний корінь як чисельника, так і знаменника.

$$\begin{aligned} x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{\sqrt{4 a^{2}}} \\ x+\dfrac{b}{2 a} &=\pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Simplify: } \sqrt{4 a^{2}}=2 a \\ x &=-\dfrac{b}{2 a} \pm \dfrac{\sqrt{b^{2}-4 a c}}{2 a} \quad \color {Red} \text { Subtract } b /(2 a) \text { from both sides } \end{aligned} \nonumber$$

Оскільки обидва дроби мають однаковий знаменник, ми можемо додавати і віднімати чисельники і поставити відповідь над спільним знаменником.

$$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber$$

Квадратична формула

Рівняння$a x^{2}+b x+c=0$ називається квадратним рівнянням. Її розв'язки задаються $$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber$$ так званої квадратичної формулою.

Ух! На щастя, результат набагато простіше застосувати, ніж розвивати! Спробуємо кілька прикладів.

Приклад$\PageIndex{1}$

Вирішити для$x: x^{2}-4 x-5=0$

Рішення

Пара цілих чисел$1,−5$ має$ac = −5$ добуток і суму$b = −4$. Звідси і це триноміальні чинники.

$$\begin{array}{r}{x^{2}-4 x-5=0} \\ {(x+1)(x-5)=0}\end{array} \nonumber$$

Тепер ми можемо використовувати властивість нульового продукту для запису:

$$\begin{array}{rlrl}{x+1} & {=0} & {\text { or }} & {x-5} & {=0} \\ {x} & {=-1} & {} & {x} & {=5}\end{array} \nonumber$$

Таким чином, рішення є$x =−1$ і$x = 5$. Тепер давайте дамо квадратичну формулу спробувати. Спочатку ми повинні порівняти наше рівняння з квадратним рівнянням, потім визначити значення$a$$b$, і$c$.

$$\begin{array}{l}{a x^{2}+b x+c=0} \\ {x^{2}-4 x-5=0}\end{array} \nonumber$$

Порівнюючи рівняння, ми бачимо$a = 1$, що$b = −4$, і$c = −5$. Тепер ми підключимо ці числа в квадратичну формулу. Спочатку замініть кожне входження$a$$b$, а$c$ в квадратичній формулі відкритими дужками.

\ [\ почати {вирівняний}
х &=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ quad\ color {Червоний}\ текст {Квадратична формула.}\\ x& = {\ dfrac {- (\ quad)\ pm\ sqrt {(\ quad) ^ {2} -4 ()}} {2 (2})}\ quad\ quad\ color {Червоний}\ текст {Замінити} a, b,\ text {і} c\ text {з відкритими дужками.}}\ end {вирівняний}\ номер\]

Тепер ми можемо підставити:$1$ for$a$,$−4$ for$b$, і$−5$ for$c$.

$$\begin{array}{ll}{x=\dfrac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-5)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a,-4 \text { for } b} \\ {x=\dfrac{4 \pm \sqrt{16+20}}{2}} & \color {Red} {\text { Simplify. Exponent first, then }} \\ {x=\dfrac{4 \pm \sqrt{36}}{2}} & \color {Red} {\text { Add: } 16+20=36} \\ {x=\dfrac{4 \pm 6}{2}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber$$

Зверніть увагу, що через символу «плюс або мінус» у нас є дві відповіді.

$$\begin{array}{ll}{x=\dfrac{4-6}{2}} & \text {or} & {x=\dfrac{4+6}{2}} \\ {x=\dfrac{-2}{2}} && {x=\dfrac{10}{2}} \\ {x=-1} && {x=5}\end{array} \nonumber$$

Зауважте, що ці відповіді відповідають відповідям, знайденим за допомогою тесту ac-test для фактора триноміалу.

Вправа$\PageIndex{1}$

Вирішити для$x: x^{2}-8x+12=0$

Відповідь

$2$,$6$

Приклад$\PageIndex{2}$

Вирішити для$x : x^{2}=5 x+7$

Рішення

Рівняння нелінійне, зробіть одну сторону нулем.

$$\begin{array}{rlrl}{x^{2}} & {=5 x+7} & {} & \color {Red} {\text { Original equation. }} \\ {x^{2}-5 x-7} & {=0} & {} & \color {Red} {\text { Nonlinear. Make one side zero. }}\end{array} \nonumber$$

Порівняйте$x^2 −5x−7 = 0$ з$ax^2 + bx + c = 0$ і зверніть увагу$a = 1$, що$b = −5$,, і$c = −7$. Замініть кожне входження$a$$b$, і$c$ відкритими дужками підготувати квадратичну формулу для підстановки.

$$\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color {Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color {Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber$$

Замінник$a$,$1$$−5$ для$b$, і$−7$ для$c$.

$$\begin{array}{ll}{x=\dfrac{-(-5) \pm \sqrt{(-5)^{2}-4(1)(-7)}}{2(1)}} & \color {Red} {\text { Substitute: } a=1, b=-5, c=-7} \\ {x=\dfrac{5 \pm \sqrt{25+28}}{2}} & \color {Red} {\text { Exponents and multiplication first. }} \\ {x=\dfrac{5 \pm \sqrt{53}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber$$

Перевірка: Використовуйте калькулятор для перевірки кожного рішення (див. Рис.$\PageIndex{1}$). Зверніть увагу, що при$\mathbf{X}$ зберіганні$(5-\sqrt{53}) / 2$ в, ми повинні оточити чисельник в дужках.

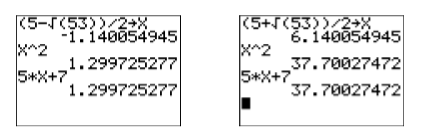
Малюнок$\PageIndex{1}$: Перевірка$(5-\sqrt{53}) / 2$ і$(5+\sqrt{53}) / 2$.

На кожному зображенні на малюнку$\PageIndex{1}$, після зберігання рішення в$\mathbf{X}$, зверніть увагу, що ліва і права сторони вихідного рівняння$x^2 =5 x + 7$ дають однакове число, перевіряючи, що наші рішення правильні.

Вправа$\PageIndex{2}$

Вирішити для$x : x^{2}+7 x=10$

Відповідь

$(-7+\sqrt{89}) / 2,(-7-\sqrt{89}) / 2$

Окрім розміщення всіх квадратних коренів у просту радикальну форму, іноді потрібно звести відповідь до найнижчих показників.

Приклад$\PageIndex{3}$

Вирішити для$x : 7 x^{2}-10 x+1=0$

Рішення

Порівняйте$7x^2 −10x + 1 = 0$ з$ax^2 + bx + c = 0$ і зверніть увагу$a = 7$, що$b = −10$,, і$c = 1$. Замініть кожне входження$a$$b$, і$c$ відкритими дужками підготувати квадратичну формулу для підстановки.

\ [\ почати {вирівняний}
х &=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\ квадратний\ колір {Червоний}\ текст {Квадратична формула.}\\
x &=\ dfrac {- (\ quad)\ pm\ sqrt {() ^ {2} -4 () ()}} {2} quad\ color {Red}\ text {Замінити} a, b,\ text {і} c\ text {з відкритими дужками.}
\ кінець {вирівняний}\ nonumber\]

Замінник$a$,$7$$−10$ для$b$, і$1$ для$c$.

$$\begin{array}{ll}{x=\dfrac{-(-10) \pm \sqrt{(-10)^{2}-4(7)(1)}}{2(7)}} & \color {Red} {\text { Substitute: } 7 \text { for } a} \\ {x=\dfrac{10 \pm \sqrt{100-28}}{14}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {x=\dfrac{10 \pm \sqrt{72}}{14}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber$$

У цьому випадку зверніть увагу, що ми можемо виділити ідеальний квадрат, а саме$\sqrt{36}$.

$$\begin{array}{ll}{x=\dfrac{10 \pm \sqrt{36} \sqrt{2}}{14}} & \color {Red} {\sqrt{72}=\sqrt{36} \sqrt{2}} \\ {x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber$$

Нарешті, зверніть увагу, що і чисельник, і знаменник діляться на$2$.

\ [\ begin {вирівняний}
x&=\ dfrac {\ tfrac {10\ pm 6\ sqrt {2}} {2}} {\ tfrac {14} {2}}\ quad\ color {Червоний}\ text {Розділити чисельник і знаменник на} 2. \\
x&=\ dfrac {\ trac {10} {2}\ pm\ tfrac {6\ sqrt {2}} {\ trac {14} {2}}\ квадратний\ колір {Червоний}\ текст {Розподілити} 2.\\ x&=\ dfrac {5\ pm 3\ sqrt {2}} {7}\ квадратний\\ квадратний\ {Червоний}\ текст {Спрощення.}
\ кінець {вирівняний}\ nonumber\]

Альтернативне спрощення: Замість того, щоб ділити чисельник і знаменник на$2$, деякі вважають за краще множник і скасувати, як показано нижче.

$$\begin{array}{ll}{x=\dfrac{10 \pm 6 \sqrt{2}}{14}} & \color {Red} {\text { Original answer. }} \\ {x=\dfrac{2(5 \pm 3 \sqrt{2})}{2(7)}} & \color {Red} {\text { Factor out a } 2} \\ {x=\dfrac{\not{2}(5 \pm 3 \sqrt{2})}{\not{2}(7)}} & \color {Red} {\text { Cancel. }} \\ {x=\dfrac{5 \pm 3 \sqrt{2}}{7}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber$$

Зверніть увагу, що ми отримуємо той же відповідь, використовуючи цю методику.

Вправа$\PageIndex{3}$

Вирішити для$x : 3 x^{2}+8 x+2=0$

Відповідь

$(-4+\sqrt{10}) / 3,(-4-\sqrt{10}) / 3$

Приклад$\PageIndex{4}$

Об'єкт запускається вертикально, а його висота$y$ (у футах) над рівнем землі задається рівнянням$y = 320+192t−16t^2$, де - час (у секундах), який минув з моменту його запуску. Скільки часу має пройти після запуску, перш ніж об'єкт повернеться на рівень землі? Розмістивши відповідь в простій формі і зменшивши, скористайтеся вашим калькулятором, щоб округлити відповідь до найближчої десятої частки секунди.

Рішення

Коли об'єкт повертається на рівень землі, його висота$y$ над рівнем землі становить$y = 0$ фути. Щоб знайти час, коли це відбувається, підставляємо$y = 0$ формулу$y = 320 + 192t−16t^2$ і вирішуємо для$t$.

$$\begin{array}{ll}{y=320+192 t-16 t^{2}} & \color {Red} {\text { Original equation. }} \\ {0=320+192 t-16 t^{2}} & \color {Red} {\text { Set } y=0}\end{array} \nonumber$$

Кожен з коефіцієнтів ділиться на$−16$.

$$0=t^{2}-12 t-20 \quad \color{Red} \text { Divide both sides by }-16 \nonumber$$

Порівняйте$t^2−12t−20 = 0$ з$at^2 +bt+c = 0$ і зверніть увагу$a = 1$, що$b = −12$,, і$c = −20$. Замініть кожне входження$a$$b$, і$c$ відкритими дужками підготувати квадратичну формулу для підстановки. Зауважте, що ми вирішуємо для цього часу, ні$x$.

$$\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color {Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color {Red} {\text { Replace } a, b, \text { and } c \text { with open parentheses. }}\end{array} \nonumber$$

Замінник$a$,$1$$−12$ для$b$, і$−20$ для$c$.

$$\begin{array}{ll}{t=\dfrac{-(-12) \pm \sqrt{(-12)^{2}-4(1)(-20)}}{2(1)}} & \color {Red} {\text { Substitute: } 1 \text { for } a} \\ {t=\dfrac{12 \pm \sqrt{144+80}}{2}} & \color {Red} {\text { Exponent, then multiplication. }} \\ {t=\dfrac{12 \pm \sqrt{224}}{2}} & \color {Red} {\text { Simplify. }}\end{array} \nonumber$$

Відповідь не в простій формі, оскільки ми можемо врахувати$\sqrt{16}$.

$$\begin{array}{ll}{t=\dfrac{12 \pm \sqrt{16} \sqrt{14}}{2}} & \color {Red} {\sqrt{224}=\sqrt{16} \sqrt{14}} \\ {t=\dfrac{12 \pm 4 \sqrt{14}}{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber$$

Використовуйте розподільну властивість, щоб розділити обидва члени в чисельнику на$2$.

$$\begin{array}{ll}{t=\dfrac{12}{2} \pm \dfrac{4 \sqrt{14}}{2}} & \color{Red} {\text { Divide both terms by } 2} \\ {t=6 \pm 2 \sqrt{14}} & \color {Red} {\text { Simplify }}\end{array} \nonumber$$

Таким чином, у нас є два рішення,$t=6-2 \sqrt{14}$ і$t=6+2 \sqrt{14}$. Використовуйте калькулятор, щоб знайти десяткові наближення, а потім округлити до найближчої десятої.

Малюнок$\PageIndex{2}$: Використання калькулятора для пошуку десяткових наближень

$$t \approx-1.5,13.5 \nonumber$$

Негативний час не має значення, тому до найближчої десятої частки секунди об'єкту потрібно приблизно$13.5$ секунди, щоб повернутися на рівень землі.

Вправа$\PageIndex{4}$

Об'єкт запускається вертикально, а його висота$y$ (у футах) над рівнем землі задається рівнянням$y = 160 + 96t−16t^2$, де$t$ - час (у секундах), який минув з моменту його запуску. Скільки часу має пройти після запуску, перш ніж об'єкт повернеться на рівень землі?

Відповідь

$3+\sqrt{19} \approx 7.4$секунд

Приклад$\PageIndex{5}$

Арні сідає на свій велосипед опівдні і починає їздити через північ з постійною швидкістю$12$ миль на годину. О 1:00 PM Барбара сідає на свій велосипед в тій же відправній точці і починає їздити на схід з постійною швидкістю$8$ миль на годину. В який час доби вони будуть один від$50$ одного (як ворона летить)? Не турбуйтеся про просту форму, просто повідомте час доби, виправте до найближчої хвилини.

Рішення

На даний момент вони знаходяться в$50$ милі один від одного, давайте$t$ представляємо час, коли Арні їхав з полудня. Оскільки Барбара почала о 1:00 вечора, вона їхала на годину менше, ніж Арні. Отже, давайте$t−1$ представляємо кількість годин, які Барбара їхала в даний момент, вони знаходяться в$50$ милі один від одного.

Тепер, якщо Арні годинами їхав з постійною швидкістю$12$ миль на$t$ годину, значить, він пройшов відстань в$12t$ милі. Оскільки Барбара годинами їздила з постійною швидкістю$8$ миль на$t−1$ годину, вона пройшла відстань у$8(t−1)$ милі.

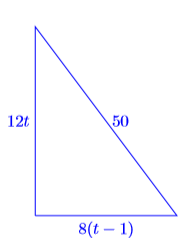
Малюнок$\PageIndex{3}$:$50$ милі один від одного.

Відстань і напрямок, пройдене Арні і Барбарою, позначені на малюнку$\PageIndex{3}$. Зверніть увагу, що у нас є прямокутний трикутник, тому сторони трикутника повинні задовольняти теоремі Піфагора. Тобто,

$$(12 t)^{2}+[8(t-1)]^{2}=50^{2} \quad \color{Red} \text { Use the Pythagorean Theorem. } \nonumber$$

Розподіліть$8$.

$$(12 t)^{2}+(8 t-8)^{2}=50^{2} \quad \color{Red} \text { Distribute the } 8 \nonumber$$

Квадратний кожен член. $(a−b)^2 = a^2 −2ab + b^2$Використовувати для розширення$(8t−8)^2$.

$$\begin{aligned} 144 t^{2}+64 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Square each term. } \\ 208 t^{2}-128 t+64 &=2500 \quad \color{Red} \text { Simplify: } 144 t^{2}+64 t^{2}=208 t^{2} \end{aligned} \nonumber$$

Отримане рівняння нелінійне. Зробіть одну сторону рівною нулю.

$$\begin{array}{rlrl}{208 t^{2}-128 t-2436} & {=0} & {} & \color{Red} {\text { Subtract } 2500 \text { from both sides. }} \\ {52 t^{2}-32 t-609} & {=0} & {} & \color{Red} {\text { Divide both sides by } 4 .}\end{array} \nonumber$$

Порівняйте$52t^2 −32t−609 = 0$ з$at^2 + bt + c = 0$ і зверніть увагу$a = 52$, що$b = −32$,, і$c = −609$. Замініть кожне входження$a$$b$, і$c$ відкритими дужками підготувати квадратичну формулу для підстановки. Зауважте, що ми вирішуємо на$t$ цей час, ні$x$.

$$\begin{array}{ll}{x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} & \color{Red} {\text { The quadratic formula. }} \\ {x=\dfrac{-( ) \pm \sqrt{( )^{2}-4( )( )}}{2( )}} & \color{Red} {\text { Replace } a, b, \text { and } c \text { with }}\end{array} \nonumber$$

Замінник$a$,$52$$−32$ для$b$, і$−609$ для$c$.

$$\begin{align*} t &= \dfrac{-(-32) \pm \sqrt{(-32)^{2}-4(52)(-609)}}{2(52)} \quad \color {Red} \text { Substitute: } 52 \text { for } a\\ t &= \dfrac{32 \pm \sqrt{1024+126672}}{104} \quad \color {Red} \text {Exponent, then multiplication.}\\ t &= \dfrac{32 \pm \sqrt{127696}}{104} \quad \color {Red} \text { Simplify. } \end{align*} \nonumber$$
Тепер, оскільки запит розрахований на приблизний час, ми не будемо морочитися з простою формою і скороченням, а перейдемо відразу до калькулятора, щоб наблизити цей останній результат (див. Малюнок$\PageIndex{4}$). Таким чином, Арні їхав приблизно$3.743709336$ годинами. Щоб змінити дробову частину$0.743709336$ годин на хвилини, помножте на$60$ хв/год.

Малюнок$\PageIndex{4}$: Приблизний час, коли Арні їхав.

$$0.743709336 \mathrm{hr}=0.743709336 \mathrm{hr} \times \dfrac{60 \mathrm{min}}{\mathrm{hr}}=44.62256016 \mathrm{min} \nonumber$$

Округляючи до найближчої хвилини, Арні їхав приблизно$3$ годинами і$45$ хвилинами. Оскільки Арні почав їздити опівдні, час, коли він і Барбара знаходяться в$50$ милі один від одного, становить приблизно 3:45 вечора.

Вправа$\PageIndex{5}$

О 6:00 ранку вантажний поїзд проходить через Sagebrush Junction, прямуючи на захід$40$ зі швидкістю миль на годину. О 8:00 ранку пасажирський поїзд проходить через перехрестя, що прямує на південь зі швидкістю$60$ миль на годину. В який час доби, поправте до найближчої хвилини, чи будуть два поїзди відстані один$180$ від одного?

Відповідь

9:42 РАНКУ