5.2: Квадратичні функції

Last updated
Save as PDF

Page ID: 59608

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Розпізнати характеристики парабол.
Зрозумійте, як графік параболи пов'язаний з її квадратичною функцією.
Визначте мінімальне або максимальне значення квадратичної функції.
Вирішувати задачі, що включають мінімальне або максимальне значення квадратичної функції.

Вигнуті антени, такі як показані на малюнку$\PageIndex{1}$, зазвичай використовуються для фокусування мікрохвильових хвиль та радіохвиль для передачі телевізійних та телефонних сигналів, а також супутникового та космічного зв'язку. Перетин антени має форму параболи, яку можна описати квадратичної функцією.

$Супутникові антени.$

Малюнок$\PageIndex{1}$: Масив супутникових антен. (кредит: Метью Колвін де Валле, Flickr)

У цьому розділі ми досліджуємо квадратичні функції, які часто моделюють задачі, пов'язані з рухом площі та снаряда. Робота з квадратичними функціями може бути менш складною, ніж робота з функціями більш високого ступеня, тому вони дають хорошу можливість для детального вивчення поведінки функцій.

Визнання характеристик парабол

Графік квадратичної функції - це U-подібна крива, яка називається параболою. Однією з важливих особливостей графіка є те, що він має крайню точку, звану вершиною. Якщо парабола відкривається, вершина представляє найнижчу точку на графіку, або мінімальне значення квадратичної функції. Якщо парабола відкривається вниз, вершина представляє найвищу точку на графіку, або максимальне значення. У будь-якому випадку вершина є поворотною точкою на графіку. Графік також симетричний з вертикальною лінією, проведеної через вершину, званої віссю симетрії. Ці особливості проілюстровані на рис$\PageIndex{2}$.

альт — Малюнок$\PageIndex{2}$: Графік параболи, що показує, де знаходяться$x$ і$y$ перехоплює, вершина та вісь симетрії.

Y-перехоплення - це точка, в якій парабола перетинає$y$ вісь -. X-перехоплення - це точки, в яких парабола перетинає$x$ вісь -. Якщо вони існують, то x-перехоплення представляють нулі, або коріння, квадратичної функції, значення$x$ при якій$y=0$.

Приклад$\PageIndex{1}$: Identifying the Characteristics of a Parabola

Визначте вершину, вісь симетрії, нулі та y-перехоплення параболи, наведеного на малюнку$\PageIndex{3}$.

Графік параболи з вершиною в (3, 1) і y-перехопленням в (0, 7). — Малюнок$\PageIndex{3}$.

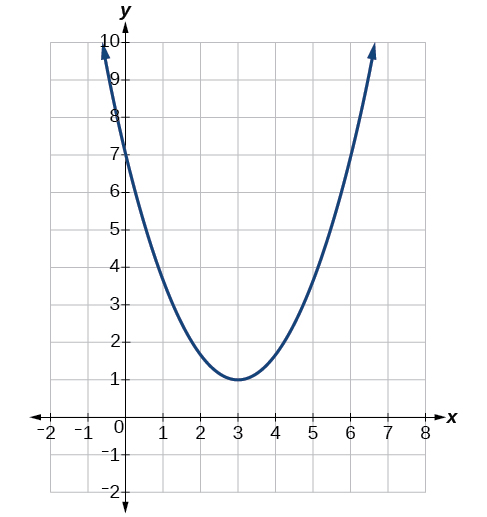
Рішення

Вершина є точкою повороту графа. Ми бачимо, що вершина знаходиться в$(3,1)$. Оскільки ця парабола відкривається вгору, вісь симетрії - це вертикальна лінія, яка перетинає параболу у вершині. Отже, вісь симетрії є$x=3$. Ця парабола не перетинає вісь x, тому не має нулів. Він перетинає$y$ вісь -на$(0,7)$ так що це перехоплення y-перехоплення.

Розуміння того, як графіки парабол пов'язані з їх квадратичними функціями

Загальна форма квадратичної функції представляє функцію у вигляді

\[f(x)=ax^2+bx+c\]

де$a$$b$, і$c$ є дійсними числами і$a{\neq}0$. Якщо$a>0$, парабола відкривається вгору. Якщо$a<0$, парабола відкривається вниз. Ми можемо використовувати загальну форму параболи, щоб знайти рівняння для осі симетрії.

Вісь симетрії визначається по$x=−\frac{b}{2a}$. Якщо використовувати квадратичну формулу$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$, щоб вирішити$ax^2+bx+c=0$ для x-перехоплення, або нулів, ми знайдемо значення$x$ півдорозі між ними завжди$x=−\frac{b}{2a}$, рівняння для осі симетрії.

Малюнок$\PageIndex{4}$ являє собою графік квадратичної функції, записаний у загальному вигляді як$y=x^2+4x+3$. У такому вигляді,$a=1$,$b=4$, і$c=3$. Тому що$a>0$, парабола відкривається вгору. Вісь симетрії є$x=−\frac{4}{2(1)}=−2$. Це також має сенс, оскільки ми бачимо з графіка, що вертикальна лінія$x=−2$ ділить графік навпіл. Вершина завжди виникає уздовж осі симетрії. Для параболи, яка відкривається вгору, вершина зустрічається в найнижчій точці на графіку, в даному випадку,$(−2,−1)$. X-перехоплення, ті точки, де парабола перетинає вісь х, відбуваються при$(−3,0)$ і$(−1,0)$.

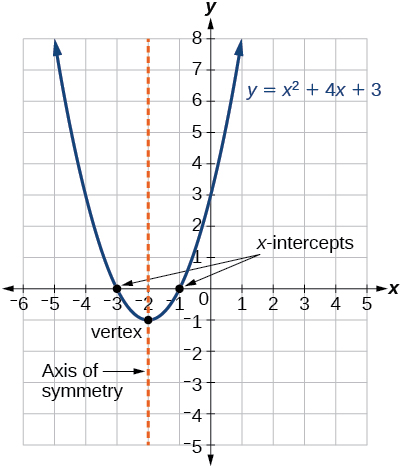
Графік параболи, що показує, де x та y перехоплюють, вершину та вісь симетрії для функції y=x^2+4x+3. — Рисунок$\PageIndex{4}$: Графік параболи, що показує, де$x$ і$y$ перехоплює, вершина та вісь симетрії для функції$y=x^2+4x+3$.

Стандартна форма квадратичної функції представляє функцію у вигляді

\[f(x)=a(x−h)^2+k\]

де$(h, k)$ - вершина. Оскільки вершина з'являється у стандартній формі квадратичної функції, ця форма також відома як вершинна форма квадратичної функції.

Як і при загальній формі$a>0$, якщо, парабола відкривається вгору і вершина мінімальна. Якщо$a<0$, парабола відкривається вниз, а вершина - максимум. Малюнок$\PageIndex{5}$ являє собою графік квадратичної функції, записаної в стандартному вигляді як$y=−3(x+2)^2+4$. Так як$x–h=x+2$ в даному прикладі,$h=–2$. У такому вигляді,$a=−3$,$h=−2$, і$k=4$. Тому що$a<0$, парабола відкривається вниз. Вершина знаходиться в$(−2, 4)$.

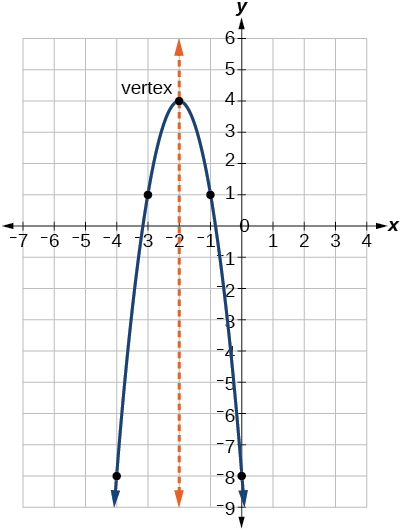
Графік параболи, що показує, де x та y перехоплюють, вершину та вісь симетрії для функції y=-3 (x+2) ^2+4. — Рисунок$\PageIndex{5}$: Графік параболи, що показує, де$x$ і$y$ перехоплює, вершина та вісь симетрії для функції$y=-3(x+2)^2+4$.

Стандартна форма корисна для визначення того, як графік трансформується з графіка$y=x^2$. Малюнок$\PageIndex{6}$ - це графік цієї основної функції.

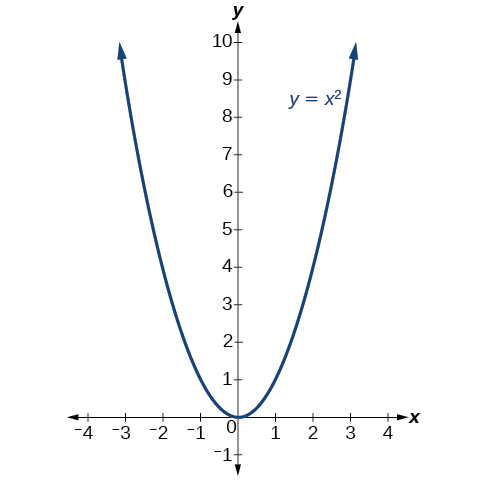
Графік y=x^2. — Малюнок$\PageIndex{6}$: Графік$y=x^2$.

Якщо$k>0$, графік зміщується вгору, тоді як якщо$k<0$, графік зміщується вниз. На малюнку$\PageIndex{5}$$k>0$, таким чином графік зміщений на 4 одиниці вгору. Якщо$h>0$, графік зміщується вправо, а якщо$h<0$, графік зміщується вліво. На малюнку$\PageIndex{5}$$h<0$, таким чином графік зміщений на 2 одиниці вліво. Величина$a$ вказує на розтягнення графіка. Якщо точка$|a|>1$, пов'язана з певним значенням x, зміщується далі від осі x, отже, графік стає більш вузьким, і виникає вертикальне розтягнення. Але якщо точка$|a|<1$, пов'язана з певним значенням x, зсувається ближче до осі x, значить, графік стає ширшим, але насправді відбувається вертикальне стиснення. На малюнку$\PageIndex{5}$$|a|>1$, таким чином, графік стає вужчим.

Стандартна форма і загальна форма - еквівалентні методи опису однієї і тієї ж функції. Ми можемо переконатися в цьому, розгорнувши загальну форму і встановивши її рівною стандартній формі.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

Щоб лінійні долі були рівними, коефіцієнти повинні бути рівними.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

Це вісь симетрії, яку ми визначили раніше. Встановлення постійних членів, рівних:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

На практиці, однак, як правило, легше запам'ятати, що$k$ є вихідним значенням функції, коли вхід є$h$, так що$f(h)=k$.

Визначення: Форми квадратичних функцій

Квадратична функція - це функція другого ступеня. Графік квадратичної функції - парабола.

Загальна форма квадратичної функції - це$f(x)=ax^2+bx+c$ де$a$$b$, і є$c$ дійсними числами і$a{\neq}0$.
Стандартною формою квадратичної функції є$f(x)=a(x−h)^2+k$.
Вершина$(h,k)$ розташована на\[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO: Написати квадратичну функцію в загальному вигляді

Задано графік квадратичної функції, запишіть рівняння функції в загальному вигляді.

Визначте горизонтальний зсув параболи; це значення є$h$. Визначте вертикальний зсув параболи; це значення є$k$.
Підставляємо значення горизонтального і вертикального зсуву для$h$ і$k$. у функції$f(x)=a(x–h)^2+k$.
Підставити значення будь-якої точки, крім вершини, на графі параболи для$x$ і$f(x)$.
Вирішити для коефіцієнта розтягування,$|a|$.
Якщо парабола розкривається,$a>0$. Якщо парабола відкривається вниз,$a<0$ так як це означає, що графік відбився навколо осі х.
Розгорнути і спростити написання в загальному вигляді.

Приклад$\PageIndex{2}$: Writing the Equation of a Quadratic Function from the Graph

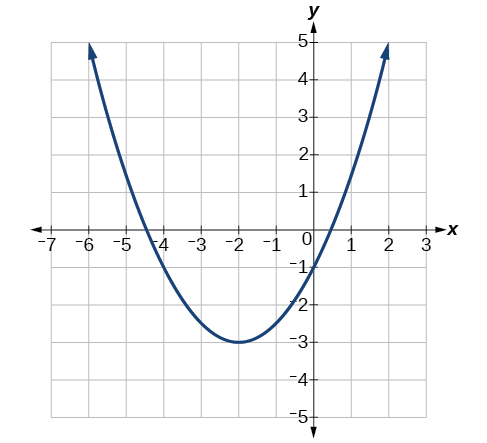
Напишіть рівняння для квадратичної функції на$g$ малюнку$\PageIndex{7}$ як перетворення$f(x)=x^2$, а потім розгорніть формулу і спростіть терміни, щоб записати рівняння в загальному вигляді.

Рішення

Ми можемо бачити графік$g$ це графік$f(x)=x^2$ зрушеного вліво 2 і вниз 3, даючи формулу у вигляді$g(x)=a(x+2)^2–3$.

Підставляючи координати точки на кривій, наприклад$(0,−1)$, ми можемо вирішити для коефіцієнта розтягування.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

У стандартному вигляді алгебраїчна модель для цього графа є$g(x)=\dfrac{1}{2}(x+2)^2–3$.

Щоб записати це в загальному многочленном вигляді, ми можемо розширити формулу і спростити терміни.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Зверніть увагу, що горизонтальні і вертикальні зсуви основного графіка квадратичної функції визначають розташування вершини параболи; на вершину не впливають розтяжки і стиснення.

Аналіз

Ми можемо перевірити нашу роботу за допомогою функції таблиці на графічній утиліті. Спочатку введіть$\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}$. Далі виберіть$\mathrm{TBLSET}$, потім використовуйте$\mathrm{TblStart=–6}$ і$\mathrm{ΔTbl = 2}$, і виберіть$\mathrm{TABLE}$. Див. Таблицю$\PageIndex{1}$

Таблиця$\PageIndex{1}$
$x$	-6	-4	-2	0	2
$y$	-5	-1	-3	-1	5

Впорядковані пари в таблиці відповідають точкам на графіку.

Вправа$\PageIndex{2}$

Координатна сітка була накладена на квадратичну траєкторію баскетболу на малюнку$\PageIndex{8}$. Знайдіть рівняння для шляху руху кулі. Чи робить стрілок кошик?

$альт$

Малюнок$\PageIndex{8}$: Зупиніть рухомий малюнок хлопчика, який кидає баскетбол у обруч, щоб показати параболічну криву, яку він робить.
(Кредит: модифікація роботи Дена Мейєра)

Відповідь: Шляхи проходять через початок і має вершину в$(−4, 7)$, так що$h(x)=–\frac{7}{16}(x+4)^2+7$. Щоб зробити постріл, потрібно$h(−7.5)$ було б близько 4 але$h(–7.5){\approx}1.64$; він не робить це.

$альт$ Задано квадратичну функцію в загальному вигляді, знайдіть вершину параболи.

Визначити$a$,$b$, і$c$.
Знайти$h$, x-координату вершини, шляхом підстановки$a$ і$b$ в$h=–\frac{b}{2a}$.
Знайти$k$, y-координату вершини, шляхом оцінки$k=f(h)=f\Big(−\frac{b}{2a}\Big)$.

Приклад$\PageIndex{3}$: Finding the Vertex of a Quadratic Function

Знайдіть вершину квадратичної функції$f(x)=2x^2–6x+7$. Перепишіть квадратику в стандартну форму (вершинна форма).

Рішення

Горизонтальна координата вершини буде на

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

Вертикальна координата вершини буде на

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Переписуючи в стандартну форму, коефіцієнт розтягування буде таким же, як і$a$ в оригінальній квадратиці.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Використовуючи вершину для визначення зрушень,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

Аналіз

Одна з причин, по якій ми можемо захотіти визначити вершину параболи, полягає в тому, що ця точка повідомить нам, що таке максимальне або мінімальне значення функції$(k)$, і де вона виникає$(h)$.

Вправа$\PageIndex{3}$

З огляду на рівняння$g(x)=13+x^2−6x$, запишіть рівняння в загальному вигляді, а потім в стандартному вигляді.

Відповідь: $g(x)=x^2−6x+13$в загальному вигляді;$g(x)=(x−3)^2+4$ в стандартній формі.

Пошук області та діапазону квадратичної функції

Будь-яке число може бути вхідним значенням квадратичної функції. Тому область будь-якої квадратичної функції - це всі дійсні числа. Оскільки параболи мають максимальну або мінімальну точку, діапазон обмежений. Оскільки вершина параболи буде або максимумом, або мінімумом, діапазон буде складатися з усіх значень y, більших або рівних y-координаті в точці повороту або менше або дорівнює координаті y в точці повороту, залежно від того, відкривається парабола вгору або вниз.

Визначення: Область та діапазон квадратичної функції

Доменом будь-якої квадратичної функції є всі дійсні числа.

Діапазон квадратичної функції, записаної в загальному вигляді$f(x)=ax^2+bx+c$ з додатним$a$ значенням$f(x){\geq}f ( −\frac{b}{2a}\Big)$, дорівнює, або$[ f(−\frac{b}{2a}),∞ ) $; діапазон квадратичної функції, записаної в загальному вигляді з від'ємним значенням a$f(x) \leq f(−\frac{b}{2a})$, або$(−∞,f(−\frac{b}{2a})]$.

Діапазон квадратичної функції, записаної в стандартній формі$f(x)=a(x−h)^2+k$ з додатним$a$ значенням, є$f(x) \geq k;$ діапазоном квадратичної функції, записаної в стандартному вигляді з від'ємним$a$ значенням$f(x) \leq k$.

$альт$ Задано квадратичну функцію, знайдіть область і діапазон.

Визначте область будь-якої квадратичної функції як всі дійсні числа.
$a$Визначте, позитивний чи негативний. Якщо$a$ позитивний, то парабола має мінімум. Якщо$a$ негативний, то парабола має максимум.
Визначте максимальне або мінімальне значення параболи,$k$.
Якщо парабола має мінімум, діапазон задається$f(x){\geq}k$, або$\left[k,\infty\right)$. Якщо парабола має максимум, дальність задається$f(x){\leq}k$, або$\left(−\infty,k\right]$.

Приклад$\PageIndex{4}$: Finding the Domain and Range of a Quadratic Function

Знайдіть домен і діапазон доменів$f(x)=−5x^2+9x−1$.

Рішення

Як і у випадку з будь-якою квадратичною функцією, домен - це всі дійсні числа.

$a$Оскільки негативна, парабола відкривається вниз і має максимальне значення. Нам потрібно визначити максимальне значення. Ми можемо почати з пошуку значення x вершини.

\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]

Максимальне значення задається за допомогою$f(h)$.

\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]

Діапазон - це$f(x){\leq}\frac{61}{20}$, або$\left(−\infty,\frac{61}{20}\right]$.

Вправа$\PageIndex{4}$

Знайдіть домен і діапазон доменів$f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}$.

Відповідь: Домен - це всі дійсні числа. Діапазон - це$f(x){\geq}\frac{8}{11}$, або$\left[\frac{8}{11},\infty\right)$.

Визначення максимальних і мінімальних значень квадратичних функцій

Виходом квадратичної функції на вершині є максимальне або мінімальне значення функції, що залежить від орієнтації параболи. Максимальне і мінімальне значення ми можемо побачити на малюнку$\PageIndex{9}$.

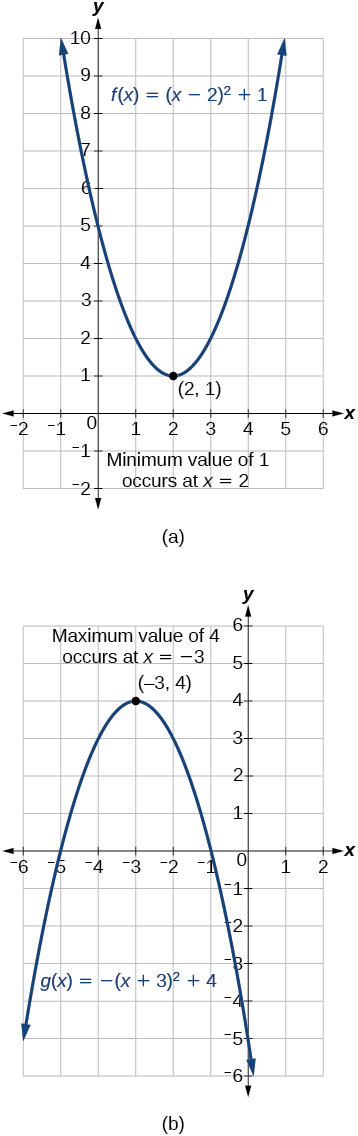
Два графіки, де перший графік показує максимальне значення для f (x) = (x-2) ^2+1, яке відбувається при (2, 1), а другий графік показує мінімальне значення для g (x) =- (x+3) ^2+4, яке відбувається при (-3, 4). — Малюнок$\PageIndex{9}$: Мінімум і максимум двох квадратичних функцій.

Існує багато реальних сценаріїв, які передбачають знаходження максимального або мінімального значення квадратичної функції, таких як додатки, що стосуються площі та доходу.

Приклад$\PageIndex{5}$: Finding the Maximum Value of a Quadratic Function

Фермер на задньому дворі хоче облагородити прямокутний простір для нового саду в її обгородженому дворі. Вона придбала 80 футів дротяної огорожі, щоб обкласти три сторони, і вона буде використовувати секцію огорожі заднього двору як четверту сторону.

Знайдіть формулу для площі, огородженої парканом, якщо сторони огорожі перпендикулярні існуючому паркану мають довжину$L$.
Якими габаритами вона повинна зробити свій сад, щоб максимально закрити закриту територію?

Рішення

Давайте використаємо діаграму типу Figure$\PageIndex{10}$ для запису заданої інформації. Також корисно ввести тимчасову змінну$W$, щоб представити ширину саду та довжину секції паркану паралельно паркану на задньому дворі.

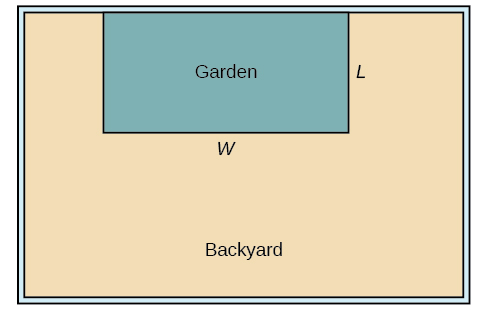
Малюнок$\PageIndex{10}$: Схема саду і присадибної ділянки.

a Ми знаємо, що у нас є тільки 80 футів паркану доступні$L+W+L=80$, і, простіше кажучи,$2L+W=80$. Це дозволяє нам представляти ширину$W$, з точки зору$L$.

\[W=80−2L\]

Тепер ми готові написати рівняння для площі, яку огороджує паркан. Ми знаємо, що площа прямокутника дорівнює довжині, помноженої на ширину, так

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

Ця формула представляє площу огорожі в перерахунку на змінну довжину$L$. Функція, написана в загальному вигляді, є

\[A(L)=−2L^2+80L\].

Квадратика має негативний провідний коефіцієнт, тому графік відкриється вниз, а вершина буде максимальним значенням для площі. Знаходячи вершину, ми повинні бути обережними, оскільки рівняння не записується в стандартній поліноміальній формі з спадними ступенями. Саме тому ми переписали функцію в загальному вигляді вище. Так як$a$ є коефіцієнт квадрата члена,$a=−2$,$b=80$, і$c=0$.

Щоб знайти вершину:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

Максимальне значення функції - площа 800 квадратних футів, яка виникає при$L=20$ футах. Коли коротші сторони 20 футів, для довшої сторони залишається 40 футів огорожі. Щоб максимізувати площу, вона повинна огородити сад так, щоб дві коротші сторони мали довжину 20 футів, а довша сторона, паралельна існуючому паркану, має довжину 40 футів.

Аналіз

Цю проблему також можна вирішити шляхом побудови графіків квадратичної функції. Ми можемо побачити, де максимальна площа відбувається на графіку квадратичної функції на малюнку$\PageIndex{11}$.

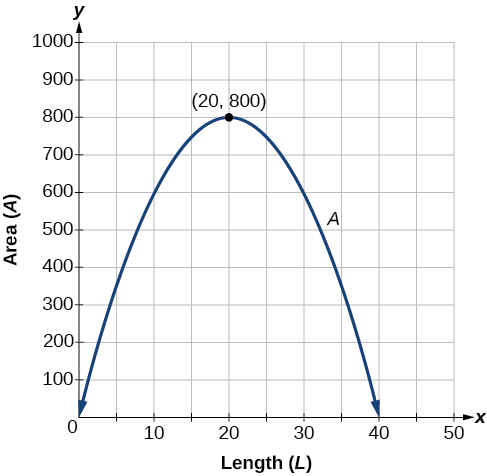
Графік параболічної функції A (L) =-2L^2+80L, на якій вісь x позначена Length (L), а вісь y - Area (A). Вершина знаходиться в (20, 800). — Малюнок$\PageIndex{11}$: Графік параболічної функції$A(L)=-2L^2+80L$

$альт$ З огляду на додаток, що передбачає дохід, використовуйте квадратне рівняння, щоб знайти максимум.

Напишіть квадратне рівняння доходу.
Знайдіть вершину квадратного рівняння.
Визначте значення y вершини.

Приклад$\PageIndex{6}$: Finding Maximum Revenue

Ціна одиниці товару впливає на його попит і пропозицію. Тобто, якщо ціна за одиницю піде вгору, попит на товар, як правило, зменшиться. Наприклад, місцева газета наразі має 84 000 передплатників за щоквартальну плату в розмірі 30 доларів. Дослідження ринку припускають, що якщо власники підвищать ціну до 32 доларів, вони втратять 5000 передплатників. Припускаючи, що підписки лінійно пов'язані з ціною, яку ціну повинна стягувати газета за квартальну підписку, щоб максимізувати свій дохід?

Рішення

Дохід - це сума грошей, яку компанія приносить. В цьому випадку дохід можна знайти, помноживши ціну за підписку на кількість передплатників, або кількість. Ми можемо ввести змінні,$p$ для ціни за підписку та$Q$ для кількості, даючи нам рівняння$\text{Revenue}=pQ$.

Оскільки кількість передплатників змінюється разом з ціною, нам потрібно знайти зв'язок між змінними. Ми знаємо, що в даний час$p=30$ і$Q=84,000$. Ми також знаємо, що якщо ціна підвищиться до 32 доларів, газета втратить 5000 передплатників, даючи другу пару цінностей,$p=32$ і$Q=79,000$. З цього ми можемо знайти лінійне рівняння, що стосується двох величин. Ухил буде

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

Це говорить нам, що папір втратить 2500 передплатників за кожен долар, який вони підвищують ціну. Потім ми можемо вирішити для y-перехоплення.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

Це дає нам лінійне рівняння,$Q=−2,500p+159,000$ що стосується вартості та абонентів. Тепер ми повернемося до нашого рівняння доходів.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

Тепер у нас є квадратична функція доходу як функція плати за підписку. Щоб знайти ціну, яка дозволить максимізувати дохід для газети, ми можемо знайти вершину.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

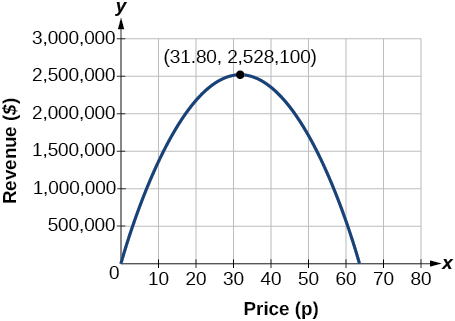
Модель говорить нам, що максимальний дохід відбудеться, якщо газета стягне 31,80 долара за підписку. Щоб дізнатися, який максимальний дохід, оцінюємо функцію доходу.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

Аналіз

Це також може бути вирішено графіком квадратичного зображення, як на малюнку$\PageIndex{12}$. Максимальний дохід ми можемо побачити на графіку квадратичної функції.

Графік параболічної функції, на якій вісь x позначається Price (p), а вісь y - позначена Revenue ($). Вершина знаходиться в (31.80, 258100). — Малюнок$\PageIndex{12}$: Графік параболічної функції

Пошук x- та Y-перехоплень квадратичної функції

Так само, як ми робили в прикладних задачах вище, нам також потрібно знайти перехоплення квадратичних рівнянь для графічних парабол. Нагадаємо, що ми знаходимо y-перехоплення квадратичного шляхом оцінки функції на вході нуля, і знаходимо x-перехоплення в місцях, де вихід дорівнює нулю. Зверніть увагу на малюнку$\PageIndex{13}$, що кількість x-перехоплень може змінюватися залежно від місця розташування графіка.

" src="https://math.libretexts.org/@api/dek..._03_02_013.jpg">

Малюнок$\PageIndex{13}$: Кількість x-перехоплень параболи.

$альт$ Задано квадратичну функцію$f(x)$, знайдіть y- та x-перехоплення.

Оцініть$f(0)$, щоб знайти y-перехоплення.
Розв'яжіть квадратне рівняння,$f(x)=0$ щоб знайти х-перехоплення.

Приклад$\PageIndex{7}$: Finding the y- and x-Intercepts of a Parabola

Знайдіть y- і x-перехоплення квадратичного$f(x)=3x^2+5x−2$.

Рішення

Знаходимо y-перехоплення шляхом оцінки$f(0)$.

\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]

Таким чином, y-перехоплення знаходиться на$(0,−2)$.

Для x-перехоплень знаходимо всі рішення$f(x)=0$.

\[0=3x^2+5x−2\]

При цьому квадратичність може бути врахована легко, надаючи найпростіший спосіб вирішення.

\[0=(3x−1)(x+2)\]

\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]

Таким чином, Х-перехоплення знаходяться в$(\frac{1}{3},0)$ і$(−2,0)$.

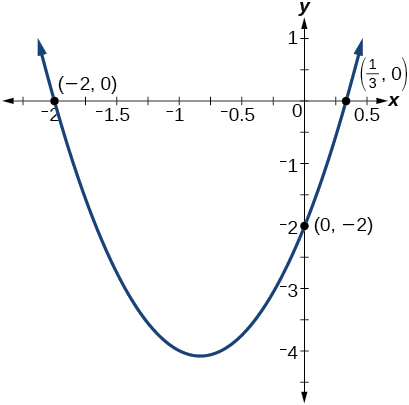
Аналіз

Графікуючи функцію, ми можемо підтвердити, що графік перетинає$y$ -вісь на$(0,−2)$. Ми також можемо підтвердити, що графік перетинає вісь x в$\Big(\frac{1}{3},0\Big)$ і$(−2,0)$. Див$\PageIndex{14}$. Малюнок.

Графік параболи, яка має наступні перехоплення (-2, 0), (1/3, 0) та (0, -2). — Малюнок$\PageIndex{14}$: Графік параболи.

Рерайтинг квадратики в стандартному вигляді

У$\PageIndex{7}$ прикладі квадратика легко вирішувалася факторингом. Однак є багато квадратиків, які не можуть бути враховані. Ми можемо вирішити ці квадратики, попередньо переписавши їх в стандартному вигляді.

$альт$ Задано квадратичну функцію, знайдіть x-перехоплення шляхом перезапису в стандартному вигляді.

Підставляємо а і$b$ в$h=−\frac{b}{2a}$.
$x=h$Підставляємо в загальну форму квадратичної функції, щоб знайти$k$.
Перепишіть квадратику в стандартному вигляді за допомогою$h$ і$k$.
Вирішіть, коли вихід функції буде нульовим, щоб знайти x-перехоплення.

Приклад$\PageIndex{8}$: Finding the x-Intercepts of a Parabola

Знайдіть x-перехоплення квадратичної функції$f(x)=2x^2+4x−4$.

Рішення

Починаємо з вирішення, коли на виході буде нуль.

\[0=2x^2+4x−4 \nonumber\]

Оскільки квадратичне не є легко факторинним у цьому випадку, ми вирішуємо для перехоплень, спочатку переписуючи квадратику в стандартному вигляді.

\[f(x)=a(x−h)^2+k\nonumber\]

Ми це знаємо$a=2$. Тоді вирішуємо за$h$ і$k$.

\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]

Так що тепер ми можемо переписати в стандартному вигляді.

\[f(x)=2(x+1)^2−6\nonumber\]

Тепер ми можемо вирішити, коли на виході буде нуль.

\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]

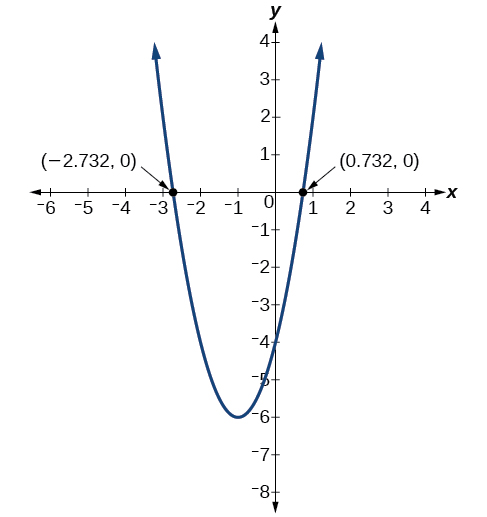
Графік має x-перехоплення в$(−1−\sqrt{3},0)$ і$(−1+\sqrt{3},0)$.

Аналіз

Ми можемо перевірити нашу роботу, намалювавши задану функцію на графічній утиліті та спостерігаючи за перехопленнями x. Див$\PageIndex{15}$. Малюнок.

Графік параболи, що має наступні x-перехоплення (-2.732, 0) та (0.732, 0). — Малюнок$\PageIndex{15}$: Графік параболи, яка має такі x-перехоплення:$(-2.732, 0)$ і$(0.732, 0)$.

Вправа$\PageIndex{1}$

У Try$\PageIndex{1}$ It ми знайшли стандартну та загальну форму функції$g(x)=13+x^2−6x$. Тепер знайдіть y- і x-перехоплення (якщо такі є).

Відповідь: y-перехоплення at$(0, 13)$, немає x-перехоплення

Приклад$\PageIndex{9}$: Solving a Quadratic Equation with the Quadratic Formula

Вирішити$x^2+x+2=0$.

Рішення

Почнемо з написання квадратичної формули:$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$.

При застосуванні квадратичної формули виділяємо коефіцієнти$a$,$b$ і$c$. Для$x^2+x+2=0$ рівняння ми маємо$a=1$,$b=1$, і$c=2$. Підставляючи ці значення в формулу, ми маємо:

\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]

Розв'язками рівняння є$x=\frac{−1+i\sqrt{7}}{2}$ і$x=\frac{−1-i\sqrt{7}}{2}$ або$x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}$ і$x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}$.

Приклад$\PageIndex{10}$: Applying the Vertex and x-Intercepts of a Parabola

М'яч кидається вгору з вершини 40 футів висотою будівлі зі швидкістю 80 футів в секунду. Висота кулі над землею може бути змодельована рівнянням$H(t)=−16t^2+80t+40$.

Коли м'яч досягає максимальної висоти?
Яка максимальна висота кулі?
Коли м'яч б'є об землю?

Куля досягає максимальної висоти у вершини параболи.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

М'яч досягає максимальної висоти через 2,5 секунди.

Щоб знайти максимальну висоту, знайдіть y-координату вершини параболи.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

М'яч досягає максимальної висоти 140 футів.

Щоб знайти, коли м'яч вдариться об землю, нам потрібно визначити, коли висота дорівнює нулю,$H(t)=0$.

Використовуємо квадратичну формулу.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Оскільки квадратний корінь не спрощує красиво, ми можемо скористатися калькулятором для наближення значень рішень.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

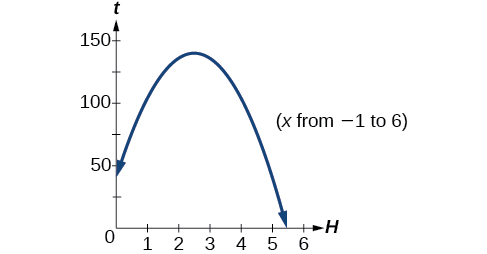
Друга відповідь знаходиться поза розумною сферою нашої моделі, тому ми робимо висновок, що м'яч вдарить об землю приблизно через 5.458 секунд. Див$\PageIndex{16}$. Малюнок.

$альт$ $\PageIndex{5}$: Скеля кидається вгору з вершини 112-футової скелі з видом на океан зі швидкістю 96 футів в секунду. Висота скелі над океаном може бути змодельована рівнянням$H(t)=−16t^2+96t+112$.

Коли скеля досягає максимальної висоти?
Яка максимальна висота породи?
Коли скеля потрапила в океан?

Рішення

a. 3 секунди б. 256 футів c. 7 секунд

Ключові рівняння

загальна форма квадратичної функції:$f(x)=ax^2+bx+c$
квадратична формула:$x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}$
стандартна форма квадратичної функції:$f(x)=a(x−h)^2+k$

Ключові поняття

Поліноміальна функція другого ступеня називається квадратичною функцією.
Графік квадратичної функції - парабола. Парабола - це U-подібна крива, яка може відкриватися або вгору, або вниз.
Віссю симетрії є вертикальна лінія, що проходить через вершину. Нулі, або x-перехоплення, - це точки, в яких парабола перетинає вісь x. Y-перехоплення - це точка, в якій парабола перетинає$y$ вісь -.
Квадратичні функції часто пишуться в загальному вигляді. Стандартна або вершинна форма корисна для легкого визначення вершини параболи. Будь-яка форма може бути записана з графіка.
Вершину можна знайти з рівняння, що представляє квадратичну функцію.
Область квадратичної функції - це всі дійсні числа. Діапазон варіюється в залежності від функції.
Мінімальне або максимальне значення квадратичної функції задається значенням y вершини.
Мінімальне або максимальне значення квадратичної функції може бути використано для визначення діапазону функції та для вирішення багатьох видів реальних проблем, включаючи проблеми, пов'язані з площею та доходами.
Деякі квадратні рівняння повинні бути вирішені за допомогою квадратичної формули.
Вершина та перехоплення можуть бути ідентифіковані та інтерпретовані для вирішення реальних проблем.

Глосарій

вісь симетрії
- вертикальна лінія, проведена через вершину параболи, навколо якої парабола симетрична; вона визначається$x=−\frac{b}{2a}$.

загальна форма квадратичної функції функція
, яка описує параболу, записану у вигляді$f(x)=ax^2+bx+c$, де$a,b,$ і$c$ є дійсними числами і a0.

стандартна форма квадратичної функції
- функція, яка описує параболу, записану у вигляді$f(x)=a(x−h)^2+k$, де$(h, k)$ знаходиться вершина.

вершина
- точка, в якій парабола змінює напрямок, що відповідає мінімальному або максимальному значенню квадратичної функції

вершинна форма квадратичної функції
інша назва стандартної форми квадратичної функції

нулі
в заданій функції, значення$x$ при яких$y=0$, також називаються корінням

Таблиця\(\PageIndex{1}\)
\(x\)	-6	-4	-2	0	2
\(y\)	-5	-1	-3	-1	5