4.3: Рівняння абсолютних значень
- Page ID
- 58165
У попередньому розділі ми визначилися
\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x \geq 0}\end{array}\right.\]
і ми побачили, що графік функції абсолютного значення, визначеної f (x) = |x| має «V-подібну форму», показану на рис\(\PageIndex{1}\).
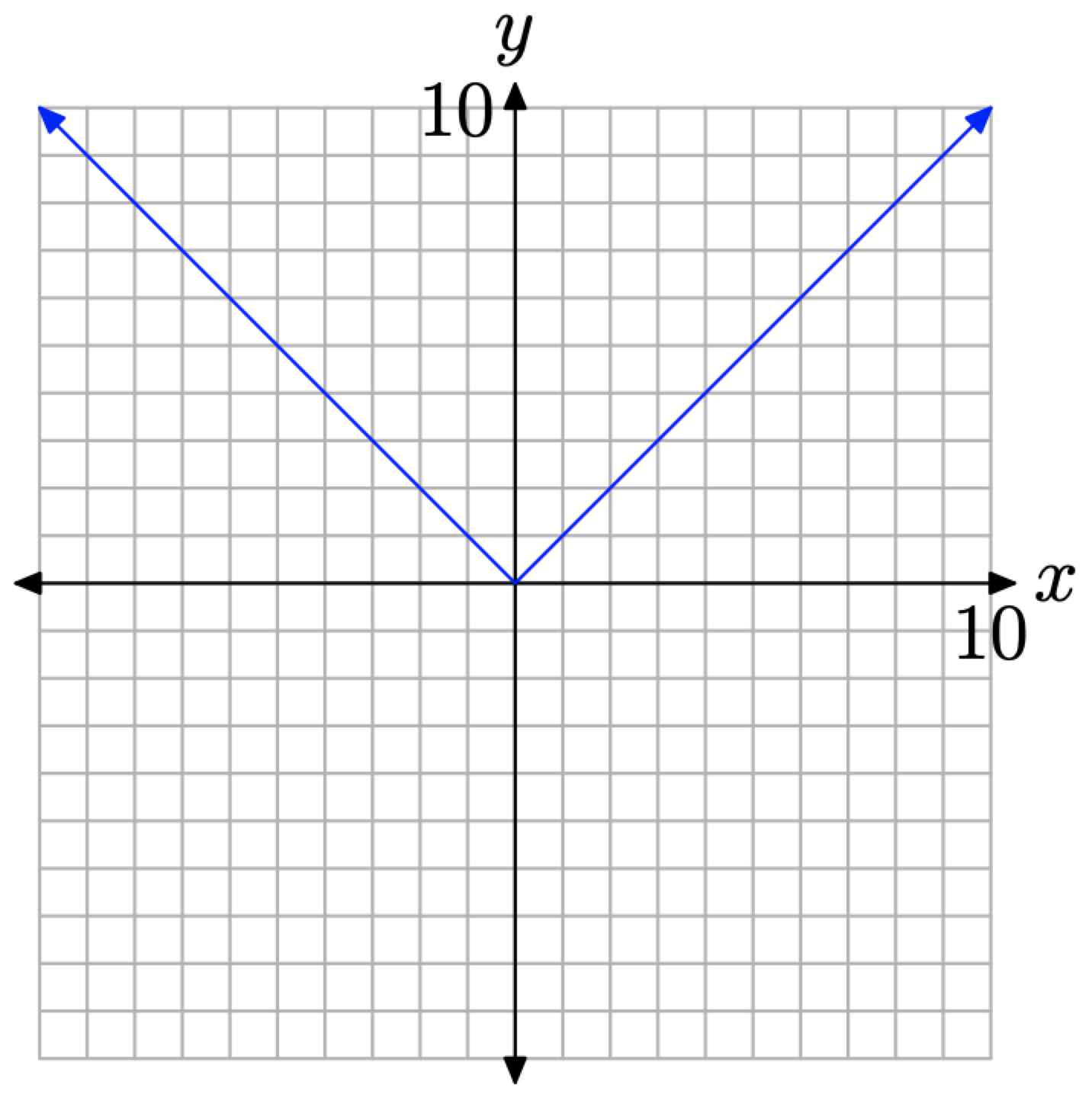
Важливо зазначити, що рівнянням лівої гілки «V» є y = −x. Типовими точками на цій гілці є (−1, 1), (−2, 2), (−3, 3) тощо. Не менш важливо зазначити, що права гілка «V» має рівняння y = x. Типовими точками на цій гілці є (1, 1), (2, 2), (2), (2), (3, 3) і т.д.
Рішення |x| = a
Ми зараз обговоримо розв'язки рівняння
\[|x|=a\]
Існує три окремі випадки для обговорення, кожен з яких залежить від значення та знака числа a.
- Випадок I: a < 0
Якщо a < 0, то графік y = a є горизонтальною лінією, яка лежить строго нижче осі x, як показано на малюнку\(\PageIndex{2}\) (а). У цьому випадку рівняння |x| = a не має розв'язків, оскільки графіки y = a і y = |x| не перетинаються.
- Випадок II: а = 0
Якщо a = 0, то графік y = 0 є горизонтальною лінією, яка збігається з віссю x, як показано на малюнку\(\PageIndex{2}\) (b). У цьому випадку рівняння |x| = 0 має єдине рішення x = 0, тому що горизонтальна лінія y = 0 перетинає графік y = |x| рівно в одній точці, в x = 0.
- Випадок III: а > 0
Якщо a > 0, то графік y = a - це горизонтальна лінія, яка лежить строго над віссю x, як показано на малюнку\(\PageIndex{2}\) (в). У цьому випадку рівняння |x| = a має два розв'язки, тому що графіки y = a і y = |x| мають дві точки перетину.
Нагадаємо, що ліва гілка y = |x| має рівняння y = −x, а точки на цій гілці мають вигляд (−1, 1), (−2, 2) тощо Оскільки точка, де граф y = a перетинає ліву гілку y = |x| має y-координату y = a, координата x цієї точки перетину дорівнює x = −a. розв'язок |x| = a.
Нагадаємо, що права гілка y = |x| має рівняння y = x, а точки на цій гілці мають вигляд (1, 1), (2, 2) і т.д. тому що точка, де граф y = a перетинає праву гілку y = |x| має y-координату y = a, x-координата цієї точки перетину x = a. це друга розв'язок |x| = a.
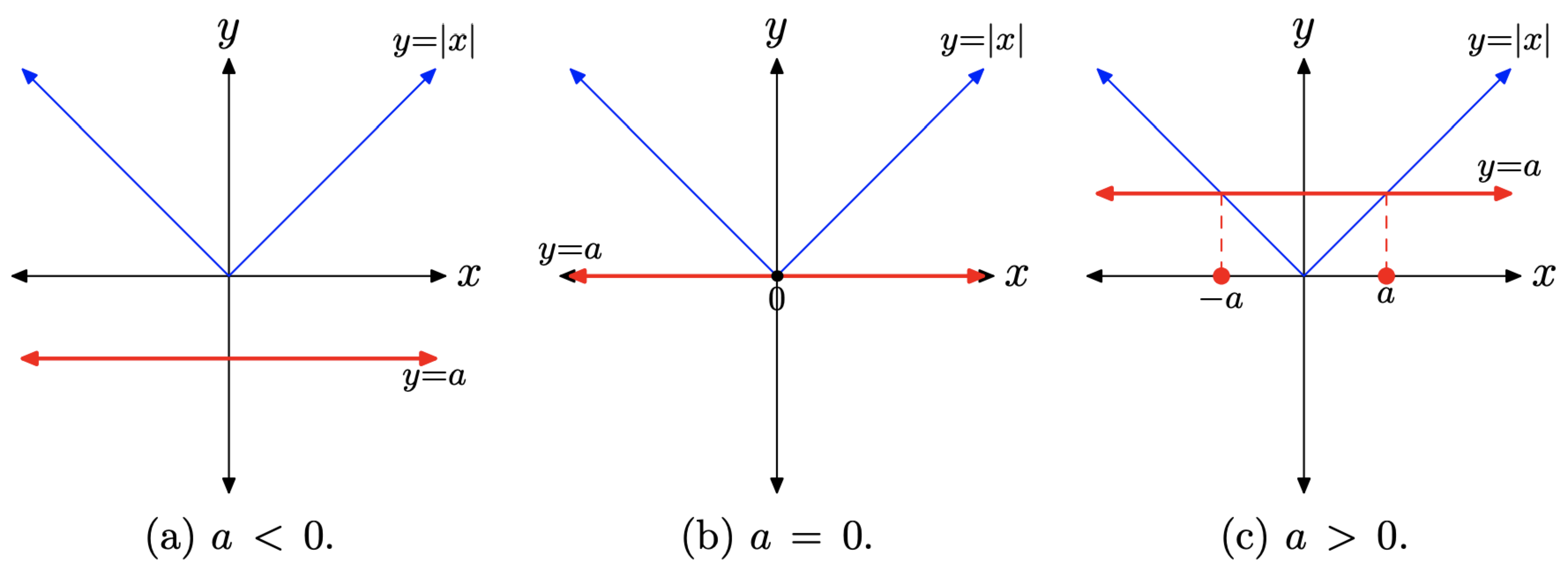
Ця дискусія призводить до наступного ключового результату.
Нерухомість 2
Розв'язок |x| = a залежить від значення та знака a.
- Випадок I: a < 0
Рівняння |x| = a не має розв'язків.
- Випадок II: а = 0
Рівняння |x| = 0 має одне рішення, x = 0.
- Випадок III: а > 0
Рівняння |x| = a має два розв'язки, x = −a або x = a.
Давайте розглянемо кілька прикладів.
Приклад\(\PageIndex{1}\)
Вирішити |x| = −3 для x.
Рішення
Графік лівої частини |x| = −3 є «V» малюнка\(\PageIndex{2}\) (a). Графік правої частини |x| = −3 є горизонтальною лінією на три одиниці нижче осі x. Це має вигляд ескізу на малюнку\(\PageIndex{2}\) (а). Графіки не перетинаються. Тому рівняння |x| = −3 не має розв'язків.
Альтернативним підходом є врахування того факту, що абсолютне значення x ніколи не може дорівнювати −3. Абсолютне значення числа завжди невід'ємне (нуль або додатне). Отже, рівняння |x| = −3 не має розв'язків.
Приклад\(\PageIndex{2}\)
Вирішити |x| = 0 для х
Рішення
Це той випадок, який зображений на малюнку\(\PageIndex{2}\) (б). Графік лівої частини |x| = 0 перетинає графік правої частини |x| = 0 при x = 0. Таким чином, єдиним рішенням |x| = 0 є x = 0.
Думаючи про це алгебраїчно замість графічно, ми знаємо, що 0 = 0, але немає іншого числа з абсолютним значенням нуля. Отже, інтуїтивно, єдиним рішенням |x| = 0 є x = 0.
Приклад\(\PageIndex{3}\)
Вирішити |x| = 4 для х.
Рішення
Графік лівої частини |x| = 4 - це «V» малюнка\(\PageIndex{2}\) (c). Графік правого боку являє собою горизонтальну лінію на 4 одиниці вище осі х. Це має вигляд ескізу на малюнку\(\PageIndex{2}\) (в). Графіки перетинаються в (−4, 4) і (4, 4). Тому розв'язки |x| = 4 є x = −4 або x = 4.
Крім того, | − 4| = 4 та |4| = 4, але жодне інше дійсне число не має абсолютного значення, рівного 4. Отже, єдиними розв'язками |x| = 4 є x = −4 або x = 4.
Приклад\(\PageIndex{4}\)
Розв'яжіть рівняння |3 − 2x| = −8 для x.
Рішення
Якби рівняння було |x| = −8, ми б не вагалися. Рівняння |x| = −8 не має розв'язків. Однак міркування, застосоване до простого випадку |x| = −8, однаково добре працює з рівнянням |3 − 2x| = −8. Ліва частина цього рівняння повинна бути невід'ємною, тому його графік повинен лежати вище або на осі x. Праворуч |3−2x| = −8 є горизонтальною лінією на 8 одиниць нижче осі x. Графіки не можуть перетинатися, тому рішення не існує.
Ми можемо перевірити цей аргумент за допомогою графічного калькулятора. Завантажте ліву та праву сторони |3 − 2x| = −8 у Y1 та Y2 відповідно, як показано на малюнку\(\PageIndex{3}\) (a). Натисніть кнопку MATH на калькуляторі, а потім стрілку вправо до меню NUM, як показано на малюнку\(\PageIndex{3}\) (b). Використовуйте 1: abs (щоб ввести абсолютне значення, показане на Y1 на малюнку\(\PageIndex{3}\) (а). У меню ZOOM виберіть 6:ZStandard, щоб створити зображення, показане на малюнку\(\PageIndex{3}\) (c).
Зауважте, що, як передбачалося вище, графік y = |3 − 2x| лежить на осі x або вище, а графік y = −8 лежить строго нижче осі x. Отже, графіки не можуть перетинатися, а рівняння |3 − 2x| = −8 не має розв'язків.
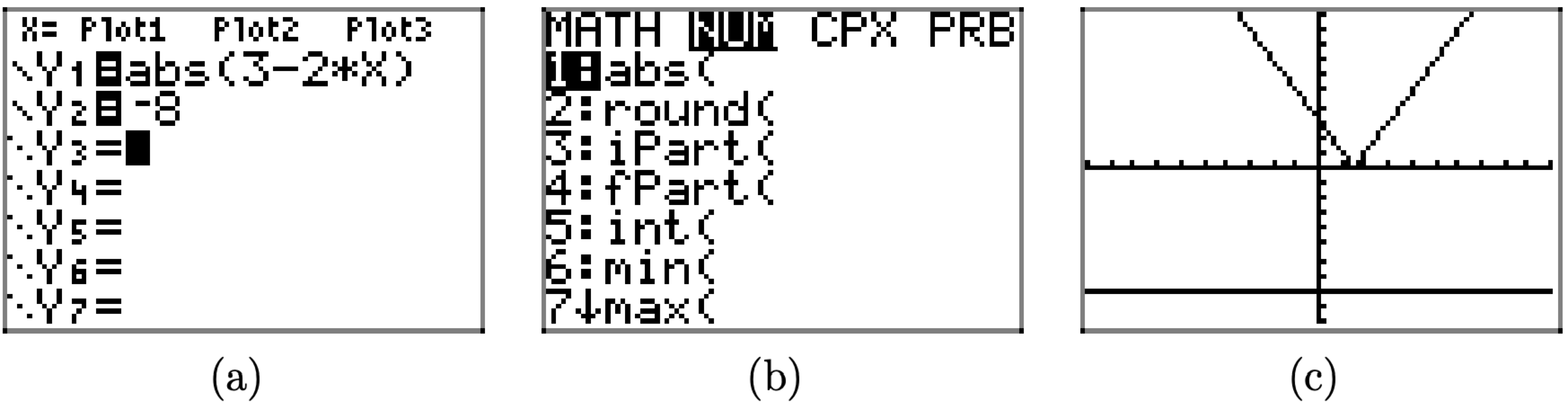
Крім того, ми можемо надати цілком інтуїтивне рішення |3 − 2x| = −8, аргументуючи, що ліва частина цього рівняння невід'ємна, а права - негативна. Це неможлива ситуація. Значить, рівняння не має розв'язків.
Приклад\(\PageIndex{5}\)
Розв'яжіть рівняння |3 − 2x| = 0 для x.
Рішення
Ми стверджували, що єдиним рішенням |x| = 0 є x = 0. Подібні міркування вказують на те, що |3 − 2x| = 0 тільки тоді, коли 3 − 2x = 0. Вирішуємо це рівняння самостійно.
\[\begin{aligned} 3-2 x &=0 \\-2 x &=-3 \\ x &=\frac{3}{2} \end{aligned}\]
Таким чином, єдиним рішенням |3 − 2x| = 0 є x = 3/2.
Варто вказати, що «верхівка» або «вершина» «V» на малюнку\(\PageIndex{3}\) (в) розташована на x = 3/2. Це єдине місце, де перетинаються графіки y = |3 − 2x| та y = 0.
Приклад\(\PageIndex{6}\)
Розв'яжіть рівняння |3 − 2x| = 6 для x.
Рішення
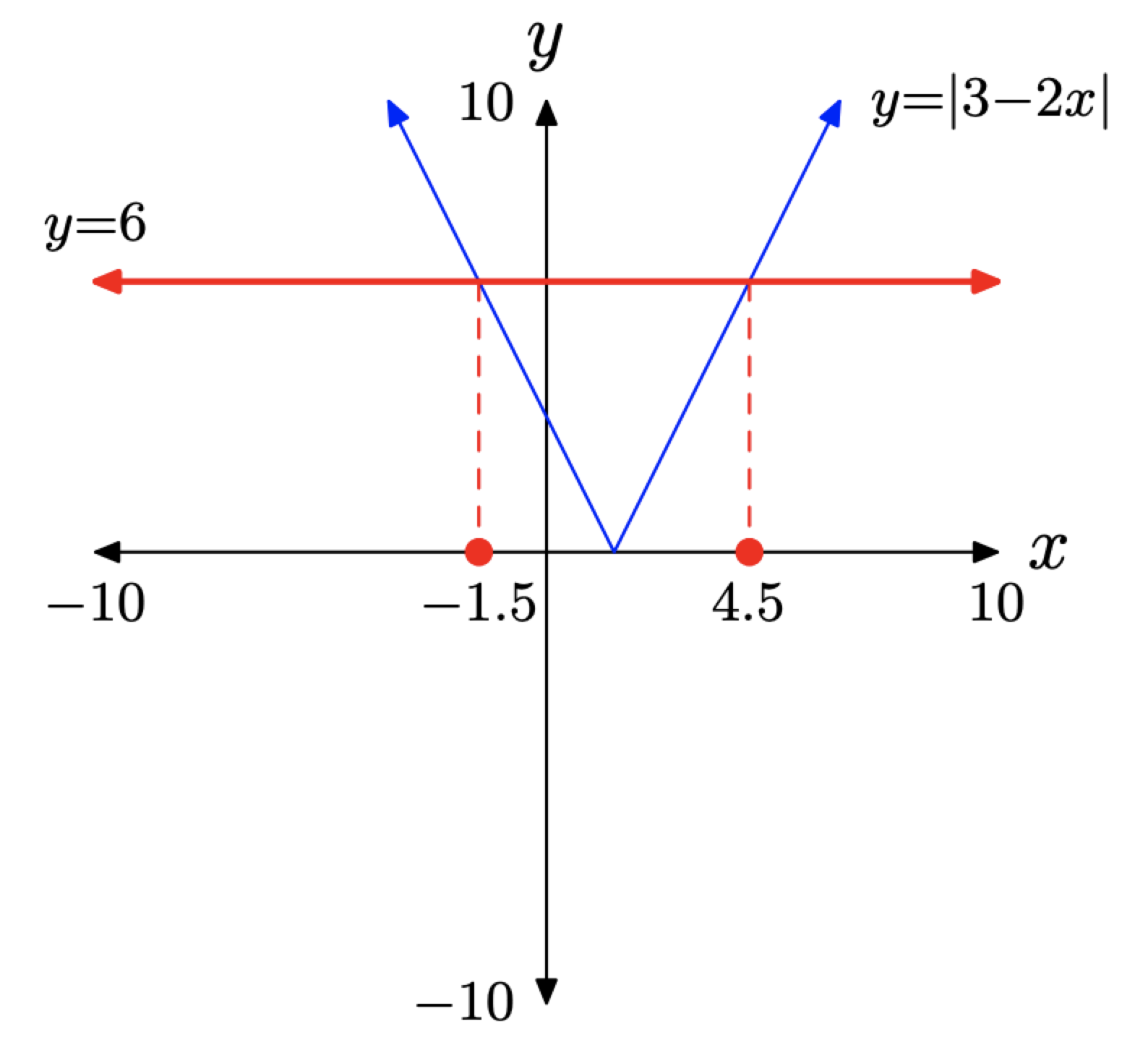
У цьому прикладі графік y = 6 є горизонтальною лінією, яка лежить на 6 одиниць над віссю x, а графік y = |3 − 2x| перетинає графік y = 6 у двох місцях. Ви можете використовувати утиліту intersect, щоб знайти точки перетину графіків, як ми маємо на малюнку\(\PageIndex{4}\) (b) і (c).
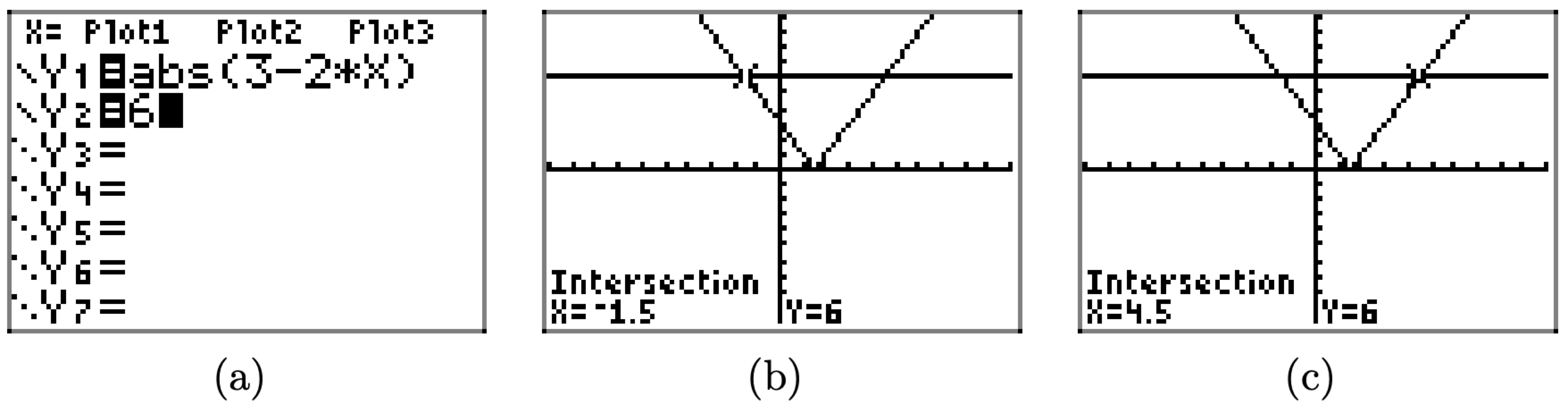
Нам потрібен спосіб підсумовування цього графічного калькулятора підхід на нашому домашньому папері. По-перше, намалюйте розумний факсиміле вікна перегляду вашого калькулятора на домашньому папері. Використовуйте лінійку, щоб намалювати всі лінії. Заповніть наступний контрольний список.
- Позначте кожну вісь, в даному випадку з x і y.
- Масштабуйте кожну вісь. Для цього натисніть кнопку WINDOW на вашому калькуляторі, після чого повідомте значення xmin, xmax, ymin та ymax на відповідній осі.
- Позначте кожен граф своїм рівнянням.
- Відкиньте пунктирні вертикальні лінії від точок перетину до осі x. Затіньте і позначте ці розв'язки рівняння на осі х.
Дотримуючись вказівок у наведеному вище контрольному списку, ми отримуємо зображення на малюнку\(\PageIndex{5}\).
Алгебраїчний підхід. Також можна скористатися алгебраїчною технікою для пошуку двох розв'язків |3 − 2x| = 6. Наскільки |x| = 6 має розв'язки x = −6 або x = 6, рівняння
\[|3-2 x|=6\]
можливий, лише якщо вираз всередині абсолютних значень дорівнює −6 або 6. Тому пишіть
\[3-2 x=-6 \qquad \text { or } \qquad 3-2 x=6\]
і вирішити ці рівняння самостійно
\[\begin{array}{rlrrrl}{3-2 x}&{=}&{-6} & {\text { or }} & {3-2 x}&{=}&{6} \\ {-2 x}&{=}&{-9} && {-2 x}&{=}&{3} \\ {x}&{=}&{\frac{9}{2}} && {x}&{=}&{-\frac{3}{2}}\end{array}\]
Оскільки −3/2 = −1.5 та 9/2 = 4.5, ці точні розв'язки точно узгоджуються з графічними розв'язками на рисунках\(\PageIndex{4}\) (b) та (c).
Підсумуємо методику, яка бере участь у вирішенні цієї важливої справи.
Примітка
Розв'язування |вираз | = a, коли a > 0. Вирішити рівняння
\[| \text { expression } |=a, \quad \text { when } a>0\]
набір
\[\text { expression }=-a \qquad \text { or } \qquad \text { expression }=a\]
потім вирішити кожне з цих рівнянь самостійно.
Наприклад:
• Щоб вирішити |2x + 7| = 5, задайте\[2x + 7 = −5 \qquad or \qquad 2x + 7 = 5\], потім вирішуйте кожне з цих рівнянь незалежно.
• Щоб розв'язати |3 − 5x| = 9, задайте\[3 − 5x = −9 \qquad or \qquad 3 − 5x = 9\], потім вирішуйте кожне з цих рівнянь незалежно.
• Зауважте, що цей метод не слід застосовувати до рівняння |2x + 11| = −10, оскільки права частина рівняння не є додатним числом. Дійсно, у цьому випадку жодне значення x не зробить ліву частину цього рівняння рівнянням −10, тому рівняння не має розв'язків.
Іноді нам доводиться робити невелику алгебру, перш ніж видаляти стовпчики абсолютних значень.
Приклад\(\PageIndex{7}\)
Розв'яжіть рівняння\[|x+2|+3=8\] для x.
Рішення
Спочатку відніміть 3 з обох сторін рівняння. \[\begin{aligned}|x+2|+3 &=8 \\|x+2|+3-3 &=8-3 \end{aligned}\]
Це спрощує\[|x+2|=5\]
Тепер, або\[x+2=-5 \qquad \text { or } \qquad x+2=5\]
кожне з яких можна вирішити окремо.
\[\begin{array}{rrlrrl}{x+2} & {=} & {-5} & {\text { or }} & {x+2} & {=} & {5} \\ {x+2-2} & {=} & {-5-2} && {x+2-2} & {=} & {5-2} \\ {x} & {=} & {-7} && {x} & {=} & {3}\end{array}\]
Приклад\(\PageIndex{8}\)
Розв'яжіть рівняння\[3|x-5|=6\] для x.
Рішення
Спочатку розділіть обидві сторони рівняння на 3
\[\begin{aligned} 3|x-5| &=6 \\ \frac{3|x-5|}{3} &=\frac{6}{3} \end{aligned}\]
Це спрощує\[|x-5|=2\]
Тепер, або\[x-5=-2 \qquad \text { or } \qquad x-5=2\]
кожне з яких можна вирішити окремо.
\[\begin{array}{rllrrl}{x-5} & {=} & {-2} & {\text { or }} & {x-5} & {=} & {2} \\ {x-5+5} & {=} & {-2+5} && {x-5+5} & {=} & {2+5} \\ {x} & {=} & {3} && {x} & {=} & {7}\end{array}\]
Властивості абсолютного значення
Приклад буде мотивувати необхідність деякого обговорення властивостей абсолютної величини.
Приклад\(\PageIndex{9}\)
Розв'яжіть рівняння\[\left|\frac{x}{2}-\frac{1}{3}\right|=\frac{1}{4}\] для x.
Рішення
Заманливо помножити обидві сторони цього рівняння на загальний знаменник наступним чином.
\[\begin{array}{l}{\left|\dfrac{x}{2}-\dfrac{1}{3}\right|=\dfrac{1}{4}} \\ {12\left|\dfrac{x}{2}-\dfrac{1}{3}\right|=12\left(\dfrac{1}{4}\right)}\end{array}\]
Якщо допустимо переміщати 12 всередині абсолютних значень, то ми могли б поступити наступним чином.
\[\begin{aligned}\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right| &=3 \\|6 x-4| &=3 \end{aligned}\]
Припускаючи на той момент, що цей останній хід допустимий, або
\[6 x-4=-3 \qquad \text { or } \qquad 6 x-4=3\]
Кожне з них можна вирішити окремо, спочатку додаючи 4 до обох сторін рівнянь, потім діливши на 6.
\[\begin{array}{rllrrl}{6 x-4} & {=} & {-3} & {\text { or }} & {6 x-4} & {=} & {3} \\ {6 x} & {=} & {1} & &{6 x} & {=} & {7} \\ {x} & {=} & {1 / 6} && {x} & {=} & {7 / 6}\end{array}\]
Оскільки ми використовували дещо сумнівний крок у отриманні цих рішень, було б розумно перевірити наші результати. По-перше, підставити x = 1/6 у вихідне рівняння.
\[\begin{aligned}\left|\frac{x}{2}-\frac{1}{3}\right| &=\frac{1}{4} \\\left|\frac{1 / 6}{2}-\frac{1}{3}\right| &=\frac{1}{4} \\\left|\frac{1}{12}-\frac{1}{3}\right| &=\frac{1}{4} \end{aligned}\]
Запишіть еквівалентні дроби із загальним знаменником і відніміть.
\[\begin{aligned}\left|\frac{1}{12}-\frac{4}{12}\right| &=\frac{1}{4} \\\left|-\frac{3}{12}\right| &=\frac{1}{4} \\\left|-\frac{1}{4}\right| &=\frac{1}{4} \end{aligned}\]
Зрозуміло, х = 1/6 чеків. Перевірку другого рішення залишимо нашим читачам.
Ну, ми перевірили наші рішення, і вони правильні, тому це повинно бути так, що
\[12\left|\frac{x}{2}-\frac{1}{3}\right|=\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right|\]
Але чому? Зрештою, бари абсолютних значень, хоча вони діють як символи групування, мають трохи більш обмежувальне значення, ніж звичайні символи групування, такі як дужки, дужки та дужки.
Викладемо першу властивість абсолютних значень.
Нерухомість
Якщо a і b є будь-якими дійсними числами, то
\[|a b|=|a||b|\]
Ми можемо продемонструвати дійсність цього майна, просто перевіривши випадки.
- Якщо a і b обидва позитивні дійсні числа, то так само ab і\(|a||b|=a b\). З іншого боку,\(|a||b|=a b\). Таким чином,\(|ab| = |a||b|\).
- Якщо a і b обидва є від'ємними дійсними числами, то ab є додатним і\(|ab| = ab\). З іншого боку,\(|a||b| = (−a)(−b) = ab\). Таким чином,\(|ab| = |a||b|\).
Ми залишимо докази інших двох випадків як вправи. Ми можемо використовувати,\(|a||b| = |ab|\) щоб продемонструвати, що
\[12\left|\frac{x}{2}-\frac{1}{3}\right|=|12|\left|\frac{x}{2}-\frac{1}{3}\right|=\left|12\left(\frac{x}{2}-\frac{1}{3}\right)\right|\]
Це підтверджує метод атаки, який ми використовували для розв'язання рівняння (12) у прикладі\(\PageIndex{9}\).
Попередження 14
З іншого боку, не припустимо множити на від'ємне число і просто ковзати від'ємне число всередині барів абсолютних значень. Наприклад,
\[-2|x-3|=|-2(x-3)|\]
явно помилка (ну, він працює для х = 3). Для будь-якого x, крім 3, лівою стороною цього результату є від'ємне число, але права - додатне число. Їм явно немає рівних.
Подібним чином можна продемонструвати друге корисна властивість, що передбачає абсолютну величину.
Визначення
Якщо a і b - будь-які дійсні числа, то\[\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\] передбачено, звичайно, що\(b \neq 0\).
Знову ж таки, це можна довести, перевіривши чотири випадки. Наприклад, якщо a є додатним дійсним числом, а b - від'ємним дійсним числом, то a/b є негативним і\(|a/b| = −a/b\). З іншого боку,\(|a|/|b| = a/(−b) = −a/b\).
Доказ решти трьох випадків залишаємо як вправи.
Ця властивість стане в нагоді в певних ситуаціях. Наприклад, якщо ви хочете розділити\(|2x − 4|\) на 2, ви будете діяти наступним чином.
\[\frac{|2 x-4|}{2}=\frac{|2 x-4|}{|2|}=\left|\frac{2 x-4}{2}\right|=|x-2|\]
Ця методика стане в нагоді в декількох ситуаціях. Наприклад, якщо ви хочете вирішити рівняння\(|2x − 4| = 6\), ви можете розділити обидві сторони на 2 і застосувати частку властивість абсолютних значень.
Відстань переглянуто
Нагадаємо, що для будь-якого дійсного числа x абсолютне значення x визначається як відстань між дійсним числом x і початком на дійсній прямій. У цьому розділі ми просунемо цю концепцію відстані трохи далі.
Припустимо, що у вас два дійсних числа на дійсному рядку. Наприклад, на наступному малюнку ми розмістили 3 та −2 на дійсному рядку.

Ви можете визначити відстань між двома точками, віднімаючи число зліва від числа праворуч. Тобто відстань між двома точками дорівнює d = 3 − (−2) = 5 одиниць. Якщо відняти в іншому напрямку, ви отримаєте від'ємне значення відстані, як у −2 − 3 = −5 одиниць. Звичайно, відстань є невід'ємною величиною, тому цей негативний результат не може відображати відстань між двома точками. Отже, щоб знайти відстань між двома точками на реальній прямій, потрібно завжди відняти число зліва від числа праворуч.
Однак, якщо взяти абсолютне значення різниці, ви отримаєте правильний результат незалежно від напрямку віднімання.
\[d=|3-(-2)|=|5|=5 \quad \text { and } \quad d=|-2-3|=|-5|=5\]
Ця дискусія призводить до наступної ключової ідеї.
Нерухомість 16.
Припустимо, що a і b - це два числа на дійсному рядку

Визначити відстань d між a і b на дійсній прямій можна, взявши абсолютне значення їх різниці. Тобто,
\[d=|a-b|\]
Звичайно, можна було б відняти в іншому напрямку, отримуючи\(d = |b − a|\). Це теж правильно.
Тепер, коли ця геометрія відстані введена, корисно вимовляти символіку |a−b| як «відстань між a та b» замість того, щоб говорити «абсолютне значення мінус b».
Приклад\(\PageIndex{10}\)
Розв'яжіть рівняння\[|x − 3| = 8\] для x.
Рішення
Ось ідеальна ситуація для застосування нашої нової концепції відстані. Замість того, щоб сказати «абсолютне значення х мінус 3 дорівнює 8», ми вимовляємо рівняння\(|x − 3| = 8\) як «відстань між x і 3 дорівнює 8».
Намалюйте цифру і знайдіть цифру 3 на лінії.

Нагадаємо, що «відстань між х і 3 дорівнює 8». Сказавши це, відзначте дві точки на реальній лінії, які знаходяться на відстані 8 одиниць від 3.
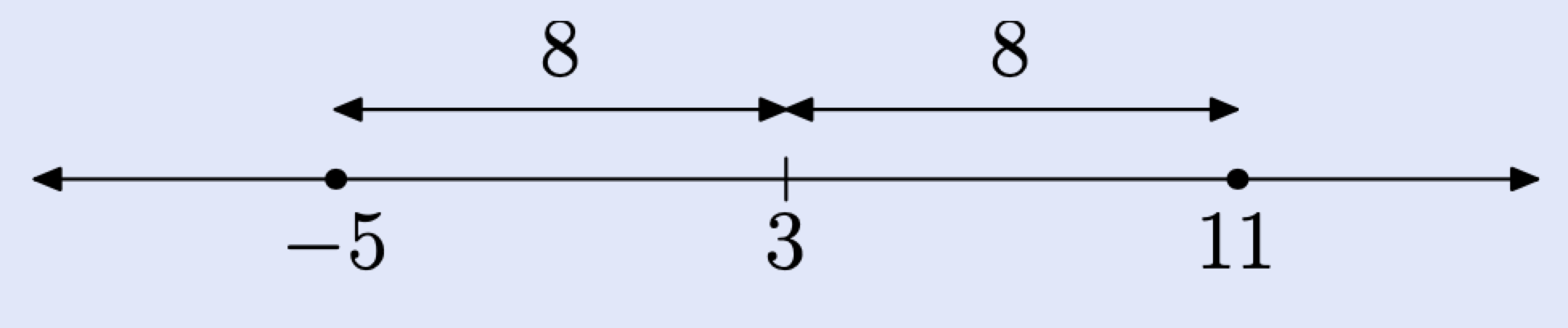
Таким чином, розв'язки |x − 3| = 8 складають x = −5 або x = 11
Приклад\(\PageIndex{11}\)
Розв'яжіть рівняння\[|x + 5| = 2\] для x.
Рішення
Перепишіть рівняння як різницю. \[|x − (−5)| = 2\]Це вимовляється «відстань між x і −5 дорівнює 2». Знайдіть дві точки на числовому рядку, що знаходяться на відстані 2 одиниць від −5.
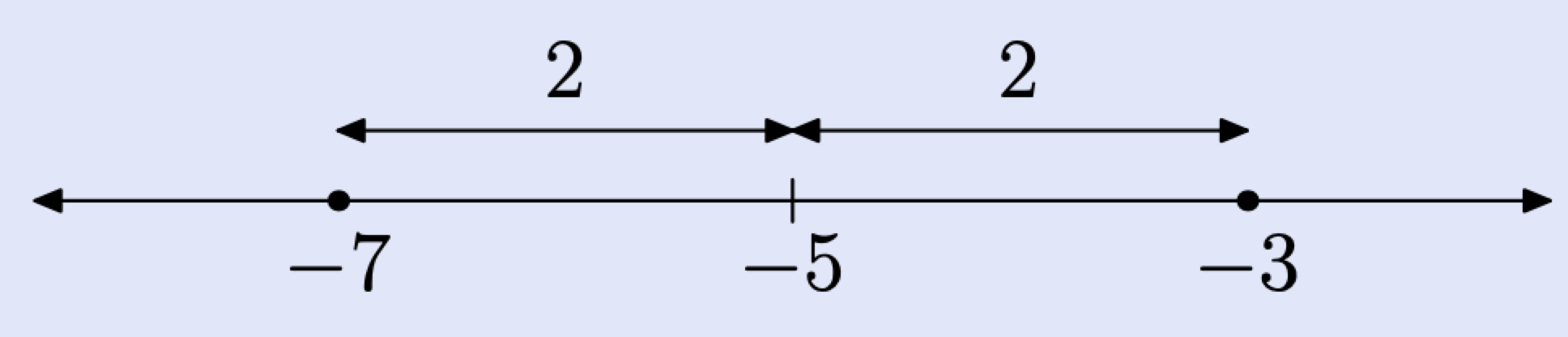
Отже,\(|x + 5| = 2\) розв'язки х = −7 або x = −3.
Вправа
Для кожного з рівнянь у вправах 1 - 4 виконайте кожне з наступних завдань.
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь.
- Намалюйте графік кожної сторони рівняння без допомоги калькулятора. Позначте кожен граф своїм рівнянням.
- Затіньте рішення рівняння на осі x (якщо є), як показано на малюнку 5 (читайте «Очікування») в оповіданні. Тобто відкиньте пунктирні лінії від точок перетину до осі, потім затіньте і позначте рішення, встановлене на осі х.
Вправа\(\PageIndex{1}\)
|х| = −2
- Відповідь
-
Ніяких рішень.
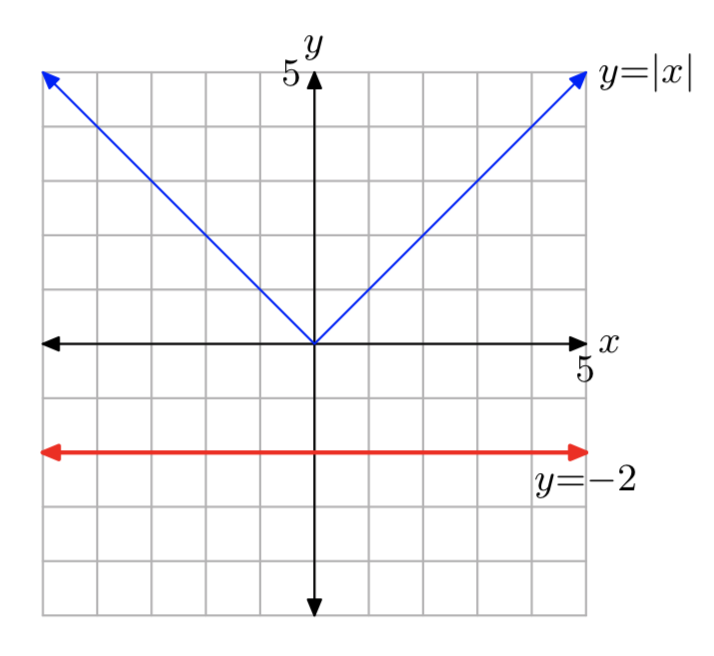
Вправа\(\PageIndex{2}\)
|х| = 0
Вправа\(\PageIndex{3}\)
|х| = 3
- Відповідь
-
Розв'язок: х = −3 або х = 3.
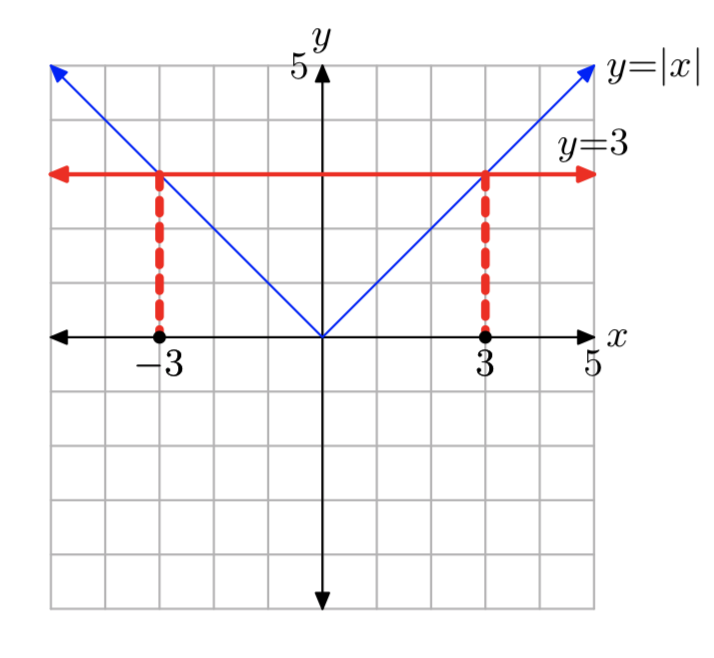
Вправа\(\PageIndex{4}\)
|х| = 2
Для кожного з рівнянь у вправах 5 - 8 виконайте кожне з наступних завдань.
- Завантажте кожну сторону рівняння в меню Y = вашого калькулятора. оголошення- просто оглядове вікно, щоб у вікні перегляду були видні всі точки перетину двох графіків.
- Скопіюйте зображення на екрані перегляду на домашній папір. Позначте кожну вісь та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте кожен граф своїм рівнянням.
- Використовуйте утиліту Intersect в меню CALC для визначення точок перетину. Заштрихуйте і позначте кожне рішення, як показано на малюнку 5 (читайте «Очікування») в розповіді. Тобто відкиньте пунктирні лінії від точок перетину до осі, потім затіньте і позначте рішення, встановлене на осі х.
Вправа\(\PageIndex{5}\)
|3−2х| = 5
- Відповідь
-
Розчини: х = −1 або х = 4.
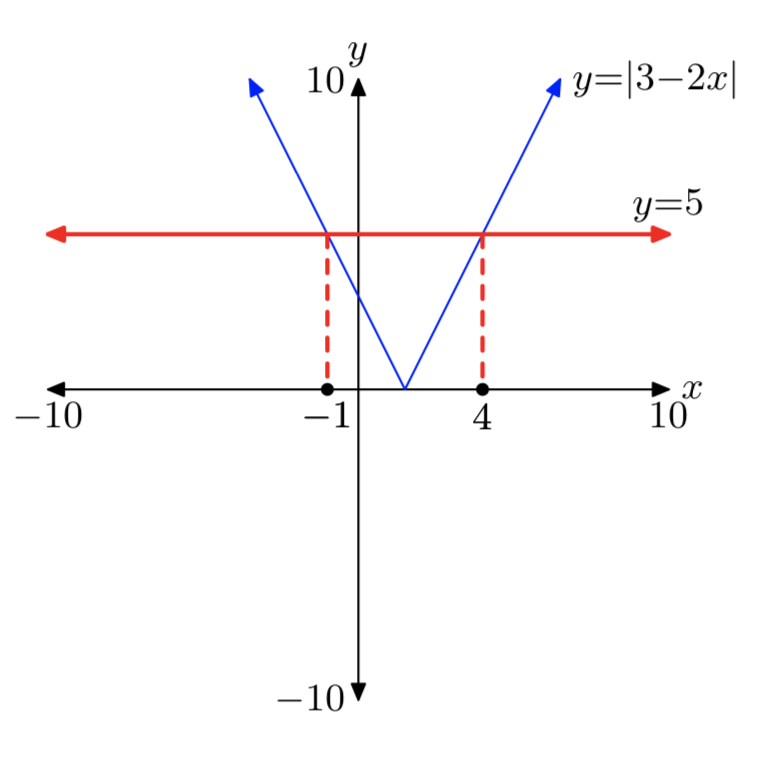
Вправа\(\PageIndex{6}\)
|2х+7| = 4
Вправа\(\PageIndex{7}\)
|4х+5| = 7
- Відповідь
-
Розчини: х = −3 або х = 0,5.
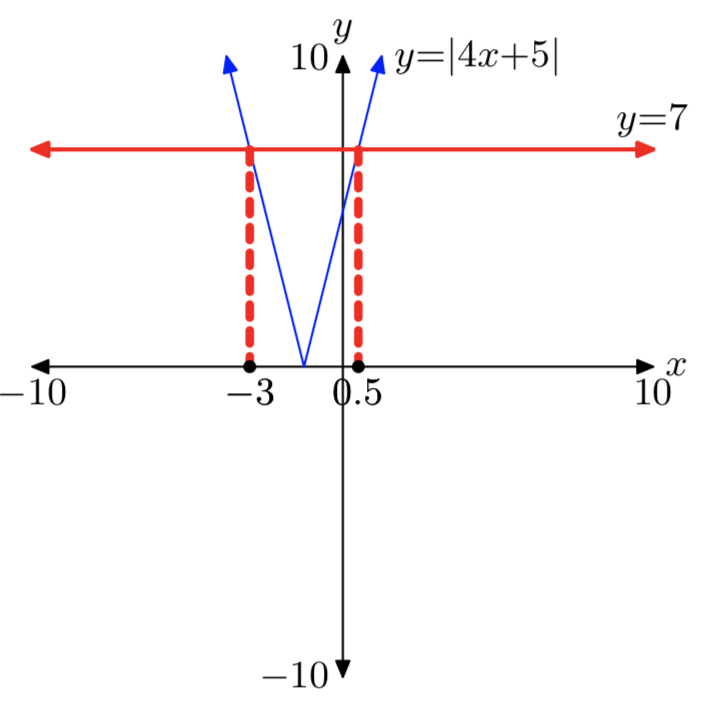
Вправа\(\PageIndex{8}\)
|5x−7| = 8
Для кожного з рівнянь у вправах 9 - 14 надайте чисто алгебраїчне рішення без використання калькулятора. Влаштуйте свою роботу так, як показано в прикладах 6, 7 і 8 в оповіданні, але не використовуйте калькулятор.
Вправа\(\PageIndex{9}\)
|4х+3| = 0
- Відповідь
-
\(x = −\frac{3}{4}\)
Вправа\(\PageIndex{10}\)
|3х−11| = −5
Вправа\(\PageIndex{11}\)
|2х+7| = 14
- Відповідь
-
\(x = −\frac{21}{2}\)або\(x = \frac{7}{2}\)
Вправа\(\PageIndex{12}\)
|7−4х| = 8
Вправа\(\PageIndex{13}\)
|3−2x| = −1
- Відповідь
-
Ніяких рішень.
Вправа\(\PageIndex{14}\)
|4х+9| = 0
Для кожного з рівнянь у вправах 15 - 20 виконайте кожне з наступних завдань.
- Розташуйте кожну з наступних частин на домашньому папері в тому ж місці. Не розміщуйте алгебраїчну роботу на одній сторінці, а графічну роботу на іншій.
- Дотримуйтесь кожного з вказівок, наведених для вправ 5 - 8, щоб знайти та записати рішення за допомогою графічного калькулятора.
- Надайте чисто алгебраїчне рішення, показуючи всі етапи вашої роботи. Чи вигідно ці рішення відрізняються від тих, що знайдені за допомогою графічного калькулятора в частині (ii)? Якщо немає, шукайте помилку у своїй роботі.
Вправа\(\PageIndex{15}\)
|х−8| = 7
- Відповідь
-
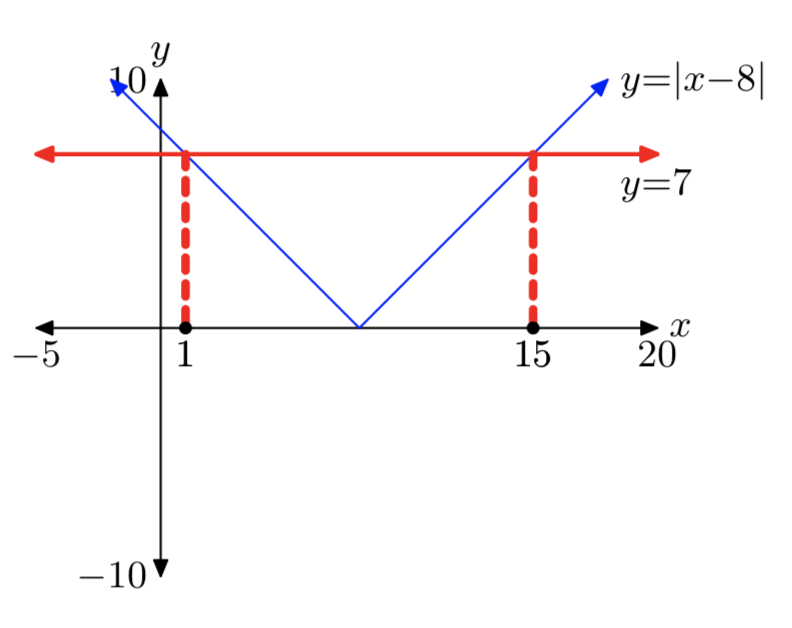
х = 1 або х = 15
Вправа\(\PageIndex{16}\)
|2х−15| = 5
Вправа\(\PageIndex{17}\)
|2х+11| = 6
- Відповідь
-
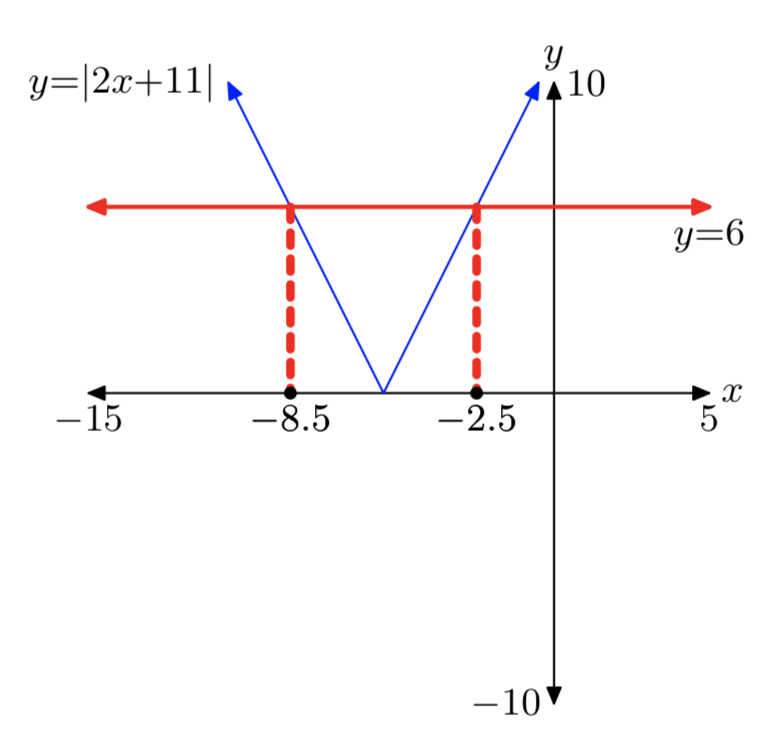
x = −8,5 або х = −2,5
Вправа\(\PageIndex{18}\)
|5x−21| = 7
Вправа\(\PageIndex{19}\)
|х−12| = 6
- Відповідь
-
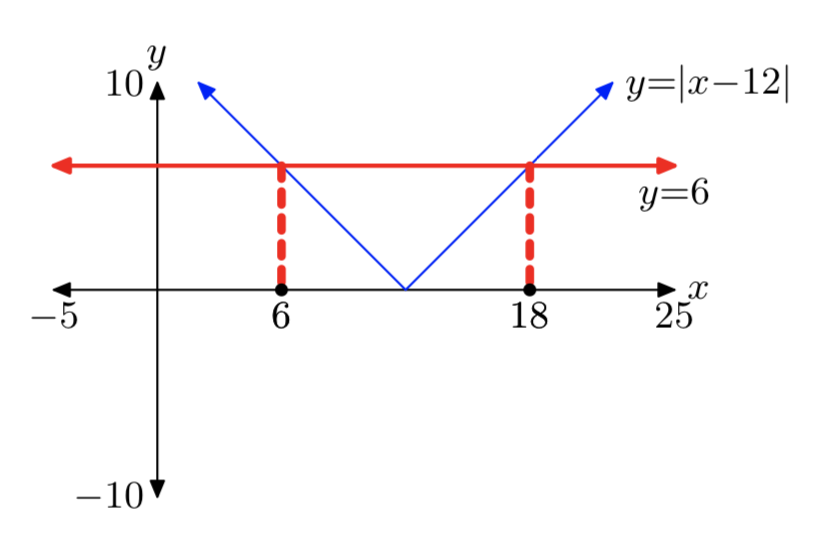
х = 6 або х = 18
Вправа\(\PageIndex{20}\)
|х+11| = 5
Використовуйте строго алгебраїчну техніку для вирішення кожного з рівнянь у Вправи 21 - 28. Не використовуйте калькулятор.
Вправа\(\PageIndex{21}\)
|х+2|−3 = 4
- Відповідь
-
х = −9 або х = 5
Вправа\(\PageIndex{22}\)
3|х+5| = 6
Вправа\(\PageIndex{23}\)
−2|3−2x| = −6
- Відповідь
-
х = 0 або х = 3
Вправа\(\PageIndex{24}\)
|4−х|+5 = 12
Вправа\(\PageIndex{25}\)
3|х+2|−5 = |х+2|+7
- Відповідь
-
х = −8 або х = 4
Вправа\(\PageIndex{26}\)
4−3|4−х| = 2|4−х|−1
Вправа\(\PageIndex{27}\)
\(|\frac{x}{3}−\frac{1}{4}| = \frac{1}{12}\)
- Відповідь
-
\(x = \frac{1}{2}\)або х = 1
Вправа\(\PageIndex{28}\)
\(|\frac{x}{4}−\frac{1}{2}| = \frac{2}{3}\)
Використовуйте техніку відстані на числовій лінії, продемонстровану в прикладах 16 і 17, для вирішення кожного з рівнянь у вправах 29 - 32. Надайте ескізи числових рядків на домашньому папері, як показано в прикладах 16 та 17 в розповіді.
Вправа\(\PageIndex{29}\)
|х−5| = 8
- Відповідь
-
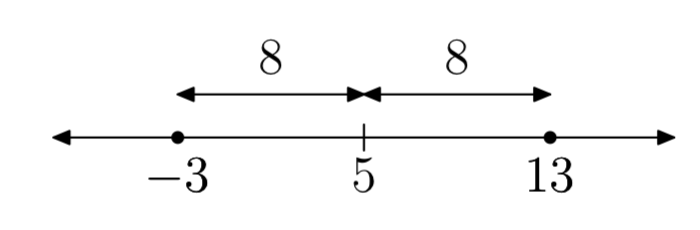
х = −3 або х = 13
Вправа\(\PageIndex{30}\)
|х−2| = 4
Вправа\(\PageIndex{31}\)
|х+4| = 3
- Відповідь
-
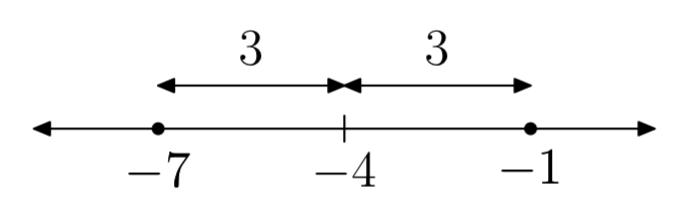
x = −7 або x = −1
Вправа\(\PageIndex{32}\)
|х+2| = 11
Використовуйте інструкції, наведені в Вправи 5 - 8, для вирішення рівнянь у Вправи 33 - 34.
Вправа\(\PageIndex{33}\)
\(|x+2| = \frac{1}{3}x+5\)
- Відповідь
-
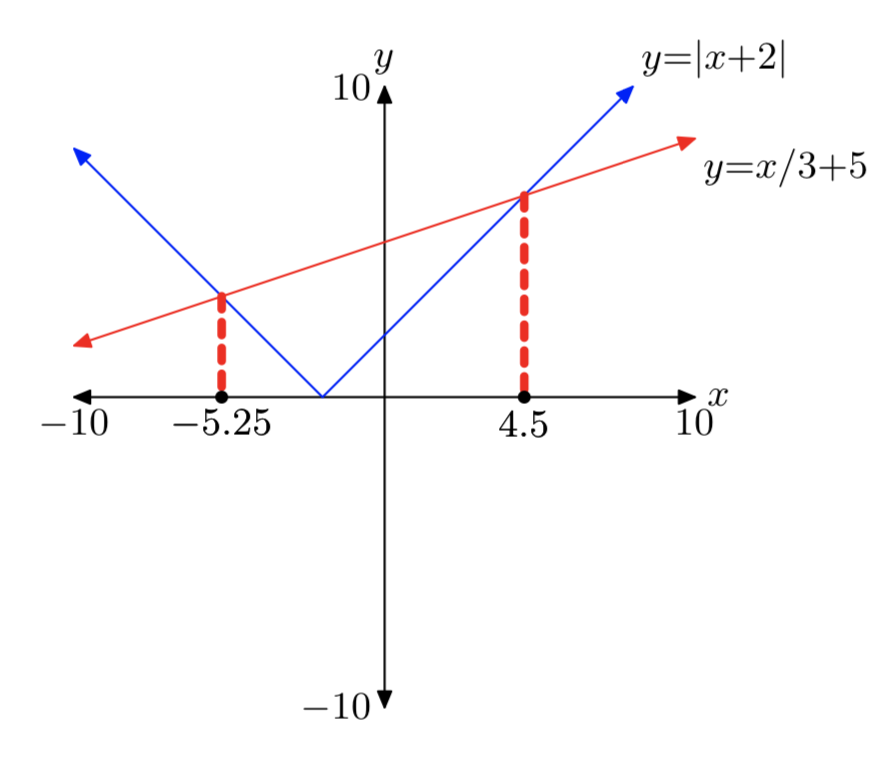
Вправа\(\PageIndex{34}\)
\(|x−3|=5−\frac{1}{2}x\)
У Вправах 35 - 36 виконайте кожне з наступних завдань.
- Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь.
- Без використання калькулятора накидайте графіки лівої і правої сторін даного рівняння. Позначте кожен граф своїм рівнянням.
- Відкиньте пунктирні вертикальні лінії від кожної точки перетину до осі x. Заштрихуйте і позначте кожен розчин на осі х (вам доведеться наблизити).
Вправа\(\PageIndex{35}\)
\(|x−2| = \frac{1}{3}x+2\)
- Відповідь
-
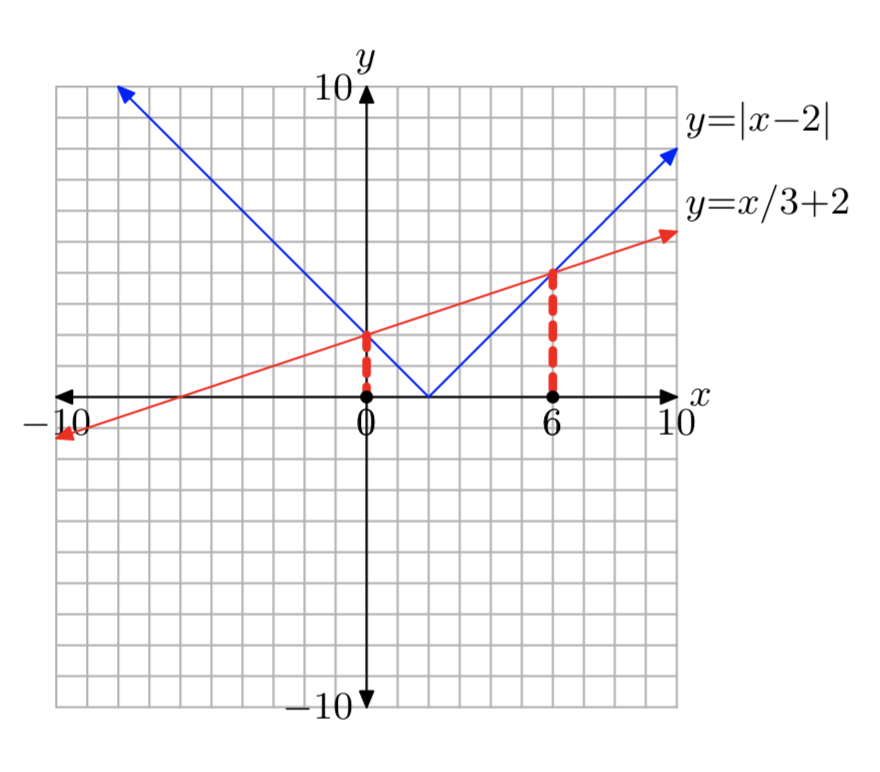
Вправа\(\PageIndex{36}\)
\(|x+4| = \frac{1}{3}x+4\)
Вправа\(\PageIndex{37}\)
Враховуючи, що < 0 and b > 0, довести, що |ab| = |a||b|.
- Відповідь
-
Якщо a є від'ємним дійсним числом, а b - додатним дійсним числом, то ab є від'ємним, отже |ab| = −ab. З іншого боку, негативний також означає, що |a| = −a, а b додатне означає, що |b| = b, так що |a||b| = −a (b) = −ab. Порівнюючи ці результати, ми бачимо, що |ab| і |a||b| рівні одне і те ж, і тому вони повинні дорівнювати один одному.
Вправа\(\PageIndex{38}\)
Враховуючи, що a>0 і b<0, довести, що |ab| = |a||b|.
Вправа\(\PageIndex{39}\)
В оповіданні ми довели, що якщо a > 0 і b < 0, то\(|\frac{a}{b}| = \frac{|a|}{|b|}\). Доведіть інші три випадки.
- Відповідь
-
Кейс I. (a, b > 0) Якщо a і b є додатними дійсними числами, то\(\frac{a}{b}\) це додатне і так\(|\frac{a}{b}| = \frac{a}{b}\). З іншого боку, позитив також означає, що |a| = a, а b позитивний означає, що |b| = b, так що\(\frac{|a|}{|b|} = \frac{a}{b}\). Порівнюючи ці два результати, ми бачимо, що\(|\frac{a}{b}|\) і\(\frac{|a|}{|b|}\) рівні одне і те ж, і тому вони повинні бути рівні один одному.
Справа II. (a, b < 0) Якщо a і b є від'ємними дійсними числами, то\(\frac{a}{b}\) це додатне і так\(|\frac{a}{b}| = \frac{a}{b}\). З іншого боку, негативний також означає, що |a| = −a, а b негативний означає, що |b| = −b, отже\(\frac{|a|}{|b|} = \frac{−a}{(−b)} = \frac{a}{b}\). Порівнюючи ці два результати, ми бачимо, що\(|\frac{a}{b}|\) і\(\frac{|a|}{|b|}\) рівні одне і те ж, і тому вони повинні бути рівні один одному.
Справа III. (a < 0, b > 0) Якщо a є від'ємним дійсним числом, а b - додатним дійсним числом,\(\frac{a}{b}\) то від'ємне і так\(|\frac{a}{b}| =−(\frac{a}{b})\). З іншого боку, негативне також означає, що |a| = −a, а b додатне означає, що |b| = b, так що\(\frac{|a|}{|b|} = −\frac{a}{b} = −(\frac{a}{b})\). Порівнюючи ці два результати, ми бачимо, що\(|\frac{a}{b}|\) і\(\frac{|a|}{|b|}\) рівні одне і те ж, і тому вони повинні бути рівні один одному.
