4.1: Кусково визначені функції

При підготовці до визначення функції абсолютного значення вкрай важливо добре зрозуміти поняття кусково визначеної функції. Однак, перш ніж ми стрибати в бій, давайте поглянемо на особливий тип функції називається постійною функцією.

Одним із способів розуміння постійної функції є погляд на її графік.

Приклад\(\PageIndex{1}\)

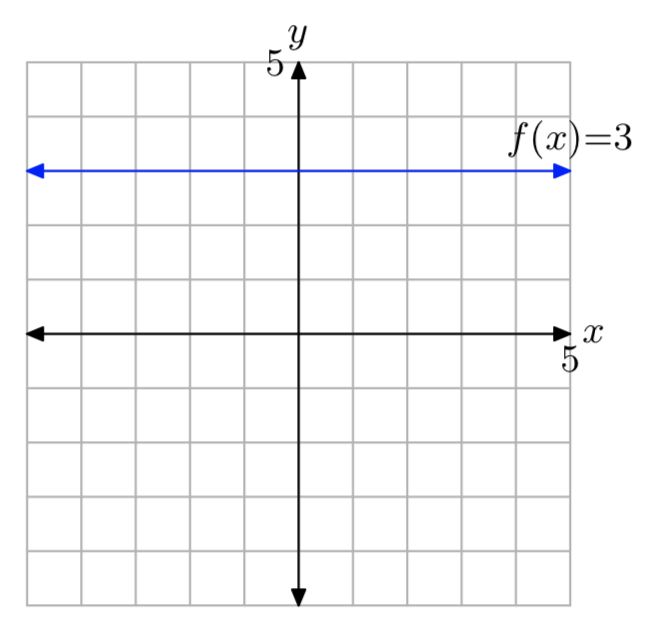
Намалюйте графік постійної функції f (x) = 3.

Рішення

Оскільки позначення f (x) = 3 еквівалентно позначенню y = 3, ми можемо намалювати графік f, намалювавши графік горизонтальної лінії, що має рівняння y = 3, як показано на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\). Графік постійної функції - горизонтальна лінія.

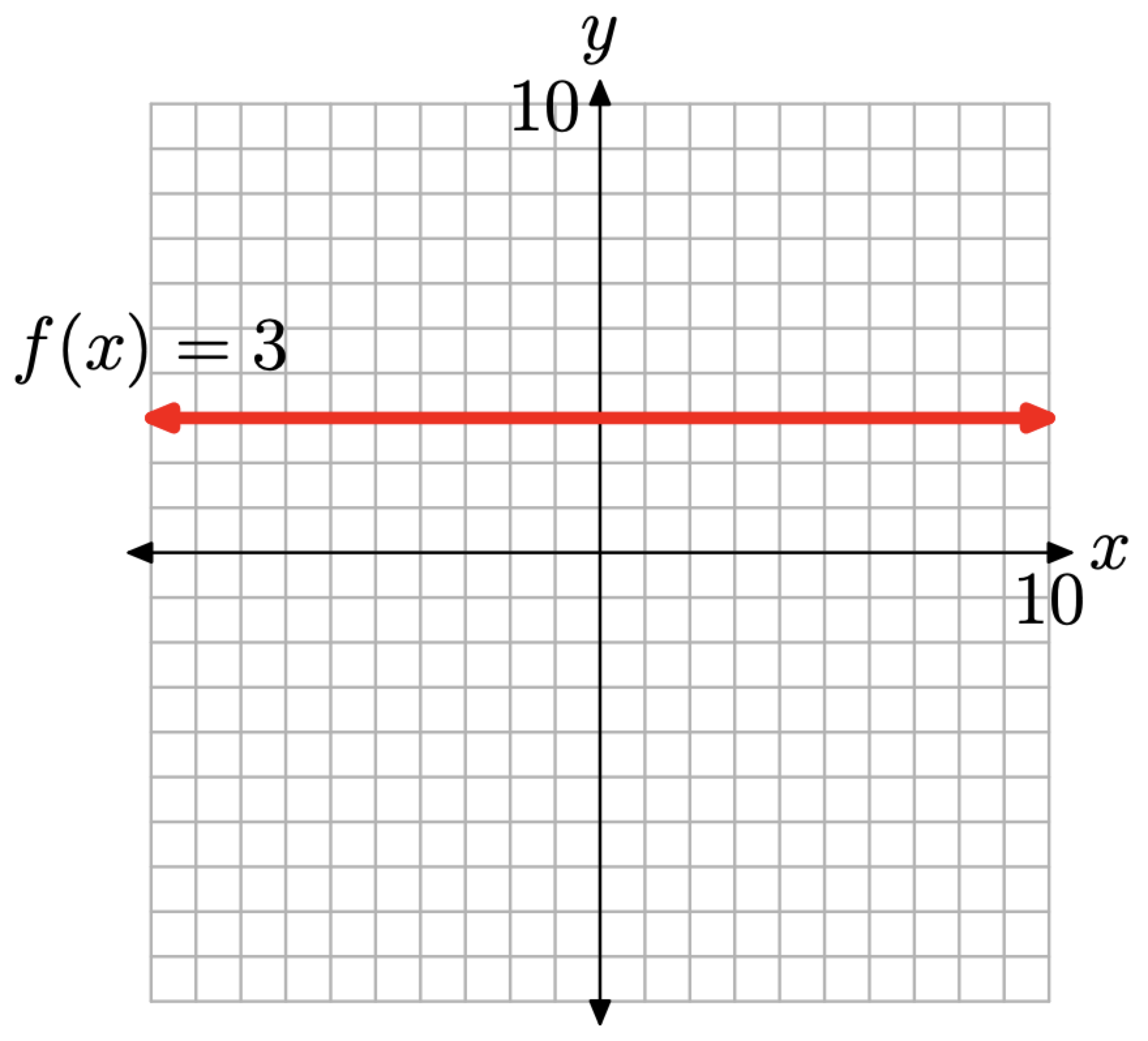
Коли ви дивитеся на графік на малюнку 1, зверніть увагу, що кожна точка на горизонтальній лінії, що має рівняння f (x) = 3, має значення y, рівне 3. Ми говоримо, що значення y на цій горизонтальній лінії постійні, з тієї простої причини, що вони постійно рівні 3.

Функціональна форма працює точно так само. Подивіться ще раз на позначення\[f(x)=3\]

Зверніть увагу, що незалежно від того, яке число ви підставите для x в лівій частині f (x) = 3, права сторона постійно дорівнює 3. Таким чином,

\[f(-5)=3, \quad f(-1 / 2)=3, \quad f(\sqrt{2})=3, \quad \text { or } \quad f(\pi)=3\]

Вищевикладене обговорення призводить до наступного визначення.

Визначення

Функція, визначена f (x) = c, де c - константа (фіксоване дійсне число), називається постійною функцією.

Два зауваження по порядку:

1. f (x) = c для всіх дійсних чисел x.
2. Графік f (x) = c - горизонтальна лінія. Він складається з усіх точок (x, y), що мають значення y, рівне c.

Кусково постійні функції

Кускові функції - улюбленець інженерів. Давайте розглянемо приклад.

Приклад\(\PageIndex{2}\)

Припустимо, що акумулятор не забезпечує напругу ланцюга при розімкнутому вимикачі. Потім, починаючи на час\(t = 0\), вимикач закривається і акумулятор забезпечує постійне 5 вольт з цього часу вперед. Створіть кускову функцію моделювання обмежень задачі та намалюйте її графік.

Рішення

Це досить проста вправа, але нам доведеться ввести деякі нові позначення. Перш за все, якщо час t менше нуля (\(t < 0\)), то напруга дорівнює 0 вольт. Якщо час t більше або дорівнює нулю (\(t \geq 0\)), то напруга постійне 5 вольт. Ось позначення, яке ми будемо використовувати, щоб узагальнити цей опис напруги.

\[V(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0} \\ {5,} & {\text { if } t \geq 0}\end{array}\right.\]

Деякі зауваження по порядку:

• Різниця напруг, що забезпечується акумулятором в ланцюзі, є функцією часу. Таким чином, V (t) являє собою напругу в момент t.
• Позначення, що використовуються в (4), універсально приймаються математиками в ситуаціях, коли функція змінює визначення в залежності від значення незалежної змінної. Таке визначення функції V називається «кусковим визначенням». Оскільки кожна з частин у цьому визначенні є постійною, функція V називається кусково-постійною функцією.
• Ця особлива функція має дві частини. Функція - це постійна функція\(V (t) = 0\)\(t < 0\), коли, але інша постійна функція\(V (t) = 5\), коли\(t \geq 0\).

Якщо\(t<0, V(t)=0 .\) Наприклад, для\(t=-1, t=-10,\) і\(t=-100\)

\[V(-1)=0, \quad V(-10)=0, \quad \text { and } \quad V(-100)=0\]

З іншого боку, якщо\(t \geq 0,\) тоді\(V(t)=5 .\) Наприклад, для\(t=0, t=10,\) і\(t=100\)

\[V(0)=5, \quad V(10)=5, \quad \text { and } \quad V(100)=5\]

Перш ніж представити графік кусково-постійної функції V, давайте зупинимося на мить, щоб переконатися, що ми розуміємо деякі стандартні геометричні терміни.

Геометричні терміни

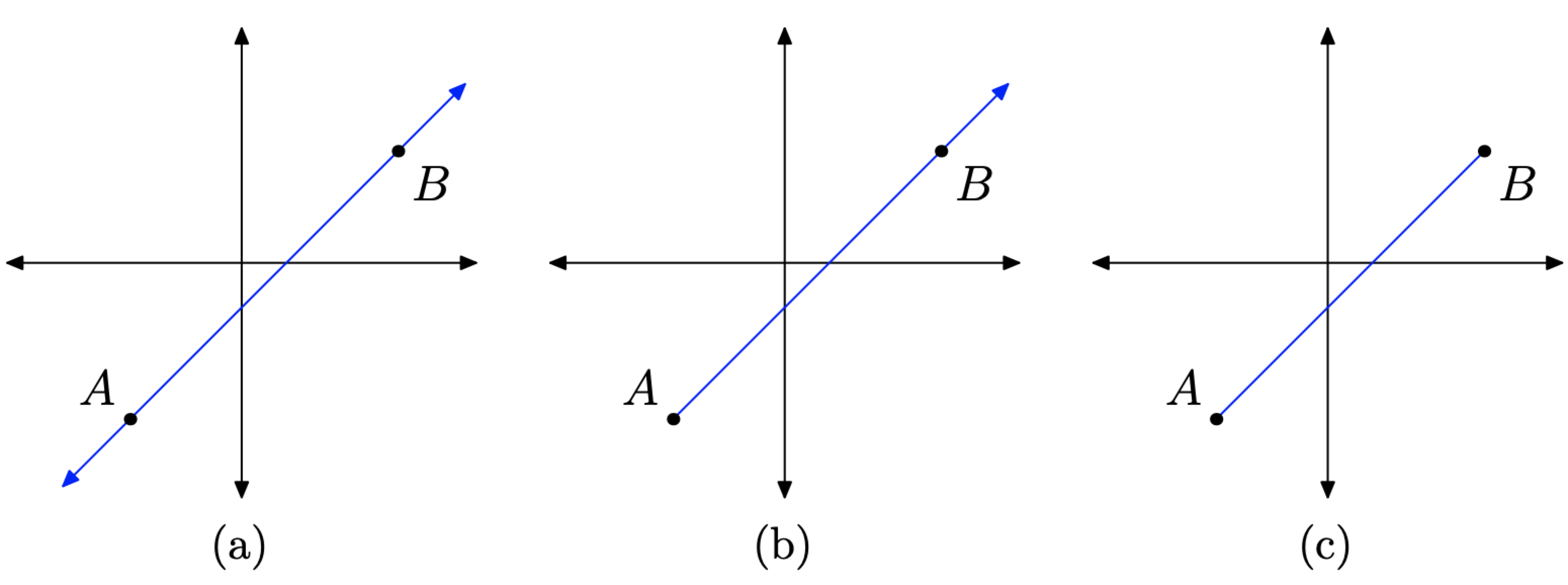
• Лінія розтягується нескінченно в двох напрямках, як показано на малюнку\(\PageIndex{2}\) (а).
• Якщо лінія має фіксовану кінцеву точку і розтягується на невизначений час тільки в одному напрямку, як показано на малюнку\(\PageIndex{2}\) (b), то вона називається променем.
• Якщо частина лінії закріплена на кожному кінці, як показано на малюнку\(\PageIndex{2}\) (в), то вона називається відрізком лінії.

Малюнок\(\PageIndex{2}\). Лінії, промені та сегменти.

Маючи в руках ці терміни, звернемо увагу на графік напруги, визначеного рівнянням (4). Коли\(t < 0\), то\(V (t) = 0\). Зазвичай графік\(V (t) = 0\) буде горизонтальною лінією, де кожна точка на лінії має V -значення, рівне нулю. Однак\(V (t) = 0\) тільки в тому випадку\(t < 0\), якщо таким чином графік є горизонтальним променем, який починається від початку, то переміщається на невизначений час вліво, як показано на малюнку\(\PageIndex{3}\). Тобто горизонтальна лінія\(V = 0\) була обмежена доменом\(\{t : t<0\}\) і існує лише зліва від початку.

Аналогічно\(t \geq 0\), коли,\(V (t) = 5\) то горизонтальний промінь показаний на рис\(\PageIndex{3}\). Кожна точка на промені має V -значення, рівне 5.

Малюнок\(\PageIndex{3}\). Напруга як функція часу t.

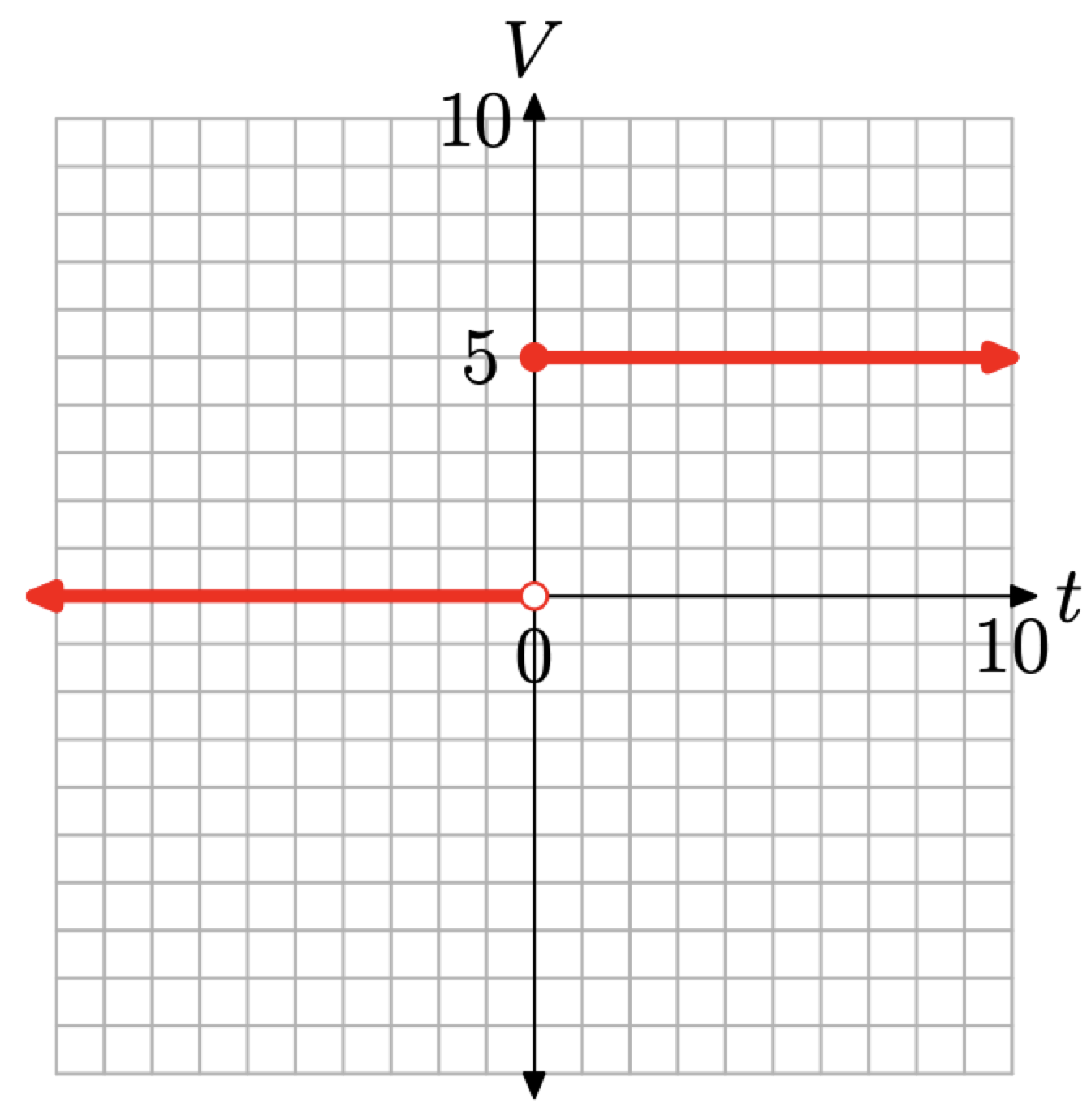
Два зауваження по порядку:

• Тому що\(V (t) = 0\) тільки коли t < 0, точка (0, 0) незаповнена (це відкрите коло). Відкрите коло в (0, 0) - це спосіб математика сказати, що ця конкретна точка не побудована або затінена.
• Тому що\(V (t) = 5\) коли\(t \geq 0\), точка (0, 5) заповнена (це заповнене коло). Заповнене коло в (0, 5) - це спосіб математика сказати, що ця конкретна точка побудована або затінена.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{3}\)

Розглянемо кусково визначену функцію

\[f(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {1,} & {\text { if } 0 \leq x<2} \\ {2,} & {\text { if } x \geq 2}\end{array}\right.\]

Оцініть f (x) при x = −1, 0, 1, 2 та 3. Намалюйте графік кускової функції f.

Рішення

Оскільки кожна частина функції в (6) є постійною, оцінка функції досить проста. Вам просто потрібно вибрати правильний шматок.

• Зауважте, що x = −1 менше 0, тому ми використовуємо перший шматок і запишемо f (−1) = 0.

• Зверніть увагу, що х = 0 задовольняє\(0 \leq x<2\), тому використовуємо другий шматок і пишемо f (0) = 1.

• Зверніть увагу, що х = 1 задовольняє\(0 \leq x<2\), тому використовуємо другий шматок і пишемо f (1) = 1.

• Зверніть увагу, що х = 2 задовольняє\(x \geq 2\), тому використовуємо третій шматок і пишемо f (2) = 2.

• Нарешті, зауважте, що х = 3 задовольняє\(x \geq 2\), тому використовуємо третій шматок і пишемо f (3) = 2. Графік так само простий для ескізу.

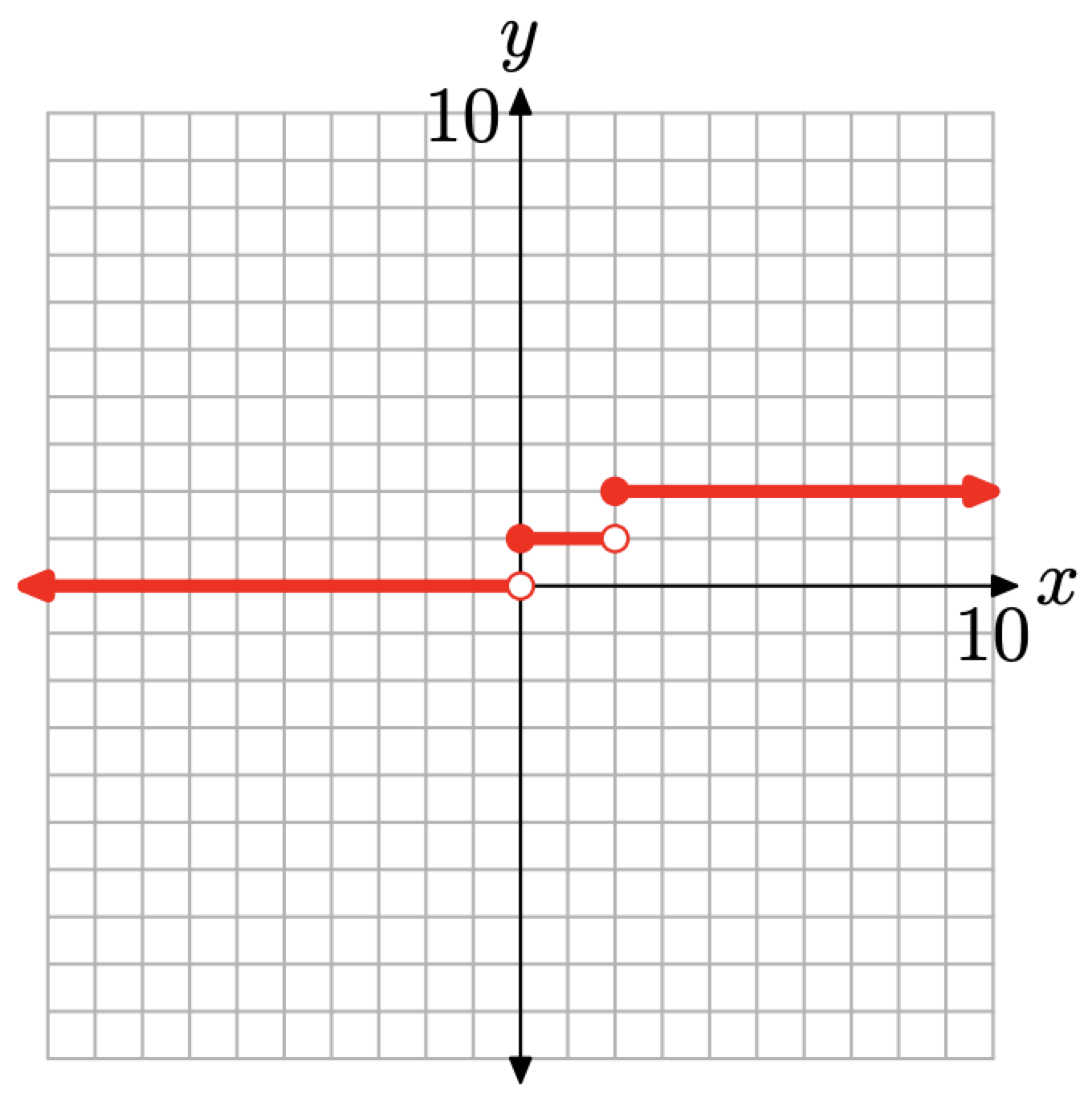
• Оскільки f (x) = 0 для x < 0, графік цього фрагмента є горизонтальним променем з кінцевою точкою x = 0. Кожна точка цього променя матиме значення y, рівне нулю, і промінь буде лежати повністю лівіше x = 0, як показано на малюнку\(\PageIndex{4}\).

• Оскільки f (x) = 1 for\(0 \leq x<2\), графік цього фрагмента є горизонтальним відрізком з однією кінцевою точкою в x = 0, а інший при x = 2. Кожна точка на цьому відрізку матиме значення y, рівне 1, як показано на малюнку\(\PageIndex{4}\).

• Оскільки f (x) = 2 for\(x \geq 2\), графік цього фрагмента є горизонтальним променем з кінцевою точкою в x = 2. Кожна точка цього променя має значення y, рівне 2, і промінь лежить повністю праворуч від x = 2, як показано на малюнку\(\PageIndex{4}\).

Кілька зауважень по порядку:

• Функція дорівнює нулю ліворуч від початку (для x < 0), але не на початку. На це вказує порожнє коло біля початку, вказівка на те, що ми не будуємо цю конкретну точку.

• Для\(0 \leq x<2\), функція дорівнює 1. Тобто функція постійно дорівнює 1 для всіх значень x між 0 і 2, включаючи нуль, але не включаючи 2. Ось чому ви бачите заповнене коло на (0, 1) і порожнє коло в (2, 1).

• Нарешті, для\(x \geq 2\), функція дорівнює 2. Тобто функція постійно дорівнює 2, коли x більше або дорівнює 2. Ось чому ви бачите заповнене коло на (2, 2).

Малюнок\(\PageIndex{4}\). Ескіз графіка кускової функції (6).

Кусково визначені функції

Тепер, давайте подивимося на більш загальну ситуацію, що включає кусково визначені функції - той, де шматки не обов'язково є постійними. Найкращий спосіб вчитися - це робити, тому почнемо з прикладу.

Приклад\(\PageIndex{4}\)

Розглянемо кусково визначену функцію

\[f(x)=\left\{\begin{array}{ll}{-x+2,} & {\text { if } x<2} \\ {x-2,} & {\text { if } x \geq 2}\end{array}\right.\]

Оцініть f (x) для x = 0, 1, 2, 3 і 4, потім намалюйте графік кусково визначеної функції.

Рішення

Функція змінює визначення при x = 2. Якщо x < 2, то f (x) = −x + 2. Оскільки обидва 0 і 1 строго менше 2, ми оцінюємо функцію з цієї першої частини визначення.

\[\begin{array}{ll}{f(x)=-x+2} &\text{and} & {f(x)=-x+2} \\ {f(0)=-0+2} & &{f(1)=-1+2} \\ {f(0)=2} & &{f(1)=1}\end{array}\]

З іншого боку, якщо\(x \geq 2\), то\(f(x) = x − 2\). Оскільки 2, 3 і 4 все більше або дорівнює 2, ми оцінюємо функцію з цієї другої частини визначення.

\[\begin{array}{lll}{f(x)=x-2}&{\text { and }} & {f(x)=x-2} & {\text { and }} & {f(x)=x-2} \\ {f(2)=2-2} &{\text { and }}& {f(3)=3-2} &{\text { and }}& {f(4)=4-2} \\ {f(2)=0} &{\text { and }}& {f(3)=1} & {\text { and }}&{f(4)=2}\end{array}\]

Одним з можливих підходів до графіка f є розміщення точок, які ми вже обчислили, плюс пару додаткових, в таблиці (див. Рисунок\(\PageIndex{5}\) (а)), побудувати їх (див. Рисунок\(\PageIndex{5}\) (b)), а потім інтуїтивно зрозуміти форму графіка з доказів, наданих побудованими точками. Це робиться на малюнку\(\PageIndex{5}\) (в).

Малюнок\(\PageIndex{5}\). Побудова графіка кускової функції, визначеної в (8).

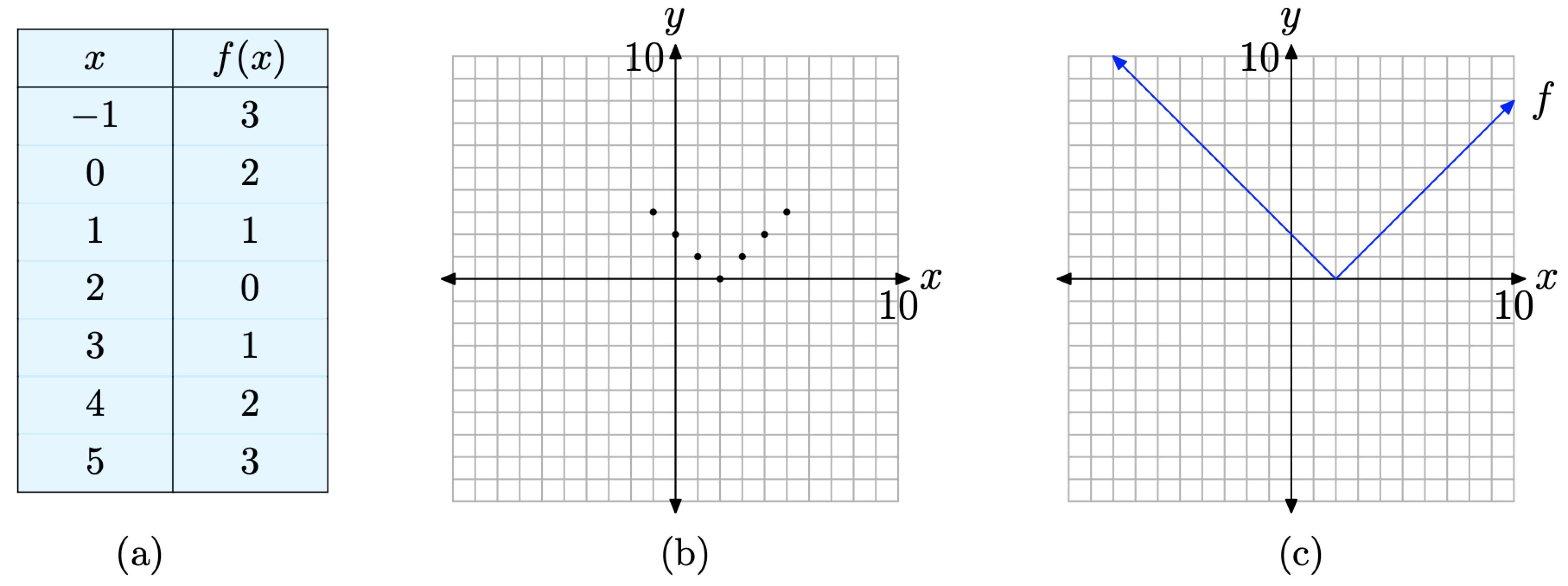
Однак прагматичний, цей точковий підхід є трохи втомливим; але, що ще важливіше, він не забезпечує фон, необхідний для обговорення функції абсолютного значення в наступному розділі. Нам потрібно розтягнути наше розуміння на більш високий рівень. На щастя, всі основи на місці. Нам потрібно лише застосувати те, що ми вже знаємо про рівняння ліній, щоб відповідати цій кусковій ситуації.

Альтернативний підхід. Давайте скористаємося нашими знаннями рівняння прямої (тобто y = mx + b), щоб допомогти намалювати графік кускової функції, визначеної в (8).

Давайте намалюємо перший шматок функції f, визначеної в (8). У нас є f (x) = −x+ 2, за умови x < 2. Зазвичай це буде лінія (з нахилом −1 і перехопленням 2), але ми маємо намалювати лише частину цієї лінії, частину, де x < 2 (x ліворуч від 2). Таким чином, цей шматок графіка буде промінням, починаючи з точки, де x = 2, потім рухаючись на невизначений час вліво.

Найпростіший спосіб намалювати промінь - спочатку обчислити і побудувати його фіксовану кінцеву точку (в даному випадку при x = 2), потім побудувати другу точку на промені, що має рентгенівське значення менше 2, потім за допомогою лінійки намалювати промінь.

З огляду на цю думку, щоб знайти координати кінцевої точки променя, підставити x = 2 in f (x) = −x + 2, щоб отримати f (2) = 0. Тепер, технічно, ми не повинні використовувати цей шматок функції, якщо х строго менше 2, але ми могли б використовувати його з х = 1.9, або х = 1.99, або х = 1.999, і т.д. так що давайте йти вперед і використовувати х = 2 в цій частині функції, але вказуємо, що ми насправді не повинні використовувати цю точку, малюючи» порожнє коло» в (2, 0), як показано на малюнку\(\PageIndex{6}\) (а).

Щоб завершити сюжет променя, нам знадобиться друга точка, яка лежить зліва від його кінцевої точки в (2, 0). Зверніть увагу, що x = 0 знаходиться ліворуч від x = 2. Оцінити f (x) = −x + 2 при x = 0, щоб отримати f (0) = −0 + 2 = 2. Це дає нам другу точку (0, 2), яку ми будуємо, як показано на малюнку\(\PageIndex{6}\) (а). Нарешті, намалюйте промінь з кінцевою точкою в (2, 0) і другою точкою в (0, 2), як показано на малюнку\(\PageIndex{6}\) (а).

Малюнок\(\PageIndex{6}\). Намалюйте кожен шматок окремо

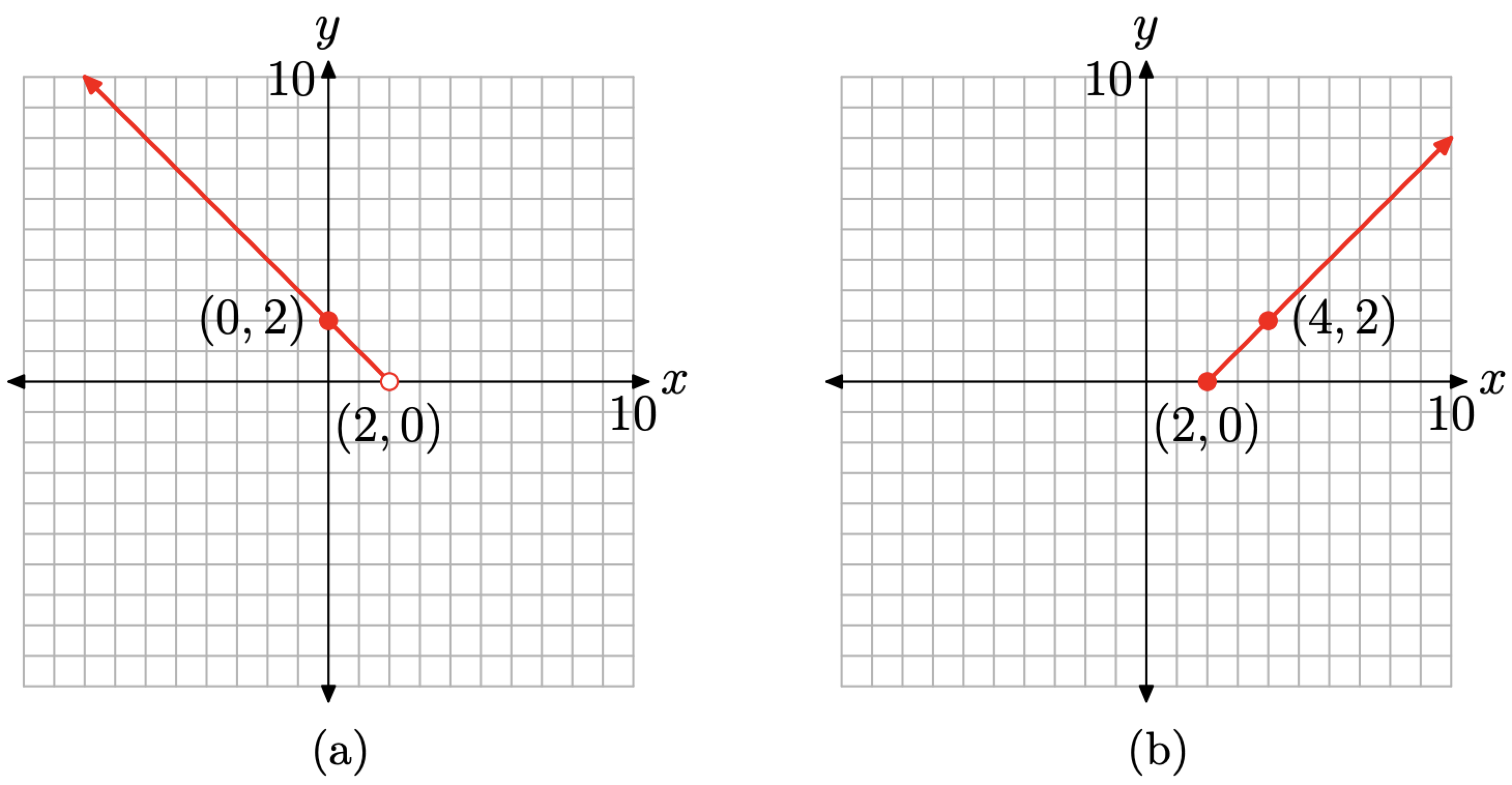
Тепер ми повторюємо цей процес для другої частини функції, визначеної в (8). Рівняння другого фрагмента дорівнює f (x) = x − 2, надано\(x \geq 2\). Зазвичай f (x) = x − 2 буде лінією (з нахилом 1 та перехопленням −2), але ми маємо намалювати лише ту частину лінії, яка лежить праворуч від x = 2. Таким чином, графік цього другого шматка являє собою промінь, починаючи з точки з x = 2 і продовжуючи вправо. Якщо оцінювати f (x) = x − 2 при x = 2, то f (2) = 2 − 2 = 0. Таким чином, фіксована кінцева точка променя знаходиться в точці (2, 0). Оскільки ми насправді повинні використовувати цей шматок з х = 2, ми вказуємо цей факт із заповненою окружністю в (2, 0), як показано на малюнку\(\PageIndex{6}\) (b).

Нам потрібна друга точка праворуч від цієї фіксованої кінцевої точки, тому ми оцінюємо f (x) = x−2 при x = 4, щоб отримати f (4) = 4 − 2 = 2. Таким чином, друга точка на промені - це точка (4, 2). Нарешті, ми просто малюємо промінь, починаючи з кінцевої точки (2, 0) і проходячи через другу точку в (4, 2), як показано на малюнку\(\PageIndex{6}\) (b).

Щоб завершити графік кускової функції f, визначеної в рівнянні (8), просто об'єднайте дві частини на малюнку\(\PageIndex{6}\) (а) та малюнку\(\PageIndex{6}\) (b), щоб отримати готовий графік на малюнку\(\PageIndex{7}\). Зверніть увагу, що графік на малюнку\(\PageIndex{7}\) ідентичний попередньому результату на малюнку\(\PageIndex{5}\) (c).

Спробуємо цю альтернативну процедуру в іншому прикладі.

Приклад\(\PageIndex{5}\)

Джерело забезпечує напругу ланцюга згідно з кусковим визначенням.

\[V(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0} \\ {t,} & {\text { if } t \geq 0}\end{array}\right.\]

Намалюйте графік напруги V проти часу t.

Рішення

За весь час t, що менше нуля, напруга V дорівнює нулю. Графік V (t) = 0 є постійною функцією, тому його графік зазвичай є горизонтальною лінією. Однак ми повинні обмежити

Малюнок\(\PageIndex{7}\). Поєднання обох частин.

графік до області\((-\infty, 0)\), тому цей шматок рівняння (10) буде горизонтальним променем, починаючи від початку і рухаючись на невизначений час вліво, як показано на малюнку\(\PageIndex{8}\) (а).
З іншого боку, V (t) = t для всіх значень t, які більше або рівні нулю. Зазвичай це буде лінія з нахилом 1 і перехоплює нуль. Однак ми повинні обмежити область до\([0, \infty)\), тому цей шматок рівняння (10) буде промінням, починаючи від початку і рухаючись на невизначений час вправо.

• Кінцева точка цього променя починається з t = 0. Тому що V (t) = t, V (0) = 0. Отже, кінцева точка цього променя знаходиться в точці (0, 0).
• Виберіть будь-яке значення t, яке більше нуля. Ми виберемо t = 5. Тому що V (t) = t, V (5) = 5. Це дає нам другу точку на промені в (5, 5), як показано на малюнку\(\PageIndex{8}\) (b).

Малюнок\(\PageIndex{8}\).

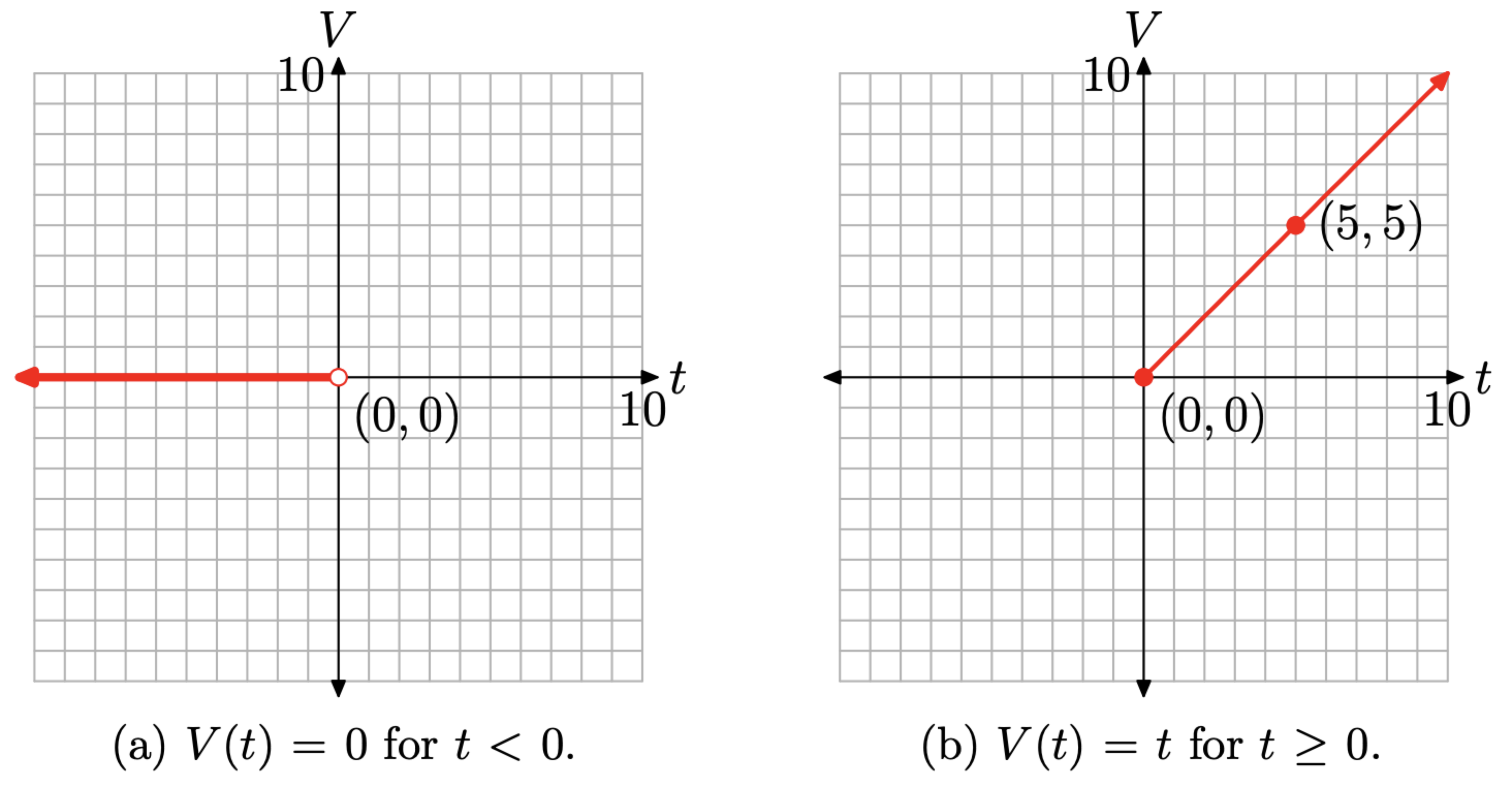
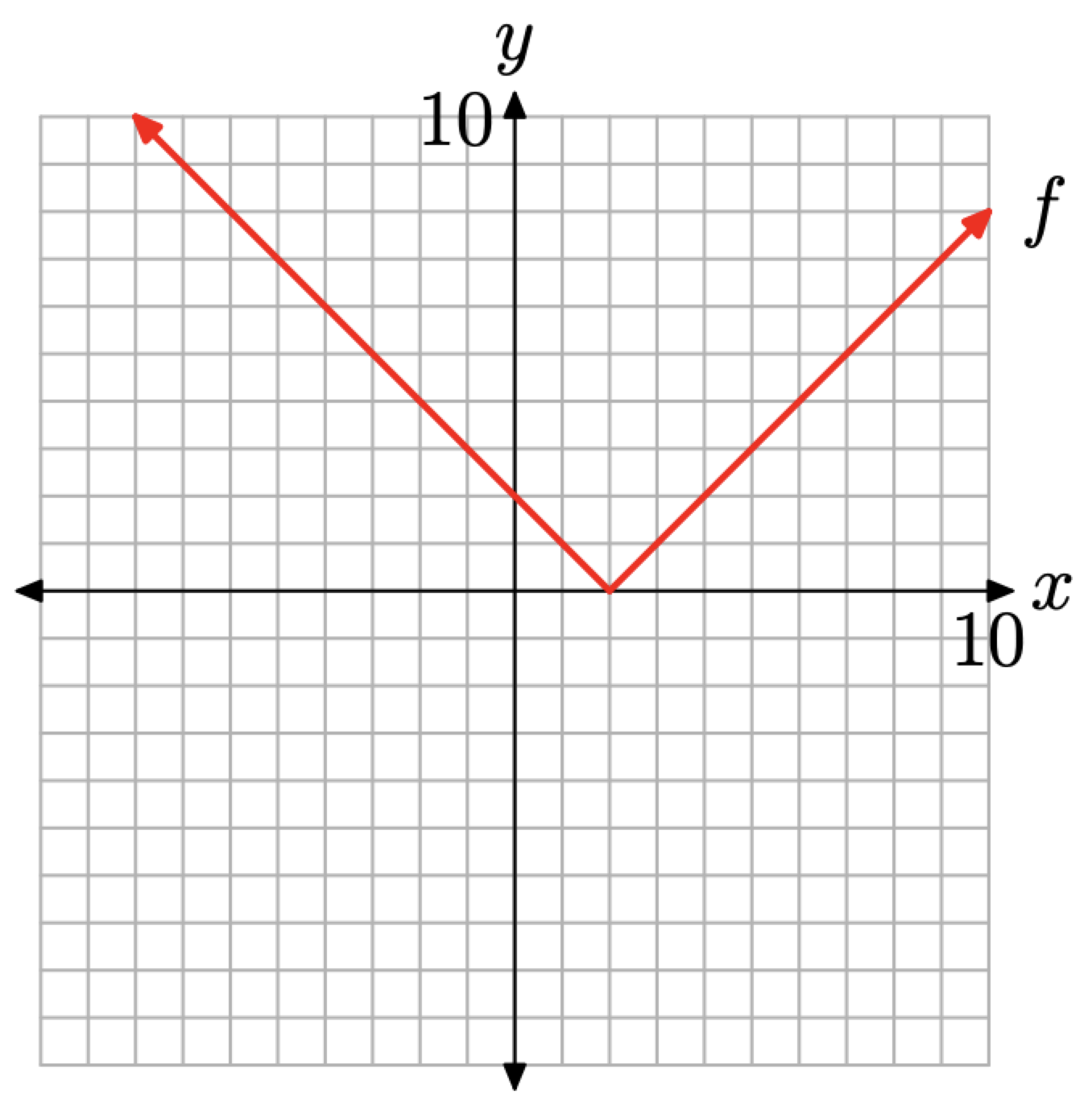
Нарешті, щоб забезпечити повний графік функції напруги, визначеної рівнянням (10), ми об'єднаємо графіки кожного фрагмента визначення, показаного на малюнках\(\PageIndex{8}\) (а) і (b).

Результат показаний на малюнку\(\PageIndex{9}\). Інженери називають цей тип вхідної функції «функцією рампи».

Малюнок\(\PageIndex{9}\). Графік функції пандуса визначається рівнянням (10).

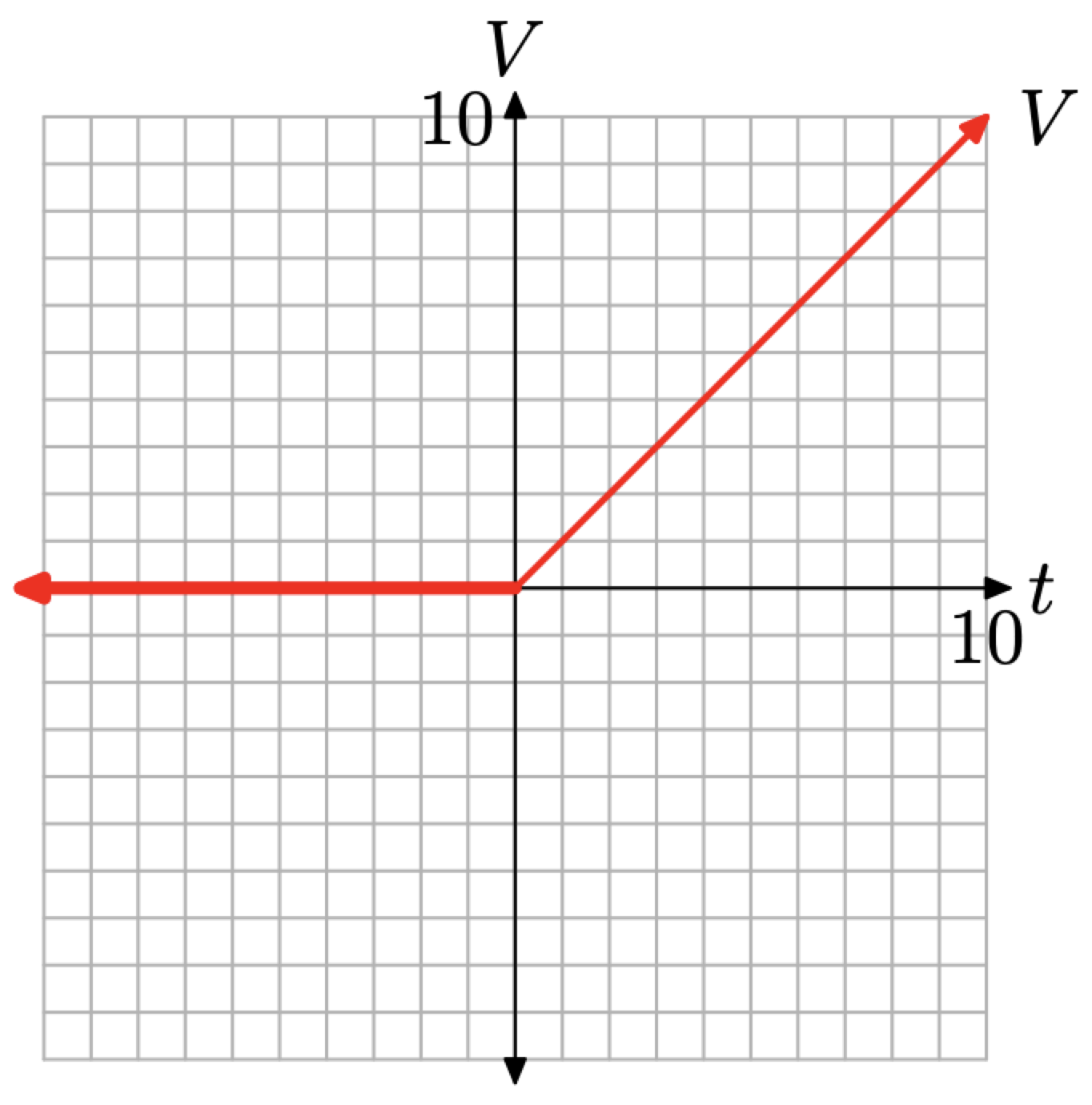
Давайте розглянемо дуже практичне застосування кускових функцій.

Приклад\(\PageIndex{6}\)

Ставки федерального податку на прибуток для єдиного подавача в 2005 році наведені в табл\(\PageIndex{1}\).

Табл\(\PageIndex{1}\). 2005 Федеральні ставки податку на прибуток для єдиного подавача.

Дохід	Ставка податку
До 7 150 доларів	10%
7 151$ - 29 050$	15%
$29,051-$70,350	25%
$70 351 - $146 750	28%
$146 751-319 100	33%
$319,101 або більше	35%

Створіть кускове визначення, яке передбачає ставку податку як функцію доходу фізичних осіб.

Рішення

У звітності про оподатковуваний дохід суми округляються до найближчого долара на федеральній формі податку на прибуток. Технічно домен дискретний. Ви можете повідомити про оподатковуваний дохід у розмірі $35,000 або $35,001, але цифри між цими двома доходами не використовуються на федеральній формі податку на прибуток. Однак ми будемо думати про дохід як про континуум, що дозволяє доходу бути будь-яким реальним числом, більшим або рівним нулю. Якби ми цього не зробили, то наш графік був би серію крапок - по одній на кожну суму долара. Ми повинні були б побудувати багато точок!

Ми дозволимо R представляти ставку податку, а я представляю дохід. Мета полягає у визначенні R як функції I.

• Якщо дохід I є будь-якою сумою, більшою або рівною нулю, і менше або дорівнює $7,150, ставка податку R становить 10% (тобто R = 0,10). Таким чином, якщо\(\$ 0 \leq I \leq \$ 7,150\), R (I) = 0,10.
• Якщо дохід I - це будь-яка сума, яка строго перевищує $7,150, але менше або дорівнює $29,050, то ставка податку R становить 15% (тобто R = 0,15). Таким чином, якщо $7, 150 < I ≤ $29, 050, то R (I) = 0,15.

Продовжуючи таким чином, ми можемо побудувати кускове визначення ставки R як функції оподатковуваного доходу I.

\[R(I)=\left\{\begin{array}{ll}{0.10,} & {\text { if } \$ 0 \leq I \leq \$ 7,150} \\ {0.15,} & {\text { if } \$ 7,150<I \leq \$ 29,050} \\ {0.25,} & {\text { if } \$ 29,050<I \leq \$ 70,350} \\ {0.28,} & {\text { if } \$ 70,350<I \leq \$ 146,750} \\ {0.33,} & {\text { if } \$ 146,750<I \leq \$ 319,100} \\ {0.35,} & {\text { if } I>\$ 319,100}\end{array}\right.\]

Звернемо увагу на графік цієї кусково визначеної функції. Всі частини є постійними функціями, тому кожен шматок буде горизонтальною лінією на рівні, що вказує ставку податку. Однак кожен з перших п'яти частин функції, визначеної в рівнянні (12), є сегментами, оскільки ставка визначається на інтервалі з початковим і кінцевим доходом. Шостий і останній шматок - це промінь, оскільки він має початкову кінцеву точку, але ставка залишається постійною для всіх доходів понад 319 100 доларів. Ми використовуємо ці знання для побудови графіка, показаного на малюнку\(\PageIndex{10}\).

Перша ставка становить 10%, і це призначається оподатковуваному доходу, починаючи з $0 і закінчуючи $7,150 включно. Таким чином, зверніть увагу на перший горизонтальний відрізок лінії на малюнку\(\PageIndex{10}\), який проходить від $0 до $7150 на висоті R = 0,10. Зверніть увагу, що кожна з кінцевих точок заповнена колами.

Друга ставка становить 15%, і це призначається оподатковуваним доходам більше 7150 доларів, але менше або дорівнює $29,050. Другий відрізок горизонтальної лінії на малюнку 10 проходить від $7,150 до $29,050 при висоті R = 0,15. Зауважте, що кінцевою точкою лівого кінця цього горизонтального відрізка є відкритим колом, тоді як кінцева точка на правому кінці - це заповнене коло, оскільки оподатковувані доходи коливаються на $7150 < I ≤ $29 050. Таким чином, виключаємо ліву кінцеву точку і включаємо праву кінцеву точку.

Решта відрізки малюються аналогічним чином.

Останній шматок призначає ставку R = 0,35 всім оподатковуваним доходам строго вище $319 100. Отже, останній шматок - горизонтальний промінь, починаючи з ($319 100, 0,35) і продовжується на невизначений термін вправо. Зверніть увагу, що ліва кінцева точка цього променя є відкритим колом, оскільки ставка R = 0,35 застосовується до оподатковуваних доходів I > $319, 100.

Поговоримо момент про область і діапазон функції R, визначеної рівнянням (12). Графік R зображений на малюнку\(\PageIndex{10}\). Якщо ми спроектуємо всі точки на графіку на горизонтальну вісь, вся вісь буде «лежати в тіні». Таким чином, спочатку

Малюнок\(\PageIndex{10}\). Графік ставки податку R в порівнянні з оподатковуваним доходом І.

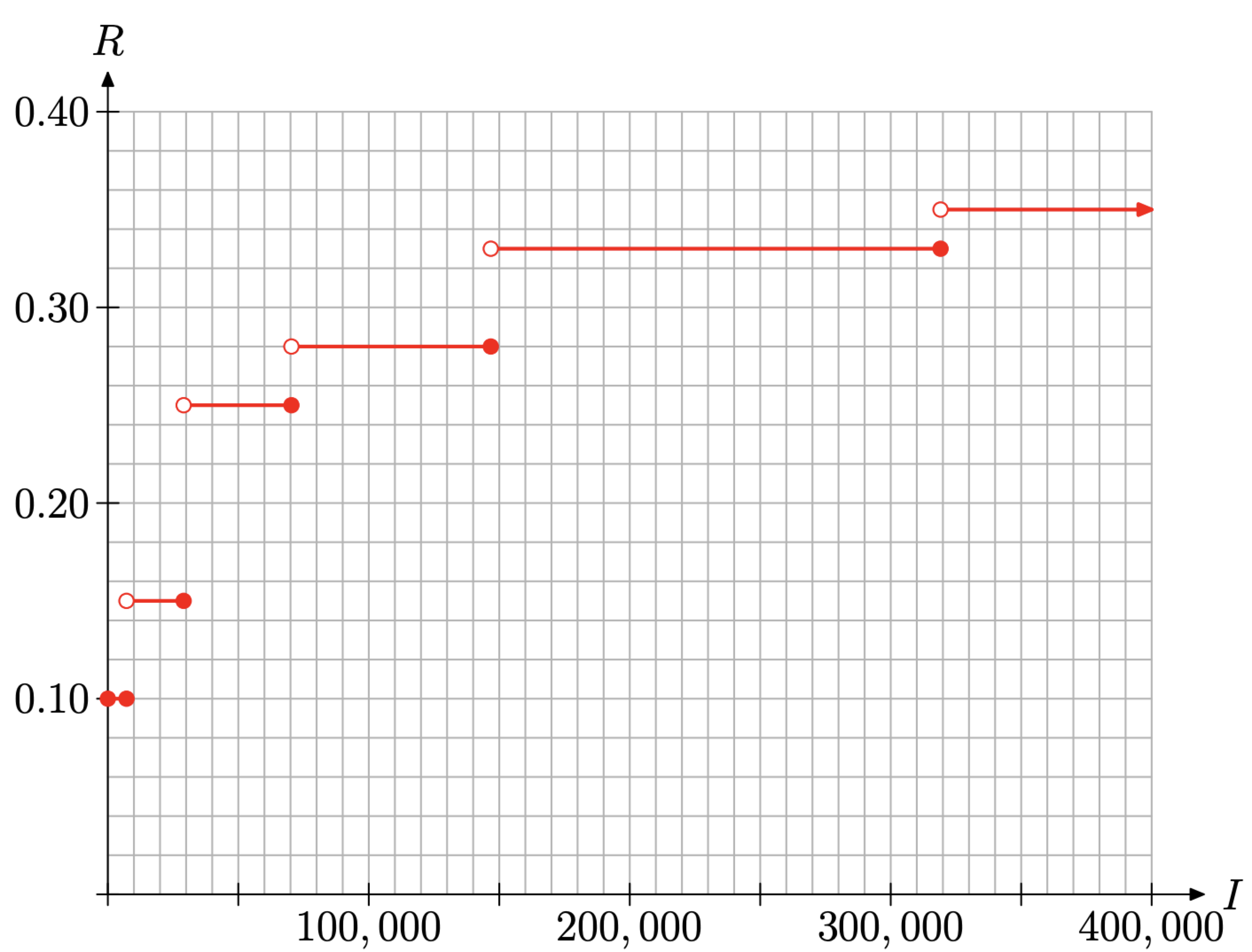
погляд, можна стверджувати, що область R - це набір всіх дійсних чисел, які більше або рівні нулю.

Однак пам'ятайте, що ми вирішили моделювати дискретну ситуацію з континуумом. Оподатковуваний дохід завжди округляється до найближчого долара на федеральних формах податку на прибуток. Таким чином, домен насправді всі цілі числа більше або рівні нулю. В символах,

\[\text { Domain }=\{I \in \mathbb{W} : I \geq 0\}\]

Щоб знайти діапазон R, ми б проектувати всі точки на графіку R на малюнку\(\PageIndex{10}\) на вертикальну вісь. Результатом буде те, що шість точок будуть затінені на вертикальній осі, по одній на 0,10, 0,15, 0,25, 0,28, 0,33 та 0,35. Таким чином, діапазон є кінцевим дискретним набором, тому його найкраще описати, просто перерахувавши його членів.

\[\text { Range }=\{0.10,0.15,0.25,0.28,0.33,0.35\}\]

Вправа

Вправа\(\PageIndex{1}\)

З огляду на функцію, визначену правилом f (x) = 3, оцінюють f (−3), f (0) та f (4), потім накидають графік f.

Відповідь

f (−3) = 3, f (0) = 3, а f (4) = 3.

Вправа\(\PageIndex{2}\)

З огляду на функцію, визначену правилом g (x) = 2, обчислити g (−2), g (0) і g (4), потім накреслити графік g.

Вправа\(\PageIndex{3}\)

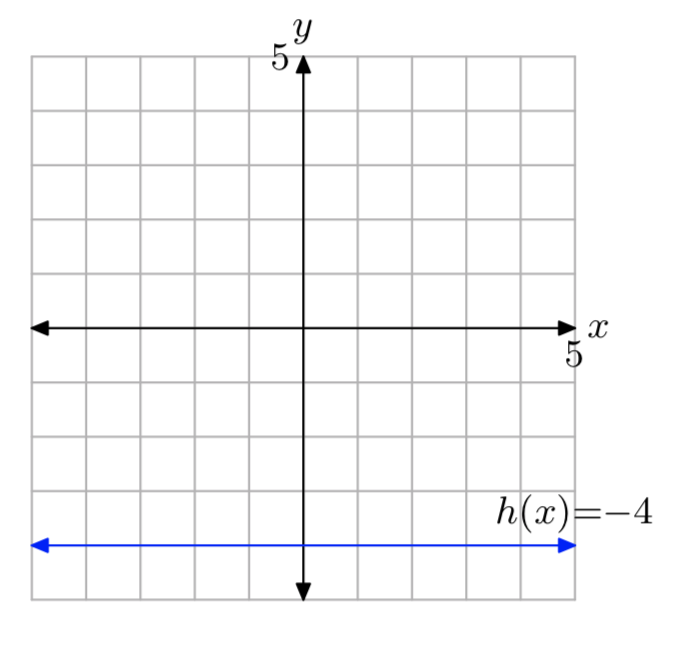
З огляду на функцію, визначену правилом h (x) = −4, обчислити h (−2), h (a) та h (2x+3), потім накреслити графік h.

Відповідь

h (−2) = −4, h (a) = −4, а h (2x+3) = −4.

Вправа\(\PageIndex{4}\)

Враховуючи функцію, визначену правилом f (x) = −2, обчислити f (0), f (b) та f (5−4x), потім намалюйте графік f.

Вправа\(\PageIndex{5}\)

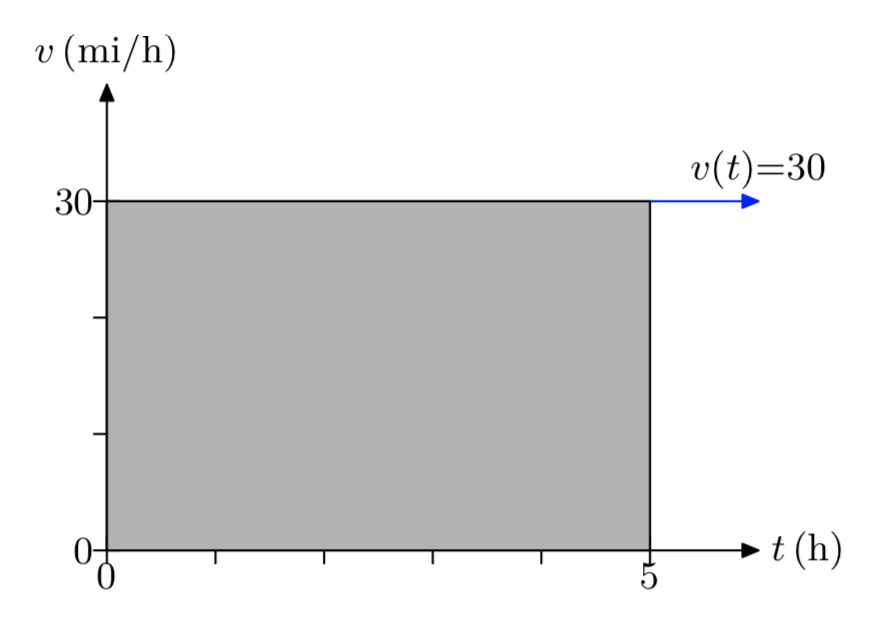
Швидкість автомобіля, що рухається по шосе, є функцією часу і описується постійною функцією v (t) = 30, де t вимірюється в годинами, а v вимірюється в милі на годину. Намалюйте графік v проти t Обов'язково позначте кожну вісь відповідними одиницями. Затіньте область під графіком v протягом часового інтервалу [0,5] годин. Що таке площа під графіком v за цей часовий проміжок і що вона собою являє?

Відповідь

Площа під кривою становить 150 миль. Це відстань, пройдене автомобілем.

Вправа\(\PageIndex{6}\)

Швидкість скейтбордиста, коли вона рухається вниз по схилу, є функцією часу і описується постійною функцією v (t) = 8, де t вимірюється в секундах, а v вимірюється в футах в секунду. Намалюйте графік v проти t Обов'язково позначте кожну вісь відповідними одиницями. Затінюйте область під графіком v протягом часового інтервалу [0,60] секунд. Що таке площа під графіком v за цей часовий проміжок і що вона собою являє?

Вправа\(\PageIndex{7}\)

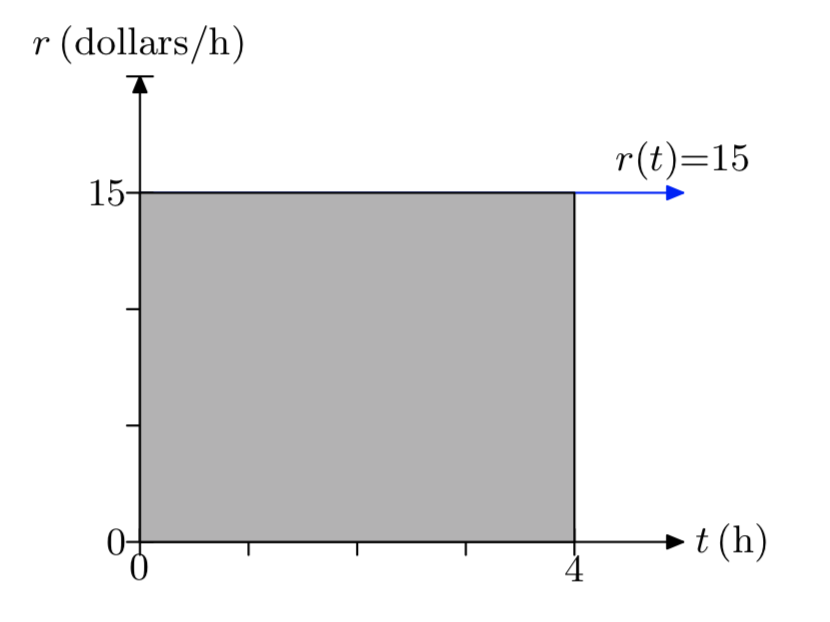
Неліцензований сантехнік стягує 15 доларів за кожну годину праці. Визначимо цю норму як функцію часу по r (t) = 15, де t вимірюється в годинами, а r вимірюється в доларах на годину. Намалюйте графік r проти t. Обов'язково позначте кожну вісь відповідними одиницями. Затінюйте область під графіком r за часовим інтервалом [0,4] годин. Що таке площа під графіком r за цей проміжок часу і що вона собою являє?

Відповідь

Площа під кривою становить 150 миль. Це відстань, пройдене автомобілем.

Вправа\(\PageIndex{8}\)

Тесляр стягує фіксовану ставку за кожну годину праці. Опишемо цю швидкість як функцію часу на r (t) = 25, де t вимірюється в годинами, а r вимірюється в доларах на годину. Намалюйте графік r проти t. Обов'язково позначте кожну вісь відповідними одиницями. Затіньте область під графіком r протягом часового інтервалу [0, 5] годин. Що таке площа під графіком r за цей часовий проміжок і що вона собою являє?

Вправа\(\PageIndex{9}\)

Задано функцію, визначену правилом

\[f(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {2,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

оцініть f (−2), f (0) та f (3), потім намалюйте графік f на аркуші графічного паперу. Вказати домен і діапазон f.

Відповідь

f (−2) = 0, f (0) = 2, а f (3) = 2.

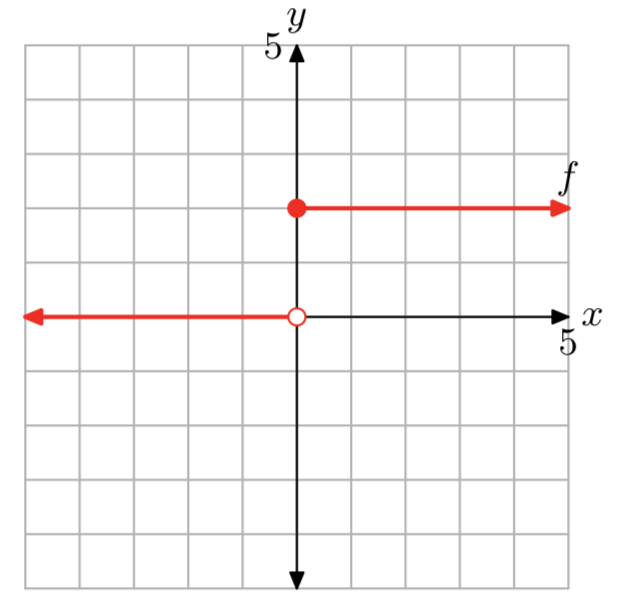
Домен f - це множина всіх дійсних чисел. Діапазон f дорівнює {0, 2}.

Вправа\(\PageIndex{10}\)

Задано функцію, визначену правилом

\[f(x)=\left\{\begin{array}{ll}{2,} & {\text { if } x<0} \\ {0,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

оцініть f (−2), f (0) та f (3), потім намалюйте графік f на аркуші графічного паперу. Вказати домен і діапазон f.

Вправа\(\PageIndex{11}\)

Задано функцію, визначену правилом

\[f(x)=\left\{\begin{array}{ll}{-3,} & {\text { if } x<0} \\ {1,} & {\text { if } -2 \le x < 2}\\ {3,} &{\text{ if } x \ge 2} \nonumber \end{array}\right.\]

оцініть g (−3), g (−2) та g (5), потім намалюйте графік g на аркуші графського паперу. Вказати домен і діапазон g.

Відповідь

g (−3) = −3, g (−2) = 1, а g (5) = 3

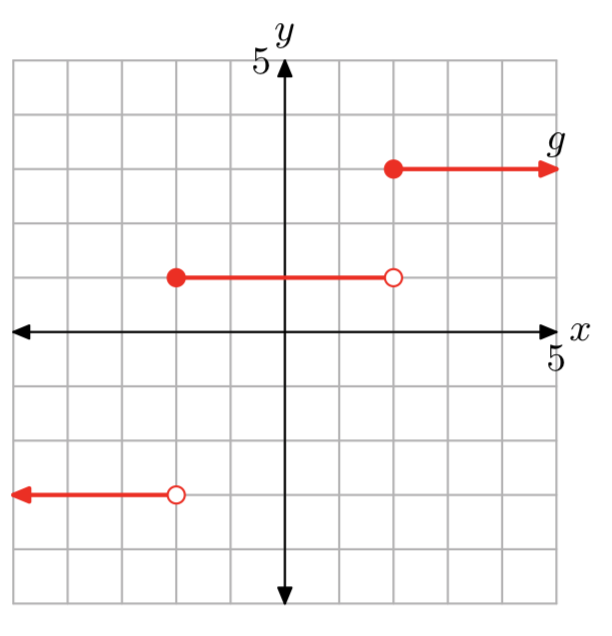
Домен g - це всі дійсні числа. Діапазон g дорівнює {−3, 1, 3}.

Вправа\(\PageIndex{12}\)

Задано функцію, визначену правилом

\[f(x)=\left\{\begin{array}{ll}{4,} & {\text { if } x \le -1} \\ {2,} & {\text { if } -1 < x \le 2}\\ {-3,} &{\text{ if } x > 2} \nonumber \end{array}\right.\]

оцініть g (−1), g (2) та g (3), потім намалюйте графік g на аркуші графського паперу. Вказати домен і діапазон g.

У вправах 13 - 16 визначте кускове визначення функції, описаної графіками, потім вкажіть область і діапазон функції.

Вправа\(\PageIndex{13}\)

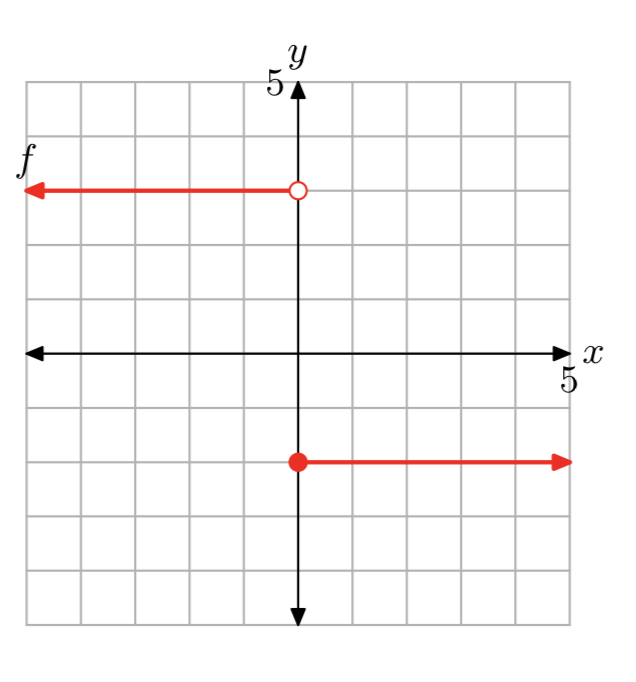
Відповідь

\[f(x)=\left\{\begin{array}{ll}{3,} & {\text { if } x<0} \\ {-2,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

Домен f - це множина всіх дійсних чисел. Діапазон f дорівнює {−2, 3}.

Вправа\(\PageIndex{14}\)

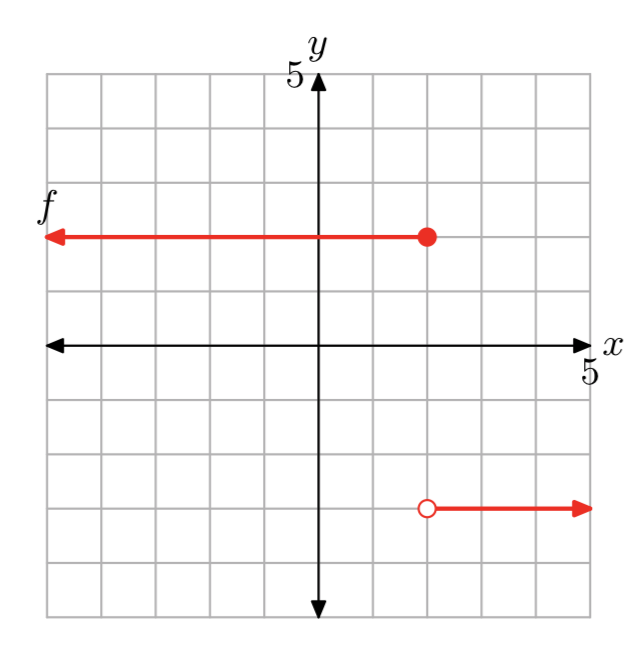
Вправа\(\PageIndex{15}\)

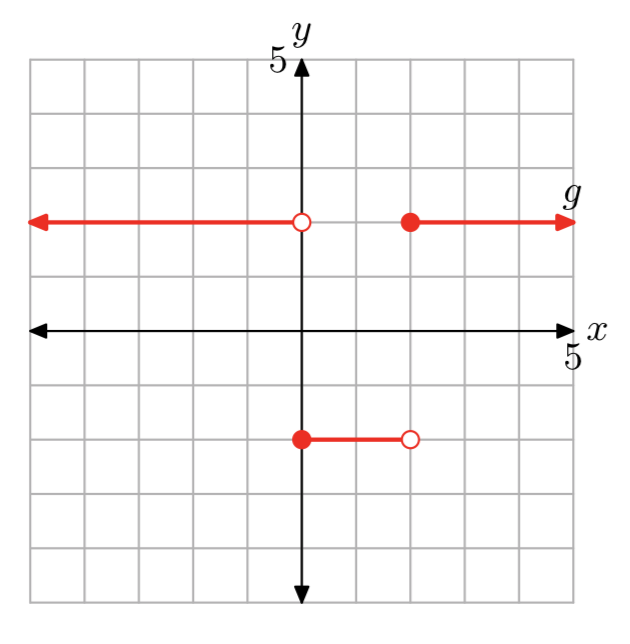
Відповідь

\[g(x)=\left\{\begin{array}{ll}{2,} & {\text { if } x < 0} \\ {-2,} & {\text { if } 0 \le x < 2}\\ {2,} &{\text{ if } x > 2} \nonumber \end{array}\right.\]

Домен f - це множина всіх дійсних чисел. Діапазон f дорівнює {−2, 2}.

Вправа\(\PageIndex{16}\)

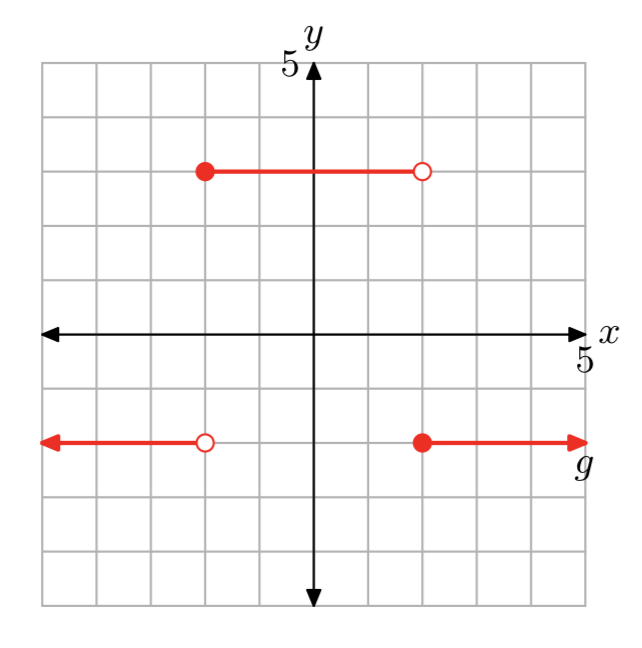
Вправа\(\PageIndex{17}\)

Задана кускова функція

\[f(x)=\left\{\begin{array}{ll}{-x-3,} & {\text { if } x<-3} \\ {x+3,} & {\text { if } x \ge -3} \nonumber \end{array}\right.\]

оцініть f (−4) і f (0), потім намалюйте графік f на аркуші графського паперу. Створіть домен і діапазон функції.

Відповідь

f (−4) = 1 і f (0) = 3.

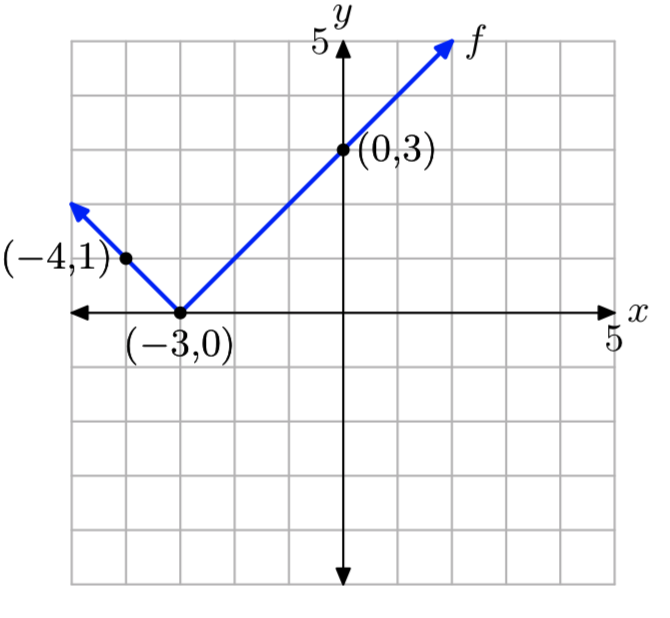
Домен f - це множина всіх дійсних чисел. Діапазон вимкнено {y:\(y \ge 0\)}.

Вправа\(\PageIndex{18}\)

Задана кускова функція

\[f(x)=\left\{\begin{array}{ll}{-x+1,} & {\text { if } x<1} \\ {x-1,} & {\text { if } x \ge 1} \nonumber \end{array}\right.\]

оцініть f (−2) і f (3), потім намалюйте графік f на аркуші графського паперу. Створіть домен і діапазон функції.

ФІЗИЧНІ ВПРАВИ\(\PageIndex{19}\)

Задана кускова функція

\[g(x)=\left\{\begin{array}{ll}{-2x+3,} & {\text { if } x<\frac{3}{2}} \\ {2x-3,} & {\text { if } x \ge \frac{3}{2}} \nonumber \end{array}\right.\]

оцінити g (0) і g (3), потім намалювати графік f на аркуші графського паперу. Створіть домен і діапазон функції.

Відповідь

г (−2) = 7 і г (2) = 1.

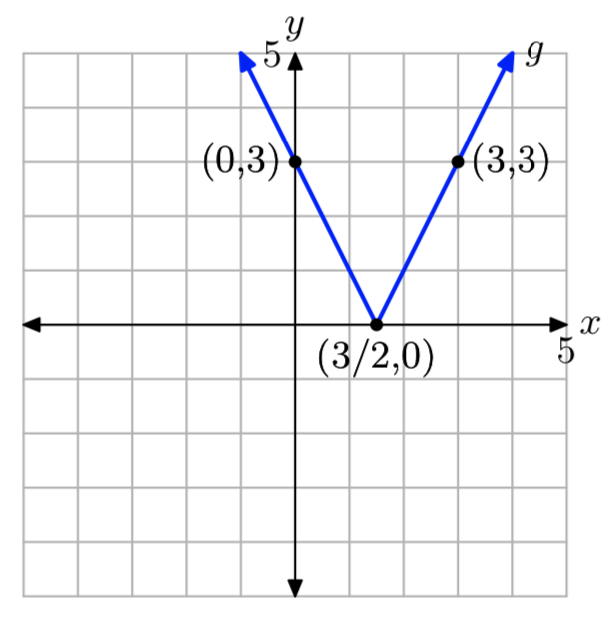
Домен g - це сукупність всіх дійсних чисел. Діапазон вимкнено {y:\(y \ge 0\)}.

Вправа\(\PageIndex{20}\)

Задана кускова функція

\[g(x)=\left\{\begin{array}{ll}{-3x-4,} & {\text { if } x<-\frac{4}{3}} \\ {3x+4,} & {\text { if } x \ge -\frac{4}{3}} \nonumber \end{array}\right.\]

оцінити g (−2) і g (3), потім намалювати графік f на аркуші графського паперу. Створіть домен і діапазон функції.

Вправа\(\PageIndex{21}\)

Акумулятор подає напругу в електричний ланцюг наступним чином. До часу t = 0 секунд вимикач відкритий, тому напруга, що подається акумулятором, дорівнює нулю вольт. За часом t = 0 секунд вимикач замикається і батарея починає подавати постійне 3 вольта в ланцюг. За часом t = 2 секунди перемикач знову відкривається, і напруга, що подається акумулятором, падає відразу до нуля вольт. Намалюйте графік напруги vversus time t, позначте кожну вісь відповідними одиницями, потім надайте кускове визначення напруги v, що подається акумулятором як функція часу t.

Відповідь

Далі йде графік.

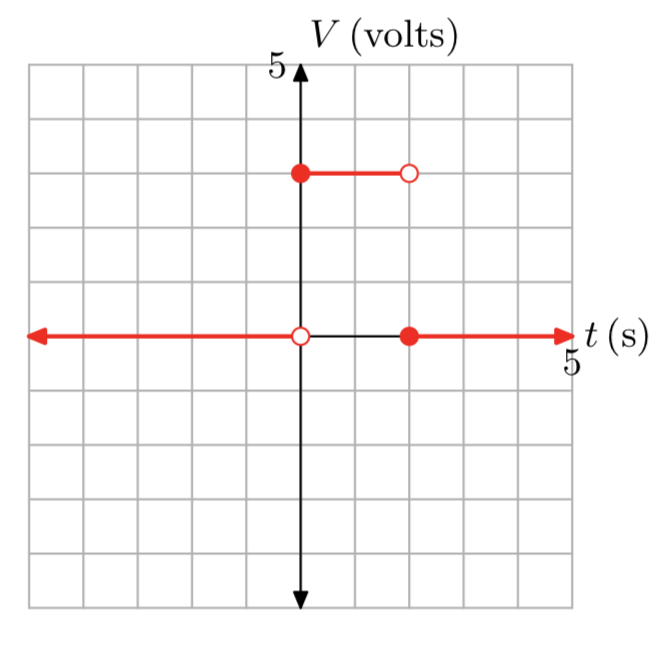
\[g(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {3,} & {\text { if } 0 \le x < 2}\\ {0,} & {\text{ if } x \ge 2} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{22}\)

До часу t = 0 хвилин барабан порожній. Під час t = 0 хвилин включається шланг і рівень води в барабані починає підвищуватися з постійною швидкістю 2 дюйми кожну хвилину. Нехай h представляють рівень води (в дюймах) в час t (в хвилинах). Намалюйте графік h проти, позначте осі відповідними одиницями, потім надайте кускове визначення має функцію t.