4.4: Нерівності абсолютних значень
- Page ID
- 58166
В останньому розділі ми розв'язали рівняння абсолютних значень. У цьому розділі ми звернемо увагу на нерівності, пов'язані з абсолютною цінністю.
Рішення |x| < a
Розв'язки\[|x|<a\] знову залежать від значення та знака числа a. Щоб розв'язати |x| < a графічно, ми повинні визначити, де графік лівої сторони лежить нижче графіка правої частини нерівності |x| < a. Існує три випадки, які слід розглянути.
- Випадок I: a < 0
При цьому графік y = a лежить строго нижче осі х. Як видно на малюнку\(\PageIndex{1}\) (a), графік y = |x| ніколи не лежить нижче графіка y = a, отже, нерівність |x| < a не має розв'язків.
- Випадок II: а = 0
При цьому графік y = 0 збігається з віссю x. Як видно на малюнку\(\PageIndex{1}\) (b), графік y = |x| ніколи не лежить строго нижче осі х. Отже, нерівність |x| < 0 не має розв'язків.
- Випадок III: а > 0
При цьому графік y = a лежить строго над віссю х. На малюнку\(\PageIndex{1}\) (c) графік y = |x| і y = a перетинається при x = −a і x = a. На малюнку\(\PageIndex{1}\) (c) ми також бачимо, що графік y = |x| лежить строго нижче графіка y = a, коли x знаходиться між −a і a; тобто коли −a < x < a.
На малюнку\(\PageIndex{1}\) (c) ми скинули пунктирні вертикальні лінії від точок перетину двох графіків до осі x. На осі x ми затінювали розв'язок |x| < a, тобто −a < x < a.

Це обговорення призводить до наступної властивості ключа.
властивість 1
Розв'язок |x| < a залежить від значення та знака a.
- Випадок I: a < 0
Нерівність |x| < a не має розв'язку.
- Випадок II: а = 0
Нерівність |x| < 0 не має розв'язку.
- Випадок III: а > 0
Нерівність |x| < a має набір розв'язків {x: −a < x < a}.
Давайте розглянемо кілька прикладів.
Приклад\(\PageIndex{1}\)
Розв'яжіть нерівність |x| < −5 для x.
Рішення
Графік лівої частини |x| < −5 є «V» малюнка\(\PageIndex{1}\) (a). Графік правої частини |x| < −5 — це горизонтальна лінія, розташована на 5 одиниць нижче осі x. Така ситуація показана на малюнку\(\PageIndex{1}\) (а). Тому графік y = |x| ніколи не знаходиться нижче графіка y = −5. Таким чином, нерівність |x| < −5 не має розв'язку.
Альтернативним підходом є врахування того факту, що абсолютне значення x завжди є невід'ємним і ніколи не може бути меншим за −5. Таким чином, нерівність |x| < −5 не має розв'язку.
Приклад\(\PageIndex{2}\)
Розв'яжіть нерівність |x| < 0 для x.
Рішення
Це той випадок, який зображений на малюнку\(\PageIndex{1}\) (б). Графік y = |x| ніколи не знаходиться строго нижче осі x. Таким чином, нерівність |x| < 0 не має розв'язку.
Приклад\(\PageIndex{3}\)
Розв'яжіть нерівність |x| < 8 для x.
Рішення
Графік лівої частини |x| < 8 - це «V» малюнка\(\PageIndex{1}\) (c). Графік правої частини |x| < 8 - це горизонтальна лінія, розташована на 8 одиниць вище осі x. Така ситуація зображена на малюнку\(\PageIndex{1}\) (в). Графіки перетинаються в (−8, 8) та (8, 8), а графік y = |x| лежить строго під графіком y = 8 для значень x між −8 і 8. Таким чином, розв'язок |x| < 8 дорівнює −8 < x < 8.
Допомагає інтуїція, якщо перевірити результати останнього прикладу. Зауважте, що числа від −8 до 8, такі як −7.75, −3 та 6.8 задовольняють нерівності,
\[|-7.75|<8 \qquad \text { and } \quad|-3|<8 \quad \text { and } \quad|6.8|<8\]
тоді як значення, які не лежать між −8 і 8, не задовольняють нерівності. Наприклад, жодне з чисел −9.3, 8.2 та 11.7 не знаходиться між −8 і 8, і кожне з наведених нижче твердження є помилковим.
\[|-9.3|<8 \quad \text { and } \qquad|8.2|<8 \qquad \text { and } \qquad|11.7|<8 \quad \text { (all are false) }\]
Якщо ви поміркуєте над цими результатами, вони допоможуть закріпити уявлення про те, що розчином |x| < 8 є усіма значеннями x, що задовольняють −8 < x < 8.
Приклад\(\PageIndex{4}\)
Розв'яжіть нерівність |5 − 2x| < −3 для x.
Рішення
Якби нерівність була |x| < −3, ми б не вагалися. Це ситуація, зображена на малюнку\(\PageIndex{1}\) (a), і нерівність |x| < −3 не має розв'язків. Міркування, застосоване до |x| < −3, однаково добре працює для нерівності |5 − 2x| < −3. Ліва частина цієї нерівності повинна бути невід'ємною, тому її графік повинен лежати на осі x або над нею. Праворуч |5 − 2x| < −3 є горизонтальною лінією, розташованою на 3 одиниці нижче осі x. Отже, графік y = |5 − 2x| ніколи не може лежати нижче графіка y = −3, а нерівність |5 − 2x| < −3 не має розв'язку.
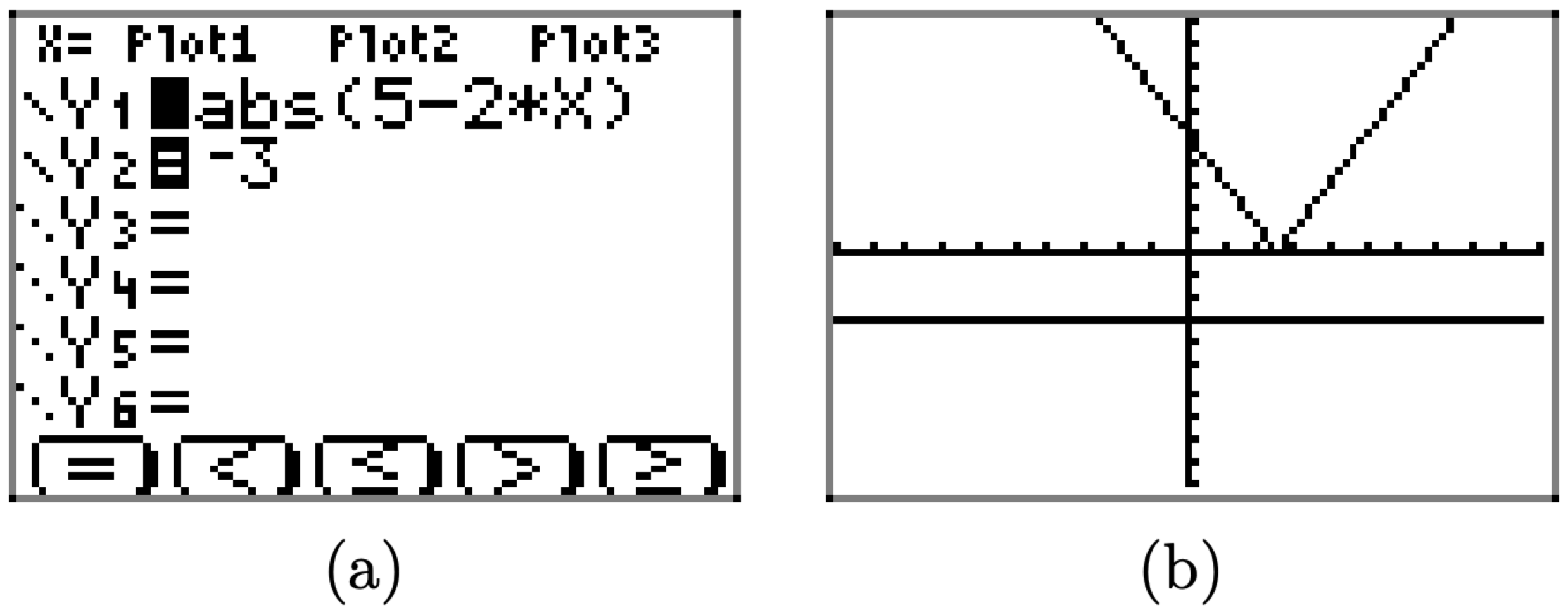
Ми можемо перевірити цей результат за допомогою графічного калькулятора. Завантажте ліву та праву сторони |5 − 2x| < −3 у Y1 та Y2 відповідно, як показано на малюнку\(\PageIndex{2}\) (a). У меню ZOOM виберіть 6:ZStandard, щоб створити зображення, показане на малюнку\(\PageIndex{2}\) (b).
Як і передбачалося, графік y = |5 − 2x| ніколи не лежить нижче графіка y = −3, тому нерівність |5 − 2x| < −3 не має розв'язку.
Приклад\(\PageIndex{5}\)
Розв'яжіть нерівність |5 − 2x| < 0 для x.
Рішення
Відомо, що ліва частина нерівності |5 − 2x| < 0 має форму «V», зазначену на малюнку\(\PageIndex{1}\) (b). Графік «торкається» осі x, коли |5 − 2x| = 0, або коли
\[\begin{aligned} 5-2 x &=0 \\-2 x &=-5 \\ x &=\frac{5}{2} \end{aligned}\]
Однак графік y = |5 − 2x| ніколи не опускається нижче осі x, тому нерівність |5 − 2x| < 0 не має розв'язку.
Інтуїтивно має бути зрозуміло, що нерівність |5−2x| < 0 не має розв'язку. Дійсно, ліва сторона цієї нерівності завжди ненегативна, і ніколи не може бути строго менше нуля.
Приклад\(\PageIndex{6}\)
Розв'яжіть нерівність |5 − 2x| < 3 для x.
Рішення
У цьому прикладі графік правої частини нерівності |5 − 2x| < 3 є горизонтальною лінією, розташованою на 3 одиниці вище осі x. Графік лівої частини нерівності має форму «V», показану на малюнку\(\PageIndex{3}\) (b) і (c). Ви можете скористатися утилітою intersect на графічному калькуляторі, щоб знайти точки перетину графіків y = |5 − 2x| і y = 3, як це було зроблено на малюнках\(\PageIndex{3}\) (b) та (c). Зверніть увагу, що калькулятор вказує дві точки перетину, одна при x = 1 і друга при x = 4.

Графік y = |5 − 2x| опускається нижче графіка y = 3 для всіх значень x між 1 і 4. Отже, розв'язком нерівності |5 − 2x| < 3 є множиною всіх x, що задовольняють 1 < x < 4; тобто {x: 1 < x < 4}.
Очікування:
Нам потрібен спосіб підсумовування цього графічного калькулятора підхід на нашому домашньому папері. По-перше, намалюйте розумний факсиміле вікна перегляду вашого калькулятора на домашньому папері. Використовуйте лінійку, щоб намалювати всі лінії. Заповніть наступний контрольний список.
- Позначте кожну вісь, в даному випадку з x і y.
- Масштабуйте кожну вісь. Для цього натисніть кнопку WINDOW на вашому калькуляторі, після чого повідомте значення xmin, xmax, ymin та ymax на відповідній осі.
- Позначте кожен граф своїм рівнянням.
- Відкиньте пунктирні вертикальні лінії від точок перетину до осі x. Затіньте та позначте набір розв'язків нерівності на осі x.
Дотримуючись вказівок у наведеному вище контрольному списку, ми отримуємо зображення на малюнку\(\PageIndex{4}\).

Алгебраїчний підхід. Розглянемо алгебраїчний розв'язок нерівності |5 − 2x| < 3. Так само, як |x| < 3 означає, що −3 < x < 3 нерівність
\[|5-2 x|<3\]
вимагає, щоб
\[-3<5-2 x<3\]
Ми можемо відняти 5 з усіх трьох членів цієї останньої нерівності, а потім спростити.
\[\begin{aligned}-3-5 &<5-2 x-5<3-5 \\ &-8<-2 x<-2 \end{aligned}\]
Розділіть усі три члени цієї останньої нерівності на −2, змінюючи символи нерівності, коли ви йдете.
\[4>x>1\]
Ми вважаємо за краще, щоб наші нерівності читалися від «малого до великого», тому ми пишемо
\[1<x<4\]
Ця форма відповідає порядку затіненого рішення на числовому рядку на малюнку\(\PageIndex{4}\), який ми знайшли за допомогою графічного калькулятора.
Алгебраїчна техніка цього останнього прикладу призводить нас до наступного властивості.
Нерухомість 8
Якщо a > 0, то нерівність |x| < a еквівалентна нерівності −a < x < a.
Ця властивість надає простий метод розв'язання нерівностей виду |x| < a. Давайте застосуємо цю алгебраїчну техніку в наступному прикладі.
Приклад\(\PageIndex{7}\)
Розв'яжіть нерівність |4x + 5| < 7 для x.
Рішення
Першим кроком є використання Property 8, щоб написати, що\[|4 x+5|<7\]
еквівалентний нерівності
\[-7<4 x+5<7\]
Звідси ми можемо вирішити для x, спочатку віднімаючи 5 з усіх трьох членів, а потім розділивши через 4.
\[\begin{array}{l}{-12<4 x<2} \\ {-3<x<\frac{1}{2}}\end{array}\]
Ми можемо накидати рішення на числовій лінії.

І ми можемо описати рішення як в інтервалі, так і в позначеннях set-builder наступним чином.
\[\left(-3, \frac{1}{2}\right)=\left\{x :-3<x<\frac{1}{2}\right\}\]
Припускаючи, що a > 0, нерівність\(|x| \leq a\) вимагає знайти, де абсолютне значення x або «менше» a або «дорівнює» a. Ми знаємо, що |x| < a при −a < x < a і ми знаємо, що |x| = a, коли x = −a або x = a. Таким чином, розв'язком\(|x| \leq a\) є «об'єднання» цих двох розв'язків.
Цей аргумент призводить до наступної властивості.
Нерухомість 10
Якщо\(a > 0\), то нерівність\(|x| \leq a\) еквівалентна нерівності\(−a \leq x \leq a\).
Приклад\(\PageIndex{8}\)
Розв'яжіть нерівність\(5 − 3|x − 4| \geq −4\) для x.
Рішення
На перший погляд, нерівність\[5-3|x-4| \geq-4\] має форму, досить несхожу з тим, що ми зробили до цього часу. Однак давайте віднімемо 5 з обох сторін нерівності.
\[-3|x-4| \geq-9\]
Тепер давайте розділимо обидві сторони цієї останньої нерівності на −3, змінивши знак нерівності.
\[|x-4| \leq 3\]
Ага! Знайомий грунт. Використовуючи властивість 10, ця остання нерівність еквівалентна
\[-3 \leq x-4 \leq 3\]
і коли ми додаємо 4 до всіх трьох членів, ми маємо рішення.
\[1 \leq x \leq 7\]
Ми можемо накидати рішення на числовій лінії

І ми можемо описати рішення з інтервальними і set-builder позначеннями.
\[[1,7]=\{x : 1 \leq x \leq 7\}\]
Рішення |x| > a
Розв'язки |x| > a знову залежать від значення і знака а, щоб розв'язати |x| > a графічно, ми повинні визначити, де граф y = |x| лежить над графіком y = a. знову розглянемо три випадки.
- Випадок I: a < 0
При цьому графік y = a лежить строго нижче осі х. Тому графік y = |x| на малюнку\(\PageIndex{5}\) (а) завжди лежить над графіком y = a. отже, всі дійсні числа є розв'язками нерівності |x| > a.
- Випадок II: а = 0
При цьому графік y = 0 збігається з віссю x. Як показано на малюнку\(\PageIndex{5}\) (b), графік y = |x| буде лежати строго над графіком y = 0 для всіх значень x за одним винятком, а саме x не може дорівнювати нулю. Отже, кожне дійсне число, крім x = 0, є розв'язком |x| > 0. На малюнку\(\PageIndex{5}\) (b) ми затінювали розв'язок |x| > 0, а саме набір всіх дійсних чисел, крім x = 0.
- Випадок III: а > 0
При цьому графік y = a лежить строго над віссю х. На малюнку\(\PageIndex{5}\) (c) графік y = |x| перетинає графік y = a при x = −a і x = a. на малюнку\(\PageIndex{5}\) (c) ми бачимо, що графік y = |x| лежить строго над графіком y = a, якщо x менше −a або більше a.
На малюнку\(\PageIndex{5}\) (c) ми скинули пунктирні вертикальні лінії від точок перетину до осі x. На осі х ми затінювали розв'язок |x| > a, а саме набір всіх дійсних чисел x, таких як x < −a or x > a.

Це обговорення призводить до наступного властивості.
Нерухомість 12
Розв'язок |x| > a залежить від значення та знака a.
- Випадок I: a < 0
Усі дійсні числа є розв'язками нерівності |x| > a.
- Випадок II: а = 0
Усі дійсні числа, за винятком x = 0, є розв'язками |x| > 0.
- Випадок III: а > 0
Нерівність |x| > a має набір розв'язків {x: x < −a or x > a}.
Приклад\(\PageIndex{9}\)
Створіть рішення кожного з наступних нерівностей.
\[\text { a. }|x|>-5 \qquad \text { b. }|x|>0 \qquad \text { c. }|x|>4\]
Рішення
a. Розв'язок |x| > −5 є дійсними числами.
b Розв'язок |x| > 0 є усіма дійсними числами, крім нуля.
c Розв'язок |x| > 4 є множиною всіх дійсних чисел, менших за −4 або більше 4.
Приклад\(\PageIndex{10}\)
Розв'яжіть нерівність |4 − x| > −5 для x.
Рішення
Ліва частина нерівності |4 − x| > −5 невід'ємна, тому графік y = |4 − x| повинен лежати вище або на осі x. Графік правої частини |4 − x| > −5 — це горизонтальна лінія, розташована на 5 одиниць нижче осі x. Тому графік y = |4 − x| завжди лежить над графіком y = −5. Таким чином, всі дійсні числа є розв'язками нерівності |4 − x| > −5.
Ми можемо перевірити наше мислення за допомогою графічного калькулятора. Завантажте ліву та праву сторони нерівності |4 − x| > −5 у Y1 та Y2 відповідно, як показано на малюнку\(\PageIndex{6}\) (a). У меню ZOOM виберіть 6:ZStandard, щоб створити зображення, показане на малюнку\(\PageIndex{6}\) (b).
Як і передбачалося, графік y = |4 − x| лежить над графіком y = −5 для всіх дійсних чисел.

Інтуїтивно, абсолютне значення будь-якого числа завжди є невід'ємним, тому |4−x| > −5 для всіх дійсних значень x.
Приклад\(\PageIndex{11}\)
Розв'яжіть нерівність |4 − x| > 0 для x.
Рішення
Як ми бачили на малюнку\(\PageIndex{6}\) (b), графік y = |4 − x| лежить на осі x або над нею для всіх дійсних чисел. Він «торкається» осі х у «вершини» «V», де\[|4-x|=0\]
Це може статися тільки в тому випадку, якщо
\[\begin{aligned} 4-x &=0 \\-x &=-4 \\ x &=4 \end{aligned}\]
Таким чином, графік y = |4 − x| знаходиться строго вище осі x для всіх дійсних чисел, крім x = 4. Тобто, розв'язок |4 − x| > 0 дорівнює {x: x 6= 4}.
Приклад\(\PageIndex{12}\)
Розв'яжіть нерівність |4 − x| > 5 для x.
Рішення
У цьому прикладі графік правої частини |4 − x| > 5 є горизонтальною лінією, розташованою на 5 одиниць вище осі x. Графік y = |4 − x| має форму «V», показану на малюнку\(\PageIndex{6}\) (c). Ви можете скористатися утилітою intersect на графічному калькуляторі для наближення точок перетину графіків y = |4 − x| і y = 5, як ми зробили на малюнку\(\PageIndex{7}\) (c) та (d). Калькулятор вказує дві точки перетину: одна при x = −1 і друга при x = 9.

Графік y = |4 − x| лежить над графіком y = 5 для всіх значень x, які лежать ліворуч від −1 або праворуч від 9. Отже, розв'язок |4 − x| > 5 є множиною {x: x < −1 or x > 9}.
Дотримуючись вказівок, встановлених у прикладі\(\PageIndex{6}\), ми створюємо зображення, показане\(\PageIndex{8}\) на малюнку на нашому домашньому папері. Зверніть увагу, що ми позначили кожну вісь, масштабували кожну вісь за допомогою xmin, xmax, ymin та ymax, позначили кожен графік своїм рівнянням, а також затінювали та позначили рішення на осі x.

Алгебраїчний підхід. Розглянемо алгебраїчний розв'язок |4 − x| > 5. Багато в чому так само, як |x| > 5 призводить до умов x < −5 or x > 5, нерівність
\[|4-x|>5\]
вимагає, щоб
\[4-x<-5 \qquad \text { or } \qquad 4-x>5\]
Ми можемо вирішити кожну з них самостійно, спочатку віднімаючи 4 з кожної сторони нерівності, а потім помноживши обидві сторони кожної нерівності на −1, змінюючи кожну нерівність, як ми робимо це.
\[\begin{array}{rllrrl}{4-x} & {<} & {-5} & {\text { or }} & {4-x} & {>} & {5} \\ {-x} & {<} & {-9} && {-x} & {>} & {1} \\ {x} & {>} & {9} && {x} & {<} & {-1}\end{array}\]
Ми вважаємо за краще писати це рішення в порядку
\[x<-1 \qquad \text { or } \qquad x>9\]
оскільки він відповідає порядку графічного рішення, затіненого на рис\(\PageIndex{8}\). Тобто набір розв'язків - {x: x < −1 or x > 9}.
Алгебраїчна техніка цього останнього прикладу призводить до наступної властивості.
Нерухомість 17
Якщо a > 0, то нерівність |x| > a еквівалентна складній нерівності x < −a or x > a.
Ця властивість надає простий алгебраїчний метод розв'язання нерівностей виду |x| > a, коли a > 0. Давайте сконцентруємося на цій техніці в наступних прикладах.
Приклад\(\PageIndex{13}\)
Розв'яжіть нерівність |4x − 3| > 1 для x.
Рішення
Першим кроком є використання Property 17 для запису,\[|4 x-3|>1\] що еквівалентно
\[4 x-3<-1 \qquad \text { or } \qquad 4 x-3>1\]
Тепер ми можемо вирішити кожну нерівність самостійно. Починаємо з додавання по 3 до обох сторін кожної нерівності, потім ділимо обидві сторони отриманих нерівностей на 4.
\[\begin{array}{rrlrrl}{4 x-3} & {<} & {-1} & {\text { or }} & {4 x-3} & {>} & {1} \\ {4 x} & {<} & {2} && {4 x} & {>} & {4} \\ {x} & {<} & {\frac{1}{2}} & &{x} & {>} & {1}\end{array}\]
Ми можемо накидати рішення на числовій лінії.

І ми можемо описати рішення за допомогою інтервалу та позначення set-builder.
\[(-\infty, 1 / 2) \cup(1, \infty)=\{x : x<1 / 2 \text { or } x>1\}\]
Знову ж таки, нехай a > 0. Як ми зробили з\(|x| \leq a\), ми можемо взяти об'єднання розв'язків |x| = a та |x| > a, щоб знайти рішення\(|x| \geq a\). Це призводить до наступного властивості.
Визначення
Якщо a > 0, то нерівність\(|x| \geq a\) еквівалентна нерівності\(x \leq −a\) або\(x \geq a\).
Приклад\(\PageIndex{14}\)
Розв'яжіть нерівність\(3|1 − x| − 4 \geq |1 − x|\) для x.
Рішення
Знову ж таки, на перший погляд, нерівність\[3|1-x|-4 \geq|1-x|\]
виглядає на відміну від будь-якої нерівності, яку ми намагалися до цього моменту. Однак якщо відняти |1 − x| з обох сторін нерівності, то додати 4 до обох сторін нерівності, отримаємо
\[3|1-x|-|1-x| \geq 4\]
Зліва у нас є подібні терміни. Зауважте, що 3|1−x|−|1−x| = 3|1−x|−1|1−x| = 2|1−x|. Таким чином,
\[2|1-x| \geq 4\]
Розділіть обидві сторони останнього нерівності на 2.
\[|1-x| \geq 2\]
Тепер ми можемо використовувати Property 19 для написання
\[1-x \leq-2 \quad \text { or } \qquad 1-x \geq 2\]
Кожне з цих нерівностей ми можемо вирішити самостійно. Спочатку відніміть 1 з обох сторін кожної нерівності, а потім помножте обидві сторони кожної результуючої нерівності на −1, змінюючи кожну нерівність, коли ви йдете.
\[\begin{array}{rllrrl}{1-x } & {\leq} & {-2} & {\text { or }} & {1-x } & {\geq} & { 2} \\ {-x } & {\leq} & {-3} && {-x } & {\geq } & {1} \\ {x} & { \geq } & {3} & &{x} & { \leq} & {-1}\end{array}\]
Ми вважаємо за краще писати це в порядку
\[x \leq-1 \qquad \text { or } \qquad x \geq 3\]
Ми можемо накидати рішення на числовій лінії.

І ми можемо описати рішення за допомогою інтервальних і set-builder позначень.
\[(-\infty,-1] \cup[3, \infty)=\{x : x \leq-1 \text { or } x \geq 3\}\]
Повторне відвідування відстані
Якщо a і b - будь-які числа на дійсній прямій, то відстань між a і b знаходять, взявши абсолютне значення їх різниці. Тобто відстань d між a і b обчислюється з d = |a − b|. Що ще важливіше, ми навчилися вимовляти символіку |a − b| як «відстань між a та b». Ця вимова набагато корисніше, ніж сказати «абсолютне значення a мінус b».
Приклад\(\PageIndex{15}\)
Розв'яжіть нерівність |x − 3| < 8 для x.
Рішення
Ця нерівність вимовляється «відстань між х і 3 менше 8». Намалюйте цифрову лінію, знайдіть 3 на лінії, потім відзначте дві точки, які знаходяться на відстані 8 одиниць від 3.

Тепер нам потрібно затінювати точки, які менше 8 одиниць з 3.

Отже, розв'язком нерівності |x − 3| < 8 є\[(-5,11)=\{x :-5<x<11\}\]
Приклад\(\PageIndex{16}\)
Розв'яжіть нерівність |x + 5| > 2 для x.
Рішення
По-перше, запишіть нерівність як різницю.
\[|x-(-5)|>2\]
Ця остання нерівність вимовляється «відстань між x та −5 більша за 2». Намалюйте числову лінію, знайдіть −5 на числовій лінії, потім зверніть увагу на дві точки, які є 2 одиницями від −5.

Тепер нам потрібно затінювати точки, які більші за 2 одиниці від −5.
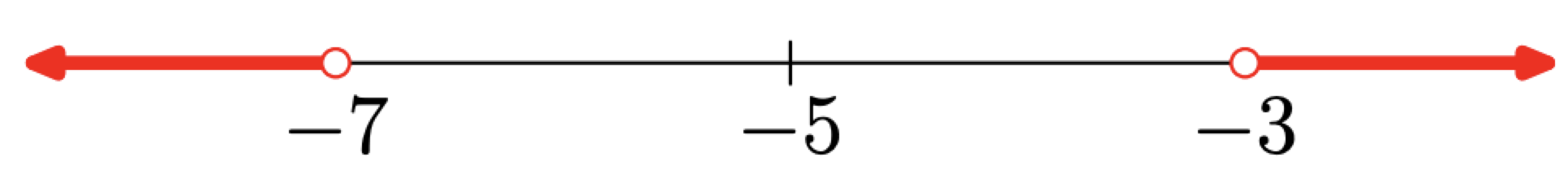
Отже, розв'язком нерівності |x + 5| > 2 є
\[(-\infty,-7) \cup(-3, \infty)=\{x : x<-7 \quad \text { or } \quad x>-3\}\]
Вправа
Для кожного з нерівностей у вправах 1 - 10 виконайте кожне з наступних завдань.
- Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь.
- Намалюйте графік кожної сторони нерівності без допомоги калькулятора. Позначте кожен граф своїм рівнянням.
- Затіньте розв'язок нерівності на осі x (якщо така є) у спосіб, показаний на рисунках 4 та 8 в оповіданні. Тобто відкиньте пунктирні лінії від точок перетину до осі, потім затіньте і позначте рішення, встановлене на осі х. Використовуйте set-builder і інтервальні позначення (якщо це можливо) для опису вашого набору рішень.
Вправа\(\PageIndex{1}\)
|x| > −2
- Відповідь
-
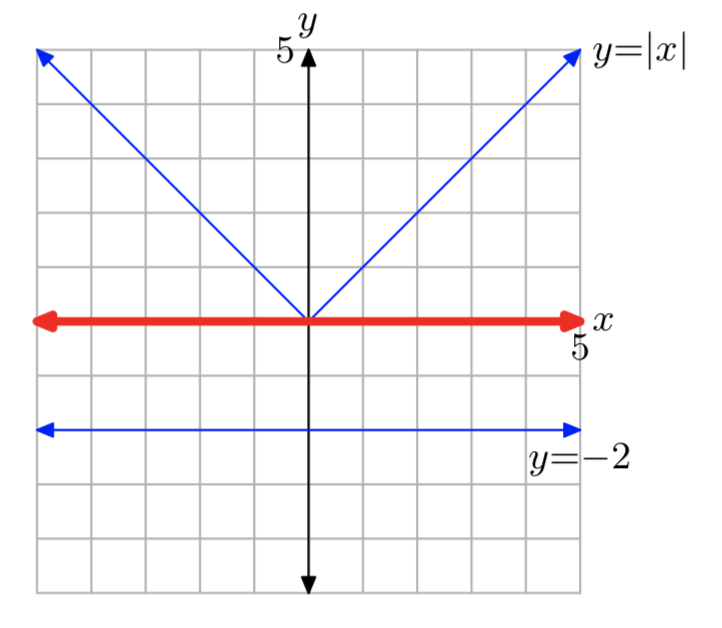
Рішення:\(\mathbb{R} = (−\infty, \infty)\)
Вправа\(\PageIndex{2}\)
|x| > 0
Вправа\(\PageIndex{3}\)
|x| < 3
- Відповідь
-
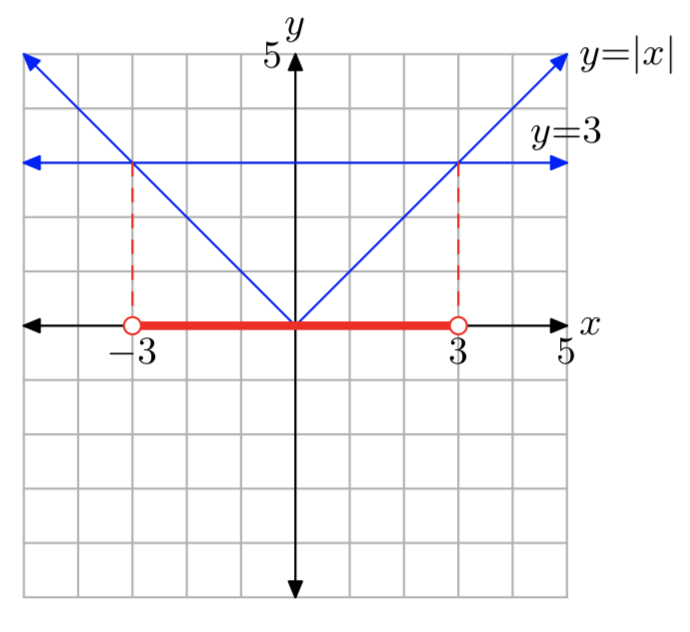
Розв'язок: (−3, 3) = {x: −3 < x < 3}
Вправа\(\PageIndex{4}\)
|x| > 2
Вправа\(\PageIndex{5}\)
|x| > 1
- Відповідь
-
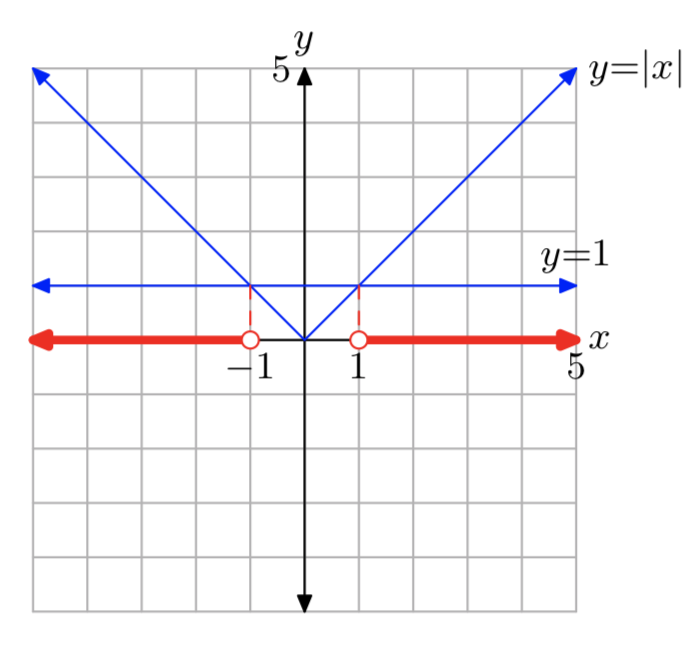
\((−\infty,−1) \cup (1,\infty)\)Розв'язок: = {x: x <−1 або x > 1}.
Вправа\(\PageIndex{6}\)
|x| < 4
Вправа\(\PageIndex{7}\)
|x| ≤ 0
- Відповідь
-
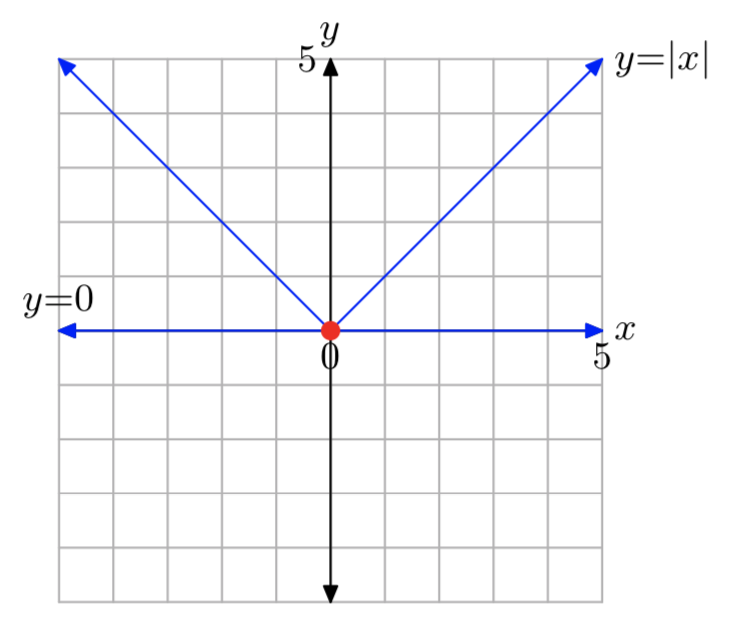
Рішення: {x: x = 0}
Вправа\(\PageIndex{8}\)
|x| ≤ −2
Вправа\(\PageIndex{9}\)
|x| ≤ 2
- Відповідь
-

Розв'язок: [−2, 2] = {x:\(−2 \le x \le 2\)}.
Вправа\(\PageIndex{10}\)
|x| ≥ 1
Для кожного з нерівностей у вправах 11 - 22 виконайте кожне з наступних завдань.
- Завантажте кожну сторону нерівності в меню Y = вашого калькулятора. Налаштуйте вікно перегляду так, щоб у вікні перегляду були видні всі точки перетину двох графіків.
- Скопіюйте зображення на екрані перегляду на домашній папір. Позначте кожну вісь та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте кожен граф своїм рівнянням.
- Використовуйте утиліту Intersect в меню CALC для визначення точок перетину. Затіньте розв'язок нерівності на осі x (якщо така є) у спосіб, показаний на рисунках 4 та 8 в оповіданні. Тобто відкиньте пунктирні лінії від точок перетину до осі, потім затіньте і позначте рішення, встановлене на осі x. Використовуйте set- builder і інтервальні позначення (якщо це доречно) для опису вашого набору рішень.
Вправа\(\PageIndex{11}\)
|3−2х| > 5
- Відповідь
-
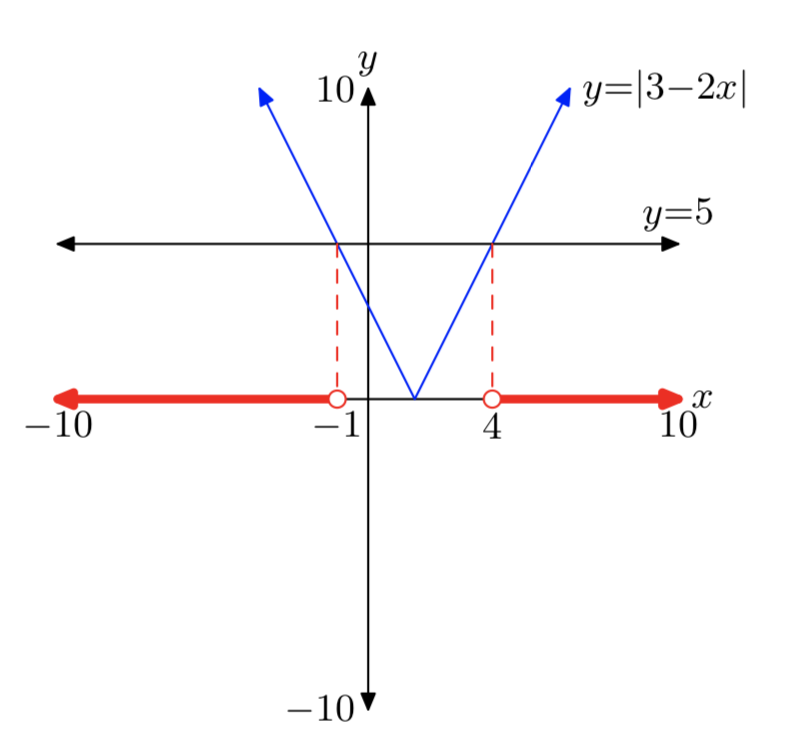
\((−\infty, −1) \cup (4, \infty)\)Розв'язок: = {x: x <−1 або x > 4}.
Вправа\(\PageIndex{12}\)
|2х+7| < 4
Вправа\(\PageIndex{13}\)
|4x+5| < 7
- Відповідь
-
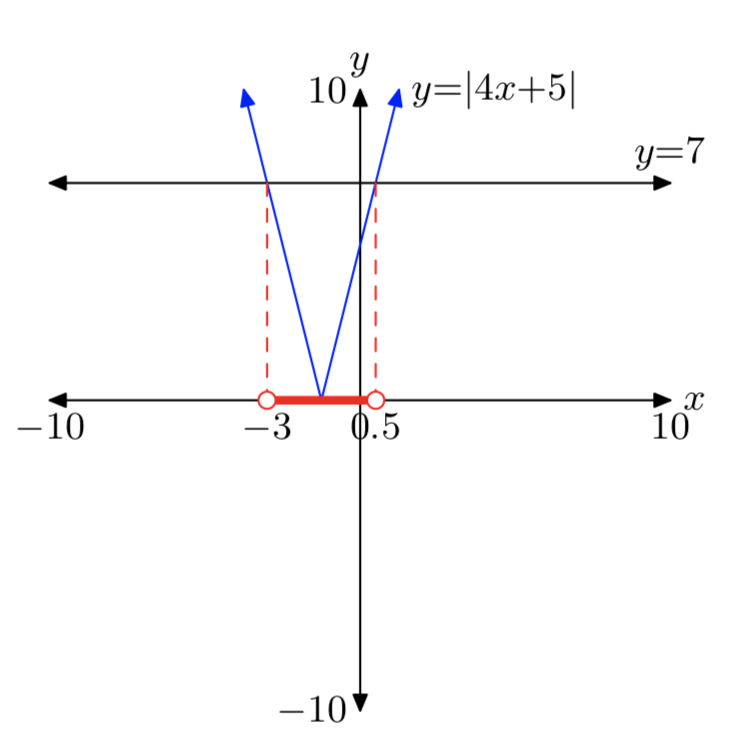
Розв'язок: (−3, 0,5) = {x: −3 < x < 0,5}.
Вправа\(\PageIndex{14}\)
|5x−7| > 8
Вправа\(\PageIndex{15}\)
|4x+5| > −2
- Відповідь
-
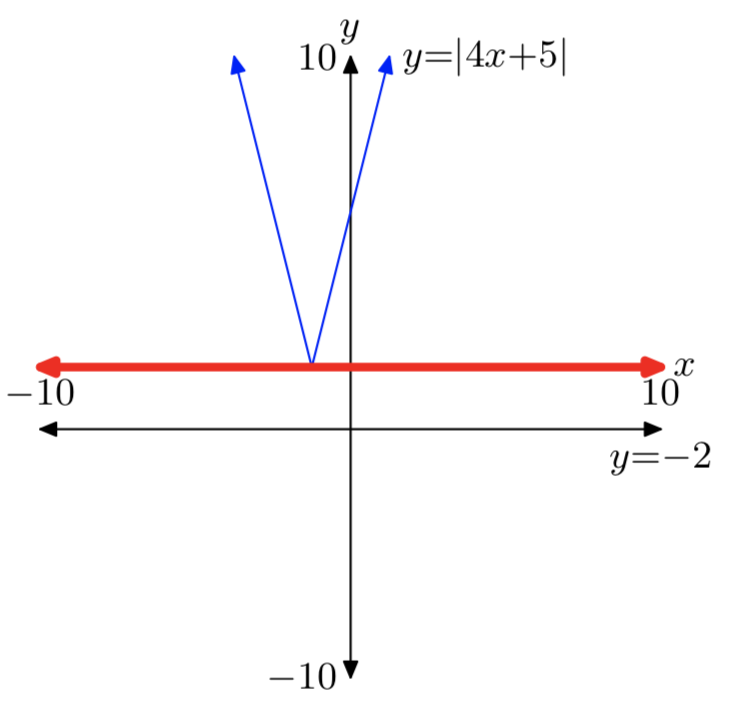
Рішення:\(\mathbb{R} = (−\infty, \infty)\)
Вправа\(\PageIndex{16}\)
|3х−5| < −3
Вправа\(\PageIndex{17}\)
\(|2x−9| \ge 6\)
- Відповідь
-
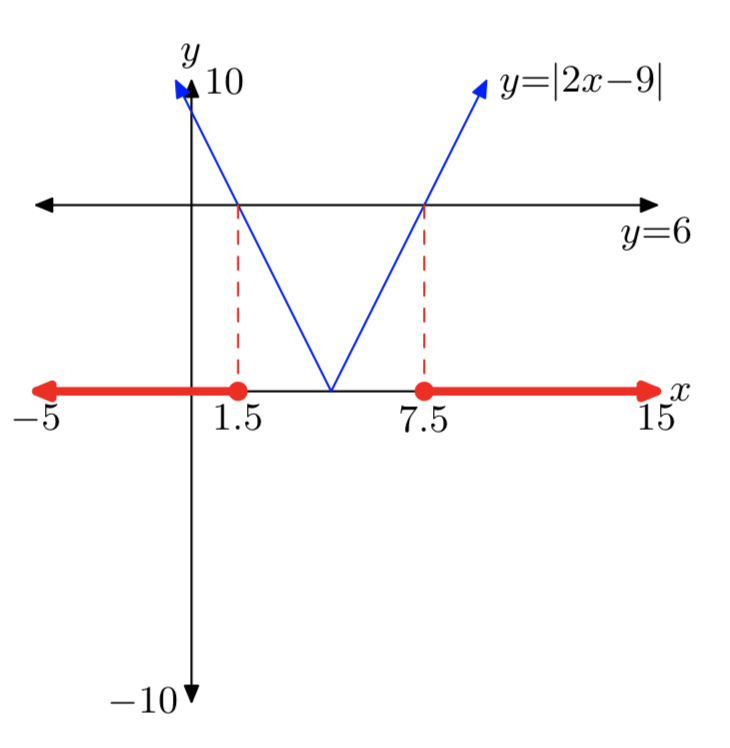
Рішення:\((−\infty, 1.5] \cup [7.5, \infty)\) = {x:\(x \ le 1.5 or x \ge 7.5\)}.
Вправа\(\PageIndex{18}\)
\(|3x+25| \ge 8\)
Вправа\(\PageIndex{19}\)
\(|13−2x| \le 7\)
- Відповідь
-

Рішення: [3, 10] = {x:\(3 \le x \le 10\)}.
Вправа\(\PageIndex{20}\)
\(|2x+15| \le 7\)
Вправа\(\PageIndex{21}\)
\(|3x−11| > 0\)
- Відповідь
-

Рішення: {x:\(x \ne \frac{11}{3}\)}
Вправа\(\PageIndex{22}\)
\(|4x+19| \le 0\)
Для кожного з нерівностей у вправах 23 - 32 надайте чисто алгебраїчне рішення без використання калькулятора. Покажіть всю вашу роботу, яка веде до рішення, затіньте набір рішення на числовому рядку, а потім скористайтеся конструктором наборів та інтервальними позначеннями (якщо можливо), щоб описати свій набір рішень.
Вправа\(\PageIndex{23}\)
|4x+3| < 8
- Відповідь
-

(\(−\frac{11}{4}, \frac{5}{4}\)) = {x:\(−\frac{11}{4} < x < \frac{5}{4}\)}
Вправа\(\PageIndex{24}\)
|3х−5| > 11
Вправа\(\PageIndex{25}\)
\(|2x−3| \le 10\)
- Відповідь
-

[\(−\frac{7}{2}, \frac{13}{2}\)] = {x:\(−\frac{7}{2} \le x \le \frac{13}{2}\)}
Вправа\(\PageIndex{26}\)
\(|3−5x| \ge 15\)
Вправа\(\PageIndex{27}\)
|3х−4| < 7
- Відповідь
-

(−1,\(\frac{11}{3}\)) = {x:\(−1 < x < \frac{11}{3}\)}
Вправа\(\PageIndex{28}\)
|5−2х| > 10
Вправа\(\PageIndex{29}\)
\(|3−7x| \ge 5\)
- Відповідь
-

\((−\infty,−\frac{2}{7}] \cup [\frac{8}{7}, \infty)\)= {x:\(x \le −\frac{2}{7}\) або\(x \ge \frac{8}{7}\)}
Вправа\(\PageIndex{30}\)
\(|2−11x| \le 6\)
Вправа\(\PageIndex{31}\)
\(|x+2| \ge −3\)
- Відповідь
-

\(\mathbb{R} = (−\infty, \infty)\)
Вправа\(\PageIndex{32}\)
|x+5| < −4
Для кожного з нерівностей у вправах 33 - 38 виконайте кожне з наступних завдань.
- Розташуйте кожну з наступних частин на домашньому папері в тому ж місці. Не розміщуйте алгебраїчну роботу на одній сторінці, а графічну роботу на іншій.
- Дотримуйтесь кожного з вказівок, наведених для вправ 11 - 22, щоб знайти та записати рішення за допомогою графічного калькулятора.
- Надайте чисто алгебраїчне рішення, показуючи всі етапи вашої роботи. Намалюйте рішення на числовому рядку, а потім використовуйте конструктор наборів та інтервальні позначення для опису вашого набору рішень. Чи вигідно ці рішення відрізняються від тих, які знайшли за допомогою графічного калькулятора в частині (2)? Якщо немає, шукайте помилку у своїй роботі.
Вправа\(\PageIndex{33}\)
|x−8| < 7
- Відповідь
-
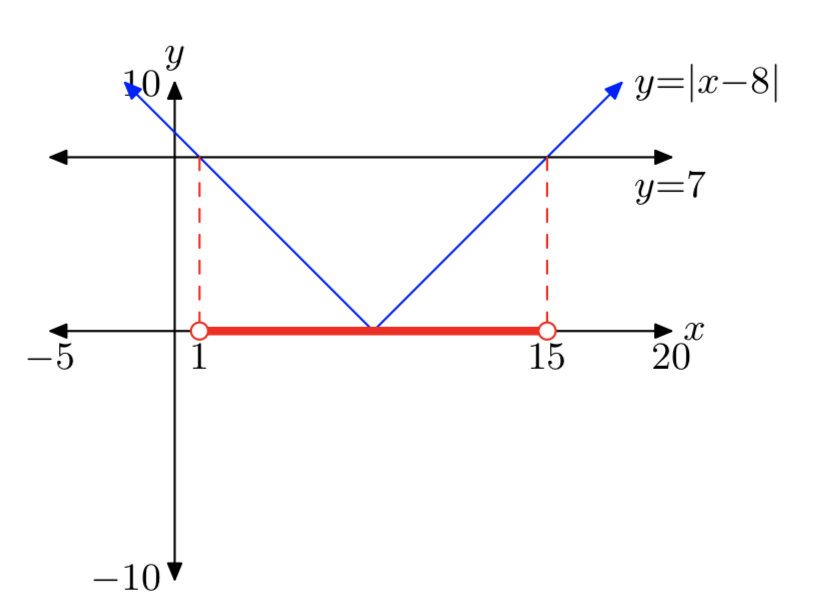
(1, 15) = {x: 1 < х < 15}
Вправа\(\PageIndex{34}\)
|2x−15| > 5
Вправа\(\PageIndex{35}\)
\(|2x+11| \ge 6\)
- Відповідь
-
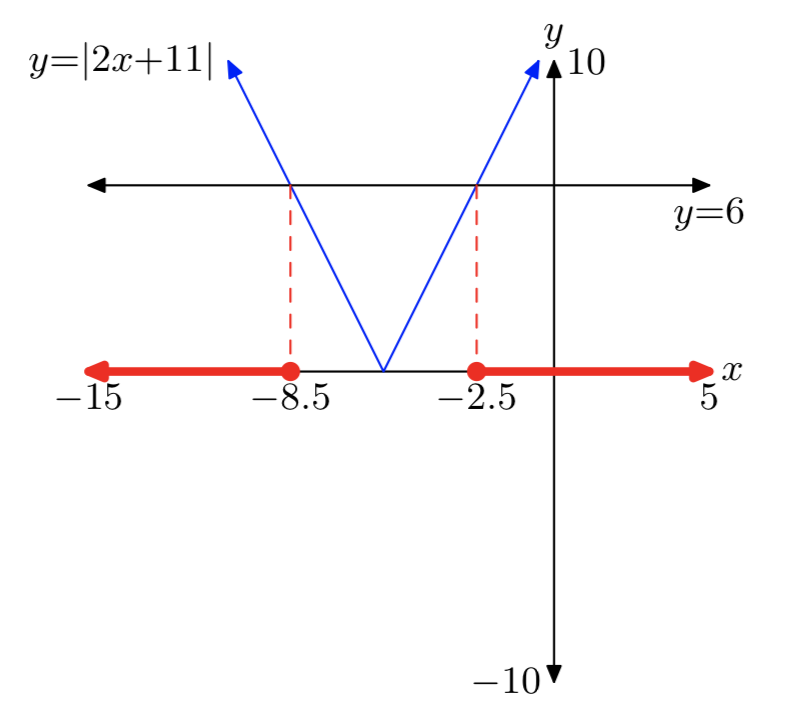
\((−\infty, −8.5] \cup [−2.5, \infty)\)= {x:\(x \le −8.5\) або\(x \ge −2.5\)}
Вправа\(\PageIndex{36}\)
\(|5x−21| \le 7\)
Вправа\(\PageIndex{37}\)
|х−12| > 6
- Відповідь
-
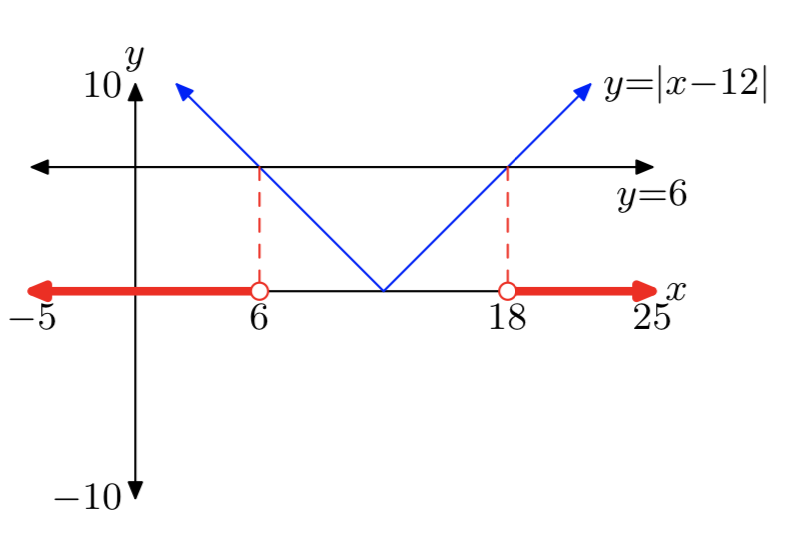
\((−\infty, 6) \cup (18, \infty)\)= {x: х < 6 or x > 18}
Вправа\(\PageIndex{38}\)
|х+11| < 5
Використовуйте строго алгебраїчну техніку для вирішення кожного з рівнянь у Вправи 39 - 46. Не використовуйте калькулятор. Затіньте набір рішення на числовому рядку та опишіть набір розв'язків, використовуючи як конструктор наборів, так і інтервальну нотацію.
Вправа\(\PageIndex{39}\)
|x+2|−3> 4
- Відповідь
-

\((−\infty, −9) \cup (5, \infty)\)= {x: x < −9 or x > 5}
Вправа\(\PageIndex{40}\)
3|х+5| < 6
Вправа\(\PageIndex{41}\)
\(−2|3−2x| \le −6\)
- Відповідь
-

\((−\infty, 0] \cup [3, \infty)\)= {x:\(x \le 0\) або\(x \ge 3\)}
Вправа\(\PageIndex{42}\)
\(|4−x|+5 \ge 12\)
Вправа\(\PageIndex{43}\)
3|х+2|−5 > |х+2|+7
- Відповідь
-

\((−\infty, −8) \cup (4, \infty)\)= {x: x < −8 or x > 4}
Вправа\(\PageIndex{44}\)
4−3|4−x| > 2|4−x|−1
Вправа\(\PageIndex{45}\)
\(|\frac{x}{3}−\frac{1}{4}| \le \frac{1}{12}\)
- Відповідь
-

[\(\frac{1}{2}\), 1] = {x:\(\frac{1}{2} \le x \le 1\)}
Вправа\(\PageIndex{46}\)
\(|\frac{x}{4}−\frac{1}{2}| \ge \frac{2}{3}\)
Використовуйте техніку відстані на числовій лінії, продемонстровану в прикладах 21 і 22, для розв'язання кожної з нерівностей у вправах 47 - 50. Надайте ескізи числових рядків, як у прикладі 17 в оповіданні. Опишіть набір рішень, використовуючи як set-builder, так і інтервальну нотацію.
Вправа\(\PageIndex{47}\)
|x−5| < 8
- Відповідь
-
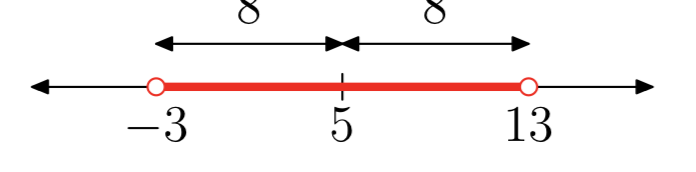
(−3, 13) = {x: −3 < x < 13}
Вправа\(\PageIndex{48}\)
|x−2| > 4
Вправа\(\PageIndex{49}\)
\(|x+4| \ge 3\)
- Відповідь
-
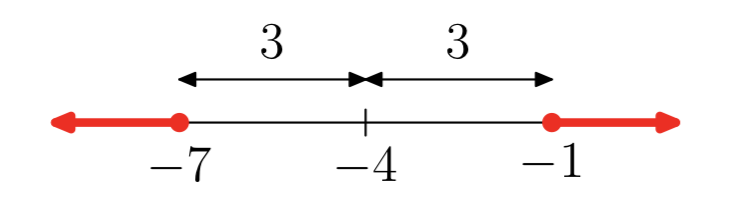
\((−\infty, −7] \cup [−1, \infty)\)= {x:\(x \le −7\) або\(x \ge −1\)}
Вправа\(\PageIndex{50}\)
\(|x+2| \le 11\)
Скористайтеся інструкціями, наведеними у Вправах 11 - 22, щоб вирішити нерівності у вправах 51 - 52. Опишіть набір рішень, використовуючи як set-builder, так і інтервальну нотацію.
Вправа\(\PageIndex{51}\)
\(|x+2| < \frac{1}{3}x+5\)
- Відповідь
-
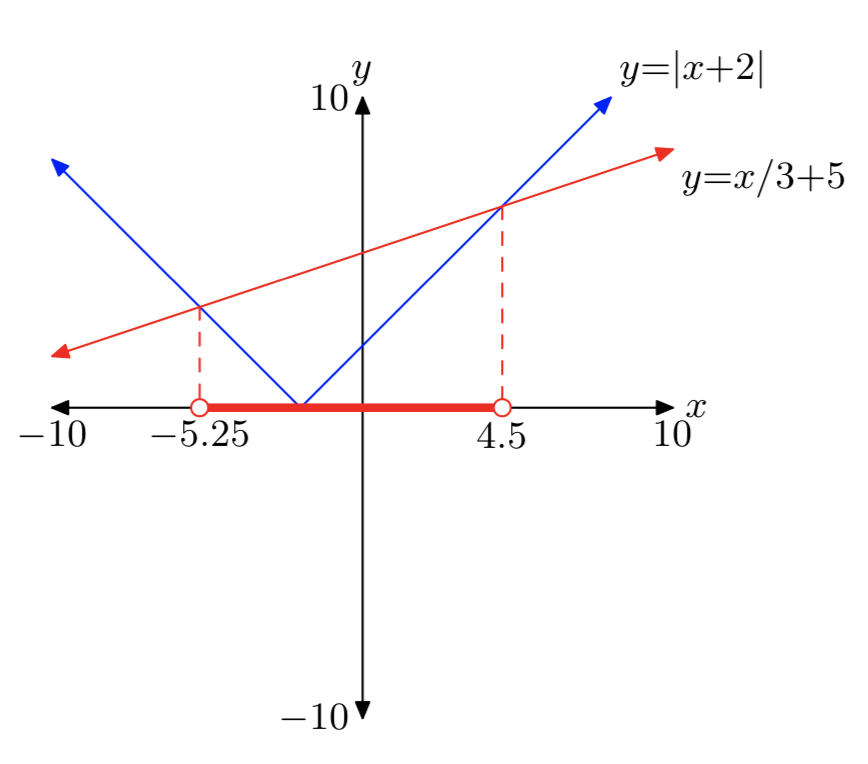
(−5,25, 4.5) = {x: −5,25 < х < 4,5}
Вправа\(\PageIndex{52}\)
\(|x−3| > 5−\frac{1}{2}x\)
У вправах 53 - 54 виконайте кожне з наступних завдань.
- Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь.
- Без використання калькулятора накидайте графіки лівої і правої сторін заданої нерівності. Позначте кожен граф своїм рівнянням.
- Затіньте розв'язок нерівності на осі x (якщо така є) у спосіб, показаний на рисунках 4 та 8 в оповіданні. Тобто відкиньте пунктирні лінії від точок перетину до осі, потім затіньте і позначте рішення, встановлене на осі х (доведеться наблизити). Опишіть набір рішень, використовуючи як set-builder, так і інтервальну нотацію.
Вправа\(\PageIndex{53}\)
\(|x−2| > \frac{1}{3}x+2\)
- Відповідь
-

\((−\infty, 0) \cup (6, \infty)\)= {x: х < 0 or x > 6}
Вправа\(\PageIndex{54}\)
\(|x+4| < \frac{1}{3}x+4\)
