4.2: Абсолютне значення

Тепер, коли у нас є основи кусково визначених функцій, ми готові ввести функцію абсолютного значення. Для початку давайте викласти тривіальне нагадування про те, що означає приймати абсолютне значення дійсного числа.

У певному сенсі абсолютне значення числа - це міра його величини, без (без) його знака. Таким чином,

\[|7|=7 \qquad \text { and } \qquad |-7| =7\]

Ось формальне визначення абсолютного значення дійсного числа.

Визначення: Абсолютне значення

Щоб знайти абсолютне значення будь-якого дійсного числа, спочатку знайдіть число на дійсному рядку.

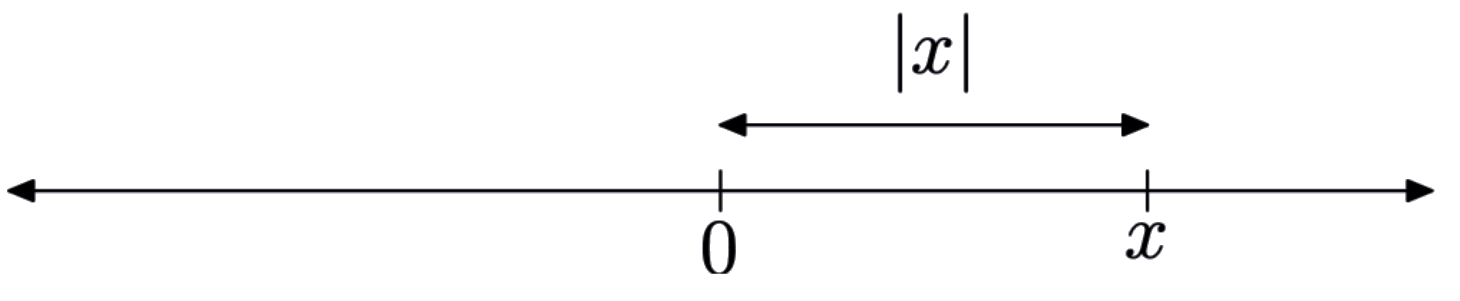
Абсолютне значення числа визначається як його відстань від початку.

Наприклад, щоб знайти абсолютне значення 7, знайдіть 7 на реальній лінії, а потім знайдіть її відстань від початку.

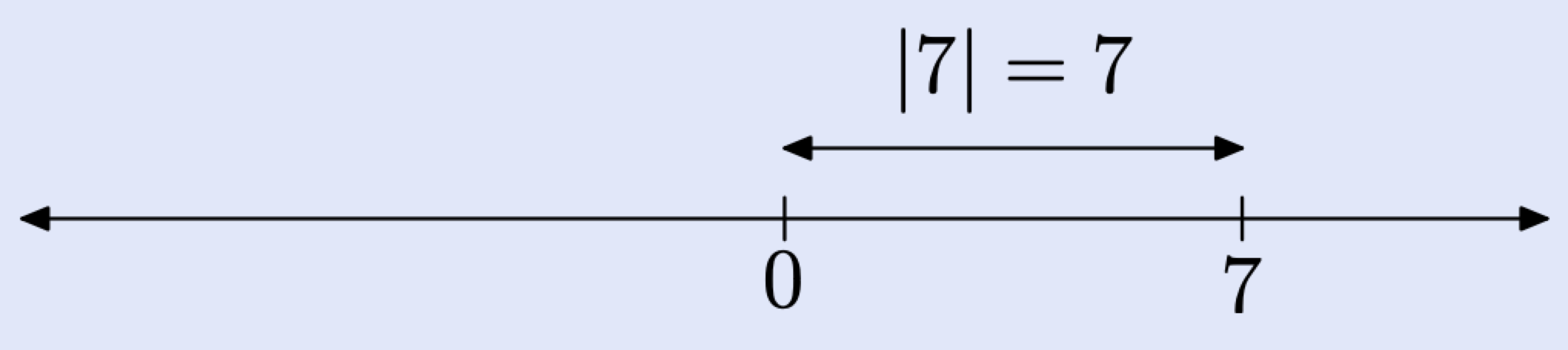
Щоб знайти абсолютне значення −7, знайдіть −7 на дійсному рядку, а потім знайдіть його відстань від початку.

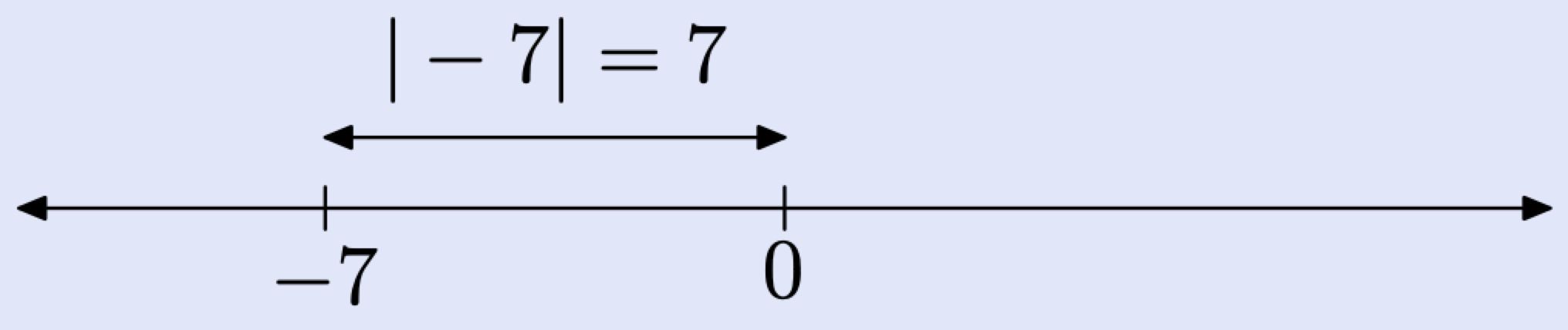
Деякі люблять говорити, що прийняття абсолютного значення «виробляє число, яке завжди є позитивним». Однак це ігнорує важливе виняток, тобто

\[|0|=0\]

Таким чином, правильним твердженням є «абсолютне значення будь-якого дійсного числа або додатне, або воно дорівнює нулю», тобто абсолютне значення дійсного числа «не від'ємне» 2 Замість використання фрази «не негативний», математики віддають перевагу слову «ненегативний». Коли ми приймаємо абсолютне значення числа, результат завжди невід'ємний; тобто результат або позитивний, або нуль. В символах,

\[|x| \geq 0 \text { for all real numbers } x\]

Це має сенс у світлі визначення 2. Відстань завжди невід'ємна.

Однак обговорення вище не має достатньої глибини для вирішення більш складних проблем, пов'язаних з абсолютним значенням.

Кускове визначення абсолютної величини

Оскільки абсолютне значення тісно пов'язане з відстанню, математики та вчені вважають його безцінним інструментом для вимірювання та аналізу помилок. Однак нам знадобиться формульне визначення абсолютної величини, якщо ми хочемо використовувати цей інструмент змістовно. Потрібно розробити кускове визначення функції абсолютного значення, яка буде визначати абсолютне значення для будь-якого довільного дійсного числа x.

Почнемо з кількох спостережень. Пам'ятайте, що абсолютне значення числа завжди невід'ємне (додатне або нуль).

1. Якщо число від'ємне, заперечення цього числа зробить його додатним. | − 5| = − (−5) = 5, і аналогічно | − 12| = − (−12) = 12. Таким чином, якщо x < 0 (якщо x від'ємний), то |x| = −x.
2. Якщо x = 0, то |x| = 0.
3. Якщо число позитивне, прийняття абсолютного значення цього числа не змінить нічого.

\[|5|=5, \text { and similarly, }|12|=12\]

Таким чином, якщо\(x>0\) (якщо\(x\) позитивний), то\(|x|=x\).

Ми можемо узагальнити ці три випадки з кусковим визначенням.

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {0,} & {\text { if } x=0} \\ {x,} & {\text { if } x>0}\end{array}\right.\]

Це перший рядок у нашому кусковому визначенні (4), який зазвичай залишає студентів дряпають голови. Вони можуть сказати: «Я думав, що абсолютне значення робить число позитивним (або нульовим), але у вас є\(|x| = −x\); тобто у вас є абсолютне значення x рівне від'ємному x». Намагайтеся, як би вони не могли, це здається суперечливим. Вам так здається?

Однак протиріччя немає. Якщо x < 0, тобто, якщо x є від'ємним числом, то −x є додатним числом, і наше інтуїтивне поняття абсолютного значення не відрізняється від нашого кускового визначення (4). Наприклад, якщо x = −8, то −x = 8, і хоча ми говоримо «від'ємний x», у цьому випадку −x є додатним числом.

Якщо ви все ще заплуталися з пантелику, врахуйте простий факт, що x і −x повинні мати «протилежні знаки». Якщо один позитивний, інший - негативний, і навпаки. Отже,

• якщо x є додатним, то −x є від'ємним, але
• якщо x від'ємний, то −x є додатним.

Давайте підсумуємо те, що ми дізналися до цих пір.

Підведення підсумків визначення на числовому рядку

Ми любимо використовувати числовий рядок, щоб допомогти підсумувати визначення абсолютного значення x.

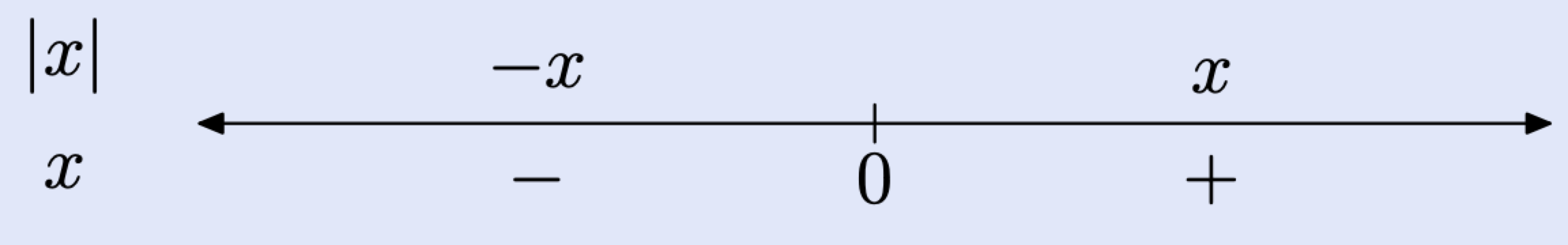
Деякі зауваження для того, щоб це резюме на числовому рядку.

• Спочатку ми малюємо реальну лінію, потім відзначаємо «критичне значення» для виразу всередині барів абсолютних значень на числовій лінії. Число нуль є критичним значенням для виразу x, тому що х змінює знак при переході з однієї сторони нуля на іншу.
• Зліва від нуля x - від'ємне число. Ми вказуємо це знаком мінус під цифровим рядком. Праворуч від нуля x - додатне число, позначене знаком плюс під цифровим рядком.
• Над числовим рядком спрощуємо вираз |x|. Ліворуч від нуля x є від'ємним числом (дивіться нижче рядка), отже |x| = −x. Зверніть увагу, як результат −x розміщується над рядком ліворуч від нуля. Аналогічно праворуч від нуля x - додатне число (дивіться нижче рядка), тому |x| = x. зверніть увагу, як результат x розміщується над рядком праворуч від нуля.

У кусковому визначенні |x| in (4) зауважте, що у нас є три окремі частини, по одній для кожного випадку, розглянутого вище. Однак, оскільки |0| = 0, ми можемо включити цей випадок з шматочком |x| = x, якщо ми відрегулюємо умову, щоб включити нуль.

Визначення

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x \geq 0}\end{array}\right.\]

Зауважимо, що це кускове визначення узгоджується з нашим обговоренням на сьогоднішній день.

1. У першому рядку рівняння (6), якщо x є від'ємним числом (тобто if\(x < 0\)), то абсолютне значення має змінити x на додатне число шляхом заперечення. Тобто, |x| = −x.
2. У другому рядку рівняння (6), якщо x є додатним або нульовим (тобто якщо\(x \geq 0\)), то нічого не робити, окрім як видалити стовпчики абсолютних значень. Тобто |x| = х.

Оскільки |0| = −0, ми могли б так само включити випадок для нуля ліворуч, визначаючи абсолютне значення за допомогою

\[|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x \leq 0} \\ {x,} & {\text { if } x>0}\end{array}\right.\]

Однак у цьому тексті ми завжди будемо включати критичне значення праворуч, як показано у Визначенні 5.

Побудова кускових визначень

Давайте подивимося, якщо ми можемо визначити кускові визначення для інших виразів, що включають абсолютне значення.

Приклад\(\PageIndex{1}\)

Визначте кускове визначення для |x − 2|.

Рішення

Спочатку встановіть вираз всередині барів абсолютних значень, рівних нулю, і вирішіть для x.

\[\begin{aligned} x-2 &=0 \\ x &=2 \end{aligned}\]

Зауважте, що x − 2 = 0 при x = 2. Це «критичне значення» для цього виразу. Намалюйте реальну лінію і позначте це критичне значення x на лінії. Помістіть вираз x − 2 під рядком у лівому кінці.

Далі визначте знак x − 2 для значень x з кожного боку 2. Це легко зробити шляхом «тестування» точки з кожного боку 2 у виразі x − 2.

• Візьмемо х = 1, який лежить зліва від критичного значення 2 на нашій числовій рядку. Підставляємо це значення x у вираз x − 2, отримавши

\[x-2=1-2=-1\]

який є негативним. Дійсно, незалежно від того, яке значення x ви обрали ліворуч від 2, при вставці у вираз x − 2, ви отримаєте негативний результат (ви повинні перевірити це для інших значень x ліворуч від 2). Ми вказуємо, що вираз x − 2 є від'ємним для знаків x ліворуч від 2, розмістивши знак мінус (−) під числовим рядком ліворуч від 2.

• Далі вибираємо x = 3, який лежить праворуч від критичного значення 2 на числовій лінії. Підставляємо це значення x у вираз x − 2, отримавши

\[x-2=3-2=1\]

що є позитивним. Дійсно, незалежно від того, яке значення x ви обрали праворуч від 2, при вставці у вираз x − 2 ви отримаєте позитивний результат (ви повинні перевірити це для інших значень x праворуч від 2). Ми вказуємо, що вираз x − 2 є додатним для значень x праворуч від 2, розмістивши знак плюс (+) під числовим рядком праворуч від 2 (див. Числовий рядок вище).

Наступним кроком буде вилучення стовпчиків абсолютних значень з виразу |x−2|, залежно від знака x − 2.

• Ліворуч від 2 вираз x − 2 від'ємний (зверніть увагу на знак мінус (−) під числовим рядком), тому |x − 2| = − (x − 2). Тобто, ми повинні заперечувати x − 2, щоб зробити його позитивним. На це вказується розміщенням − (x − 2) над лінією ліворуч від 2.

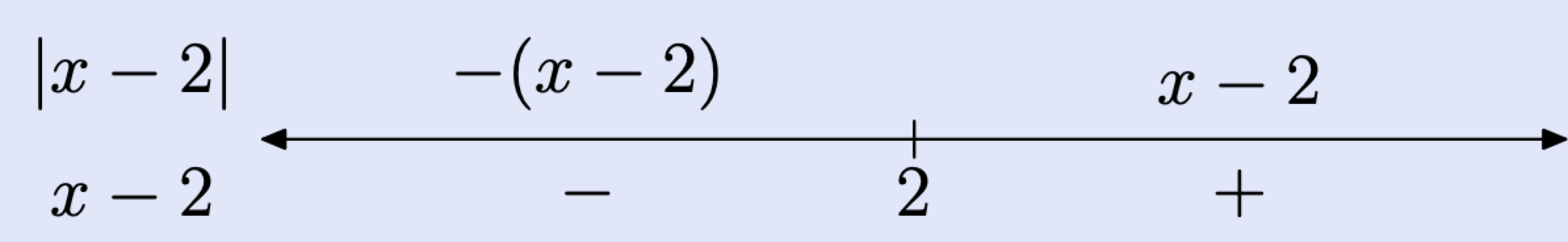
• Праворуч від 2 вираз x − 2 є додатним (зверніть увагу на знак плюса (+) нижче рядка), тому |x − 2| = x − 2. Тобто ми просто видаляємо бари абсолютного значення, оскільки кількість всередині вже позитивна. На це вказується розміщенням x − 2 над рядком праворуч від 2 (див. числовий рядок вище).

Ми можемо скористатися цим підсумком останнього числового рядка для побудови кускового визначення виразу |x − 2|.

\[|x-2|=\left\{\begin{array}{ll}{-(x-2),} & {\text { if } x<2,} \\ {x-2,} & {\text { if } x \geq 2}\end{array}=\left\{\begin{array}{ll}{-x+2,} & {\text { if } x<2} \\ {x-2,} & {\text { if } x \geq 2}\end{array}\right.\right.\]

Наш числовий рядок і кускове визначення узгоджуються: |x − 2| = − (x − 2) ліворуч від 2 та |x − 2| = x − 2 праворуч від 2. Крім того, зверніть увагу, як ми включили критичне значення 2 «праворуч» в нашому кусковому визначенні.

Давайте підсумуємо метод, який ми слідували, щоб побудувати кускову функцію вище.

Побудова кускового визначення абсолютної величини

Якщо представлено абсолютне значення алгебраїчного виразу, виконайте наступні кроки, щоб видалити бруски абсолютних значень та побудувати еквівалентне кускове визначення.

1. Візьміть вираз, який знаходиться всередині барів абсолютних значень, і встановіть цей вираз рівним нулю. Потім вирішіть для x Це значення x називається «критичним значенням». (Примітка: Вираз всередині барів абсолютних значень може мати більше одного критичного значення. Ми не будемо стикатися з такими проблемами в цьому тексті.)
2. Помістіть критичне значення на числовому рядку.
3. Помістіть вираз всередині рядків абсолютних значень під числовим рядком у лівому кінці.
4. Перевірте знак виразу всередині рядків абсолютних значень, вставивши значення x з кожного боку критичного значення та позначивши результат знаком плюс (+) або мінус (−) під числовим рядком.
5. Помістіть вихідний вираз, який включає смуги абсолютних значень, над числовим рядком у лівому кінці.
6. Використовуйте знак виразу всередині барів абсолютних значень (позначені знаками плюс і мінус під числовим рядком), щоб видалити стовпчики абсолютних значень, розмістивши результати над числовим рядком з кожного боку критичного значення.
7. Побудувати кускове визначення, яке імітує результати на числовому рядку.

Давайте застосуємо цю техніку до іншого прикладу.

Приклад\(\PageIndex{2}\)

Визначте кускове визначення для |3 − 2x|.

Рішення

Крок 1: Спочатку встановіть вираз всередині барів абсолютних значень, рівних нулю, і вирішіть для x.

\[\begin{aligned} 3-2 x &=0 \\ x &=3 / 2 \end{aligned}\]

Зауважте, що 3 − 2x = 0 при x = 3/2. Це «критичне значення» для цього виразу.

Кроки 2 і 3: Намалюйте цифрову лінію і позначте це критичне значення на лінії. Наступний крок вимагає, щоб ми розмістили вираз всередині рядків абсолютних значень, а саме 3 − 2x, під лінією в лівому кінці.

Крок 4: Далі визначте знак 3 − 2x для значень x з кожного боку 3/2. Це легко зробити шляхом «тестування» точки з кожного боку 3/2 у виразі 3 − 2x.

• Візьміть х = 1, який лежить зліва від 3/2. Підставляємо це значення x у вираз 3 − 2x, отримання\[3-2 x=3-2(1)=1\] якого є додатним. Вкажіть цей результат, помістивши знак плюс (+) під цифровим рядком ліворуч від 3/2.

• Далі вибираємо х = 2, який лежить праворуч від 3/2. Підставляємо це значення x у вираз 3 − 2x, отримання\[3-2 x=3-2(2)=-1\] якого є від'ємним. Вкажіть цей результат, розмістивши від'ємний знак (−) нижче рядка праворуч від 3/2 (див. номер рядка вище).

Кроки 5 і 6: Помістіть вихідний вираз, а саме |3 − 2x|, над числовим рядком у лівому кінці. Наступним кроком буде вилучення стовпчиків абсолютних значень з виразу |3 − 2x|.

• Ліворуч від 3/2 вираз 3 − 2x є додатним (зверніть увагу на знак плюс (+) під числовим рядком), отже |3−2x| = 3−2x. Вкажіть цей результат, розмістивши вираз 3 − 2x над числовим рядком ліворуч від 3/2.

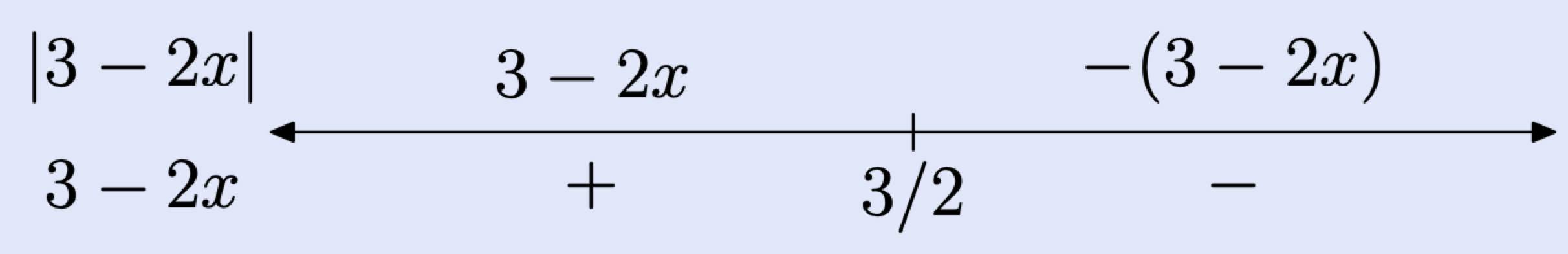
• Праворуч від 3/2 вираз 3−2x є від'ємним (зверніть увагу на знак мінус (−) під числовим рядком), отже |3−2x| = − (3−2x). Тобто, ми повинні заперечувати 3−2x, щоб зробити його позитивним. На це вказується розміщенням виразу − (3 − 2x) над рядком праворуч від 3/2 (див. числовий рядок вище).

Крок 7: Ми можемо використати цей останній номер рядка для написання кускового визначення виразу |3 − 2x|.

\[|3-2 x|=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2 .} \\ {-(3-2 x),} & {\text { if } x \geq 3 / 2}\end{array}=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2} \\ {-3+2 x,} & {\text { if } x \geq 3 / 2}\end{array}\right.\right.\]

Знову ж таки, зверніть увагу, як ми включили критичне значення 3/2 «праворуч».

Креслення графіка функції абсолютного значення

Тепер, коли ми знаємо, як побудувати кускове визначення для виразу, що містить стовпчики абсолютних значень, ми можемо використовувати те, що ми дізналися в попередньому розділі, щоб намалювати графік.

Приклад\(\PageIndex{3}\)

Намалюйте графік функції f (x) = |3 − 2x|.

Рішення

У\(\PageIndex{2}\) прикладі ми побудували наступне кускове визначення.

\[f(x)=|3-2 x|=\left\{\begin{array}{ll}{3-2 x,} & {\text { if } x<3 / 2} \\ {-3+2 x,} & {\text { if } x \geq 3 / 2}\end{array}\right.\]

Тепер ми ескіз кожен шматок цієї функції.

• Якщо x < 3/2, то f (x) = 3 − 2x (див. Рівняння (10)). Це промінь, що починається з х = 3/2 і тягнеться вліво. При х = 3/2,

\[f(3 / 2)=3-2(3 / 2)=3-3=0\]

Таким чином, кінцева точка променя розташовується в (3/2, 0).

Далі виберіть значення x, яке лежить ліворуч від 3/2. При х = 0,

\[f(0)=3-2(0)=3-0=3\]

Таким чином, друга точка на промені дорівнює (0, 3).

Таблиця, що містить дві оцінені точки і ескіз супутнього променя наведені на малюнку\(\PageIndex{1}\). Оскільки f (x) = 3 − 2x, лише якщо x строго менше 3/2, точка в (3/2, 0) незаповнена.

Рис\(\PageIndex{1}\). f (x) = 3 − 2x при x < 3/2.

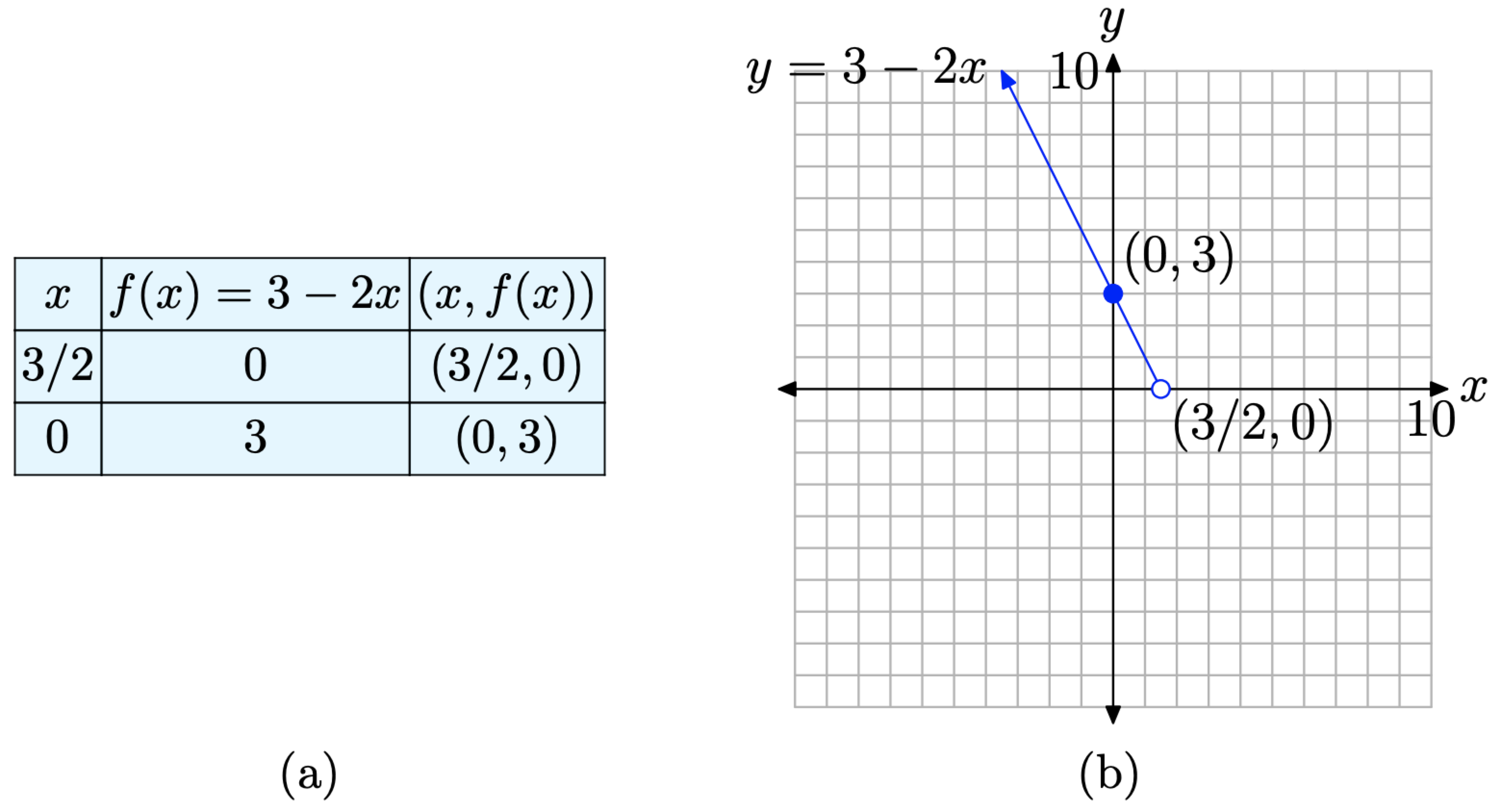
• Якщо x ≥ 3/2, то f (x) = −3 + 2x (див. Рівняння (10)). Це промінь, що починається з х = 3/2 і тягнеться вправо. При х = 3/2,\[f(3 / 2)=-3+2(3 / 2)=-3+3=0\]

Таким чином, кінцева точка променя розташовується в (3/2, 0).

Далі виберіть значення x, яке лежить праворуч від 3/2. При х = 3,\[f(3)=-3+2(3)=-3+6=3\]

Таким чином, друга точка на промені - це (3, 3). Таблиця, що містить дві оцінені точки і ескіз супутнього променя наведені на малюнку\(\PageIndex{2}\). Оскільки f (x) = −3 + 2x для всіх значень x, які більше або рівні 3/2, точка в (3/2, 0) заповнюється на цьому графіку.

Мал\(\PageIndex{2}\). f (x) = −3 + 2x при\(x \geq 3/2\).

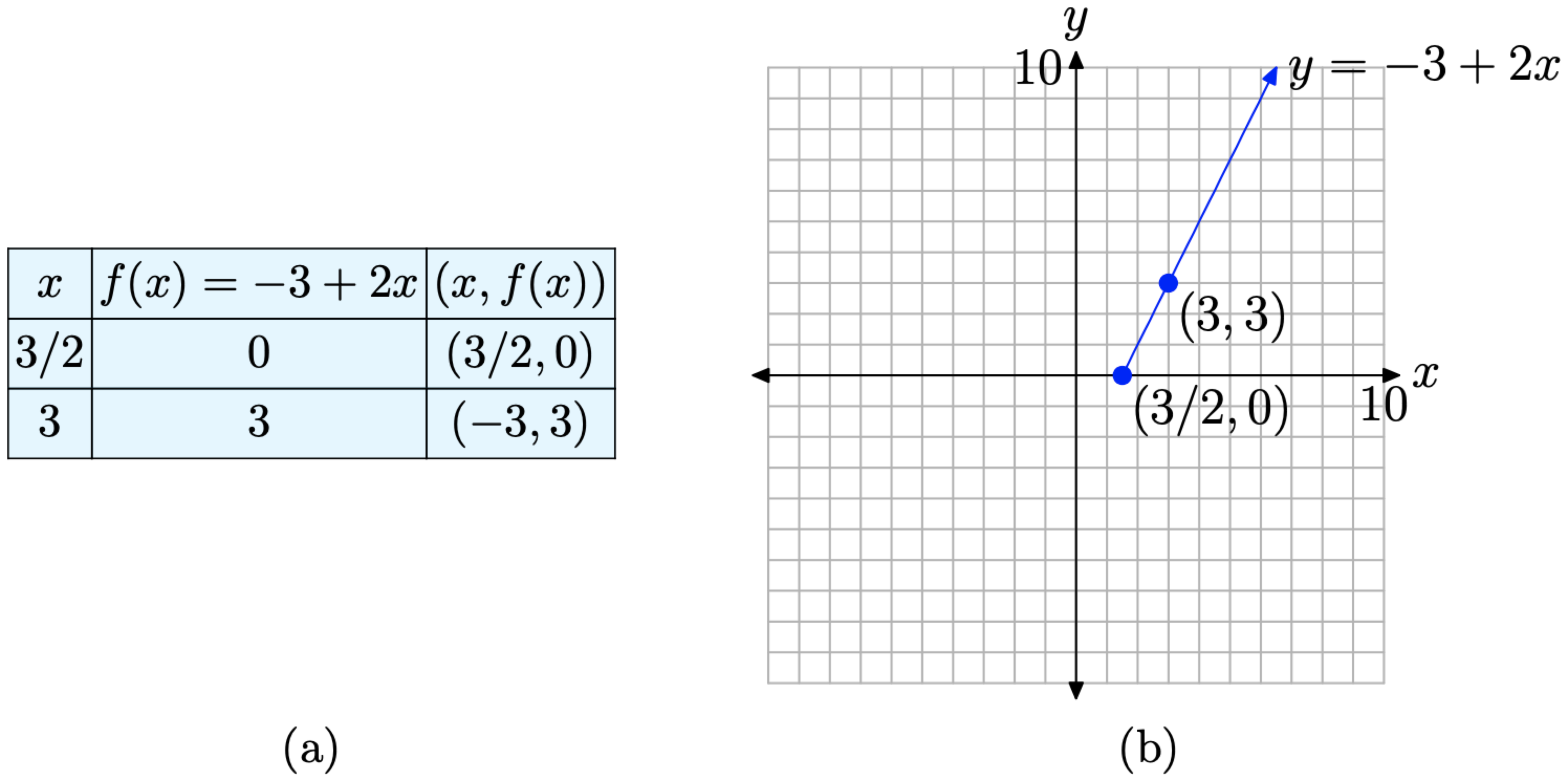
• Щоб намалювати графік f (x) = |3 − 2x|, нам потрібно об'єднати лише дві частини з малюнків\(\PageIndex{1}\) і\(\PageIndex{2}\). Результат показаний на малюнку\(\PageIndex{3}\).

Малюнок\(\PageIndex{3}\). Графік f (x) = |3 − 2x|.

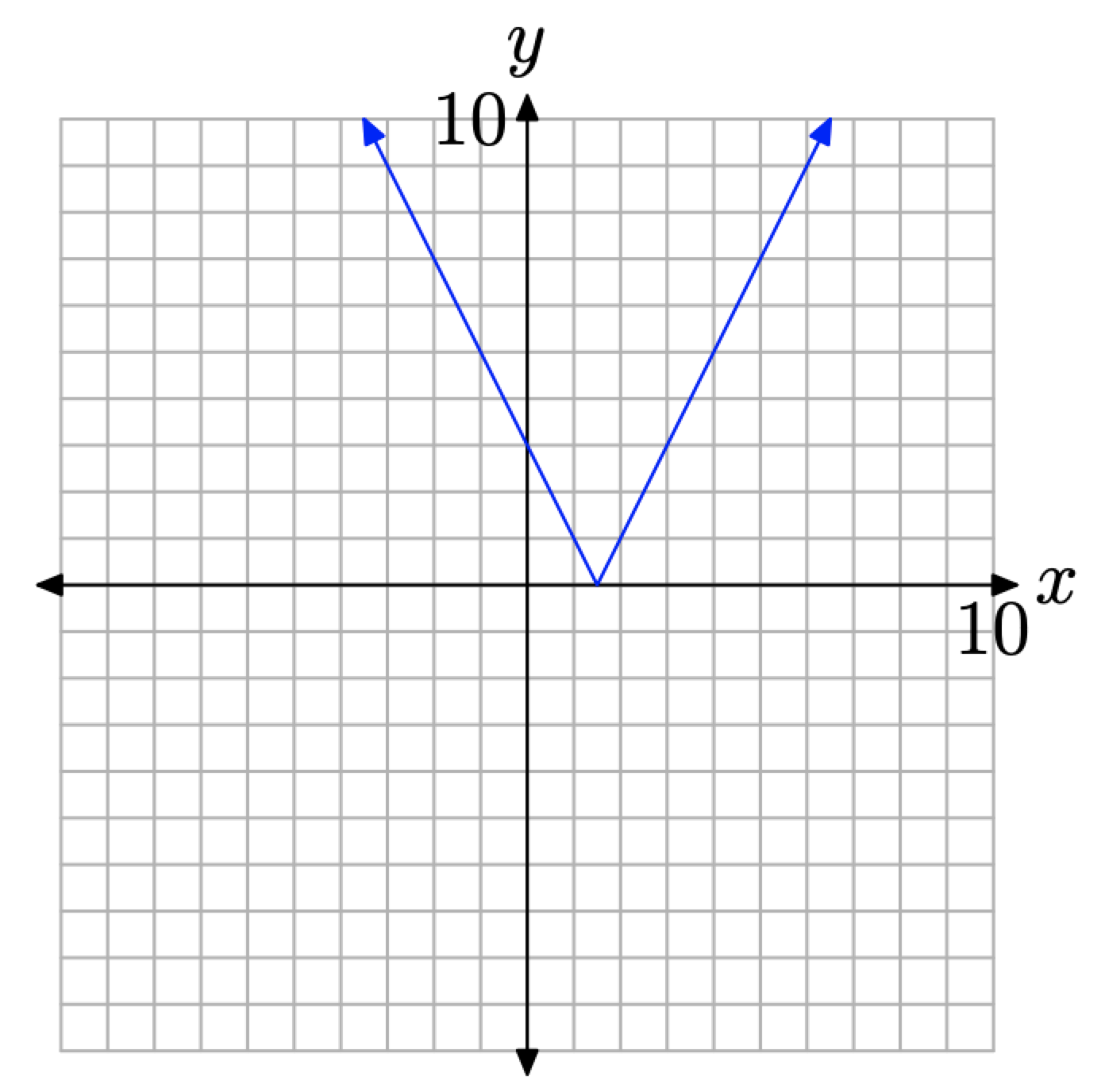
Зверніть увагу на «V-подібну форму» графіка. Ми будемо називати точку на кінчику «V» вершиною функції абсолютного значення.

На\(\PageIndex{3}\) малюнку рівняння лівої гілки «V» дорівнює y = 3 − 2x. Альтернативним підходом до малювання цієї гілки є зауваження, що її графік міститься у графіку повної лінії y = 3 − 2x, яка має нахил −2 та перехоплення y (0, 3). Таким чином, можна намалювати повну лінію, використовуючи нахил і y-перехоплення, а потім стерти ту частину лінії, яка лежить праворуч від x = 3/2. Аналогічна стратегія працювала б для правої гілки y = |3 − 2x|.

Використання перетворень

Розглянемо ще раз основне визначення абсолютного значення х.

\[f(x)=|x|=\left\{\begin{array}{ll}{-x,} & {\text { if } x<0} \\ {x,} & {\text { if } x \geq 0}\end{array}\right.\]

Деякі основні спостереження:

• Якщо x < 0, то f (x) = −x. Цей промінь починається з початку і тягнеться вліво з нахилом −1. Його графік зображений на малюнку\(\PageIndex{4}\) (а).
• Якщо\(x \geq 0\), то f (x) = x Цей промінь починається з початку і тягнеться вправо з нахилом 1. Його графік зображений на малюнку\(\PageIndex{4}\) (б).
• Об'єднуємо графіки на рисунках\(\PageIndex{4}\) (a) і\(\PageIndex{4}\) (b), щоб отримати графік f (x) = |x| на малюнку\(\PageIndex{4}\) (c).

Малюнок\(\PageIndex{4}\). Об'єднайте ліву та праву гілки, щоб отримати основний графік f (x) = |x|.

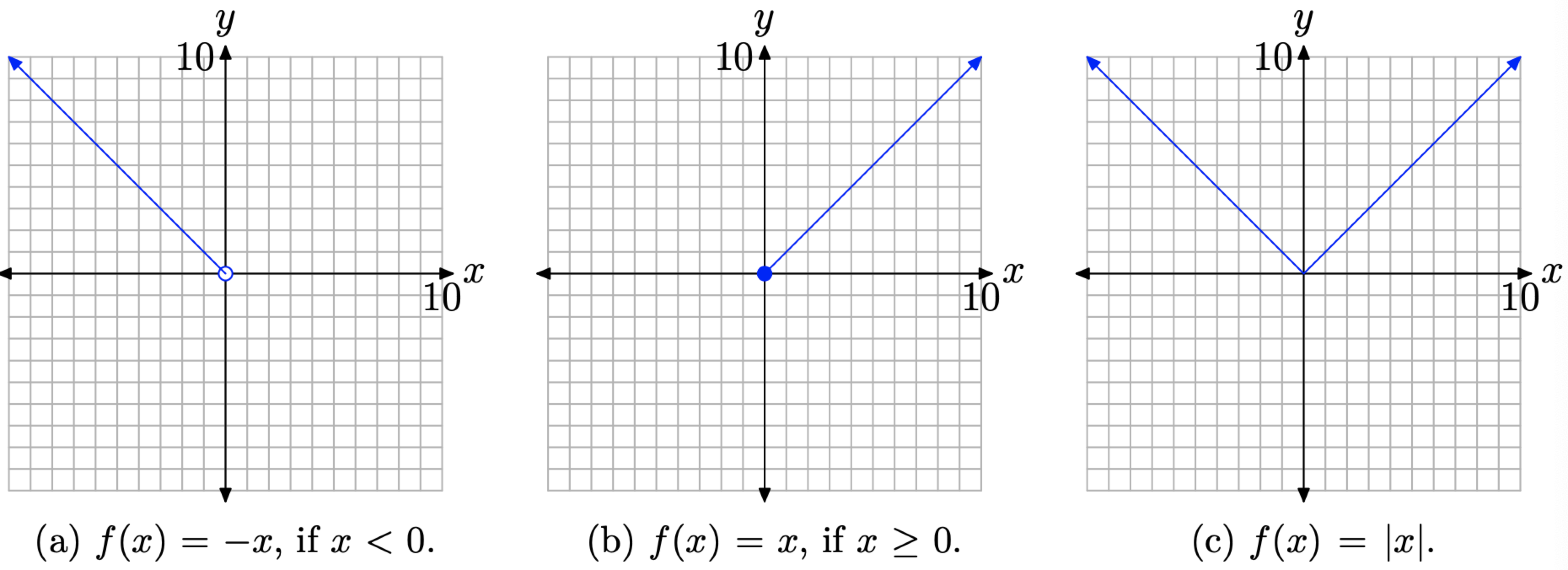
Ви повинні зафіксувати граф f (x) = |x| до пам'яті. Речі, які слід зазначити:

• Графік f (x) = |x| - «V-подібний».
• Вершина графа знаходиться в точці (0, 0).
• Ліва гілка має рівняння y = −x та нахил −1.
• Права гілка має рівняння y = x і нахил 1.
• Кожна гілка графа f (x) = |x| утворює ідеальний кут 45◦ з віссю x.

Тепер, коли ми знаємо, як намалювати графік f (x) = |x|, ми можемо використовувати перетворення, які ми дізналися в Главі 2 (розділи 5 і 6), щоб намалювати ряд простих графіків, що включають абсолютне значення.

Приклад\(\PageIndex{4}\)

Намалюйте графік f (x) = |x − 3|.

Рішення

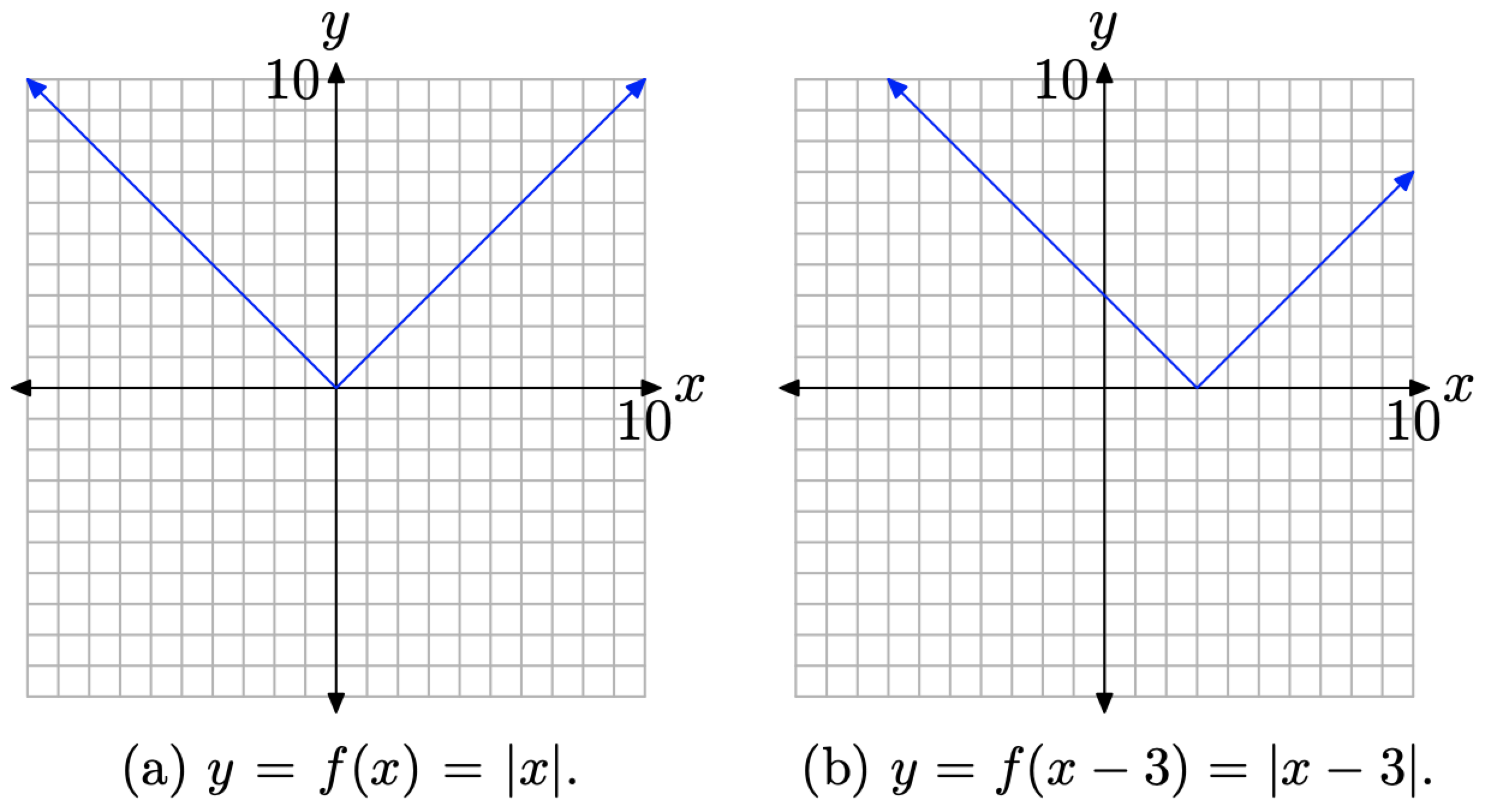
Спочатку намалюйте графік y = f (x) = |x|, як показано на малюнку\(\PageIndex{5}\) (а). Зверніть увагу, що якщо f (x) = |x|, то

\[y=f(x-3)=|x-3|\]

Щоб накреслити графік y = f (x − 3) = |x − 3|, зрушуємо графік y = f (x) = |x| три одиниці вправо, отримавши результат, показаний на малюнку\(\PageIndex{5}\) (b).

Малюнок\(\PageIndex{5}\). Щоб намалювати графік y = |x − 3|, зрушуємо графік y = |x| на три одиниці вправо.

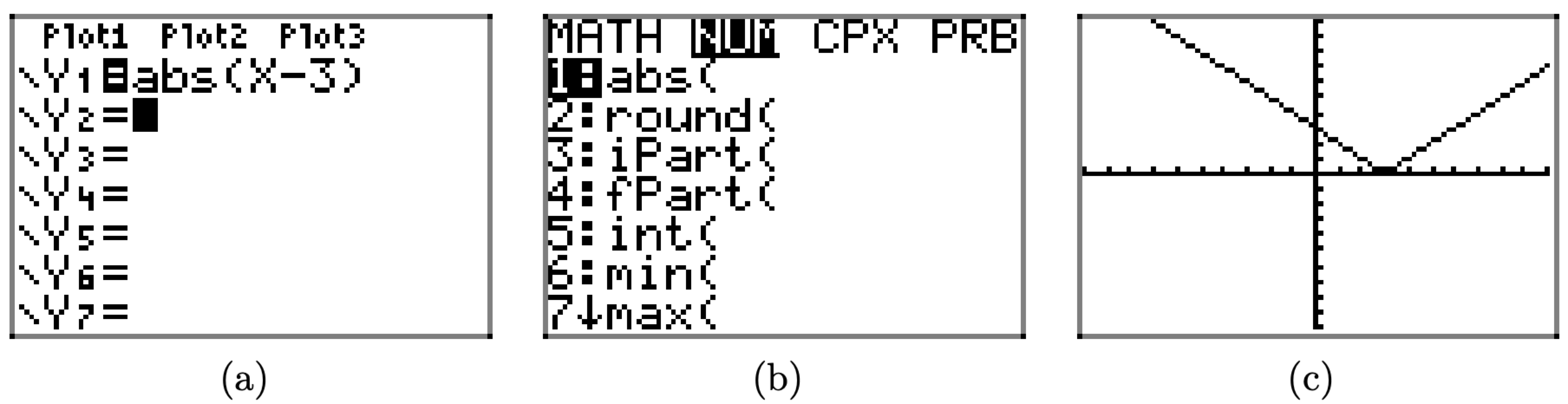
Ми можемо перевірити цей результат за допомогою графічного калькулятора. Завантажте функцію f (x) = |x − 3| у Y1 у меню Y= на графічному калькуляторі, як показано на малюнку\(\PageIndex{6}\) (a). Натисніть кнопку MATH, стрілка праворуч до меню NUM, потім виберіть 1:abs ((див. Рис.\(\PageIndex{6}\) (b)), щоб ввести абсолютне значення в Y1. Натисніть кнопку ZOOM, а потім виберіть 6:ZStandard, щоб створити зображення, показане на малюнку\(\PageIndex{6}\) (c).

Малюнок\(\PageIndex{6}\). За допомогою графічного калькулятора можна намалювати графік f (x) = |x − 3|.

Давайте розглянемо ще один простий приклад.

Приклад\(\PageIndex{5}\)

Намалюйте графік f (x) = |x| − 4.

Рішення

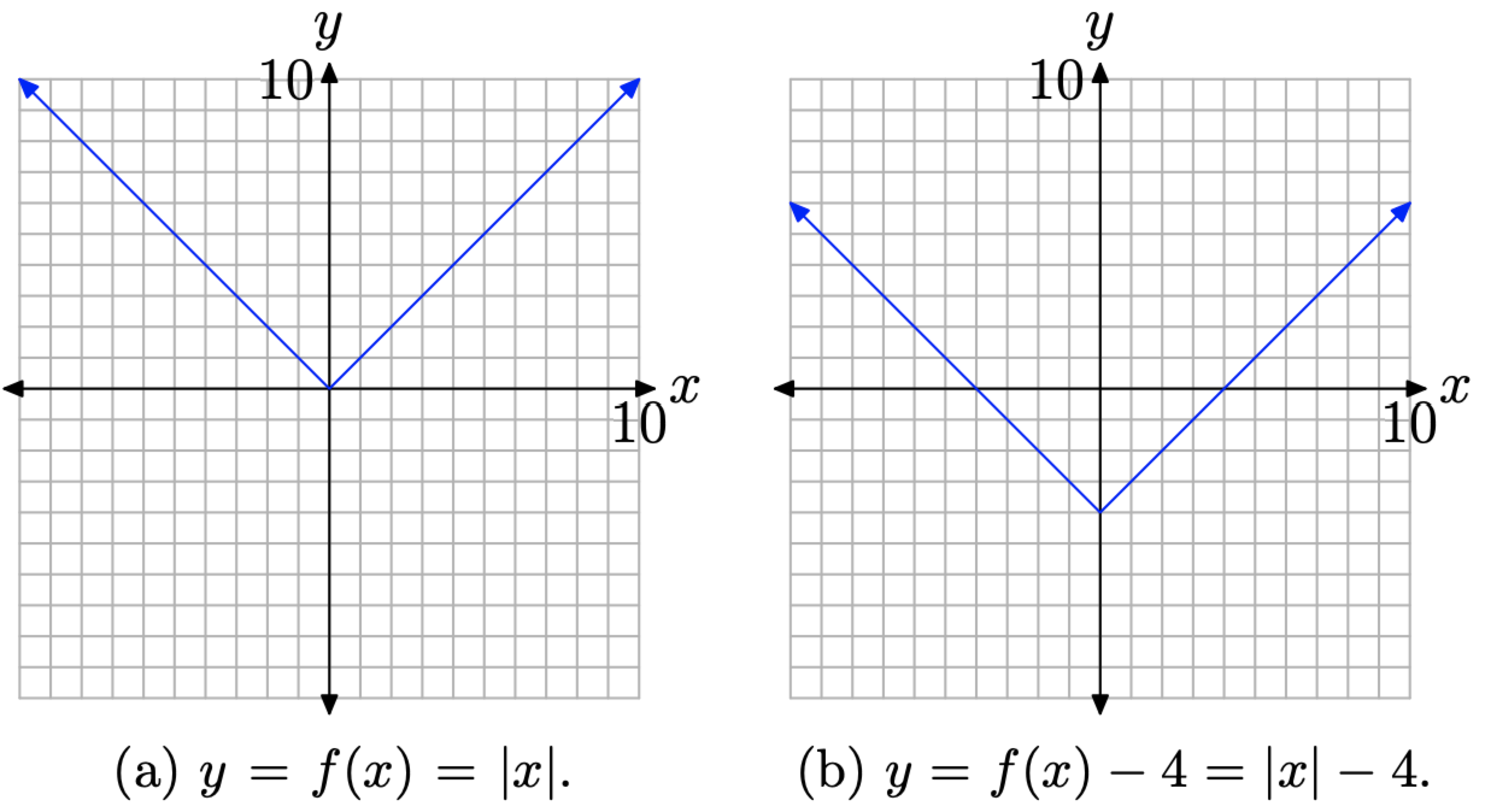
Спочатку намалюйте графік y = f (x) = |x|, як показано на малюнку\(\PageIndex{7}\) (а). Зверніть увагу, що якщо f (x) = |x|, то\[y=f(x)-4=|x|-4\]

Для накреслення графіка y = f (x) − 4 = |x| − 4 зрушуємо графік y = f (x) = |x| вниз на 4 одиниці, отримавши результат, показаний на малюнку\(\PageIndex{5}\) (b).

Малюнок\(\PageIndex{7}\). Щоб намалювати графік y = |x| − 4, зрушуємо графік y = |x| вниз на 4 одиниці.

Давайте розглянемо один остаточний приклад.

Приклад\(\PageIndex{6}\)

Намалюйте графік f (x) = −|x| + 5. Вкажіть домен і діапазон цієї функції.

Рішення

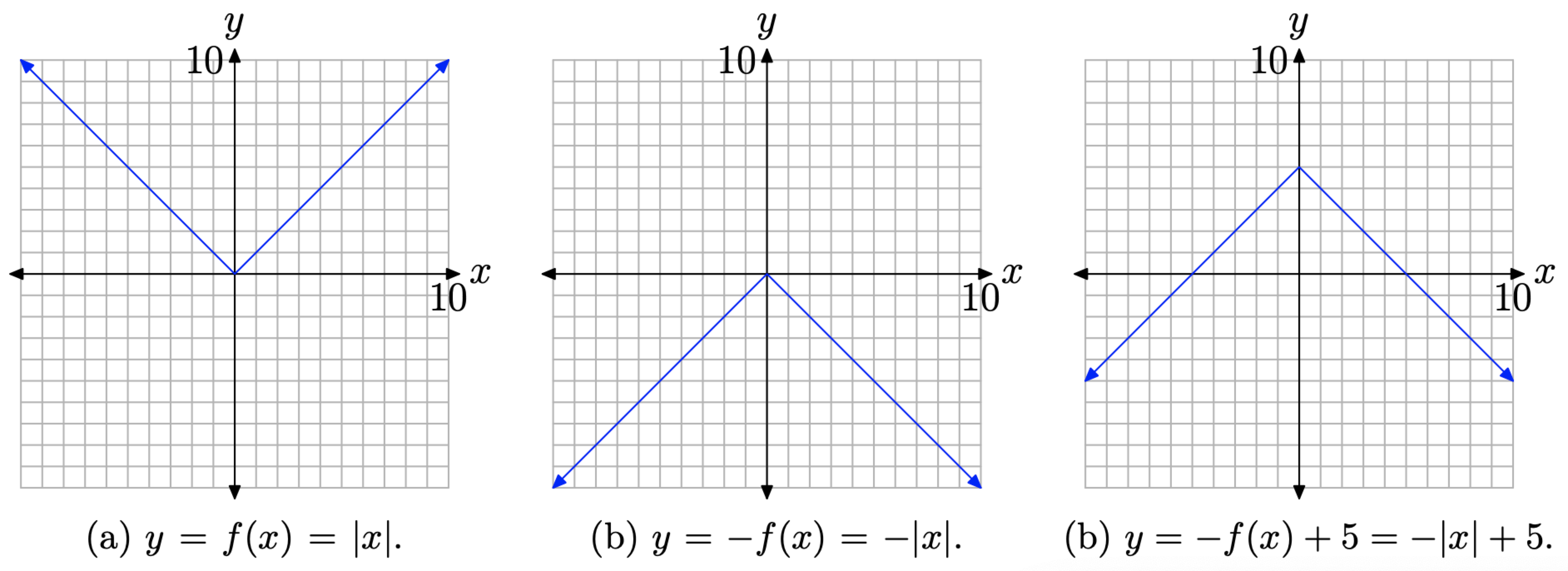
• Спочатку намалюйте графік y = f (x) = |x|, як показано на малюнку\(\PageIndex{8}\) (а).
• Далі намалюйте графік y = −f (x) = −|x|, який є відображенням графіка y = f (x) = |x| поперек осі x і зображений на малюнку\(\PageIndex{8}\) (b).
• Нарешті, ми хочемо намалювати графік y = −f (x) + 5 = −|x| + 5. Для цього зрушуємо графік y = −f (x) = −|x| на малюнку\(\PageIndex{8}\) (b) вгору на 5 одиниць, щоб отримати результат на малюнку\(\PageIndex{8}\) (c).

Щоб знайти область f (x) = −|x| + 5, спроектуйте всі точки на графіку на вісь x, як показано на малюнку\(\PageIndex{9}\) (a). Таким чином, домен f є\((-\infty, \infty)\). Щоб знайти діапазон, спроектуйте всі точки на графіку на вісь y, як показано на малюнку\(\PageIndex{9}\) (b). Таким чином, діапазон є\((-\infty, 5]\).

Малюнок\(\PageIndex{8}\). Щоб намалювати графік y = −|x| + 5, спочатку відобразіть графік y = |x| по осі x, щоб створити графік y = −|x|, потім зсуньте цей результат на 5 одиниць, щоб отримати графік y = −|x| + 5.

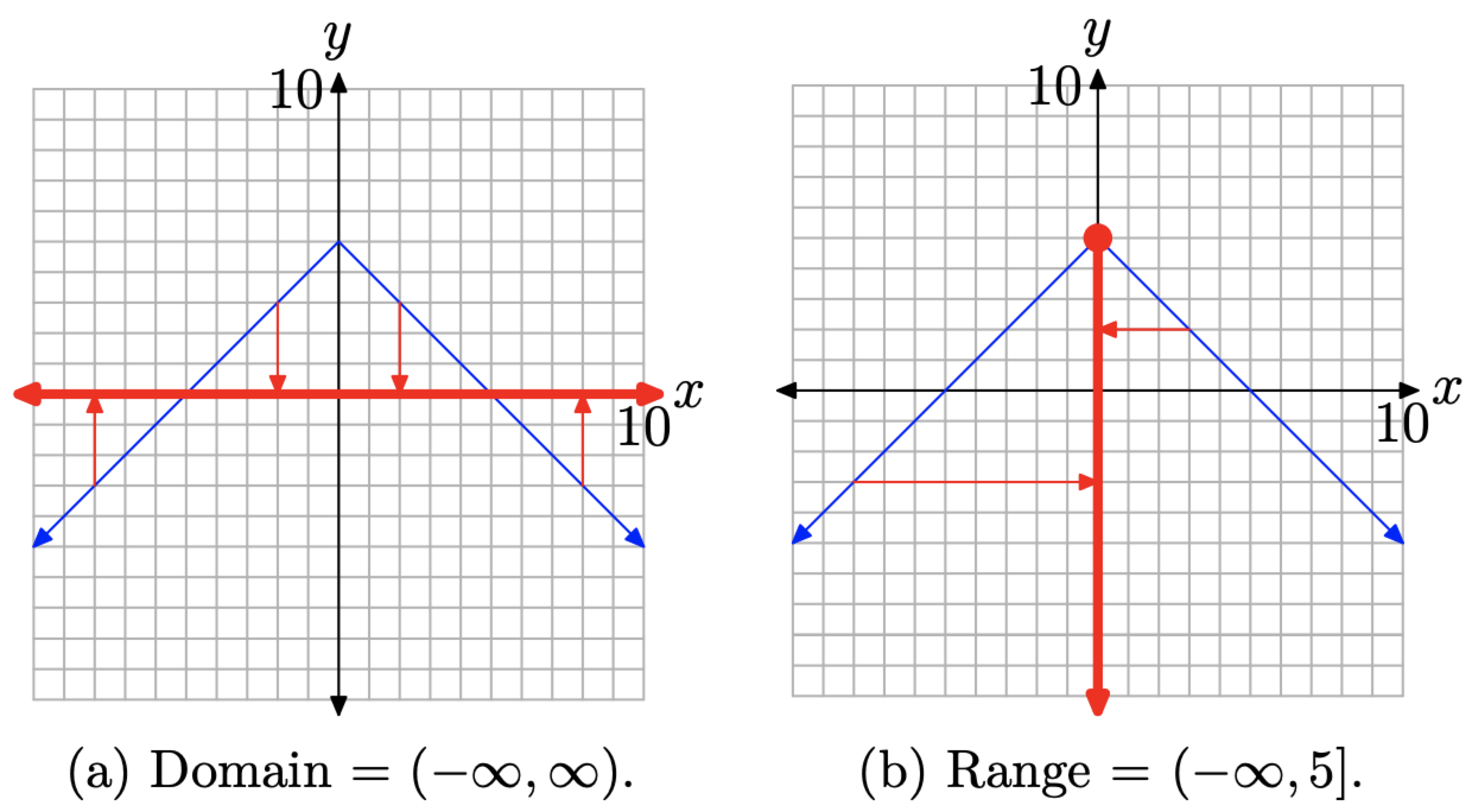
Малюнок\(\PageIndex{9}\). Проектування на осі для пошуку домену та діапазону

Вправа

Для кожної з функцій у вправах 1 - 8, як у прикладах 7 і 8 в оповіданні, відзначте «критичне значення» на числовому рядку, потім позначте знак виразу всередині стовпчиків абсолютних значень нижче числової лінії. Над числовим рядком видаліть стовпчики абсолютних значень відповідно до знака виразу, який ви позначили під числовим рядком. Після завершення зведення числового рядка створіть кускове визначення для заданої функції абсолютного значення.

Вправа\(\PageIndex{1}\)

ф (х) = |х+1|

Відповідь

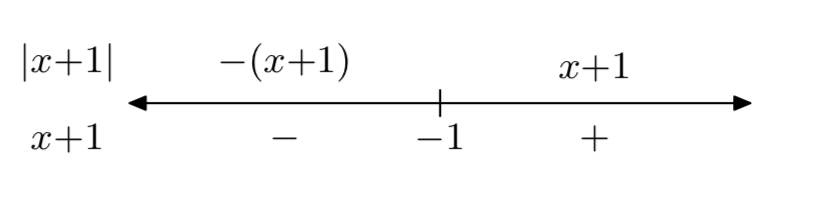
\[f(x)=\left\{\begin{array}{ll}{-x-1,} & {\text { if } x<-1} \\ {x+1,} & {\text { if } x \ge -1} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{2}\)

f (x) = |х−4|

Вправа\(\PageIndex{3}\)

г (х) = |4−5x|

Відповідь

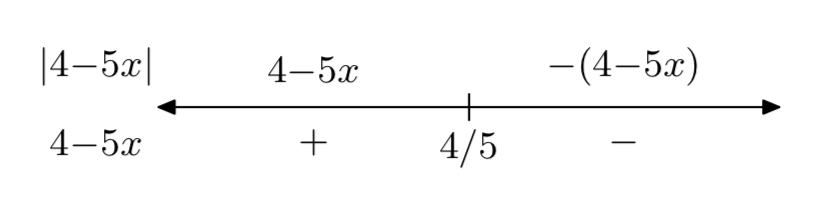
\[g(x)=\left\{\begin{array}{ll}{4-5x,} & {\text { if } x<\frac{4}{5}} \\ {-4+5x,} & {\text { if } x \ge \frac{4}{5}} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{4}\)

г (х) = |3−2х|

Вправа\(\PageIndex{5}\)

h (x) = |−х−5|

Відповідь

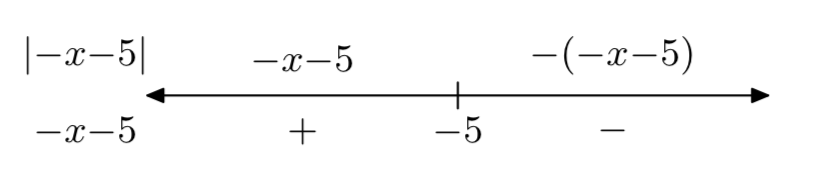
\[h(x)=\left\{\begin{array}{ll}{-x-5,} & {\text { if } x<-5} \\ {x+5,} & {\text { if } x \ge -5} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{6}\)

h (x) = |−х−3|

Вправа\(\PageIndex{7}\)

ф (х) = х+|х|

Відповідь

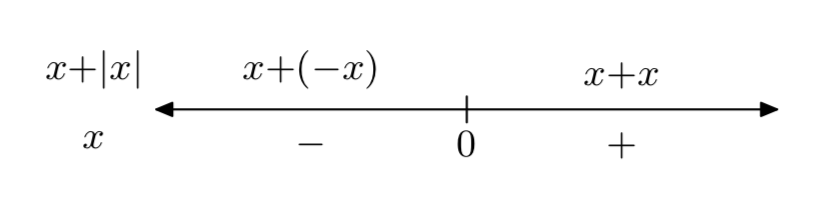
\[f(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {2x,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{8}\)

\(f(x) = \frac{|x|}{x}\)

Для кожної з функцій у Вправи 9 - 16 виконайте кожну з наступних завдань.

1. Створіть кускове визначення для даної функції, використовуючи техніку в Вправи 1 - 8 і Приклади 7 і 8 в оповіданні.
2. Слідуючи свинцю в прикладі 9 в оповіданні, використовуйте своє кускове визначення, щоб намалювати графік даної функції на аркуші графського паперу. Будь ласка, розмістіть кожну вправу на власну систему координат.

Вправа\(\PageIndex{9}\)

f (x) = |х−1|

Відповідь

\[f(x)=\left\{\begin{array}{ll}{-x+1,} & {\text { if } x<1} \\ {x-1,} & {\text { if } x \ge 1} \nonumber \end{array}\right.\]

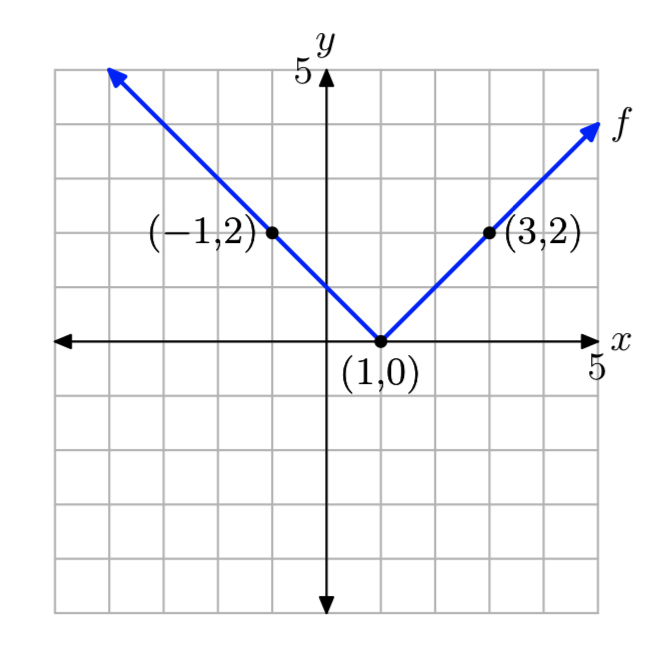
Вправа\(\PageIndex{10}\)

ф (х) = |х+2|

Вправа\(\PageIndex{11}\)

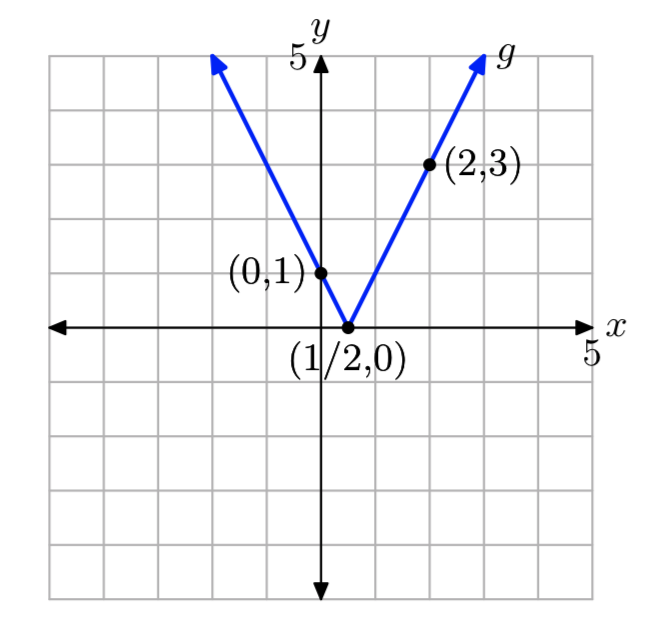
г (х) = |2х−1|

Відповідь

\[g(x)=\left\{\begin{array}{ll}{-2x+1,} & {\text { if } x<\frac{1}{2}} \\ {2x-1,} & {\text { if } x \ge \frac{1}{2}} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{12}\)

г (х) = |5−2х|

Вправа\(\PageIndex{13}\)

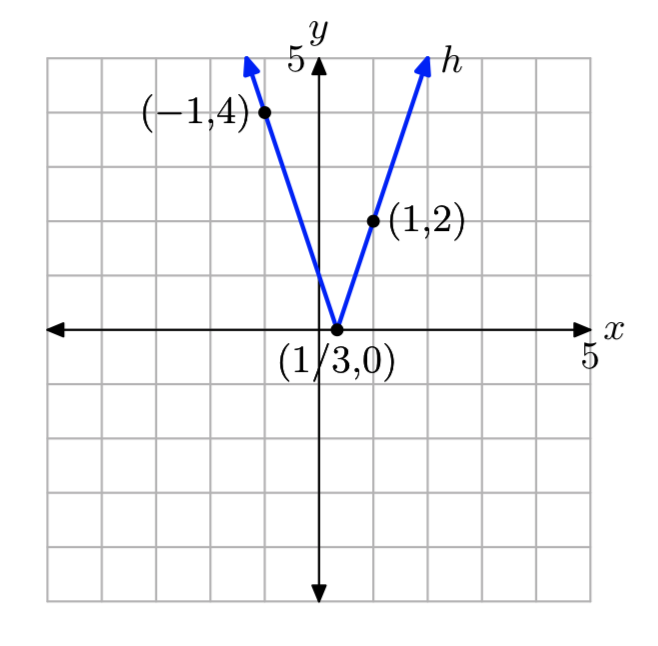
ч (х) = |1−3х|

Відповідь

\[h(x)=\left\{\begin{array}{ll}{1-3x,} & {\text { if } x<\frac{1}{3}} \\ {-1+3x,} & {\text { if } x \ge \frac{1}{3}} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{14}\)

ч (х) = |2х+1|

Вправа\(\PageIndex{15}\)

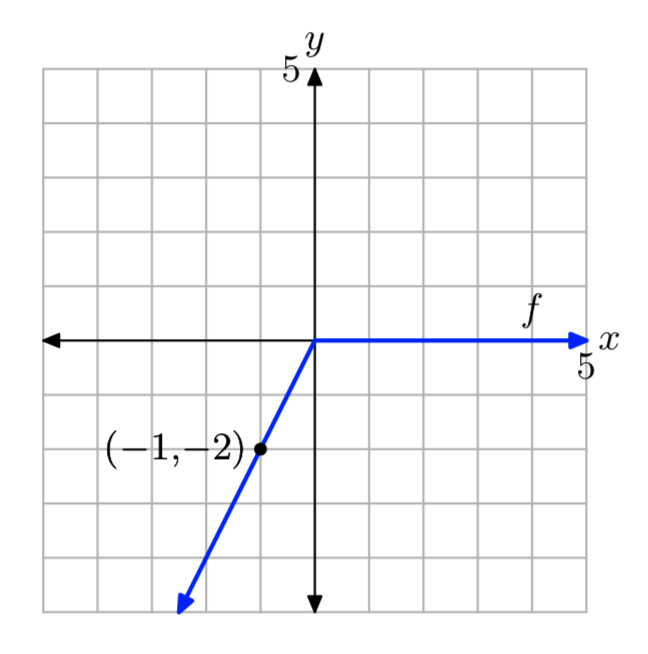
f (x) = x−|x|

Відповідь

\[f(x)=\left\{\begin{array}{ll}{2x,} & {\text { if } x<0} \\ {0,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

Вправа\(\PageIndex{16}\)

f (x) = х+|х−1|

Вправа\(\PageIndex{17}\)

Використовуйте графічний калькулятор, щоб намалювати графіки y = |x|, y = 2|x|, y = 3|x| та y = 4|x| у тому ж вікні перегляду. Своїми словами поясніть, що ви дізналися в цій вправі.

Відповідь

Множення на коефіцієнт a > 1, як у y = a|x|, розтягує графік y = |x| по вертикалі на коефіцієнт a Чим вище значення a, тим більше він розтягується по вертикалі.

Вправа\(\PageIndex{18}\)

Використовуйте графічний калькулятор, щоб намалювати графіки y = |x|, y = (1/2) |x|, y = (1/3) |x| та y = (1/4) |x| на одному оглядовому вікні. Своїми словами поясніть, що ви дізналися в цій вправі.

Вправа\(\PageIndex{19}\)

Використовуйте калькулятор графіків, щоб намалювати графіки y = |x|, y = |x−2|, y =|x−4| та y = |x−6| у одному вікні перегляду. Своїми словами поясніть, що ви дізналися в цій вправі.

Відповідь

Віднімання додатного значення a, як у y = |x−a|, зрушує графік a одиниць вправо.

Вправа\(\PageIndex{20}\)

Використовуйте графічний калькулятор, щоб намалювати графіки y = |x|, y = |x+2|, y = |x+4| та y = |x+6| у тому ж вікні перегляду. Своїми словами поясніть, що ви дізналися в цій вправі.

У Вправах 21 - 36 виконайте кожне з наступних завдань. Не соромтеся перевіряти свою роботу за допомогою графічного калькулятора, але ви повинні мати можливість виконувати всю роботу вручну.

1. Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь. Створіть точний графік функції y = |x| на вашій системі координат і позначте цей графік рівнянням.
2. Використовуйте техніку прикладів 12,13 та 14 в оповіданні, щоб допомогти вибрати відповідні геометричні перетворення для перетворення рівняння y = |x| у форму функції, наведеної у вправі. На тій самій системі координат використовуйте олівець або ручку іншого кольору, щоб намалювати графік функції, отриманої в результаті застосованого перетворення. Позначте отриманий графік його рівнянням.
3. Використовуйте інтервальне позначення для опису області та діапазону заданої функції.

Вправа\(\PageIndex{21}\)

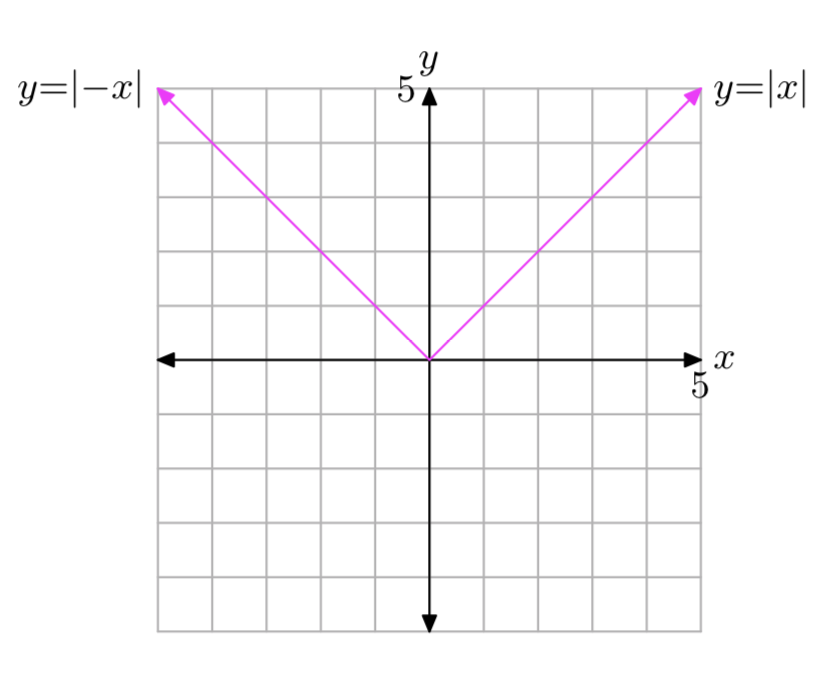
f (x) = |−х|

Відповідь

Графіки y = |x| і y = |−x| збігаються. Домен є\((−\infty, \infty)\) і діапазон є\([0, \infty)\).

Вправа\(\PageIndex{22}\)

f (x) = −|x|

Вправа\(\PageIndex{23}\)

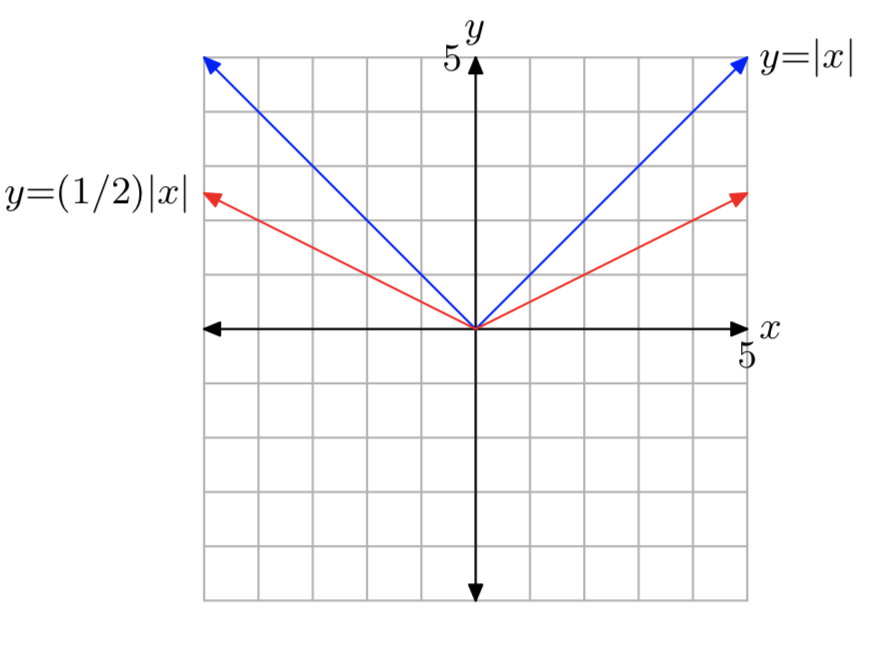
\(f(x) = \frac{1}{2}|x|\)

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\([0, \infty)\).

Вправа\(\PageIndex{24}\)

f (x) = −2|х|

Вправа\(\PageIndex{25}\)

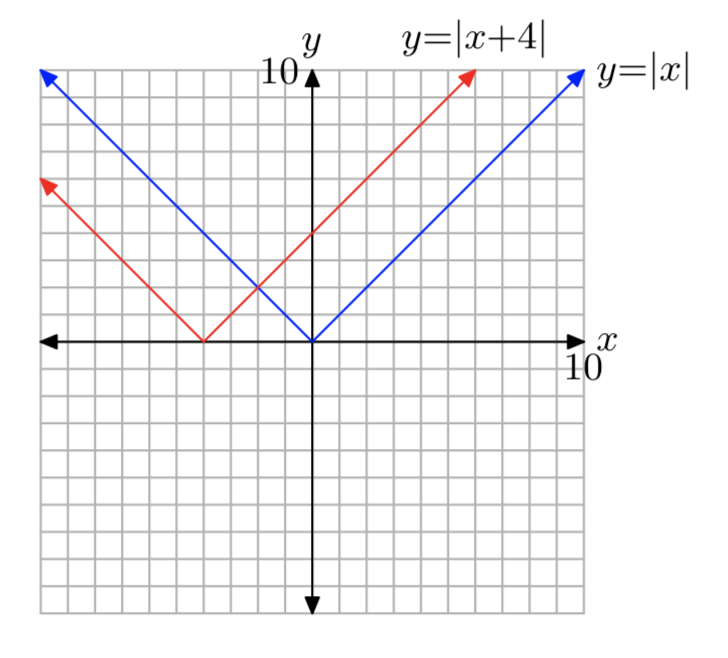
ф (х) = |х+4|

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\([0, \infty)\).

Вправа\(\PageIndex{26}\)

f (x) = |х−2|

Вправа\(\PageIndex{27}\)

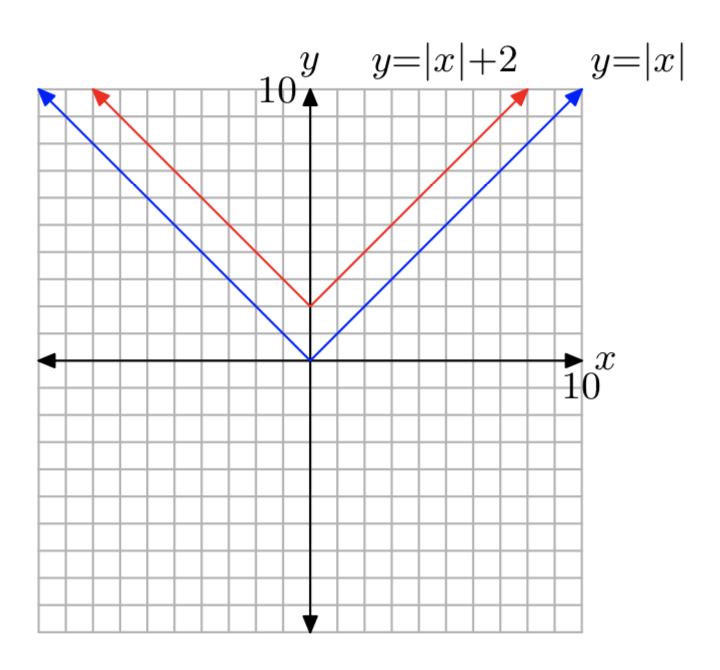
f (х) = |х|+2

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\([2, \infty)\).

Вправа\(\PageIndex{28}\)

f (x) = |х|−3

Вправа\(\PageIndex{29}\)

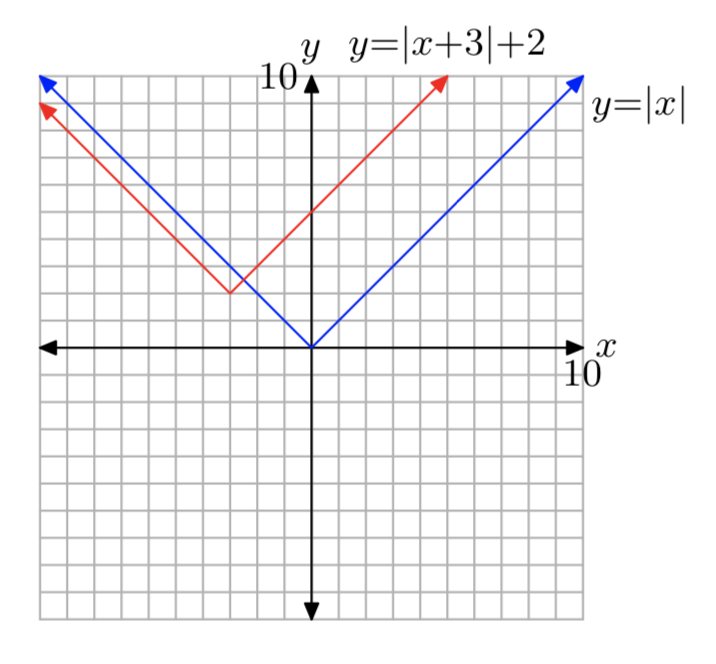
f (х) = |х+3|+2

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\([2, \infty)\).

Вправа\(\PageIndex{30}\)

f (x) = |х−3|−4

Вправа\(\PageIndex{31}\)

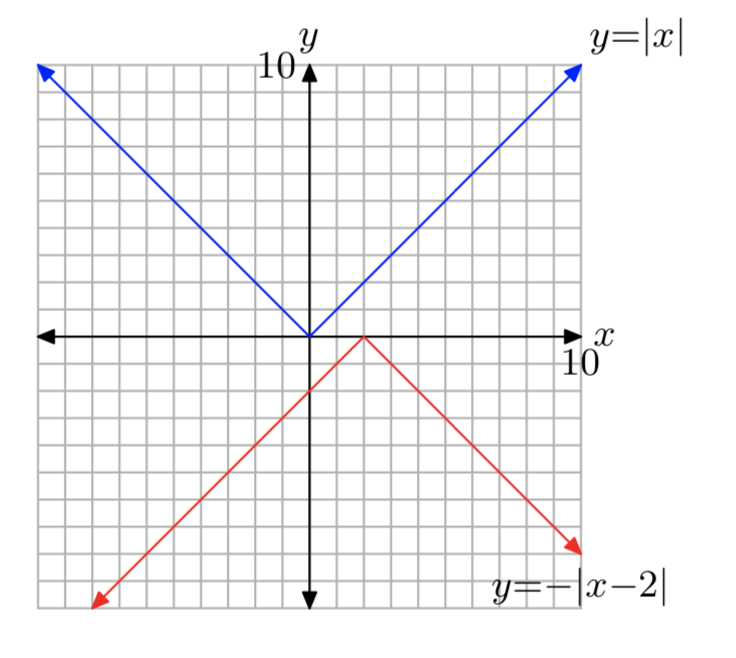
f (x) = −|х−2|

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\((−\infty, 0]\).

Вправа\(\PageIndex{32}\)

f (x) = −|х|−2

Вправа\(\PageIndex{33}\)

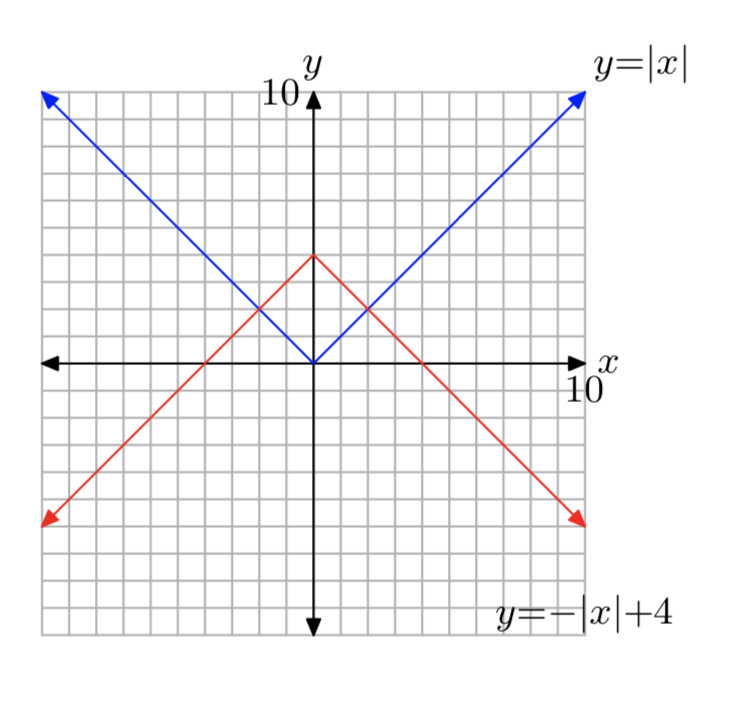
f (x) = −|х|+4

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\((−\infty, 4]\).

Вправа\(\PageIndex{34}\)

f (x) = −|х+4|

Вправа\(\PageIndex{35}\)

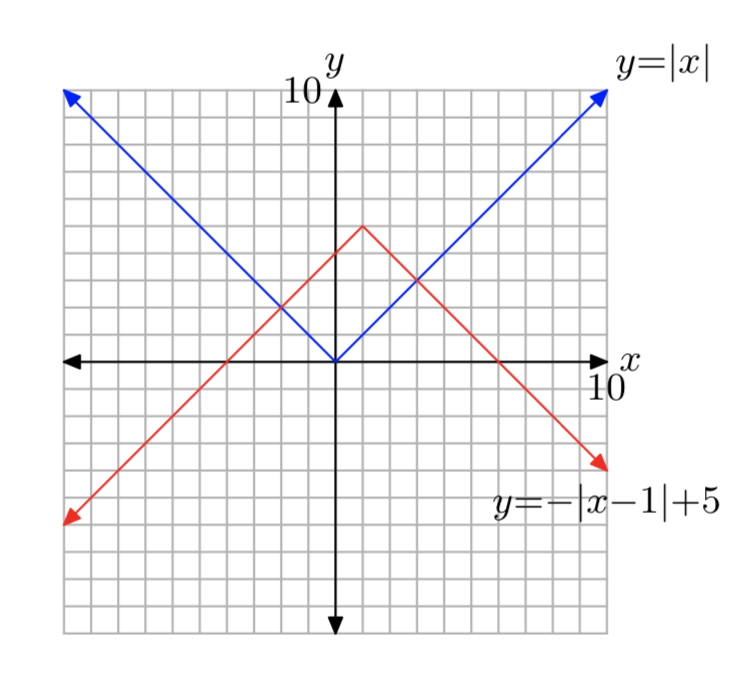
f (x) = −|х−1|+5

Відповідь

Домен є\((−\infty, \infty)\) і діапазон є\((−\infty, 5]\).

Вправа\(\PageIndex{36}\)

f (x) = −|х+5|+2