2.7: Інші типи рівнянь

Цілі навчання

• Розв'яжіть рівняння за участю раціональних показників.
• Вирішити рівняння за допомогою факторингу.
• Вирішити радикальні рівняння
• Вирішити рівняння абсолютних значень.
• Розв'яжіть інші типи рівнянь.

Ми розв'язували лінійні рівняння, раціональні рівняння та квадратні рівняння кількома методами. Однак існує багато інших типів рівнянь, і ми дослідимо ще кілька типів у цьому розділі. Ми розглянемо рівняння, що включають раціональні показники, поліноміальні рівняння, радикальні рівняння, рівняння абсолютної величини, рівняння в квадратичній формі та деякі раціональні рівняння, які можуть бути перетворені в квадратики. Однак рішення будь-якого рівняння використовує ті ж основні алгебраїчні правила. Ми вивчимо деякі нові методи, оскільки вони застосовуються до певних рівнянь, але алгебра ніколи не змінюється.

Розв'язування рівнянь за участю раціональних показників

Раціональні експоненти - це показники, які є дробами, де чисельник - це ступінь, а знаменник - корінь. Наприклад,${16}^{\tfrac{1}{2}}$ це ще один спосіб написання$\sqrt{16}$;$8^{\tfrac{1}{3}}$ це ще один спосіб написання$\sqrt[3]{8}$. Уміння працювати з раціональними показниками - корисний навик, оскільки він дуже застосуємо в обчисленні.

Ми можемо вирішити рівняння, в яких змінна піднімається до раціонального показника шляхом підняття обох сторін рівняння до зворотної показника. Причина, по якій ми піднімаємо рівняння до зворотного показника, полягає в тому, що ми хочемо усунути показник на змінному члені, і число, помножене на його взаємні рівні$1$. Наприклад,

$$\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber$$

$$3\left (\dfrac{1}{3} \right )=1, \nonumber$$

і так далі.

РАЦІОНАЛЬНІ ПОКАЗНИКИ

Раціональний показник вказує на ступінь в чисельнику і корінь в знаменнику. Існує кілька способів написання виразу, змінної або числа з раціональним показником:

$$a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m$$

Приклад$\PageIndex{1}$: Evaluating a Number Raised to a Rational Exponent

Оцінити$8^{\tfrac{2}{3}}$

Рішення

Чи беремо ми корінь першим або потужність спочатку залежить від числа. Легко знайти кубічний корінь$8$, тому перепишіть$8^{\tfrac{2}{3}}$ як${\left (8^{\tfrac{1}{3}} \right )}^2$.

$$\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}$$

Вправа$\PageIndex{1}$

Оцінити${64}^{-\tfrac{1}{3}}$

Відповідь

$\dfrac{1}{4}$

Приклад$\PageIndex{2}$: Solve the Equation Including a Variable Raised to a Rational Exponent

Розв'яжіть рівняння, в якому змінна підвищується до раціонального показника:$x^{\tfrac{5}{4}} = 32$.

Рішення

Спосіб видалення показника$x$ полягає в тому, щоб підняти обидві сторони рівняння до ступеня, яка є зворотною$\dfrac{5}{4}$, яка є$\dfrac{4}{5}$.

$$\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}$$

Вправа$\PageIndex{2}$

Розв'яжіть рівняння$x^{\tfrac{3}{2}} = 125$.

Відповідь

$25$

Приклад$\PageIndex{3}$: Solving an Equation Involving Rational Exponents and Factoring

Вирішити$3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}$.

Рішення

Це рівняння включає раціональні показники, а також факторинг раціональних показників. Давайте зробимо це по одному кроку за раз. Спочатку поставте змінні члени на одній стороні знака рівності і встановіть рівняння, рівне нулю.

$$\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}$$

Тепер, схоже, ми повинні враховувати ліву сторону, але що ми враховуємо? Ми завжди можемо врахувати термін з найнижчим показником. Перепишіть$x^{\tfrac{1}{2}}$ як$x^{\tfrac{2}{4}}$. Потім, фактор$x^{\tfrac{2}{4}}$ з обох термінів ліворуч.

$$\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}$$

Звідки$x^{\tfrac{1}{4}}$ взялися? Пам'ятайте, коли ми множимо два числа з однаковою базою, ми додаємо показники. Тому, якщо ми помножимо$x^{\tfrac{2}{4}}$ назад у використанні розподільної властивості, ми отримаємо вираз, який ми мали до факторингу, що і повинно статися. Нам потрібен показник такий, що при додаванні до$\dfrac{2}{4}$ рівних$\dfrac{3}{4}$. Таким чином, показник на$x$ в дужках є$\dfrac{1}{4}$.

Давайте продовжимо. Тепер ми маємо два множники і можемо використовувати теорему нульового фактора.

\ [\ почати {вирівнювати*}
x^ {\ tfrac {2} {4}}\ ліворуч (3x^ {\ tfrac {1} {4}} -1\ праворуч) &= 0\\
x^ {\ tfrac {2} {4}} &= 0\\ x&= 0\\

3x^ {\ tfrac {1} {4}} -1&= 0\\ x&= 0\\
3x^ {\ tfrac {1} {4}} -1&= 0\\ 3x^ {\ trac {1} {4}} &= 1\\
x^ {\ trac {1} {4}} &=\ dfrac {1} {3},\ qquad\ текст {Розділити обидві сторони на 3.} \\
{\ ліворуч (x^ {\ tfrac {1} {4}}\ праворуч)} ^4&= {\ ліворуч (\ dfrac {1} {3}\ праворуч)} ^4,\ qquad\ text

ParseError: EOF expected (click for details)

Callstack:
    at (Математика/Алгебра/Карта:_Коледж_алгебри_(OpenStax)/02:_Рівняння_та_нерівності/2.07:_Інші_типи_рівнянь), /content/body/div[2]/div[6]/div/p[9]/span, line 1, column 3

\]

Два рішення - це$0$ і$\dfrac{1}{81}$.

Вправа$\PageIndex{3}$

Вирішити:${\left(x+5\right)}^{\tfrac{3}{2}}=8$.

Відповідь

$-1$

Розв'язування рівнянь з використанням факторингу

Ми використовували факторинг для вирішення квадратних рівнянь, але це метод, який ми можемо використовувати з багатьма типами поліноміальних рівнянь, які є рівняннями, що містять рядок термінів, включаючи числові коефіцієнти та змінні. Коли ми стикаємося з рівнянням, що містить поліноми ступеня вище$2$, ми часто можемо вирішити їх шляхом факторингу.

РІВНЯННЯ ПОЛІНОМА

Многочлен ступеня$n$ - це вираз типу

$$a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0$$

де$n$ is a positive integer and $a_n ,…, a_0$ are real numbers and $a_n≠0$.

Встановлення многочлена, рівного нулю, дає поліноміальне рівняння. Загальна кількість розв'язків (дійсних і комплексних) поліноміального рівняння дорівнює найвищому показнику$n$.

Приклад$\PageIndex{4}$: Solving a Polynomial by Factoring

Розв'яжіть многочлен шляхом факторингу:$5x^4 = 80x^2$.

Рішення

Спочатку встановіть рівняння рівне нулю. Потім визначте, що є спільним для обох термінів, GCF.

$$\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}$$

Зверніть увагу, що у нас є різниця квадратів в$x^2−16$ коефіцієнті, який ми продовжимо множити і отримати два рішення. Перший термін генерує технічно два рішення, як показник є$2$, але вони є одним і тим же рішенням.$5x^2$

$$\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}$$

Розчини бувають$0$ (подвійне рішення)$4$, і$−4$.

Аналіз

Розв'язки ми можемо побачити на графіку на малюнку$\PageIndex{1}$. X-координати точок, де графік перетинає$x$ вісь - це рішення$x$ - перехоплення. Зверніть увагу на графіку, що у$0$ розв'язку графік торкається$x$ осі -і відскакує назад. Вона не перетинає$x$ -вісь. Це характерно для подвійних рішень.

Малюнок$\PageIndex{1}$

Вправа$\PageIndex{4}$

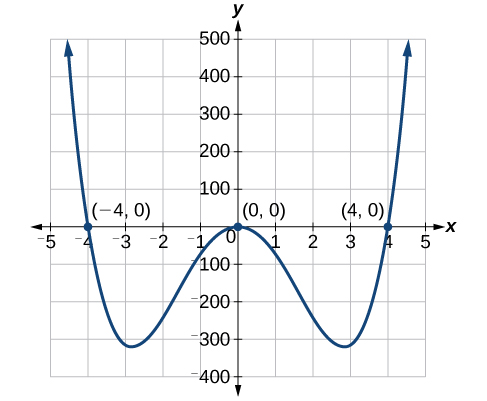
Вирішити шляхом факторингу:$12x^4 = 3x^2$.

Відповідь

$x=0, x=12, x=−12$

Приклад$\PageIndex{5}$: Solve a Polynomial by Grouping

Розв'яжіть многочлен шляхом групування:$x^3+x^2−9x−9=0$.

Рішення

Цей многочлен складається з$4$ термінів, які ми можемо вирішити шляхом групування. Процедури групування вимагають факторингу перших двох термінів, а потім факторингу останніх двох термінів. Якщо фактори в дужках ідентичні, ми можемо продовжити процес і вирішити, якщо не буде запропоновано більше факторингу.

$$\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}$$

Процес групування закінчується тут, оскільки ми можемо фактор,$x^2−9$ використовуючи формулу різниці квадратів.

$$\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}$$

Рішення є$3$$−3$, і$−1$. Зауважте, що найвищим показником є$3$ і ми отримали$3$ рішення. Ми можемо побачити рішення, X-перехоплення, на графіку на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$

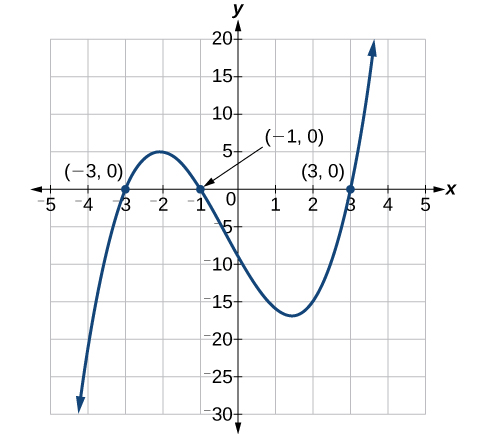
Аналіз

Ми розглянули рішення квадратичних рівнянь шляхом факторингу, коли провідний коефіцієнт є$1$. Коли провідного коефіцієнта немає$1$, ми вирішуємо групуванням. Для групування потрібні чотири члени, які ми отримали шляхом розщеплення лінійного члена квадратних рівнянь. Ми також можемо використовувати групування для деяких поліномів ступеня вище$2$, ніж, як ми бачили тут, оскільки було вже чотири члени.

Рішення радикальних рівнянь

Радикальні рівняння - це рівняння, які містять змінні в радиканді (вираз під радикальним символом), такі як

$$\sqrt{3x+18}=x \nonumber$$

$$\sqrt{x+3}=x-3 \nonumber$$

$$\sqrt{x+5}-\sqrt{x-3}=2 \nonumber$$

Радикальні рівняння можуть мати один або кілька радикальних членів, і вирішуються шляхом усунення кожного радикала по одному. Ми повинні бути обережними при вирішенні радикальних рівнянь, так як незвично знайти сторонні рішення, корені, які, по суті, не є розв'язками рівняння. Ці розв'язки не пов'язані з помилкою в методі розв'язання, а є результатом процесу підняття обох сторін рівняння до степеня. Однак перевірка кожної відповіді у вихідному рівнянні підтвердить справжні рішення.

РАДИКАЛЬНІ РІВняння

Рівняння, що містить члени зі змінною в радикані називається радикальним рівнянням.

Howto: З огляду на радикальне рівняння, розв'яжіть його

1. Виділяють радикальний вираз з одного боку знака рівності. Всі залишилися терміни покладіть на іншу сторону.
2. Якщо радикал - квадратний корінь, то квадрат обидві сторони рівняння. Якщо це кубічний корінь, то підніміть обидві сторони рівняння до третьої степені. Іншими словами, для$n^{th}$ кореневого радикала підніміть обидві сторони до$n^{th}$ влади. Це усуває радикальний символ.
3. Вирішити залишилося рівняння.
4. Якщо радикальний термін все ще залишається, повторіть кроки 1—2.
5. Підтвердіть розв'язки, підставивши їх у вихідне рівняння.

Приклад$\PageIndex{6}$: Solving an Equation with One Radical

Вирішити$\sqrt{15−2x}=x$.

Рішення

Радикал вже ізольований з лівого боку рівної сторони, тому приступайте до квадрату обидві сторони.

$$\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}$$

Ми бачимо, що решта рівняння є квадратичним. Встановіть його рівним нулю і вирішіть.

$$\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}$$

Запропонованими рішеннями є$−5$ і$3$. Давайте перевіримо кожне рішення назад у вихідному рівнянні. Спочатку перевірте$x=−5$.

$$\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}$$

Це стороннє рішення. Поки не було допущено жодної помилки при вирішенні рівняння, ми знайшли рішення, яке не задовольняє вихідному рівнянню.

Перевірте$x=3$.

$$\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}$$

Рішення є$3$.

Вправа$\PageIndex{5}$

Розв'яжіть радикальне рівняння:$\sqrt{x+3}=3x-1$

Відповідь

$x=1$, стороннє рішення$x=−\dfrac{2}{9}$

Приклад$\PageIndex{7}$: Solving a Radical Equation Containing Two Radicals

Вирішити$\sqrt{2x+3}+\sqrt{x-2}=4$

Рішення

Оскільки це рівняння містить два радикали, ми виділяємо один радикал, усуваємо його, а потім виділяємо другий радикал.

$$\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber$$

$$\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}$$

Використовуйте ідеальну формулу квадрата, щоб розширити праву сторону:${(a−b)}^2=a^2−2ab+b^2$.

$$\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}$$

Тепер, коли обидва радикали були усунені, встановіть квадратику рівну нулю і вирішіть.

$$\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}$$

Запропонованими рішеннями є$3$ і$83$. Перевірте кожне рішення у вихідному рівнянні.

$$\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}$$

Одним з рішень є$3$.

Перевірте$x=83$.

$$\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}$$

Єдине рішення - це$3$. Ми бачимо, що$x=83$ це стороннє рішення.

Вправа$\PageIndex{6}$

Розв'яжіть рівняння двома радикалами:$\sqrt{3x+7}+\sqrt{x+2}=1$

Відповідь

$x=−2$, стороннє рішення$x=−1$

Розв'язування рівняння абсолютного значення

Далі ми навчимося вирішувати рівняння абсолютного значення. Щоб вирішити таке рівняння$|2x−6|=8$, як, ми помічаємо, що абсолютне значення буде дорівнює,$8$ якщо величина всередині барів абсолютного значення дорівнює$8$ або$−8$. Це призводить до двох різних рівнянь, які ми можемо вирішити самостійно.

$$\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}$$

АБО

$$\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}$$

Знати, як вирішувати проблеми, пов'язані з функціями абсолютних значень, корисно. Наприклад, нам може знадобитися визначити числа або точки на лінії, які знаходяться на певній відстані від заданої контрольної точки.

РІВНЯННЯ АБСОЛЮТНОГО ЗНАЧЕННЯ

Абсолютна величина$x$ записується як$|x|$. Він володіє наступними властивостями:

Якщо$x≥0$, то$|x|=x$ .If$x<0$, то$x=−x$.

Для дійсних чисел$A$ і$B$, рівняння виду$|A|=B$, з$B≥0$, матиме рішення коли$A=B$ або$A=−B$. Якщо$B<0$, рівняння не$|A|=B$ має розв'язку.

Рівняння абсолютного значення у вигляді$|ax+b|=c$ має такі властивості:

• Якщо$c<0$, не$|ax+b|=c$ має рішення.
• Якщо$c=0$,$|ax+b|=c$ є одне рішення.
• Якщо$c>0$,$|ax+b|=c$ має два рішення.

Як

Задано рівняння абсолютного значення, розв'яжіть його.

1. Виділіть вираз абсолютного значення на одній стороні знака рівності.
2. Якщо$c>0$, запишіть і вирішите два рівняння:$ax+b=c$ і$ax+b=−c$.

Приклад$\PageIndex{8}$: Solving Absolute Value Equations

Вирішіть наступні рівняння абсолютних значень:

1. $|6x+4|=8$
2. $|3x+4|=−9$
3. $|3x−5|−4=6$
4. $|−5x+10|=0$

Рішення

1. $|6x+4|=8$

Напишіть два рівняння і вирішіть кожне:

$$\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}$$

АБО

$$\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}$$

Два рішення - це$\dfrac{2}{3}$ і$−2$.

2. $|3x+4|=−9$

Рішення не існує, оскільки абсолютне значення не може бути від'ємним.

3. $|3x−5|−4=6$

Виділіть вираз абсолютного значення, а потім запишіть два рівняння.

$$\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}$$

АБО

$$\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}$$

Є два рішення:$5$, і$-\dfrac{5}{3}$.

4. $|−5x+10|=0$

Рівняння встановлюється рівним нулю, тому ми повинні написати тільки одне рівняння.

$$\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}$$

Є одне рішення:\ (2\).

Вправа$\PageIndex{7}$

Розв'яжіть рівняння абсолютного значення:$|1−4x|+8=13$.

Відповідь

$x=−1, x=\dfrac{3}{2}$

Розв'язування інших типів рівнянь

Існує багато інших типів рівнянь на додаток до тих, які ми обговорювали досі. Ми побачимо більше їх у всьому тексті. Тут ми обговоримо рівняння, що знаходяться в квадратичній формі, і раціональні рівняння, що призводять до квадратичного.

Розв'язування рівнянь у квадратичній формі

Рівняння в квадратичній формі - це рівняння з трьома долями. Перший термін має силу, відмінну від$2$. Середній термін має показник, який є половиною показника провідного терміну. Третій термін - константа. Ми можемо розв'язувати рівняння в такому вигляді так, ніби вони квадратичні. Кілька прикладів цих рівнянь включають$x^4−5x^2+4=0$,$x^6+7x^3−8=0$, і$x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0$. У кожному з них подвоєння показника середнього члена дорівнює показнику на провідному терміні. Ми можемо вирішити ці рівняння, підставивши змінну на середній член.

КВАДРАТИЧНА ФОРМА

Якщо показник середнього члена дорівнює половині показника на провідному члені, ми маємо рівняння в квадратичній формі, яке ми можемо вирішити так, ніби це квадратичне. Підставляємо змінну для середнього члена для розв'язання рівнянь у квадратичній формі.

Howto: З огляду на квадратне рівняння за формою, розв'яжіть його

1. Визначте показник на провідному терміні та визначте, чи є він подвійним показником у середньостроковій перспективі.
2. Якщо це так, підставити змінну$u$, наприклад, для змінної частини середнього члена.
3. Перепишіть рівняння так, щоб воно прийняло стандартну форму квадратики.
4. Вирішуйте, використовуючи один із звичайних методів розв'язування квадратичного.
5. Замініть змінну підстановки початковим терміном.
6. Вирішити залишилося рівняння.

Приклад$\PageIndex{9}$: Solving a Fourth-degree Equation in Quadratic Form

Розв'яжіть це рівняння четвертого ступеня:$3x^4−2x^2−1=0$.

Рішення

Це рівняння відповідає основним критеріям, що влада на провідному члені вдвічі більша за владу на середньостроковій. Далі ми зробимо підстановку змінного члена посередині. Нехай$u =x^2$. Перепишіть рівняння в$u$.

$$3u^2−2u−1=0 \nonumber$$

Тепер вирішуйте квадратичну.

$$\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}$$

Вирішіть кожен фактор і замініть початковий термін для$u$.

$$\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}$$

Рішення є$x=±i\sqrt{\dfrac{1}{3}}$ і$x=±1$

Вправа$\PageIndex{8}$

Вирішити за допомогою підміни:$x^4−8x^2−9=0$.

Відповідь

$x=−3,3,−i,i$

Приклад$\PageIndex{10}$: Solving an Equation in Quadratic Form Containing a Binomial

Розв'яжіть рівняння в квадратичному вигляді:${(x+2)}^2+11(x+2)−12=0$.

Рішення

Це рівняння містить біноміал замість єдиної змінної. Тенденція полягає в розширенні того, що представлено. Однак визнання того, що він відповідає критеріям знаходження в квадратичній формі, робить все різниця в процесі вирішення. Спочатку зробіть заміну, здаючи в оренду$u =x+2$. Потім перепишіть рівняння в$u$.

$$\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}$$

Вирішіть, використовуючи властивість нульового фактора, а потім замініть$u$ оригінальним виразом.

$$\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}$$

Другий фактор призводить до

$$\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}$$

У нас є два рішення:$−14$, і$−1$.

Вправа$\PageIndex{9}$

Вирішити:${(x−5)}^2−4(x−5)−21=0$.

Відповідь

$x=2,x=12$

Розв'язування раціональних рівнянь, що призводять до квадратичного

Раніше ми вирішували раціональні рівняння. Іноді рішення раціонального рівняння призводить до квадратичного. Коли це станеться, ми продовжуємо рішення, спрощуючи квадратне рівняння одним із методів, які ми бачили. Може виявитися, що рішення немає.

Приклад$\PageIndex{11}$: Solving a Rational Equation Leading to a Quadratic

Вирішіть наступне раціональне рівняння:$\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}$

Рішення

Ми хочемо, щоб усі знаменники у факторованій формі знайшли РК-дисплей. Два знаменники не можуть бути враховані далі. Однак,$x^2−1=(x+1)(x−1)$. Потім, РК-дисплей є$(x+1)(x−1)$. Далі множимо все рівняння на РК-дисплей.

\ [\ почати {вирівнювати*} (x+1) (x-1)\ ліворуч (\ dfrac {-4x} {x-1} +\ dfrac {4} {x+1}\ праворуч) &=\ ліворуч (\ dfrac {-8} {x^2-1}\ праворуч) (x+1) (x-1)\ -4x (x+1) +4 (x-1) +4 (x-1) +4 (x-1) &= -8\\ -4x^2-4x+4x-4&= -8\\ -4x^2+4&= 0\\\
-4 (х ^ 2-1) &= 0\\ -4 (х+1) (x-1) &= 0\\ x &= -1\\ x & = 1\ кінець {вирівняй*}\]

У цьому випадку будь-яке рішення дає нуль у знаменнику у вихідному рівнянні. Таким чином, рішення не існує.

Вправа$\PageIndex{10}$

Вирішити$\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}$

Відповідь

$x=−1, x= 0$це не рішення.

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з різними типами рівнянь.

1. Раціональне рівняння без розв'язку
2. Розв'язування рівнянь з раціональними показниками з використанням взаємних ступенів
3. Розв'язування радикальних рівнянь частина 1 з 2
4. Розв'язування радикальних рівнянь частина 2 з 2

Ключові концепції

• Раціональні показники можуть бути переписані декількома способами в залежності від того, що найбільш зручно для проблеми. Для розв'язання обидві сторони рівняння піднімаються до степеня, яка надасть показник на змінній рівній$1$. Див. розділ Приклад, Приклад та Приклад.
• Факторинг поширюється на поліноми вищого порядку, коли він передбачає факторинг GCF або факторинг шляхом групування. Див. Приклад і Приклад.
• Ми можемо розв'язати радикальні рівняння, ізолюючи радикал і піднімаючи обидві сторони рівняння до потужності, яка відповідає індексу. Див. Приклад і Приклад.
• Щоб розв'язати рівняння абсолютних значень, нам потрібно написати два рівняння, одне для додатного значення і одне для від'ємного значення. Див. Приклад.
• Рівняння в квадратичній формі легко помітити, оскільки показник на першому члені вдвічі перевищує показник другого члена, а третій член - константа. Ми також можемо побачити біноміальне замість однієї змінної. Використовуємо підміну для вирішення. Див. Приклад і Приклад.
• Розв'язування раціонального рівняння також може призвести до квадратного рівняння або рівняння в квадратичній формі. Див. Приклад.