1.1: Огляд функцій
- Page ID
- 62355
- Використовуйте функціональні позначення для оцінки функції.
- Визначте область і діапазон функції.
- Намалюйте графік функції.
- Знайти нулі функції.
- Розпізнати функцію з таблиці значень.
- Створюйте нові функції з двох або більше заданих функцій.
- Опишіть властивості симетрії функції.
У цьому розділі ми надаємо формальне визначення функції та розглянемо декілька способів представлення функцій, а саме через таблиці, формули та графіки. Вивчаються формальні позначення та терміни, пов'язані з функціями. Визначено склад функцій та властивості симетрії. Більшість цього матеріалу буде для вас оглядом, але він служить зручною довідкою, щоб нагадати вам про деякі алгебраїчні прийоми, корисні для роботи з функціями.
Функції
Задано дві\(A\)\(B\) множини та множина з елементами, які\(x\) є впорядкованими парами,\((x,y)\) де елемент\(A\) і\(y\)\(B,\) є елементом - це відношення від\(A\) до\(B\). Відношення від\(A\) до\(B\) визначає зв'язок між цими двома множинами. Функція - це особливий тип зв'язку, при якому кожен елемент першої множини пов'язаний рівно з одним елементом другого множини. Елемент першого множини називається вхідним; елемент другого множини називається виходом. Функції використовуються весь час в математиці для опису зв'язків між двома множинами. Для будь-якої функції, коли ми знаємо вхід, визначається вихід, тому ми говоримо, що вихід є функцією входу. Наприклад, площа квадрата визначається його довжиною сторони, тому ми говоримо, що площа (вихід) є функцією його довжини сторони (вхід). Швидкість кулі, кинутого в повітря, може бути описана як функція кількості часу, коли м'яч знаходиться в повітрі. Вартість розсилки посилки - це функція ваги посилки. Оскільки функції мають так багато застосувань, важливо мати точні визначення та термінологію для їх вивчення.

Функція\(f\) складається з набору входів, набору виходів і правила призначення кожного входу рівно одному виводу. Безліч входів називається доменом функції. Безліч виходів називається діапазоном функції.
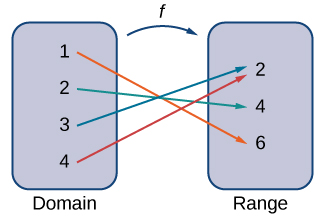
Наприклад, розглянемо функцію\(f\), де домен - це набір всіх дійсних чисел і правило полягає в квадраті вхідних даних. Потім вхід\(x=3\) призначається виводу\(3^2=9\).
Оскільки кожне невід'ємне дійсне число має дійсний квадратний корінь, кожне невід'ємне число є елементом діапазону цієї функції. Оскільки немає дійсного числа з квадратом, який є негативним, негативні дійсні числа не є елементами діапазону. Зроблено висновок, що діапазон є множиною невід'ємних дійсних чисел.
Для загальної функції\(f\) з доменом\(D\) ми часто використовуємо для\(x\) позначення вхідних даних і\(y\) для позначення вихідних даних, пов'язаних з\(x\). При цьому ми називаємо незалежну змінну і\(y\) як залежну змінну, оскільки вона залежить від\(x\).\(x\) Використовуючи позначення функції, ми пишемо\(y=f(x)\), і читаємо це рівняння як «\(y\)дорівнює\(f\)»\(x.”\) Для описаної раніше функції квадратури ми пишемо\(f(x)=x^2\).
Поняття функції можна візуалізувати за допомогою Figures\(\PageIndex{1}\) -\(\PageIndex{3}\).
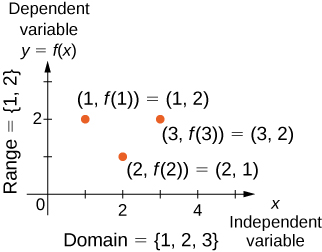
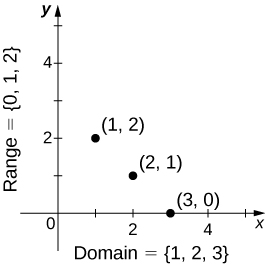
Ми також можемо візуалізувати функцію шляхом побудови точок\((x,y)\) в координатній площині де\(y=f(x)\). Графік функції - це множина всіх цих точок. Для прикладу розглянемо функцію\(f\), де домен - це безліч,\(D=\{1,2,3\}\) а правило -\(f(x)=3−x\). На\(\PageIndex{4}\) малюнку ми будуємо графік цієї функції.
Кожна функція має домен. Однак іноді функція описується рівнянням, як у\(f(x)=x^2\), без вказаної конкретної області. При цьому домен приймається за набір всіх дійсних чисел,\(x\) для яких\(f(x)\) є дійсним числом. Наприклад, оскільки будь-яке дійсне число може бути зведене в квадрат, якщо не вказано іншого домену, ми вважаємо домен to набором всіх дійсних чисел.\(f(x)=x^2\) З іншого боку, функція квадратного кореня дає реальний результат\(f(x)=\sqrt{x}\) лише у тому випадку, якщо він\(x\) невід'ємний. Тому область функції\(f(x)=\sqrt{x}\) - це множина невід'ємних дійсних чисел, іноді званих природним доменом.
Для функцій\(f(x)=x^2\) і\(f(x)=\sqrt{x}\), доменів є множини з нескінченною кількістю елементів. Зрозуміло, що ми не можемо перерахувати всі ці елементи. При описі множини з нескінченною кількістю елементів часто корисно використовувати set-builder або інтервальні позначення. При використанні позначення set-builder для опису підмножини всіх дійсних чисел, що позначаються\(R\), пишемо
\[\{x\,|\,\textit{x has some property}\}. \nonumber \]
Ми читаємо це як набір дійсних чисел,\(x\) таких, що\(x\) має деяку властивість. Наприклад, якби нас зацікавив набір дійсних чисел, які більше одиниці, але менше п'яти, ми могли б позначити цей набір, використовуючи нотації set-builder шляхом написання
\[\{x\,|\,1<x<5\}.\nonumber \]
Такий набір, як this, який містить всі числа більше\(a\) і менше, також\(b,\) можна позначити за допомогою інтервальних позначень\((a,b)\). Тому,
\[(1,5)=\{x\,|\,1<x<5\}.\nonumber \]
Цифри\(1\) і\(5\) називаються кінцевими точками цієї множини. Якщо ми хочемо розглянути набір, який включає кінцеві точки, ми б позначили цей набір, написавши
\[[1,5]=\{x\,|\,1 \le x \le 5\}.\nonumber \]
Ми можемо використовувати подібні позначення, якщо хочемо включити одну з кінцевих точок, але не іншу. Для позначення множини невід'ємних дійсних чисел ми використали б позначення set-builder
\[\{x\,|\,x\ge 0\}.\nonumber \]
Найменше число в цьому наборі дорівнює нулю, але цей набір не має найбільшого числа. Використовуючи інтервальне позначення, ми б використали символ,\(∞,\) який посилається на позитивну нескінченність, і ми б написали набір як
\[[0,∞)=\{x\,|\,x\ge 0\}.\nonumber \]
Важливо відзначити, що\(∞\) це не реальне число. Тут символічно використовується для позначення того, що цей набір включає всі дійсні числа, більші або рівні нулю. Аналогічно, якби ми хотіли описати набір всіх непозитивних чисел, ми могли б написати
\[(−∞,0]=\{x\,|\,x≤0\}.\nonumber \]
Тут позначення\(−∞\) відноситься до негативної нескінченності, і це вказує на те, що ми включаємо всі числа менше або рівні нулю, незалежно від того, наскільки малі. Набір
\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\nonumber \]
відноситься до множини всіх дійсних чисел. Деякі функції визначаються за допомогою різних рівнянь для різних частин їх області. Ці типи функцій відомі як кусково визначені функції. Наприклад, припустимо, ми хочемо визначити функцію\(f\) з доменом, який є множиною всіх дійсних чисел, таких, що\(f(x)=3x+1\) for\(x≥2\) і\(f(x)=x^2\) for\( x<2\). Позначимо цю функцію записом
\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\nonumber \]
При оцінці цієї функції для вхідних даних рівняння\(x\), яке слід використовувати, залежить від того, чи є\(x≥2\) чи\(x<2\). Наприклад, так як\(5>2\), ми використовуємо той факт, що\(f(x)=3x+1\) для\(x≥2\) і бачимо, що\(f(5)=3(5)+1=16\). З іншого боку, для\(x=−1\), ми використовуємо той факт, що\(f(x)=x^2\) для\(x<2\) і бачимо, що\(f(−1)=1\).
Для функції\(f(x)=3x^2+2x−1\) оцініть:
- \(f(−2)\)
- \(f(\sqrt{2})\)
- \(f(a+h)\)
Рішення
Підставляємо задане значення для\(x\) у формулу для\(f(x)\).
- \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
- \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
- \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)
Для\(f(x)=x^2−3x+5\), оцінити\(f(1)\) і\(f(a+h)\).
- Підказка
-
\(1\)Підставляємо і\(a+h\) для\(x\) в формулі для\(f(x)\).
- Відповідь
-
\(f(1)=3 \)і\(f(a+h)=a^2+2ah+h^2−3a−3h+5\)
Для кожної з наступних функцій визначте i. домен і ii. діапазон.
- \(f(x)=(x−4)^2+5\)
- \(f(x)=\sqrt{3x+2}−1\)
- \(f(x)=\dfrac{3}{x−2}\)
Рішення
а. розглянути\(f(x)=(x−4)^2+5.\)
1. Оскільки\(f(x)=(x−4)^2+5\) є дійсним числом для будь-якого дійсного числа\(x\), домен\(f\) - це інтервал\((−∞,∞)\).
2. Так як\((x−4)^2≥0\), ми знаємо\(f(x)=(x−4)^2+5≥5\). Тому діапазон повинен бути підмножиною\(\{y\,|\,y≥5\}.\) Щоб показати, що кожен елемент у цьому наборі знаходиться в діапазоні, ми повинні показати, що для даного\(y\) в цьому наборі, є дійсне число\(x\) таке, що\(f(x)=(x−4)^2+5=y\). Вирішуючи це рівняння,\(x,\) ми бачимо, що нам потрібно\(x\) таке, що
\((x−4)^2=y−5.\)
Це рівняння задовольняється до тих пір, поки існує дійсне число\(x\) таке, що
\(x−4=±\sqrt{y−5}\)
Так як\(y≥5\), квадратний корінь чітко виражений. Ми робимо висновок, що для\(x=4±\sqrt{y−5},\)\(f(x)=y,\) і, отже, діапазон\(\{y\,|\,y≥5 \}.\)
б) Розглянемо\(f(x)=\sqrt{3x+2}−1\).
1. Щоб знайти домен\(f\), нам знадобиться вираз\(3x+2≥0\). Вирішуючи цю нерівність, робимо висновок, що доменом є\(\{x\,|\,x≥−2/3\}.\)
2. Щоб знайти діапазон\(f\), відзначимо, що з\(\sqrt{3x+2}≥0,\)\(f(x)=\sqrt{3x+2}−1≥−1\). Тому діапазон\(f\) повинен бути підмножиною множини\(\{y\,|\,y≥−1\}\). Щоб показати, що кожен елемент у цьому наборі знаходиться в діапазоні\(f\), ми повинні показати, що для всіх\(y\) в цьому наборі, існує дійсне число\(x\) в домені такий, що\(f(x)=y.\) Нехай\(y≥−1.\) Тоді,\(f(x)=y\) якщо і тільки якщо
\(\sqrt{3x+2}−1=y.\)
Вирішуючи це рівняння,\(x,\) ми бачимо, що\(x\) має вирішити рівняння
\(\sqrt{3x+2}=y+1.\)
Так як\(y≥−1\), таке\(x\) могло існувати. Квадратуючи обидві сторони цього рівняння, ми маємо\(3x+2=(y+1)^2.\)
Тому нам потрібно
\(3x=(y+1)^2−2,\)
що має на увазі
\(x=\frac{1}{3}(y+1)^2−\frac{2}{3}.\)
Нам просто потрібно перевірити, що\(x\) знаходиться в домені\(f\). Оскільки домен\(f\) складається з усіх дійсних чисел, більших або рівних\(\frac{−2}{3}\), і
\(\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3},\)
існує\(x\) в домені домену\(f\). Робимо висновок, що діапазон\(f\)\(\{y\,|\,y≥−1\}.\)
c Розглянемо\(f(x)=\dfrac{3}{x−2}.\)
1. Оскільки\(3/(x−2)\) визначається, коли знаменник ненульовий, домен\(\{x\,|\,x≠2\}.\)
2. Щоб знайти діапазон\(f,\) нам потрібно знайти значення\(y\) таких, що існує дійсне число\(x\) в домені з властивістю, яка
\(\dfrac{3}{x−2}=y.\)
Вирішуючи це рівняння,\(x,\) ми знаходимо, що
\(x=\dfrac{3}{y}+2.\)
Тому до тих пір\(y≠0\), поки існує дійсне число\(x\) в домені таке, що\(f(x)=y\). Таким чином, діапазон\(\{y\,|\,y≠0\}.\)
Пошук домену та діапазону для\(f(x)=\sqrt{4−2x}+5.\)
- Підказка
-
Використання\(4−2x≥0\).
- Відповідь
-
Домен =\(\{x\,|\,x≤2\}\) і діапазон =\(\{y\,|\,y≥5\}\)
Представлення функцій
Як правило, функція представлена за допомогою одного або декількох таких інструментів:
- Стіл
- Графік
- Формула
Ми можемо визначити функції в кожній формі, але ми також можемо використовувати їх разом. Наприклад, ми можемо побудувати на графіку значення з таблиці або створити таблицю з формули.
Столи
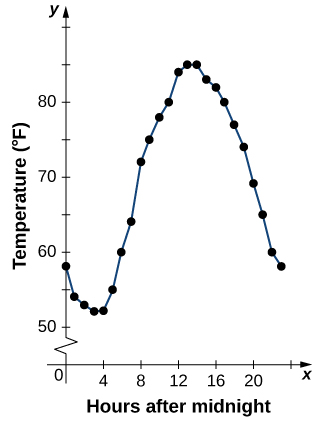
Функції, описані за допомогою таблиці значень, часто виникають у реальних додатках. Розглянемо наступний простий приклад. Ми можемо описати температуру в даний день як функцію часу доби. Припустимо, ми записуємо температуру щогодини протягом 24-годинного періоду, починаючи з півночі. Ми дозволяємо нашій вхідній змінній\(x\) бути час після півночі, вимірюється в годинами, а вихідна\(y\) змінна - температура\(x\) годин після півночі, виміряна в градусах Фаренгейта. Записуємо наші дані в табл\(\PageIndex{1}\).
| Година після півночі | Температура (° F) | Година після півночі | Температура (° F) |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
З таблиці видно, що температура - це функція часу, а температура зменшується, то збільшується, а потім знову зменшується. Однак ми не можемо отримати чітке уявлення про поведінку функції без її графіків.
Графіки
З огляду на функцію,\(f\) описану таблицею, ми можемо надати наочну картину функції у вигляді графіка. Графік температур, перелічених у таблиці,\(\PageIndex{1}\) може дати нам краще уявлення про їх коливання протягом дня. \(\PageIndex{5}\)На малюнку показаний графік температурної функції.
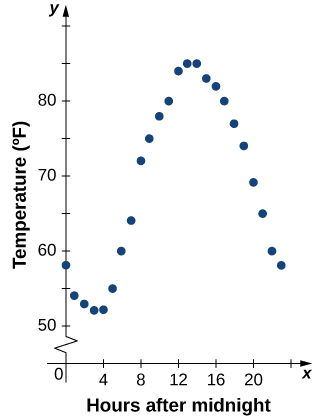
З точок, нанесених на графіку на малюнку\(\PageIndex{5}\), ми можемо візуалізувати загальну форму графіка. Часто корисно з'єднати точки на графіку, які представляють дані з таблиці. У цьому прикладі, хоча ми не можемо зробити жодного остаточного висновку щодо того, якою була температура в будь-який час, для якого температура не була зафіксована, враховуючи кількість зібраних точок даних та закономірність у цих точках, розумно підозрювати, що температури в інший час слідували за аналогічний візерунок, як ми бачимо на малюнку\(\PageIndex{6}\).
Алгебраїчні формули
Іноді нам не дають значення функції в табличній формі, скоріше нам дають значення в явній формулі. Формули виникають у багатьох додатках. Наприклад, площа кола радіуса\(r\) задається за формулою\(A(r)=πr^2\). Коли об'єкт викидається вгору від землі з початковою швидкістю\(v_{0}\) ft/s, його висота над землею з моменту його викидання до моменту його потрапляння на землю задається формулою\(s(t)=−16t^2+v_{0}t\). Коли\(P\) долари інвестуються на рахунок за річною процентною\(r\) ставкою, що збільшується безперервно, сума грошей через\(t\) роки дається за формулою\(A(t)=Pe^{rt}\). Алгебраїчні формули є важливими інструментами для обчислення значень функцій. Часто ми також представляємо ці функції візуально у вигляді графіка.
Дано алгебраїчну формулу для функції\(f\), графом\(f\) є множина точок\((x,f(x))\), де\(x\) знаходиться в області\(f\) і\(f(x)\) знаходиться в діапазоні. Для побудови графіка функції, заданої формулою, корисно почати з використання формули для створення таблиці входів і виходів. Якщо домен\(f\) складається з нескінченної кількості значень, ми не можемо перерахувати їх усі, але оскільки перерахування деяких входів та виходів може бути дуже корисним, це часто хороший спосіб почати.
Створюючи таблицю входів і виходів, ми зазвичай перевіряємо, чи є нуль виходом. Ті значення\(x\) де\(f(x)=0\) називаються нулями функції. Наприклад, нулі від\(f(x)=x^2−4\) є\(x=±2\). Нулі визначають, де графік\(f\) перетинає\(x\) -вісь, що дає нам більше інформації про форму графіка функції. Графік функції ніколи не може перетинатися з\(x\) -віссю, або вона може перетинатися кілька (або навіть нескінченно багато) разів.
Ще однією точкою інтересу є\(y\) -перехоплення, якщо він існує. \(y\)-Перехоплення задається\((0,f(0))\).
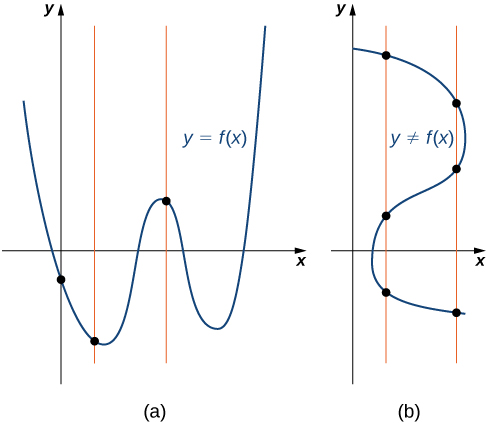
Оскільки функція має рівно один вихід для кожного входу, графік функції може мати, максимум, один\(y\) -перехоплення. Якщо\(x=0\) знаходиться в області функції,\(f,\) то\(f\) має рівно один\(y\) -перехоплення. Якщо не\(x=0\) знаходиться в домені,\(f,\) то не\(f\) має\(y\) -перехоплення. Аналогічно, для будь-якого дійсного числа,\(c,\) якщо\(c\) знаходиться в області\(f\), є рівно один вихід\(f(c),\) і лінія\(x=c\) перетинає графік\(f\) рівно один раз. З іншого боку, якщо не\(c\) знаходиться в області не визначено і лінія\(x=c\) не перетинається з графіком\(f\).\(f,\)\(f(c)\) Ця властивість підсумовується в тесті вертикальної лінії.
Задана функція\(f\), кожна вертикальна лінія, яка може бути намальована, перетинає графік\(f\) не більше одного разу. Якщо будь-яка вертикальна лінія перетинає безліч точок більше одного разу, множина точок не представляє функції.
Ми можемо використовувати цей тест, щоб визначити, чи є набір побудованих точок графіком функції (рис.\(\PageIndex{7}\)).
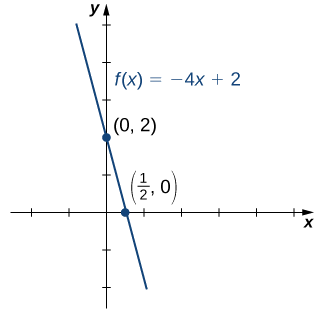
Розглянемо функцію\(f(x)=−4x+2.\)
- Знайти всі нулі\(f\).
- Знайти\(y\) -перехоплення (якщо є).
- Намалюйте графік\(f\).
Рішення
1. Щоб знайти нулі, вирішуйте\(f(x)=−4x+2=0\). Ми виявляємо, що\(f\) має один нуль при\(x=1/2\).
2. \(y\)-Перехоплення задається\((0,f(0))=(0,2).\)
3. Враховуючи, що\(f\) є лінійною функцією форми,\(f(x)=mx+b\) яка проходить через точки\((1/2,0)\) і\((0,2)\), можна накидати графік\(f\) (рис.\(\PageIndex{8}\)).
Розглянемо функцію\(f(x)=\sqrt{x+3}+1\).
- Знайти всі нулі\(f\).
- Знайти\(y\) -перехоплення (якщо є).
- Намалюйте графік\(f\).
Рішення
1. Щоб знайти нулі, вирішуйте\(\sqrt{x+3}+1=0\). Це рівняння має на увазі\(\sqrt{x+3}=−1\). Так як\(\sqrt{x+3}≥0\) для всіх\(x\) це рівняння не має розв'язків, а тому не\(f\) має нулів.
2.The\(y\) -перехоплення дається\((0,f(0))=(0,\sqrt{3}+1)\).
3. Для графіка цієї функції складаємо таблицю значень. Так як нам потрібно\(x+3≥0\), нам потрібно вибирати значення\(x≥−3\). Ми вибираємо значення, які полегшують оцінку функції квадратного кореня.
| \(x\) | -3 | -2 | 1 |
|---|---|---|---|
| \(f(x)\) | 1 | 2 | 3 |
Використовуючи таблицю і знаючи, що, оскільки функція є квадратним коренем, графік\(f\) повинен бути схожий на графік\(y=\sqrt{x}\), ми накидаємо графік (рис.\(\PageIndex{9}\)).
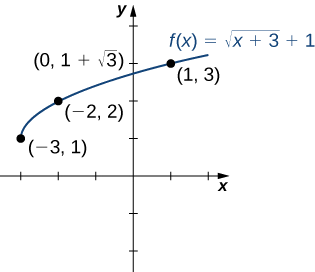
Знайти нулі\(f(x)=x^3−5x^2+6x.\)
- Підказка
-
Фактор многочлена.
- Відповідь
-
\(x=0,2,3\)
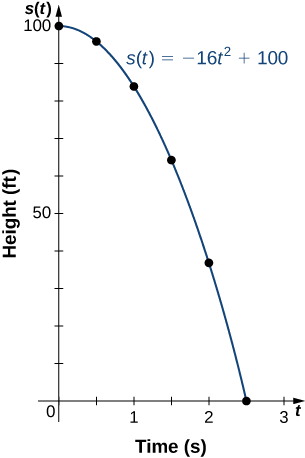
Якщо м'яч скидається з висоти 100 футів, його висота s в час\(t\) задається функцією\(s(t)=−16t^2+100\), де s вимірюється в футах і\(t\) вимірюється в секундах. Домен обмежений інтервалом,\([0,c],\) де\(t=0\) час падіння м'яча і час, коли м'яч\(t=c\) потрапляє на землю.
- Створіть таблицю із зазначенням висоти s (t), коли\(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\) і\(2.5\). Використовуючи дані з таблиці, визначте домен для цієї функції. Тобто знайти час,\(c\) коли м'яч вдариться об землю.
- Намалюйте графік\(s\).
Рішення
| \(t\) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| \(s(t)\) | 100 | 96 | 84 | 64 | 36 | 0 |
Так як м'яч б'є об землю коли\(t=2.5\), доменом цієї функції є інтервал\([0,2.5]\).
2.
Ми говоримо, що функція\(f\) збільшується на інтервалі,\(I\) якщо для всіх\(x_{1},\, x_{2}∈I,\)
\(f(x_{1})≤f(x_{2})\)коли\(x_{1}<x_{2}.\)
Ми говоримо\(f\) строго збільшується на інтервалі,\(I\) якщо для всіх\(x_{1},x_{2}∈I,\)
\(f(x_{1})<f(x_{2})\)коли\(x_{1}<x_{2}.\)
Ми говоримо, що функція\(f\) зменшується на інтервалі,\(I\) якщо для всіх\(x_{1},x_{2}∈I,\)
\(f(x_{1})≥f(x_{2})\)якщо\(x_{1}<x_{2}.\)
Ми говоримо, що функція\(f\) строго зменшується на інтервалі\(I\) якщо для всіх\(x_{1},x_{2}∈I\),
\(f(x_{1})>f(x_{2})\)якщо\(x_{1}<x_{2}.\)
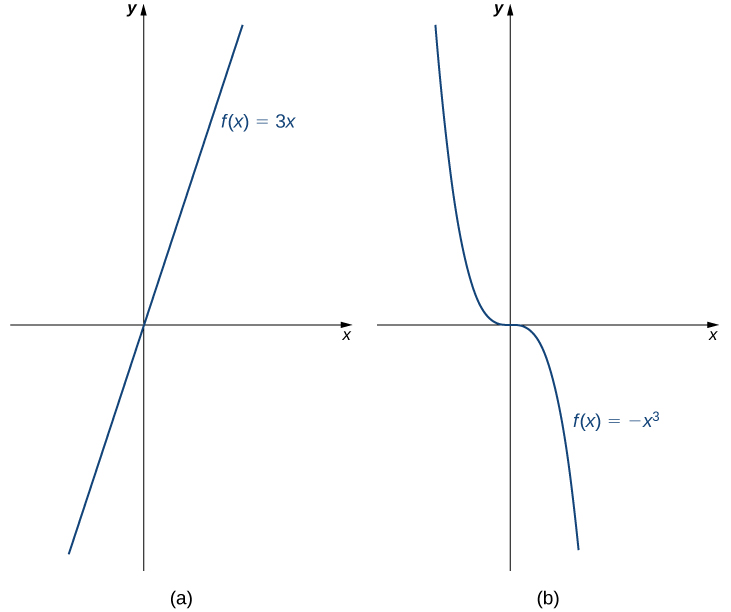
Наприклад, функція\(f(x)=3x\) збільшується на інтервалі,\((−∞,∞)\) тому що\(3x_{1}<3x_{2}\) коли завгодно\(x_{1}<x_{2}\). З іншого боку, функція\(f(x)=−x^3\) зменшується на інтервалі,\((−∞,∞)\) тому що\(−x^3_{1}>−x^3_{2}\) всякий раз\(x_{1}<x_{2}\) (рис.\(\PageIndex{10}\)).
Поєднання функцій
Тепер, коли ми розглянули основні характеристики функцій, ми можемо побачити, що відбувається з цими властивостями, коли ми поєднуємо функції по-різному, використовуючи основні математичні операції для створення нових функцій. Наприклад, якщо вартість компанії на виготовлення\(x\) предметів описується функцією,\(C(x)\) а виручка, створювана реалізацією\(x\) предметів, описується функцією\(R(x)\), то прибуток від виготовлення і продажу\(x\) предметів визначається як\(P(x)=R(x)−C(x)\). Використовуючи різницю між двома функціями, ми створили нову функцію.
Крім того, ми можемо створити нову функцію, склавши дві функції. Наприклад, з урахуванням функцій\(f(x)=x^2\) і\(g(x)=3x+1\), складена функція\(f∘g\) визначається таким чином, що
\[(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2. \nonumber \]
Композитна функція\(g∘f\) визначається таким чином, що
\[(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1. \nonumber \]
Зверніть увагу, що ці дві нові функції відрізняються один від одного.
Поєднання функцій з математичними операторами
Для об'єднання функцій за допомогою математичних операторів ми просто запишемо функції з оператором і спрощуємо. З огляду на дві функції\(f\) і\(g\), ми можемо визначити чотири нові функції:
| \((f+g)(x)=f(x)+g(x)\) | Сума |
| \((f−g)(x)=f(x)−g(x)\) | Різниця |
| \((f·g)(x)=f(x)g(x)\) | Продукт |
| \((\frac{f}{g})(x)=\frac{f(x)}{g(x)}\)для\(g(x)≠0\) | Частка |
З огляду на функції\(f(x)=2x−3\) і\(g(x)=x^2−1\), знайти кожну з наступних функцій і вказати її область.
- \((f+g)(x)\)
- \((f−g)(x)\)
- \((f·g)(x)\)
- \(\left(\dfrac{f}{g}\right)(x)\)
Рішення
1. \((f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.\)
Доменом цієї функції є інтервал\((−∞,∞)\).
2. \((f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.\)
Доменом цієї функції є інтервал\((−∞,∞)\).
3. \((f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.\)
Доменом цієї функції є інтервал\((−∞,∞)\).
4. \(\left(\dfrac{f}{g}\right)(x)=\dfrac{2x−3}{x^2−1}\).
Доменом цієї функції є\(\{x\,|\,x≠±1\}.\)
Для\(f(x)=x^2+3\) і\(g(x)=2x−5\), знайти\((f/g)(x)\) і вказати його домен.
- Підказка
-
Нова функція\((f/g)(x)\) є часткою двох функцій. Для яких значень\(x\) знаходить знаменник нуль?
- Відповідь
-
\(\left(\dfrac{f}{g}\right)(x)=\frac{x^2+3}{2x−5}.\)Домен\(\{x\,|\,x≠\frac{5}{2}\}.\)
Функція Склад
Коли ми складаємо функції, ми приймаємо функцію функції. Наприклад, припустимо, що температура\(T\) в даний день описується як функція часу\(t\) (вимірюється в годинами після півночі), як в табл\(\PageIndex{1}\). Припустимо\(C\), вартість, щоб обігріти або охолодити будівлю за 1 годину, можна описати як функцію температури\(T\). Поєднуючи ці дві функції, ми можемо описати витрати на опалення або охолодження будівлі як функцію часу шляхом оцінки\(C(T(t))\). Ми визначили нову функцію, позначену\(C∘T\), яка визначається таким чином, що\((C∘T)(t)=C(T(t))\) для всіх\(t\) в області\(T\). Ця нова функція називається складовою функцією. Зауважимо, що оскільки вартість - це функція температури, а температура - це функція часу, має сенс визначити цю нову функцію\((C∘T)(t)\). Це не має сенсу розглядати\((T∘C)(t)\), тому що температура не є функцією вартості.
Розглянемо функцію\(f\) з доменом\(A\) і діапазоном\(B\), а функцію\(g\) з доменом\(D\) і діапазоном\(E\). Якщо\(B\) є підмножиною\(D\), то складеною функцією\((g∘f)(x)\) є функція з областю\(A\) такої, що
\[(g∘f)(x)=g(f(x)) \nonumber \]
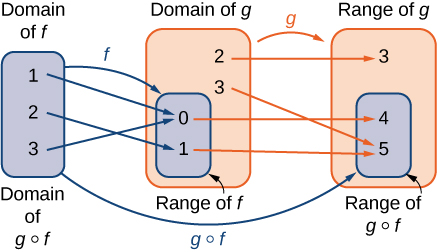
Складену функцію\(g∘f\) можна переглянути в два етапи. По-перше, функція\(f\) відображає кожен вхід\(x\) в області\(f\) до його виходу\(f(x)\) в діапазоні\(f\). По-друге, оскільки діапазон\(f\) є підмножиною області\(g\), вихід\(f(x)\) є елементом в області\(g\), і тому він зіставляється на вихід\(g(f(x))\) в діапазоні\(g\). На малюнку\(\PageIndex{11}\) ми бачимо наочне зображення складеної функції.
Розглянемо функції\(f(x)=x^2+1\) і\(g(x)=1/x\).
- Знайдіть\((g∘f)(x)\) і вкажіть його домен і діапазон.
- Оцінити\((g∘f)(4),\)\((g∘f)(−1/2)\).
- Знайдіть\((f∘g)(x)\) і вкажіть його домен і діапазон.
- Оцінити\((f∘g)(4),\)\((f∘g)(−1/2)\).
Рішення
1. Ми можемо знайти формулу для\((g∘f)(x)\) двома різними способами. Ми могли б написати
\((g∘f)(x)=g(f(x))=g(x^2+1)=\dfrac{1}{x^2+1}\).
Як варіант, ми могли б написати
\((g∘f)(x)=g(f(x))=\dfrac{1}{f(x)}=\dfrac{1}{x^2+1}.\)
Оскільки\(x^2+1≠0\) для всіх дійсних\(x,\) чисел домен\((g∘f)(x)\) - це набір всіх дійсних чисел. Так як\(0<1/(x^2+1)≤1\), діапазон - це, максимум, інтервал\((0,1]\). Щоб показати, що діапазон - це весь цей інтервал, ми дозволяємо\(y=1/(x^2+1)\) і вирішуємо це рівняння,\(x\) щоб показати\((0,1]\), що для всіх\(y\) в інтервалі існує дійсне число\(x\) таке, що\(y=1/(x^2+1)\). Вирішуючи це рівняння\(x^2+1=1/y\),\(x,\) ми бачимо, що
\(x=±\sqrt{\frac{1}{y}−1}\)
Якщо\(y\) знаходиться в інтервалі\((0,1]\), вираз під радикалом є невід'ємним, і тому існує дійсне число\(x\) таке, що\(1/(x^2+1)=y\). Робимо висновок, що діапазон\(g∘f\) - це інтервал\((0,1].\)
2. \((g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\)
\((g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)
3. Ми можемо знайти формулу для двома\((f∘g)(x)\) способами. По-перше, ми могли б написати
\((f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.\)
Як варіант, ми могли б написати
\((f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.\)
Домен\(f∘g\) - це сукупність всіх дійсних чисел,\(x\) таких, що\(x≠0\). Щоб знайти діапазон,\(f,\) нам потрібно знайти всі значення,\(y\) для яких існує дійсне число\(x≠0\) таке, що
\(\left(\dfrac{1}{x}\right)^2+1=y.\)
Вирішуючи це рівняння,\(x,\) ми бачимо, що нам потрібно\(x\) задовольнити
\(\left(\dfrac{1}{x}\right)^2=y−1,\)
що спрощує
\(\dfrac{1}{x}=±\sqrt{y−1}\)
Нарешті, отримуємо
\(x=±\dfrac{1}{\sqrt{y−1}}.\)
Оскільки\(1/\sqrt{y−1}\) є дійсним числом тоді і тільки тоді\(y>1,\), коли діапазон\(f\) є встановленим\(\{y\,|\,y≥1\}.\)
4. \((f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\)
\((f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5\)
У\(\PageIndex{7}\) прикладі ми бачимо, що\((f∘g)(x)≠(g∘f)(x)\). Це говорить нам, в загальних рисах, що порядок, в якому ми складаємо функції, має значення.
Нехай\(f(x)=2−5x\). Дозвольте\(g(x)=\sqrt{x}.\) знайти\((f∘g)(x)\).
Рішення
\((f∘g)(x)=2−5\sqrt{x}.\)
Розглянемо функції\(f\) і\(g\) описуємо
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
| \(x\) | -4 | -2 | 0 | 2 | 4 |
|---|---|---|---|---|---|
| \(g(x)\) | 1 | 0 | 3 | 0 | 5 |
- Оцініть\((g∘f)(3)\),\((g∘f)(0)\).
- Вказати домен і діапазон домену\((g∘f)(x)\).
- Оцініть\((f∘f)(3)\),\((f∘f)(1)\).
- Вказати домен і діапазон домену\((f∘f)(x)\).
Рішення:
1. \((g∘f)(3)=g(f(3))=g(−2)=0\)
\((g∘f)(0)=g(4)=5\)
2. Домен\(g∘f\) - це набір\(\{−3,−2,−1,0,1,2,3,4\}.\) Оскільки діапазон\(f\) - це набір\(\{−2,0,2,4\},\), діапазон\(g∘f\) - це набір\(\{0,3,5\}.\)
3. \((f∘f)(3)=f(f(3))=f(−2)=4\)
\((f∘f)(1)=f(f(1))=f(−2)=4\)
4. Домен\(f∘f\) - це набір\(\{−3,−2,−1,0,1,2,3,4\}.\) Оскільки діапазон\(f\) - це набір\(\{−2,0,2,4\},\), діапазон\(f∘f\) - це набір\(\{0,4\}.\)
Магазин рекламує продаж 20% від усіх товарів. Керолайн має купон, який дає їй право на додаткову знижку 15% на будь-який товар, включаючи товари для продажу. Якщо Керолайн вирішить придбати товар з початковою ціною\(x\) доларів, скільки вона в кінцевому підсумку заплатить, якщо застосує свій купон до ціни продажу? Вирішити цю задачу можна за допомогою складеної функції.
Рішення
Оскільки ціна продажу становить 20% від початкової ціни, якщо товар є\(x\) доларами, його ціна продажу визначається\(f(x)=0.80x\). Оскільки купон дає право фізичній особі на 15% від ціни будь-якого товару, якщо товар є\(y\) доларами, ціна, після застосування купона, дається g (y) = 0.85y. Тому, якщо ціна спочатку\(x\) долари, її ціна продажу буде,\(f(x)=0.80x\) а потім остаточна ціна після купона буде\(g(f(x))=0.85(0.80x)=0.68x\).
Якщо товари продаються за 10% від початкової ціни, а клієнт має купон на додаткову знижку 30%, якою буде остаточна ціна товару, який спочатку становить\(x\) долари, після застосування купона до ціни продажу?
Підказка
Ціна продажу товару з початковою ціною\(x\) доларів становить\(f(x)=0.90x\). Купонна ціна на товар, який є\(y\) доларами, становить\(g(y)=0.70y\).
Рішення
\((g∘f)(x)=0.63x\)
Симетрія функцій
Графіки певних функцій мають властивості симетрії, які допомагають нам зрозуміти функцію та форму її графіка. Для прикладу розглянемо функцію,\(f(x)=x^4−2x^2−3\) зображену на малюнку\(\PageIndex{12a}\). Якщо взяти частину кривої, яка лежить праворуч від\(y\) -осі, і перевернути її над\(y\) -вісь, вона лежить точно на вершині кривої зліва від\(y\) -осі. У цьому випадку ми говоримо, що функція має симетрію щодо\(y\) -осі. З іншого боку, розглянемо функцію,\(f(x)=x^3−4x\) показану на малюнку\(\PageIndex{12b}\). Якщо ми візьмемо графік і\(180°\) повернемо його навколо початку, новий графік буде виглядати точно так само. У цьому випадку ми говоримо, що функція має симетрію щодо походження.
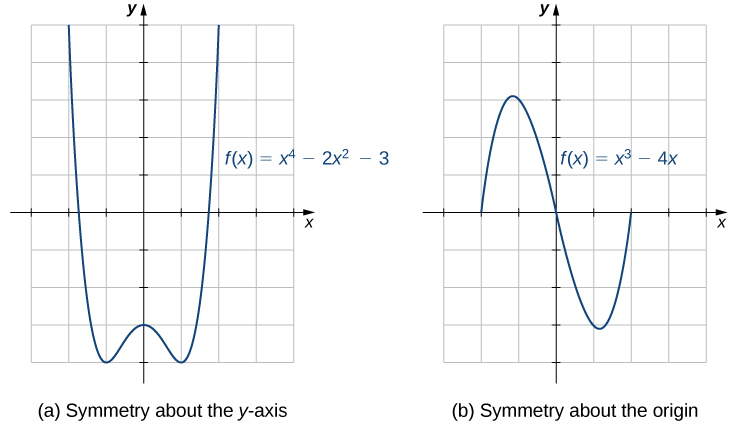
Якщо нам задано графік функції, то легко побачити, чи має графік одну з цих властивостей симетрії. Але без графіка, як ми можемо алгебраїчно визначити, чи\(f\) має функція симетрію? Подивившись на Малюнок\(\PageIndex{12a}\) знову, ми бачимо,\(f\) що оскільки симетрична щодо\(y\) -осі, якщо точка\((x,y)\) знаходиться на графіку, точка\((−x,y)\) знаходиться на графіку. Іншими словами,\(f(−x)=f(x)\). Якщо функція\(f\) має цю властивість, ми говоримо, що\(f\) це парна функція, яка має симетрію щодо\(y\) -осі. Наприклад,\(f(x)=x^2\) це навіть тому, що
\(f(−x)=(−x)^2=x^2=f(x).\)
На відміну від цього,\(\PageIndex{12b}\) знову подивившись на малюнок, якщо функція\(f\) симетрична щодо початку, то всякий раз, коли точка\((x,y)\) знаходиться на графіку, точка також\((−x,−y)\) знаходиться на графіку. Іншими словами,\(f(−x)=−f(x)\). Якщо\(f\) має цю властивість, ми говоримо, що\(f\) це непарна функція, яка має симетрію щодо походження. Наприклад,\(f(x)=x^3\) це непарно, тому що
\(f(−x)=(−x)^3=−x^3=−f(x).\)
- Якщо\(f(x)=f(−x)\) для всіх\(x\) в області\(f\), то\(f\) є парна функція. Парна функція симетрична щодо\(y\) -осі.
- Якщо\(f(−x)=−f(x)\) для всіх\(x\) в області\(f\), то\(f\) є непарною функцією. Непарна функція симетрична щодо походження.
Визначте, чи є кожна з наступних функцій парною, непарною чи ні.
- \(f(x)=−5x^4+7x^2−2\)
- \(f(x)=2x^5−4x+5\)
- \(f(x)=\frac{3x}{x^2+1}\)
Рішення
Щоб визначити, парна чи непарна функція, оцінюємо\(f(−x)\) і порівняємо її з\(f(x)\) і\(−f(x)\).
1. \(f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x).\)Тому\(f\) є рівним.
2. \(f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5.\)Тепер,\(f(−x)≠f(x).\) Крім того, зазначивши\(−f(x)=−2x^5+4x−5\), що, ми бачимо, що\(f(−x)≠−f(x)\). Тому не\(f\) буває ні парним, ні непарним.
3. \(f(−x)=3(−x)/((−x)2+1)\)\(=−3x/(x^2+1)=\)\(−[3x/(x^2+1)]=−f(x).\)Тому\(f\) це непарно.
\(f(x)=4x^3−5x\)Визначте, парне, непарне чи ні.
- Підказка
-
Порівняйте\(f(−x)\) з\(f(x)\) і\(−f(x)\).
- Відповідь
-
\(f(x)\)непарний.
Однією симетричною функцією, яка виникає часто, є функція абсолютного значення, записана як\(|x|\). Функція абсолютного значення визначається як
\[f(x)=\begin{cases} -x, & \text{if }x<0 \\ x, & \text{if } x≥0 \end{cases} \nonumber \]
Деякі студенти описують цю функцію, заявляючи, що вона «робить все позитивним». За визначенням функції абсолютного значення ми бачимо, що якщо\(x<0\), то\(|x|=−x>0,\) і якщо\(x>0\), то\(|x|=x>0.\) Однак, для\(x=0,\)\(|x|=0.\) Тому точніше сказати, що для всіх ненульових входів вихід позитивний, а якщо\(x=0\), вихід\(|x|=0\). Зроблено висновок, що діапазон функції абсолютного значення дорівнює\(\{y\,|\,y≥0\}.\) На рис.\(\PageIndex{13}\), Ми бачимо, що функція абсолютного значення симетрична щодо\(y\) -осі і тому є парною функцією.
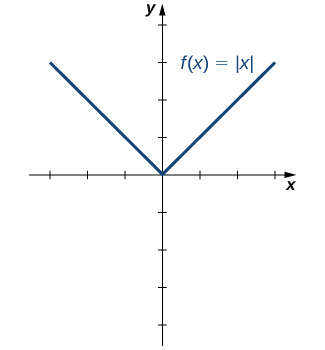
Знайдіть домен і діапазон функції\(f(x)=2|x−3|+4\).
Рішення
Оскільки функція абсолютного значення визначена для всіх дійсних чисел, область цієї функції є\((−∞,∞)\). Так як\(|x−3|≥0\) для всіх\(x\) функція\(f(x)=2|x−3|+4≥4\). Тому діапазон є, максимум, набір\(\{y\,|\,y≥4\}.\) Щоб побачити, що діапазон, по суті, весь цей набір, нам потрібно показати, що для\(y≥4\) існує дійсне число\(x\) таке, що
\(2|x−3|+4=y\)
Справжнє число\(x\) задовольняє цьому рівнянню до тих пір, поки
\(|x−3|=\frac{1}{2}(y−4)\)
Оскільки\(y≥4\), ми знаємо\(y−4≥0\), і, таким чином, права частина рівняння невід'ємна, тому цілком можливо, що є рішення. Крім того,
\(|x−3|=\begin{cases} −(x−3), & \text{if } x<3\\x−3, & \text{if } x≥3\end{cases}\)
Тому ми бачимо, що є два рішення:
\(x=±\frac{1}{2}(y−4)+3\).
Діапазон дії цієї функції дорівнює\(\{y\,|\,y≥4\}.\)
Для функції\(f(x)=|x+2|−4\) знайдіть домен і діапазон.
- Підказка
-
\(|x+2|≥0\)для всіх дійсних чисел\(x\).
- Відповідь
-
Домен =\((−∞,∞)\), діапазон =\(\{y\,|\,y≥−4\}.\)
Ключові поняття
- Функція - це відображення з набору входів до набору виходів з рівно одним виходом для кожного входу.
- Якщо для функції не вказано жодного\(y=f(x),\) домену, домен вважається множиною всіх дійсних чисел,\(x\) для яких визначена функція.
- Під час ескізу графіка функції\(f,\) кожна вертикальна лінія може перетинати графік, максимум, один раз.
- Функція може мати будь-яку кількість нулів, але вона має, максимум, один\(y\) -перехоплення.
- Щоб визначити склад\(g∘f\), діапазон\(f\) повинен міститися в області\(g\).
- Парні функції симетричні щодо\(y\) -осі, тоді як непарні функції симетричні щодо походження.
Ключові рівняння
- Склад двох функцій
\((g∘f)(x)=g\big(f(x)\big)\)
- Функція абсолютного значення
\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
Глосарій
- функція абсолютного значення
- \(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
- композитна функція
- задано дві функції\(f\) і\(g\), нова функція, позначається\(g∘f\), така, що\((g∘f)(x)=g(f(x))\)
- зменшення на інтервалі\(I\)
- функція, що зменшується на інтервалі\(I\) if, для всіх\(x_1,\,x_2∈I,\;f(x_1)≥f(x_2)\) if\(x_1<x_2\)
- залежна змінна
- вихідна змінна для функції
- домен
- набір входів для функції
- парна функція
- функція навіть якщо\(f(−x)=f(x)\) для всіх\(x\) у домені\(f\)
- функція
- набір входів, набір виходів і правило для відображення кожного входу рівно до одного виходу
- граф функції
- множина\((x,y)\) таких точок, що\(x\) знаходиться в області\(f\) і\(y=f(x)\)
- збільшення на інтервалі\(I\)
- функція, що збільшується на інтервалі\(I\) if для всіх\(x_1,\,x_2∈I,\;f(x_1)≤f(x_2)\) if\(x_1<x_2\)
- незалежна змінна
- вхідна змінна для функції
- непарна функція
- функція непарна, якщо\(f(−x)=−f(x)\) для всіх\(x\) в області\(f\)
- діапазон
- набір виходів для функції
- симетрія про походження
- графік функції\(f\) симетричний щодо походження, якщо\((−x,−y)\) знаходиться на графіку кожного разу,\(f\) коли\((x,y)\) знаходиться на графіку
- симетрія навколо\(y\) -осі
- графік функції\(f\) симетричний щодо\(y\) -осі, якщо\((−x,y)\) знаходиться на графіку кожного разу,\(f\) коли\((x,y)\) знаходиться на графіку
- таблиця значень
- таблиця, що містить список входів і відповідних їм виходів
- тест вертикальної лінії
- враховуючи графік функції, кожна вертикальна лінія перетинає графік, максимум, один раз
- нулі функції
- коли\(x\) дійсне число дорівнює нулю функції\(f,\;f(x)=0\)
