2.5: Вертикальні перетворення

Last updated
Save as PDF

Page ID: 58162

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми вивчаємо мистецтво перетворень: масштабування, рефлексії та переклади. Ми обмежимо свою увагу перетвореннями у вертикальному або y-напрямку. Наша мета - застосувати певні перетворення до рівняння функції, а потім запитати, який вплив воно має на графіку функції.

Ми починаємо наше завдання з прикладу, який вимагає, щоб ми прочитали графік функції, щоб захопити кілька ключових точок, які лежать на графіку функції.

Приклад$\PageIndex{1}$

Розглянемо графік f, представлений на малюнку$\PageIndex{1}$ (а). Використовуйте графік f, щоб заповнити таблицю на малюнку$\PageIndex{1}$ (b).

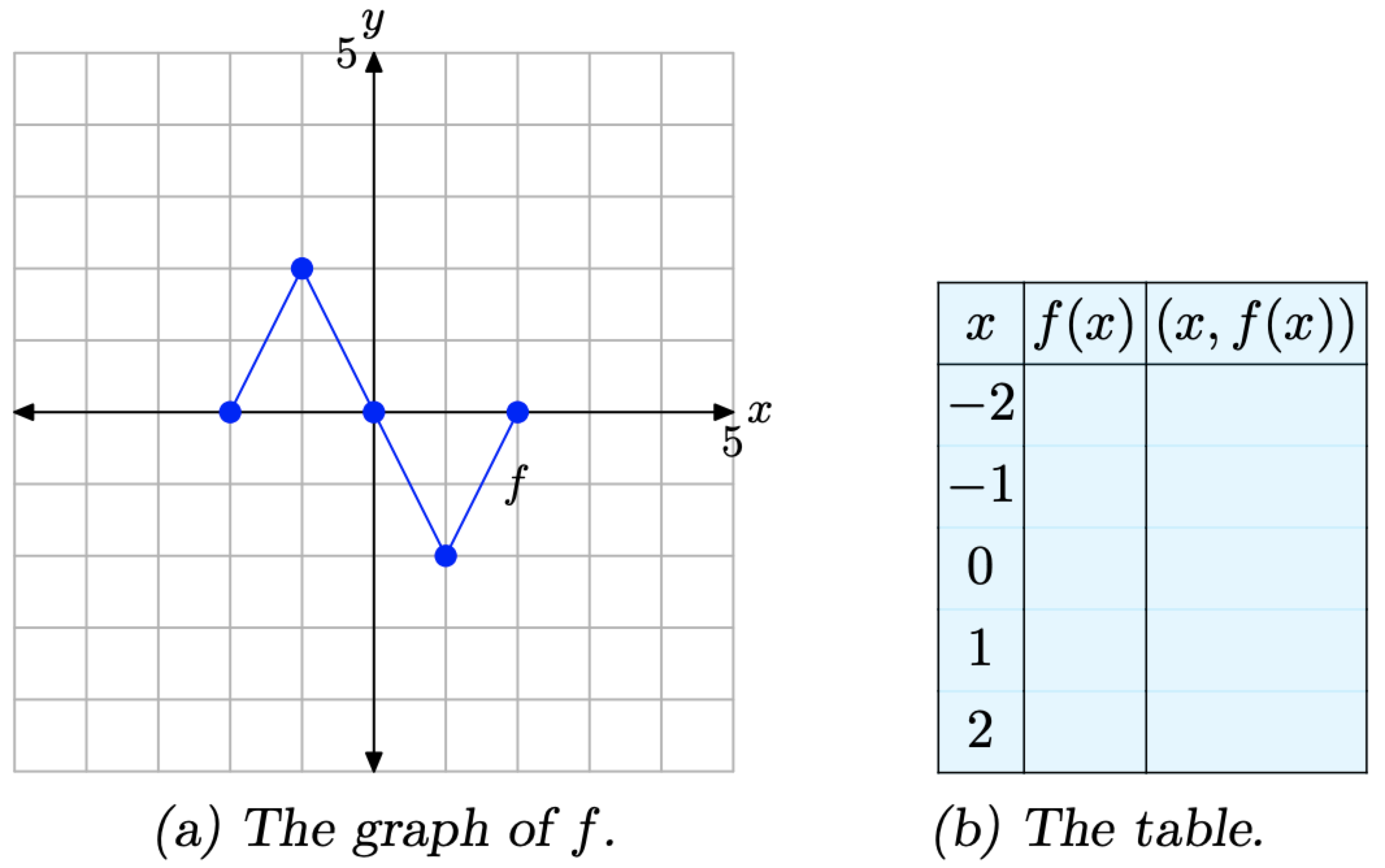
$WeChat231fdb846a5a57b3b7017acff5673b7e.png$

Малюнок$\PageIndex{1}$. Читання ключових значень з графіка f.

Рішення

Щоб обчислити f (−1), ми знаходимо −1 на осі x, намалюємо вертикальну стрілку до графіка f, потім горизонтальну стрілку до осі y, як показано на малюнку$\PageIndex{2}$ (a). Значення y цього кінцевого призначення є значенням f (−1). Тобто f (−1) = 2. Це дозволяє нам заповнити один запис у таблиці, як показано на малюнку$\PageIndex{2}$ (b). Продовжуйте таким чином завершити всі записи в таблиці. Результат показаний на малюнку$\PageIndex{2}$ (в).

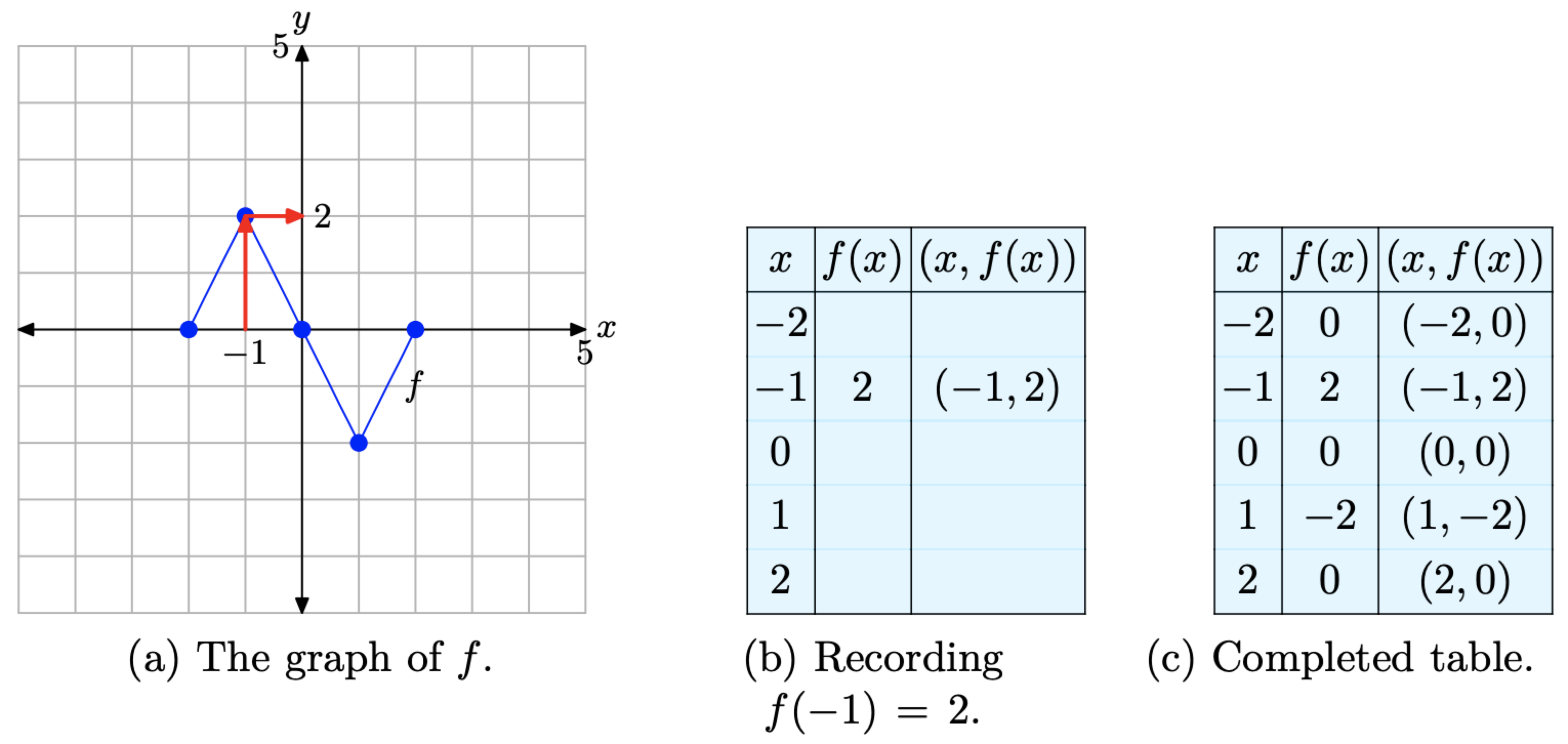
$WeChat3ca39b7081394e6f8965adb0dd945e1e.png$

Малюнок$\PageIndex{2}$. Запис координат точок на графіку f в таблицях.

Вертикальне масштабування

У наступному розповіді ми матимемо повторну потребу в графіку на малюнку$\PageIndex{2}$ (а) та таблиці на малюнку$\PageIndex{2}$ (c). Вони характеризують основну функцію, яка стане відправною точкою для понять масштабування, рефлексії та перекладу, які ми розробляємо в цьому розділі. Отже, давайте розмістимо їх пліч-о-пліч для акценту на малюнку$\PageIndex{3}$.

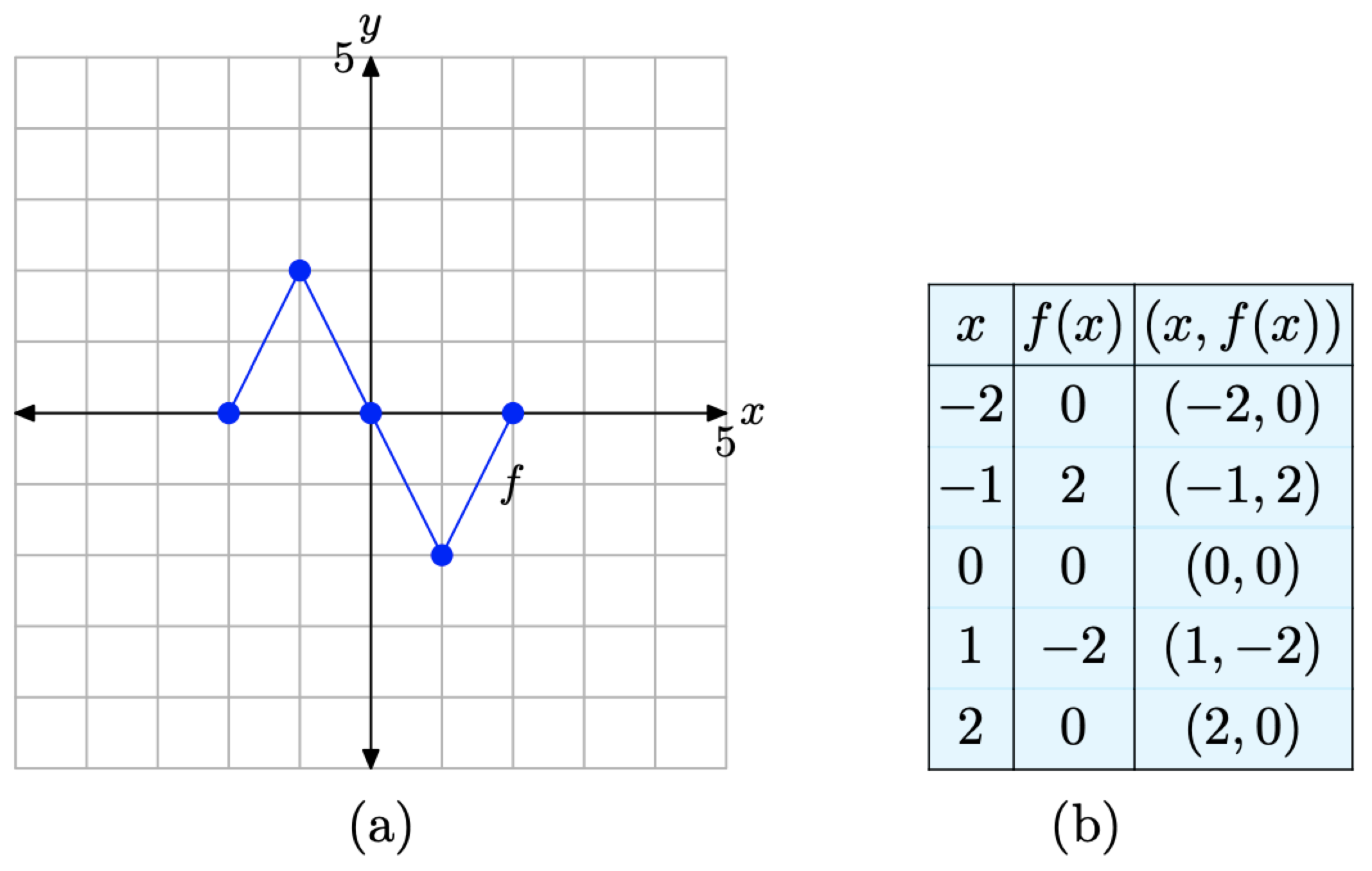
$WeChat121beb889b53c2b82eca4e9b45e08663.png$

Малюнок$\PageIndex{3}$. Вихідний графік f і таблиця ключових точок на графіку f.

Тепер ми будемо масштабувати графік f у вертикальному напрямку.

Приклад$\PageIndex{2}$

Якщо y = f (x) має графік, показаний на малюнку$\PageIndex{3}$ (a), намалюйте графік y = 2f (x).

Рішення

Що ми робимо, коли зустрічаємо графік, у формі якого ми не впевнені? Відповідь на це питання полягає в тому, що ми будуємо деякі точки, які задовольняють рівнянню, щоб отримати уявлення про форму графіка. Маючи на увазі цю думку, давайте оцінимо функцію y = 2f (x) при x = −2.

Буква f відноситься до вихідної функції, показаної на малюнку$\PageIndex{3}$ (a), а таблиця на малюнку$\PageIndex{3}$ (b) містить значення цієї функції при заданих значеннях x. Таким чином, при обчисленні y = 2f (−2) першим кроком є пошук значення f (−2) у таблиці на малюнку$\PageIndex{3}$ (b). Там ми знаходимо, що f (−2) = 0. Таким чином, ми можемо написати\[y=2 f(-2)=2(0)=0\]

Аналогічним чином оцінимо функцію y = 2f (x) при x = −1. Спочатку знайдіть значення f (−1) у таблиці на малюнку$\PageIndex{3}$ (b). Там ми знаходимо, що f (−1) = 2. Таким чином, ми можемо написати\[y=2 f(-1)=2(2)=4\]

Закінчуємо оцінкою функції y = 2f (x) при x = 0, 1 і 2. Кожен раз, коли потрібно оцінювати функцію f за числом, візьміть результат з таблиці або графіка на малюнку 3. Далі наведено оцінки y = 2f (x) при x = −2, −1, 0, 1 та 2.

\[\begin{array}{l}{y=2 f(-2)=2(0)=0} \\ {y=2 f(-1)=2(2)=4} \\ {y=2 f(0)=2(0)=0} \\ {y=2 f(1)=2(-2)=-4} \\ {y=2 f(2)=2(0)=0}\end{array}\]

Ми можемо розташувати ці результати в таблиці, наведеній на малюнку$\PageIndex{4}$ (b), а потім побудувати їх на малюнку, показаному на малюнку$\PageIndex{4}$ (а).

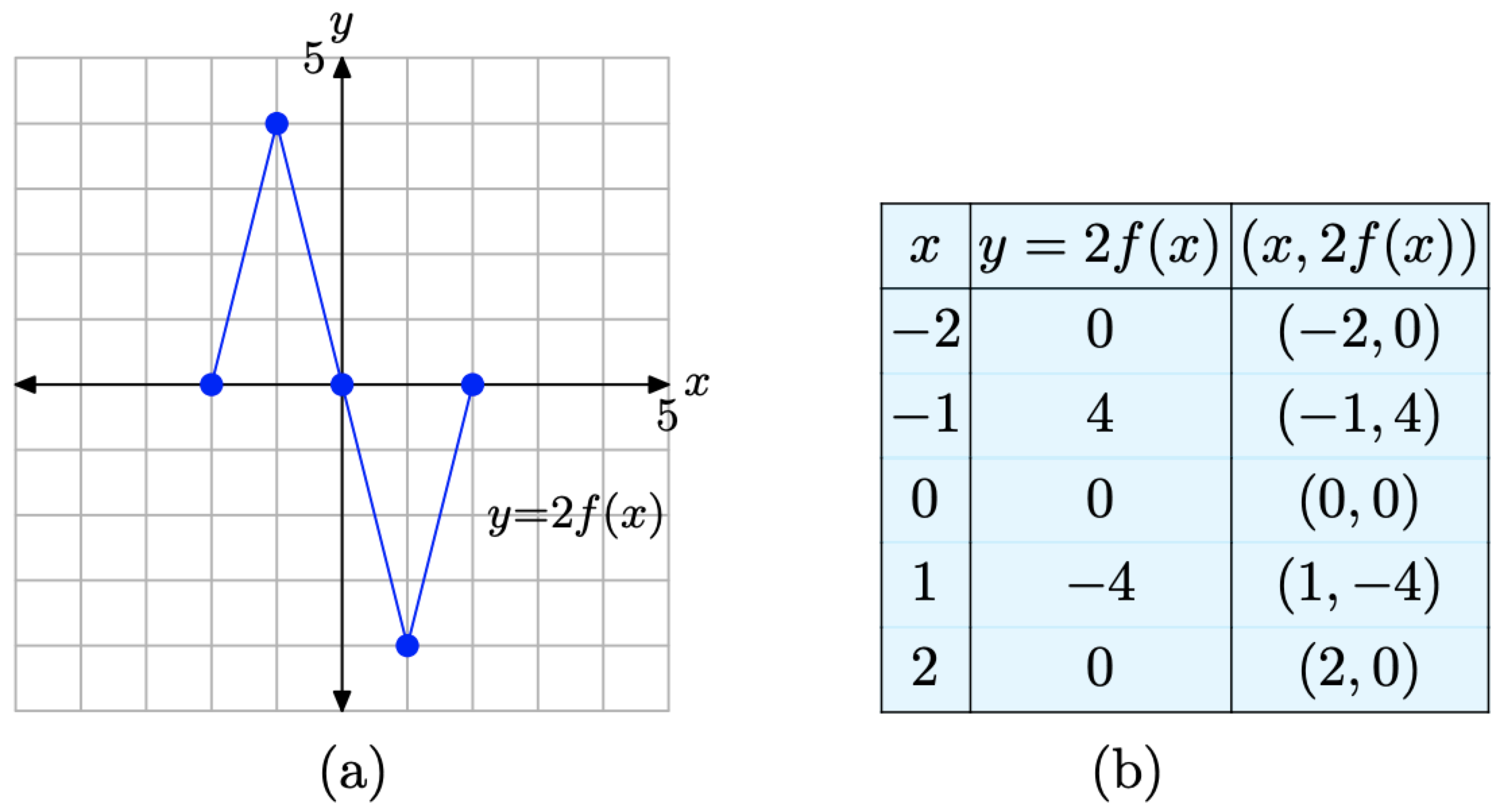
$WeChat8bab2e9940b274f4aa16178936431d15.png$

Малюнок$\PageIndex{4}$. Точки в таблиці - це точки на графіку y = 2f (x).

На даний момент існує ряд порівнянь, які ви можете зробити.

Порівняйте дані в таблицях на малюнку$\PageIndex{3}$ (b) і малюнку$\PageIndex{4}$ (b). Зверніть увагу, що значення x ідентичні. В обох таблицях x = −2, −1, 0, 1 та 2. Однак зауважте, що кожне значення y в таблиці на малюнку$\PageIndex{4}$ (b) точно вдвічі перевищує відповідне значення y в таблиці на малюнку$\PageIndex{3}$ (b).
Порівняйте графіки на малюнку$\PageIndex{3}$ (а) та малюнку$\PageIndex{4}$ (а). Зверніть увагу, що значення y кожної точки на графіку y = 2f (x) на малюнку$\PageIndex{4}$ (a) точно вдвічі перевищує значення y відповідної точки на малюнку$\PageIndex{3}$ (а).

Зверніть увагу на результат. Графік y = 2f (x) розтягнутий вертикально (від осі x), як позитивно, так і негативно, в 2 рази.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{3}$

Якщо y = f (x) має графік, показаний на малюнку$\PageIndex{3}$ (а), намалюйте графік y = (1/2) f (x).

Рішення

Почнемо з обчислення функції y = (1/2) f (x) при x = −2. Спочатку знайдіть значення f (−2) у таблиці на малюнку$\PageIndex{3}$ (b). Там ми знаходимо, що f (−2) = 0. Таким чином, ми можемо написати\[y=(1 / 2) f(-2)=(1 / 2)(0)=0\]

Аналогічним чином оцінимо функцію y = (1/2) f (x) при x = −1. Спочатку знайдіть значення f (−1) у таблиці на малюнку$\PageIndex{3}$ (b). Там ми знаходимо, що f (−1) = 2. Таким чином, ми можемо написати\[y=(1 / 2) f(-1)=(1 / 2)(2)=1\]

Продовжуючи таким чином, ми можемо оцінити функцію y = (1/2) f (x) при x = 0, 1 і 2.

\[\begin{array}{l}{y=(1 / 2) f(0)=(1 / 2)(0)=0} \\ {y=(1 / 2) f(1)=(1 / 2)(-2)=-1} \\ {y=(1 / 2) f(2)=(1 / 2)(0)=0}\end{array}\]

Результати заносяться в таблицю на малюнку$\PageIndex{5}$ (б). Замість того, щоб подвоювати кожне значення y, як це зробила функція y = 2f (x) у прикладі$\PageIndex{2}$, ця функція y = (1/2) f (x) половина кожного значення y Графік y = (1/2) f (x) та таблиця ключових точок на графіку представлені на малюнках$\PageIndex{5}$ (a) та (b) відповідно.

Знову ж таки, існує ряд порівнянь.

Порівняйте дані в таблицях на малюнку$\PageIndex{5}$ (b) і малюнку$\PageIndex{3}$ (b). Зверніть увагу, що значення x ідентичні. В обох таблицях x = −2, −1, 0, 1 та 2. Однак зауважте, що кожне значення y в таблиці на малюнку$\PageIndex{5}$ (b) точно дорівнює половині відповідного значення y в таблиці на малюнку$\PageIndex{3}$ (b).
Коли ви порівнюєте графік y = (1/2) f (x) на малюнку$\PageIndex{5}$ (a) з вихідним графіком y = f (x) на малюнку$\PageIndex{3}$ (a), зверніть увагу, що кожна точка на графіку y = (1/2) f (x) має значення y, яке рівно становить половину відповідного значення y на вихідному графіку y = f (x) на малюнку$\PageIndex{3}$ (а).

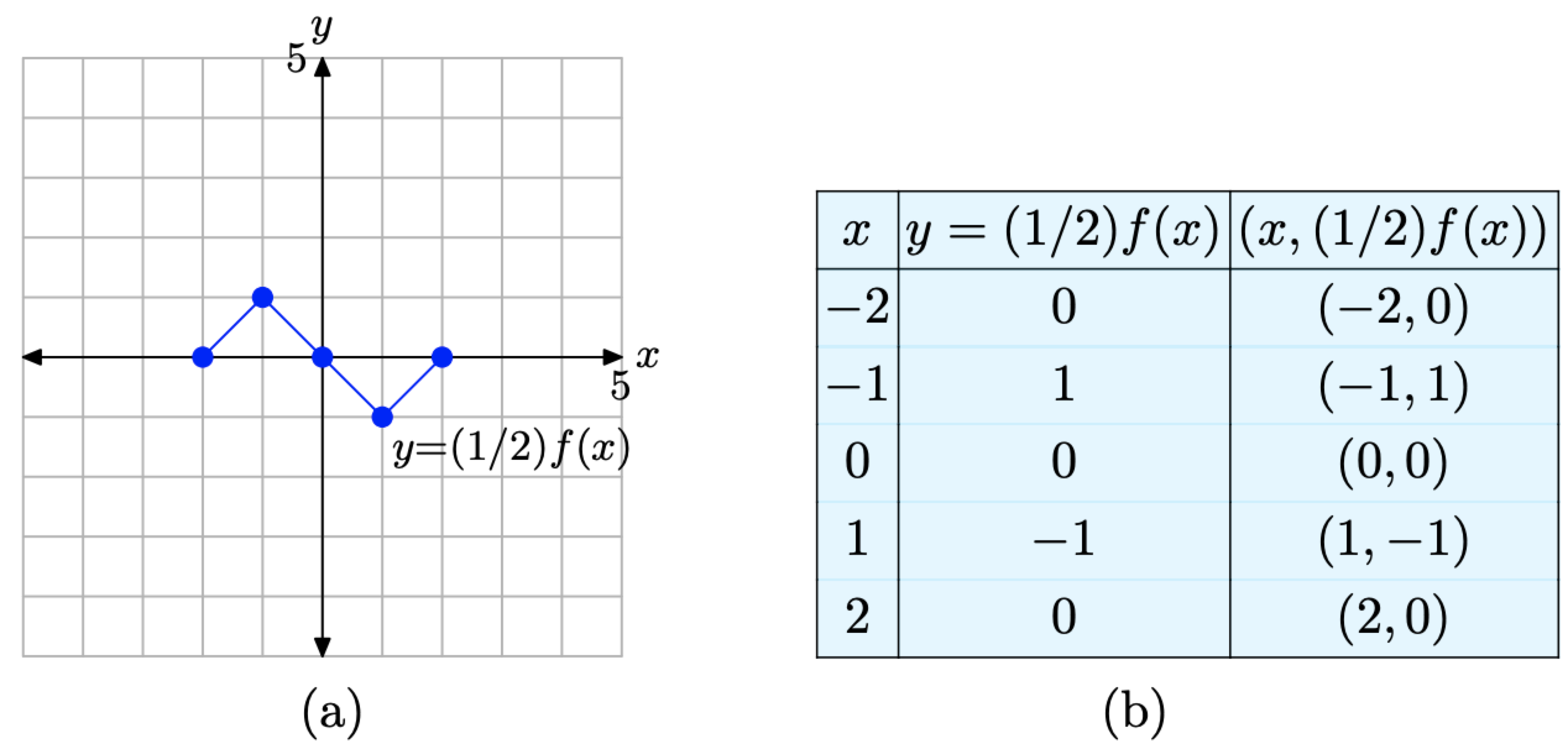
$WeChat4c2b144dcb3ff59dc8405501f815a912.png$

Малюнок$\PageIndex{5}$. Точки в таблиці - це точки на графіку y = (1/2) f (x).

Зверніть увагу на результат. Графік f був стиснутий вертикально (до осі x), як позитивно, так і негативно, в 2 рази.

Давайте підсумуємо наші висновки.

Візуальний підсумок - вертикальне масштабування.

Розглянемо зображення на малюнку$\PageIndex{6}$.

На малюнку$\PageIndex{6}$ (a) ми бачимо на фото графік вихідної функції y = f (x).
На малюнку$\PageIndex{6}$ (b) зверніть увагу, що кожна ключова точка на графіку y = 2f (x) має значення y, яке точно вдвічі перевищує значення y відповідної точки на графіку y = f (x) на малюнку$\PageIndex{6}$ (а).
На малюнку$\PageIndex{6}$ (c) зверніть увагу, що кожна ключова точка на графіку y = (1/2) f (x) має значення y, яке точно дорівнює половині значення y відповідної точки на графіку y = f (x) на малюнку$\PageIndex{6}$ (а).
Зверніть увагу, що значення x кожної трансформованої точки залишається незмінним.

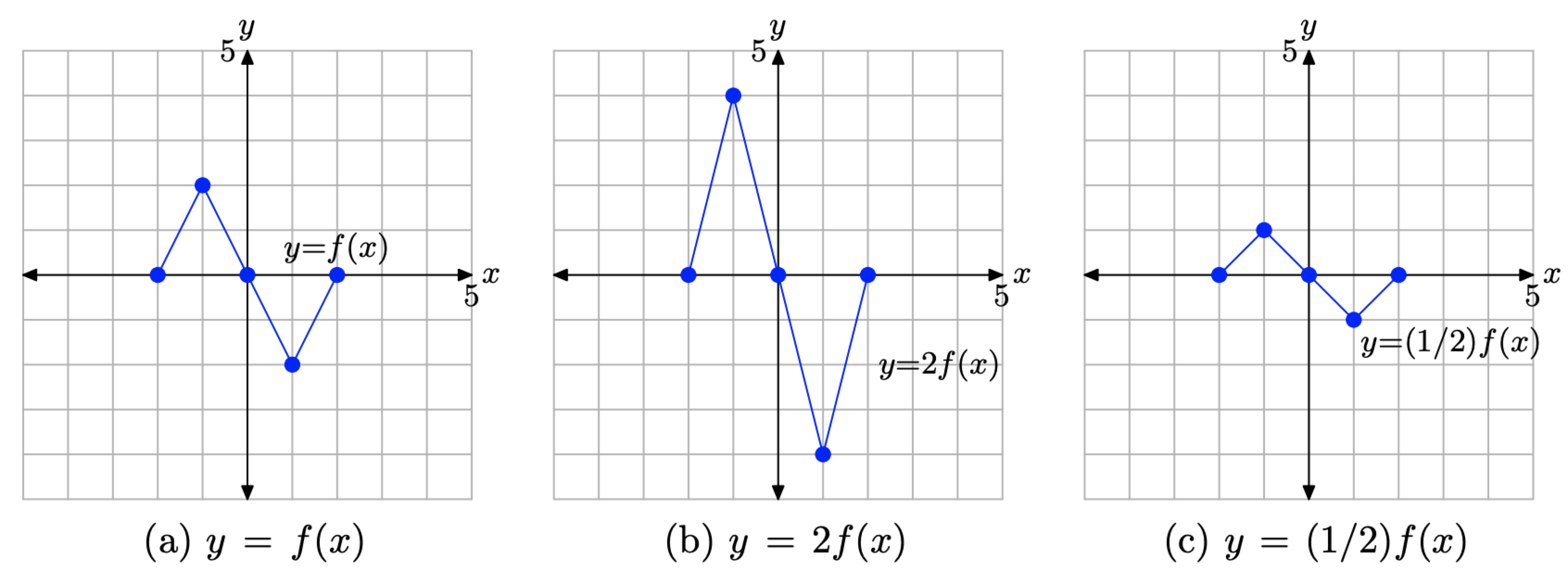
$WeChat45e5c0f5b7d7ed643f9c06f046d84386.png$

Малюнок$\PageIndex{6}$. Графік y = 2f (x) розтягується вертикально (від осі x) в 2 рази. Графік y = (1/2) f (x) стискає вертикально (до осі x) в 2 рази.

Візуальне резюме на малюнку$\PageIndex{6}$ робить ескіз графіків y = 2f (x) та y = (1/2) f (x) легким завданням.

З огляду на графік y = f (x), щоб намалювати графік y = 2f (x), просто візьміть кожну точку на графіку y = f (x) і подвоїти її значення y, зберігаючи однакове значення x.
З огляду на графік y = f (x), щоб намалювати графік y = (1/2) f (x), просто візьміть кожну точку на графіку y = f (x) і вдвічі зменшіть її значення y, зберігаючи однакове значення x.

Виконайте ті ж процедури для інших факторів масштабування. Наприклад, у випадку y = 3f (x) візьміть кожну точку на графіку y = f (x) і помножте її значення y на 3, зберігаючи однакове значення x. З іншого боку, щоб намалювати графік y = (1/3) f (x), візьміть кожну точку на графіку f і помножте її значення y на 1/3, зберігаючи однакове значення y.

Загалом, можна констатувати наступне.

резюме

Припустимо, нам дано графік y = f (x).

Якщо a > 1, то графік y = af (x) розтягується вертикально (від осі x), як позитивно, так і негативно, в рази a.
Якщо 0 < a < 1, то графік y = af (x) стискається вертикально (до осі x), як позитивно, так і негативно, в рази 1/a.

Другий пункт в резюме вимагає слова пояснення. Порівняйте загальну форму y = af (x) з функцією Приклад$\PageIndex{3}$, y = (1/2) f (x). У цьому випадку a = 1/2, так\[\frac{1}{a}=\frac{1}{1 / 2}=1 \times 2=2\]

Другий пункт говорить, що при 0 < a < 1 графік y = af (x) стискається вертикально коефіцієнтом 1/a. дійсно, це саме те, що відбувається у випадку y = (1/2) f (x), який стискається коефіцієнтом 1/ (1/2), або 2.

Вертикальні роздуми

Для зручності почнемо з повторення вихідного графіка y = f (x) і супутніх йому даних.

Тепер ми будемо відображати графік у вертикальному напрямку (поперек осі x).

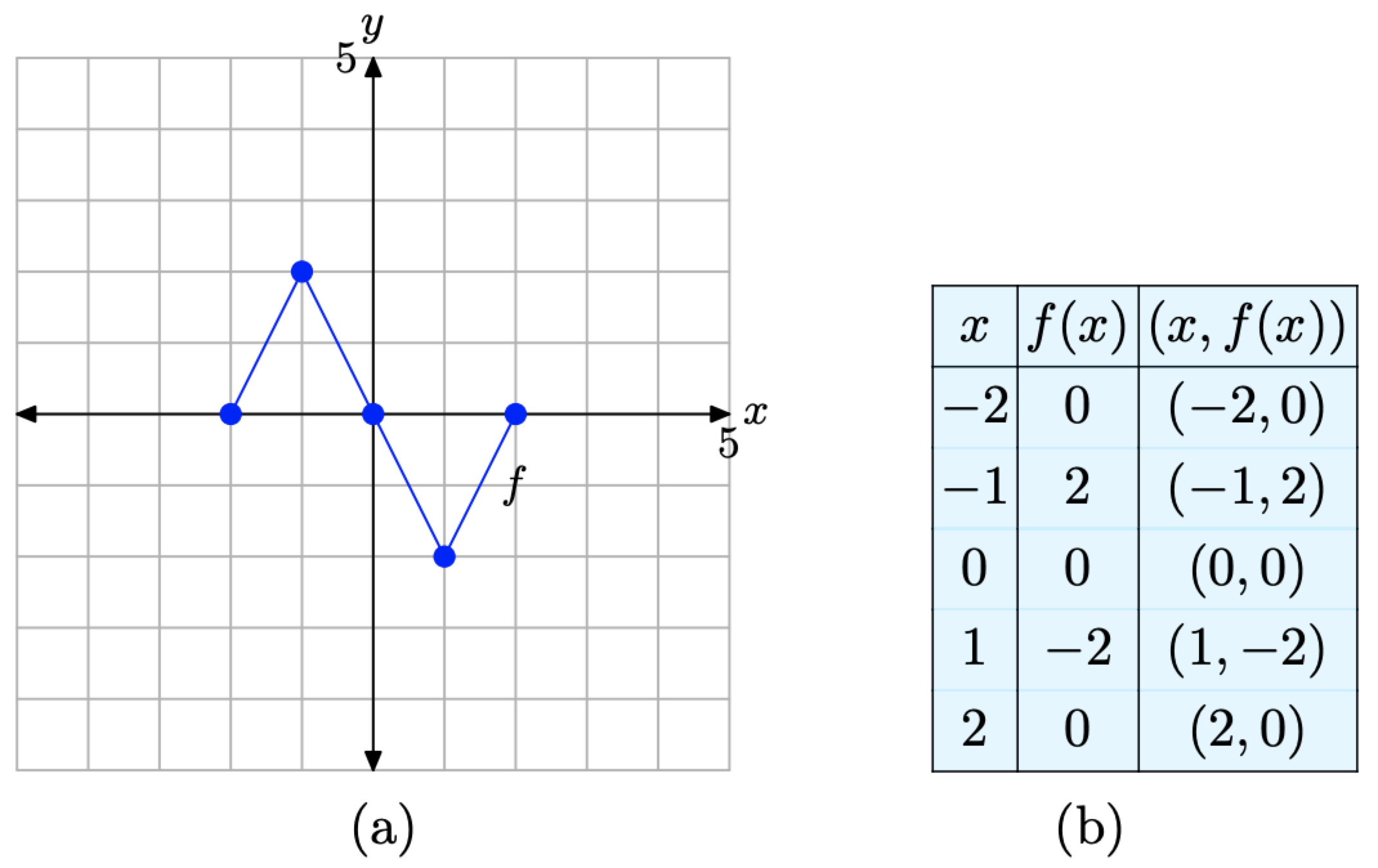
$WeChat28f413c47b5cadc6612b803db3aa404a.png$

Малюнок$\PageIndex{7}$. Вихідний графік f і таблиця ключових точок на графіку f.

Приклад$\PageIndex{4}$

Якщо y = f (x) має графік, показаний на малюнку$\PageIndex{7}$ (a), намалюйте графік y = −f (x).

Рішення

Щоб налаштувати таблицю точок під час підготовки до графіку y = −f (x), ми використаємо точно ті самі значення x, які ви бачите в таблиці на малюнку$\PageIndex{7}$ (b), а саме x = −2, −1, 0, 1 і 2. Щоб оцінити y = −f (x) при першому значенні x, а саме x = −2, зробимо наступний розрахунок,

\[y=-f(-2)=-(0)=0\]

де ми використали той факт, що f (−2) = 0 з таблиці на малюнку$\PageIndex{7}$ (b). Аналогічним чином ми оцінюємо y = −f (x) на кожному з решти значень x, а саме x = −1, 0, 1 та 2.

\[\begin{aligned} y &=-f(-1)=-(2)=-2 \\ y &=-f(0)=-(0)=0 \\ y &=-f(1)=-(-2)=2 \\ y &=-f(2)=-(0)=0 \end{aligned}\]

Збираємо ці точки в таблиці на малюнку$\PageIndex{8}$ (б) і будуємо їх на малюнку$\PageIndex{8}$ (а).

Зауважте, що графік y = −f (x) на малюнку$\PageIndex{8}$ (a) є відображенням графіка y = f (x) на малюнку$\PageIndex{7}$ (a) по осі x.

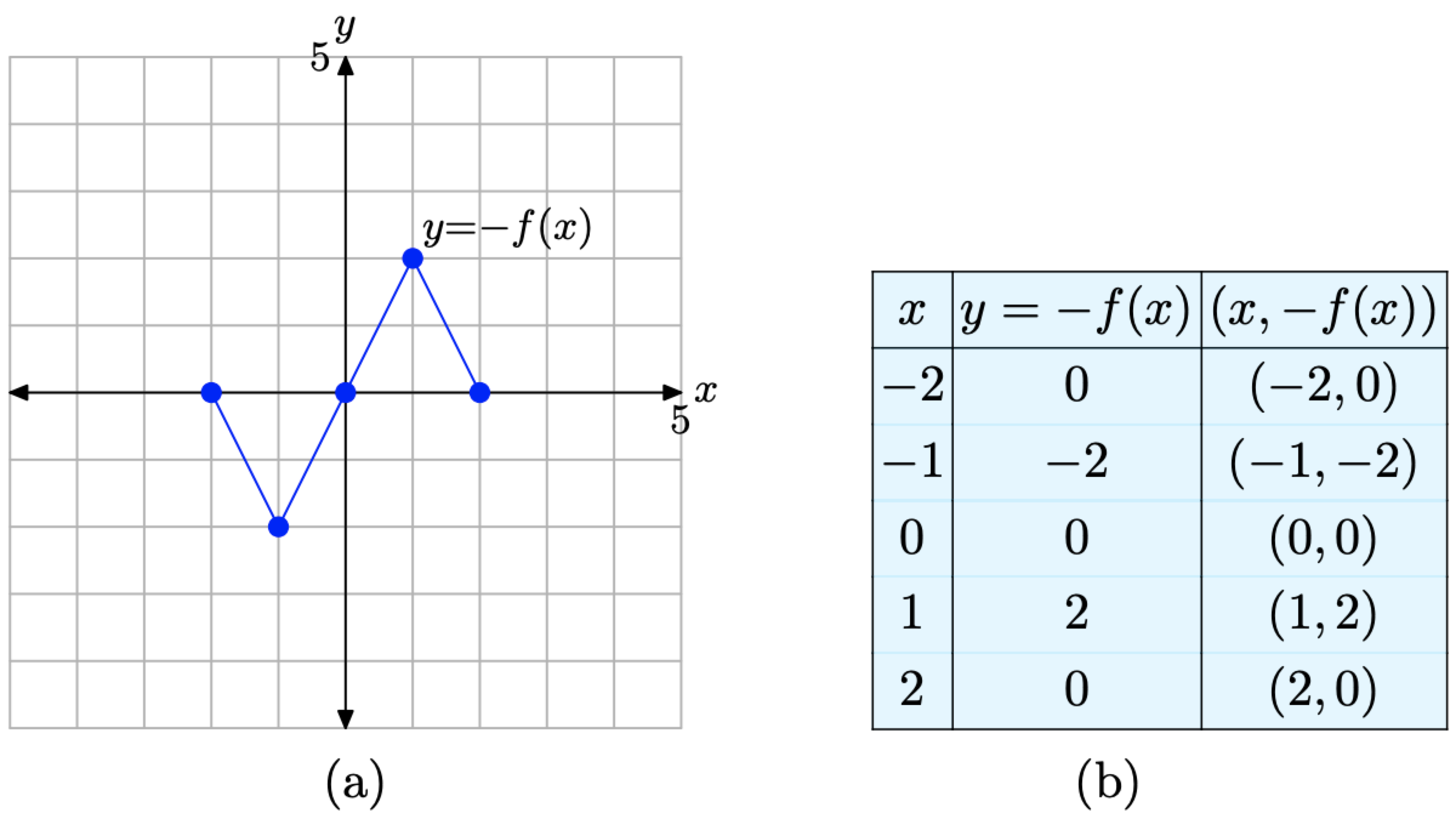
$WeChat8ecae9b9acd1d041ee2ca7bb5f9ff5ba.png$

Малюнок$\PageIndex{8}$. Графік y = −f (x) та таблиця ключових точок на графіку.

Давайте підсумуємо те, що ми дізналися про вертикальні відображення.

Візуальне резюме - вертикальні роздуми

Розглянемо зображення на малюнку$\PageIndex{9}$.

На малюнку$\PageIndex{9}$ (а) ми бачимо на фото оригінальний графік y = f (x).
На малюнку$\PageIndex{9}$ (b) графік y = −f (x) є відображенням графіка y = f (x) по осі x.

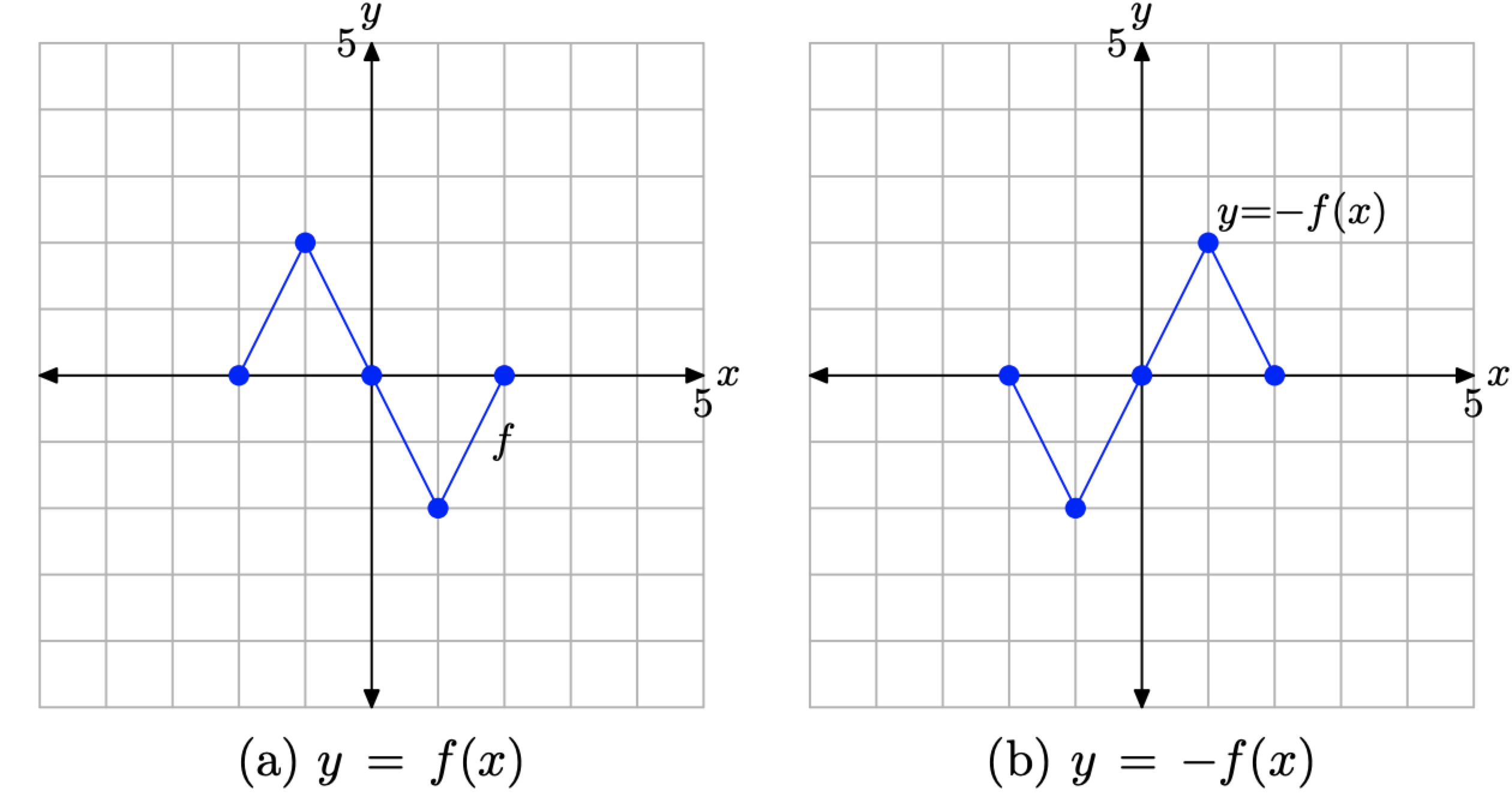
$WeChatf832c6332119614ecf42647cfe91a5c7.png$

Малюнок$\PageIndex{9}$. Графік y = −f (x) є відображенням графіка y = f (x) по осі x.

Таким чином, враховуючи графік y = f (x), намалювати графік y = −f (x) є простим завданням.

Щоб намалювати графік y = −f (x), візьміть кожну точку на графіку y = f (x) і відобразіть її по осі x, зберігаючи значення x однаковим, але заперечуючи значення y.

Вертикальні переклади

Переклади, мабуть, найлегша трансформація з усіх. Переклад - це «зрушення» або «слайд». Прикиньте, на мить, що ви розмістили прозорий аркуш тонкого пластику поверх аркуша графічного паперу. Ви намалювали декартову систему координат на графічному папері, але ви намалювали графік на прозорому аркуші пластику. Тепер «зрушуйте» або «ковзайте» прозорість на графічному папері в постійному напрямку, не обертаючи прозорість. Це те, що ми маємо на увазі під «перекладом». У цьому розділі ми зупинимося строго на вертикальних перекладах.

Для зручності почнемо з повторення вихідного графіка y = f (x) і супутніх до нього даних на малюнку$\PageIndex{10}$ (а) і (b) відповідно. Тепер ми переведемо цей графік у вертикальному напрямку.

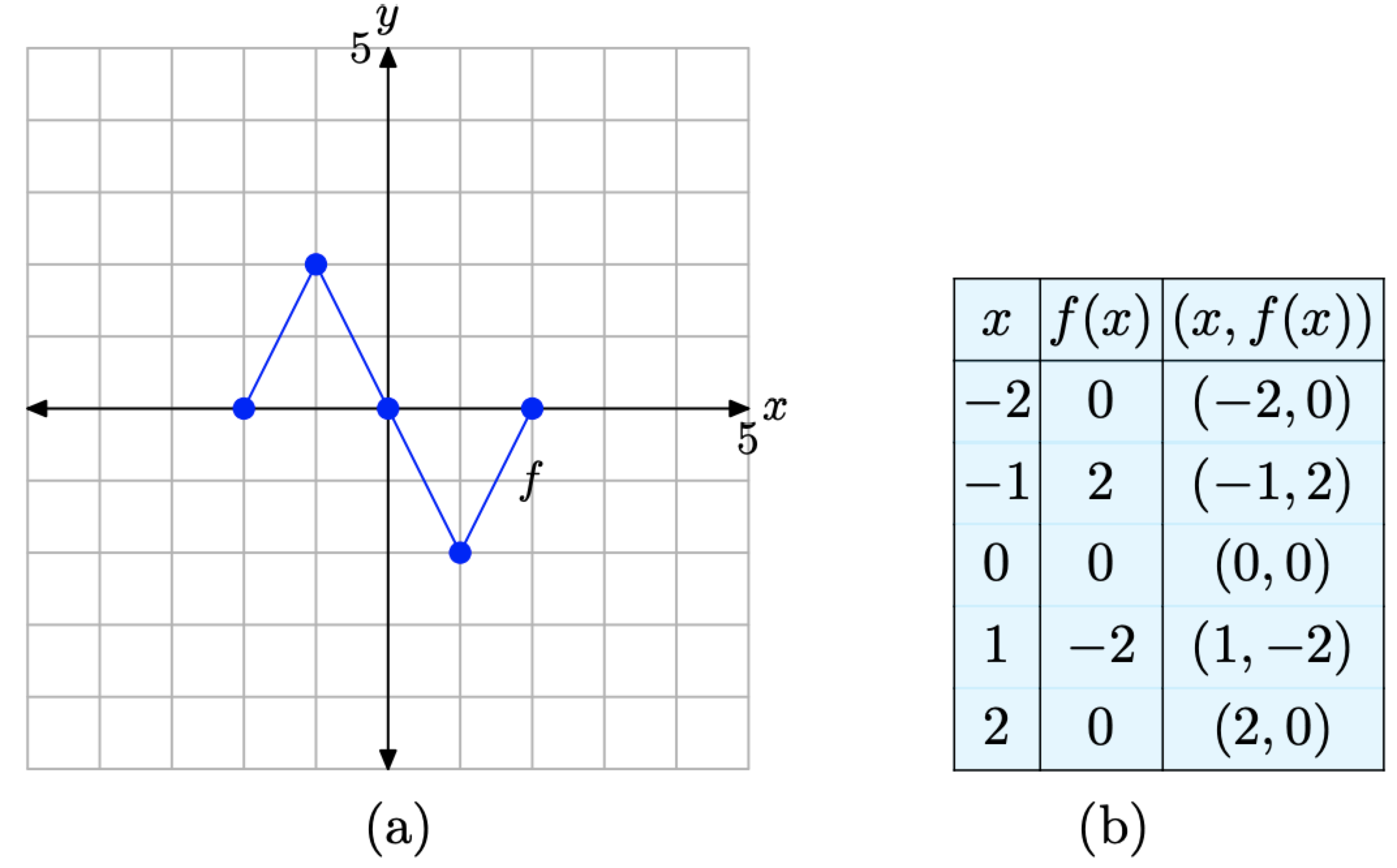
$WeChat18f468b011e27a8f2b0bc874ff92e6f2.png$

Малюнок$\PageIndex{10}$. Вихідний графік f і таблиця ключових точок на графіку f.

Приклад$\PageIndex{5}$

Якщо y = f (x) має графік, показаний на малюнку$\PageIndex{10}$ (a), намалюйте графік y = f (x) + 1.

Рішення

Ми будемо оцінювати y = f (x) +1 за тими ж значеннями, показаними в таблиці на малюнку$\PageIndex{10}$ (b), а саме x = −2, −1, 0, 1 і 2. Для оцінки y = f (x) +1 при першому значенні x, а саме x = −2, зробимо наступний розрахунок\[y=f(-2)+1=0+1=1\]

де ми використовували той факт, що f (−2) = 0 з таблиці на малюнку$\PageIndex{10}$ (b). Аналогічним чином ми можемо оцінити y = f (x) + 1 при кожному з решти значень x, а саме x = −1, 0, 1 і 2.

\[\begin{array}{l}{y=f(-1)+1=2+1=3} \\ {y=f(0)+1=0+1=1} \\ {y=f(1)+1=-2+1=-1} \\ {y=f(2)+1=0+1=1}\end{array}\]

Збираємо ці точки в таблиці на малюнку$\PageIndex{11}$ (б) і будуємо їх на малюнку$\PageIndex{11}$ (а).

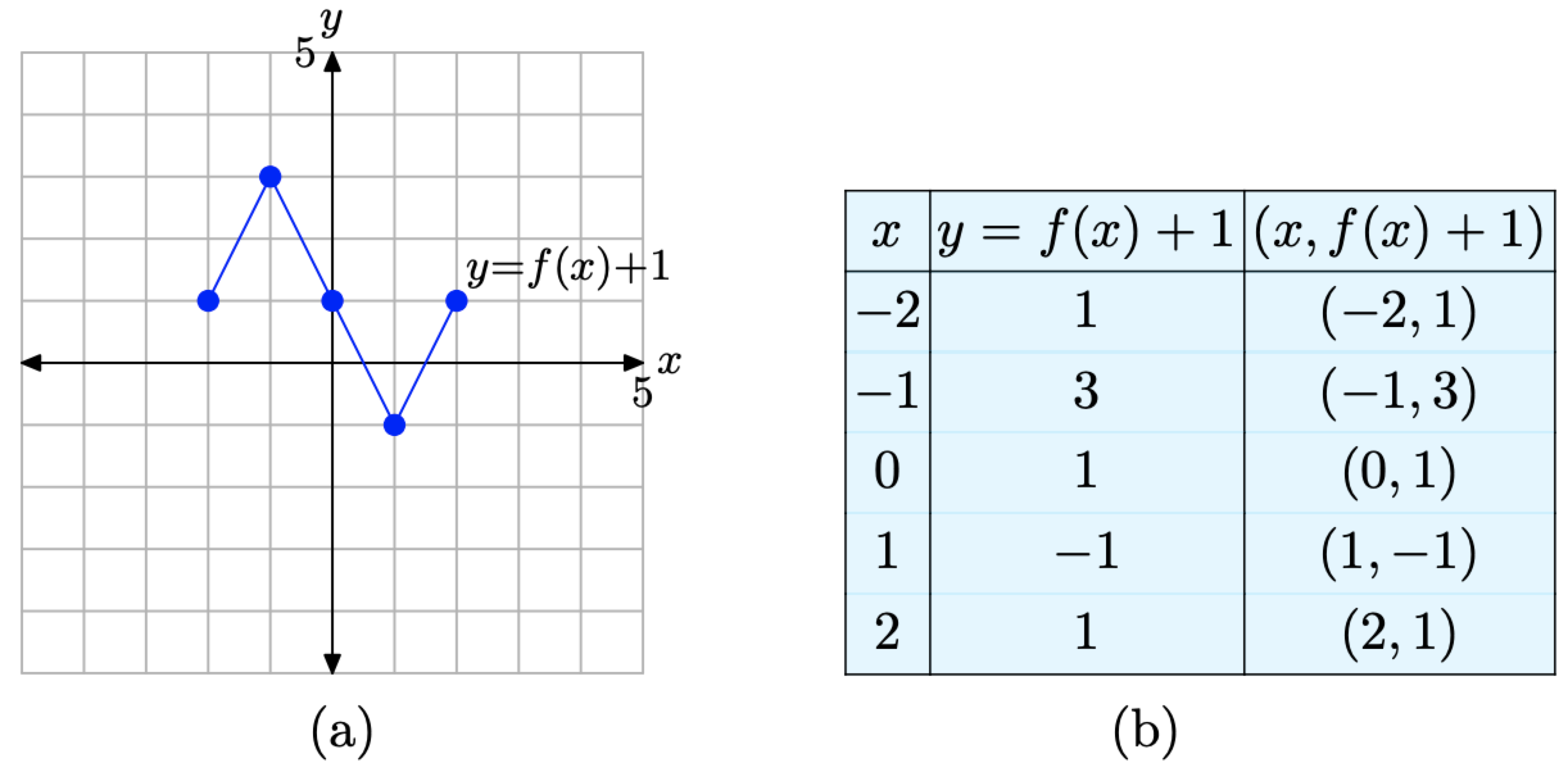
$WeChat1bcc53c1d90bf053fbdca96da5c88ac9.png$

Малюнок$\PageIndex{11}$. Графік y = f (x) + 1 і таблиця ключових точок на графіку.

При порівнянні записів в таблиці на рис$\PageIndex{11}$. (б) з початковими значеннями в таблиці на рис$\PageIndex{10}$. (b), ви зауважте, що значення x у кожній таблиці ідентичні, але значення y в таблиці на малюнку$\PageIndex{11}$. (b) всі збільшені на 1. Це має сенс, тому що це y-значення точок, пов'язаних з функцією y = f (x) + 1. Звичайно, всі значення y повинні бути на 1 більше, ніж значення y, пов'язані з вихідним рівнянням y = f (x).

Зверніть увагу на результат. Графік y = f (x) + 1 на малюнку$\PageIndex{11}$ (а) при порівнянні з графіком y = f (x) на малюнку$\PageIndex{10}$ (а) зміщується на 1 одиницю вгору.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{6}$

Якщо y = f (x) має графік, показаний на малюнку$\PageIndex{10}$ (a), намалюйте графік y = f (x) − 2.

Рішення

Оцініть функцію y = f (x) − 2 при кожному значенні x у таблиці на малюнку$\PageIndex{10}$ (b). При х = −2,\[y=f(-2)-2=0-2=-2\]

Аналогічним чином оцініть y = f (x) − 2 при кожному залишковому значенні x у таблиці на малюнку$\PageIndex{10}$ (b).

\[\begin{aligned} y &=f(-1)-2=2-2=0 \\ y &=f(0)-2=0-2=-2 \\ y &=f(1)-2=-2-2=-4 \\ y &=f(2)-2=0-2=-2 \end{aligned}\]

Збираємо ці точки в таблиці на малюнку$\PageIndex{12}$ (б) і будуємо їх на малюнку$\PageIndex{12}$ (а).

Коли ви порівнюєте записи в таблиці на малюнку$\PageIndex{12}$ (b) з початковими значеннями в таблиці на малюнку$\PageIndex{10}$ (b), ви зауважите, що значення x у кожній таблиці ідентичні, але значення y в таблиці на малюнку$\PageIndex{12}$ (b) зменшуються на 2. Це робить

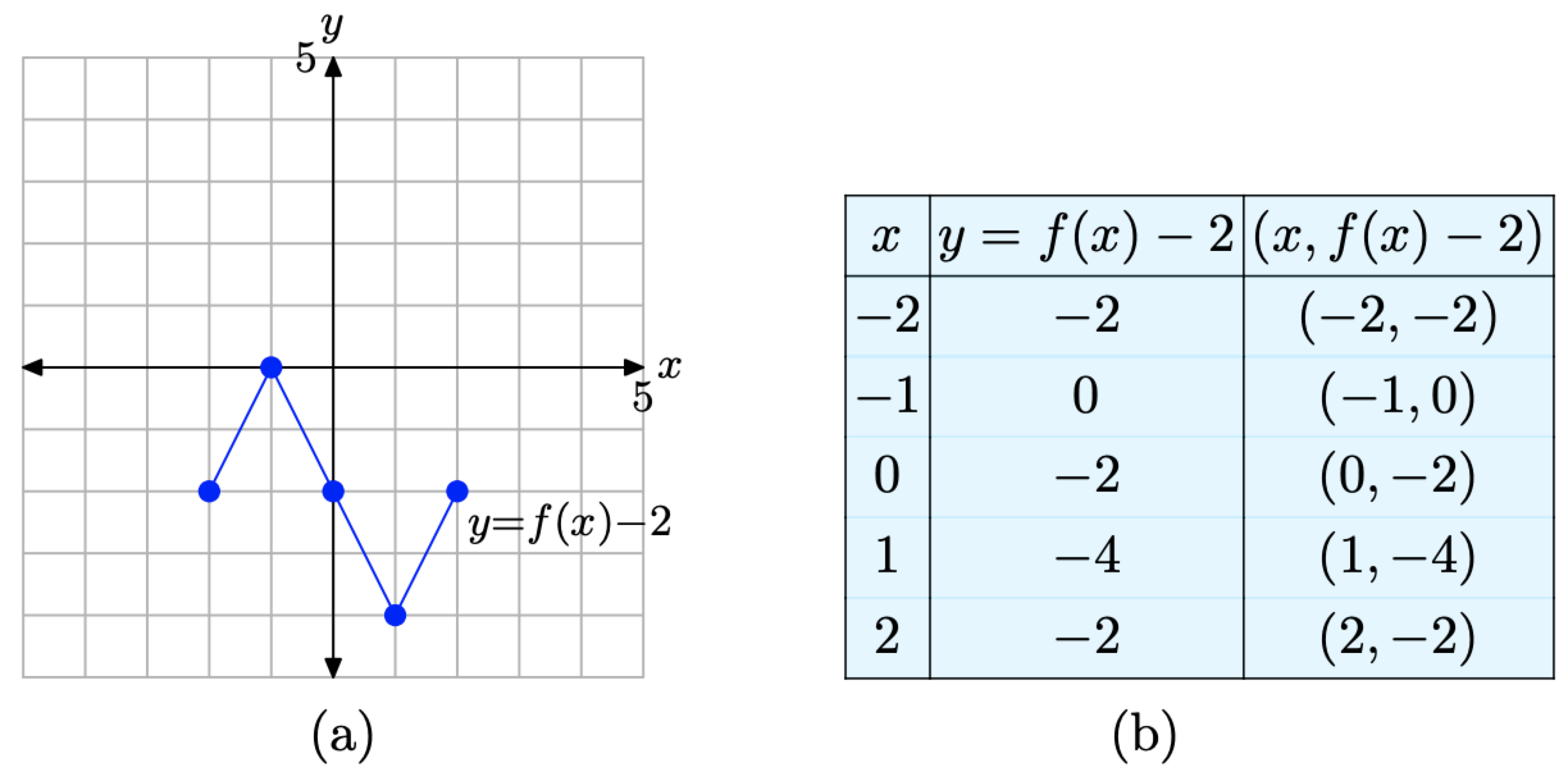
$WeChat3e19d071a3a0907d7ee21b7043eff748.png$

Малюнок$\PageIndex{12}$. Графік y = f (x) − 2 та таблиця ключових точок на графіку.

сенсу, тому що це y-значення точок, пов'язаних з функцією y = f (x) − 2. Звичайно, всі значення y повинні бути на 2 менше значень y, пов'язаних з вихідним рівнянням y = f (x).

Зверніть увагу на результат. Графік y = f (x) − 2 на малюнку$\PageIndex{12}$ (a) при порівнянні з графіком y = f (x) на малюнку$\PageIndex{10}$ (a) зміщується вниз на 2 одиниці.

Давайте підсумуємо те, що ми дізналися про вертикальні переклади.

Візуальний підсумок - вертикальні переклади (зрушення)

Розглянемо зображення на малюнку$\PageIndex{13}$.

На малюнку$\PageIndex{13}$ (a) ми бачимо на фото графік вихідної функції y = f (x).
На малюнку$\PageIndex{13}$ (b) зверніть увагу, що кожна ключова точка на графіку y = f (x) + 1 має значення y, яке точно на 1 одиницю більше значення y відповідної точки на графіку y = f (x) на малюнку$\PageIndex{13}$ (а).
На малюнку$\PageIndex{13}$ (c) зауважте, що кожна ключова точка на графіку y = f (x) − 2 має значення y, яке точно на 2 одиниці менше значення y відповідної точки на графіку y = f (x) на малюнку$\PageIndex{13}$ (а).
Зверніть увагу, що значення x кожної трансформованої точки залишається незмінним.

Візуальне резюме на малюнку$\PageIndex{13}$ робить ескіз графіків y = f (x) + 1 та y = f (x) − 2 простим завданням.

З огляду на графік y = f (x), щоб намалювати графік y = f (x) + 1, просто візьміть кожну точку на графіку y = f (x) і перемістіть її вгору на 1 одиницю, зберігаючи однакове значення x.
Враховуючи графік y = f (x), щоб намалювати графік y = f (x) − 2, просто візьміть кожну точку на графіку y = f (x) і перемістіть її вниз на 2 одиниці, зберігаючи однакове значення x.

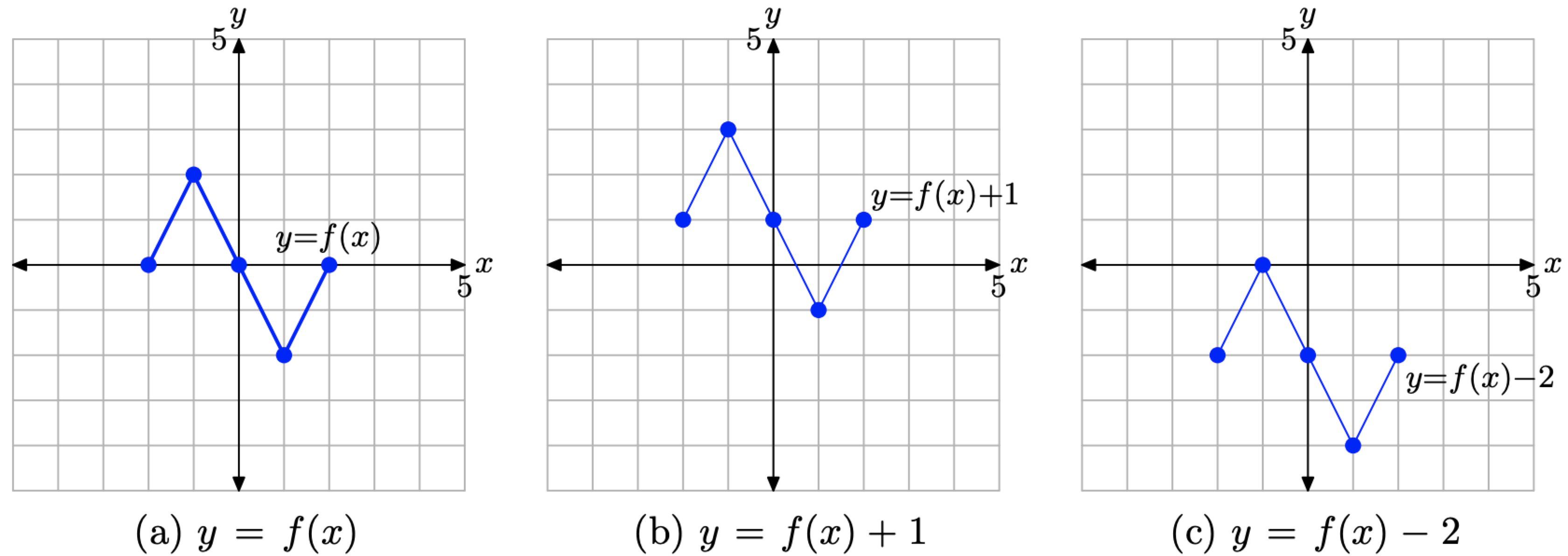
$WeChat20d85db2c4d982b69b890d936fa7cafa.png$

Малюнок$\PageIndex{13}$. Графік y = f (x) + 1 формується зміщенням (вертикально) графіка y = f (x) вгору на 1 одиницю. Графік y = f (x) − 2 формується зміщенням (вертикально) графіка y = f (x) вниз на 2 одиниці.

Загалом, можна констатувати наступне.

резюме

Припустимо, що нам дано графік y = f (x) і припустимо, що c - будь-яке додатне дійсне число.

Графік y = f (x) +c зміщений c одиницями вгору від графіка y = f (x).
Графік y = f (x) − c зміщений на c одиниць вниз від графіка y = f (x).

Складання перетворень

Іноді нам захочеться виконати одне перетворення, потім взяти результат першого перетворення і застосувати друге перетворення. Давайте розглянемо приклад.

Приклад$\PageIndex{7}$

Розглянемо графік y = f (x), представлений на малюнку$\PageIndex{14}$.

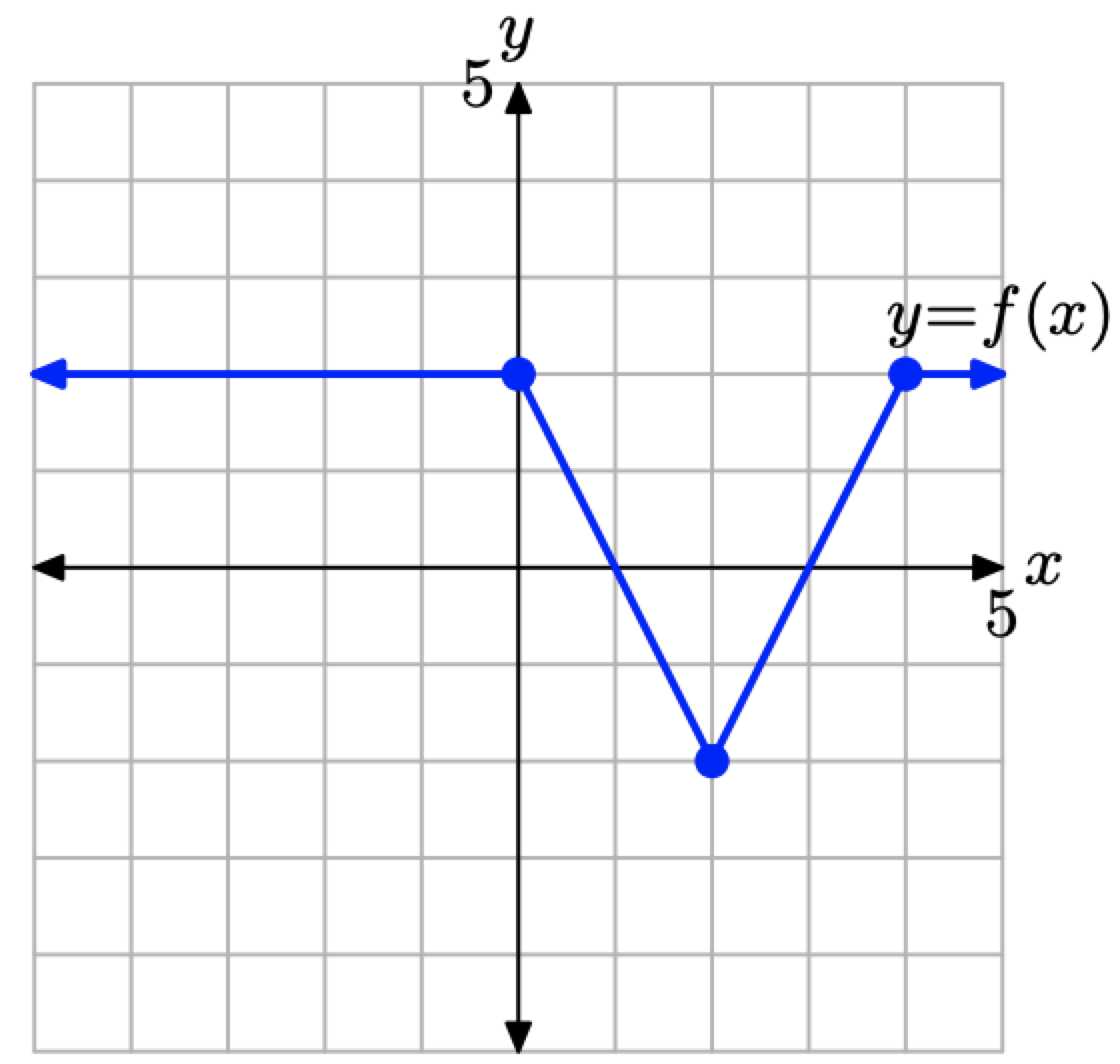
$WeChat937ead318813960d5bf0b08ccf94ade9.png$

$\PageIndex{14}$Рисунок Графік y = f (x), який буде перетворений у Приклад$\PageIndex{7}$.

Використовуйте концепції, розглянуті у Візуальних резюме, щоб намалювати графік y = −2f (x), не створюючи та посилаючись на таблицю точок.

Рішення

Зауважте, що рівняння y = −2f (x) може бути утворено послідовністю двох перетворень.

Спочатку масштабуйте вихідну функцію y = f (x), щоб отримати рівняння y = 2f (x).
По-друге, звести нанівець отриману функцію y = 2f (x), щоб отримати рівняння y = −2f (x).

Таким чином, графік y = −2f (x) можна сформувати наступним чином:

Почніть з графіка y = f (x) і подвоюйте значення y кожної точки на графіку y = f (x), зберігаючи однакове значення x. Результатом є графік y = 2f (x), показаний на малюнку$\PageIndex{15}$ (b).
Далі звести нанівець значення y кожної точки на графіку y = 2f (x), зберігаючи однакове значення x. Результатом є графік y = −2f (x) на малюнку$\PageIndex{15}$ (c).

$WeChat7c00a30968686057ddb449a6b65db15a.png$

Малюнок$\PageIndex{15}$. Перетворення графа y = f (x) з послідовністю двох перетворень.

Цікаво відзначити, що такий же результат ви отримаєте, якщо спочатку звести нанівець, потім масштабувати результат. Ми залишимо це нашим читачам, щоб перевірити, чи це правда.

Давайте розглянемо один остаточний приклад.

Приклад$\PageIndex{8}$

Розглянемо графік y = f (x), представлений на малюнку$\PageIndex{16}$.

Використовуйте концепції, розглянуті у Візуальних резюме, щоб намалювати графік y = −f (x) +2, не створюючи і посилаючись на таблицю точок.

Рішення

Зауважте, що рівняння y = −f (x) + 2 може бути утворено послідовністю двох перетворень.

Спочатку заперечуйте вихідну функцію y = f (x), щоб отримати рівняння y = −f (x).
По-друге, додайте 2 до отриманої функції y = −f (x), щоб отримати рівняння y = −f (x) + 2.

Таким чином, графік y = −f (x) + 2 можна сформувати наступним чином.

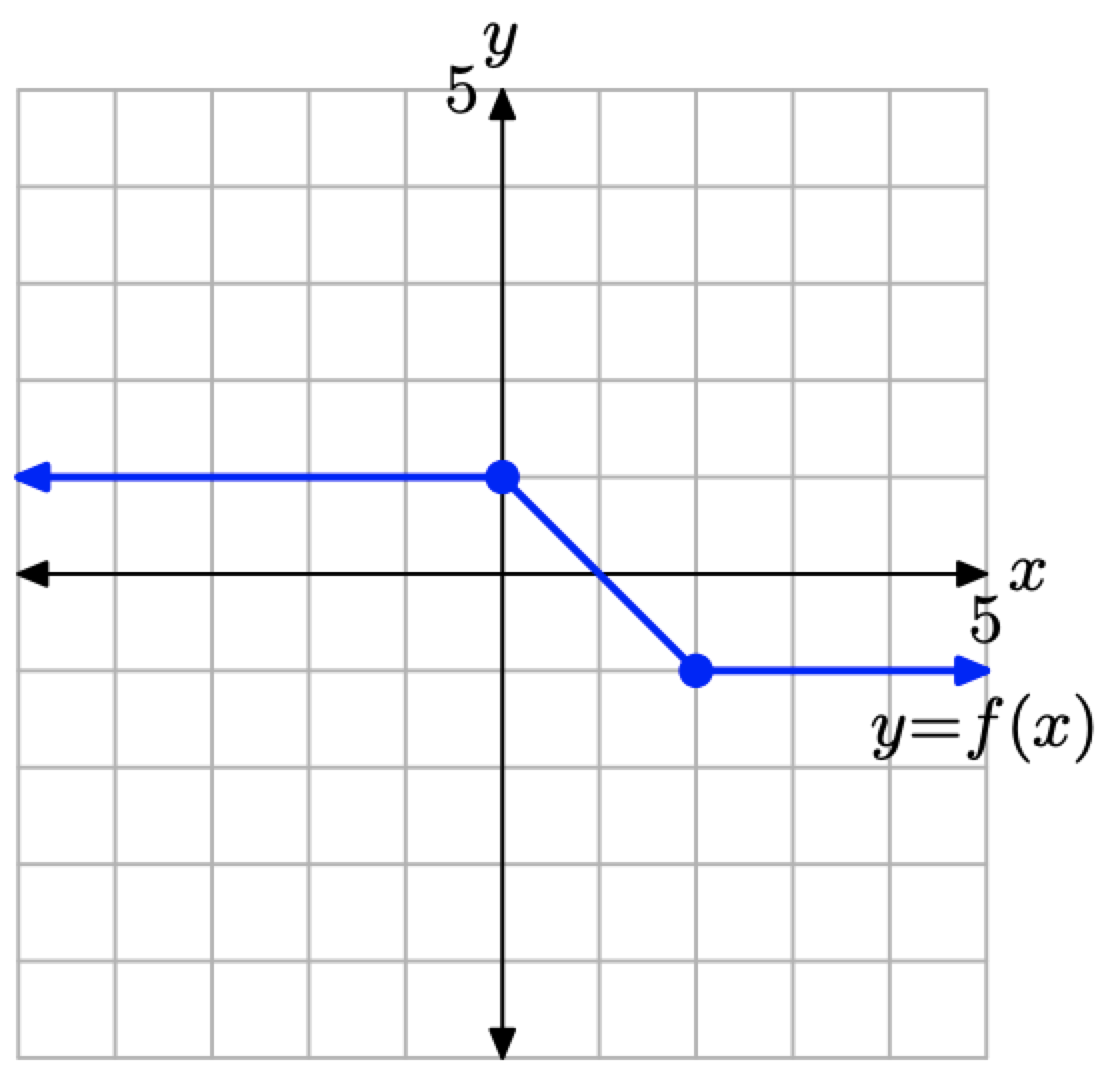
$WeChat6c4dcdb2dd6f7993faa7d1dc766c1bec.png$

Малюнок$\PageIndex{16}$. Графік y = f (x), який буде перетворений у прикладі$\PageIndex{8}$.

1. Спочатку почніть з графіка y = f (x) на малюнку$\PageIndex{17}$ (a) і зведіть нанівець значення y кожної точки, щоб отримати графік y = −f (x) Рисунок$\PageIndex{17}$ (b).

2. Далі додайте 2 до значення y кожної точки на графіку y = −f (x) на малюнку$\PageIndex{17}$ (b), щоб отримати графік y = −f (x) + 2 на малюнку$\PageIndex{17}$ (c).

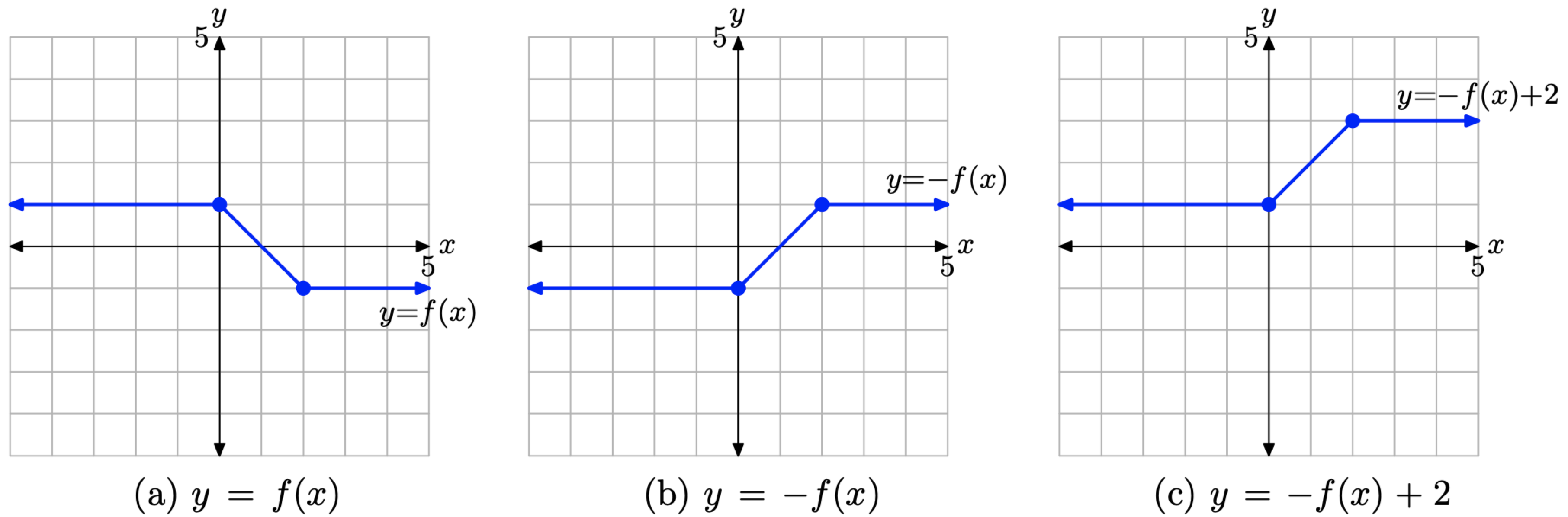
$WeChat890a4972b242609b51359f499af540fc.png$

Малюнок$\PageIndex{17}$. Трансформуючи графік y = f (x), спочатку відбиваючи поперек осі x, потім зміщуючи 2 одиниці вгору для отримання графіка y = −f (x) + 2.

У прикладі$\PageIndex{7}$, де ми почали з графа y = f (x), а потім графували y = 2f (x), порядок перетворень не мав значення. Масштабувати на 2, потім звести нанівець, або звести нанівець і масштабувати на 2, ви отримаєте той же результат (читачі повинні перевірити це твердження). Однак у цьому прикладі порядок, в якому застосовуються перетворення, має значення. Щоб переконатися в цьому, давайте зробимо наступне:

Додайте 2, щоб зрушити графік y = f (x) на малюнку$\PageIndex{18}$ (a) дві одиниці вгору, щоб отримати графік y = f (x) + 2 на малюнку$\PageIndex{18}$ (b).
Зніміть значення y кожної точки на графіку y = f (x) + 2 на малюнку$\PageIndex{18}$ (b), щоб отримати графік y = − (f (x) + 2) на малюнку$\PageIndex{18}$ (c). Зверніть увагу, що ми повинні звести нанівець все значення y. Звідси дужки.

На жаль, графік y = − (f (x) + 2) на малюнку$\PageIndex{18}$ (c) не збігається з графіком y = −f (x) + 2 на малюнку$\PageIndex{17}$ (c). Але звичайно, це має повний сенс, так як рівняння (у випадку з малюнком$\PageIndex{18}$ (в))

\[y=-(f(x)+2)=-f(x)-2\]

і (у випадку з малюнком$\PageIndex{17}$ (c))

\[y=-f(x)+2\]

теж не однакові.

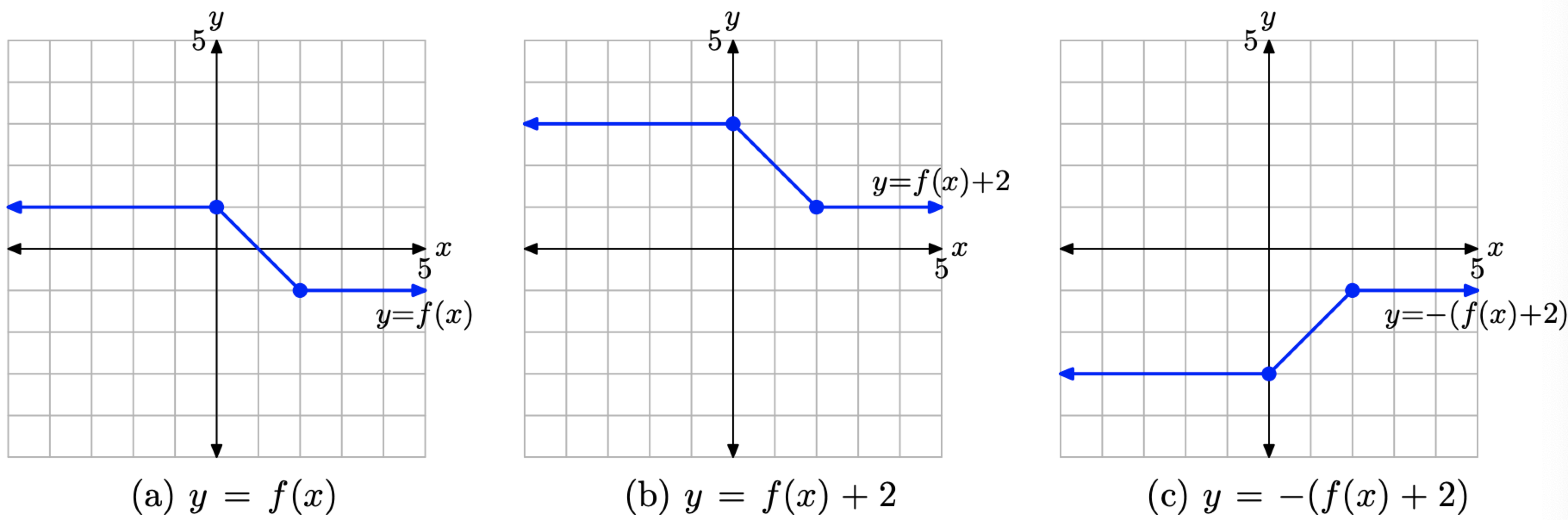
$WeChatbf6ad2cde0793cd167583aec2ba44f13.png$

Малюнок$\PageIndex{18}$. Трансформуючи графік y = f (x), зміщуючи 2 одиниці вгору для отримання графіка y = f (x) + 2, потім відбиваючи поперек осі x для отримання графіка y = − (f (x) + 2).

Тому слід дотримуватися обережності при застосуванні не одного перетворення. Ось гарне правило, щоб жити.

Спочатку виконуйте вертикальні масштабування та відображення, потім вертикальні переклади. При виконанні послідовності вертикальних перетворень зазвичай простіше (менш заплутано) застосовувати вертикальні масштабування та відображення перед вертикальними перекладами.

Однак, поки ви виконуєте перетворення правильно, ви повинні отримати правильний результат. У прикладі$\PageIndex{8}$, якщо ви хочете намалювати графік y = −f (x) +2, виконавши перший переклад, правильний шлях буде наступним (хоча дещо неінтуїтивним):

Спочатку зсуньте графік y = f (x) вниз на 2 одиниці, щоб отримати графік y = f (x) − 2.
По-друге, відобразіть графік y = f (x) − 2 по осі x, щоб отримати графік y = − (f (x) − 2). Знову ж таки, зверніть увагу на використання дужок, оскільки ми заперечуємо все значення y.

Нарешті, зауважте, що\[y=-(f(x)-2)=-f(x)+2\]

Ми залишимо це нашим читачам, щоб показати, що ця послідовність дає правильний результат, графік, ідентичний правильній відповіді, показаній на малюнку$\PageIndex{17}$ (c).

Резюме

У цьому розділі ми бачили, як кілька перетворень значно покращують наші можливості графіків. Ми закінчуємо цей розділ перерахуванням перетворень, представлених у цьому розділі, та їх впливу на графік функції.

Вертикальні перетворення.

Вертикальні перетворення. Припустимо, нам дано графік y = f (x).

Якщо$a > 1$, то графік y = af (x) розтягується вертикально (від осі х), як позитивно, так і негативно, в рази a.
Якщо$0 < a < 1$, то графік y = af (x) стискається вертикально (до осі х), як позитивно, так і негативно, в рази 1/a.
Графік y = −f (x) є відображенням графіка y = f (x) по осі x.
Якщо$c > 0$, то графік y = f (x) + c зміщений c одиницями вгору від графа y = f (x).
Якщо$c > 0$, то графік y = f (x) − c зміщується на c одиниць вниз від графа y = f (x).