1.3: Логіка
- Page ID
- 58055
Два найтонших слова в англійській мові - це слова «і» і «або». Одна має всього три літери, дві інші, але абсолютно дивно, скільки плутанини ці два крихітних слова можуть викликати. Наш намір у цьому розділі полягає в тому, щоб очистити таємницю навколо цих слів і підготувати вас до математики, яка залежить від ретельного розуміння слів «і» і «або».
Встановити позначення
Починаємо з визначення набору.
Визначення 1
Набір - це сукупність предметів.
Об'єктами в наборі може бути взагалі що завгодно: цифри, букви, імена, міста, ви називаєте його. У цьому розділі мова піде про набори чисел, але важливо розуміти, що об'єкти в наборі можуть бути якими б ви їх не вибрали.
Якщо кількість об'єктів у множині кінцева і досить мала, ми можемо описати множину просто перерахувавши елементи (об'єкти) у множині. Зазвичай це робиться шляхом укладення списку об'єктів у множині фігурними дужками. Наприклад, нехай
\[A=\{1,3,5,7,9,11\}\]
Тепер, коли ми посилаємося на набір\(A\) в оповіданні, кожен повинен знати, що ми говоримо про набір чисел 1, 3, 5, 7, 9 та 11.
Також можна описати безліч\(A\) словами. Хоча існує багато способів зробити це, одним з можливих описів може бути «\(A\)Дозволяти бути набір непарних натуральних чисел між 1 і 11 включно». Цей описовий метод особливо ефективний, коли набір, який ви описуєте, є або нескінченним, або занадто великим, щоб перерахувати у списку.
Наприклад, ми можемо сказати «нехай\(A\) буде набір всіх дійсних чисел, які більше, ніж\(4.\)» Це набагато краще, ніж намагатися перерахувати кожне з чисел у множині\(A\), що було б марно в цьому випадку. Інша можливість - поєднати позначення фігурної дужки з текстовим описом і написати щось на кшталт
\[A=\{ \text{real numbers that are greater than }4\}\]
Якщо ми покликані прочитати це позначення вголос, ми б сказали, що «\(A\)це набір всіх дійсних чисел, які більше, ніж\(4,\)» або щось подібне.
Існує ряд більш складних методів, які ми можемо використовувати для опису набору. Один опис, який ми часто використовуватимемо, називається позначенням set-builder і має наступний вигляд.
\[A=\{x : \text{some statement describing }x\}\]
Стандартно читати позначення\(\{x : \quad\}\) вголос наступним чином: «Безліч всього\(x\) такого, що». Тобто товста кишка вимовляється «такий що». Тоді ви б прочитали опис, що слідує за двокрапкою. Наприклад, набір
\[A=\{x : x<3\}\]
читається вголос «\(A\)це набір всіх\(x\) таких, що\(x\) менше, ніж\(3.\)» Деякі люди вважають за краще використовувати «бар» замість двокрапки, і вони пишуть
\[A=\{x \, | \,\text { some statement describing } x\}\]
Це також вимовляється «\(A\)є набір всіх\(x\) таких, що», і тоді ви б прочитали текстовий опис, який слідує за «планкою». Таким чином, позначення
\[A=\{x \, | \, x<3\}\]
ідентичний позначенню,\(A=\{x : x<3\}\) використаному вище, і читається точно так само: «A - це набір всіх\(x\) таких, що\(x\) менше 3». Ми віддаємо перевагу позначенню двокрапки, але сміливо використовуйте «бар», якщо вам це більше подобається. Це означає те ж саме.
Мить думка розкриє той факт, що позначення не\(A=\{x : x<3\}\) зовсім описове. Напевно, можна з упевненістю сказати, оскільки опис\(x\) є «\(x < 3,\)», що це позначення стосується чисел, які менше 3, але які числа? Натуральні числа? Цілі числа? Раціональні числа? Ірраціональні числа? Реальні числа? Позначення насправді\(A=\{x : x<3\}\) не розповідають всю історію.
Ми виправимо цей недолік за мить, але спочатку нагадаємо, що в нашому попередньому розділі ми використовували конкретні символи для представлення певних наборів чисел. Дійсно, ми використовували наступне:
\[\begin{aligned} \mathbb{N} &=\{\text { natural numbers }\} \\ \mathbb{Z} &=\{\text { integers }\} \\ \mathbb{Q} &=\{\text { rational numbers }\} \\ \mathbb{R} &=\{\text { real numbers }\} \end{aligned}\]
Ми можемо використовувати ці символи, щоб допомогти позначити тип числа, описаного за допомогою нашої нотації setbuilder. Наприклад, якщо ми пишемо
\[A=\{x \in \mathbb{N} : x<3\}\]
то ми говоримо «A - це множина всіх х в натуральних числах, таких, що х менше 3,» або простіше кажучи, «множина всіх натуральних чисел, які менше 3.» Символ\(∈\) є грецькою літерою «епсилон», і при використанні в позначенні множників він вимовляється «є елементом», або «знаходиться в». Звичайно, єдиними натуральними числами\(\mathbb{N}=\{1,2,3, \ldots\}\), які менше 3, є натуральні числа 1 і 2. Таким чином\(A = {1, 2}\), «набір, членами якого є 1 і 2».
З іншого боку, якщо ми пишемо
\[A=\{x \in \mathbb{Z} : x<3\}\]
то ми говоримо, що «\(A\)є множиною\(x\) в множині цілих чисел, таких,\(x\) що менше 3,» або більш неформально, «\(A\)є множиною всіх цілих чисел менше 3.» Звичайно, цілі числа\(\mathbb{Z}=\{0, \pm 1, \pm 2, \pm 3, \ldots\}^{2}\) менше 3 нескінченні за кількістю. Ми не можемо перерахувати їх усіх, якщо не звернемося до уяви чимось на зразок
\[A=\{\ldots,-3,-2,-1,0,1,2\}\]
Трикрапка.. означає «і т.д.» Ми перерахували достатню кількість чисел, щоб встановити шаблон, тому нам дозволено сказати «і так далі». Зчитувач розуміє, що ранніми номерами у списку є −4, −5 тощо.
Давайте розглянемо інший приклад. Припустимо, що ми пишемо\[A=\{x \in \mathbb{R} : x<3\}\]
Тоді ми говоримо «\(A\)це множина всіх\(x\) у множині дійсних чисел, таких,\(x\) що менше 3», або більш неформально, «\(A\)є множиною всіх дійсних чисел менше 3». Звичайно, це ще один нескінченний набір і неважко уявити, що позначення,\(\{x \in \mathbb{R} : x<3\}\) використані вище, вже оптимальні для опису цього набору дійсних чисел.
У цьому тексті ми в основному будемо мати справу з наборами дійсних чисел. Таким чином, з цього моменту вперед, якщо ми пишемо
\[A=\{x : x<3\}\]
ми будемо вважати, що ми маємо на увазі сказати, що «\(A\)це набір всіх дійсних чисел менше 3». Тобто, якщо ми пишемо\(A=\{x : x<3\}\), ми розуміємо, що це означає\(A=\{x \in \mathbb{R} : x<3\}\). У разі, коли ми хочемо використовувати певний набір чисел, ми вкажемо, що, як ми це робили вище, наприклад, в\(A=\{x \in \mathbb{N} : x<3\}\).
Позначення дійсної лінії та інтервалу
Припустимо, що ми намалюємо лінію (ласкаво відому як «реальна лінія»), потім намалюємо точку в будь-якому місці цієї лінії, а потім зіставляємо число нуль до цієї точки (називається «походження»), як показано на малюнку\(\PageIndex{1}\). По-друге, визначитеся з одиницею відстані і зіставте число 1 до цієї точки, знову показано на малюнку\(\PageIndex{1}\).
Тепер, коли ми встановили одиницю відстані, кожне дійсне число відповідає точці на реальній лінії. Навпаки, кожна точка на дійсній прямій відповідає дійсному числу. Це визначає відповідність один до одного між дійсними числами в\(\mathbb{R}\) і точками на дійсній лінії. Таким чином, точка на лінії і дійсне число можна розглядати як синоніми. \(\PageIndex{2}\)На малюнку показано кілька дійсних чисел, нанесених на дійсну лінію.
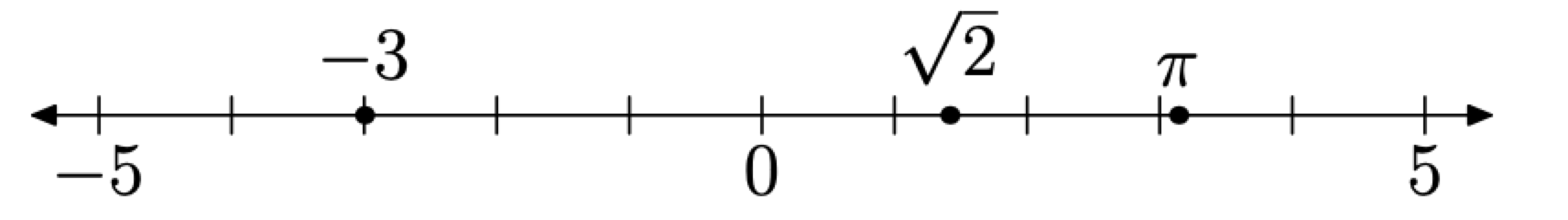
Малюнок\(\PageIndex{2}\) Приклад чисел на дійсному рядку.
Тепер, припустимо, що нас просять затінювати всі дійсні числа в наборі\(\{x : x>3\}\). Оскільки це вимагає, щоб ми затінювали кожне дійсне число, яке більше 3 (праворуч від 3), ми використовуємо затінення, показане на малюнку,\(\PageIndex{3}\) щоб представити набір\(\{x : x>3\}\).
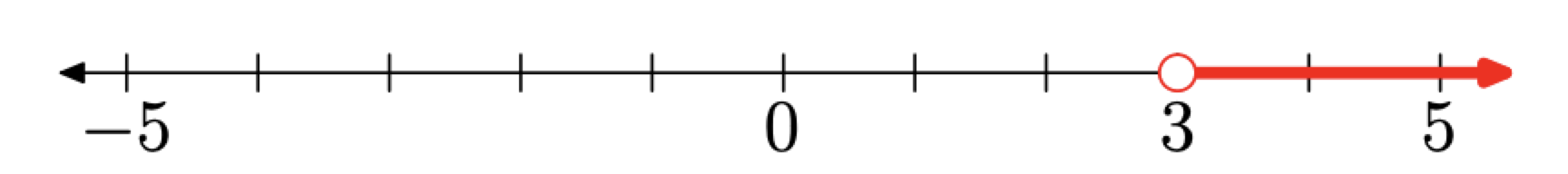
Хоча технічно коректно, зображення на малюнку 3 містить більше інформації, ніж насправді потрібно. Картина прийнятна, але багатолюдна. Дійсно важливою інформацією є той факт, що затінення починається з 3, потім рухається вправо. Крім того, оскільки 3 немає в множині\({x : x > 3}\), тобто 3 не більше 3, ми не затінюємо точку, відповідну дійсному числу 3. Зверніть увагу, що ми вказали цей факт з «порожнім» колом на 3 на реальній лінії.
Таким чином, при затіненні множини\({x : x > 3}\) на реальній лінії нам потрібно лише позначити кінцеву точку на 3, використовувати «порожнє» коло в 3 і затінювати всі дійсні числа праворуч від 3, як показано на малюнку\(\PageIndex{4}\).

Малюнок\(\PageIndex{4}\). Затінення всіх дійсних чисел більше 3. Кінцева точка - єдина інформація, яку потрібно позначити. Не потрібно показувати будь-які інші точки та/або мітки.
Оскільки ми затінюємо всі числа від 3 до позитивної нескінченності на малюнку\(\PageIndex{4}\), ми будемо використовувати наступні інтервальні позначення для представлення цього «інтервалу» чисел (все між 3 і позитивною нескінченністю).
\[(3, \infty)=\{x : x>3\}\]
Аналогічно, Таблиця\(\PageIndex{1}\) перераховує позначення set-builder та інтервалу, а також затінення множин на реальному рядку, для кількох ситуацій, включаючи щойно обговорювану.
Існує кілька точок акценту щодо інтервалів в табл\(\PageIndex{1}\).
1. Коли ми хочемо підкреслити, що ми не включаємо точку на реальній лінії, ми використовуємо «порожнє коло». І навпаки, «заповнене коло» означає, що ми включаємо точку на реальній лінії. Таким чином, дійсні рядки в перших двох рядках Таблиці\(\PageIndex{1}\) не включають число 3, але реальні рядки в останніх двох рядках таблиці\(\PageIndex{1}\) включають число 3.
2. Використання дужки в інтервальних позначеннях означає, що ми не включаємо цю кінцеву точку в інтервал. Таким чином, використання дужок\((-\infty, 3)\) у другому рядку таблиці\(\PageIndex{1}\) означає, що ми не включаємо число 3 в інтервал.
| Номер рядка | Позначення Set-Builder | Інтервальні позначення |
|---|---|---|
 |
\(\{x : x > 3\}\) | \((3, \infty)\) |
 |
\(\{x : x < 3\}\) | \((-\infty, 3)\) |
 |
\(\{x : x \geq 3\}\) | \([3, \infty)\) |
 |
\(\{x : x \leq 3\}\) | \((-\infty, 3]\) |
3. Використання дужки в інтервальних позначеннях означає, що ми включаємо в інтервал число в дужках. Таким чином, дужка використовується в\([3, \infty)\), як видно в третьому рядку таблиці\(\PageIndex{1}\), означає, що ми включаємо число 3 в інтервал.
4. Використання\(\infty\)\((3, \infty)\) в рядку один з таблиці\(\PageIndex{1}\) означає, що ми включаємо кожне дійсне число більше 3. Використання\(-\infty\) в\((-\infty, 3]\) означає, що ми включаємо кожне дійсне число менше або дорівнює 3. Оскільки\(-\infty\) і не\(\infty\) є фактичними цифрами, немає сенсу включати їх за допомогою дужки. Отже, ви завжди повинні використовувати дужки з\(-\infty\) або\(\infty\).
Союз і перетин
Перетин двох множин\(A\) і\(B\) визначається наступним чином.
Визначення 3
Перетин множин\(A\) і\(B\) є сукупністю всіх об'єктів, які знаходяться в\(A\) і в\(B\). В символах пишемо
\[A \cap B=\{x : x \in A \text { and } x \in B\}\]
Для того щоб зрозуміти це визначення, абсолютно важливо, щоб ми розуміли значення слова «і». Слово «і» - це сполучник, що використовується між\(Q\) твердженнями\(P\) і, як у «Сьогодні йде дощ, і мій найкращий друг - Самотній рейнджер». Для того щоб визначити правдивість або неправдивість цього твердження, необхідно спочатку вивчити істинність або неправдивість висловлювань\(P\) і з кожного\(Q\) боку слова «і».
Єдиний спосіб, яким оратор говорить правду, - це якщо обидва твердження\(P\) і\(Q\) вірні. Іншими словами, твердження «Сьогодні йде дощ, і мій найкращий друг - Самотній рейнджер» вірно тоді і лише тоді, коли твердження «Сьогодні йде дощ», і твердження «мій найкращий друг - Самотній рейнджер» також вірно. Логікам подобається складати конструкцію, яка називається таблицею істинності, подібно до тієї, що наведена в табл\(\PageIndex{2}\).
Пункти в таблиці\(\PageIndex{2}\), які слід враховувати:
| \(P\) | \(Q\) | \(P\)і\(Q\) |
|---|---|---|
| \ (P\) ">Т | \ (Q\) ">Т | \ (Р\) і\(Q\) «>Т |
| \ (P\) ">Т | \ (Q\) ">F | \ (P\) і\(Q\) «>F |
| \ (P\) ">F | \ (Q\) ">Т | \ (P\) і\(Q\) «>F |
| \ (P\) ">F | \ (Q\) ">F | \ (P\) і\(Q\) «>F |
- У першому рядку (після рядка заголовка) таблиці\(\PageIndex{2}\), якщо оператори\(P\) і обидва\(Q\) істинні (позначені буквою T), то твердження «\(P\)і\(Q\)» також вірно.
- В інших рядках\(\PageIndex{2}\) Таблиці одне або інше твердження\(P\) або\(Q\) є помилковими (позначені F), тому твердження «\(P\)і\(Q\)» також є помилковим.
Тому твердження «\(P\)і\(Q\)» вірно тоді і тільки тоді, коли\(P\) є істинним і\(Q\) є істинним.
Приклад\(\PageIndex{1}\)
Якщо\(A = \{1, 3, 5, 7, 9\}\) і\(B = \{2, 5, 7, 8, 11\},\) знайти перетин\(A\) і\(B.\)
Рішення
Як нагадування, перетин множин\(A\) і\(B\) є
\[A \cap B=\{x : x \in A \text { and } x \in B\}\]
Таким чином, ми шукаємо об'єкти, які знаходяться в\(A\) і в\(B.\) Єдині об'єкти, які знаходяться в\(A\) і в\(B\) (пам'ятайте, обидва твердження «in\(A\)» і «in\(B\)» повинні бути істинними) є 5 і 7, тому ми пишемо:
\[A \cap B=\{5,7\}\]
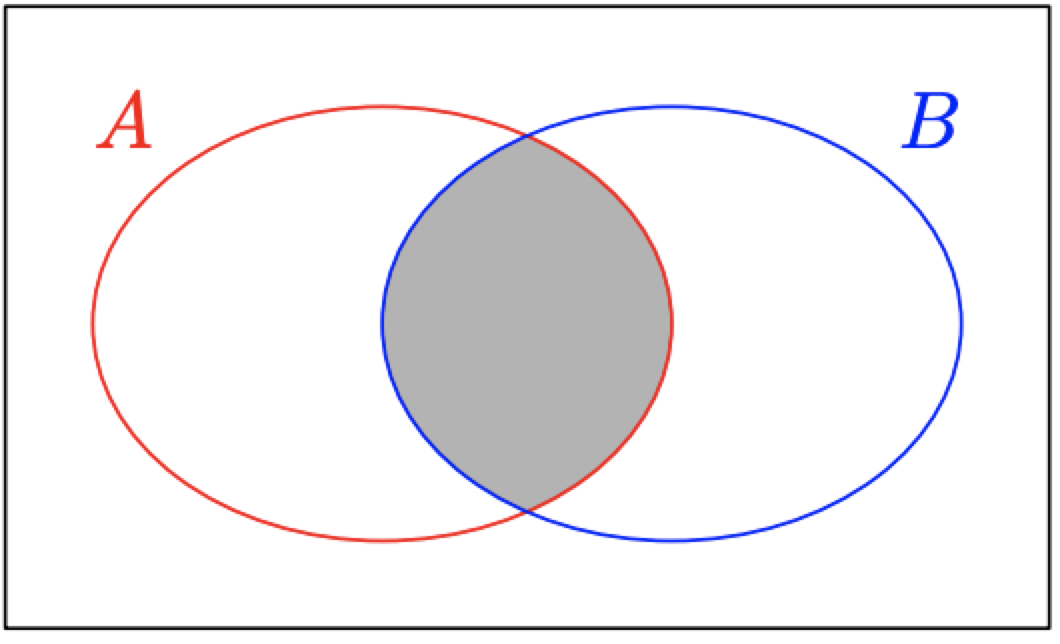
Математики та логіки використовують наочний посібник під назвою діаграма Венна для представлення множин. Джон Венн був англійським математиком, який розробив цю візуалізацію логічних зв'язків. Розглянемо еліпс\(A\) на малюнку\(\PageIndex{5}\). Все, що знаходиться всередині кордону цього еліпса, становить безліч\(A = \{1, 3, 5, 7, 9\}.\) Ось чому ви бачите ці числа всередині кордону цього еліпса.
Розглянемо еліпс\(B\) на малюнку\(\PageIndex{5}\). Все, що знаходиться всередині кордону цього еліпса, становить безліч\(B = \{2, 5, 7, 8, 11\}.\) Ось чому ви бачите ці числа всередині кордону цього еліпса.
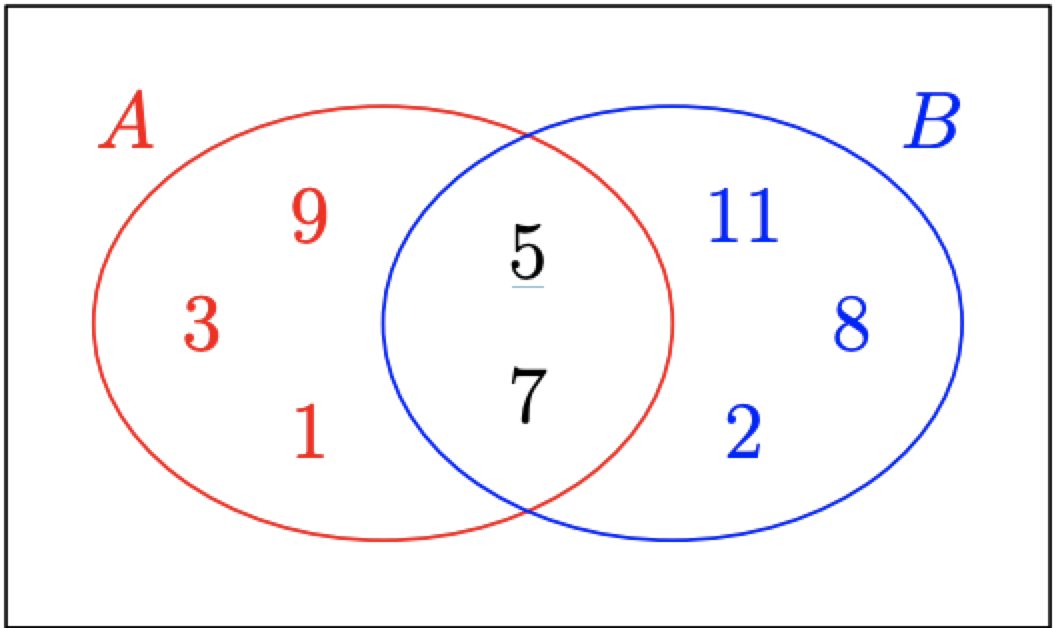
Тепер зверніть увагу, що тільки два числа,\(5\) і\(7,\) містяться в межах обох\(A\) і\(B.\) Це числа, які знаходяться в перетині множин\(A\) і\(B.\)
Затінена область на малюнку\(\PageIndex{6}\) - це область, яка належить до обох наборів,\(A\) і\(B.\) Зверніть увагу, як ця затінена область влучно називається «перетином множин\(A\) і\(B.\)» Це область, яка є спільною для множин\(A\) і\(B,\) область, де \(A\)множини і\(B\) перекриваються або «перетинаються».
Це призводить до наступних важливих порад.
Примітка
Коли просять знайти перетин двох множин\(A\) і\(B,\) подивитися, де множини перетинаються або перекриваються. Тобто подивіться, щоб побачити елементи, які є в обох наборах\(A\) і\(B.\)
Перейдемо до визначення об'єднання двох множин\(A\) і\(B.\)
Визначення
Об'єднання множин\(A\) і\(B\) являє собою сукупність всіх об'єктів, які знаходяться в\(A\) або в символах\(B.\) В, ми пишемо
\[A \cup B=\{x : x \in A \text { or } x \in B\}\]
Для того щоб зрозуміти це визначення, дуже важливо, щоб ми розуміли значення слова «або». Слово «або» - це диз'юнкція, що використовується між твердженнями\(P\) і\(Q,\) як у «Сьогодні йде дощ або мій найкращий друг - самотній рейнджер». Для того щоб визначити правдивість або неправдивість цього твердження, необхідно спочатку вивчити істинність або неправдивість висловлювань\(P\) і з кожного\(Q\) боку слова «або».
Доповідач говорить правду, якщо будь-яке твердження\(P\) є істинним, або твердження\(Q\) є правдою. Іншими словами, твердження «Сьогодні йде дощ або мій найкращий друг - Самотній рейнджер» вірно тоді і лише тоді, коли твердження «Сьогодні йде дощ» або твердження «мій найкращий друг - Самотній рейнджер» вірно. Логікам подобається складати конструкцію, яка називається таблицею істинності, подібно до тієї, що наведена в табл\(\PageIndex{3}\).
| \(P\) | \(Q\) | \(P\)або\(Q\) |
|---|---|---|
| \ (P\) ">Т | \ (Q\) ">Т | \ (Р\) або\(Q\) «>Т |
| \ (P\) ">Т | \ (Q\) ">F | \ (Р\) або\(Q\) «>Т |
| \ (P\) ">F | \ (Q\) ">Т | \ (Р\) або\(Q\) «>Т |
| \ (P\) ">F | \ (Q\) ">F | \ (P\) або\(Q\) «>F |
Пункти в таблиці\(\PageIndex{3}\), які слід враховувати:
- В останньому рядку таблиці\(\PageIndex{3}\) обидва твердження\(P\) і\(Q\) є помилковими (позначені з F), тому твердження\(P\) або також\(Q\) є помилковим.
- У перших трьох рядках (після рядка заголовка) таблиці\(\PageIndex{3}\), або оператор\(P\) true, або оператор true (\(Q\)позначається з T), тому твердження\(P\) або\(Q\) також true.
Тому твердження «\(P\)або\(Q\)» є істинним тоді і тільки тоді, коли або твердження,\(P\) або\(Q,\) є істинним.
Приклад\(\PageIndex{2}\)
Якщо\(A = \{1, 3, 5, 7, 9\}\) і\(B = \{2, 5, 7, 8, 11\},\) знайти союз\(A\) і\(B.\)
Рішення
Як нагадування, об'єднання\(A\) і\(B\) є\[A \cup B=\{x : x \in A \text { or } x \in B\}\]
Таким чином, об'єкт знаходиться в об'єднанні\(A\) і\(B\) якщо і тільки в тому випадку, якщо він знаходиться в будь-якому наборі. Числа, які знаходяться в будь-якому наборі, - це цифри\[A \cup B=\{1,2,3,5,7,8,9,11\}\]
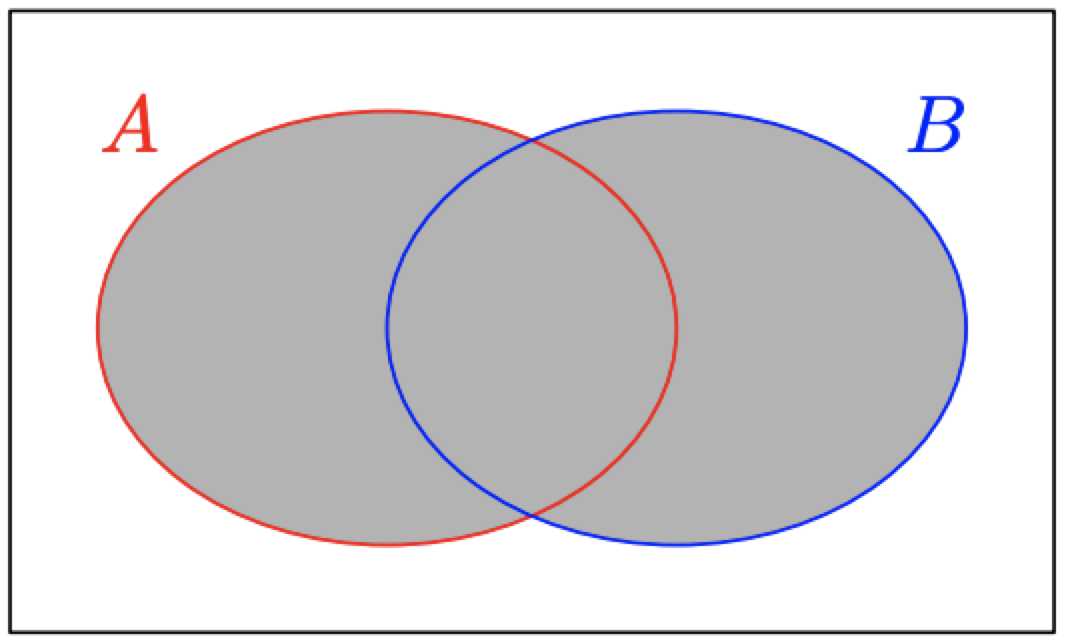
Якщо ми знову подивимося на діаграму Венна на малюнку\(\PageIndex{5}\), ми бачимо, що це об'єднання\(A \cup B = \{1, 2, 3, 5, 7, 8, 9, 11\}\) перераховує кожне число, яке знаходиться в будь-якому встановленому на малюнку\(\PageIndex{5}\).
Таким чином, затінена область на малюнку\(\PageIndex{7}\) є об'єднанням множин\(A\) і\(B.\) Зверніть увагу, як ця область добре названа, як це те, що ви насправді робите, беручи «об'єднання» двох множин\(A\) і\(B.\) тобто об'єднання містить всі елементи, які належать або\(A\) або \(B.\)Менш формально союз - це спосіб об'єднання всього, що відбувається в будь-якому наборі.
Це призводить до наступних важливих порад.
Примітка
Коли вас попросять знайти об'єднання двох наборів\(A\) і\(B,\) у вашій відповіді, включіть все з обох наборів.
Прості складні нерівності
Давайте застосуємо те, що ми навчилися, щоб знайти об'єднання і/або перетину інтервалів дійсних чисел. Найпростіший підхід - через низку прикладів. Почнемо.
Приклад\(\PageIndex{3}\)
На реальному рядку намалюйте набір дійсних чисел у множині\(\{x : x < 3\) або\(x < 5\}.\) Використовуйте інтервальне позначення для опису вашої остаточної відповіді.
Рішення
Спочатку давайте накидаємо два\(\{x : x < 3\}\) набори, і\(\{x : x < 5\},\) на окремих реальних лініях, один поверх іншого, як показано на малюнку\(\PageIndex{8}\).
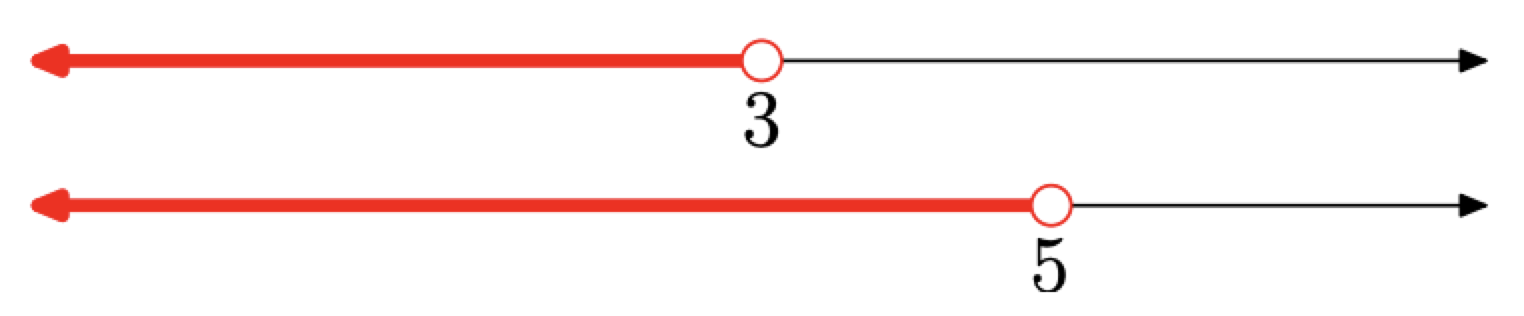
Тепер, щоб накидати рішення, зверніть увагу на слово «або» в наборі\(\{x : x < 3\) або\(x < 5\}.\) Таким чином, нам потрібно взяти об'єднання двох затінених реальних ліній на малюнку\(\PageIndex{8}\). Тобто нам потрібно затінювати все, що затінено на будь-якій з двох числових рядків. Звичайно, це було б все менше 5, як показано на малюнку\(\PageIndex{9}\).

Таким чином, кінцевим рішенням є те,\(\{x : x < 5\},\) що в інтервальних позначеннях, є\((-\infty, 5)\).
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{4}\)
На реальному рядку намалюйте набір дійсних чисел у множині\(\{x : x < 3\) та\(x < 5\}.\) Використовуйте інтервальне позначення для опису вашої остаточної відповіді.
Рішення
У\(\PageIndex{3}\) прикладі вас попросили затінювати набір\(\{x : x < 3\) або\(x < 5\}\) на реальну лінію. У цьому прикладі нам пропонується намалювати набір\(\{x : x < 3\) і\(x < 5\}.\) Зауважте, що позначення set-builder ідентичні, за винятком однієї зміни, «або» Прикладу\(\PageIndex{3}\) було замінено словом «і».
Знову накидайте два\(\{x : x < 3\}\) набори, і\(\{x : x < 5\},\) на окремих реальних лініях, один поверх іншого, як показано на малюнку\(\PageIndex{10}\).
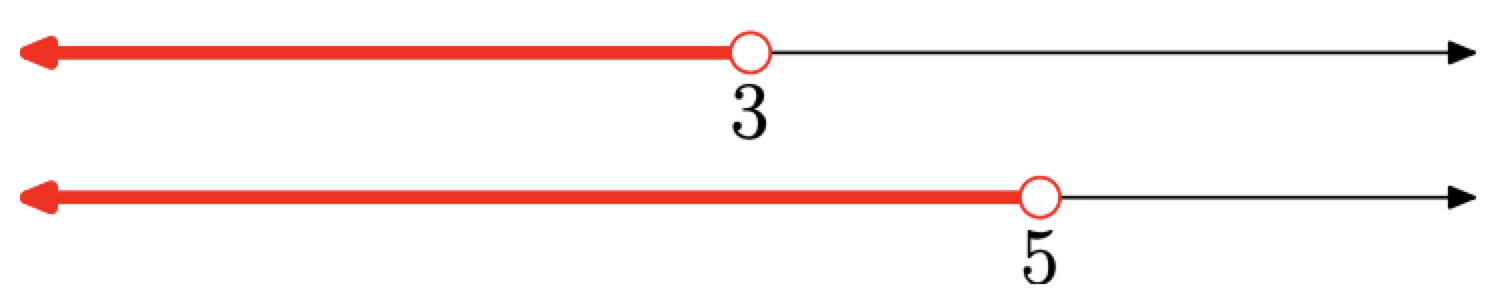
Тепер, щоб накидати рішення, зверніть увагу на слово «і» в\(\{x : x < 3\) наборі і\(x < 5\}.\) Таким чином, нам потрібно взяти перетин двох заштрихованих реальних ліній на малюнку\(\PageIndex{10}\). Тобто нам потрібно затінювати все, що є загальним для двох числових рядків. Звичайно, це було б все менше 3, як показано на малюнку\(\PageIndex{11}\).

Таким чином, кінцевим рішенням є те,\(\{x : x < 3\},\) що в інтервальних позначеннях, є\((-\infty, 3)\).
Примітка
Якщо ви відповідаєте «або», коли відповідь вимагає «і» або навпаки, ви не зробили незначної помилки. Дійсно, це величезна помилка, як продемонстровано в Example\(\PageIndex{3}\) і Example\(\PageIndex{4}\).
Перш ніж спробувати інший приклад, ми робимо паузу, щоб визначити трохи позначення, яке буде надзвичайно важливим у нашій майбутній роботі.
Визначення
позначення
\[a<x<b\]
інтерпретується як означає
\[x>a \text { and } x<b\]
Крім того, ми могли б сказати, що\(a < x < b\) це ідентично висловлюванню «\(a < x\)і\(x < b,\)», але сказати «\(a < x\)» - це те саме, що сказати «\(x > a.\)» Ми вважаємо за краще говорити «\(x > a\)і\(x < b,\)» і будемо використовувати цей порядок протягом всієї нашої роботи, але форма «\(a < x\)і\(x < b\)» однаково дійсний.
Дійсно ключовим моментом, який слід зробити тут, є той факт, що твердження\(a < x < b\) є твердженням «і». Якщо він використовується належним чином, це хороший спосіб описати числа, які лежать між\(a\) і\(b.\)
Давайте розглянемо приклад.
Приклад\(\PageIndex{5}\)
На реальному рядку намалюйте набір дійсних чисел у множині\(\{x : 3 < x < 5\}.\) Використовуйте інтервальне позначення для опису вашої відповіді.
Рішення
Спочатку напишемо, що мається на увазі під\(\{x : 3 < x < 5\}.\) позначенням. За визначенням цей набір збігається з множиною
\[\{x : x>3 \text { and } x<5\}\nonumber\]
Таким чином, першим кроком є ескіз множин\(\{x : x > 3\}\) і\(\{x : x < 5\}\) на окремих реальних лініях, укладених одна на іншу, як показано на малюнку\(\PageIndex{12}\).

Тепер, щоб накидати рішення, зверніть увагу на слово «і» в\(\{x : x > 3\) наборі і\(x < 5\}.\) Таким чином, нам потрібно взяти перетин двох ліній на малюнку\(\PageIndex{12}\). Тобто нам потрібно затінювати числа на дійсній лінії, які є загальними для двох рядків, показаних на малюнку\(\PageIndex{12}\). Цифри 3 і 5 не затінені в обох наборах на малюнку\(\PageIndex{12}\), тому вони не будуть затінені в нашому остаточному рішенні. Однак усі дійсні числа між 3 та 5 затінені в обох наборах на малюнку\(\PageIndex{12}\), тому ці числа будуть затінені в остаточному рішенні, показаному на малюнку\(\PageIndex{13}\).

Найбільш природним чином інтервальне позначення для затіненого розчину на малюнку\(\PageIndex{13}\) є\((3, 5).\) Тобто
\[(3,5)=\{x : 3<x<5\}\]
Аналогічно, ось set-builder і інтервальні позначення, а також затінення множин на реальній лінії, для декількох ситуацій, включаючи щойно обговорювану.
| Номер рядка | Позначення Set-Builder | Інтервальні позначення |
|---|---|---|
 |
\(\{x : 3 < x < 5\}\) | \((3,5)\) |
 |
\(\{x : 3 \leq x \leq 5\}\) |
\([3,5]\) |
 |
\(\{x : 3 \leq x < 5\}\) | \([3,5)\) |
 |
\(\{x : 3 < x \leq 5\}\) | \((3,5]\) |
Існує кілька точок акценту щодо інтервалів в табл\(\PageIndex{4}\).
- Коли ми хочемо підкреслити, що ми не включаємо точку на реальній лінії, ми використовуємо «порожнє коло». І навпаки, «заповнене коло» означає, що ми включаємо точку на реальній лінії. Таким чином, інтервал у першому рядку таблиці\(\PageIndex{4}\) не включає кінцеві точки на 3 і 5, але інтервал у другому рядку таблиці\(\PageIndex{4}\) включає кінцеві точки на 3 і 5.
- Використання дужки в інтервальних позначеннях означає, що ми не включаємо цю кінцеву точку в інтервал. Таким чином, дужки, використані\((3, 5)\) в першому рядку таблиці,\(\PageIndex{4}\) означає, що ми не включаємо числа 3 і 5 в цьому інтервалі.
- Використання дужки в інтервальних позначеннях означає, що ми включаємо в інтервал число в дужках. Таким чином, дужки, використані в,\([3, 5],\) як видно в другому рядку таблиці\(\PageIndex{4}\), означає, що ми включаємо числа 3 і 5 в інтервал.
- Нарешті, зауважте, що деякі з наших інтервалів «відкриті» на одному кінці, але «закриті» (заповнені) на іншому кінці, наприклад, у рядках 3 та 4 таблиці\(\PageIndex{4}\).
Визначення
Деяка термінологія:
- Інтервал\((3, 5)\) відкритий з кожного кінця. Тому ми називаємо інтервал відкритим\((3, 5)\) інтервалом.
- Інтервал\([3, 5]\) закривається (заповнюється) на кожному кінці. Тому ми називаємо\([3, 5]\) інтервал замкнутим інтервалом.
- Інтервали\((3, 5]\) і не\([3, 5)\) є ні відкритими, ні закритими.
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{6}\)
На реальній лінії накидайте множину всіх дійсних чисел в\(\{x : x > 3\) множині або\(x < 5\}\). Використовуйте інтервальне позначення для опису вашої відповіді.
Рішення
Зауважте, що єдиною відмінністю між цим\(\PageIndex{4}\) поточним прикладом і набором затінених у Прикладі є те, що ми замінили слово «\(\{x : x > 3\)і\(x < 5\}\)» на слово «або» в\(\{x : x > 3\) або\(x < 5\}\). Але, як ми бачили раніше, це може змінити світ.
Таким чином, першим кроком є ескіз множин\(\{x : x > 3\}\) і\(\{x : x < 5\}\) на окремих реальних лініях, укладених одна на іншу, як показано на малюнку\(\PageIndex{14}\).

Тепер, щоб накидати рішення, зверніть увагу на слово «або» в наборі\(\{x : x > 3 or x < 5\}\). Таким чином, нам потрібно взяти об'єднання двох рядків на малюнку\(\PageIndex{14}\). Тобто нам потрібно затінювати числа на дійсній лінії, які затінені на будь-якій з двох ліній, показаних на малюнку\(\PageIndex{14}\). Однак це означає, що нам доведеться затінювати кожне число на лінії, як показано на малюнку\(\PageIndex{15}\). Ви не помітили жодних міток для 3 та 5 на реальному рядку на малюнку\(\PageIndex{15}\), оскільки в цьому рішенні немає кінцевих точок. Кінцеві точки, якщо хочете, знаходяться в негативній і позитивній нескінченності.

Таким чином, найбільш природним чином інтервальні позначення для затіненого розчину на малюнку\(\PageIndex{15}\) є\((-\infty, \infty)\).
Давайте розглянемо інший приклад.
Приклад\(\PageIndex{7}\)
На реальній лінії накидайте множину всіх дійсних чисел в\(\{x : x < −1\) множині або\(x > 3\}\). Використовуйте інтервальне позначення для опису вашої відповіді.
Рішення
Насамперед необхідно накидати\(\{x : x < −1\}\) набори і\(\{x : x > 3\}\) на окремих реальних лініях, укладаються одна на іншу, як показано на малюнку\(\PageIndex{16}\).

Щоб накидати рішення, зверніть увагу на слово «або» в наборі\(\{x : x < −1\) або\(x > 3\}\). Таким чином, нам потрібно взяти об'єднання двох затінених реальних ліній на малюнку\(\PageIndex{16}\). Тобто нам потрібно затінювати числа на реальній лінії, які затінені на будь-якій реальній лінії на малюнку\(\PageIndex{16}\). Таким чином, затінюється кожне число менше −1, а також кожне число більше 3. Результат показаний на рис\(\PageIndex{17}\).

Ось важлива порада.
Примітка
Якщо ви хочете правильно використовувати інтервальні позначення, дотримуйтесь одного простого правила: Завжди змітайте очі зліва направо, описуючи те, що ви бачите затіненим на реальній лінії.
Якщо ми дотримуємось цієї поради, коли ми проведемо очі зліва направо через реальну лінію, затінену на малюнку\(\PageIndex{17}\), ми побачимо, що числа затінені від негативної нескінченності до −1, а від 3 до позитивної нескінченності. Таким чином, найбільш природним чином інтервальне позначення для затіненого розчину, встановленого на малюнку\(\PageIndex{17}\), є
\[(-\infty,-1) \cup(3, \infty)\nonumber\]
Тут слід зробити кілька важливих моментів:
Зверніть увагу, як ми використовували символ об'єднання\(\cup\) для об'єднання двох інтервалів природним чином.\((-\infty,-1) \cup(3, \infty)\)
Символ об'єднання використовується між множинами чисел, в той час як слово «або» використовується між твердженнями про числа. Некоректно обмінюватися ролями символу союзу і словом «або». Таким чином, написання\(\{x : x<-1 \cup x>3\}\) некоректно, як це було б також написати\((-\infty,-1)\) або\((3, \infty)\).
Ми підкріплюємо попередню дискусію про різницю між «заповненими» та «відкритими» колами, дужками та дужками в таблиці 5, де ми включаємо кілька порівнянь позначення інтервалу та конструктора наборів, включаючи поточне рішення для Прикладу\(\PageIndex{7}\).
| Номер рядка | Позначення Set-Builder | Інтервальні позначення |
|---|---|---|
 |
\(\{x : x<-1\)або\(x>3\}\) | \((-\infty,-1) \cup(3, \infty)\) |
 |
\(\{x : x \leq-1\)або\(x \geq 3\}\) | \((-\infty,-1] \cup[3, \infty)\) |
 |
\(\{x : x \leq-1\)або\(x>3\}\) | \((-\infty,-1] \cup(3, \infty)\) |
 |
\(\{x : x<-1\)або\(x \geq 3\}\) | \((-\infty,-1) \cup[3, \infty)\) |
Знову підкріплюємо наступні моменти.
- Зверніть увагу, як підмітати очі зліва направо, описуючи те, що затінено на реальній лінії, гарантує, що ви пишете інтервальні позначення в правильному порядку.
- Дужка еквівалентна заповненій крапці і включає кінцеву точку, тоді як дужка еквівалентна відкритій точці і не включає кінцеву точку.
Давайте зробимо останній приклад, який повинен назавжди закріпити уявлення про те, що існує величезна різниця між словами «і» і «або».
Приклад\(\PageIndex{8}\)
На реальній лінії накидайте множину всіх дійсних чисел в множині\(\{x : x<-1\) і\(x>3\}\). Опишіть своє рішення.
Рішення
Перш за все, зверніть увагу, що єдина відмінність між цим прикладом і прикладом\(\PageIndex{6}\) полягає в тому, що ми змінили «\(\{x : x<-1\)або»\(x>3\}\) в або на «і» в\(\{x : x<-1\) і\(x>3\}\). Попередні ескізи ідентичні тим, що наведені на малюнку\(\PageIndex{16}\).

Тепер зверніть увагу на слово «і» в\(\{x : x < −1\text{ and }x > 3\}\). Таким чином, нам потрібно взяти перетин затінених реальних ліній на малюнку\(\PageIndex{18}\). Тобто нам потрібно затінювати на одній дійсній лінії всі числа, які затінені на обох реальних лініях на малюнку\(\PageIndex{18}\). Однак на реальних лініях на малюнку немає загальних точок\(\PageIndex{18}\), тож набір рішень порожній, як показано на малюнку\(\PageIndex{19}\).

Досить вражає! Останні два приклади наочно демонструють, що якщо ви поміняєтеся ролями «і» і «або», ви не зробили незначної помилки. Дійсно, ви змінили весь сенс проблеми. Так що будьте обережні зі своїми «руками» і «орсами».
