8.2: Спрощення радикальних виразів
- Page ID
- 58132
Цілі навчання
- Спростіть радикальні вирази, використовуючи добуток і часткове правило для радикалів.
- Використовуйте формули за участю радикалів.
- Оцінити задані функції квадратного кореня та кубового кореня.
Спрощення радикальних виразів
Алгебраїчний вираз, що містить радикали, називається радикальним виразом. Ми використовуємо продукт і правила коефіцієнта, щоб спростити їх.
Приклад\(\PageIndex{1}\)
Спростити:
\(\sqrt[3]{8 y^{3}}\)
Рішення:
Використовуйте той факт, що\(\sqrt[n]{a^{n}}=a\) коли n непарне.
\(\begin{aligned} \sqrt[3]{8 y^{3}} &=\sqrt[3]{2^{3} \cdot y^{3}} \qquad\quad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.}\\ &=\sqrt[3]{2^{3}} \cdot \sqrt[3]{y^{3}}\quad\:\:\:\color{Cerulean}{Simplify.} \\ &=2 y \end{aligned}\)
Відповідь:
\(2y\)
Приклад\(\PageIndex{2}\)
Спростити:
\(\sqrt{9 x^{2}}\)
Рішення:
Квадратний корінь має індекс 2; використовуйте той факт, що\(\sqrt[n]{a^{n}}=a\) коли n парне.
\(\begin{aligned} \sqrt{9 x^{2}} &=\sqrt{3^{2} x^{2}}\qquad\quad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.} \\ &=\sqrt{3^{2}} \cdot \sqrt{x^{2}}\quad\:\color{Cerulean}{Simplify.} \\ &=3|x| \end{aligned}\)
Оскільки x є змінною, вона може представляти від'ємне число. Таким чином, нам потрібно переконатися, що результат позитивний, включивши оператор абсолютного значення.
Відповідь:
\(3|x|\)
Примітка
Як правило, на цьому етапі початку алгебри тексти відзначають, що всі змінні приймаються позитивними. Якщо це так, то x в попередньому прикладі позитивний і оператор абсолютного значення не потрібен. Приклад можна спростити наступним чином:
\(\sqrt{9x^{2}}=\sqrt{3^{2}x^{2}}=\sqrt{3^{2}}\cdot\sqrt{x^{2}}=3x\)
У цьому розділі будемо вважати, що всі змінні позитивні. Це дозволяє зосередитися на розрахунку в коренях без технічних нюансів, пов'язаних з принципом в кореневій проблемі. З цієї причини ми будемо використовувати наступну властивість для решти розділу:
\(\sqrt[n]{a^{n}}=a\), якщо\(a≥0\) в корені
При спрощенні радикальних виразів шукайте фактори з повноваженнями, які відповідають індексу.
Приклад\(\PageIndex{3}\)
Спростити:
\(\sqrt{18x^{3}y^{4}}\)
Рішення:
Почніть з визначення квадратних коефіцієнтів\(18, x^{3}\), і\(y^{4}\).
\( \ \begin{aligned} 18 &=2 \cdot \color{Cerulean}{3^{2}} \\ x^{3} &=\color{Cerulean}{x^{2}}\color{black}{ \cdot} x \\ y^{4} &=\color{Cerulean}{\left(y^{2}\right)^{2}} \end{aligned} \ \qquad\color{Cerulean}{Square\:factors}\)
Зробіть ці заміни, а потім застосуйте правило продукту для радикалів і спростіть.
\(\begin{aligned} \sqrt{18 x^{3} y^{4}} &=\sqrt{\color{Cerulean}{2}\color{black}{ \cdot} 3^{2} \cdot x^{2} \cdot \color{Cerulean}{x}\color{black}{ \cdot}\left(y^{2}\right)^{2}}\qquad\qquad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.} \\ &=\sqrt{3^{2}} \cdot \sqrt{x^{2}} \cdot \sqrt{\left(y^{2}\right)^{2}} \cdot \color{black}{\sqrt{\color{Cerulean}{2 x}}}\quad\color{Cerulean}{Simplify.} \\ &=3 \cdot x \cdot y^{2} \cdot \sqrt{2 x} \\ &=3 x y^{2} \sqrt{2 x} \end{aligned}\)
Відповідь:
\(3 x y^{2} \sqrt{2 x}\)
Приклад\(\PageIndex{4}\)
Спростити:
\(\sqrt{4a^{5}b^{6}}\)
Рішення:
Почніть з визначення квадратних коефіцієнтів\(4, a^{5}\), і\(b^{6}\).
\(\begin{array}{l}{4=\color{Cerulean}{2^{2}}} \\ {a^{5}=a^{2} \cdot a^{2} \cdot a=\color{Cerulean}{\left(a^{2}\right)^{2}}\color{black}{ \cdot} a} \\ {b^{6}=b^{3} \cdot b^{3}=\color{Cerulean}{\left(b^{3}\right)^{2}}}\end{array} \qquad\color{Cerulean}{Square\:factors}\)
Зробіть ці заміни, а потім застосуйте правило продукту для радикалів і спростіть.
\(\begin{aligned} \sqrt{\frac{4 a^{5}}{b^{6}}} &=\sqrt{\frac{2^{2}\left(a^{2}\right)^{2} \cdot a}{\left(b^{3}\right)^{2}}}\qquad\qquad\color{Cerulean}{Apply\:the\:product\:and\:quotient\:rule\:for\:radicals.} \\ &=\frac{\sqrt{2^{2}} \cdot \sqrt{\left(a^{2}\right)^{2}} \cdot \sqrt{a}}{\sqrt{\left(b^{3}\right)^{2}}}\quad\color{Cerulean}{Simplify.} \\ &=\frac{2 a^{2} \sqrt{a}}{b^{3}} \end{aligned}\)
Відповідь:
\(\frac{2 a^{2} \sqrt{a}}{b^{3}}\)
Приклад\(\PageIndex{5}\)
Спростити:
\(\sqrt[3]{80x^{5}y^{7}}\)
Рішення:
Почніть з визначення кубічних факторів\(80, x^{5}\), і\(y^{7}\).
\(\begin{array}{l}{80=2^{4} \cdot 5=\color{Cerulean}{2^{3}}\color{black}{ \cdot} 2 \cdot 5} \\ {x^{5}=\color{Cerulean}{x^{3}}\color{black}{ \cdot} x^{2}} \\ {y^{7}=y^{6} \cdot y=\color{Cerulean}{\left(y^{2}\right)^{3}}\color{black}{ \cdot} y}\end{array} \qquad\color{Cerulean}{Cubic\:factors}\)
Зробіть ці заміни, а потім застосуйте правило продукту для радикалів і спростіть.
\(\begin{aligned} \sqrt[3]{80 x^{5} y^{7}} &=\sqrt[3]{\color{Cerulean}{2^{3}}\color{black}{ \cdot} 2 \cdot 5 \cdot \color{Cerulean}{x^{3}}\color{black}{ \cdot} x^{2} \cdot\color{Cerulean}{\left(y^{2}\right)^{3}}\color{black}{ \cdot} y} \qquad\qquad\qquad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.}\\ &=\color{black}{\sqrt[3]{\color{Cerulean}{2^{3}}}} \cdot \color{black}{\sqrt[3]{\color{Cerulean}{x^{3}}}} \cdot \color{black}{\sqrt[3]{\color{Cerulean}{\left(y^{2}\right)^{3}}}} \cdot \sqrt[3]{2 \cdot 5 \cdot x^{2} \cdot y} \quad\:\:\color{Cerulean}{Simplify.} \\ &=2 \cdot x \cdot y^{2} \cdot \sqrt[3]{10 x^{2} y} \\ &=2 x y^{2} \sqrt[3]{10 x^{2} y} \end{aligned}\)
Відповідь:
\(2 x y^{2} \sqrt[3]{10 x^{2} y}\)
Приклад\(\PageIndex{6}\)
Спростити:
\(\sqrt[3]{9x^{6}y^{3}z^{9}}\)
Рішення:
Коефіцієнт\(9=3^{2}\) і, таким чином, не має досконалих кубових факторів. Він залишиться єдиним радикалом, оскільки всі інші фактори є кубами, як показано нижче:
\(\begin{aligned} x^{6} &=\left(x^{2}\right)^{3} \\ y^{3} &=(y)^{3} \\ z^{9} &=\left(z^{3}\right)^{3} \end{aligned}\qquad \color{Cerulean}{Cubic\:factors}\)
Замініть змінні цими еквівалентами, застосуйте правило продукту та частки для радикалів, а потім спростіть.
\(\begin{aligned} \sqrt[3]{\frac{9 x^{6}}{y^{3} z^{9}}} &=\sqrt[3]{\frac{3^{2} \cdot\left(x^{2}\right)^{3}}{y^{3} \cdot\left(z^{3}\right)^{3}}} \\ &=\frac{\sqrt[3]{3^{2}} \cdot \sqrt[3]{\left(x^{2}\right)^{3}}}{\sqrt[3]{y^{3}} \cdot \sqrt[3]{\left(z^{3}\right)^{3}}} \\ &=\frac{\sqrt[3]{3^{2}} \cdot x^{2}}{y \cdot z^{3}} \\ &=\frac{\sqrt[3]{9} \cdot x^{2}}{y \cdot z^{3}} \end{aligned}\)
Відповідь:
\(\frac{\sqrt[3]{9} \cdot x^{2}}{y \cdot z^{3}}\)
Приклад\(\PageIndex{7}\)
Спростити:
\(\sqrt[4]{81a^{4}b^{5}}\)
Рішення:
Визначте всі фактори, які можна записати як досконалі сили 4. Тут важливо це побачити\(b^{5}=b^{4}⋅b\). Звідси фактор\(b\) залишиться всередині радикала.
\(\begin{aligned} \sqrt[4]{81 a^{4} b^{5}} &=\sqrt[4]{3^{4} \cdot a^{4} \cdot b^{4} \cdot b} \\ &=\sqrt[4]{3^{4}} \cdot \sqrt[4]{a^{4}} \cdot \sqrt[4]{b^{4}} \cdot \sqrt[4]{b} \\ &=3 \cdot a \cdot b \cdot \sqrt[4]{b} \end{aligned}\)
Відповідь:
\(3ab\sqrt[4]{b}\)
Приклад\(\PageIndex{8}\)
Спростити:
Рішення:
Зверніть увагу, що змінний коефіцієнт x не може бути записаний як ступінь 5 і, таким чином, залишиться всередині радикала. Крім того, для\(y^{6}=y^{5}⋅y\); фактор y залишиться всередині радикала, а також.
Відповідь:
\(-2yz\sqrt[5]{x^{3}y}\)
Вправа\(\PageIndex{1}\)
Спростити:
\(\sqrt{192x^{6}y^{7}z^{12}}\)
(Припустимо, що всі змінні є позитивними.)
- Відповідь
-
\(8x^{3}y^{3}z^{6}\sqrt{3y}\)
Примітка
Щоб легко спростити і в корені, ми можемо розділити повноваження на індекс.
\(\sqrt{a^{6}}=a^{3}\), який є\(a^{6÷2}= a^{3}\)\(\sqrt[3]{b^{6}}=b^{2}\), який є\(b^{6÷3}=b^{2}\)\(\sqrt[6]{c^{6}}=c\), який\(c^{6÷6}=c^{1}\)
Якщо індекс не ділиться на потужність рівномірно, то ми можемо використовувати частку і залишок для спрощення. Наприклад,
\(\sqrt{a^{5}}=a^{2}⋅\sqrt{a}\), який є\(a^{5÷2}=a^{2}_{r\:1}\)\(\sqrt[3]{b^{5}}=b⋅\sqrt[3]{b^{2}}\), який є\(b^{5÷3}=b^{1}_{r\:2}\)\(\sqrt[5]{c^{14}}=c^{2}⋅\sqrt[5]{c^{4}}\), який\(c^{14÷5}=c^{2}_{r\:4}\)
Коефіцієнт є показником фактора поза радикалом, а залишок - показник фактора, що залишився всередині радикала.
Формули за участю радикалів
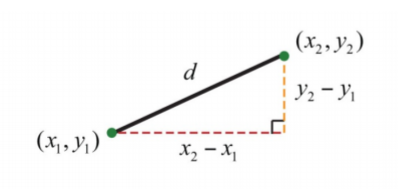
Далі розглядаємо формулу відстані. З огляду на два пункти\((x_{1}, y_{1})\) і\((x_{2}, y_{2})\),
.png)
Відстань, d, між ними задається за такою формулою:
Формула відстані:
\[d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\]
Нагадаємо, що ця формула була виведена з теореми Піфагора.
Приклад\(\PageIndex{9}\)
Обчисліть відстань між\((−4, 7)\) і\((2, 1)\).
Рішення:
Використовуйте формулу відстані з наступними пунктами.
\(\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\left(x_{2}, y_{2}\right)} \\ {(\color{Cerulean}{-4}\color{black}{,}\color{OliveGreen}{7}\color{black}{)}} & {(\color{Cerulean}{2}\color{black}{,}\color{OliveGreen}{1}\color{black}{)}}\end{array}\)
Хорошою практикою є включення формули в загальному вигляді перед підстановкою значень для змінних; це покращує читабельність і зменшує ймовірність помилок.
\(\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{(\color{Cerulean}{2}\color{black}{-}(\color{Cerulean}{-4}\color{black}{)})^{2}+(\color{OliveGreen}{1}\color{black}{-}\color{OliveGreen}{7}\color{black}{)}^{2}} \\ &=\sqrt{(2+4)^{2}+(1-7)^{2}} \\ &=\sqrt{(6)^{2}+(-6)^{2}} \\ &=\sqrt{72} \\ &=\sqrt{36 \cdot 2} \\ &=6 \sqrt{2} \end{aligned}\)
Відповідь:
\(6\sqrt{2}\)одиниць
Приклад\(\PageIndex{10}\)
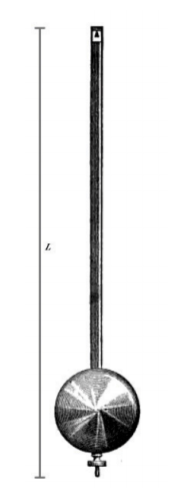
Період, T, маятника в секундах задається за формулою
\[T=2 \pi \sqrt{\frac{L}{32}}\]
де L представляє довжину маятника в футах. Якщо довжина маятника вимірює 6 футів, то обчисліть період, округлений до найближчої десятої частки секунди.
.png)
Рішення:
Підставити 6 на L, а потім спростити.
\(\begin{aligned} T &=2 \pi \sqrt{\frac{L}{32}} \\ &=2 \pi \sqrt{\frac{6}{32}}\quad\color{Cerulean}{Reduce.} \\ &=2 \pi \sqrt{\frac{3}{16}} \quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals.}\\ &=2 \pi \frac{\sqrt{3}}{\sqrt{16}} \quad\color{Cerulean}{Simplify.}\\ &=\frac{2 \pi \sqrt{3}}{4}\quad\:\:\:\color{Cerulean}{Use\:a\:calculator.} \\ & \approx 2.7 \end{aligned}\)
Відповідь:
Період становить приблизно 2,7 секунди.
Функції квадратного кореня та кореня куба
Починаємо з функції квадратного кореня:
\(f(x)=\sqrt{x}\)
Ми знаємо, що квадратний корінь не є дійсним числом, коли радиканд х є негативним. Тому робимо висновок, що домен складається з усіх дійсних чисел, більших або рівних 0. Тут ми вибираємо 0 і деякі позитивні значення для x, обчислюємо відповідні y -значення і будуємо отримані впорядковані пари.
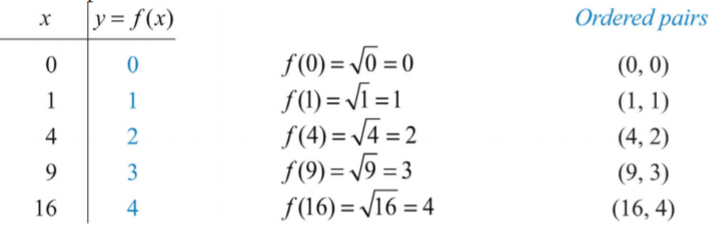.png)
Після побудови точок, ми можемо накидати графік функції квадратного кореня.
.png)
Приклад\(\PageIndex{11}\)
Задано функцію\(f(x)=\sqrt{x+2}\), знайдіть f (−2), f (2) та f (6).
Рішення:
Замініть x на кожне з заданих значень.
\(f(x)=\sqrt{x+2}\)
\(\begin{aligned} f(\color{OliveGreen}{-2}\color{black}{)} &=\sqrt{\color{OliveGreen}{-2}\color{black}{+}2}=\sqrt{0}=0 \\ f(\color{OliveGreen}{2}\color{black}{)} &=\sqrt{\color{OliveGreen}{2}\color{black}{+}2}=\sqrt{4}=2 \\ f(\color{OliveGreen}{6}\color{black}{)} &=\sqrt{\color{OliveGreen}{6}\color{black}{+}2}=\sqrt{8}=\sqrt{4 \cdot 2}=2 \sqrt{2} \end{aligned}\)
Відповідь:
\(f(−2)=0, f(2)=2\), і\(f(6)=2\sqrt{2}\)
Далі розглянемо функцію кореня куба:
\(f(x)=\sqrt[3]{x}\)
Оскільки кубічний корінь може бути як негативним, так і позитивним, робимо висновок, що домен складається з усіх дійсних чисел. Для повноти виберіть деякі позитивні і від'ємні значення для x, а також 0, а потім обчислити відповідні y -значення
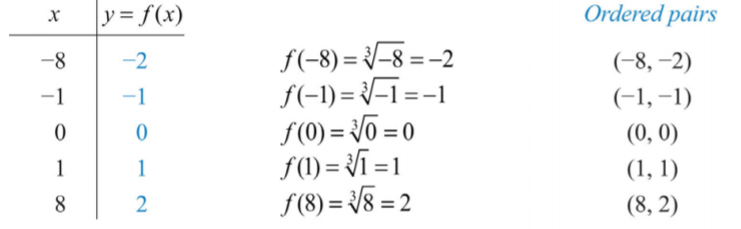.png)
Побудуйте точки та намалюйте графік функції кореня куба.
.png)
Приклад\(\PageIndex{12}\)
Задано функцію\(g(x)=\sqrt[3]{x-1}\), знайдіть g (−7), g (0) та g (55).
Рішення:
Замініть x на кожне з заданих значень.
\(g(x)=\sqrt[3]{x-1}\)
Відповідь:
\(g(−7)=−2, g(0)=−1\), і\(g(55)=3\sqrt[3]{2}\)
Ключові винос
- На початку алгебри ми зазвичай припускаємо, що всі змінні вирази в межах радикала є позитивними. Це дозволяє зосередитися на спрощенні радикалів без технічних проблем, пов'язаних з основним n-м коренем.
- Щоб спростити радикальні вирази, шукайте фактори радиканда з повноваженнями, які відповідають індексу. Якщо вони виявлені, їх можна спростити, застосувавши продукт і правила частки для радикалів, а також властивість\(\sqrt[n]{a^{n}}=a\), де\(a\) позитивно.
Вправа\(\PageIndex{2}\) simplifying radical expressions
Спростити. (Припустимо, що всі змінні представляють собою позитивні числа.)
- \(\sqrt{36a^{2}}\)
- \(\sqrt{121b^{2}}\)
- \(\sqrt{x^{2}y^{2}}\)
- \(\sqrt{25x^{2}y^{2}z^{2}}\)
- \(\sqrt{180x^{3}}\)
- \(\sqrt{150y^{3}}\)
- \(\sqrt{49a^{3}b^{2}}\)
- \(\sqrt{4a^{4}b^{3}c}\)
- \(\sqrt{45x^{5}y^{3}}\)
- \(\sqrt{50x^{6}y^{4}}\)
- \(\sqrt{64r^{2}s^{6}t^{5}}\)
- \(\sqrt{144r^{8}s^{6}t^{2}}\)
- \(\sqrt{(x + 1 )^{2}}\)
- \(\sqrt{( 2 x + 3 )^{2}}\)
- \(\sqrt{4 ( 3 x − 1 )^{2}}\)
- \(\sqrt{9 ( 2 x + 3 )^{2}}\)
- \(\sqrt{9x^{3}5y^{2}}\)
- \(\sqrt{4x^{5}9y^{4}}\)
- \(\sqrt{m^{7}36 n^{4}}\)
- \(\sqrt{147 m^{9}n^{6}}\)
- \(\sqrt{2 r^{2}s^{5}25t^{4}}\)
- \(\sqrt{36 r^{5} s^{2} t^{6}}\)
- \(\sqrt[3]{27 a^{ 3}}\)
- \(\sqrt[3]{125 b^{3}}\)
- \(\sqrt[3]{250 x^{4}y^{3}}\)
- \(\sqrt[3]{162 a^{3} b^{5}}\)
- \(\sqrt[3]{64 x^{3}y^{6} z^{9}}\)
- \(\sqrt[3]{216 x^{12}y^{3}}\)
- \(\sqrt[3]{8 x^{3}y^{4}}\)
- \(\sqrt[3]{27 x^{5}y^{3}}\)
- \(\sqrt[3]{a^{4} b^{5} c^{6}}\)
- \(\sqrt[3]{a^{7} b^{5} c^{3}}\)
- \(\sqrt[3]{8 x^{4}27y^{3}}\)
- \(\sqrt[3]{x^{5}125y^{6}}\)
- \(\sqrt[3]{360 r^{5} s^{12} t^{13}}\)
- \(\sqrt[3]{540r^{3}s^{2}t^{9}}\)
- \(\sqrt[4]{81x^{4}}\)
- \(\sqrt[4]{x^{4}y^{4}}\)
- \(\sqrt[4]{16x^{4}y^{8}}\)
- \(\sqrt[4]{81x^{12}y^{4}}\)
- \(\sqrt[4]{a^{4}b^{5}c^{6}}\)
- \(\sqrt[4]{54a^{6}c^{8}}\)
- \(\sqrt[4]{128x^{6}}\)
- \(\sqrt[4]{243y^{7}}\)
- \(\sqrt[5]{32m^{10}n^{5}}\)
- \(\sqrt[5]{37m^{9}n^{10}}\)
- \(-3\sqrt{4x^{2}}\)
- \(7\sqrt{9y^{2}}\)
- \(-5\sqrt{x4x^{2}y}\)
- \(−3\sqrt{y^{16}x^{3}y^{2}}\)
- \(12ab\sqrt{a^{5}b^{3}}\)
- \(6a^{2}b^{9}\sqrt{a^{7}b^{2}}\)
- \(2x\sqrt[3]{8x^{6}}\)
- \(−5x^{2}\sqrt[3]{27x^{3}}\)
- \(2ab\sqrt[3]{−8a^{4}b^{5}}\)
- \(5a^{2}b\sqrt[3]{−27a^{3}b^{3}}\)
- Відповідь
-
1. \(6a\)
3. \(xy\)
5. \(6x \sqrt{5x}\)
7. \(7ab\sqrt{a}\)
9. \(3x^{2}y\sqrt{5xy}\)
11. \(8rs^{3}t^{2}\sqrt{t}\)
13. \(x+1\)
15. \(2(3x−1)\)
17. \(3xy\sqrt{5x}\)
19. \(6n^{2}m^{3}\sqrt{m}\)
21. \(5\sqrt{2s}rt^{2}s^{2}\)
23. \(3a\)
25. \(5xy\sqrt[3]{2x}\)
27. \(4xy^{2}z^{3}\)
29. \(2xy\sqrt[3]{y}\)
31. \(abc^{2}\sqrt[3]{ab^{2}}\)
33. \(6yx\sqrt[3]{x}\)
35. \(2rs^{4}t^{4}\sqrt[3]{45r^{2}t}\)
37. \(3x\)
39. \(2xy^{2}\)
41. \(abc\sqrt[4]{bc^{2}}\)
43. \(2x\sqrt[4]{8x^{2}}\)
45. \(2^{m}2^{n}\)
47. \(−6x\)
49. \(−10 x\sqrt{xy}\)
51. \(12 a^{3} b^{2}\sqrt{ab}\)
53. \(4x^{3}\)
55. \(− 4 a^{ 2} b^{ 2}\sqrt[3]{ab^{2}}\)
Вправа\(\PageIndex{3}\) simplifying radical expressions
Перепишіть наступне як радикальний вираз з коефіцієнтом 1.
- \(5\sqrt{2x}\)
- \(2\sqrt{3y}\)
- \(2x\sqrt{3}\)
- \(3y\sqrt{2}\)
- \(ab\sqrt{10a}\)
- \(2ab\sqrt{2a}\)
- \(m^{2}n\sqrt{mn}\)
- \(2m^{2}n^{3}\sqrt{3n}\)
- \(5\sqrt[3]{2x}\)
- \(3\sqrt[3]{5y}\)
- \(2x\sqrt[3]{3}\)
- \(3y\sqrt[3]{2}\)
- Відповідь
-
1. \(\sqrt{50 x}\)
3. \(\sqrt{12 x^{2}}\)
5. \(\sqrt{10 a^{3} b^{2}}\)
7. \(\sqrt{m^{5} n^{3}}\)
9. \(\sqrt[3]{250 x}\)
11. \(\sqrt[3]{24 x^{3}}\)
Вправа\(\PageIndex{4}\) simplifying radical expressions
Припустимо, що змінна може представляти будь-яке дійсне число, а потім спростити.
- \(\sqrt{4x^{2}}\)
- \(\sqrt{25y^{2}}\)
- \(\sqrt[3]{8y^{3}}\)
- \(\sqrt[3]{125a^{3}}\)
- \(\sqrt[4]{64x^{4}}\)
- \(\sqrt[4]{81y^{4}}\)
- \(\sqrt{36a^{4}}\)
- \(\sqrt{100a^{8}}\)
- \(\sqrt{4a^{6}}\)
- \(\sqrt{a^{10}}\)
- \(\sqrt{18a^{4}b^{5}}\)
- \(\sqrt{48a^{5}b^{3}}\)
- \(\sqrt[6]{128x^{6}y^{8}}\)
- \(\sqrt[6]{a^{6}b^{7}c^{8}}\)
- Відповідь
-
1. \(2 | x | \)
3. \(2y \)
5. \(2 | x | \)
7. \(6 a^{2}\)
9. \(2| a^{3}|\)
11. \(3 a^{2} b^{2}\sqrt{2 b}\)
13. \(2 |xy |\sqrt[6]{ 2y^{2}}\)
Вправа\(\PageIndex{5}\) formulas involving radicals
Y -перехоплення для будь-якого графа матиме вигляд (0, y), де y - дійсне число. Тому, щоб знайти y -перехоплення, встановіть x = 0 і вирішіть для y. Знайдіть y -перехоплення для наступного.
- \(y=\sqrt{x+4}−1\)
- \(y=\sqrt{x+1}−3\)
- \(y=\sqrt[3]{x−1}+2\)
- \(y=\sqrt[3]{x+1}−3\)
- Відповідь
-
1. \((0, 1)\)
3. \((0, 1)\)
Вправа\(\PageIndex{6}\) formulas involving radicals
Використовуйте формулу відстані для обчислення відстані між заданими двома точками.
- \((5, −7)\)і\((3, −8)\)
- \((−9, 7)\)і\((−8, 4)\)
- \((−3, −4)\)і\((3, −6)\)
- \((−5, −2)\)і\((1, −6)\)
- \((−1, 1)\)і\((−4, 10)\)
- \((8, −3)\)і\((2, −12)\)
- Відповідь
-
1. \(\sqrt{5}\)
3. \(2\sqrt{10}\)
5. \(3\sqrt{10}\)
Вправа\(\PageIndex{7}\) formulas involving radicals
Фактор радиканд, а потім спростити. (Припустимо, що всі вирази позитивні.)
- \(\sqrt{x^{2}−6x+9}\)
- \(\sqrt{x^{2}−10x+25}\)
- \(\sqrt{4x^{2}+12x+9}\)
- \(\sqrt{9x^{2}+6x+1}\)
- Швидкість транспортного засобу до того, як були застосовані гальма, можна оцінити по довжині слідів занесення, залишених на дорозі. На сухому тротуарі швидкість, v, в милі на годину можна оцінити за формулою\(v=\sqrt{5d}\), де d представляє довжину слідів занесення в футах. Оцініть швидкість транспортного засобу перед застосуванням гальм на сухому тротуарі, якщо сліди ковзання залишили позаду вимірювання 36 футів.
- Радіус, r, сфери можна обчислити за формулою\(r=\sqrt[3]{\frac{3 V}{4 \pi}}\), де V представляє об'єм сфери. Який радіус кулі, якщо обсяг\(36π\) кубічних сантиметрів?
- Відповідь
-
1. \(x − 3\)
3. \(2 x + 3\)
5. \(30\)миль на годину
Вправа\(\PageIndex{8}\) formulas involving radicals
Період, T, маятника в секундах задається за формулою
\(T=2 \pi \sqrt{\frac{L}{32}}\)
де L представляє довжину в футах. Розрахуйте період, враховуючи наступні довжини. Дайте точне значення і приблизне значення округлені до найближчої десятої частки секунди.
- 8 футів
- 32 фути
- 1/2 фута
- 1/8 фута
- Відповідь
-
1. \(π≈3.1\)секунд
3. \(\frac{π}{4} ≈0.8\)секунд
Вправа\(\PageIndex{9}\) formulas involving radicals
Час, t, у секундах, коли об'єкт знаходиться у вільному падінні, задається формулою
\(s=16\cdot t^{2}\)
де s являє собою відстань, яку вона впала в ноги. Розрахуйте час, який потрібно об'єкту для падіння, враховуючи наступні відстані. Дайте точне значення і приблизне значення округлені до найближчої десятої частки секунди.
- 48 футів
- 80 футів
- 192 футів
- 288 футів
- Відповідь
-
1. \(\sqrt{3} ≈1.7\)секунд
3. \(2\sqrt{3} \approx 3.5\)секунд
Вправа\(\PageIndex{10}\) radical functions
З огляду на функцію, обчислити наступне.
- \(f(x)=\sqrt{x−1}\), знайти f (1), f (2) і f (5)
- \(f(x)=\sqrt{x+5}\), знайти f (−5), f (−1) та f (20)
- \(f(x)=\sqrt{x}+3\), знайти f (0), f (1) і f (16)
- \(f(x)=\sqrt{x}−5\), знайти f (0), f (1) і f (25)
- \(g(x)=\sqrt[3]{x}\), знайти g (−1), g (0) та g (1)
- \(g(x)=\sqrt[3]{x+7}\), знайти g (−15), g (−7) та g (20)
- \(g(x)=\sqrt[3]{x}−2\), знайти g (−1), g (0) та g (8)
- \(g(x)=\(\sqrt[3]{x−1}+2\), знайти g (0), g (2) і g (9)
- Відповідь
-
1. \(f(1)=0, f(2)=1\), і\(f(5)=2\)
3. \(f(0)=3, f(1)=4\), і\(f(16)=7\)
5. \(g(−1)=−1, g(0)=0\), і\(g(1)=1\)
7. \(g(−1)=−3, g(0)=−2\), і\(g(8)=0\)
Вправа\(\PageIndex{11}\) radical functions
Для кожної функції заповніть таблицю.
- \(f(x)=\sqrt{x+1}\)
.png)
Малюнок\(\PageIndex{7}\) - \(f(x)=\sqrt{x−2}\)
.png)
Малюнок\(\PageIndex{8}\) - \(f(x)=\sqrt[3]{x}+1\)
.png)
Малюнок\(\PageIndex{9}\) - \(f(x)=\sqrt[3]{x+2}\)
.png)
Малюнок\(\PageIndex{10}\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{11}\) 3.
.png)
Малюнок\(\PageIndex{12}\)
Вправа\(\PageIndex{12}\) discussion board
- Дайте значення для x таке, що\(\sqrt{x^{2}}≠x\). Поясніть, чому важливо припустити, що змінні представляють собою позитивні числа.
- Досліджуйте та обговоріть досягнення Крістофа Рудольфа. За що йому зараховують?
- Дослідити та обговорити методи, що використовуються для обчислення квадратних коренів перед загальним використанням електронних калькуляторів.
- Що таке сурд, і звідки береться слово?
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
