6.4: Факторинг спеціальних біноміалів
- Page ID
- 58032
Цілі навчання
- Факторні біноміали, які є відмінностями квадратів.
- Факторні біноміали, які є сумами та відмінностями кубів.
Різниця квадратів
Біноміал - це многочлен з двома долями. Почнемо з нашого першого спеціального біноміала, який називається різницею квадратів:
\[a^{2}-b^{2}=(a+b)(a-b)\]
Щоб перевірити наведену вище формулу, помножте:
\(\begin{aligned} (a+b)(a-b)&=a^{2}-ab+ba-b^{2} \\&=a^{2}\color{red}{-ab+ab}\color{black}{-b^{2}} \\ &=a^{2}-b^{2} \end{aligned}\)
Цю формулу ми використовуємо для множення певних спеціальних біноміалів.
Приклад\(\PageIndex{1}\)
Фактор:
\(x^{2}-16\).
Рішення:
Крок 1: Визначте біноміальне як різницю квадратів та визначте квадратні множники кожного члена.
.png)
Тут ми можемо написати
\(x^{2}-16=(\color{Cerulean}{x}\color{black}{)^{2}-(}\color{Cerulean}{4}\color{black}{)^{2}}\)
Терміни - квадрати\(x\) і\(4\). Звідси\(a=x\) і\(b=4\).
Крок 2: Підставте в різницю квадратів формулу.
\(\begin{aligned}a^{2}-b^{2}&=(a+b)(a-b) \\ &\:\:\color{Cerulean}{\:\quad\downarrow\quad\:\downarrow\quad\downarrow\quad\downarrow} \\ x^{2}-16&=(x+4)(x-4) \end{aligned}\)
Крок 3: Множте, щоб перевірити. Цей крок необов'язковий.
Відповідь:
\((x+4)(x-4)\)
Варто взяти деякий додатковий час на цей момент, щоб переглянути всі квадрати цілих чисел від\(1\) до\(12\).
\(\begin{array}{ll}{1^{2}=1}&{7^{2}=49}\\{2^{2}=4}&{8^{2}=64}\\{3^{2}=9}&{9^{2}=81}\\{4^{2}=16}&{10^{2}=100}\\{5^{2}=25}&{11^{2}=121}\\{6^{2}=36}&{12^{2}=144} \end{array}\)
Розпізнавання цих ідеальних квадратних цілих чисел допомагає прискорити процес факторингу.
Приклад\(\PageIndex{2}\)
Фактор:
\(9x^{2}-121\).
Рішення:
Віднімання вказує на те, що це різниця. Крім того, ми визнаємо, що терміни є квадратами.
\(9x^{2}-121=(\color{Cerulean}{3x}\color{black}{)^{2}-(}\color{Cerulean}{11}\color{black}{)^{2}}\)
В даному випадку\(a=3x\) і\(b=11\). Підставляємо в формулу різниці квадратів.
\(\begin{aligned} a^{2}-b^{2}&=(a+b)(a-b) \\ 9x^{2}-121&=(3x+11)(3x-11) \end{aligned}\)
Відповідь:
\((3x+11)(3x-11)\)
Може бути так, що терміни біноміала мають загальний фактор. Якщо так, буде важко визначити ідеальні квадрати, поки ми спочатку не перерахуємо GCF.
Приклад\(\PageIndex{3}\)
Фактор:
\(12y^{2}−75\).
Рішення:
Терміни не є ідеальними квадратами. Однак зауважте, що вони мають загальний фактор. По-перше, фактор з GCF,\(3\).
\(12y^{2}-75=3(4y^{2}-25)\)
Отриманий біноміальний коефіцієнт є різницею квадратів з\(a=2y\) і\(b=5\).
\(\begin{aligned} 12y^{2}-75&=3(4y^{2}-25) \\ &=3(2y+5)(2y-5) \end{aligned}\)
Відповідь:
\(3(2y+5)(2y-5)\)
Приклад\(\PageIndex{4}\)
Фактор:
\(49x^{2}−100y^{2}\).
Рішення:
Тут ми маємо біном з двома змінними і визнаємо, що це різниця квадратів.
\(49x^{2}-100y^{2}=(\color{Cerulean}{7x}\color{black}{)^{2}-(}\color{Cerulean}{10y}\color{black}{)^{2}}\)
Тому\(a=7x\) і\(b=10y\). Підставляємо в формулу різниці квадратів.
\(\begin{aligned} a^{2}-b^{2}&=(a+b)(a-b) \\ 49x^{2}-100y^{2}&=(7x+10y)(7x-10y) \end{aligned}\)
Відповідь:
\((7x+10y)(7x-10y)\)
Вправа\(\PageIndex{1}\)
Фактор:
\(36x^{2}−1\).
- Відповідь
-
\((6x+1)(6x−1)\)
Задано будь-яке дійсне число\(b\), многочлен форми\(x^{2}+b^{2}\) є простим.
Крім того, сума квадратів\(a^{2}+b^{2}\) не має загального факторного еквівалента. Слід подбати про те, щоб не переплутати це з ідеальним квадратним триноміалом:
\(\begin{aligned}(a+b)^{2}&=(a+b)(a+b) \\ &=a^{2}+ab+ba+b^{2} \\ &=a^{2}+2ab+b^{2} \end{aligned}\)
Тому
\[(a+b)^{2}\neq a^{2}+b^{2}\]
Коли ступінь спеціального біноміала більше двох, нам може знадобитися застосувати формулу різниці квадратів кілька разів. Поліном повністю враховується, коли жоден з факторів не може бути врахований далі.
Приклад\(\PageIndex{5}\)
Фактор повністю:
\(x^{4}−16\).
Рішення:
Спочатку визначте, що знаходиться в квадраті:
\(x^{4}-16=(\quad )^{2}-(\quad )^{2}\)
Для цього слід згадати правило потужності для експонентів,\((x^{m})^{^{n}}=x^{m^{n}}\). Коли експоненти піднімаються до степеня, помножте їх. Маючи це на увазі, визначте, що\((x^{2})^{^{2}}=x^{4}\) і напишіть
\(x^{4}-16=(x^{2})^{^{2}}-(4)^{2}\)
Тому\(a=x^{2}\) і\(b=4\). Підставляємо в формулу різниці квадратів.
\(x^{4}-16=(x^{2}+4)(x^{2}-4)\)
На цьому етапі зверніть увагу, що коефіцієнт сам по собі\((x^{2}−4)\) є різницею двох квадратів і, таким чином, може бути додатково врахований за допомогою\(a=x\) і\(b=2\). Коефіцієнт\((x^{2}+4)\) - це сума квадратів, які не можуть бути враховані за допомогою дійсних чисел.
\(\begin{aligned} x^{4}-16&=(x^{2}+4)(x^{2}-4) \\ &=(x^{2}+4)(x+2)(x-2) \end{aligned}\)
Відповідь:
\((x^{2}+4)(x+2)(x-2)\)
Вправа\(\PageIndex{2}\)
Фактор повністю:
\(81x^{4}−1\).
- Відповідь
-
\((9x^{2}+1)(3x+1)(3x−1)\)
Сума і різниця кубів
Два інших спеціальних бінома, що цікавлять, - це сума і різниця кубів:
\[ a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2}) \]
\[ a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2}) \]
Ми можемо перевірити ці формули, перемноживши:
\(\begin{aligned} (a+b)(a^{2}-ab+b^{2})&=a^{3}-a^{2}b+ab^{2}-ab^{2}+b^{3} \\ &=a^{3}+b^{3}\quad\color{Cerulean}{\checkmark} \\ (a-b)(a^{2}+ab+b^{2})&=a^{3}+a^{2}b+ab^{2}=a^{2}b-ab^{2}-b^{3} \\ &=a^{3}-b^{3}\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Процес факторингу суми та різниці кубів дуже схожий на процес для різниці квадратів. Спочатку визначаємо,\(a\)\(b\) а потім підставляємо у відповідну формулу. Окремі формули для суми та різниці кубів дозволяють завжди\(b\) вибирати\(a\) і бути позитивними.
Приклад\(\PageIndex{6}\)
Фактор:
\(x^{3}+8\).
Рішення:
Знак плюса і те, що терміни - кубики, вказують нам, що це сума кубів.
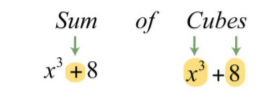.png)
Далі визначте, що відбувається в кубі.
\(x^{3}+8=(\color{Cerulean}{x}\color{black}{)^{3}+(}\color{Cerulean}{2}\color{black}{)^{3}}\)
В даному випадку\(a=x\) і\(b=2\). Підставляємо в суму кубиків формулу.
\(\begin{aligned} a^{3}+b^{3}&=(a+b)(a^{2}-a\:\:b+\:\:b^{2}) \\ &\color{Cerulean}{\:\:\quad\downarrow\:\:\quad\downarrow\quad\downarrow\:\:\quad\downarrow\:\:\:\downarrow\quad\:\:\downarrow} \\ x^{3}+8&=(x+2)(x^{2}-x\cdot 2+2^{2}) \\ &=(x+2)(x^{2}-2x+4) \end{aligned}\)
Отриманий триноміал є простим, а факторинг завершений. Ми можемо перевірити цю факторизацію шляхом множення.
\(\begin{aligned} (x+2)(x^{2}-2x+4)&= x^{3}-2x^{2}+4x+2x^{2}-4x+8 \\ &=x^{3} -\color{Cerulean}{\cancel{\color{black}{2x^{2}}}}\color{black}{+}\color{Cerulean}{\cancel{\color{black}{4x}}}\color{black}{+}\color{Cerulean}{\cancel{\color{black}{2x^{2}}}}\color{black}{-}\color{Cerulean}{\cancel{\color{black}{4x}}}\color{black}{+8} \\ &=x^{3}+8\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Відповідь:
\((x-2)(x^{2}-2x+4)\)
Корисно переглянути ідеальні куби цілих чисел від\(1\) до\(12\). Це допоможе вам визначити суми та відмінності кубів.
\(\begin{array}{ll} {1^{3}=1}&{y^{3}=343}\\{2^{3}=8}&{8^{3}=512}\\{3^{3}=27}&{9^{3}=729}\\{4^{3}=64}&{10^{3}=1000}\\{5^{3}=125}&{11^{3}=1331}\\{6^{3}=216}&{12^{3}=1728} \end{array}\)
Приклад\(\PageIndex{7}\)
Фактор:
\(y^{3}-125\).
Рішення:
В даному випадку у нас є різниця кубиків.
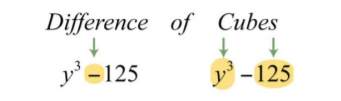.png)
Ми можемо написати
\(y^{3}-125=(\color{Cerulean}{y}\color{black}{)^{3}-(}\color{Cerulean}{5}\color{black}{)^{3}}\)
\(b=5\)Підставляємо\(a=y\) і в формулу різниці кубиків.
\(\begin{aligned} a^{3}-b^{3}&=(a-b)(a^{2}+a\:\:b+\:\:b^{2}) \\ &\color{Cerulean}{\:\:\quad\downarrow\:\:\quad\downarrow\quad\downarrow\:\:\quad\downarrow\:\:\:\downarrow\quad\:\:\downarrow} \\ y^{3}-1258&=(y-5)(y^{2}+y\cdot 5+5^{2}) \\ &=(y-5)(y^{2}+5y+25) \end{aligned}\)
Відповідь:
\((y-5)(y^{2}+5y+25)\)
Завжди шукайте загальні фактори при факторингу. Якщо терміни біноміального мають GCF\(1\), крім, то фактор, що спочатку.
Приклад\(\PageIndex{8}\)
Фактор:
\(54x^{4}+128x\).
Рішення:
Почніть з факторингу GCF\(2x\).
\(54x^{4}+128x=2x(27x^{3}+64)\)
Отриманий біноміальний коефіцієнт являє собою суму кубів, де\(a=3x\) і\(b=4\).
\(\begin{aligned} 54x^{4}+128x &=2x(27x^{3}+64) \\ &=2x(3x+4)((3x)^{2}-(3x)(4)+4^{2}) \\ &=2x(3x+4)(9x^{2}-12x+16) \end{aligned}\)
Відповідь:
\(2x(3x+4)(9x^{2}-12x+16)\)
Приклад\(\PageIndex{9}\)
Фактор:
\(x^{3}y^{3}-1\).
Рішення
Цей біноміал є різницею кубів з двома змінними. Визначте, що відбувається в кубі.
\(x^{3}y^{3}-1=(\color{Cerulean}{xy}\color{black}{)^{3}-(}\color{Cerulean}{1}\color{black}{)^{3}}\)
Ось\(a=xy\) і\(b=1\). Підставляємо у відповідну формулу і спрощуємо.
\(\begin{aligned} a^{3}-b^{3}&=(a-b)(a^{2}+ab+b^{2}) \\ x^{3}y^{3}-1&=(xy-1)((xy)^{2}+xy\cdot 1+1^{2}) \\ &=(xy-1)(x^{2}y^{2}+xy+1) \end{aligned}\)
Відповідь:
\((xy-1)(x^{2}y^{2}+xy+1)\)
Вправа\(\PageIndex{3}\)
Фактор:
\(8x^{3}+343\).
- Відповідь
-
\((2x+7)(4x^{2}−14x+49)\)
При факторингу завжди шукайте результуючі фактори для подальшого фактору.
Приклад\(\PageIndex{10}\)
Фактор повністю:
\(x^{6}−64\).
Рішення:
При зіткненні з біноміальним, який є одночасно різницею квадратів і кубів, як це є, візьміть за правило, щоб коефіцієнт, використовуючи різницю квадратів спочатку.
\(x^{6}-64=(\color{Cerulean}{x^{3}}\color{black}{)^{^{2}}-(}\color{Cerulean}{8}\color{black}{)^{2}}\)
Тому\(a=x^{3}\) і\(b=8\). Підставляємо в різницю квадратів формулу.
\(x^{6}-64=(x^{3}+8)(x^{3}-8)\)
Отримані два біноміальних множника є сумою і різницею кубів. Кожен можна врахувати далі.
\(\begin{aligned} x^{3}+8&=(x+2)(x^{2}-2x+2^{2}) \\ x^{3}-8&=(x-2)(x^{2}+2x+2^{2}) \end{aligned}\)
Тому у нас є
\(\begin{array}{ccccc} {x^{6}-64}&{=}&{(x^{3}+8)}&{\cdot}&{(x^{3}-8)}\\{}&{=}&{\color{Cerulean}{\overbrace{\color{black}{(x+2)(x^{2}-2x+4)}}}}&{\cdot}&{\color{Cerulean}{\overbrace{\color{black}{(x-2)(x^{2}+2x+4)}}}} \end{array}\)
Триноміальні фактори є простими, а вираз повністю враховано.
Відповідь:
\((x+2)(x^{2}−2x+4)(x−2)(x^{2}+2x+4)\)
Як вправу, спочатку врахуйте попередній приклад як різницю кубів, а потім порівняйте результати. Чому, на вашу думку, ми вважаємо за правило спочатку використовувати різницю квадратів?
Вправа\(\PageIndex{4}\)
Фактор:
\(x^{6}−y^{6}\).
- Відповідь
-
\((x+y)(x^{2}−xy+y2)(x−y)(x^{2}+xy+y2)\)
Ключові виноси
- При факторингу спеціальних біноміалів першим кроком є визначення його як суми або різниці. Після того, як ми ідентифікуємо біноміал, ми визначаємо значення\(a\)\(b\) і підставляємо у відповідну формулу.
- Формули для всіх спеціальних біноміалів повинні бути запам'ятовані. Крім того, щоб полегшити ідентифікацію спеціальних біноміалів, запам'ятовуйте квадрати і куби цілих чисел щонайменше\(12\).
- Якщо біноміал - це і різниця квадратів і кубів, то спочатку множьте його як різницю квадратів.
Вправа\(\PageIndex{5}\) Difference of Squares
Фактор повністю.
- \(x^{2}−9\)
- \(x^{2}−100 \)
- \(y^{2}−36 \)
- \(y^{2}−144 \)
- \(x^{2}+4 \)
- \(x^{2}−5 \)
- \(m^{2}−81 \)
- \(m^{2}−64 \)
- \(16x^{2}−9 \)
- \(25x^{2}−4 \)
- \(144x^{2}−1 \)
- \(9x^{2}−121 \)
- \(4y^{2}−81 \)
- \(100y^{2} −49 \)
- \(9 − 4 x^{2}\)
- \(100 −x^{2}\)
- \(1 −y^{2}\)
- \(25 − 9y^{2}\)
- \(− 3 x^{2} +75\)
- \(−16 x^{2} +25\)
- \(2 x^{2} −72\)
- \(20 x^{3} −45 x\)
- \(−48 x +27x^{3}\)
- \(36 x^{2} −100\)
- \(x^{2} −y^{2}\)
- \(25 x^{2} − 9y^{2}\)
- \(a^{2} − 4 b^{2}\)
- \(a^{2} b^{2} −36\)
- \(4 x^{2}y^{2} − 1\)
- \(x^{2}y^{2} −25\)
- \(2 a^{3} − 8ab^{2}\)
- \(3 a^{3} b^{4} −75ab^{2}\)
- \(−100xy^{3} + 4x^{3}y\)
- \(−18 x^{3}y^{3} +32xy\)
- \((x + 1 )^{2} −y^{2}\)
- \(x^{2}−(y − 2 )^{2}\)
- \((x − 3 )^{2}−(y + 3 )^{2}\)
- \((x^{2} + 2 )^{2}−(x − 1 )^{2}\)
- \((x^{2} − 1 )^{2}−( 2 x + 3 )^{2}\)
- \(x^{4} − 1\)
- \(x^{4} −y^{4}\)
- \(16 x^{4} −81\)
- \(a^{4}b^{4}−16\)
- \(a^{4}−16b^{4}\)
- \(x^{8}−1\)
- \(25x^{8}−1\)
- \(a^{8}−b^{2}\)
- \(a^{4}−9\)
- \(x^{8}−y^{8}\)
- \(81x^{8}−1 \)
- Висота снаряда, скинутого з\(64\) -футової вежі, задається функцією\(h(t)=−16t^{2}+64\), де\(t\) позначає час у секундах після його скидання. Перепишіть цю функцію в факторованому вигляді. (Підказка: Фактор\(−16\) спочатку.)
- Висота снаряда, скинутого з\(36\) -футової вежі, задається функцією\(h(t)=−16t^{2}+36\), де\(t\) позначає час у секундах після його скидання. Перепишіть цю функцію в факторованому вигляді.
- Відповідь
-
1. \((x+3)(x−3) \)
3. \((y+6)(y−6) \)
5. Прем'єр
7. \((m+9)(m−9) \)
9. \((4x+3)(4x−3) \)
11. \((12x+1)(12x−1) \)
13. \((2y+9)(2y−9) \)
15. \((3+2x)(3−2x) \)
17. \((1+y)(1−y) \)
19. \(−3(x+5)(x−5) \)
21. \(2(x+6)(x−6) \)
23. \(3x(3x+4)(3x−4) \)
25. \((x +y)(x −y ) \)
27. \(( a + 2 b)( a − 2 b ) \)
29. \(( 2xy + 1)( 2xy − 1 ) \)
31. \(2 a ( a + 2 b)( a − 2 b ) \)
33. \(4xy (x + 5y)(x − 5y ) \)
35. \((x + 1 +y)(x + 1 −y ) \)
37. \((x +y)(x −y − 6 ) \)
39. \((x^{2} + 2 x + 2)(x^{2} − 2 x − 4 ) \)
41. \((x^{2} +y^{2} ) (x +y)(x −y ) \)
43. \(( a^{2} b^{2} + 4 ) (ab + 2)(ab − 2 ) \)
45. \((x^{4} + 1)(x^{2} + 1 ) (x + 1)(x − 1 ) \)
47. \(( a^{4} + b)( a^{4} − b ) \)
49. \((x^{4} +y^{4})(x^{2} +y^{2} ) (x +y)(x −y )\)
51. \(h ( t)=−16 ( t + 2)( t − 2 )\)
Вправа\(\PageIndex{6}\) Sum and Difference of Cubes
Фактор повністю.
- \(x^{3}−1 \)
- \(x^{3}+1 \)
- \(y^{3}−27 \)
- \(y^{3}−8 \)
- \(8y^{3}+1 \)
- \(27y^{3}−1 \)
- \(64a^{3}−125 \)
- \(8a^{3}+27 \)
- \(a^{3}+216 \)
- \(a^{3}−125 \)
- \(x^{3}−1000 \)
- \(343m^{3}−1 \)
- \(512 n^{3} + 1 \)
- \(8 x^{3} +343 \)
- \(40y^{3} −135 \)
- \(27y^{3} +729 \)
- \(27y^{3} −64 \)
- \(x^{3} + 3 \)
- \(5 x^{3} + 1\)
- \(1 −y^{3}\)
- \(27 −1,000y^{3}\)
- \(343 +125 a^{3}\)
- \(x^{3} −y^{3}\)
- \(x^{3} +y^{3}\)
- \(x^{3}y^{3} +125\)
- \(8 x^{3}y^{3} −27\)
- \(27 a^{3} − 8 b^{3}\)
- \(16 x^{3} −250y^{3}\)
- \(128 x^{3} + 2y^{3}\)
- \(54 x^{3} − 2y^{3}\)
- \(3 a^{4} b −24ab^{4}\)
- \(a^{3} b^{3} c^{3} − 1\)
- \((x + 1 )^{3} − 8\)
- \(8 x^{3}−(x − 5 )^{3}\)
- \((x − 2 )^{3}+(x + 2 )^{3}\)
- \(( a + 3 )^{3}+( b − 3 )^{3}\)
- \(x^{6} − 1\)
- \(x^{6} + 1\)
- \(64 a^{6} − 1\)
- \(a^{6} −81 b^{6}\)
- \(x^{6} −y^{6}\)
- \(x^{6}+y^{6}\)
- Відповідь
-
1. \((x − 1 ) (x^{2} +x + 1 ) \)
3. \((y − 3 ) (y^{2} + 3 y + 9 ) \)
5. \(( 2y + 1 ) ( 4y^{2} − 2y + 1 ) \)
7. \(( 4 a − 5 ) (16 a^{2} +20 a +25 ) \)
9. \(( a + 6 ) ( a^{2} − 6 a +36 ) \)
11. \((x −10 ) (x^{2} +10 x +100 ) \)
13. \(( 8 n + 1 ) (64 n^{2} − 8 n + 1 ) \)
15. \(5 ( 2y − 3 ) ( 4y^{2} + 6y + 9 ) \)
17. \(( 3 y − 4 ) ( 9y^{2} +12y +16 ) \)
19. Прем'єр
21. \(( 3 −10y ) ( 9 +30y +100y^{2} )\)
23. \((x −y ) (x^{2} +xy +y^{2} )\)
25. \((xy + 5 ) (x^{2}y^{2} − 5xy +25 ) \)
27. \(( 3 a − 2 b ) ( 9 a^{2} + 6ab + 4 b^{2} )\)
29. \(2 ( 4 x +y ) (16 x^{2} − 4xy +y^{2} )\)
31. \(3ab(a−2b)(a^{2}+2ab+4b^{2})\)
33. \((x−1)(x^{2}+4x+7) \)
35. \(2x(x^{2}+12) \)
37. \((x+1)(x^{2}−x+1)(x−1)(x^{2}+x+1) \)
39. \((2a+1)(4a^{2}−2a+1)(2a−1)(4a^{2}+2a+1) \)
41. \((x+y)(x^{2}−xy+y^{2})(x−y)(x^{2}+xy+y^{2})\)
Вправа\(\PageIndex{7}\) Discussion Board Topics
- Якщо біноміал потрапляє в обидві категорії, різниця квадратів і різниця кубів, що було б краще врахувати його як, і чому? Створіть приклад, який ілюструє цю ситуацію, і врахуйте її за допомогою обох формул.
- Що можна сказати про ступені факторів многочлена? Наведемо приклад.
- Складіть свою власну різницю квадратів факторингу вправи та надайте відповідь. Поясніть, як ви це вирішили.
- Складіть власну суму або різницю кубиків факторингу вправи та надайте відповідь. Поясніть, як ви це вирішили.
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
