Skip to main content
LibreTexts - Ukrayinska

5.3: Додавання та віднімання многочленів

  1. Last updated
  2. Save as PDF
  • Page ID
    58039

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Додайте многочлени.
    • Відніміть многочлени.
    • Додавання та віднімання поліноміальних функцій

    Додавання многочленів

    Нагадаємо, що ми поєднуємо подібні терміни, або терміни з тією ж змінною частиною, як засіб для спрощення виразів. Для цього складають коефіцієнти термінів, щоб отримати єдиний член з однаковою змінною частиною. Наприклад,

    \[5x^{2}+8x^{2}=13x^{2}\]

    Зверніть увагу, що змінна частина\(x^{2}\), не змінюється. Це, крім комутативних і асоціативних властивостей додавання, дозволяє додавати поліноми.

    Приклад\(\PageIndex{1}\)

    Додати:

    \(3x+(4x−5)\).

    Рішення:

    Властивість\(+(a+b)=a+b\), яка була виведена за допомогою властивості distributive, дозволяє нам видалити дужки, щоб ми могли додавати подібні терміни.

    Відповідь:

    \(7x-5\)

    Приклад\(\PageIndex{2}\)

    Додати:

    \((3x^{2}+3x+5)+(2x^{2}−x−2)\).

    Рішення:

    Видаліть дужки, а потім об'єднайте подібні терміни.

    Відповідь:

    \(5x^{2}+2x+3\)

    Приклад\(\PageIndex{3}\)

    Додати:

    \((−5x^{2}y−2xy^{2}+7xy)+(4x^{2}y+7xy^{2}−3xy)\).

    Рішення:

    Пам'ятайте, що змінні частини повинні бути точно такими ж, перш ніж ми зможемо додати коефіцієнти.

    \(\begin{aligned} &(−5x^{2}y−2xy^{2}+7xy)+(4x^{2}y+7xy^{2}−3xy) \\ &=\color{Cerulean}{\underline{-5x^{2}y}}\color{black}{-}\color{OliveGreen}{\underline{\underline{2xy^{2}}}}\color{black}{+\underline{\underline{\underline{7xy}}}+}\color{Cerulean}{\underline{4x^{2}y}}\color{black}{+}\color{OliveGreen}{\underline{\underline{7xy^{2}}}}\color{black}{-\underline{\underline{\underline{3xy}}}} \\ &=-x^{2}y+5xy^{2}+4xy \end{aligned}\)

    Відповідь:

    \(-x^{2}y+5xy^{2}+4xy\)

    Загальноприйнятою практикою є представлення термінів спрощеного поліноміального виразу в порядку спадання на основі їх ступеня. Іншими словами, ми зазвичай представляємо поліноми в стандартній формі, з термінами в порядку від найвищого до нижчого ступеня.

    Приклад\(\PageIndex{4}\)

    Додати:

    \((a−4a^{3}+a^{5}−8)+(−9a^{5}+a^{4}−7a+5+a^{3})\).

    Рішення:

    Відповідь:

    \(-8a^{5}+a^{4}-3a^{3}-6a-3\)

    Вправа\(\PageIndex{1}\)

    Додати:

    \((6−5x^{3}+x^{2}−x)+(x^{2}+x+6x^{3}−1)\).

    Відповідь

    \(x^{3}+2x^{2}+5\)

    Віднімання многочленів

    При відніманні многочленів ми бачимо, що дужки стають дуже важливими. Нагадаємо, що розподільне майно дозволило нам вивести наступне:

    \[-(a+b)=-a-b\]

    Іншими словами, при відніманні алгебраїчного виразу ми прибираємо дужки, віднімаючи кожен член.

    Приклад\(\PageIndex{5}\)

    Відніміть:

    \(10x−(3x+5)\).

    Рішення:

    Відніміть кожен член в дужках, а потім об'єднайте подібні терміни.

    Відповідь:

    \(7x-5\)

    Віднімання кількості еквівалентно множенню її на\(−1\).

    Приклад\(\PageIndex{6}\)

    Відніміть:

    \((3x^{2}+3x+5)−(2x^{2}−x−2)\).

    Рішення:

    Розподіліть\(−1\), видаліть дужки, а потім об'єднайте подібні терміни.

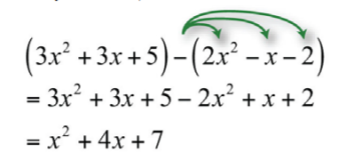    Знімок екрана (362) .png
    Малюнок\(\PageIndex{1}\)

    Відповідь:

    \(x^{2}+4x+7\)

    Множення членів многочлена на\(−1\) змінює всі ознаки.

    Приклад\(\PageIndex{7}\)

    Відніміть:

    \((−5x^{3}−2x^{2}+7)−(4x^{3}+7x^{2}−3x+2)\).

    Рішення:

    Розподіліть\(−1\), видаліть дужки, а потім об'єднайте подібні терміни.

    Відповідь:

    \(-9x^{3}-9x^{2}+3x+5\)

    Приклад\(\PageIndex{8}\)

    Відняти\(6x^{2}−3x−1\) від\(2x^{2}+5x−2\).

    Рішення

    Оскільки віднімання не є комутативним, ми повинні подбати про правильне налаштування різниці. Спочатку напишіть кількість\((2x^{2}+5x−2)\); з цього відніміть кількість\((6x^{2}−3x−1)\).

    Відповідь:

    \(-4x^{2}+8x-1\)

    Приклад\(\PageIndex{9}\)

    Спростити:

    \((2x^{2}−3x+5)−(x^{2}−3x+1)+(5x^{2}−4x−8)\).

    Рішення:

    Застосуйте розподільну властивість, видаліть дужки, а потім об'єднайте подібні терміни.

    Відповідь:

    \(6x^{2}-4x-4\)

    Вправа\(\PageIndex{2}\)

    Відніміть:

    \((8x^{2}y−5xy^{2}+6)−(x^{2}y+2xy^{2}−1)\).

    Відповідь

    \(7x^{2}y-7xy^{2}+7\)

    Додавання та віднімання поліноміальних функцій

    Ми використовуємо позначення функцій для позначення додавання та віднімання функцій наступним чином:

    Додавання функцій: \((f+g)(x)=f(x)+g(x)\)
    Віднімання функцій: \((f-g)(x)=f(x)-g(x)\)
    Таблиця\(\PageIndex{1}\)

    Використовуючи позначення функції, будьте обережні, щоб згрупувати всю функцію і відповідно додати або відняти.

    Приклад\(\PageIndex{10}\)

    Обчисліть:

    \((f+g)(x)\), з огляду на\(f(x)=−x^{2}−3x+5\) і\(g(x)=3x^{2}+2x+1\).

    Рішення:

    Позначення\((f+g)(x)\) вказує на те, що ви повинні додати функції\(f(x)+g(x)\) і збирати подібні терміни.

    \(\begin{aligned} f(x)+g(x)&=(-x^{2}-3x+5)+(3x^{2}+2x+1) \\ &=-x^{2}-3x+5+3x^{2}+2x+1 \\ &=2x^{2}-x+6 \end{aligned}\)

    Відповідь:

    \((f+g)(x) = 2x^{2}-x+6\)

    Приклад\(\PageIndex{11}\)

    Обчисліть:

    \((f−g)(x)\), з огляду на\(f(x)=2x−3\) і\(g(x)=−2x^{2}+2x+5\).

    Рішення:

    Позначення\((f−g)(x)\) вказує на те, що слід відняти функції\(f(x)−g(x)\):

    Відповідь:

    \((f-g)(x)=2x^{2}-8\)

    Нас можуть попросити оцінити суму або різницю двох функцій. У нас є можливість спочатку знайти суму або різницю і використовувати результуючу функцію для оцінки заданої змінної, або спочатку оцінити кожну функцію, а потім знайти суму або різницю.

    Приклад\(\PageIndex{12}\)

    Обчисліть:

    \((f−g)(5)\), з огляду на\(f(x)=x^{2}+x−7\) і\(g(x)=4x+10\).

    Рішення:

    Спочатку знайдіть\((f−g)(x)=f(x)−g(x)\).

    Тому

    \((f-g)(x)=x^{2}-3x-17\)

    Далі\(5\) підставляємо змінну\(x\).

    Відповідь:

    \((f-g)(5)=-7\)

    Альтернативне рішення:

    Так як\((f−g)(5)=f(5)−g(5)\), ми можемо знайти,\(f(5)\)\(g(5)\) а потім відняти результати.

    \(\begin{array}{c|c} {f(x)=x^{2}+x-7}&{g(x)=4x+10}\\{f(\color{OliveGreen}{5}\color{black}{)=(}\color{OliveGreen}{5}\color{black}{)^{2}+(}\color{OliveGreen}{5}\color{black}{)-7}}&{g(\color{OliveGreen}{5}\color{black}{)=4(}\color{OliveGreen}{5}\color{black}{)+10}}\\{=25+5-7}&{=20+10}\\{=23}&{=30} \end{array}\)

    Тому у нас є

    Відповідь:

    \((f-g)(5)=-7\)

    Ключові винос

    • При додаванні поліномів видаліть пов'язані дужки, а потім об'єднайте подібні терміни.
    • При відніманні поліномів розподіліть\(−1\) і відніміть всі члени, перш ніж видаляти дужки та поєднувати подібні терміни.
    • Позначення\((f+g)(x)\) вказує на те, що ви додаєте функції.
    • Позначення\((f−g)(x)\) вказує на те, що ви віднімаєте функції

    Вправа\(\PageIndex{3}\) Addition of Polynomials

    Додати.

    1. \((2x+1)+(−x+7)\)
    2. \((−6x+5)+(3x−1)\)
    3. \((\frac{2}{3}x+\frac{1}{2})+(\frac{1}{3}x−2)\)
    4. \((\frac{1}{3}x−\frac{3}{4})+(\frac{5}{6}x+\frac{1}{8})\)
    5. \((2x+1)+(x−3)+(5x−2)\)
    6. \((2x−8)+(−3x^{2}+7x−5)\)
    7. \((x^{2}−3x+7)+(3x^{2}−8x−5)\)
    8. \((−5x^{2}−1+x)+(−x+7x^{2}−9)\)
    9. \((\frac{1}{2}x^{2}−\frac{1}{3}x+\frac{1}{6})+(−\frac{3}{2}x^{2}+\frac{2}{3}x−1)\)
    10. \((−\frac{3}{5}x2+\frac{1}{4}x−6)+(2x^{2}−\frac{3}{8}x+\frac{5}{2})\)
    11. \((x^{2}+5)+(3x^{2}−2x+1)+(x^{2}+x−3)\)
    12. \((a^{3}−a^{2}+a−8)+(a^{3}+a^{2}+6a−2)\)
    13. \((a^{3}−8)+(−3a^{3}+5a^{2}−2)\)
    14. \((4a^{5}+5a^{3}−a)+(3a^{4}−2a^{2}+7)\)
    15. \((2x^{2}+5x−12)+(7x−5)\)
    16. \((3x+5)+(x^{2}−x+1)+(x^{3}+2x^{2}−3x+6)\)
    17. \((6x^{5}−7x^{3}+x^{2}−15)+(x^{4}+2x^{3}−6x+12)\)
    18. \((1+7x−5x^{3}+4x^{4})+(−3x^{3}+5−x^{2}+x)\)
    19. \((x^{2}y^{2}−7xy+7)+(4x^{2}y^{2}−3xy−8)\)
    20. \((x^{2}+xy−y^{2})+(7x^{2}−5xy+2y^{2})\)
    21. \((2x^{2}+3xy−7y^{2})+(−5x^{2}−3xy+8y^{2})\)
    22. \((a^{2}b^{2}−100)+(2a^{2}b^{2}−3ab+20)\)
    23. \((ab^{2}−3a^{2}b+ab−3)+(−2a^{2}b+ab^{2}−7ab−1)\)
    24. \((10a^{2}b−7ab+8ab^{2})+(6a^{2}b−ab+5ab^{2})\)
    25. Знайти суму\(2x+8\) і\(7x−1\).
    26. Знайти суму\(13x−15\) і\(16x+110\).
    27. Знайти суму\(x^{2}−10x+8\) і\(5x^{2}−2x−6\).
    28. Знайти суму\(a^{2}−5a+10\) і\(−9a^{2}+7a−11\).
    29. Знайти суму\(x^{2}y^{2}−xy+6\) і\(x^{2}y^{2}+xy−7\).
    30. Знайти суму\(x^{2}−9xy+7y^{2}\) і\(−3x^{2}−3xy+7y^{2}\).
    Відповідь

    1. \(x+8\)

    3. \(x−\frac{3}{2}\)

    5. \(8x−4\)

    7. \(4x^{2}−11x+2\)

    9. \(−x^{2}+\frac{1}{3}x−\frac{5}{6}\)

    11. \(5x^{2}−x+3\)

    13. \(−2a^{3}+5a^{2}−10\)

    15. \(2x^{2}+12x−17\)

    17. \(6x^{5}+x^{4}−5x^{3}+x^{2}−6x−3\)

    19. \(5x^{2}y^{2}−10xy−1\)

    21. \(−3x^{2}+y^{2}\)

    23. \(−5a^{2}b+2ab^{2}−6ab−4 \)

    25. \(9x+7\)

    27. \(6x^{2}−12x+2\)

    29. \(2x^{2}y^{2}−1\)

    Вправа\(\PageIndex{4}\) Subtraction of Polynomials

    Відніміть.

    1. \((5x−3)−(2x−1)\)
    2. \((−4x+1)−(7x+10)\)
    3. \((\frac{1}{4}x−\frac{3}{4})−(\frac{3}{4}x+\frac{1}{8})\)
    4. \((−\frac{3}{5}x+\frac{3}{7})−(\frac{2}{5}x−\frac{3}{2})\)
    5. \((x^{2}+7x−5)−(4x^{2}−5x+1)\)
    6. \((−6x^{2}+3x−12)−(−6x^{2}+3x−12)\)
    7. \((−3x^{3}+4x−8)−(−x^{2}+4x+10)\)
    8. \((\frac{1}{2}x^{2}+\frac{1}{3}x−\frac{3}{4})−(\frac{3}{2}x^{2}−\frac{1}{6}x+\frac{1}{2})\)
    9. \((\frac{5}{9}x^{2}+\frac{1}{5}x−\frac{1}{3})−(\frac{1}{3}x^{2}+\frac{3}{10}x+\frac{5}{9})\)
    10. \((a^{3}−4a^{2}+3a−7)−(7a^{3}−2a^{2}−6a+9)\)
    11. \((3a^{3}+5a^{2}−2)−(a^{3}−a+8)\)
    12. \((5x^{5}+4x^{3}+x^{2}−6)−(4x^{4}−3x^{3}−x+3)\)
    13. \((3−5x−x^{3}+5x^{4})−(−5x^{3}+2−x^{2}−7x)\)
    14. \((x^{5}−6x^{3}+9x)−(4x^{4}+2x^{2}−5)\)
    15. \((2x^{2}y^{2}−4xy+9)−(3x^{2}y^{2}−3xy−5)\)
    16. \((x^{2}+xy−y^{2})−(x^{2}+xy−y^{2})\)
    17. \((2x^{2}+3xy−7y^{2})−(−5x^{2}−3xy+8y^{2})\)
    18. \((ab^{2}−3a^{2}b+ab−3)−(−2a^{2}b+ab^{2}−7ab−1)\)
    19. \((10a^{2}b−7ab+8ab^{2})−(6a^{2}b−ab+5ab^{2})\)
    20. \((10a^{2}b^{2}+5ab−6)−(5a^{2}b^{2}+5ab−6)\)
    21. Відняти\(3x+1\) від\(5x−9\).
    22. Відняти\(x^{2}−5x+10\) від\(x^{2}+5x−5\).
    23. Знайдіть різницю\(3x−7\) і\(8x+6\).
    24. Знайдіть різницю\(2x^{2}+3x−5\) і\(x^{2}−9\).
    25. Вартість в доларах виробництва кавових кухлів на замовлення з логотипом компанії задається за формулою\(C=150+0.10x\), де\(x\) знаходиться кількість вироблених чашок. Виручка від продажу чашок в фірмовому магазині дається за рахунок того\(R=10x−0.05x^{2}\), де\(x\) знаходиться кількість проданих одиниць.
      1. Знайдіть формулу отримання прибутку. (прибуток = виручка − вартість)
      2. Знайти прибуток від виробництва і продажу 100 кухлів можна в фірмовому магазині.
    26. Вартість в доларах виробництва толстовки задається формулою\(C=10q+1200\), де\(C\) знаходиться вартість і\(q\) представляє кількість виробленої. Дохід, отриманий від продажу футболок за $\(37\) кожен, дається\(R=37q\), де\(q\) представляє кількість проданих. Визначте прибуток, отриманий\(125\), якщо виробляються та продаються сорочки.
    27. Зовнішній радіус шайби в\(3\) рази перевищує радіус отвору.
      Знімок екрана (363) .png
      \(\PageIndex{2}\)
      Малюнок       а. вивести формулу для площі грані шайби.
      б. яка площа шайби, якщо отвір має діаметр\(10\) міліметрів?
    28. Вивести формулу для площі поверхні наступного прямокутного тіла.
      Знімок екрана (364) .png
      Малюнок\(\PageIndex{3}\)
    Відповідь

    1. \(3x−2\)

    3. \(−\frac{1}{2}x−\frac{7}{8}\)

    5. \(−3x^{2}+12x−6\)

    7. \(−3x^{3}+x^{2}−18\)

    9. \(\frac{2}{9}x^{2}−\frac{1}{10}x−\frac{8}{9}\)

    11. \(2a^{3}+5a^{2}+a−10\)

    13. \(5x^{4}+4x^{3}+x^{2}+2x+1\)

    15. \(−x^{2}y^{2}−xy+14\)

    17. \(7x^{2}+6xy−15y^{2}\)

    19. \(4a^{2}b+3ab^{2}−6ab\)

    21. \(2x−10\)

    23. \(−5x−13 \)

    25. а.\(P=−0.05x^{2}+9.9x−150\); б. $\(340\)

    27. а.\(A=8πr^{2}\); б.\(628.32\) квадратних міліметрів

    Вправа\(\PageIndex{5}\) Addition and Subtraction of Polynomial

    Спростити.

    1. \((2x+3)−(5x−8)+(x−7) \)
    2. \((3x−5)−(7x−11)−(5x+2) \)
    3. \((3x−2)−(4x−1)+(x+7) \)
    4. \((5x−3)−(2x+1)−(x−1) \)
    5. \((5x^{2}−3x+2)−(x^{2}+x−4)+(7x^{2}−2x−6) \)
    6. \((−2x^{3}+x^{2}−8)−(3x^{2}+x−6)−(2x−1)\)
    7. \((2x−7)−(x^{2}+3x−7)+(6x−1)\)
    8. \((6x^{2}−10x+13)+(4x^{2}−9)−(9−x^{2})\)
    9. \((a^{2}−b^{2})−(2a^{2}+3ab−4b^{2})+(5ab−1)\)
    10. \((a^{2}−3ab+b^{2})−(a^{2}+  b^{2})−(3ab−5)\)
    11. \((\frac{1}{2}x^{2}−\frac{3}{4}x+\frac{1}{4})−(\frac{3}{2}x−\frac{3}{4})+(\frac{5}{4}x−\frac{1}{2})\)
    12. \((\frac{9}{5}x^{2}−\frac{1}{3}x+2)−(\frac{3}{10}x^{2}−\frac{4}{5})−(x+\frac{5}{2})\)
    Відповідь

    1. \(−2x+4\)

    3. \(6\)

    5. \(11x^{2}−6x\)

    7. \(−x^{2}+5x−1\)

    9. \(−a^{2}+2ab+3b^{2}−1\)

    11. \(12x^{2}−x+12\)

    Вправа\(\PageIndex{6}\) Addition and Subtraction of Polynomial Functions

    Знайти\((f+g)(x)\) і\((f−g)(x)\), враховуючи наступні функції.

    1. \(f(x)=4x−1\)і\(g(x)=−3x+1\)
    2. \(f(x)=−x+5\)і\(g(x)=2x−3\)
    3. \(f(x)=3x^{2}−5x+7\)і\(g(x)=−2x^{2}+5x−1\)
    4. \(f(x)=x^{3}+2x^{2}−6x+2\)і\(g(x)=2x^{3}+2x^{2}−5x−1\)
    5. \(f(x)=\frac{1}{2}x+\frac{1}{3}\)і\(g(x)=\frac{1}{5}x^{2}−\frac{3}{2}x+\frac{1}{6} \)
    6. \(f(x)=x^{2}−5x+\frac{1}{3}\)і\(g(x)=\frac{2}{3}x^{2}−x−\frac{1}{2}\)
    Відповідь

    1. \((f+g)(x)=x\)і\((f−g)(x)=7x−2\)

    3. \((f+g)(x)=x^{2}+6\)і\((f−g)(x)=5x^{2}−10x+8\)

    5. \((f+g)(x)=\frac{1}{5}x^{2}−x+\frac{1}{2}\)і\((f−g)(x)=−\frac{1}{5}x^{2}+2x+\frac{1}{6}\)

    Вправа\(\PageIndex{7}\) Addition and Subtraction of Polynomial Functions

    Дано\(f(x)=2x−3\) і\(g(x)=x^{2}+3x−1\), знайдіть наступне.

    1. \((f+g)(x) \)
    2. \((g+f)(x) \)
    3. \((f−g)(x) \)
    4. \((g−f)(x) \)
    5. \((g+g)(x) \)
    6. \((f+g)(3) \)
    7. \((f+g)(−2) \)
    8. \((f+g)(0) \)
    9. \((f−g)(0) \)
    10. \((f−g)(−2) \)
    11. \((g−f)(−2) \)
    12. \((g−f)(12)\)
    Відповідь

    1. \((f+g)(x)=x^{2}+5x−4\)

    3. \((f−g)(x)=−x^{2}−x−2\)

    5. \((g+g)(x)=2x^{2}+6x−2\)

    7. \((f+g)(−2)=−10\)

    9. \((f−g)(0)=−2\)

    11. \((g−f)(−2)=4\)

    Вправа\(\PageIndex{8}\) Addition and Subtraction of Polynomial Functions

    Дано\(f(x)=5x^{2}−3x+2\) і\(g(x)=2x^{2}+6x−4\), знайдіть наступне.

    1. \((f+g)(x) \)
    2. \((g+f)(x) \)
    3. \((f−g)(x) \)
    4. \((g−f)(x) \)
    5. \((f+g)(−2) \)
    6. \((f−g)(−2) \)
    7. \((f+g)(0) \)
    8. \((f−g)(0)\)
    Відповідь

    1. \((f+g)(x)=7x^{2}+3x−2\)

    3. \((f−g)(x)=3x^{2}−9x+6\)

    5. \((f+g)(−2)=20\)

    7. \((f+g)(0)=−2\)