5.1: Правила експонентів
- Page ID
- 58030
Цілі навчання
- Спростіть вирази, використовуючи правила показників.
- Спростіть вирази, що включають дужки та показники.
- Спростіть вирази, що беруть участь\(0\) як показник.
Продукт, частка та правило влади для експонентів
Якщо коефіцієнт повторюється кілька разів, то твір можна записати в експоненціальній формі\(x_{n}\). Позитивна ціла експонента\(n\) вказує кількість разів, коли база\(x\) повторюється як множник
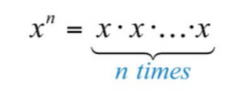.png)
Наприклад,
\(5^{4}=5\cdot 5\cdot 5\cdot 5\)
Тут база є\(5\) і експонента є\(4\). Експоненти іноді позначаються символом каретки (^), знайденим на клавіатурі:\(5\) ^\(4 = 5*5*5*5\).
Далі розглянемо твір\(2^{3}\) і\(2^{5}\),
.png)
Розширення виразу за допомогою визначення дає кілька факторів основи, що є досить громіздким, особливо коли\(n\) воно велике. З цієї причини ми розробимо кілька корисних правил, які допоможуть нам спростити вирази з показниками. У цьому прикладі зверніть увагу, що ми могли б отримати той самий результат, додаючи показники.
\(2^{3}\cdot 2^{5}=2^{3+5}=2^{8}\)
Загалом, це описує правило продукту для експонентів. Якщо\(m\) і\(n\) є натуральними числами, то
\[x^{m}\cdot x^{n} = x^{m+n}\]
Іншими словами, при множенні двох виразів з однаковою базою додайте показники.
Приклад\(\PageIndex{1}\)
Спростити:\(10^{5}\cdot 10^{18}\).
Рішення:
\(\begin{aligned} 10^{5}\cdot 10^{18}&=10^{5+18} \\ &=10^{23} \end{aligned}\)
Відповідь:
\(10^{23}\)
У попередньому прикладі зверніть увагу, що ми не множили базу в 10 разів саму. При застосуванні правила вироби складіть показники і залиште основу без змін.
Приклад\(\PageIndex{2}\)
Спростити:\(x^{6}⋅x^{12}⋅x\).
Рішення:
Нагадаємо, що\(x\) передбачається, що змінна має показник\(1: x=x^{1}\).
\(\begin{aligned} x^{6}\cdot x^{12}\cdot x &=x^{6}\cdot x^{12}\cdot x^{1} \\ &=x^{6+12+1} \\ &=x^{19} \end{aligned}\)
Відповідь:
\(x^{19}\)
Базою може бути будь-який алгебраїчний вираз.
Приклад\(\PageIndex{3}\)
Спростити:\((x+y)^{9} (x+y)^{13}\).
Рішення:
Ставтеся до виразу\((x+y)\) як до основи.
\(\begin{aligned} (x+y)^{9}(x+y)^{13}&=(x+y)^{9+13} \\ &=(x+y)^{22} \end{aligned}\)
Відповідь:
\((x+y)^{22}\)
Комутативна властивість множення дозволяє використовувати правило добутку для експонентів для спрощення факторів алгебраїчного виразу.
Приклад\(\PageIndex{4}\)
Спростити:\(2x^{8}y⋅3x^{4}y^{7}\).
Рішення:
Помножте коефіцієнти і складіть показники змінних факторів з однаковою базою.
\(\begin{aligned} 2x^{8}y\cdot 3x^{4}y^{7}&=2\cdot 3\cdot x^{8}\cdot x^{4}\cdot y^{1}\cdot y^{7} &\color{Cerulean}{Commutative\:property} \\ &=6\cdot x^{8+4}\cdot y^{1+7} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=6x^{12}y^{8} \end{aligned}\)
Відповідь:
\(6x^{12}y^{8}\)
Далі ми розробимо правило поділу, попередньо подивившись на частку\(2^{7}\) і\(2^{3}\).
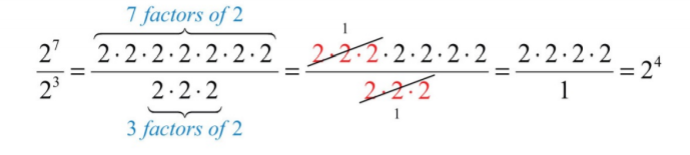.png)
Тут ми можемо скасувати фактори після застосування визначення показників. Зверніть увагу, що той же результат можна отримати, віднімаючи показники.
\[\frac{2^{7}}{2^{3}}=2^{7-3}=2^{4} \nonumber\]
Це описує часткове правило для експонентів. Якщо\(m\) і\(n\) є натуральними числами і\(x≠0\), то
\[\frac{x^{m}}{x^{n}}=x^{m-n} \nonumber\]
Іншими словами, коли ви ділите два вирази з однаковою базою, відніміть показники.
Приклад\(\PageIndex{5}\)
Спростити:\(\frac{12y^{15}}{4y^{7}}\).
Рішення:
Розділіть коефіцієнти і відніміть показники змінної\(y\).
\(\begin{aligned} \frac{12y^{15}}{4y^{7}}&=\frac{12}{4}\cdot y^{15-7}\\ &=3y^{8} \end{aligned}\)
Відповідь:
\(3y^{8}\)
Приклад\(\PageIndex{6}\)
Спростити:\(\frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}\)
Рішення:
\(\begin{aligned} \frac{20x^{10}(x+5)^{6}}{10x^{9}(x+5)^{2}}&=\frac{20}{10}\cdot x^{10-9}\cdot (x+5)^{6-2} \\ &=2x^{1}(x+5)^{4} \end{aligned}\)
Відповідь:
\(2x(x+5)^{4}\)
Тепер підніміть\(2^{3}\) до четвертої потужності наступним чином:
.png)
Після написання бази\(2^{3}\) як множник чотири рази, розширити, щоб отримати\(12\) фактори\(2\). Ми можемо отримати той самий результат, перемноживши показники.
\((2^{3})^{^{4}} = 2^{3\cdot 4} = 2^{12}\)
Загалом, це описує правило потужності для експонентів. Задано натуральні числа\(m\) і\(n\), потім
\[(x^{m})^{^{n}}=x^{m\cdot n}\]
Іншими словами, піднімаючи силу до сили, помножте показники.
Приклад\(\PageIndex{7}\)
Спростити:\((y^{6})^{^{7}}=y^{6\cdot 7}\)
Рішення:
\(\begin{aligned} (y^{6})^{^{7}}&=y^{6\cdot 7} \\ &=y^{42} \end{aligned}\)
Відповідь:
\(y^{42}\)
Підводячи підсумок, ми розробили три дуже корисні правила показників, які широко використовуються в алгебрі. Якщо задано натуральні числа\(m\) і\(n\), то
- Правило продукту:\[x^{m}\cdot x^{n}=x^{m+n}\]
- Правило частки:\[\frac{x^{m}}{x^{n}}=x^{m-n}, x\neq 0\]
- Правило харчування:\[(x^{m})^{^{n}} = x^{m\cdot n}\]
Вправа\(\PageIndex{1}\)
Спростити:\(y^{5}⋅(y^{4})^{^{6}}\).
- Відповідь
-
\(y^{29}\)
Правила харчування для продуктів і коефіцієнтів
Зараз ми розглядаємо підвищення згрупованих продуктів до влади. Наприклад,
\(\begin{aligned} (xy)^{4} &= xy\cdot xy\cdot xy\cdot xy \\ &=x\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot y\quad\color{Cerulean}{Commutative\:property} \\ &=x^{4}\cdot y^{4} \end{aligned}\)
Після розширення ми маємо чотири фактори продукту\(xy\). Це еквівалентно підняттю кожного з вихідних чинників до четвертої потужності. Загалом, це описує правило харчування для продукту. Якщо\(n\) натуральне число, то
\[(xy)^{n}=x^{n}y^{n}\]
Приклад\(\PageIndex{8}\)
Спростити:\((2ab)^{7}=2^{7}a^{7}b^{7}\).
Рішення:
Ми повинні застосувати показник\(7\) до всіх факторів, включаючи коефіцієнт,\(2\).
\(\begin{aligned} (2ab)^{7}&=2^{7}a^{7}b^{7} \\ &=128a^{7}b^{7} \end{aligned}\)
Якщо коефіцієнт підвищений до відносно невеликої потужності, то представимо еквівалент дійсного числа, як ми це робили в цьому прикладі:\(2^{7}=128\).
Відповідь:
\(128a^{7}b^{7}\)
У багатьох випадках процес спрощення виразів за участю експонентів вимагає використання декількох правил показників.
Приклад\(\PageIndex{9}\)
Спростити:\((3xy^{3})^{^{4}}\).
Рішення:
\(\begin{aligned} (3xy^{3})^{^{4}}&=3^{4}\cdot x^{4}\cdot (y^{3})^{^{4}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=3^{4}x^{4}y^{3\cdot 4} &\color{Cerulean}{Power\:rule\:for\:exponents} \\ &=81x^{4}y^{12} \end{aligned}\)
Відповідь:
\(81x^{4}y^{12}\)
Приклад\(\PageIndex{10}\)
Спростити:\((4x^{2}y^{5}z)^{^{3}}\).
Рішення:
\(\begin{aligned} (4x^{2}y^{5}z)^{^{3}}&=4^{3}\cdot(x^{2})^{^{3}}\cdot (y^{5})^{^{3}}\cdot z^{3} \\ &=64x^{6}y^{15}z^{3} \end{aligned}\)
Відповідь:
\(64x^{6}y^{15}z^{3}\)
Приклад\(\PageIndex{11}\)
Спростити:\([5(x+y)^{3}]^{^{3}}\)
Рішення:
\(\begin{aligned} [5(x+y)^{3}]^{^{3}} &=5^{3}\cdot (x+y)^{9} \\ &=125(x+y)^{9} \end{aligned}\)
Відповідь:
\(125(x+y)^{9}\)
Далі розглянемо частку, підняту до влади.
\(\begin{aligned} \left( \frac{x}{y} \right) ^{4} &= \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y}\cdot \frac{x}{y} \\ &=\frac{x\cdot x\cdot x\cdot x}{y\cdot y\cdot y\cdot y} \\ &=\frac{x^{4}}{y^{4}} \end{aligned}\)
Тут ми отримуємо чотири множники частки, що еквівалентно чисельнику і знаменнику обидва підняті до четвертої степені. Загалом, це описує правило потужності для частки. Якщо\(n\) натуральне число і\(y≠0\), то
\[\left( \frac{x}{y} \right) ^{n} = \frac{x^{n}}{y^{n}}\]
Іншими словами, враховуючи дріб, піднятий до степеня, ми можемо застосувати цей показник до чисельника та знаменника. Це правило вимагає, щоб знаменник був ненульовим. Ми зробимо це припущення для решти розділу.
Приклад\(\PageIndex{12}\)
Спростити:\(\left(\frac{3a}{b} \right) ^{3}\)
Рішення:
Спочатку застосуйте правило потужності для частки, а потім правило потужності для продукту.
\(\begin{aligned} \left(\frac{3a}{b} \right) ^{3}&=\frac{(3a)^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{3^{3}\cdot a^{3}}{b^{3}} &\color{Cerulean}{Power\:rule\:for\:a\:product} \\ &=\frac{27a^{3}}{b^{3}} \end{aligned}\)
Відповідь:
\(\frac{27a^{3}}{b^{3}}\)
На практиці ми часто поєднуємо ці два кроки, застосовуючи експоненту до всіх факторів чисельника та знаменника.
Приклад\(\PageIndex{13}\)
Спростити:\(\left( \frac{ab^{2}}{2c^{3}} \right)^{5}\)
Рішення:
Застосовуйте експоненту\(5\) до всіх факторів чисельника та знаменника.
\(\begin{aligned} \left( \frac{ab^{2}}{2c^{3}} \right)^{5}&=\frac{a^{5}(b^{2})^{^{5}}}{2^{5}(c^{3})^{^{5}}} \\ &=\frac{a^{5}b^{10}}{32c^{15}} \end{aligned}\)
Відповідь:
\(\frac{a^{5}b^{10}}{32c^{15}}\)
Приклад\(\PageIndex{14}\)
Спростити:\(\left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2}\)
Рішення:
\(\begin{aligned} \left( \frac{5x^{5}(2x-1)^{4}}{3y^{7}} \right) ^{2} &=\frac{(5x^{5}(2x-1)^{4})^{2}}{(3y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:a\:quotient} \\ &=\frac{5^{2}\cdot (x^{5})^{^{2}}\cdot [(2x-1)^{4}]^{2}}{3^{2}\cdot (y^{7})^{^{2}}} &\color{Cerulean}{Power\:rule\:for\:products} \\ &=\frac{25x^{10}(2x-1)^{8}}{9y^{14}} &\color{Cerulean}{Power\:rule\:for\:exponents} \end{aligned}\)
Відповідь:
\(\frac{25x^{10}(2x-1)^{8}}{9y^{14}}\)
Хорошою практикою є спрощення в дужках перед використанням правил харчування; це узгоджується з порядком операцій.
Приклад\(\PageIndex{15}\)
Спростити:\(\left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}\)
Рішення:
\(\begin{aligned} \left( \frac{-2x^{3}y^{4}z}{xy^{2}} \right)^{4}&=(-2\cdot x^{3-1}\cdot y^{4-2}\cdot z)^{4} &\color{Cerulean}{Simplify\:within\:the\:parentheses\:first.} \\ &=(-2\cdot x^{2}\cdot y^{2} \cdot z)^{4} &\color{Cerulean}{Apply\:the\:power\:rule\:for\:a\:product.} \\ &=(-2)^{4}\cdot (x^{2})^{^{4}}\cdot (y^{2})^{^{4}}\cdot z^{4}&\color{Cerulean}{Apply\:the\:power\:rule\:for\:exponents.} \\ &=16x^{8}y^{8}z^{4} \end{aligned}\)
Відповідь:
\(16x^{8}y^{8}z^{4}\)
Підводячи підсумок, ми розробили два нових правила, які корисні, коли символи групування використовуються спільно з експонентами. Якщо задано натуральне число\(n\), де\(y\) є ненульовим числом, то
- Правило харчування для виробу:\[(xy)^{n} = x^{n}y^{n}\]
- Правило харчування для частки:\[\left( \frac{x}{y} \right)^{n} = \frac{x^{n}}{y^{n}}\]
Вправа\(\PageIndex{2}\)
Спростити:\(\left(\frac{4x^{2}(x-y)^{3}}{3yz^{5}} \right)^{3}\)
- Відповідь
-
\(\frac{64x^{6}(x-y)^{9}}{27y^{3}z^{15}}\)
Нуль як показник
Використовуючи частне правило для експонентів, ми можемо визначити, що означає мати\(0\) як показник. Розглянемо наступний розрахунок:
\ (\ color {Cerulean} {1}\ колір {чорний} {=\ frac {8} {8} =\ frac {2^ {3}} {2^ {3}} =2^ {3-3} =}\ колір {лазурний} {2^ {0}}
Вісім ділиться на чітко\(8\) дорівнює\(1\), і коли застосовується часткове правило для експонент, ми бачимо, що\(0\) показник результатів. Це призводить нас до визначення нуля як показника, де\(x≠0\):
\[x^{0}=1\]
Важливо відзначити, що\(0^{0}\) не визначено. Якщо база негативна, то результат все одно\(+1\). Іншими словами, будь-яка ненульова база, піднята до\(0\) влади, визначається бути\(1\). У наступних прикладах припустимо, що всі змінні ненульові.
Приклад\(\PageIndex{16}\)
Спростити:
- \((-5)^{0}\)
- \(-5^{0}\)
Рішення:
- Будь-яка ненульова величина, піднята до\(0\) потужності, дорівнює\(1\).
\((-5)^{0}=1\)
б. У\(−5^{0}\) прикладі база є\(5\), а не\(−5\).
Відповідь:
- \(1\)
- \(-1\)
Приклад\(\PageIndex{17}\)
Спростити:
\((5x^{3}y^{0}z^{2})^{^{2}}\).
Рішення:
Це гарна практика, щоб спростити в дужках в першу чергу.
\(\begin{aligned} (5x^{3}\color{Cerulean}{y^{0}}\color{black}{z^{2})^{^{2}}}&=(5x^{3}\cdot\color{Cerulean}{1}\color{black}{\cdot z^{2})^{2}} \\ &=(5x^{3}z^{2})^{2} \\ &=5^{2}x^{3\cdot 2}z^{2\cdot 2} \\ &=25x^{6}z^{4} \end{aligned}\)
Відповідь:
\(25x^{6}z^{4}\)
Приклад\(\PageIndex{18}\)
Спростити:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0}\).
Рішення:
\(\left( -\frac{8a^{10}b^{5}}{5c^{12}d^{14}} \right) ^{0} =1\)
Відповідь:
\(1\)
Вправа\(\PageIndex{3}\)
Спростити:
\(5x^{0}\)і\((5x)^{0}\)
- Відповідь
-
\(5x^{0}=5\)і\((5x)^{0}=1\)
Ключові винос
- Правила показників дозволяють спростити вирази за участю експонентів.
- При множенні двох величин з однаковою базою додайте показники:\(x^{m}⋅x^{n}=x^{m+n}\).
- При діленні двох величин з однаковою базою віднімають показники:\(\frac{x^{m}}{x^{n}}=x^{m−n}\).
- При підвищенні повноважень до повноважень помножте показники:\((x^{m})^{^{n}}=x^{m⋅n}\).
- Коли згрупована величина, що включає множення та ділення, піднімається до степеня, застосуйте цю владу до всіх факторів у чисельнику та знаменнику:\((xy)^{n}=x^{n}y^{n}\) і\((\frac{x}{y})^{n}=\frac{x^{n}}{y^{n}}\).
- Будь-яка ненульова величина, піднята до\(0\) потужності, визначається рівною\(1: x^{0}=1\).
Вправа\(\PageIndex{4}\) Product, Quotient, and Power Rule for Exponents
Запишіть кожен вираз, використовуючи експоненціальну форму.
- \((2x)(2x)(2x)(2x)(2x)\)
- \((−3y)(−3y)(−3y)\)
- \(−10⋅a⋅a⋅a⋅a⋅a⋅a⋅a\)
- \(12⋅x⋅x⋅y⋅y⋅y⋅y⋅y⋅y\)
- \(−6⋅(x−1)(x−1)(x−1)\)
- \((9ab)(9ab)(9ab)(a^{2}−b)(a^{2}−b)\)
- Відповідь
-
1. \((2x)^{5}\)
3. \(-10a^{7}\)
5. \(-6(x-1)^{3}\)
Вправа\(\PageIndex{5}\) Product, Quotient, and Power Rule for Exponents
Спростити.
- \(2^{7}⋅2^{5}\)
- \(3^{9}⋅3\)
- \(−2^{4}\)
- \((−2)^{4}\)
- \(−3^{3}\)
- \((−3)^{4}\)
- \(10^{13}⋅10^{5}⋅10^{4}\)
- \(10^{8}⋅10^{7}⋅10\)
- \(\frac{5^{12}}{5^{2}}\)
- \(\frac{10^{7}}{10^{10}}\)
- \(\frac{10^{12}}{10^{9}}\)
- \((7^{3})^{^{5}}\)
- \((4^{8})^{^{4}}\)
- \(10^{6}⋅(10^{5})^{^{4}}\)
- Відповідь
-
1. \(2^{12}\)
3. \(−16\)
5. \(−27\)
7. \(10^{22}\)
9. \(5^{10}\)
11. \(10^{3}\)
13. \(4^{32}\)
Вправа\(\PageIndex{6}\) Product, Quotient, and Power Rule for Exponents
Спростити.
- \((−x)^{6}\)
- \(a^{5}⋅(−a)^{2}\)
- \(x^{3}⋅x^{5}⋅x\)
- \(y^{5}⋅y^{4}⋅y^{2}\)
- \((a^{5})^{^{2}}⋅(a^{3})^{^{4}}⋅a\)
- \((x+1)^{4}(y^{5})^{^{4}}⋅y^{2}\)
- \((x+1)^{5}(x+1)^{8}\)
- \((2a−b)^{12}(2a−b)^{9}\)
- \(\frac{(3x-1)^{5}}{(3x-1)^{2}}\)
- \(\frac{(a-5)^{37}}{(a-5)^{13}}\)
- \(xy^{2}⋅x^{2}y\)
- \(3x^{2}y^{3}⋅7xy^{5}\)
- \(−8a^{2}b⋅2ab\)
- \(−3ab^{2}c^{3}⋅9a^{4}b^{5}c^{6}\)
- \(2a^{2}b^{4}c (−3abc)\)
- \(5a^{2}(b^{3})^{^{3}}c^{3}⋅(−2)2a^{3}(b^{2})^{^{4}}\)
- \(2x^{2}(x+y)^{5}⋅3x^{5}(x+y)^{4}\)
- \(−5xy^{6}(2x−1)^{6}⋅x^{5}y(2x−1)^{3}\)
- \(x^{2}y⋅xy^{3}⋅x^{5}y^{5}\)
- \(−2x^{10}y⋅3x^{2}y^{12}⋅5xy^{3}\)
- \(3^{2}x^{4}y^{2}z⋅3xy^{4}z^{4}\)
- \((−x^{2})^{^{3}}(x^{3})^{^{2}}(x^{4})^{^{3}}\)
- \(a^{10}⋅\frac{(a^{6})^{^{3}}}{a^{3}}\)
- \(\frac{10x^{9}(x^{3})^{^{5}}}{2x^{5}}\)
- \(\frac{a^{6}b^{3}}{a^{2}b^{2}}\)
- \(\frac{m^{10}n^{7}}{m^{3}n^{4}}\)
- \(\frac{20x^{5}y^{12}z^{3}}{10x^{2}y^{10}z}\)
- \(\frac{-24a^{16}b^{12}c^{3}}{6a^{6}b^{11}c}\)
- \(\frac{16x^{4}(x+2)^{3}}{4x(x+2)}\)
- \(\frac{50y^{2}(x+y)^{20}}{10y(x+y)^{17}}\)
- Відповідь
-
1. \(x^{6}\)
3. \(x^{9}\)
5. \(a^{23}\)
7. \((x+1)^{13}\)
9. \((3x−1)^{3}\)
11. \(x^{3}y^{3}\)
13. \(−16a^{3}b^{2}\)
15. \(−6a^{3}b^{5}c^{2}\)
17. \(6x^{7}(x+y)^{9}\)
19. \(x^{8}y^{9}\)
21. \(27x^{5}y^{6}z^{5}\)
23. \(a^{25}\)
25. \(a^{4}b\)
27. \(2x^{3}y^{2}z^{2}\)
29. \(4x^{3}(x+2)^{2}\)
Вправа\(\PageIndex{7}\) Power Rules for Products and Quotients
Спростити.
- \((2x)^{5}\)
- \((−3y)^{4}\)
- \((−xy)^{3}\)
- \((5xy)^{3}\)
- \((−4abc)^{2}\)
- \(\left(\frac{7}{2x} \right)^{2}\)
- \(-\left(\frac{5}{3y} \right)^{3}\)
- \((3abc)^{3}\)
- \(\left(\frac{-2xy}{3z} \right)^{4}\)
- \(\left(\frac{5y}{(2x-1)x}\right)^{3}\)
- \((3x^{2})^{^{3}}\)
- \((−2x^{3})^{^{2}}\)
- \((xy^{5})^{^{7}}\)
- \((x^{2}y^{10})^{^{2}}\)
- \(\left(\frac{3x^{2}}{y} \right)^{3}\)
- \((2x^{2}y^{3}z^{4})^{^{5}}\)
- \(\left(\frac{-7ab^{4}}{c^{2}} \right)^{2}\)
- \([x^{5}y^{4}(x+y)^{4}]^{5}\)
- \([2y(x+1)^{5}]^{3}\)
- \((ab^{3})^{^{3}}\)
- \(\left(\frac{5a^{2}}{3b} \right)^{4}\)
- \(\left(\frac{-2x^{3}}{3y^{2}} \right)^{2}\)
- \(\left(\frac{-x^{2}}{y^{3}} \right)^{3}\)
- \(\left(\frac{ab^{2}}{3c^{3}d^{2}} \right)^{4}\)
- \(\left(\frac{2x^{7}y}{(x-1)^{3}z^{5}} \right)^{6}\)
- \((2x^{4})^{^{3}}⋅(x^{5})^{^{2}}\)
- \((x^{3}y)^{^{2}}⋅(xy^{4})^{^{3}}\)
- \((−2a^{2}b^{3})^{^{2}}⋅(2a^{5}b)^{^{4}}\)
- \((−a^{2}b)^{3}(3ab^{4})^{4}\)
- \((2x^{3}(x+y)^{4})^{5}⋅(2x^{4}(x+y)^{2})^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{3}\)
- \(\left(\frac{-3x^{5}y^{4}}{xy^{2}} \right)^{2}\)
- \(\left(\frac{-25x^{10}y^{15}}{5x^{5}y^{10}} \right)^{3}\)
- \(\left(\frac{10x^{3}y^{5}}{5xy^{2}} \right)^{2}\)
- \(\left(\frac{-24ab^{3}}{6bc} \right)^{5}\)
- \(\left(\frac{-2x^{3}y^{16}}{x^{2}y} \right)^{2}\)
- \(\left(\frac{30ab^{3}}{3abc} \right)^{3}\)
- \(\left(\frac{3s^{3}t^{2}}{2s^{2}t} \right)^{3}\)
- \(\left(\frac{6xy^{5}(x+y)^{6}}{3y^{2}z(x+y)^{2}} \right)^{5}\)
- \(\left(\frac{-64a^{5}b^{12}c^{2}(2ab-1)^{14}}{32a^{2}b^{10}c^{2}(2ab-1)^{7}} \right)^{4}\)
- Імовірність підкидання справедливої монети і отримання\(n\) голів поспіль задається формулою\(P=(12)^{n}\). Визначте ймовірність, у відсотках, кидання\(5\) голів поспіль.
- Імовірність прокатки однієї справедливої\(n\) шестигранної матриці і отримання однакових граней вгору підряд задається формулою\(P=(16)^{n}\). Визначте ймовірність, у відсотках, отримання одного і того ж лицьовою стороною вгору два рази поспіль.
- Якщо кожна сторона квадрата вимірює\(2x^{3}\) одиниці виміру, то визначте площу через змінну\(x\).
- Якщо кожне ребро куба вимірює\(5x^{2}\) одиниці виміру, то визначте обсяг через змінну\(x\).
- Відповідь
-
1. \(32x^{5}\)
3. \(−x^{3}y^{3}\)
5. \(16a^{2}b^{2}c^{2}\)
7. \(−\frac{125}{27y^{3}}\)
9. \(\frac{16x^{4}y^{4}}{81z^{4}}\)
11. \(27x^{6}\)
13. \(x^{7}y^{35}\)
15. \(\frac{27x^{6}}{y^{3}}\)
17. \(\frac{49a^{2}b^{8}}{c^{4}}\)
19. \(8y^{3}(x+1)^{15}\)
21. \(\frac{625a^{8}}{81b^{4}}\)
23. \(−\frac{x^{6}}{y^{9}}\)
25. \(\frac{64x^{42}y^{6}}{(x−1)^{18}z^{30}}\)
27. \(x^{9}y^{14}\)
29. \(−81a^{10}b^{19}\)
31. \(−27x^{12}y^{6}\)
33. \(−125x^{15}y^{15}\)
35. \(\frac{−1024a^{5}b^{10}}{c^{5}}\)
37. \(\frac{1000b^{6}}{c^{3}}\)
39. \(\frac{32x^{5}y^{15}(x+y)^{20}}{z^{5}}\)
41. \(3 \frac{1}{8}\)%
43. \(A=4x^{6}\)
Вправа\(\PageIndex{8}\) Zero Exponents
Спростити. (Припустимо, змінні ненульові.)
- \(7^{0}\)
- \((−7)^{0}\)
- \(−10^{0}\)
- \(−3^{0}⋅(−7)^{0}\)
- \(8675309^{0}\)
- \(5^{2}⋅3^{0}⋅2^{3}\)
- \(−3^{0}⋅(−2)^{2}⋅(−3)^{0}\)
- \(\frac{5x^{0}}{y^{2}}\)
- \((−3)^{2}x^{2}y^{0}z^{5}\)
- \(−3^{2}(x^{3})^{2}y^{2}(z^{3})^{0}\)
- \(2x^{3}y^{0}z⋅3x^{0}y^{3}z^{5}\)
- \(−3ab^{2}c^{0}⋅3a^{2}(b^{3}c^{2})^{0}\)
- \((−8xy^{2})^{0}\)
- \((2x^{2}y^{3})^{0}\)
- \(\frac{9x^{0}y^{4}}{3y^{3}}\)
- Відповідь
-
1. \(1\)
3. \(−1\)
5. \(1\)
7. \(−4\)
9. \(9x^{2}z^{5}\)
11. \(6x^{3}y^{3}z^{6}\)
13. \(1\)
15. \(3y\)
Вправа\(\PageIndex{9}\) Discussion Board Topics
- Рене Декарт (1637) встановив використання експоненціальної форми:\(a^{2}, a^{3}\) і так далі. До цього, як позначалися показники?
- Обговоріть досягнення, акредитовані в Al-Karismi.
- Чому не\(0^{0}\) визначено?
- Поясніть початківцю школяреві чому\(3^{4}⋅3^{2}≠9^{6}\).
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
