5.5: Ділильні многочлени
- Page ID
- 58022
Цілі навчання
- Ділимо на мономіал.
- Ділимо на многочлен за допомогою алгоритму ділення.
- Розділити поліноміальні функції.
Ділення на многочлен
Згадайте часткове правило для показників: якщо ненульові і\(m\) і\(x\)\(n\) є додатними цілими числами, то
\[\frac{x^{m}}{x^{n}}=x^{m-n}\]
Іншими словами, при діленні двох виразів з однаковою базою віднімайте показники. Це правило діє при діленні монома на мономіал. У цьому розділі будемо вважати, що всі змінні в знаменнику ненульові.
Приклад\(\PageIndex{1}\)
Розділити:
\(\frac{28y^{3}}{7y}\).
Рішення:
Розділіть коефіцієнти і відніміть показники змінної\(y\).
\(\begin{aligned} \frac{28y^{3}}{7y}&=\frac{28}{7}y^{3-1} \\ &=4y^{2} \end{aligned}\)
Відповідь:
\(4y^{2}\)
Приклад\(\PageIndex{2}\)
Розділити:
\(\frac{24x^{7}y^{5}}{8x^{3}y^{2}}\).
Рішення:
Розділіть коефіцієнти і застосуйте часткове правило, віднімаючи показники аналогічних баз.
\(\begin{aligned} \frac{24x^{7}y^{5}}{8x^{3}y^{2}}&=\frac{24}{8}x^{7-3}y^{5-2} \\ &=3x^{4}y^{3} \end{aligned}\)
Відповідь:
\(3x^{4}y^{3}\)
При діленні многочлена на мономіал ми можемо розглядати мономіал як спільний знаменник і розбивати дріб, використовуючи таку властивість:
\[\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}\]
Застосування цієї властивості призводить до термінів, які можна розглядати як коефіцієнти мономов.
Приклад\(\PageIndex{3}\)
Розділити:
\(\frac{−5x^{4}+25x^{3}−15x^{2}}{5x^{2}}\).
Рішення:
Розбийте дріб, розділивши кожен член в чисельнику на мономіал у знаменнику, а потім спростіть кожен член.
Відповідь:
\(-x^{2}+5x-3\cdot 1\)
Перевірте своє ділення, помноживши відповідь, частку, на мономіал у знаменнику, дільник, щоб побачити, чи отримаєте ви оригінальний чисельник, дивіденд.
\[\color{Cerulean}{\frac{dividend}{divisor}=quotient}\]
\(or\)
\[\color{Cerulean}{dividend=divisor\cdot quotient}\]
\(\begin{aligned} 5x^{2}\cdot (-x^{2}+5x-3) &=\color{Cerulean}{5x^{2}}\color{black}{\cdot (-x^{2})+}\color{Cerulean}{5x^{2}}\color{black}{\cdot 5x-}\color{Cerulean}{5x^{2}}\color{black}{\cdot 3} \\ &=-5x^{4}+25x^{3}-15x^{2}\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Приклад\(\PageIndex{4}\)
Розділити:
\(\frac{9a^{4}b−7a^{3}b^{2}+3a^{2}b}{−3a^{2}b}\).
Рішення:
Відповідь:
\(-3a^{2}+\frac{7}{3}ab-1\). Перевірка необов'язкова і залишається на розсуд зчитувача.
Вправа\(\PageIndex{1}\)
\((16x^{5}−8x^{4}+5x^{3}+2x^{2})÷(2x^{2})\).
- Відповідь
-
\(8x^{3}−4x^{2}+\frac{5}{2}x+1\)
Ділення на многочлен
Та ж техніка, намічена для ділення на мономіал, не працює для поліномів з двома і більше долями в знаменнику. У цьому розділі ми окреслимо процес, званий поліноміальним довгим діленням, який заснований на алгоритмі ділення дійсних чисел. Для наочності будемо вважати, що всі вирази в знаменнику ненульові.
Приклад\(\PageIndex{5}\)
Розділити:
\(\frac{x^{3}+3x^{2}−8x−4}{x−2}\).
Рішення:
\(x−2\)Ось дільник і\(x^{3}+3x^{2}−8x−4\) є дивідендом.
Крок 1: Щоб визначити перший член частки, розділіть провідний член дивіденду на провідний член дільника.
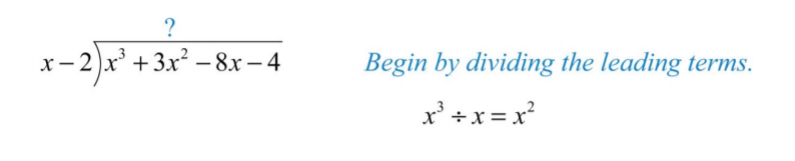.png)
Крок 2: Помножте перший член частки на дільник, не забуваючи розподіляти, і вибудовуйте як терміни з дивідендом.
.png)
Крок 3: Відніміть отриману величину з дивідендів. Подбайте про те, щоб відняти обидва терміни.
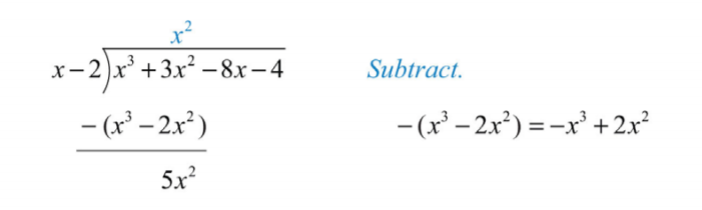.png)
Крок 4: Збийте решту термінів і повторіть процес з кроку 1.
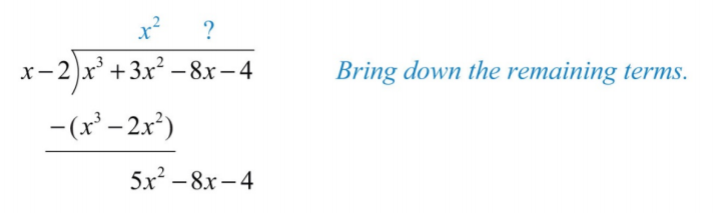.png)
Зверніть увагу, що провідний термін усувається і що результат має ступінь, яка на одиницю менше, ніж дивіденд. Повний процес ілюструється нижче:
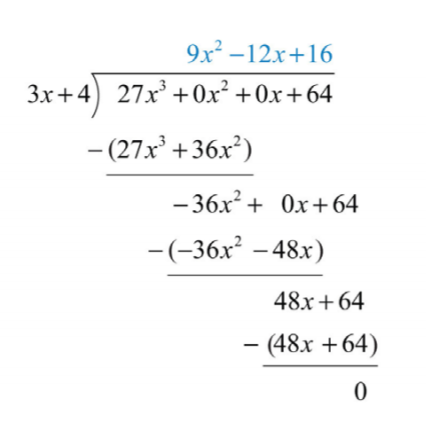.png)
Поліноміальне довге ділення закінчується тоді, коли ступінь залишку менше ступеня дільника. Тут залишок є\(0\). Тому біноміал ділить многочлен рівномірно, а відповідь - частка, показана над лінією ділення.
\(\frac{x^{3}+3x^{2}-8x-4}{x-2}=x^{2}+5x+2\)
Щоб перевірити відповідь, помножте дільник на частку, щоб побачити, чи отримаєте ви дивіденд:
\(x^{3}+3x^{2}-8x-4=(x-2)(x^{2}+5x+2)\)
Відповідь:
\(x^{2}+5x+2\)
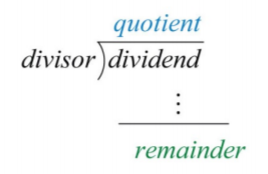
Далі демонструємо випадок, коли є ненульовий залишок.
.png)
Так само, як і у випадку з дійсними числами, остаточна відповідь додає дріб, де залишок - чисельник, а дільник - знаменник до частки. Загалом, при діленні ми маємо
\[\frac{dividend}{divisor}=\color{Cerulean}{quotient}\color{black}{+\frac{\color{OliveGreen}{remainder}}{divisor}}\]
Якщо помножити обидві сторони на дільник, отримаємо
\[dividend=\color{Cerulean}{quotient}\color{black}{\times\:divisor+}\color{OliveGreen}{remainder}\]
Приклад\(\PageIndex{6}\)
Розділити:
\(\frac{6x^{2}-5x+3}{2x-1}\)
Рішення:
Оскільки знаменник є біноміальним, почніть з налаштування багаточленного довгого ділення.
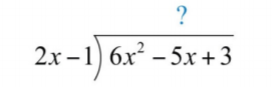.png)
Для початку визначте, які мономіальні часи\(2x−1\) призводять до провідного терміну\(6x^{2}\). Це частка заданих провідних термінів:\((6x^{2})÷(2x)=3x\). \(3x\)Помножте на дільник\(2x−1\) і вибудовуйте результат з подібними умовами дивідендів.
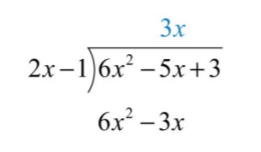.png)
Відніміть результат з дивідендів і збийте постійний термін\(+3\).
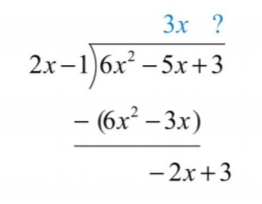.png)
Віднімання виключає провідний термін і\(−5x−(−3x)=−5x+3x=−2x\). Коефіцієнт\(−2x\) і\(2x\) є\(−1\). \(2x−1\)Помножте на\(−1\) і вибудовуйте результат.
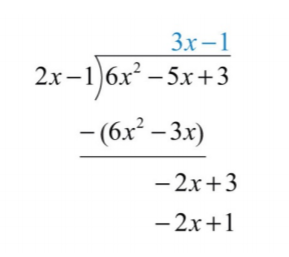.png)
Відніміть ще раз і зверніть увагу, що у нас залишився залишок.
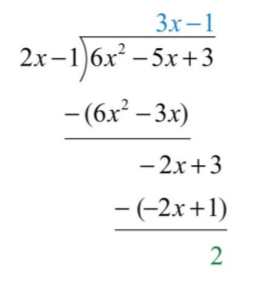.png)
Постійний термін\(2\) має ступінь\(0\), і таким чином поділ закінчується. Ми можемо написати
\(\frac{6x^{2}-5x+3}{2x-1}=\color{Cerulean}{3x-1}\color{black}{+\frac{\color{OliveGreen}{2}}{2x-1}}\)
Відповідь:
\(3x-1+\frac{2}{2x-1}\). Щоб перевірити, що цей результат правильний, множимо наступним чином:
\(\begin{aligned} \color{Cerulean}{quotient}\color{black}{\times\:divisor +}\color{OliveGreen}{remainder}&=\color{Cerulean}{(3x-1)}\color{black}{(2x-1)+}\color{OliveGreen}{2} \\ &=6x^{2}-3x-2x+1+2 \\ &=6x^{2}-5x+3 =dividend\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Іноді деякі повноваження змінних, здається, відсутні в межах полінома. Це може призвести до помилок при вишикуванні подібних термінів. Тому, коли вперше навчитеся ділити поліноми за допомогою довгого ділення, заповніть відсутні члени нульовими коефіцієнтами, званими заповнювачами.
Приклад\(\PageIndex{7}\)
Розділити:
\(\frac{27x^{3}+64}{3x+4}\).
Рішення:
Зверніть увагу, що біноміал в чисельнику не має термінів зі ступенем\(2\) або\(1\). Поділ спрощується, якщо ми перепишемо вираз із заповнювачами:
\(27x^{3}+64=27x^{3}\color{OliveGreen}{+0x^{2}+0x}\color{black}{+64}\)
Налаштуйте поліноміальне довге ділення:
.png)
Починаємо з\(27x^{3}÷3x=9x^{2}\) і опрацьовуємо інший алгоритм поділу.
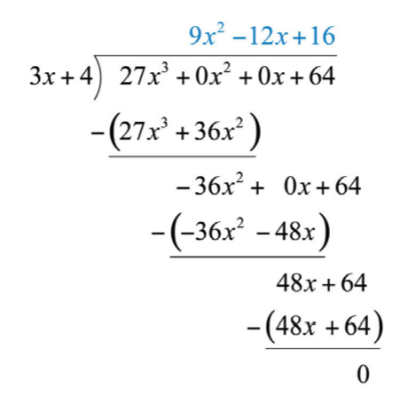.png)
Відповідь:
\(9x^{2}-12x+16\)
Приклад\(\PageIndex{8}\)
Розділити:
\(\frac{3x^{4}−2x^{3}+6x^{2}+23x−7}{x^{2}−2x+5}\).
Рішення:
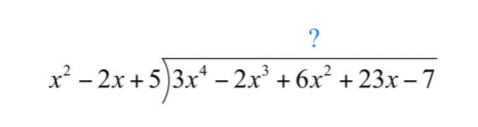.png)
Почніть процес з поділу провідних членів, щоб визначити провідний термін частки\(3x^{4}÷x^{2}=3x^{2}\). Подбайте про розподіл і вибудовуйте подібні терміни. Продовжуйте процес до тих пір, поки залишок не матиме градус менше\(2\).
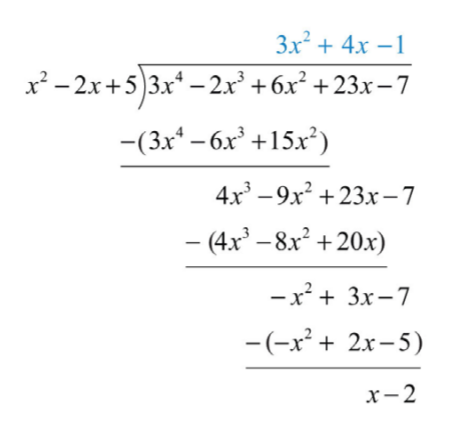.png)
Залишок - це\(x−2\). Напишіть відповідь з залишком:
\(\frac{3x^{4}-2x^{3}+6x^{2}+23x-7}{x^{2}-2x+5}=3x^{2}+4x-1+\frac{x-2}{x^{2}-2x+5}\)
Відповідь:
\(3x^{2}+4x-1+\frac{x-2}{x^{2}-2x+5}\)
Поліноміальне довге ділення вимагає часу і практики, щоб освоїти. Працюйте багато проблем і пам'ятайте, що ви можете перевірити свої відповіді, помноживши частку на дільник (і додаючи залишок, якщо він присутній), щоб отримати дивіденд.
Вправа\(\PageIndex{2}\)
Розділити:
\(\frac{20x^{4}−32x^{3}+7x^{2}+8x−10}{5x−3}\).
- Відповідь
-
\(4x^{3}−4x^{2}−x+1−\frac{7}{5}x−3\)
Функції, що ділять многочлени
Ми можемо використовувати позначення функції для позначення поділу наступним чином:
| Розподіл функцій: | \((f/g)(x)=\frac{f(x)}{g(x)}\) |
|---|
Частка двох поліноміальних функцій не обов'язково має область всіх дійсних чисел. Значення\(x\), які роблять функцію у знаменнику\(0\), обмежені доменом. Про це буде більш детально розказано пізніше. Наразі припустимо, що всі функції в знаменнику ненульові.
Приклад\(\PageIndex{9}\)
Розрахувати:
\((f/g)(x)\)дано\(f(x)=6x^{5}−36x^{4}+12x^{3}−6x^{2}\) і\(g(x)=−6x^{2}\).
Рішення:
Позначення вказує на те, що ми повинні розділити:
\(\begin{aligned} (f/g)(x)&=\frac{f(x)}{g(x)} \\ &=\frac{6x^{5}-36x^{4}+12x^{3}-6x^{2}}{-6x^{2}} \\ &=\frac{6x^{5}}{-6x^{2}}-\frac{36x^{4}}{-6x^{2}}+\frac{12x^{3}}{-6x^{2}}-\frac{6x^{2}}{-6x^{2}} \\ &=-1x^{5-2}+6x^{4-2}-2x^{3-2}+1x^{2-2} \\ &=-x^{3}+6x^{2}-2x+1 \end{aligned}\)
Відповідь:
\((f/g)(x)=-x^{3}+6x^{2}-2x+1\)
Приклад\(\PageIndex{10}\)
Розрахувати:
\((f/g)(−1)\), з огляду на\(f(x)=−3x^{3}+7x^{2}−11x−1\) і\(g(x)=3x−1\).
Рішення:
Для початку визначитеся\((f/g)(x)\).
\((f/g)(x)=\frac{f(x)}{g(x)}=\frac{-3x^{3}+7x^{2}-11x-1}{3x-1}\)
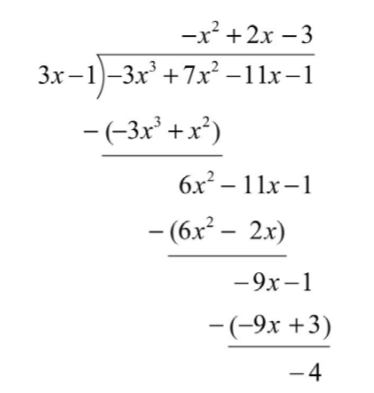.png)
Тому,
\((f/g)(x)=-x^{2}+2x-3-\frac{4}{3x-1}\)
\(−1\)Замінюємо змінну\(x\).
Відповідь:
\((f/g)(-1)=-5\)
Ключові винос
- При діленні на мономіал розділіть всі члени чисельника на мономіал, а потім спростіть кожен член. Щоб спростити кожен член, розділіть коефіцієнти і застосуйте правило частки для показників.
- При діленні многочлена на інший многочлен застосовують алгоритм ділення.
- Щоб перевірити відповідь після ділення, помножте дільник на частку і додайте залишок (при необхідності) для отримання дивіденду.
- Хорошою практикою є включення заповнювачів при виконанні поліноміального довгого ділення.
Вправа\(\PageIndex{3}\) Dividing by a Monomial
Розділити.
- \(\frac{81y^{5}}{9y^{2}}\)
- \(\frac{36y^{9}}{9y^{3}}\)
- \(\frac{52x^{2}y}{4xy}\)
- \(\frac{24xy^{5}}{2xy^{4}}\)
- \(\frac{25x^{2}y^{5}z^{3}}{5xyz}\)
- \(\frac{−77x^{4}y^{9}z^{2}}{2x^{3}y^{3}z}\)
- \(\frac{125a^{3}b^{2}c}{−10abc}\)
- \(\frac{36a^{2}b^{3}c^{5}}{−6a^{2}b^{2}c^{3}}\)
- \(\frac{9x^{2}+27x−3}{3}\)
- \(\frac{10x^{3}−5x^{2}+40x−15}{5}\)
- \(\frac{20x^{3}−10x^{2}+30x}{2x}\)
- \(\frac{10x^{4}+8x^{2}−6x}{24x}\)
- \(\frac{−6x^{5}−9x^{3}+3x}{−3x}\)
- \(\frac{36a^{12}−6a^{9}+12a^{5}}{−12a^{5}}\)
- \(\frac{−12x^{5}+18x^{3}−6x^{2}}{−6x^{2}}\)
- \(\frac{−49a^{8}+7a^{5}−21a^{3}}{7a^{3}}\)
- \(\frac{9x^{7}−6x^{4}+12x^{3}−x^{2}}{3x^{2}}\)
- \(\frac{8x^{9}+16x^{7}−24x^{4}+8x^{3}}{−8x^{3}}\)
- \(\frac{16a^{7}−32a^{6}+20a^{5}−a^{4}}{4a^{4}}\)
- \(\frac{5a^{6}+2a^{5}+6a^{3}−12a^{2}}{3a^{2}}\)
- \(\frac{−4x^{2}y^{3}+16x^{7}y^{8}−8x^{2}y^{5}}{−4x^{2}y^{3}}\)
- \(\frac{100a^{10}b^{30}c^{5}−50a^{20}b^{5}c^{40}+20a^{5}b^{20}c^{10}}{10a^{5}b^{5}c^{5}}\)
- Знайдіть частку\(−36x^{9}y^{7}\) і\(2x^{8}y^{5}\).
- Знайдіть частку\(144x^{3}y^{10}z^{2}\) і\(−12x^{3}y^{5}z\).
- Знайдіть частку\(3a^{4}−18a^{3}+27a^{2}\) і\(3a^{2}\).
- Знайдіть частку\(64a^{2}bc^{3}−16a^{5}bc^{7}\) і\(4a^{2}bc^{3}\).
- Відповідь
-
1. \(9y^{3}\)
3. \(13x\)
5. \(5xy^{4}z^{2}\)
7. \(−\frac{25}{2}a^{2}b\)
9. \(3x^{2}+9x−1\)
11. \(10x^{2}−5x+15\)
13. \(2x^{4}+3x^{2}−1\)
15. \(2x^{3}−3x+1\)
17. \(3x^{5}−2x^{2}+4x−\frac{1}{3}\)
19. \(4a^{3}−8a^{2}+5a−\frac{1}{4}\)
21. \(−4x^{5}y^{5}+2y^{2}+1\)
23. \(−18xy^{2}\)
25. \(a^{2}−6a+9\)
Вправа\(\PageIndex{4}\) Dividing by a Polynomial
Розділити.
- \((2x^{2}−5x−3)÷(x−3)\)
- \((3x^{2}+5x−2)÷(x+2)\)
- \((6x^{2}+11x+3)÷(3x+1)\)
- \((8x^{2}−14x+3)÷(2x−3)\)
- \(\frac{x^{3}−x^{2}−2x−12}{x−3}\)
- \(\frac{2x^{3}+11x^{2}+4x−5}{x+5}\)
- \(\frac{2x^{3}−x^{2}−4x+3}{2x+3}\)
- \(\frac{−15x^{3}−14x^{2}+23x−6}{5x−2}\)
- \(\frac{14x^{4}−9x^{3}+22x^{2}+4x−1}{7x−1}\)
- \(\frac{8x^{5}+16x^{4}−8x^{3}−5x^{2}−21x+10}{2x+5}\)
- \(\frac{x^{2}+8x+17}{x+5}\)
- \(\frac{2x^{2}−5x+5}{x−2}\)
- \(\frac{6x^{2}−13x+9}{−2x+1}\)
- \(\frac{−12x^{2}+x+1}{3x+2}\)
- \(\frac{x^{3}+9x^{2}+19x+1}{x+4}\)
- \(\frac{2x^{3}−13x^{2}+17x−11}{x−5}\)
- \(\frac{9x^{3}−12x^{2}+16x−15}{3x−2}\)
- \(\frac{3x^{4}−8x^{3}+5x^{2}−5x+9}{x−2}\)
- \((6x^{5}−13x^{4}+4x^{3}−3x^{2}+13x−2)÷(3x+1)\)
- \((8x^{5}−22x^{4}+19x^{3}−20x^{2}+23x−3)÷(2x−3)\)
- \(\frac{5x^{5}+12x^{4}+12x^{3}−7x^{2}−19x+3}{x^{2}+2x+3}\)
- \(\frac{6x^{5}−17x^{4}+5x^{3}+16x^{2}−7x−3}{2x^{2}−3x−1}\)
- \(\frac{x^{5}+7x^{4}−x^{3}−7x^{2}−49 x+9}{x^{2}+7x−1}\)
- \(\frac{5x^{6}−6x^{4}−4x^{2}+x+2}{5x^{2}−1}\)
- \(\frac{x^{3}−27}{x−3}\)
- \(\frac{8x^{3}+125}{2x+5}\)
- \((15x^{5}−9x^{4}−20x^{3}+12x^{2}+15x−9)÷(5x−3)\)
- \((2x^{6}−5x^{5}−4x^{4}+10x^{3}+6x^{2}−17x+5)÷(2x−5)\)
- \(\frac{x^{5}−2x^{3}+3x−1}{x−1}\)
- \(\frac{x^{4}−3x^{2}+5x−1}{3x+2}\)
- \(\frac{a^{2}−4}{a+2}\)
- \(\frac{a^{5}+1}{a^{5}+1}\)
- \(\frac{a^{6}−1}{a−1}\)
- \(\frac{x^{5}−1}{x−1}\)
- \(\frac{x^{5}+x^{4}+6x^{3}+12x^{2}−4}{x^{2}+x−1}\)
- \(\frac{50x^{6}−30x^{5}−5x^{4}+15x^{3}−5x+1}{5x^{2}−3x+2}\)
- \(\frac{5x^{5}−15x^{3}+25x^{2}−5}{5x}\)
- \(\frac{−36x^{6}+12x^{4}−6x^{2}}{6x^{2}}\)
- \(\frac{150x^{5}y^{2}z^{15}−10x^{3}y^{6}z^{5}+4x^{3}y^{2}z^{4}}{10x^{3}y^{2}z^{5}}\)
- \(\frac{27m^{6}+9m^{4}−81m^{2}+1}{9m^{2}}\)
- Розділити\(3x^{6}−2x^{5}+27x^{4}−18x^{3}−6x^{2}+7x−10\) на\(3x−2\).
- Розділити\(8x^{6}+4x^{5}−14x^{4}−5x^{3}+x^{2}−2x−3\) на\(2x+1\).
- Відповідь
-
1. \(2x+1\)
3. \(2x+3\)
5. \(x^{2}+2x+4\)
7. \(x^{2}−2x+1\)
9. \(2x^{3}−x^{2}+3x+1\)
11. \(x+3+\frac{2}{x+5}\)
13. \(−3x+5+\frac{4}{−2x+1}\)
15. \(x^{2}+5x−1+\frac{5}{x+4}\)
17. \(3x^{2}−2x+4−\frac{7}{3x−2}\)
19. \(2x^{4}−5x^{3}+3x^{2}−2x+5−\frac{7}{3x+1}\)
21. \(5x^{3}+2x^{2}−7x+1\)
23. \(x^{3}−7+\frac{2}{x^{2}+7x−1}\)
25. \(x^{2}+3x+9\)
27. \(3x^{4}−4x^{2}+3\)
29. \(x^{4}+x^{3}−x^{2}−x+2+\frac{1}{x−1}\)
31. \(a−2\)
33. \(a^{5}+a^{4}+a^{3}+a^{2}+a+1\)
35. \(x^{3}+7x+5+ \frac{2x+1}{x^{2}+x−1}\)
37. \(x^{4}−3x^{2}+5x−\frac{1}{x}\)
39. \(15x^{2}z^{10}−y^{4}+\frac{2}{5z}\)
41. \(x^{5}+9x^{3}−2x+1−\frac{8}{3x−2}\)
Вправа\(\PageIndex{5}\) Dividing Polynomial Functions
Обчисліть\((f/g)(x)\), враховуючи функції.
- \(f(x)=40x^{8}\)і\(g(x)=10x^{5}\)
- \(f(x)=54x^{5}\)і\(g(x)=9x^{3}\)
- \(f(x)=12x^{2}+24x−15\)і\(g(x)=2x+5 \)
- \(f(x)=−8x^{2}+30x−7\)і\(g(x)=2x−7 \)
- \(f(x)=18x^{2}−36x+5\)і\(g(x)=3x−5 \)
- \(f(x)=−7x^{2}+29x−6\)і\(g(x)=7x−1 \)
- \(f(x)=10x^{3}−9x^{2}+27x−10\)і\(g(x)=5x−2 \)
- \(f(x)=15x^{3}+28x^{2}−11x+56\)і\(g(x)=3x+8\)
- \(f(x)=2x^{4}+5x^{3}−11x^{2}−19x+20\)і\(g(x)=x^{2}+x−5 \)
- \(f(x)=4x^{4}−12x^{3}−20x^{2}+26x−3\)і\(g(x)=2x^{2}+2x−3\)
- Відповідь
-
1. \((f/g)(x)=4x^{3}\)
3. \((f/g)(x)=6x−3\)
5. \((f/g)(x)=6x−2−\frac{5}{3x−5}\)
7. \((f/g)(x)=2x^{2}−x+5\)
9. \((f/g)(x)=2x^{2}+3x−4\)
Вправа\(\PageIndex{6}\) Dividing Polynomial Functions
Дано\(f(x)=6x^{3}+4x^{2}−11x+3\) і\(g(x)=3x−1\), знайдіть наступне.
- \((f/g)(x)\)
- \((f/g)(−1)\)
- \((f/g)(0)\)
- \((f/g)(1)\)
- Відповідь
-
1. \((f/g)(x)=2x^{2}+2x−3\)
3. \((f/g)(0)=−3\)
Вправа\(\PageIndex{7}\) Dividing Polynomial Functions
Дано\(f(x)=5x^{3}−13x^{2}+7x+3\) і\(g(x)=x−2\), знайдіть наступне.
- \((f/g)(x)\)
- \((f/g)(−3)\)
- \((f/g)(0)\)
- \((f/g)(7)\)
- Відповідь
-
1. \((f/g)(x)=5x^{2}−3x+1+\frac{5}{x−2}\)
3. \((f/g)(0)=−\frac{3}{2}\)
Вправа\(\PageIndex{8}\) Discussion Board Topics
- Як ви використовуєте розподільну властивість при діленні многочлена на мономіал?
- Порівняйте довге ділення дійсних чисел з поліноміальним довгим діленням. Наведіть приклад кожного.
- Відповідь
-
1. Відповіді можуть відрізнятися
