Skip to main content
LibreTexts - Ukrayinska

5.2: Вступ до поліномів

  1. Last updated
  2. Save as PDF
  • Page ID
    58045

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Визначте многочлен і визначте його ступінь.
    • Оцінити многочлен для заданих значень змінних.
    • Оцінити многочлен за допомогою позначення функції.

    Визначення

    Многочлен - це спеціальний алгебраїчний вираз з термінами, які складаються з коефіцієнтів дійсних чисел і змінних факторів з цілими числовими показниками.

    \(\color{Cerulean}{Examples\:of\:polynomials:}\)

    \(3x^{2}\quad 7xy+5\quad \frac{3}{2}x^{3}+3x^{2}-\frac{1}{2}x+1\quad 6x^{2}y-4xy^{3}-4xy^{3}+7\)

    Поліноми не мають змінних у знаменнику будь-якого терміна.

    \(\color{Cerulean}{Examples\:that\:are\:not\:polynomials:}\)

    \(\frac{2x^{2}}{y} \quad 5\sqrt{x}+5\quad 5x^{2}+3x^{-2}+7\quad \frac{2}{x}-\frac{5}{y}=3\)

    Ступінь члена в поліномі визначається як показник змінної, або якщо в члені є більше однієї змінної, ступінь - це сума їх показників. Нагадаємо, що\(x^{0}=1\); будь-який постійний термін може бути записаний як твір\(x^{0}\) і самого себе. Звідси ступінь постійного терміну є\(0\).

    Термін Ступінь
    \(3x^{2}\) \(2\)
    \(6x^{2}y\) \(2+1=3\)
    \(7a^{2}b^{3}\) \(2+3=5\)
    \(8\) \(0\), так як\(8=8x^{0}\)
    \(2x\) \(1\), так як\(x=x^{1}\)
    Таблиця\(\PageIndex{1}\)

    Ступінь многочлена - найбільша ступінь з усіх його членів.

    многочлен Ступінь
    \(4x^{5}-3x^{3}+2x-1\) \(5\)
    \(6x^{2}y-5xy^{3}+7\) \(4\), тому що\(5xy^{3}\) має ступінь\(4\).
    \(12x+54\) \(1\), тому що\(x=x^{1}\)
    Таблиця\(\PageIndex{2}\)

    Класифікуємо многочлени за кількістю членів і ступенем наступним чином:

    Вираз Класифікація Ступінь
    \(5x^{7}\) Мономіал (один термін) \(7\)
    \(8x^{6}-1\) Біноміальний (два члени) \(6\)
    \(-3x^{2}+x-1\) Тримінал (три терміни) \(2\)
    \(5x^{3}-2x^{2}+3x-6\) Многочлен (багато членів) \(3\)
    Таблиця\(\PageIndex{3}\)

    У цьому тексті ми будемо називати многочлени з чотирма і більше термінами просто поліномами.

    Приклад\(\PageIndex{1}\)

    Класифікують і констатують ступінь:

    \(7x^{2}−4x^{5}−1\).

    Рішення:

    Тут є три терміни. Найвища змінна експонента є\(5\). Тому це триноміал ступеня\(5\).

    Відповідь:

    Тримінал; ступінь\(5\)

    Приклад\(\PageIndex{2}\)

    Класифікують і констатують ступінь:

    \(12a^{5}bc^{3}\).

    Рішення:

    Так як вираз складається тільки з множення, то це один член, мономіал. Змінну частину можна записати як\(a^{5}b^{1}c^{3}\); отже, її ступінь є\(5+1+3=9\).

    Відповідь:

    Мономіальна; ступінь\(9\)

    Приклад\(\PageIndex{3}\)

    Класифікують і констатують ступінь:

    \(4x^{2}y−6xy^{4}+5x^{3}y^{3}+4\).

    Рішення:

    Термін\(4x^{2}y\) має ступінь\(3\);\(−6xy^{4}\) має ступінь\(5; 5x^{3}y^{3}\) має ступінь\(6\); і постійний термін\(4\) має ступінь\(0\). Тому многочлен має\(4\) терміни зі ступенем\(6\).

    Відповідь:

    многочлен; ступінь\(6\)

    Особливий інтерес представляють поліноми з однією змінною, де кожен член має вигляд\(a_{n}x^{n}\). Тут\(a_{n}\) є будь-яке дійсне число і\(n\) будь-яке ціле число. Такі многочлени мають стандартну форму

    \[a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}\]

    Зазвичай ми влаштовуємо терміни поліномів у порядку убування на основі ступеня кожного члена. Провідним коефіцієнтом є коефіцієнт змінної з найбільшою потужністю, в даному випадку,\(a_{n}\).

    Приклад\(\PageIndex{4}\)

    Пишіть в стандартній формі:

    \(3x−4x^{2}+5x^{3}+7−2x^{4}\).

    Рішення:

    Оскільки терміни розділені додаванням, напишіть наступне:

    \(\begin{aligned} & 3x-4x^{2}+5x^{3}+7-2x^{4} \\ &=3x+(-4x^{2})+5x^{3}+7+(-2x^{4}) \end{aligned}\)

    У такому вигляді ми бачимо, що віднімання в оригіналі відповідає негативним коефіцієнтам. Оскільки додавання є комутативним, ми можемо написати терміни у порядку спадання на основі ступеня кожного члена наступним чином:

    \(\begin{aligned} &=(-2x^{4})+5x^{3}+(-4x^{2})+3x+7 \\ &=-2x^{4}+5x^{3}-4x^{2}+3x+7 \end{aligned}\)

    Відповідь:

    \(-2x^{4}+5x^{3}-4x^{2}+3x+7\)

    Ми можемо додатково класифікувати многочлени з однією змінною за їх ступенем наступним чином:

    многочлен Ім'я
    \(5\) Постійна (ступінь\(0\))
    \(2x+1\) Лінійний (ступінь\(1\))
    \(3x^{2}+5x-3\) Квадратний (градус\(2\))
    \(x^{3}+x^{2}+x+1\) Кубічний (градус\(3\))
    \(7x^{4}+3x^{3}-7x+8\) Многочлен четвертого ступеня
    Таблиця\(\PageIndex{4}\)

    У цьому тексті ми називаємо будь-який многочлен\(n\) ступеня\(n≥4\) поліномом th-го ступеня. Іншими словами, якщо ступінь є\(4\), ми називаємо многочлен поліном четвертого ступеня. Якщо ступінь є\(5\), ми називаємо це поліном п'ятого ступеня, і так далі.

    Оцінювання поліномів

    З огляду на значення змінних у многочлені, ми можемо підставити і спростити, використовуючи порядок операцій.

    Приклад\(\PageIndex{5}\)

    Оцініть:

    \(3x−1\), де\(x=−\frac{3}{2}\).

    Рішення:

    Спочатку замініть змінну дужками, а потім підставити задане значення.

    Відповідь:

    \(-\frac{11}{2}\)

    Приклад\(\PageIndex{6}\)

    Оцініть:

    \(3x^{2}+2x−1\), де\(x=−1\).

    Рішення:

    Відповідь:

    \(0\)

    Приклад\(\PageIndex{7}\)

    Оцініть:

    \(−2a^{2}b+ab^{2}−7\), Де\(a=3\) і\(b=−2\).

    Рішення:

    Відповідь:

    \(41\)

    Приклад\(\PageIndex{8}\)

    Обсяг сфери в кубічних одиницях задається за формулою\(V=\frac{4}{3}πr^{3}\), де\(r\) - радіус. Обчисліть обсяг сфери радіусом\(r=\frac{3}{2}\) метрів.

    Знімок екрана (358) .png
    Малюнок\(\PageIndex{1}\)

    Рішення:

    \(\begin{aligned} V&=\frac{4}{3}\pi r^{3} \\ &=\frac{4}{3}\pi \left( \frac{3}{2} \right)^{3} \\ &=\frac{4}{3}\pi \frac{3^{3}}{2^{3}} \\ &=\frac{\color{Cerulean}{\stackrel{1}{\cancel{\color{black}{4}}}}}{\color{Cerulean}{\stackrel{\cancel{\color{black}{3}}}{1}}} \pi \frac{\color{Cerulean}{\stackrel{9}{\cancel{\color{black}{27}}}}}{\color{Cerulean}{\stackrel{\cancel{\color{black}{8}}}{2}}} \\ &=\frac{9}{2} \pi \end{aligned}\)

    Відповідь:

    \(\frac{9}{2}\pi\)кубічних метрів

    Вправа\(\PageIndex{1}\)

    Оцініть:

    \(x^{3}−x^{2}+4x−2\), де\(x=−3\).

    Відповідь

    \(-50\)

    Функції поліномів

    Поліноміальні функції з однією змінною - це функції, які можна записати у вигляді

    \[f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + ... + a_{0}\],

    де\(a_{n}\) будь-яке дійсне число і\(n\) будь-яке ціле число. Нижче наведено кілька прикладів різних класів поліноміальних функцій:

    Функція полінома Ім'я
    \(f(x)=5\) Постійна функція (ступінь\(0\))
    \(f(x)=-2x+1\) Лінійна функція (ступінь\(1\))
    \(f(x)=5x^{2}+4x-3\) Квадратична функція (ступінь\(2\))
    \(f(x)=x^{3}-1\) Кубічна функція (ступінь\(3\))
    \(f(x)=4x^{5}+3x^{4}-7\) Функція полінома
    Таблиця\(\PageIndex{5}\)

    Оскільки обмежень на значення for немає\(x\), область будь-якої поліноміальної функції складається з усіх дійсних чисел.

    Приклад\(\PageIndex{9}\)

    Розрахувати:

    \(f(5)\), дано\(f(x)=−2x^{2}+5x+10\).

    Рішення:

    Нагадаємо, що позначення функції\(f(5)\) вказує на те, що ми повинні оцінити функцію, коли\(x=5\). Замініть кожен екземпляр змінної\(x\) значенням\(5\).

    Відповідь:

    \(f(5)=-15\)

    Приклад\(\PageIndex{10}\)

    Розрахувати:

    \(f(−1)\), дано\(f(x)=−x^{3}+2x^{2}−4x+1\).

    Рішення:

    Замініть\(x\) змінну на\(−1\).

    \(\begin{aligned} f(\color{OliveGreen}{-1}\color{black}{)} &=-(\color{OliveGreen}{-1}\color{black}{)^{3}+2(}\color{OliveGreen}{-1}\color{black}{)^{2}-4(}\color{OliveGreen}{-1}\color{black}{)+1} \\ &=-(-1)+2\cdot 1 +4+1 \\ &=1+2+4+1 \\ &=8 \end{aligned}\)

    Відповідь:

    \(f(-1)=8\)

    Вправа\(\PageIndex{2}\)

    Дано\(g(x)=x^{3}−2x^{2}−x−4\), розрахуйте\(g(−1)\).

    Відповідь

    \(g(−1)=−6\)

    Ключові винос

    • Поліноми - це спеціальні алгебраїчні вирази, де члени є добутком дійсних чисел і змінних з цілими числовими показниками.
    • Ступінь многочлена з однією змінною є найбільшим показником змінної, знайденої в будь-якому терміні.
    • Терміни многочлена, як правило, розташовані в порядку спадання на основі ступеня кожного члена.
    • При оцінці полінома доцільною практикою є заміна всіх змінних дужками, а потім підставити відповідні значення.
    • Всі многочлени є функціями.

    Вправа\(\PageIndex{3}\) Definitions

    Класифікуйте заданий многочлен як лінійний, квадратичний або кубічний.

    1. \(2x+1\)
    2. \(x^{2}+7x+2\)
    3. \(2−3x^{2}+x\)
    4. \(4x\)
    5. \(x^{2}−x^{3}+x+1\)
    6. \(5−10x^{3}\)
    Відповідь

    1. Лінійний

    3. Квадратичний

    5. Кубічний

    Вправа\(\PageIndex{4}\) Definitions

    Класифікуйте даний многочлен як мономіальний, біноміальний або триноміальний і вкажіть ступінь.

    1. \(x^{3}−1\)
    2. \(x^{2}y^{2}\)
    3. \(x−x^{5}+1\)
    4. \(x^{2}+3x−1\)
    5. \(5ab^{4}\)
    6. \(13x−12\)
    7. \(−5x^{3}+2x+1\)
    8. \(8x^{2}−9\)
    9. \(4x^{5}−5x^{3}+6x\)
    10. \(8x^{4}−x^{5}+2x−3\)
    11. \(9x+7\)
    12. \(x^{5}+x^{4}+x^{3}+x^{2}−x+1\)
    13. \(6x−1+5x^{4}−8\)
    14. \(4x−3x^{2}+3\)
    15. \(7\)
    16. \(x^{2}\)
    17. \(4x^{2}y−3x^{3}y^{3}+xy^{3}\)
    18. \(a^{3}b^{2}−6ab\)
    19. \(a^{3}b^{3}\)
    20. \(x^{2}y−y^{2}x\)
    21. \(xy−3\)
    22. \(a^{5}bc^{2}+3a^{9}−5a^{4}b^{3}c\)
    23. \(−3x^{10}y^{2}z−xy^{12}z+9x^{13}+30\)
    24. \(7x^{0}\)
    Відповідь

    1. Біноміальна; ступінь\(3\)

    3. Тримінал; ступінь\(5\)

    5. Мономіальна; ступінь\(5\)

    7. Тримінал; ступінь\(3\)

    9. Тримінал; ступінь\(5\)

    11. Біноміальна; ступінь\(1\)

    13. Чи не многочлен

    15. Мономіальна; ступінь\(0\)

    17. Тримінал; ступінь\(6\)

    19. Мономіальна; ступінь\(6\)

    21. Біноміальна; ступінь\(2\)

    23. многочлен; ступінь\(14\)

    Вправа\(\PageIndex{5}\) Definitions

    Напишіть наступні многочлени в стандартній формі.

    1. \(1−6x+7x^{2}\)
    2. \(x−9x^{2}−8\)
    3. \(7−x^{3}+x^{7}−x^{2}+x−5x^{5}\)
    4. \(a^{3}−a^{9}+6a^{5}−a+3−a^{4}\)
    Відповідь

    1. \(7x^{2}−6x+1\)

    3. \(x^{7}−5x^{5}−x^{3}−x^{2}+x+7\)

    Вправа\(\PageIndex{6}\) Evaluating Polynomials

    1. Заповніть наступну діаграму:
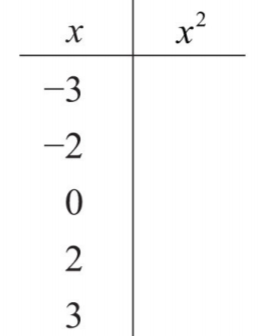      Скріншот (359) .png
      Малюнок\(\PageIndex{2}\)
    2. Заповніть наступну діаграму:
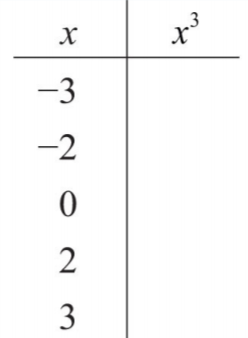      Знімок екрана (360) .png
      Малюнок\(\PageIndex{3}\)
    Відповідь

    1.

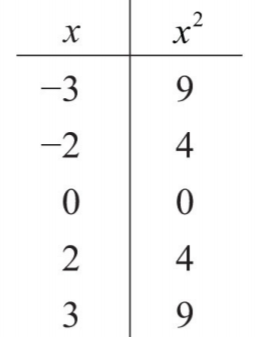    Знімок екрана (361) .png
    Малюнок\(\PageIndex{4}\)

    Вправа\(\PageIndex{7}\) Evaluating Polynomials

    Оцінити.

    1. \(2x−3\), де\(x=3\)
    2. \(x^{2}−3x+5\), де\(x=−2\)
    3. \(−12x+13\), де\(x=−13\)
    4. \(−x^{2}+5x−1\), де\(x=−12\)
    5. \(−2x^{2}+3x−5\), де\(x=0\)
    6. \(8x^{5}−27x^{3}+81x−17\), де\(x=0\)
    7. \(y^{3}−2y+1\), де\(y=−2\)
    8. \(y^{4}+2y^{2}−32\), де\(y=2\)
    9. \(a^{3}+2a^{2}+a−3\), де\(a=−3\)
    10. \(x^{3}−x^{2}\), де\(x=5\)
    11. \(34x^{2}−12x+36\), де\(x=−23\)
    12. \(58x^{2}−14x+12\), де\(x=4\)
    13. \(x^{2}y+xy^{2}\), де\(x=2\) і\(y=−3\)
    14. \(2a^{5}b−ab^{4}+a^{2}b^{2}\), де\(a=−1\) і\(b=−2\)
    15. \(a^{2}−b^{2}\), де\(a=5\) і\(b=−6\)
    16. \(a^{2}−b^{2}\), де\(a=34\) і\(b=−14\)
    17. \(a^{3}−b^{3}\), де\(a=−2\) і\(b=3\)
    18. \(a^{3}+b^{3}\), де\(a=5\) і\(b=−5\)
    Відповідь

    1. \(3\)

    3. \(\frac{1}{2}\)

    5. \(−5\)

    7. \(−3\)

    9. \(−15\)

    11. \(\frac{7}{6}\)

    13. \(6\)

    15. \(−11\)

    17. \(−35\)

    Вправа\(\PageIndex{8}\) Evaluating Polynomials

    Для кожної задачі оцінюйте\(b^{2}−4ac\), враховуючи наступні значення.

    1. \(a=−1, b=2\), і\(c=−1\)
    2. \(a=2, b=−2\), і\(c=12\)
    3. \(a=3, b=−5, c=0\)
    4. \(a=1, b=0\), і\(c=−4\)
    5. \(a=14, b=−4\), і\(c=2\)
    6. \(a=1, b=5\), і\(c=6\)
    Відповідь

    1. \(0\)

    3. \(25\)

    5. \(14\)

    Вправа\(\PageIndex{9}\) Evaluating Polynomials

    Обсяг сфери в кубічних одиницях задається за формулою\(V=\frac{4}{3}πr^{3}\), де\(r\) - радіус. Для кожної задачі обчислити об'єм сфери з урахуванням наступних радіусів.

    1. \(r = 3\)сантиметри
    2. \(r = 1\)сантиметр
    3. \(r = \frac{1}{2}\)стопи
    4. \(r = \frac{3}{2}\)стопи
    5. \(r = 0.15\)в
    6. \(r = 1.3\)дюймів
    Відповідь

    1. \(36π\)кубічні сантиметри

    3. \(\frac{π}{6}\)кубічні фути

    5. \(0.014\)кубічних дюймів

    Вправа\(\PageIndex{10}\) Evaluating Polynomials

    Висота в ногах снаряда, запущеного вертикально від землі з початковою швидкістю\(v_{0}\) в футах в секунду, задається формулою\(h=−16t^{2}+v_{0}t\), де\(t\) позначає час у секундах. Для кожної задачі обчислити висоту снаряда, враховуючи наступну початкову швидкість і час.

    1. \(v_{0}=64\)фути/секунду, в рази\(t = 0, 1, 2, 3, 4\) секунди
    2. \(v_{0}=80\)фути/секунду, в рази\(t = 0, 1, 2, 2.5, 3, 4, 5\) секунди
    Відповідь

    1.

    Час Висота
    \(t=0\)секунд \(h=0\)стопи
    \(t=1\)другий \(h=48\)стопи
    \(t=2\)секунд \(h=64\)стопи
    \(t=3\)секунд \(h=48\)стопи
    \(t=4\)секунд \(h=0\)стопи
    Таблиця\(\PageIndex{6}\)

    Вправа\(\PageIndex{11}\) Evaluating Polynomials

    Гальмівний шлях автомобіля з урахуванням середнього часу реакції можна оцінити за формулою\(d=0.05v^{2}+1.5\), де\(d\) знаходиться в футах і\(v\) - швидкість в милі на годину. Для кожної задачі розрахуйте гальмівний шлях автомобіля, що рухається на заданих швидкостях.

    1. \(20\)миль на годину
    2. \(40\)миль на годину
    3. \(80\)миль на годину
    4. \(100\)миль на годину
    Відповідь

    1. \(21.5\)стопи

    3. \(321.5\)стопи

    Вправа\(\PageIndex{12}\) Polynomial Functions

    З огляду на лінійну функцію\(f(x)=\frac{2}{3}x+6\), оцініть кожну з наступних дій.

    1. \(f(−6)\)
    2. \(f(−3)\)
    3. \(f(0)\)
    4. \(f(3)\)
    5. Знайти\(x\), коли\(f(x)=10\).
    6. Знайти\(x\), коли\(f(x)=−4\).
    Відповідь

    1. \(2\)

    3. \(6\)

    5. \(x=6\)

    Вправа\(\PageIndex{13}\) Polynomial Functions

    З огляду на квадратичну функцію\(f(x)=2x^{2}−3x+5\), оцініть кожну з наступних дій.

    1. \(f(−2)\)
    2. \(f(−1)\)
    3. \(f(0)\)
    4. \(f(2)\)
    Відповідь

    1. \(19\)

    3. \(5\)

    Вправа\(\PageIndex{14}\) Polynomial Functions

    З огляду на кубічну функцію\(g(x)=x^{3}−x^{2}+x−1\), оцініть кожну з наступних дій.

    1. \(g(−2)\)
    2. \(g(−1)\)
    3. \(g(0)\)
    4. \(g(1)\)
    Відповідь

    1. \(-15\)

    3. \(-1\)

    Вправа\(\PageIndex{15}\) Polynomial Functions

    Висота в ногах снаряда, запущеного вертикально від землі з початковою швидкістю\(128\) ніг в секунду, задається функцією\(h(t)=−16t^{2}+128t\), де\(t\) знаходиться в секундах. Обчисліть і інтерпретувати наступне.

    1. \(h(0)\)
    2. \(h(12) \)
    3. \(h(1) \)
    4. \(h(3) \)
    5. \(h(4) \)
    6. \(h(5) \)
    7. \(h(7) \)
    8. \(h(8)\)
    Відповідь

    1. Снаряд запускається з землі.

    3. Снаряд знаходиться\(112\) ногами над землею\(1\) другий після запуску.

    5. Снаряд знаходиться\(256\) ногами над землею через\(4\) кілька секунд після запуску.

    7. Снаряд знаходиться\(112\) ногами над землею через\(7\) кілька секунд після запуску.

    Вправа\(\PageIndex{16}\) Discussion Board Topics

    1. Знайти і поділитися деякими графіками поліноміальних функцій.
    2. Поясніть, як перетворити фути в секунду в милі на годину.
    3. Знайдіть і діліться іменами поліномів четвертого ступеня, п'ятого ступеня та вищого рівня.
    Відповідь

    1. Відповіді можуть відрізнятися

    3. Відповіді можуть відрізнятися