5.4: Множення многочленів
- Page ID
- 58029
Цілі навчання
- Помножте многочлен на моном.
- Помножте многочлен на біном.
- Помножте многочлен на многочлен будь-якого розміру.
- Розпізнавати і розрахувати спеціальні продукти.
- Множення поліноміальних функцій.
Множення на мономіал
Згадайте правило добутку для показників: якщо\(m\) і\(n\) є натуральними числами, то
\[x^{m}\cdot x^{n}=x^{m+n}\]
Іншими словами, при множенні двох виразів з однаковою базою додайте показники. Це правило діє при множенні мономіала на мономіал. Щоб знайти добуток мономіалів, помножте коефіцієнти і складіть показники змінних факторів з однаковою базою. Наприклад,
\(\begin{array} {cl} {3x\cdot 5x^{2} = 3\cdot 5\cdot x^{1}\cdot x^{2}}&{\color{Cerulean}{Commutative\: property}}\\{=15x^{1+2}}&{\color{Cerulean}{Product\:rule\:for\:exponents}}\\{=15x^{3}}&{} \end{array}\)
Щоб помножити многочлен на мономіал, застосуйте розподільну властивість, а потім спростіть кожен член.
Приклад\(\PageIndex{1}\)
Помножити:
\(−5x(4x−2)\).
Рішення:
В цьому випадку помножте мономіал\(−5x\),, на біноміальний,\(4x−2\). Застосовуємо розподільну властивість, а потім спрощуємо.
.png)
Відповідь:
\(-20x^{2}+10x\)
Приклад\(\PageIndex{2}\)
Помножити:
\(2x^{2}(3x^{2}−5x+1)\).
Рішення:
Застосовуємо розподільну властивість, а потім спрощуємо.
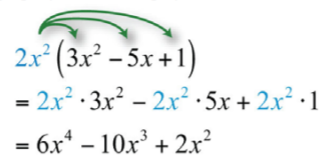.png)
Відповідь:
\(6x^{4}-10x^{3}+2x^{2}\)
Приклад\(\PageIndex{3}\)
Помножити:
\(−3ab^{2}(a^{2}b^{3}+2a^{3}b−6ab−4)\).
Рішення:
Відповідь:
Підводячи підсумок, множення полінома на мономіал передбачає розподільну властивість та правило добутку для експонентів. Помножте всі члени многочлена на мономіал. Для кожного члена помножте коефіцієнти і додайте показники змінних, де основи однакові.
Вправа\(\PageIndex{1}\)
Помножити:
\(−5x^{2}y(2xy^{2}−3xy+6x^{2}y−1)\).
- Відповідь
-
\(−10x^{3}y^{3}+15x^{3}y^{2}−30x^{4}y^{2}+5x^{2}y\)
Множення на біноміал
Точно так само, як ми використовували розподільну властивість, щоб знайти добуток мономіального та біноміального, ми будемо використовувати його, щоб знайти добуток двох біноміалів.
\[\begin{aligned} \color{Cerulean}{(a+b)}\color{black}{(c+d)} \\ &=\color{Cerulean}{(a+b)}\color{black}{\cdot c+}\color{Cerulean}{(a+b)}\color{black}{\cdot d} \\ &=ac+bc+ad+bd \\ &=ac+ad+bc+bd \end{aligned}\]
Тут ми застосовуємо властивість distributive кілька разів, щоб отримати кінцевий результат. Цей же результат виходить за один крок, якщо застосувати розподільну властивість до\(a\) і\(b\) окремо наступним чином:
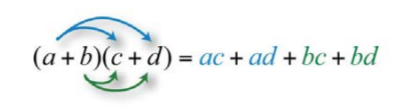.png)
Це часто називають методом FOIL. Ми додаємо продукти перших членів кожного біноміала\(ac\), зовнішніх\(o\) термінів\(ad\), внутрішніх термінів\(i\) і\(bc\), нарешті, останніх термінів\(bd\). Цей мнемонічний пристрій працює лише для продуктів біноміалів; отже, найкраще просто пам'ятати, що застосовується розподільна властивість.
Приклад\(\PageIndex{4}\)
Помножити:
\((2x+3)(5x−2)\).
Рішення:
Розподілити,\(2x\) а потім розподілити\(3\).
Спростіть, комбінуючи подібні терміни.
\(=10x^{2}+11x-6\)
Відповідь:
\(10x^{2}+11x-6\)
Приклад\(\PageIndex{5}\)
Помножити:
\((\frac{1}{2}x−\frac{1}{4})(\frac{1}{2}x+\frac{1}{4})\).
Рішення:
Розподілити,\(\frac{1}{2}x\) а потім розподілити\(−\frac{1}{4}\).
\(\begin{aligned} (\frac{1}{2}x−\frac{1}{4})(\frac{1}{2}x+\frac{1}{4}) &=\color{Cerulean}{\frac{1}{2}x}\color{black}{\frac{1}{2}x+}\color{Cerulean}{\frac{1}{2}x}\color{black}{\cdot\frac{1}{4}+}\color{OliveGreen}{\left( -\frac{1}{4} \right)}\color{black}{\cdot\frac{1}{2}x+}\color{OliveGreen}{\left(-\frac{1}{4} \right)}\color{black}{\cdot\frac{1}{4}} \\ &=\frac{1}{4}x^{2}+\frac{1}{8}x-\frac{1}{8}x-\frac{1}{16} \\ &=\frac{1}{4}x^{2}-\frac{1}{16} \end{aligned}\)
Відповідь:
\(\frac{1}{4}x^{2}-\frac{1}{16}\)
Приклад\(\PageIndex{6}\)
Помножити:
\((3y^{2}−1)(2y+1)\).
Рішення:
Відповідь:
\(6y^{3}+3y^{2}-2y-1\)
Після застосування розподільного майна комбінуйте будь-які подібні терміни.
Приклад\(\PageIndex{7}\)
Помножити:
\((x^{2}−5)(3x^{2}−2x+2)\).
Рішення:
Після множення кожного члена триноміала на\(x^{2}\) і\(−5\), спростити.
Відповідь:
\(3x^{4}-2x^{3}-13x^{2}+10x-10\)
Приклад\(\PageIndex{8}\)
Помножити:
\((2x−1)^{3}\).
Рішення:
Виконуйте по одному виробу за раз.
.png)
Відповідь:
\(8x^{3}-12x^{2}+6x-1\)
На цьому етапі варто вказати на поширену помилку:
\((2x-1)^{3}\neq (2x)^{3}-(1)^{3}\)
Плутанина походить від продукту до силового правила експонентів, де ми застосовуємо владу до всіх факторів. Оскільки в дужках є два терміни, це правило не застосовується. Слід подбати про те, щоб зрозуміти, чим відрізняється в наступних двох прикладах:
\(\begin{aligned} (xy)^{2} &=x^{2}y^{2}\quad\color{Cerulean}{\checkmark} \\ (x+y)^{2} &\neq x^{2}+y^{2}\quad\color{red}{x} \end{aligned}\)
Вправа\(\PageIndex{2}\)
Помножити:
\((2x−3)(7x^{2}−5x+4)\).
- Відповідь
-
\(14x^{3}-31x^{2}+23x-12\)
добуток многочленів
При множенні многочленів ми застосовуємо розподільне властивість багато разів. Помножте всі члени кожного многочлена, а потім об'єднайте як члени.
Приклад\(\PageIndex{9}\)
Помножити:
\((2x^{2}+x−3)(x^{2}−2x+5)\).
Рішення:
Помножте кожен член першого тріноміалу на кожен член другого триноміалу, а потім об'єднайте подібні члени.
Вирівнювання подібних термінів у стовпцях, як у нас тут, допомагає в процесі спрощення
Відповідь:
\(2x^{4}-3x^{3}+5x^{2}+11x-15\)
Зверніть увагу, що при множенні тріноміала на триноміал ми отримуємо дев'ять членів перед спрощенням. Фактично, при множенні\(n\) -членного многочлена на m-членний многочлен ми\(n × m\) отримаємо члени. У попередньому прикладі нас попросили помножити і виявили, що
\((2x^{2}+x-3)(x^{2}-2x+5)=2x^{4}-3x^{3}+5x^{2}+11x-15\)
Оскільки легко зробити невелику помилку обчислення, гарною практикою є простежити кроки подумки, щоб переконатися, що операції були виконані правильно. Крім того, ми можемо перевірити, оцінюючи будь-яке значення для\(x\) обох виразів, щоб переконатися, що результати однакові. Тут вибираємо\(x = 2\):
\(\begin{aligned} (2x^{2}+x-3)(x^{2}-2x+5)&=(2(\color{OliveGreen}{2}\color{black}{)^{2}+(}\color{OliveGreen}{2}\color{black}{)-3)((}\color{OliveGreen}{2}\color{black}{)^{2}-2(}\color{OliveGreen}{2}\color{black}{)+5)} \\ &=(8+2-3)(4-4+5) \\ &=(7)(5) \\ &=35 \end{aligned}\)
Оскільки результати випадково можуть бути однаковими, перевірка шляхом оцінки не обов'язково доводить, що ми правильно помножили. Однак, перевіривши кілька значень, ми можемо бути досить впевнені, що продукт правильний.
Вправа\(\PageIndex{3}\)
Помножити:
\((x^{2}−2x−3)^{2}\).
- Відповідь
-
\(x^{4}−4x^{3}−2x^{2}+12x+9\)
Спеціальні продукти
У цьому розділі мета полягає в тому, щоб розпізнати певні спеціальні продукти, які часто зустрічаються при нашому вивченні алгебри. Ми розробимо три формули, які будуть дуже корисні в міру просування. Три слід запам'ятати. Почнемо з розгляду наступних двох розрахунків:
\(\begin{array}{r|r} {(a+b)^{2}=(a+b)(a+b)}&{(a-b)^{2}=(a-b)(a-b)}\\{=a^{2}+ab+ba+b^{2}}&{=a^{2}-ab-ba+b^{2}}\\{=a^{2}+ab+ab+b^{2}}&{=a^{2}-ab-ab+b^{2}}\\{=a^{2}+2ab+b^{2}}&{=a^{2}-2ab+b^{2}} \end{array}\)
Це призводить нас до двох формул, які описують ідеальні квадратні триноми:
\[ (a+b)^{2}=a^{2}+2ab+b^{2} \]
\[ (a-b)^{2}=a^{2}-2ab+b^{2}\]
Ми можемо використовувати ці формули, щоб швидко квадратувати біном.
Приклад\(\PageIndex{10}\)
Помножити:
\((3x+5)^{2}\).
Рішення:
Ось\(a=3x\) і\(b=5\). Застосовуємо формулу:
\(\begin{aligned} \color{Cerulean}{(a+b)^{2}} &\color{Cerulean}{ =\:\: a^{2}\:\:\:\:+2\:\:\:\:\:\:a\:\:\:\:\:b\:\:+\:\:b^{2}} \\ &\color{Cerulean}{\quad\:\:\: \downarrow\qquad\qquad\:\: \downarrow\:\:\:\:\: \downarrow\qquad\downarrow} \\ (3x+5)^{2}&=(3x)^{2}+2\cdot(3x)(5)+(5)^{2} \\ &=9x^{2}+30x+25\end{aligned}\)
Відповідь:
\(9x^{2}+30x+25\)
Цей процес повинен стати рутинним досить, щоб його виконували подумки.
Приклад\(\PageIndex{11}\)
Помножити:
\((x−4)^{2}\).
Рішення:
Ось\(a=x\) і\(b=4\). Застосовують відповідну формулу наступним чином:
\(\begin{aligned} \color{Cerulean}{(a-b)^{2}} &\color{Cerulean}{ =\:\: a^{2}\:\:\:\:-2\:\:\:\:a\:\:\:b\:\:+\:b^{2}} \\ &\color{Cerulean}{\quad\:\:\: \downarrow\qquad\quad\:\:\:\: \downarrow\:\:\: \downarrow\quad\:\:\:\downarrow} \\ (x-4)^{2}&=(x)^{2}-2\cdot(x)(4)+(4)^{2} \\ &=x^{2}-8x+16\end{aligned}\)
Відповідь:
\(x^{2}-8x+16\)
Наш третій спеціальний продукт:
\(\begin{aligned}(a+b)(a-b)&=a^{2}-ab+ba-b^{2} \\ &=a^{2}\color{red}{-ab+ab}\color{black}{-b^{2}}\\&=a^{2}-b^{2} \end{aligned}\)
Цей твір називається різницею квадратів:
\[(a+b)(a-b)=a^{2}-b^{2}\]
Біноміали\((a+b)\) і\((a−b)\) називаються сполученими біномами. Тому при множенні сполучених бічленів середній термін усуває, а твір сам по собі є біноміальним.
Приклад\(\PageIndex{12}\)
Помножити:
\((7x+4)(7x−4)\).
Рішення:
Відповідь:
\(49x^{2}-16\)
Вправа\(\PageIndex{4}\)
Помножити:
\((−5x+2)^{2}\).
- Відповідь
-
\(25x^{2}−20x+4\)
Множення многочленних функцій
Ми використовуємо позначення функцій для позначення множення наступним чином:
| Множення функцій: | \((f\cdot g)(x)=f(x)\cdot g(x)\) |
|---|
Приклад\(\PageIndex{13}\)
Обчисліть:
\((f⋅g)(x)\), з огляду на\(f(x)=5x^{2}\) і\(g(x)=−x^{2}+2x−3\).
Рішення:
Помножте всі члени триноміала на мономіальну функцію\(f(x)\).
\(\begin{aligned} (f\cdot g)(x)&=f(x)\cdot g(x) \\ &=5x^{2}\cdot (-x^{2}+2x-3) \\ &=-5x^{4}+10x^{3}-15x^{2} \end{aligned}\)
Відповідь:
\((f\cdot g)(x)=-5x^{4}+10x^{3}-15x^{2}\)
Приклад\(\PageIndex{14}\)
Обчисліть:
\((f⋅g)(−1)\), з огляду на\(f(x)=−x+3\) і\(g(x)=4x^{2}−3x+6\).
Рішення:
Для початку визначитеся\((f⋅g)(x)\).
\(\begin{aligned} (f\cdot g)(x) &=f(x)\cdot g(x) \\ &=(-x+3)(4x^{2}-3x+6) \\ &=-4x^{3}+3x^{2}-6x+12x^{2}-9x+18 \\ &=-4x^{3}+15x^{2}-15x+18 \end{aligned}\)
У нас є
\ (f\ точка г) (х) = -4x^ {3} +15х^ {2} -15х+18
Далі\(−1\) підставляємо змінну\(x\).
\(\begin{aligned} (f\cdot g)(\color{OliveGreen}{-1}\color{black}{)}&=-4(\color{OliveGreen}{-1}\color{black}{)^{3}+15(}\color{OliveGreen}{-1}\color{black}{)^{2}-15(}\color{OliveGreen}{-1}\color{black}{)+18} \\ &=-4\cdot (-1)+15\cdot 1+15+18 \\ &=4+15+15+18 \\ &=52 \end{aligned}\)
Відповідь:
\((f\cdot g)(-1)=52\)
\((f⋅g)(−1)=f(−1)⋅g(−1)\)Тому що ми могли б альтернативно обчислити\(f(−1)\) і\(g(−1)\) окремо, а потім помножити результати (спробуйте це як вправу). Однак, якби нас попросили оцінити кілька значень для функції\((f⋅g)(x)\), найкраще спочатку визначити загальну форму, як ми маємо в попередньому прикладі.
Ключові винос
- Щоб помножити многочлен на мономіал, застосуйте розподільну властивість, а потім спростіть кожен з отриманих членів.
- Щоб помножити многочлени, помножте кожен член у першому многочлені з кожним членом у другому многочлені. Потім комбінуйте подібні терміни.
- Добуток\(n\) -членного многочлена і\(m\) -членного полінома призводить до того, що\(m × n\) термін поліном перед об'єднанням подібних термінів.
- Перевірте результати, оцінюючи значення у вихідному виразі та у вашій відповіді, щоб переконатися, що результати однакові.
- Використовуйте формули для спеціальних продуктів, щоб швидко розмножити біноміали, які часто зустрічаються в алгебрі.
Вправа\(\PageIndex{5}\) Product of a Monomial and a Polynomial
Помножити.
- \(5x(−3x^{2}y)\)
- \((−2x^{3}y^{2})(−3xy^{4})\)
- \(\frac{1}{2}(4x−3)\)
- \(−\frac{3}{4}(\frac{2}{3}x−6)\)
- \(3x(5x−2)\)
- \(−4x(2x−1)\)
- \(x^{2}(3x+2)\)
- \(−6x^{2}(5x+3)\)
- \(2ab(4a−2b)\)
- \(5a^{2}b(a^{2}−b^{2})\)
- \(6x^{2}y^{3}(−3x^{3}y+xy^{2})\)
- \(3ab^{3}(−5ab^{3}+6a^{2}b)\)
- \(−\frac{1}{2}x^{2}y(4xy−10)\)
- \(−3x^{4}y^{2}(3x^{8}y^{3})\)
- \(2x^{2}(−5x^{3})(3x^{4})\)
- \(4ab(a^{2}b^{3}c)(a^{4}b^{2}c^{4})\)
- \(−2(5x^{2}−3x+4)\)
- \(\frac{4}{5}(25x^{2}−50xy+5y^{2})\)
- \(3x(5x^{2}−2x+3)\)
- \(−x(x^{2}+x−1)\)
- \(x^{2}(3x^{2}−5x−7)\)
- \(x^{3}(−4x^{2}−7x+9)\)
- \(\frac{1}{4}x^{4}(8x^{3}−2x^{2}+\frac{1}{2}x−5)\)
- \(−\frac{1}{3}x^{3}(\frac{3}{2}x^{5}−\frac{2}{3}x^{3}+\frac{9}{2}x−1)\)
- \(a^{2}b(a^{2}−3ab+b^{2})\)
- \(6a^{2}bc^{3}(2a−3b+c^{2})\)
- \(\frac{2}{3}xy^{2}(9x^{3}y−27xy+3xy^{3})\)
- \(−3x^{2}y^{2}(12x^{2}−10xy−6y^{2})\)
- Знайдіть продукт\(3x\) і\(2x^{2}−3x+5\).
- Знайдіть продукт\(−8y\) і\(y^{2}−2y+12\).
- Знайдіть продукт\(−4x\) і\(x^{4}−3x^{3}+2x^{2}−7x+8\).
- Знайдіть продукт\(3xy^{2}\) і\(−2x^{2}y+4xy−xy^{2}\).
- Відповідь
-
1. \(−15x^{3}y\)
3. \(2x−\frac{3}{2}\)
5. \(15x^{2}−6x\)
7. \(3x^{3}+2x^{2}\)
9. \(8a^{2}b−4ab^{2}\)
11. \(−18x^{5}y^{4}+6x^{3}y^{5}\)
13. \(−2x^{3}y^{2}+5x^{2}y\)
15. \(−30x^{9}\)
17. \(−10x^{2}+6x−8\)
19. \(15x^{3}−6x^{2}+9x\)
21. \(3x^{4}−5x^{3}−7x^{2}\)
23. \(2x^{7}−\frac{1}{2}x^{6}+\frac{1}{8}x^{5}−\frac{5}{4}x^{4}\)
25. \(a^{4}b−3a^{3}b^{2}+a^{2}b^{3}\)
27. \(6x^{4}y^{3}−18x^{2}y^{3}+2x^{2}y^{5}\)
29. \(6x^{3}−9x^{2}+15x\)
31. \(−4x^{5}+12x^{4}−8x^{3}+28x^{2}−32x\)
Вправа\(\PageIndex{6}\) Product of a Binomial and a Polynomial
Помножити.
- \((3x−2)(x+4) \)
- \((x+2)(x−3) \)
- \((x−1)(x+1) \)
- \((3x−1)(3x+1) \)
- \((2x−5)(x+3) \)
- \((5x−2)(3x+4) \)
- \((−3x+1)(x−1) \)
- \((x+5)(−x+1) \)
- \((y−\frac{2}{3})(y+\frac{2}{3})\)
- \((\frac{1}{2}x+\frac{1}{3})(\frac{3}{2}x−\frac{2}{3})\)
- \((\frac{3}{4}x+\frac{1}{5})(\frac{1}{4}x+\frac{2}{5})\)
- \((\frac{1}{5}x+\frac{3}{10})(\frac{3}{5}x−\frac{5}{2})\)
- \((y^{2}−2)(y+2)\)
- \((y^{3}−1)(y^{2}+2)\)
- \((a^{2}−b^{2})(a^{2}+b^{2})\)
- \((a^{2}−3b)^{2}\)
- \((x−5)(2x^{2}+3x+4) \)
- \((3x−1)(x^{2}−4x+7) \)
- \((2x−3)(4x^{2}+6x+9) \)
- \((5x+1)(25x^{2}−5x+1) \)
- \((x−\frac{1}{2})(3x^{2}+4x−1) \)
- \((\frac{1}{3}x−\frac{1}{4})(3x^{2}+9x−3) \)
- \((x+3)^{3}\)
- \((x−2)^{3}\)
- \((3x−1)^{3}\)
- \((2x+y)^{3}\)
- \((5x−2)(2x^{3}−4x^{2}+3x−2)\)
- \((x^{2}−2)(x^{3}−2x^{2}+x+1)\)
- Відповідь
-
1. \(3x^{2}+10x−8 \)
3. \(x^{2}−1 \)
5. \(2x^{2}+x−15 \)
7. \(−3x^{2}+4x−1 \)
9. \(y^{2}−\frac{4}{9}\)
11. \(\frac{3}{16}x^{2}+\frac{7}{20}x+\frac{2}{25}\)
13. \(y^{3}+2y^{2}−2y−4\)
15. \(a^{4}−b^{4}\)
17. \(2x^{3}−7x^{2}−11x−20 \)
19. \(8x^{3}−27 \)
21. \(3x^{3}+\frac{5}{2}x^{2}−3x+12\)
23. \(x^{3}+9x^{2}+27x+27\)
25. \(27x^{3}−27x^{2}+9x−1 \)
27. \(10x^{4}−24x^{3}+23x^{2}−16x+4\)
Вправа\(\PageIndex{7}\) Product of Polynomials
Помножити.
- \((x^{2}−x+1)(x^{2}+2x+1)\)
- \((3x^{2}−2x−1)(2x^{2}+3x−4)\)
- \((2x^{2}−3x+5)(x^{2}+5x−1)\)
- \((a+b+c)(a−b−c)\)
- \((a+2b−c)^{2}\)
- \((x+y+z)^{2}\)
- \((x−3)^{4}\)
- \((x+y)^{4}\)
- Знайдіть об'єм прямокутного твердого тіла зі сторонами вимірювання\(x, x+2\) та\(x+4\) одиницями.
- Знайдіть об'єм куба, де кожна сторона вимірює\(x−5\) одиниці виміру.
- Відповідь
-
1. \(x^{4}+x^{3}+x+1\)
3. \(2x^{4}+7x^{3}−12x^{2}+28x−5\)
5. \(a^{2}+4ab−2ac+4b^{2}−4bc+c^{2}\)
7. \(x^{4}−12x^{3}+54x^{2}−108x+81\)
9. \(x^{3}+6x^{2}+8x\)
Вправа\(\PageIndex{8}\) Special Products
Помножити.
- \((x+2)^{2}\)
- \((x−3)^{2}\)
- \((2x+5)^{2}\)
- \((3x−7)^{2}\)
- \((−x+2)^{2}\)
- \((−9x+1)^{2}\)
- \((a+6)^{2}\)
- \((2a−3b)^{2}\)
- \((\frac{2}{3}x+\frac{3}{4})^{2}\)
- \((\frac{1}{2}x−\frac{3}{5})^{2}\)
- \((x^{2}+2)^{2}\)
- \((x^{2}+y^{2})^{2}\)
- \((x+4)(x−4)\)
- \((2x+1)(2x−1)\)
- \((5x+3)(5x−3)\)
- \((\frac{1}{5}x−\frac{1}{3})(\frac{1}{5}x+\frac{1}{3})\)
- \((\frac{3}{2}x+\frac{2}{5})(\frac{3}{2}x−\frac{2}{5})\)
- \((2x−3y)(2x+3y)\)
- \((4x−y)(4x+y)\)
- \((a^{3}−b^{3})(a^{3}+b^{3})\)
- Виготовляється коробочка, вирізаючи кути і склавши вгору краю квадратного шматка картону. Надано шаблон для картонної коробки висотою в\(2\) дюйми. Знайдіть формулу для обсягу, якщо початковий шматок картону являє собою квадрат зі сторонами, що вимірюють\(x\) дюйми.
.png)
Малюнок\(\PageIndex{5}\) - Надано шаблон для картонної коробки висотою в\(x\) дюйми. Знайдіть формулу для обсягу, якщо початковий шматок картону являє собою квадрат зі сторонами, що вимірюють\(12\) дюйми.
.png)
Малюнок\(\PageIndex{6}\)
- Відповідь
-
1. \(x^{2}+4x+4 \)
3. \(4x^{2}+20x+25 \)
5. \(x^{2}−4x+4 \)
7. \(a^{2}+12a+36 \)
9. \(\frac{4}{9}x^{2}+x+\frac{9}{16}\)
11. \(x^{4}+4x^{2}+4\)
13. \(x^{2}−16 \)
15. \(25x^{2}−9 \)
17. \(\frac{9}{4}x^{2}−\frac{4}{25}\)
19. \(16x^{2}−y^{2}\)
21. \(V=2x^{2}−16x+32\)кубічних дюймів
Вправа\(\PageIndex{9}\) Multiplying Polynomial Functions
Для кожної задачі обчислити\((f⋅g)(x)\), враховуючи функції.
- \(f(x)=8x\)і\(g(x)=3x−5\)
- \(f(x)=x^{2}\)і\(g(x)=−5x+1\)
- \(f(x)=x−7\)і\(g(x)=6x−1\)
- \(f(x)=5x+3\)і\(g(x)=x^{2}+2x−3\)
- \(f(x)=x^{2}+6x−3\)і\(g(x)=2x^{2}−3x+5\)
- \(f(x)=3x^{2}−x+1\)і\(g(x)=−x^{2}+2x−1\)
- Відповідь
-
1. \((f⋅g)(x)=24x^{2}−40x\)
3. \((f⋅g)(x)=6x^{2}−43x+7\)
5. \((f⋅g)(x)=2x^{4}+9x^{3}−19x^{2}+39x−15\)
Вправа\(\PageIndex{10}\) Multiplying Polynomial Functions
Дано\(f(x)=2x−3\) і\(g(x)=3x−1\), знайдіть наступне
- \((f⋅g)(x)\)
- \((g⋅f)(x)\)
- \((f⋅g)(0)\)
- \((f⋅g)(−1)\)
- \((f⋅g)(1)\)
- \((f⋅g)(\frac{1}{2})\)
- Відповідь
-
1. \((f⋅g)(x)=6x^{2}−11x+3\)
3. \((f⋅g)(0)=3\)
5. \((f⋅g)(1)=−2\)
Вправа\(\PageIndex{11}\) Multiplying Polynomial Functions
Дано\(f(x)=5x−1\) і\(g(x)=2x^{2}−4x+5\), знайдіть наступне.
- \((f⋅g)(x) \)
- \((g⋅f)(x) \)
- \((f⋅g)(0) \)
- \((f⋅g)(−1) \)
- \((f⋅g)(1) \)
- \((f⋅g)(\frac{1}{2})\)
- \((f⋅f)(x) \)
- \((g⋅g)(x)\)
- Відповідь
-
1. \((f⋅g)(x)=10x^{3}−22x^{2}+29x−5\)
3. \((f⋅g)(0)=−5\)
5. \((f⋅g)(1)=12\)
7. \((f⋅f)(x)=25x^{2}−10x+1\)
Вправа\(\PageIndex{12}\) Discussion Board Topics
- Поясніть чому\((x+y)^{2}\neq x^{2}+y{2}\).
- Поясніть, як швидко помножити біном з його сполученим. Наведемо приклад.
- Які переваги і недоліки використання мнемонічного приладу ФОЛЬГА?
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
