5.6: Негативні показники

Last updated
Save as PDF

Page ID: 58021

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Спростіть вирази з від'ємними цілими показниками.
Робота з науковими позначеннями.

Негативні показники

У цьому розділі ми визначаємо, що означає мати від'ємні цілі показники. Почнемо з наступних еквівалентних дробів:

$\frac{1}{8}=\frac{4}{32}$

Зверніть увагу$4, 8$, що, і$32$ всі повноваження$2$. Отже, ми можемо писати$4=2^{2}, 8=2^{3}, and 32=2^{5}$.

$\frac{1}{2^{3}}=\frac{1}{8}=\frac{4}{32}=\frac{2^{2}}{2^{5}}$

Якщо показник терміна в знаменнику більше показника терміна в чисельнику, то застосування правила частки для показників призводить до негативного показника. В даному випадку ми маємо наступне:

$\color{Cerulean}{\frac{1}{2^{3}}}\color{black}{=\frac{1}{8}=\frac{4}{32}=\frac{2^{2}}{2^{5}}=2^{2-5}=}\color{Cerulean}{2^{-3}}$

Ми робимо висновок, що$2^{−3}=\frac{1}{2}^{3}$. Це вірно в цілому і призводить до визначення негативних показників. Задано будь-яке ціле число$n$ і$x≠0$, потім

\[x^{-n}=\frac{1}{x^{n}}\]

Тут$x≠0$ тому, що\ frac {1} {0}\) не визначено. Для наочності в цьому розділі припустимо, що всі змінні ненульові.

Спрощення виразів з негативними показниками вимагає, щоб ми переписали вираз з позитивними показниками.

Приклад$\PageIndex{1}$

Спростити:

$10^{-2}$.

Рішення:

$\begin{aligned} 10^{-2}&=\frac{1}{10^{2}} \\ &=\frac{1}{100} \end{aligned}$

Відповідь:

$\frac{1}{100}$

Приклад$\PageIndex{2}$

Спростити:

$(-3)^{-1}$.

Рішення:

$\begin{aligned} (-3)^{-1}&=\frac{1}{(-3)^{1}} \\ &=-\frac{1}{3} \end{aligned}$

Відповідь:

$-\frac{1}{3}$

Приклад$\PageIndex{3}$

Спростити:

$\frac{1}{y^{-3}}$.

Рішення:

$\begin{aligned} \frac{1}{y^{-3}} &=\frac{1}{\frac{1}{y^{3}}} \\ &=1\cdot \frac{y^{3}}{1} \\ &=y^{3} \end{aligned}$

Відповідь:

$y^{3}$

На цьому етапі ми виділяємо два дуже важливі приклади,

Знімок екрана (387) .png — Малюнок$\PageIndex{1}$

Якщо згрупована величина піднімається до від'ємного показника, то застосуєте визначення і записуєте всю згруповану величину в знаменник. Якщо групування немає, то застосовуйте визначення тільки до бази, що передує показнику.

Приклад$\PageIndex{4}$

Спростити:

$(2ab)^{-3}$.

Рішення:

Спочатку застосуйте визначення −3 як експоненти, а потім застосуйте силу правила добутку.

$\begin{aligned} (2ab)^{-3} &=\frac{1}{(2ab)^{3}} \qquad\color{Cerulean}{Apply\:the\:negative\:exponent.} \\ &=\frac{1}{2^{3}a^{3}b^{3}} \qquad\color{Cerulean}{Apply\:the\:power\:rule\:for\:a\:product.} \\ &=\frac{1}{8a^{3}b^{3}} \end{aligned}$

Відповідь:

$\frac{1}{8a^{3}b^{3}}$

Приклад$\PageIndex{5}$

Спростити:

$(-3xy^{3})^{-2}$.

Рішення:

$\begin{aligned} (-3xy^{3})^{-2}&=\frac{1}{(-3xy^{3})^{2}} \\&=\frac{1}{(-3)^{2}x^{2}(y^{3})^{2}} \\ &=\frac{1}{9x^{2}y^{6}} \end{aligned}$

Відповідь:

$\frac{1}{9x^{2}y^{6}}$

Приклад$\PageIndex{6}$

Спростити:

$\frac{x^{-3}}{y^{-4}}$.

Рішення:

$\frac{x^{-3}}{y^{-4}}=\frac{\frac{1}{x^{3}}}{\frac{1}{y^{4}}}=\frac{1}{x^{3}}\cdot\frac{y^{4}}{1}=\frac{y^{4}}{x^{3}}$

Відповідь:

$\frac{y^{4}}{x^{3}}$

Попередній приклад пропонує властивість коефіцієнтів з негативними показниками. Якщо задано будь-які цілі числа$m$ і$n$, де$x≠0$ і$y≠0$, то

\[\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}\]

Іншими словами, негативні показники в чисельнику можуть бути записані як позитивні показники в знаменнику, а негативні показники в знаменнику можуть бути записані як позитивні показники в чисельнику.

Приклад$\PageIndex{7}$

Спростити:

$\frac{-2x^{-5}y^{3}}{z^{-2}}$.

Рішення:

Подбайте про коефіцієнт$−2$; визнайте, що це основа і що показник насправді$+1:\: −2=(−2)^{1}$. Звідси правила негативних показників не поширюються на цей коефіцієнт; залиште його в чисельнику.

$\begin{aligned} \frac{-2x^{-5}y^{3}}{z^{-2}}&=\frac{-2\color{Cerulean}{x^{-5}}\color{black}{y^{3}}}{\color{OliveGreen}{z^{-2}}} \\ &=\frac{-2y^{3}\color{OliveGreen}{z^{2}}}{\color{Cerulean}{x^{5}}} \end{aligned}$

Відповідь:

$\frac{-2y^{3}z^{2}}{x^{5}}$

Приклад$\PageIndex{8}$

Спростити:

$\frac{(-3x^{-4})^{-3}}{y^{-2}}$.

Рішення:

$\begin{aligned} \frac{(-3x^{-4})^{-3}}{y^{-2}}&=\frac{(-3)^{-3}(x^{-4})^{-3}}{y^{-2}} &\color{Cerulean}{Apply\:the\:product\:to\:a\:power\:rule.} \\ &=\frac{(-3)^{-3}x^{12}}{y^{-2}} &\color{Cerulean}{Power\:rule} \\ &=\frac{x^{12}y^{2}}{(-3)^{3}} &\color{Cerulean}{Negative\:exponents} \\ &=\frac{x^{12}y^{2}}{-27} \\ &-\frac{x^{12}y^{2}}{27} \end{aligned}$

Відповідь:

$-\frac{x^{12}y^{2}}{27}$

Приклад$\PageIndex{9}$

Спростити:

$\frac{(3x^{2})^{-4}}{(-2y^{-1}z^{3})^{-2}}$.

Рішення:

$\begin{aligned} \frac{(3x^{2})^{-4}}{(-2y^{-1}z^{3})^{-2}}&=\frac{3^{-4}(x^{2})^{-4}}{(-2)^{-2}(y^{-1})^{-2}(z^{3})^{-2}} &\color{Cerulean}{Product\:to\:a\:power\:rule} \\ &=\frac{3^{-4}x^{-8}}{(-2)^{-2}y^{2}z^{-6}} &\color{Cerulean}{Power\:rule} \\ &=\frac{(-2)^{2}z^{6}}{3^{4}x^{8}y^{2}} &\color{Cerulean}{Negative\:exponents} \\&=\frac{4z^{6}}{81x^{8}y^{2}} \end{aligned}$

Відповідь:

$\frac{4z^{6}}{81x^{8}y^{2}}$

Приклад$\PageIndex{10}$

Спростити:

$\frac{(5x^{2}y)^{3}}{x^{-5}y^{-3}}$.

Рішення:

Спочатку застосуйте силу правила продукту, а потім правило частки.

$\frac{(5x^{2})^{3}}{x^{-5}y^{-3}} = \frac{5^{3}x^{6}y^{3}}{x^{-5}y^{-3}}=5^{3}x^{6-(-5)}y^{3-(-3)}=5^{3}x^{6+5}y^{3+3}=125x^{11}y^{6}$

Відповідь:

$125x^{11}y^{6}$

Підводячи підсумок, ми маємо такі правила для від'ємних цілих показників з ненульовими основами:

Таблиця$\PageIndex{1}$
Негативні показники:	$x^{-n}=\frac{1}{x^{n}}$
Коефіцієнти з негативними показниками:	$\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}$

Вправа$\PageIndex{1}$

Спростити:

$\frac{(-5xy^{-3})^{-2}}{5x^{4}y^{-4}}$.

Відповідь: $\frac{y^{10}}{125x^{6}}$

Наукові позначення

Дійсні числа, виражені в науковому позначенні, мають вигляд

$a\times 10^{n}$

де$n$ - ціле число і$1≤a<10$. Ця форма особливо корисна, коли цифри дуже великі або дуже малі. Наприклад,

$\begin{array}{cc}{9,460,000,000,000,000m=9.46\times 10^{15}m}&{\color{Cerulean}{One\:light\:year}}\\{0.000000000025m=2.5\times 10^{-11}m}&{\color{Cerulean}{Radius\:of\:a\:hydrogen\:atom}} \end{array}$

Громіздко записувати всі нулі в обох цих випадках. Наукові позначення є альтернативним, компактним поданням цих чисел. Коефіцієнт$10^{n}$ вказує на потужність$10$ помножити коефіцієнт на перетворення назад в десятковий вигляд:

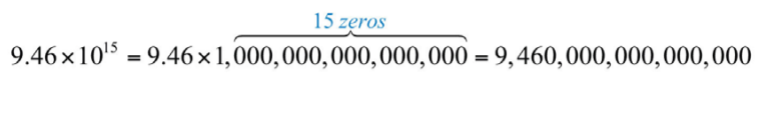Скріншот (388) .png — Малюнок$\PageIndex{2}$

Це еквівалентно переміщенню десяткового числа в коефіцієнті п'ятнадцять знаків вправо. Негативний показник вказує на те, що число дуже мало:

Знімок екрана (389) .png — Малюнок$\PageIndex{3}$

Це еквівалентно переміщенню десяткового числа в коефіцієнті одинадцять знаків вліво.

Перетворення десяткового числа в наукові позначення передбачає переміщення десяткового числа, а також. Розглянемо всі еквівалентні форми$0.00563$ з факторами$10$, які слідують:

$\begin{aligned} 0.00563&=0.0563\times 10^{-1} \\ &=0.563\times 10^{-2} \\&\color{Cerulean}{=5.63\times 10^{-3}} \\&=56.3\times 10^{-4} \\&=563\times 10^{-5} \end{aligned}$

Хоча всі вони рівні,$5.63×10^{−3}$ це єдина форма, яка вважається вираженою в науковому позначенні. Це пояснюється тим, що коефіцієнт$5.63$ знаходиться між$1$ і$10$ відповідно до вимог визначення. Зверніть увагу, що ми можемо перетворити$5.63×10^{−3}$ назад в десяткову форму, як перевірку, переміщаючи десятковий ліворуч три місця.

Приклад$\PageIndex{11}$

Пишіть,$1,075,000,000,000$ використовуючи наукові позначення.

Рішення:

Тут ми вважаємо дванадцять десяткових знаків зліва від десяткової крапки, щоб отримати число$1.075$.

$1,075,000,000,000=1.075\times 10^{12}$

Відповідь:

$1.075\times 10^{12}$

Приклад$\PageIndex{12}$

Пишіть,$0.000003045$ використовуючи наукові позначення.

Рішення:

Тут ми вважаємо шість знаків після коми праворуч для отримання$3.045$.

$0.000003045=3.045\times 10^{-6}$

Відповідь:

$3.045\times 10^{-6}$

Часто нам потрібно буде виконувати операції при використанні чисел в наукових позначеннях. Всі правила експонентів, розроблені до теперішнього часу, також стосуються чисел у наукових позначеннях.

Приклад$\PageIndex{13}$

Помножити:

$(4.36×10^{−5})(5.3×10^{12})$.

Рішення:

Використовуйте той факт, що множення є комутативним, і застосуйте правило добутку для показників.

$\begin{aligned} (4.36×10^{−5})(5.3×10^{12})&=(4.36\cdot 5.30)\times (10^{-5}\cdot 10^{12}) \\&=\color{Cerulean}{23.108}\color{black}{\times 10^{-5+12}} \\&=\color{Cerulean}{2.3108\times 10^{1}}\color{black}{\times 10^{7}} \\&=2.3108\times 10^{1+7} \\ &=2.3108\times 10^{8} \end{aligned}$

Відповідь:

$2.3108\times 10^{8}$

Приклад$\PageIndex{14}$

Розділити:

$(3.24\times 10^{8})\div (9.0\times 10^{-3})$.

Рішення:

$\begin{aligned} \frac{(3.24\times 10^{8})}{(9.0\times 10^{-3})}&= \left( \frac{3.24}{9.0} \right) \times \left( \frac{10^{8}}{10^{-3}} \right) \\ &=0.36\times 10^{8-(-3)} \\&=\color{Cerulean}{0.36}\color{black}{\times 10^{8+3}} \\&=\color{Cerulean}{3.6\times 10^{-1}}\color{black}{\times 10^{11}} \\&=3.6\times 10^{-1+11} \\ &=3.6\times 10^{10} \end{aligned}$

Відповідь:

$3.6\times 10^{10}$

Приклад$\PageIndex{15}$

Швидкість світла становить приблизно$6.7×10^{8}$ милі на годину. Висловіть цю швидкість в милі в секунду.

Рішення:

Одиничний аналіз вказує на те, що ми повинні розділити число на$3,600$.

$\begin{aligned} 6.7\times 10^{8} \:mph &=\frac{6.7\times 10^{8}miles}{1\cancel{\color{red}{hour}}}\color{black}{\cdot}\left( \frac{1\cancel{\color{red}{hour}}}{60\cancel{\color{OliveGreen}{minutes}}} \right)\cdot \left( \frac{1\cancel{\color{OliveGreen}{minutes}}}{60 seconds} \right) \\&=\frac{6.7\times 10^{8}miles}{3600 seconds} \\&=\left(\frac{6.7}{3600} \right)\times 10^{8} \\ &\approx\color{Cerulean}{0.0019}\color{black}{\times 10^{8}} \qquad\color{Cerulean}{Rounded\:to\:two\:significant\:digits} \\ &=\color{Cerulean}{1.9\times 10^{-3}}\color{black}{\times 10^{8}} \\ &=1.9\times 10^{-3+8} \\ &=1.9\times 10^{5} \end{aligned}$

Відповідь:

Швидкість світла становить приблизно$1.9×10^{5}$ милі в секунду.

Приклад$\PageIndex{16}$

За яким фактором радіус сонця більше радіуса землі?

$\begin{aligned} 6,300,000m &=6.3\times 10^{6}m\qquad\color{Cerulean}{Radius\:of\:Earth} \\ 700,000,000m &=7.0\times 10^{8}m\qquad\color{Cerulean}{Radius\:of\:the\:Sun} \end{aligned}$

Рішення:

Ми хочемо знайти число, яке при множенні на радіус землі дорівнює радіусу сонця.

$\begin{aligned}n\cdot \color{Cerulean}{radius\:of\:the\:Earth}&=\color{OliveGreen}{radius\:of\:the\:Sun} \\n&=\frac{\color{OliveGreen}{radius\:of\:the\:Sun}}{\color{Cerulean}{radius\:of\:the\:Earth}} \end{aligned}$

Тому,

$\begin{aligned} n&=\frac{7.0\times 10^{8}m}{6.3\times 10^{6}m} \\ &=\frac{7.0}{6.3}\times\frac{10^{8}}{10^{6}} \\ &\approx 1.1\times 10^{8-6} \\ &=1.1\times 10^{2} \\ &=110 \end{aligned}$

Вправа$\PageIndex{2}$

Розділити:

$(6.75\times 10^{-8})\div (9\times 10^{-17})$.

Відповідь: $7.5\times 10^{8}$

Ключові винос

Вирази з від'ємними показниками в чисельнику можна переписати як вирази з додатними показниками в знаменнику.
Вирази з від'ємними показниками в знаменнику можна переписати як вирази з додатними показниками в чисельнику.
Подбайте про те, щоб відрізнити негативні коефіцієнти від негативних показників.
Наукові позначення особливо корисні при роботі з числами, які є дуже великими або дуже маленькими.

Вправа$\PageIndex{3}$ Negative Exponents

Спростити. (Припустимо, змінні ненульові.)

$5^{−1}$
$5^{−2}$
$(−7)^{−1}$
$−7^{−1}$
$\frac{1}{2}^{−3}$
$\frac{5}{3}^{−2}$
$(\frac{3}{5})^{−2}$
$(\frac{1}{2})^{−5}$
$(−\frac{2}{3})^{−4}$
$(−\frac{1}{3})^{−3}$
$x^{−4}$
$y^{−1}$
$3x^{−5}$
$(3x)^{−5}$
$\frac{1}{y^{−3}}$
$\frac{5}{2}x^{−1}$
$\frac{x^{−1}}{y^{−2}}$
$\frac{1}{(x−y)^{−4}}$
$\frac{x^{2}y^{−3}}{z^{−5}}$
$\frac{x}{y^{−3}}$
$(ab)^{−1}$
$\frac{1}{(ab)^{−1}}$
$−5x^{−3}y^{2}z^{−4}$
$\frac{3}{−2x^{3}y^{−5}z}$
$3x^{-4}y^{2}\cdot 2x^{-1}y^{3}$
$−10a^{2}b^{3}⋅2a^{−8}b^{−10}$
$(2a^{−3})^{−2}$
$(−3x^{2})^{−1}$
$(5a^{2}b^{−3}c)^{−2}$
$(7r^{3}s^{−5}t)^{−3}$
$(−2r^{2}s^{0}t^{−3})^{−1}$
$(2xy^{−3}z^{2})^{−3}$
$(−5a^{2}b^{−3}c^{0})^{4}$
$(−x^{−2}y^{3}z^{−4})^{−7}$
$(\frac{1}{2}x^{−3})^{−5}$
$(2xy^{2})^{−2}$
$(x^{2}y^{−1})^{−4}$
$(−3a^{2}bc^{5})^{−5}$
$(\frac{20x^{−3}y^{2}}{5yz^{−1}})^{−1}$
$(\frac{4r^{5}s^{−3}t^{4}}{2r^{3}st^{0}})^{−3}$
$(\frac{2xy^{3}z^{−1}}{y^{2}z^{3}})^{−3}$
$(−\frac{3a^{2}bc}{ab^{0}c^{4}})^{2}$
$(\frac{−xyz}{x^{4}y^{−2}z^{3}})^{−4}$
$(−\frac{125x^{−3}y^{4}z^{−5}}{5x^{2}y^{4}(x+y)^{3}})^{0}$
$(x^{n})^{−2}$
$(x^{n}y^{n})^{−2}$

Відповідь

1. $\frac{1}{5}$

3. $−\frac{1}{7}$

5. $8$

7. $\frac{25}{9}$

9. $\frac{81}{16}$

11. $\frac{1}{x^{4}}$

13. $3x^{5}$

15. $y^{3}$

17. $\frac{y^{2}}{x}$

19. $\frac{x^{2}z^{5}}{y^{3}}$

21. $\frac{1}{ab}$

23. $\frac{−5y^{2}}{x^{3}z^{4}}$

25. $\frac{6y^{5}}{x^{5}}$

27. $\frac{a^{6}}{4}$

29. $\frac{b^{6}}{25a^{4}c^{2}}$

31. $−\frac{t^{3}}{2r^{2}}$

33. $\frac{625a^{8}}{b^{12}}$

35. $32x^{15}$

37. $\frac{y^{4}}{x^{8}}$

39. $\frac{x^{3}}{4yz}$

41. $\frac{z^{12}}{8x^{3}y^{3}}$

43. $\frac{x^{12}z^{8}}{y^{12}}$

45. $\frac{1}{x^{2n}}$

Вправа$\PageIndex{4}$ Negative Exponents

Значення в доларах нового MP3-плеєра можна оцінити, скориставшись формулою$V=100(t+1)^{−1}$, де$t$ вказана кількість років після покупки.

Скільки коштував MP3-плеєр нового?
Скільки буде коштувати MP3-плеєр в$1$ рік?
Скільки буде коштувати MP3-плеєр в$4$ роки?
Скільки буде коштувати MP3-плеєр в$9$ роки?
Скільки буде коштувати MP3-плеєр в$99$ роки?
Згідно з формулою, чи буде MP3 коли-небудь марним? Поясніть.

Відповідь

1. $$100$

3. $$20$

5. $$1$

Вправа$\PageIndex{5}$ Scientific Notation

Перетворити на десяткове число.

$9.3×10^{9}$
$1.004×10^{4}$
$6.08×10^{10}$
$3.042×10^{7}$
$4.01×10^{−7}$
$1.0×10^{−10}$
$9.9×10^{−3}$
$7.0011×10^{−5}$

Відповідь

1. $9,300,000,000$

3. $60,800,000,000$

5. $0.000000401$

7. $0.0099$

Вправа$\PageIndex{6}$ Scientific Notation

Перепишіть, використовуючи наукові позначення.

$500,000,000$
$407,300,000,000,000$
$9,740,000$
$100,230$
$0.0000123$
$0.000012$
$0.000000010034$
$0.99071$

Відповідь

1. $5×10^{8}$

3. $9.74×10^{6}$

5. $1.23×10^{−5}$

7. $1.0034×10^{−8}$

Вправа$\PageIndex{7}$ Scientific Notation

Виконайте зазначені операції.

$(3×10^{5})(9×10^{4})$
$(8×10^{−22})(2×10^{−12})$
$(2.1×10^{−19})(3.0×10^{8})$
$(4.32×10^{7})(1.50×10^{−18})$
$9.12×10^{−9}3.2×10^{10}$
$1.15×10^{9}2.3×10^{−11}$
$1.004×10^{−8}2.008×10^{−14}$
$3.276×10^{25}5.2×10^{15}$
$59,000,000,000,000 × 0.000032$
$0.0000000000432 × 0.0000000000673$
$1,030,000,000,000,000,000 ÷ 2,000,000$
$6,045,000,000,000,000 ÷ 0.00000005$
Щільність населення землі відноситься до кількості людей на квадратну милю площі суші. Якщо загальна площа суші на землі становить$5.751×10^{7}$ квадратні милі, а населення в 2007 році оцінювалося як$6.67×10^{9}$ люди, то обчисліть щільність населення землі в той час.
У 2008 році населення Нью-Йорка оцінювалося в$8.364$ мільйон чоловік. Загальна площа земельної ділянки становить$305$ квадратні милі. Розрахуйте щільність населення Нью Йорка.
Маса землі -$5.97×10^{24}$ кілограми, а маса Місяця -$7.35×10^{22}$ кілограми. За яким фактором маса землі більша за масу Місяця?
Маса сонця -$1.99×10^{30}$ кілограми, а маса землі -$5.97×10^{24}$ кілограми. За яким фактором маса Сонця більша за масу землі? Висловіть свою відповідь в наукових позначеннях.
Радіус сонця -$4.322×10^{5}$ милі, а середня відстань від землі до Місяця -$2.392×10^{5}$ милі. За яким фактором радіус сонця більше середньої відстані від землі до Місяця?
Один світловий рік,$9.461×10^{15}$ метри, - це відстань, яку світло проходить у вакуумі за один рік. Якщо відстань до найближчої зірки до нашого сонця, Проксими Центавра, оцінюється як$3.991×10^{16}$ метри, то обчисліть кількість років, яке знадобиться світло, щоб пройти цю відстань.
Підраховано, що на планеті налічується близько$1$ мільйона мурах на людину. Якщо населення світу оцінювалося в$6.67$ мільярд людей у 2007 році, то оцініть світову популяцію мурашок на той час.
Сонце рухається навколо центру галактики по майже круговій орбіті. Відстань від центру нашої галактики до сонця становить приблизно$26,000$ світлові роки. Яка окружність орбіти Сонця навколо галактики в метрах?
Вода важить приблизно$18$ грам на моль. Якщо одна моль йде про$6×10^{23}$ молекули, то приблизний вага кожної молекули води.
$1×10^{9}$Гігабайт - це байти, а$1×10^{6}$ мегабайт - байти. Якщо середня пісня в форматі MP3 споживає близько$4.5$ мегабайт пам'яті, то скільки пісень поміститься на$4$ -гігабайтної карті пам'яті?

Відповідь

1. $2.7×10^{10}$

3. $6.3×10^{−11}$

5. $2.85×10^{−19}$

7. $5×10^{5}$

9. $1.888×10^{9}$

11. $5.15×10^{11}$

13. Про$116$ людей на квадратну милю

15. $81.2$

17. $1.807$

19. $6.67×10^{15}$мурахи

21. $3×10^{−23}$грам

Негативні показники:	\(x^{-n}=\frac{1}{x^{n}}\)
Коефіцієнти з негативними показниками:	\(\frac{x^{-n}}{y^{-m}}=\frac{y^{m}}{x^{n}}\)