2.6: Співвідношення та пропорції додатків

Last updated
Save as PDF

Page ID: 58204

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Зрозумійте різницю між співвідношенням і пропорцією.
Вирішіть пропорції, використовуючи перехресне множення.
Вирішуйте додатки, що включають пропорції, включаючи подібні трикутники.

Визначення

Співвідношення - це зв'язок між двома числами або величинами, які зазвичай виражаються як частка. Співвідношення, як правило, виражаються за допомогою таких позначень:

$\frac{a}{b}\qquad a\:to\:b\qquad a:b$

Все вищесказане є еквівалентними формами, що використовуються для вираження співвідношення. Однак найбільш звичний спосіб вираження співвідношення - у вигляді дробу. При написанні співвідношень важливо звертати увагу на одиниці. Якщо одиниці однакові, то співвідношення можна записати і без них.

Приклад$\PageIndex{1}$

Висловіть співвідношення$12$ стоп до$48$ стоп в зменшеному вигляді.

Рішення:

$\begin{aligned} 12\text{ feet to }48\text{ feet} &=\frac{12\text{ feet}}{48\text{ feet}} \\ &=\color{black}{\frac{12\color{Cerulean}{\div 12}}{48\color{Cerulean}{\div 12}}} &\color{Cerulean}{Reduce.} \\ &=\frac{1}{4} \end{aligned}$

Відповідь:

$1$до$4$

Якщо одиниці різні, то ми повинні обов'язково включити їх, оскільки співвідношення являє собою ставку.

Приклад$\PageIndex{2}$

Висловіть відношення$220$ миль до$4$ годин у зменшеному вигляді.

Рішення:

$\begin{aligned} 220\text{ miles to }4\text{ hours}&=\frac{220\text{ miles}}{4\text{ hours}} \\ &=\frac{55\text{miles}}{1\text{ hour}} \\ &=55\text{ miles\hour} \end{aligned}$

Відповідь:

$55$милі в$1$ години (або$55$ милі на годину)

Ставки корисні при визначенні вартості одиниці, або ціни кожної одиниці. Ми використовуємо одиничну вартість для порівняння значень, коли величини не однакові. Щоб визначити собівартість одиниці, розділіть вартість на кількість одиниць.

Приклад$\PageIndex{3}$

Місцевий супермаркет пропонує пачку$12$ газованих напоїв за $$3.48$ на продаж, а місцевий склад знижок пропонує соду в футлярі$36$ -can за $$11.52$. Що є кращою цінністю?

Рішення:

Розділіть вартість на кількість банок, щоб отримати ціну за одиницю.

Таблиця$\PageIndex{1}$
Супермаркет	Дисконтний склад
$$3.4812$ банки$=$ $$0.29$ /банка	$$11.5236$ банки$=$ $$0.32$ /банка

Відповідь:

Ціна продажу супермаркету $$3.48$ за$12$ упаковку - це краща вартість в $$0.29$ за банку.

Пропорція - це твердження рівності двох співвідношень.

\[\frac{a}{b}=\frac{c}{d}\]

Ця пропорція часто$a$ читається «$c$є$b$ як є»$d$. Ось приклад простої пропорції,

$\frac{1}{2}=\frac{2}{4}$

Якщо очистити дроби, множивши обидві сторони пропорції на добуток знаменників$8$, то отримаємо наступне істинне твердження:

$\begin{aligned}\color{Cerulean}{8\cdot}\color{black}{\frac{1}{2}}&=\color{Cerulean}{8\cdot}\color{black}{\frac{2}{4}} \\ 4\cdot 1&=2\cdot 2\\ 4&=4 \end{aligned}$

Задані будь-які ненульові дійсні числа$a, b, c,$ і$d$ які задовольняють пропорції, помножте обидві сторони на добуток знаменників, щоб отримати наступне:

$\begin{aligned} \frac{a}{b}&=\frac{c}{d} \\ \color{Cerulean}{bd}\color{black}{\cdot \frac{a}{b}}&=\color{Cerulean}{bd}\color{black}{\cdot \frac{c}{d}} \\ ad&=bc \end{aligned}$

Це показує, що перехресні продукти рівні, і їх прийнято називати перехресним множенням.

\[\text{If }\frac{a}{b}=\frac{c}{d}\text{ then }ad=bc\]

Розв'язування пропорцій

Перехресне множення, щоб вирішити пропорції, де терміни невідомі.

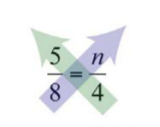
Приклад$\PageIndex{4}$

Вирішити:

$\frac{5}{8}=\frac{n}{4}$.

Рішення:

Перехресне множення, а потім вирішуйте для$n$.

$Знімок екрана (765) .png$

Малюнок$\PageIndex{1}$

$\begin{aligned} 5\cdot 4&=8\cdot n &\color{Cerulean}{Cross\:multiply.} \\ 20&=8n \\ \frac{20}{\color{Cerulean}{8}} &=\frac{8n}{\color{Cerulean}{8}} &\color{Cerulean}{Divide\:by\:8.} \\ \color{black}{\frac{20\color{Cerulean}{\div 4}}{8\color{Cerulean}{\div 4}}} &=n &\color{Cerulean}{Reduce.} \\ \frac{5}{2}&=n \end{aligned}$

Відповідь:

$n=\frac{5}{2}$

Приклад$\PageIndex{5}$

Вирішити:

$\frac{15}{x}=\frac{5}{6}$.

Рішення:

Перехресне множення потім вирішити для$x$.

$\begin{aligned} \frac{15}{x}&=\frac{5}{6} \\ 15\cdot 6&=x\cdot 5 \\ 15\cdot 6&=5x \\ \frac{15\cdot 6}{\color{Cerulean}{5}}&=\frac{5x}{\color{Cerulean}{5}} \\ 3\cdot 6&=1x \\ 18&=x \end{aligned}$

Відповідь:

$x=18$

Приклад$\PageIndex{6}$

Вирішити:

$\frac{n+3}{5}=\frac{7}{2}$.

Рішення:

При перехресному множенні обов'язково групуйте$n+3$. Застосуйте розподільну властивість на наступному кроці.

$\begin{aligned} \frac{n+3}{5}&=\frac{7}{2} &\color{Cerulean}{Cross\:multiply.} \\ (n+3)\cdot 2&=5\cdot 7 &\color{Cerulean}{Distribute.} \\ 2n+6&=35 &\color{Cerulean}{Solve.} \\ 2n+6\color{Cerulean}{-6}&=35\color{Cerulean}{-6} \\ 2n&=29 \\ \frac{2n}{\color{Cerulean}{2}}&=\frac{29}{\color{Cerulean}{2}} \\ n&=\frac{29}{2} \end{aligned}$

Відповідь:

$n=\frac{29}{2}$

Вправа$\PageIndex{1}$

Вирішити:

$\frac{5}{3}=\frac{3n−1}{2}$.

Відповідь: $n=\frac{13}{9}$

Додатки

При налаштуванні пропорцій вирішальне значення має узгодженість з одиницями кожного співвідношення. Одиниці для чисельників повинні бути однаковими, а одиниці для знаменників теж повинні бути однаковими.

Приклад$\PageIndex{7}$

Стверджується, що$2$ з$3$ стоматологів віддають перевагу певній марці зубної пасти. Якщо обстежено 600 стоматологів, то скільки скажуть, що віддають перевагу цій марці?

Рішення:

Спочатку визначте невідоме і призначте йому змінну.

Дозвольте$n$ представити кількість опитаних стоматологів, які віддають перевагу фірмовій марці.

Оскільки ви шукаєте кількість стоматологів, які віддають перевагу назву бренду із загальної кількості$600$ опитаних, побудуйте співвідношення з кількістю стоматологів, які віддають перевагу бренду в чисельнику та загальною кількістю опитаних у знаменнику.

$\begin{aligned} \underline{2}=\underline{n} &\quad\color{Cerulean}{\leftarrow\:number\:of\:dentists\:who\:prefer\:the\:brand} \\ 3\:\:600&\quad\color{Cerulean}{\leftarrow\:total\:number\:of\:dentists\:surveyed} \end{aligned}$

Перехресний множиться і вирішувати для$n$,

$\begin{aligned} 2\cdot 600&=3\cdot n \\ \frac{2\cdot 600}{\color{Cerulean}{3}}&=\frac{3\cdot n}{\color{Cerulean}{3}} \\ 2\cdot 200&=1n \\ 400&=n \end{aligned}$

Відповідь:

Претензія говорить про те, що$400$ з опитаних$600$ стоматологів віддають перевагу фірмовій марці.

Приклад$\PageIndex{8}$

У окрузі Туларе з$3$ усіх$7$ виборців сказали «так» Пропозиції 40. $42,000$Якби люди проголосували, скільки сказали «ні» Пропозиції 40?

Рішення:

Проблема дає співвідношення виборців, які сказали «так», але запитує кількість, хто сказав «ні».

Давайте$n$ представляти кількість виборців, які сказали «ні».

Якщо$3$ з$7$ сказаного так, то ми можемо припустити$4$ з$7$ сказаного ні. Налаштуйте співвідношення з кількістю виборців, які сказали «ні» в чисельнику, і загальною кількістю виборців у знаменнику.

$\begin{aligned} &\underline{4}=\:\:\:\:\underline{n}&\color{Cerulean}{\leftarrow\:voters\:who\:voted\:no} \\ &7\:\:\:\:\:\:42,000&\color{Cerulean}{\leftarrow\:total\:number\:of\:voters} \end{aligned}$

Перехресне множення і вирішуйте для$n$.

$\begin{aligned} 4\cdot 42,000&=7\cdot n \\ \frac{4\cdot 42,000}{\color{Cerulean}{7}}&=\frac{7\cdot n}{\color{Cerulean}{7}} \\ 24,000&=n \end{aligned}$

Відповідь:

$24,000$виборці з$42,000$ сказали «ні».

Приклад$\PageIndex{9}$

Сума двох цілих чисел у співвідношенні$4$ до$5$ дорівнює$27$. Знайти цілі числа.

Рішення:

Сума двох цілих чисел є$27$; використовуйте це співвідношення, щоб уникнути двох змінних.

$n$Дозволяти представляти одне з цілих чисел.

$27-n$Дозволяти представляти інше ціле число.

Задано цілі числа у співвідношенні$4$ до$5$. Налаштуйте таку пропорцію:

$\begin{aligned} \frac{4}{5}&=\frac{n}{27-n} \\ 4\cdot (27-n)&=5\cdot n \\ 108-4n&=5n \\ 108-4n\color{Cerulean}{+4n} &=5n\color{Cerulean}{+4n} \\ 108&=9n \\ \frac{108}{\color{Cerulean}{9}}&=\frac{9n}{\color{Cerulean}{9}} \\ 12&=n \end{aligned}$

Використовуйте$27 − n$ для визначення іншого цілого числа.

$27-n=27-\color{OliveGreen}{12}\color{black}{=15}$

Відповідь:

Цілими числами є$12$ і$15$.

Вправа$\PageIndex{2}$

Рецепт вимагає$5$ столових ложок цукру на кожну$8$ склянку борошна. Скільки столових ложок цукру потрібно на$32$ склянки борошна?

Відповідь: $20$столові ложки цукру

Подібні трикутники

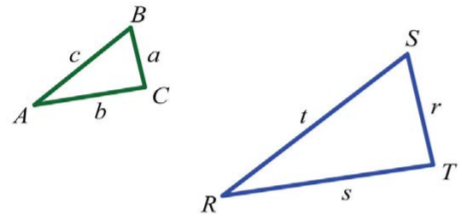
Ми часто стикаємося з проблемами пропорцій в геометрії та тригонометрії. Одна аплікація передбачає подібні трикутники, які мають однакову форму, але не обов'язково однаковий розмір. Міри відповідних кутів подібних трикутників рівні, а міри відповідних сторін пропорційні. З огляду на подібні трикутники$ABC$ і$RST$,

$Знімок екрана (766) .png$

Малюнок$\PageIndex{2}$

Ми можемо написати$ABC ~ RST$ і зробити висновок, що всі відповідні кути рівні. Позначення вказує, що кут$A$ відповідає куту$R$ і що міри цих кутів рівні:$A = R$.

$Знімок екрана (767) .png$

Малюнок$\PageIndex{3}$

Крім того, мірки інших пар відповідних кутів рівні:$B = S$ і$C = T$.

$Знімок екрана (768) .png$

Малюнок$\PageIndex{4}$

Використовуйте великі літери для кутів і малу літеру, щоб позначити сторону, протилежну заданому куту. Позначають пропорційність сторін наступним чином:

$\frac{a}{r}=\frac{b}{s}=\frac{c}{t}$

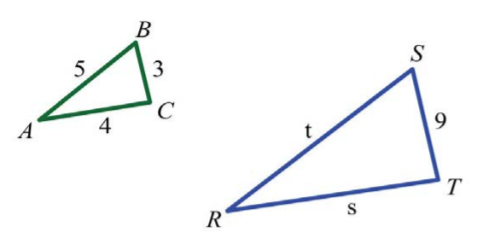
Приклад$\PageIndex{10}$

Якщо трикутник$ABC$ схожий на$RST$, де$a=3, b=4, c=5,$ і$r=9$, то знайдіть інші дві сторони.

Рішення:

Намалюйте картинку і визначте змінні наочно. Представляють залишилися невідомі сторони по$s$ і$t$. Налаштуйте пропорції і вирішуйте для відсутніх сторін.

$Знімок екрана (769) .png$

Малюнок$\PageIndex{5}$

$\begin{array}{c|c}{\underline{Find\:t}}&{\underline{Find\:s}}\\{\begin{aligned} \frac{5}{t}&=\frac{3}{9} \\ 5\cdot 9&=t\cdot 3 \\ \frac{5\cdot 9}{\color{Cerulean}{3}}&=\frac{t\cdot 3}{\color{Cerulean}{3}} \\ 5\cdot 3&=t \\ 15&=t \end{aligned}}&{\begin{aligned} \frac{4}{s}&=\frac{3}{9} \\ 4\cdot 9&=s\cdot 3 \\ \frac{4\cdot 9}{\color{Cerulean}{3}}&=\frac{s\cdot 3}{\color{Cerulean}{3}} \\ 4\cdot 3&=s \\ 12&=s \end{aligned}} \end{array}$

Відповідь:

Дві інші сторони вимірюють$12$ одиниці та$15$ одиниці виміру.

Наведене співвідношення будь-яких двох відповідних сторін подібних трикутників називається масштабним коефіцієнтом. У попередньому прикладі співвідношення двох заданих сторін$a$ і$r$ становить

$\frac{3}{9}=\frac{1}{3}$

Тому трикутник$ABC$ схожий на трикутник$RST$ з масштабним коефіцієнтом$\frac{1}{3}$. Це означає, що кожна ніжка$\frac{1}{3}$ трикутника$ABC$ має міру відповідних ніжок трикутника$RST$. Також цікавим є ще один факт, що периметри подібних трикутників знаходяться в тій же пропорції, що і їх сторони і мають один і той же масштабний коефіцієнт.

Приклад$\PageIndex{11}$

Якщо трикутник$ABC$ має периметр$12$ одиниць і схожий на$RST$ з масштабним коефіцієнтом$\frac{1}{3}$, то знайдіть периметр трикутника$RST$.

Рішення:

$x$Дозволяти представляти периметр трикутника$RST$.

Масштабний коефіцієнт$\frac{1}{3}$ має на увазі, що периметри пропорційні цьому співвідношенню. Налаштуйте пропорцію наступним чином:

$\begin{aligned} &\underline{1}=\underline{12} &\color{Cerulean}{\leftarrow\:perimeter\:of\:ABC} \\ &3\:\:\:\:\:\:x &\color{Cerulean}{\leftarrow\:perimeter\:of\:RST} \end{aligned}$

Перехресне множення і вирішуйте для$x$.

$\begin{aligned} 1\cdot x&=3\cdot 12 \\ x&=36 \end{aligned}$

Відповідь:

Периметр трикутника$RST$ -$36$ одиниці.

Ключові виноси

Розв'яжіть пропорції, множивши обидві сторони рівняння на добуток знаменників, або перехресне множення.
При налаштуванні пропорції важливо забезпечити узгоджені одиниці в чисельниках і знаменниках.
Відповідні кути подібних трикутників рівні, а відповідні їм сторони пропорційні. Співвідношення будь-яких двох відповідних сторін визначає масштабний коефіцієнт, який може бути використаний для вирішення багатьох додатків за участю подібних трикутників.

Вправа$\PageIndex{3}$ Ratios and Rates

Висловіть кожне співвідношення в зменшеному вигляді.

$100$дюйми:$250$ дюйми
$480$пікселі:$320$ пікселі
$96$стопи:$72$ стопи
$240$милі$4$ годин
$96$футів$3$ секунд
$6,000$оборотів$4$ хвилин
Середня ціна акцій Google 2008 року і прибуток на акцію становили $$465.66$ і $$14.89$ відповідно. Яким було середнє співвідношення ціни та заробітку Google у 2008 році? (Джерело: Вольфрам Альфа)
F-22 Raptor має два двигуни, кожен з яких виробляє$35,000$ фунти тяги. Якщо злітна вага цього винищувача становить$50,000$ фунти, розрахуйте співвідношення тяги до ваги літака. (Джерело: ВПС США)
Дисконтний склад пропонує коробку$55$ індивідуальних порцій вівсянки швидкого приготування за $$11.10$. Супермаркет пропонує менші коробки одного і того ж продукту, що містять$12$ окремі порції за $$3.60$. Який магазин пропонує кращу вартість?
Джо і Мері хочуть взяти подорож разом і повинні вирішити, чий автомобіль вони візьмуть. Джо підрахував, що його машина здатна проїхати$210$ милі на$12$ галоні бензину. Мері підраховує, що її машина подорожує$300$ милями на$19$ галони. Який з їхніх автомобілів отримує більше миль до галона?

Відповідь

1. $2:5$

3. $4:3$

5. $32$футів в секунду

7. $31.27$

9. Дисконтний склад

Вправа$\PageIndex{4}$ Solving Proportions

Вирішити.

$\frac{2}{3}=\frac{n}{150}$
$\frac{7}{n}=\frac{2}{15}$
$\frac{1}{3}=\frac{5}{n}$
$\frac{1}{25}=\frac{6}{n}$
$\frac{n}{8}=−\frac{3}{2}$
$\frac{n}{3}=−\frac{5}{7}$
$8=\frac{2n}{3}$
$\frac{5}{n}=−30$
$1=\frac{1}{n−1}$
$−1=−\frac{1}{n+1}$
$−\frac{40}{n}=−\frac{5}{3}$
$\frac{2n+1}{3}=−\frac{3}{5}$
$\frac{5}{3n+3}=\frac{2}{3}$
$\frac{n+1}{2n−1}=\frac{1}{3}$
$\frac{5n+7}{5}=\frac{n−1}{2}$
$−\frac{2}{n+3}=\frac{n+7}{6}$
Знайдіть два числа в співвідношенні$3$ до$5$ чиї суми$160$. (Підказка: Використовуйте$n$ і$160 − n$ для представлення двох чисел.)
Знайдіть два числа в співвідношенні$2$ до$7$ чиї суми$90$.
Знайдіть два числа в співвідношенні$−3$ до$7$ чиї суми$80$.
Знайдіть два числа в співвідношенні$−1$ до$3$ чиї суми$90$.
Більше ціле число$5$ більше, ніж менше ціле. Якщо два цілих числа мають відношення,$6$ щоб$5$ знайти цілі числа.
Більше ціле число$7$ менше, ніж в два рази менше цілого. Якщо два цілих числа мають відношення,$2$ щоб$3$ знайти цілі числа.

Відповідь

1. $n=100$

3. $n=15$

5. $n=−12$

7. $n=12$

9. $n=2$

11. $n=24$

13. $n=\frac{3}{2}$

15. $n=−\frac{19}{5}$

17. $60, 100$

19. $−60, 140$

21. $25, 30$

Вправа$\PageIndex{5}$ Solving Proportions

З огляду на наступні пропорції, визначте кожне співвідношення,$x:y$.

$\frac{x}{3}=\frac{y}{4}$
$\frac{x−2y}{3}=−\frac{3y}{5}$
$\frac{2x+4y}{2x−4y}=\frac{3}{2}$
$\frac{x+y}{x−y}=\frac{3}{5}$

Відповідь

1. $\frac{3}{4}$

3. $10$

Вправа$\PageIndex{6}$ Applications

Встановіть пропорцію, а потім вирішуйте.

Якщо з$4$ усіх$5$ виборців підтримують губернатора, то скільки з опитаних підтримують губернатора?$1,200$
Якщо кожен$1$ опитаний$3$ виборців сказав, що вони проголосували «так» на Пропозиції 23, то скільки опитаних$600$ проголосували «так»?
З опитаних$460$ студентів співвідношення підтримки проекту реконструкції студентського союзу було$3$ до$5$. Скільки студентів висловилися за перепланування?
Орієнтовні$5$ з$7$ студентів несуть заборгованість по кредитній картці. Оцініть кількість студентів, які несуть заборгованість за кредитною карткою із загальної кількості$14,000$ студентів.
Якщо співвідношення студентів жіночої та чоловічої статі в коледжі становить$6$ до$5$, то визначте кількість студентів чоловічої статі із$11,000$ загальної кількості студентів.
У 2009 році було підраховано, що в$838$ Сполучених Штатах буде смерть для кожного$100,000$ народу. Якщо загальна чисельність населення США оцінювалася як$307,212,123$ люди, то скільки смертей у Сполучених Штатах очікувалося в 2009 році? (Джерело: Світова книга фактів ЦРУ)
У 2009 році було підраховано, що в Сполучених Штатах будуть$1,382$ пологи для кожного$100,000$ народу. Якщо загальна чисельність населення США оцінювалася як$307,212,123$ люди, то скільки пологів у Сполучених Штатах очікувалося в 2009 році? (Джерело: Світова книга фактів ЦРУ)
Якщо з$2$ усіх$7$ виборців схвалюють підвищення податку з продажів, то визначте кількість виборців з$588$ опитаних, які не підтримують збільшення.
Рецепт вимагає$1$ чашки лимонного соку, щоб зробити$4$ чашки лимонаду. Скільки лимонного соку потрібно, щоб зробити$2$ галони лимонаду?
Класичний коктейль «Ширлі Темпл» вимагає$1$ частини вишневого сиропу до$4$ частин лимонно-лаймової газованої води. Скільки вишневого сиропу потрібно для змішування коктейлю, враховуючи$12$ -унцію банку лимонно-лаймової газованої води?
Принтер друкує$30$ сторінки за$1$ хвилину. Скільки часу знадобиться, щоб роздрукувати буклет$720$ -page?
Друкарка може набирати$75$ слова в хвилину. Скільки часу знадобиться, щоб друкувати$72$ сторінки, якщо на сторінці є приблизно$300$ слова?
На певній карті кожен$\frac{1}{16}$ дюйм являє собою$1$ милю. Скільки миль представляє$3\frac{1}{2}$ дюйми?
На графіку кожен$1$ сантиметр представляє$100$ фути. Який вимір на карті являє собою одну милю?
Магазин цукерок пропонує змішані цукерки$3.75$ за $ за кожен півфунта. Скільки коштуватимуть$2.6$ фунти цукерок?
Змішані горіхи коштують за ціною $$6.45$ за фунт. Скільки фунтів змішаних горіхів можна придбати за $$20.00$?
Кукурудза на фермерському ринку йде в комплекті і за ціною $$1.33$ за$6$ колосся. Скільки вух можна придбати за $$15.00$?
Якщо$4$ піци коштують $$21.00$, то скільки буде коштувати$16$ піца?
Підсолоджена каша для сніданку містить$110$ калорії в одній$\frac{3}{4}$ -чашці порції. Скільки калорій в порції$1\frac{7}{8}$ -cup?
Рис зі смаком курки містить$300$ калорії в кожній$2.5$ порції -унція. Скільки калорій в$4$ -унції совок рису зі смаком курки?
Чоловік$200$ -фунт важить близько$33.2$ фунтів на Місяці. Скільки буде важити чоловік$150$ -фунт на Місяці?
Чоловік$200$ -фунт важить близько$75.4$ фунтів на Марсі. Скільки буде важити людина$150$ -pound на Марсі?
Існує$1$ поза$6$ шансом прокатки$1$ на шестигранній матриці. Скільки разів ми можемо$1$ очікувати, що вийде в$360$ рулони штампу?
Існує$1$ поза$6$ шансом прокатки$7$ з двома шестигранними кубиками. Скільки разів ми можемо очікувати,$7$ щоб прийти в$300$ рулони?
Співвідношення арахісу до всіх горіхів в певній марці упакованих змішаних горіхів становить$3$ до$5$. Якщо в упаковці містяться$475$ горіхи, то скільки арахісу можна очікувати?
Змішаний мішок з мармуру упакований із співвідношенням$6$ помаранчевих кульок для кожного$5$ червоного мармуру. Якщо пакет містить$216$ помаранчеві кульки, то скільки червоних мармурів ми можемо очікувати?
Графічний дизайнер бажає створити захоплення екрану в$720$ масштабі пікселів. Якщо співвідношення ширини до висоти має бути$3:2$, то на скільки пікселів він повинен встановити висоту?
Якщо відеомонітор проводиться в співвідношенні ширини до висоти$16:9$ і ширини монітора$40$ дюймів, то яка висота?

Відповідь

1. $960$люди

3. $276$студенти

5. $5,000$студенти чоловічої статі

7. $4,245,672$пологів

9. $8$чашки лимонного соку

11. $24$хвилин

13. $56$миль

15. $$19.50$

17. $66$вух

19. $275$калорій

21. $24.9$фунтів

23. $60$раз

25. $285$арахіс

27. $480$пікселів

Вправа$\PageIndex{7}$ Similar Triangles

Якщо трикутник$ABC$ схожий на трикутник$RST$, знайдіть інші дві сторони з урахуванням інформації.

$a=6, b=8, c=10,$і$s=16$
$b=36, c=48, r=20,$і$t=32$
$b=2, c=4, r=6,$і$s=4$
$b=3, c=2, r=10,$і$t=12$
$a=40, c=50, s=3,$і$t=10$
$c=2, r=7, s=9,$і$t=4$
У той же час доби, дерево кидає тінь$12$ -foot, в той час як$6$ -foot людина кидає тінь$3$ -foot. Оцініть висоту дерева.
В цей же час доби батько і син, стоячи пліч-о-пліч, кидають тінь$4$ -фут і$2$ -фут відповідно. Якщо у батька високі$6$ ноги, то який зріст у нього син?
Якщо$6-8-10$$ABC$ прямокутний трикутник схожий на$RST$ з масштабним коефіцієнтом$\frac{2}{3}$, то знайдіть периметр трикутника$RST$.
Якщо$3-4-5$$ABC$ прямокутний трикутник схожий на$RST$ з масштабним коефіцієнтом$5$, то знайдіть периметр трикутника$RST$.
Рівносторонній трикутник зі сторонами вимірювальних$6$ одиниць схожий на інший з масштабним коефіцієнтом$3:1$. Знайдіть довжину кожної сторони невідомого трикутника.
Периметр рівностороннього трикутника$ABC$ вимірює$45$ одиниці виміру. Якщо трикутник$ABC ~ RST$ і$r=20$, то що таке масштабний коефіцієнт?
Периметр рівнобедреного трикутника$ABC$, де дві рівні сторони кожна вимірюють вдвічі більше основи, є$60$ одиницями. Якщо основа подібного трикутника вимірює$6$ одиниці виміру, то знайдіть його периметр.
Периметр рівнобедреного трикутника ABC вимірює$11$ одиниці та дві його рівні сторони вимірюють$4$ одиниці. Якщо трикутник$ABC$ схожий на трикутник,$RST$ а трикутник$RST$ має периметр$22$ одиниць, то знайдіть всі сторони трикутника$RST$.
$6-8-10$$ABC$Прямокутний трикутник схожий на трикутник$RST$ з$72$ одиницями периметра. Знайдіть довжину кожної ніжки трикутника$RST$.
Периметр трикутника$ABC$ - це$60$ одиниці та$b=20$ одиниці. Якщо$ABC ~ RST$ і$s=10$ одиниці, то знайдіть периметр трикутника$RST$.

Відповідь

1. $t = 20, r = 12$

3. $a = 3, t = 8$

5. $r = 8, b = 15$

7. $24$ноги

9. $36$одиниць

11. $2$одиниць

13. $30$одиниць

15. $r = 18$одиниці,$s = 24$ одиниці,$t = 30$ одиниці

Вправа$\PageIndex{8}$ Discussion Board Topics

Що таке золоте перетин і де воно з'являється?
Досліджуйте та обговоріть властивості подібних трикутників.
Обговоріть математику перспективи.
Досліджуйте та обговоріть різні пропорції, які доступні в сучасних медіа-пристроях.

Відповідь

1. Відповіді можуть відрізнятися

3. Відповіді можуть відрізнятися