2.5: Застосування лінійних рівнянь

Last updated
Save as PDF

Page ID: 58214

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте ключові слова та фрази, перекладіть речення в математичні рівняння та розробляйте стратегії вирішення проблем.
Вирішувати проблеми слів, що включають відносини між числами.
Вирішити завдання геометрії за участю периметра
Вирішити процентні та грошові проблеми, включаючи прості відсотки.
Налаштуйте та вирішуйте проблеми рівномірного руху.

Ключові слова, переклад та стратегія

Алгебра спрощує процес вирішення реальних завдань. Це робиться за допомогою букв для представлення невідомих, повторюючи задачі у вигляді рівнянь та пропонуючи систематичні методи вирішення цих рівнянь. Для вирішення завдань за допомогою алгебри спочатку перекладіть формулювання задачі в математичні твердження, які описують відносини між заданою інформацією і невідомою. Зазвичай цей переклад на математичні твердження є складним кроком у процесі. Ключ до перекладу - уважно прочитати проблему і визначити певні ключові слова і фрази.

Таблиця$\PageIndex{1}$
Ключові слова	Переклад
Сума, збільшена на, більше, ніж, плюс, додана до, загальна	$+$
Різниця, зменшена на, віднімається від, менше, мінус	$-$
Продукт, помножений на, of, раз, в два рази	$*$
Коефіцієнт, розділений на, співвідношення, на	$/$
Є, підсумок, результат	$=$

Ось кілька прикладів перекладених ключових фраз.

Таблиця$\PageIndex{2}$
Ключові фрази	Переклад
Сума числа і 7.	$x+7$
Сім більше, ніж число.	$x+7$
Різниця числа і 7.	$x-7$
Сім менше числа.
Сім віднімається з числа.
Твір 2 і число.	$2x$
Двічі число.	$2x$
Половина числа.	$\frac{1}{2}x$
Коефіцієнт числа і 7.	$\frac{x}{7}$

При перекладі пропозицій в математичні висловлювання обов'язково прочитайте пропозицію кілька разів і визначте ключові слова і словосполучення.

Приклад$\PageIndex{1}$

Перекласти:

Чотири менше ніж в два рази деяке число$16$.

Рішення:

Спочатку виберіть змінну для невідомого числа і визначте ключові слова і фрази. Нехай$x$ представляють невідоме, позначене «деяким числом».

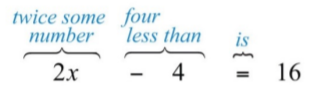$Знімок екрана (753) .png$

Малюнок$\PageIndex{1}$

Пам'ятайте, що віднімання не є комутативним. З цієї причини подбайте про налаштування відмінностей. У цьому прикладі$4−2x=16$ наведено неправильний переклад.

Відповідь:

$2x−4=16$

Важливо спочатку ідентифікувати variable— нехай х представляють... і держава словами, що невідома кількість. Цей крок не тільки робить вашу роботу більш читабельною, але і змушує задуматися про те, що ви шукаєте. Зазвичай, якщо ви знаєте, що вас просять знайти, то завдання його знайти досяжна.

Приклад$\PageIndex{2}$

Перекласти:

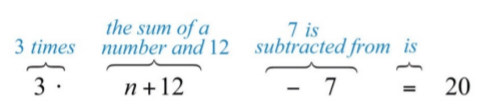
Коли$7$ віднімається від$3$ разів сума числа і$12$, результат є$20$.

Рішення:

$n$Дозволяти представляти невідоме число.

$Знімок екрана (754) .png$

Малюнок$\PageIndex{2}$

Відповідь:

$3(n+12)−7=20$

Щоб зрозуміти, навіщо потрібні дужки, вивчіть структури наступних двох пропозицій і їх переклади:

Таблиця$\PageIndex{3}$
«3 рази сума числа і 12»	$3(n+12)$
«сума в 3 рази число і 12»	$3n+12$

Ключовим є зосередження уваги на фразі «3 рази більше суми». Це спонукає нас згрупувати суму в дужках, а потім помножити на 3. Після того, як додаток перекладається в алгебраїчне рівняння, вирішіть його, використовуючи методи, які ви вивчили.

Рекомендації по налаштуванню та вирішенню проблем Word

Крок 1: Прочитайте проблему кілька разів, визначте ключові слова та фрази та впорядкуйте задану інформацію.
Крок 2: Визначте змінні, призначивши букву або вираз невідомим величинам.
Крок 3: Перекладіть та налаштуйте алгебраїчне рівняння, яке моделює задачу.
Крок 4: Розв'яжіть отримане алгебраїчне рівняння.
Крок 5: Нарешті, дайте відповідь на питання у формі речення і переконайтеся, що це має сенс (перевірте його).

Наразі налаштуйте всі свої рівняння, використовуючи лише одну змінну. Уникайте двох змінних, шукаючи зв'язок між невідомими.

Проблеми, пов'язані з відносинами між реальними числами

Ми класифікуємо додатки, пов'язані з взаємозв'язками між дійсними числами в цілому, як числові проблеми. Ці проблеми іноді можна вирішити за допомогою якоїсь творчої арифметики, ворожіння та перевірки. Рішення таким чином не є гарною практикою, і його слід уникати. Почніть з опрацювання основних кроків, викладених у загальних рекомендаціях щодо вирішення проблем слів.

Приклад$\PageIndex{3}$

Більше ціле число$2$ менше, ніж$3$ в рази менше цілого. Сума двох цілих чисел дорівнює$18$. Знайти цілі числа.

Рішення:

Визначення змінних: Почніть з призначення змінної меншому цілому числу.

$x$Дозволяти представляти менше ціле число.

Використовуйте перше речення для визначення більшого цілого числа через змінну$x$: «Більше ціле число в 2 менше, ніж в 3 рази менше».

$3x-2$Дозволяти представляти більше ціле число.

Встановіть рівняння: Додайте вирази, що представляють два цілих числа, і встановіть отриманий вираз рівним,$18$ як зазначено у другому реченні: «Сума двох цілих чисел дорівнює»$18$.

$x+(3x-2)=18$

Вирішити: Розв'яжіть рівняння, щоб отримати менше ціле число$x$.

$\begin{aligned} x+(3x-2)&=18 \\ x+3x-2&=18 \\ 4x-2&=18 \\ 4x-2\color{Cerulean}{+2}&=18\color{Cerulean}{+2} \\ 4x&=20 \\ \frac{4x}{\color{Cerulean}{4}}&=\frac{20}{\color{Cerulean}{4}} \\ x&=5 \end{aligned}$

Назад заміна: Використовуйте вираз,$3x−2$ щоб знайти велике ціле число - це називається зворотною заміною.

$3x-2=3(\color{OliveGreen}{5}\color{black}{)-2=15-2=13}$

Дайте відповідь на питання: Два цілих числа -$5$ і$13$.

Перевірка:$5 + 13 = 18$. Відповідь має сенс.

Приклад$\PageIndex{4}$

Різниця між двома цілими числами дорівнює$2$. Більше ціле число$6$ менше, ніж в два рази менше. Знайти цілі числа.

Рішення:

Використовуйте зв'язок між двома цілими числами у другому реченні «Більше ціле число на 6 менше, ніж удвічі менше», щоб визначити невідомі через одну змінну.

$x$Дозволяти представляти менше ціле число.

$2x-6$Дозволяти представляти більше ціле число.

Оскільки різниця додатна, відніміть менше ціле число з більшого.

$(2x-6)-x=2$

Вирішити.

$\begin{aligned} \color{OliveGreen}{2x}\color{black}{-6}\color{OliveGreen}{-x}&=2 \\ x-6&=2 \\ x-6\color{Cerulean}{+6}&=2\color{Cerulean}{+6} \\ x&=8 \end{aligned}$

Використовуйте$2x − 6$ для пошуку більшого цілого числа.

$2x-6=2(\color{Cerulean}{8}\color{black}{)-6=16-6=10}$

Відповідь:

Два цілих числа -$8$ і$10$. Ці цілі числа чітко вирішують задачу.

Варто ще раз згадати, що часто можна знайти рішення простих проблем шляхом ворожіння і перевірки. Це відбувається тому, що числа вибираються для спрощення процесу розв'язання, так що алгебраїчні кроки не надто виснажливі. Ви дізнаєтеся, як налаштувати алгебраїчні рівняння з більш легкими задачами, так що ви можете використовувати ці ідеї для вирішення більш складних завдань пізніше.

Приклад$\PageIndex{5}$

Сума двох послідовних парних чисел дорівнює$46$. Знайти цілі числа.

Рішення:

Ключовою фразою, на якій слід зосередитись, є «послідовні парні цілі числа».

$x$Дозволяти представляти перше парне ціле число.

$x+2$Дозволяти представляти наступне парне ціле число.

Додайте парні цілі числа і встановіть їх рівними$46$.

$x+(x+2)=46$

Вирішити.

$\begin{aligned}\color{OliveGreen}{x+x}\color{black}{+2}&=46\\2x+2&=46\\2x+2\color{Cerulean}{-2}&=46\color{Cerulean}{-2}\\2x&=44\\x&=22 \end{aligned}$

Використовуйте$x + 2$ для пошуку наступного парного цілого числа.

$x+2=\color{Cerulean}{22}\color{black}{+2=24}$

Відповідь:

Послідовні парні цілі числа -$22$ і$24$.

Повинно бути зрозуміло, що послідовні парні цілі числа розділені двома одиницями. Однак може бути не так зрозуміло, що непарні цілі числа також.

$Знімок екрана (755) .png$

Малюнок$\PageIndex{3}$

Приклад$\PageIndex{6}$

Сума двох послідовних непарних цілих чисел дорівнює$36$. Знайти цілі числа.

Рішення:

Ключовою фразою, на якій слід зосередитись, є «послідовні непарні цілі числа».

$x$Дозволяти представляти перше непарне число.

$x+2$Дозволяти представляти наступне непарне число.

Додайте два непарних цілих числа і встановіть вираз рівним$36$.

$x+(x+2)=36$

Вирішити.

$\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+2}&=36 \\ 2x+2&=36 \\ 2x+2\color{Cerulean}{-2}&=36\color{Cerulean}{-2} \\ 2x&=34 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{34}{\color{Cerulean}{2}} \\ x&=17 \end{aligned}$

Використовуйте$x + 2$ для пошуку наступного непарного цілого числа.

$x+2=\color{OliveGreen}{17}\color{black}{+2=19}$

Відповідь:

Послідовні непарні цілі числа -$17$ і$19$.

Алгебраїчна установка для парних і непарних цілих задач однакова. Поширеною помилкою є використання$x$ і$x + 3$ при ідентифікації змінних для послідовних непарних цілих чисел. Це неправильно, оскільки додавання 3 до непарного числа дає парне число: наприклад,$5 + 3 = 8$. Неправильна настройка з великою ймовірністю призведе до десяткової відповіді, що може свідчити про те, що проблема була налаштована неправильно.

Приклад$\PageIndex{7}$

Сума трьох послідовних цілих чисел дорівнює$24$. Знайти цілі числа.

Рішення:

Послідовні цілі числа відокремлюються однією одиницею.

$x$Дозволяти представляти перше ціле число.

$x+1$Дозволяти представляти наступне ціле число.

$x+2$Дозволяти представляти третє ціле число.

Додайте цілі числа і встановіть суму рівну$24$.

$x+(x+1)+(x+2)=24$

Вирішити.

$\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+1}\color{OliveGreen}{+x}\color{black}{+2}&=24\\ 3x+3&=24 \\ 3x+3\color{Cerulean}{-3}&=24\color{Cerulean}{-3} \\ 3x&=21 \\ x&=7 \end{aligned}$

Назад підставляємо, щоб знайти інші два цілих числа.

$x+1=\color{OliveGreen}{7}\color{black}{+1=8}$

$x+2=\color{OliveGreen}{7}\color{black}{+2=9}$

Відповідь:

Три послідовних цілих числа -$7, 8$ і$9$, де$7 + 8 + 9 = 24$.

Вправа$\PageIndex{1}$

Сума трьох послідовних непарних цілих чисел дорівнює$87$. Знайти цілі числа.

Відповідь: Цілі числа є$27, 29$, і$31$.

Проблеми геометрії (периметр)

Нагадаємо, що периметр багатокутника - це сума довжин всіх зовнішніх ребер. Крім того, корисно переглянути наступні формули периметра$(π≈3.14159)$.

Таблиця$\PageIndex{4}$
Периметр прямокутника:	$P=2l+2w$
Периметр квадрата:	$P=4s$
Периметр трикутника:	$P=a+b+c$
Периметр кола (окружності):	$C=2\pi r$

Майте на увазі, що ви шукаєте зв'язок між невідомими, щоб ви могли налаштувати алгебраїчні рівняння, використовуючи лише одну змінну. При роботі з проблемами геометрії часто корисно намалювати малюнок.

Приклад$\PageIndex{8}$

Прямокутник має периметр вимірювальні$64$ ноги. Довжина$4$ футів більше, ніж в$3$ рази більше ширини. Знайдіть розміри прямокутника.

Рішення:

Речення «Довжина на 4 фути більше, ніж в 3 рази більше ширини» дає зв'язок між двома змінними.

$Знімок екрана (756) .png$

Малюнок$\PageIndex{4}$

$w$Дозволяти представляти ширину прямокутника.

$3w+4$Дозволяти представляти довжину.

Речення «Прямокутник має периметр вимірювальних$64$ футів» передбачає алгебраїчну установку. $64$Підставляємо периметр і вираз довжини у відповідну формулу наступним чином:

$\begin{aligned} P&=\:\:\:\:\quad 2l + 2w \\ \color{Cerulean}{\downarrow}&\:\:\:\qquad\quad\color{Cerulean}{\downarrow} \\ \color{OliveGreen}{64}&=2(\color{OliveGreen}{3w+4}\color{black}{)+2w} \end{aligned}$

Після того, як ви встановили алгебраїчне рівняння з однією змінною, вирішіть для ширини,$w$.

$\begin{aligned} 64&=\color{OliveGreen}{6w}\color{black}{+8+}\color{OliveGreen}{2w} \\ 64&=8w+8 \\ 64\color{Cerulean}{-8}&=8w+8\color{Cerulean}{-8} \\ 56&=8w \\ \frac{56}{\color{Cerulean}{8}}&=\frac{8w}{\color{Cerulean}{8}} \\ 7&=w \end{aligned}$

Використовуйте$3w + 4$ для пошуку довжини.

$l=3w+4=3(\color{OliveGreen}{7}\color{black}{)+4=21+4=25}$

Відповідь:

Прямокутник вимірює$7$ фути за$25$ футами. Для перевірки складаємо всі сторони:

$P=7\text{ ft+}7\text{ ft+}25\text{ ft+}25\text{ ft}=64\text{ ft}$

Приклад$\PageIndex{9}$

Дві сторони трикутника$5$ і$7$ дюйми довші за третю сторону. Якщо периметр вимірює$21$ дюйми, знайдіть довжину кожної сторони.

$Знімок екрана (757) .png$

Малюнок$\PageIndex{5}$

Рішення:

Перше речення описує відносини між невідомими.

$x$Дозволяти представляти довжину третьої сторони.

Дозвольте$x+5$ і$x+7$ представляють довжини двох інших сторін.

Підставте ці вирази у відповідну формулу і використовуйте$21$ для периметра$P$.

$\begin{aligned} P&=a+b+c \\ \color{OliveGreen}{21}&=\color{OliveGreen}{x}\color{black}{+}\color{OliveGreen}{(x+5)}\color{black}{+}\color{OliveGreen}{(x+7)} \end{aligned}$

Тепер у вас є рівняння з однією змінною для вирішення.

$\begin{aligned} 21&=x+x+5+x+7 \\ 21&=3x+12 \\ 21\color{Cerulean}{-12}&=3x+12\color{Cerulean}{-12} \\ 9&=3x\\ \frac{9}{\color{Cerulean}{3}}&=\frac{3x}{\color{Cerulean}{3}} \\ 3&=x \end{aligned}$

Замінник назад.

$x+5=\color{OliveGreen}{3}\color{black}{+5=8}$

$x+5=\color{OliveGreen}{3}\color{black}{+7=10}$

Відповідь:

Три сторони трикутника вимірюють$3$ дюйми,$8$ дюйми та$10$ дюйми. Чек залишається на розгляд зчитувача.

Вправа$\PageIndex{2}$

Довжина прямокутника -$1$ фут менше, ніж в два рази більше його ширини. Якщо периметр$46$ футів, знайдіть розміри.

Відповідь: Ширина:$8$ стопи; довжина:$15$ фути

Проблеми, пов'язані з грошима та відсотками

Всякий раз, коли ви встановлюєте рівняння за участю відсотка, нам зазвичай потрібно перетворити відсоток у десятковий або дріб. Якщо питання задає відсоток, то не забудьте перевести свою відповідь на відсоток в кінці. Також, коли задіяні гроші, обов'язково округляйте до двох знаків після коми.

Приклад$\PageIndex{10}$

Якщо пара взуття коштує $,$52.50$ включаючи податок$7\frac{1}{4}$%, яка початкова вартість товару до додавання податків?

Рішення:

Почніть з перетворення$7\frac{1}{4}$% в десяткове число.

$7\frac{1}{4}%=7.25%=0.0725$

Сума податку - ця ставка, що перевищує початкову вартість товару. Початкова вартість товару - це те, що вас просять знайти.

$c$Дозволяти представляти вартість товару$\underline{\text{before taxes}}$ додаються.

$\color{Cerulean}{amount\:of\:tax\:=\:tax\:rate\:\cdot\:cost\:of\:item}$

$=0.0725\cdot c$

$\color{Cerulean}{total\:cost\:=\:cost\:of\:item\:+\:amount\:of\:tax}$

$52.50=c+0.0725c$

Використовуйте це рівняння для вирішення для$c$, початкової вартості предмета.

$\begin{aligned} 52.50&=\color{OliveGreen}{1c+0.0725c} \\ 52.50&=1.0725c \\ \frac{52.50}{\color{Cerulean}{1.0725}}&=\frac{1.0725c}{\color{Cerulean}{1.0725}} \\ 48.95& \approx c \end{aligned}$

Відповідь:

Вартість статті до оподаткування становить $$48.95$. Перевірте це,$48.95$ помноживши $ на,$0.0725$ щоб отримати податок і додати його до цієї вартості.

Приклад$\PageIndex{11}$

Враховуючи$5\frac{1}{8}$% річної процентної ставки, скільки часу знадобиться $,$1,200$ щоб отримати $$307.50$ в простих відсотках?

Рішення:

Нехай$t$ представляють час, необхідний для заробітку $$307.50$ при$5.125$%.

Організуйте дані, необхідні для використання простої формули відсотків$I=prt$.

Таблиця$\PageIndex{5}$
Надані відсотки за часовий період:	$I=$$$307.50$
Дано принципал:	$p=$$$1200$
Задана ставка:	$r=5\frac{1}{8}$%$=5.125$%$=0.05125$

Далі підставляємо всі відомі величини в формулу, а потім вирішуємо для єдиного невідомого,$t$.

$\begin{aligned} I&=prt \\ \color{OliveGreen}{307.50}&=\color{OliveGreen}{1200}\color{black}{(}\color{OliveGreen}{0.05125}\color{black}{)t} \\ 307.50&=61.5t \\ \frac{307.50}{\color{Cerulean}{61.5}}&=\frac{61.5t}{\color{Cerulean}{61.5}} \\ 5&=t \end{aligned}$

Відповідь:

Потрібні$5$ роки, щоб $$1,200$ інвестували$5\frac{1}{8}$ в%, щоб заробити $$307.50$ в простих відсотках.

Приклад$\PageIndex{12}$

Мері інвестувала свої загальні заощадження$3,400$ в розмірі $ на два рахунки. Її рахунок пайового фонду заробив$8$% минулого року, а її компакт-диск заробив$5$%. Якщо її загальний відсоток за рік склав $$245$, скільки було на кожному рахунку?

Рішення:

Відносини між двома невідомими є те, що вони становлять 3400 доларів. Коли задіяна загальна сума, загальною методикою, яка використовується для уникнення двох змінних, є представлення другої невідомої як різниці загальної кількості та першої невідомої.

Нехай$x$ представляють суму, вкладену в ПІФ, під$8$%$=0.08$.

$3,400-x$Дозволяти представляти решту суми, вкладеної в компакт-диск в$5$%$=0.05$.

Загальний відсоток - це сума відсотків, зароблених з кожного рахунку.

Таблиця$\PageIndex{6}$
Відсотки, зароблені в ПІФ:	$I=Prt=x⋅0.08⋅1=0.08x$
Відсотки, зароблені на компакт-диску:	$I=Prt=(3,400−x)⋅0.05⋅1=0.05(3,400−x)$

$\color{Cerulean}{mutual\:fund\:interest\:+\:CD\:interest\:=\:total\:interest}$

$0.08x+0.05(3,400-x)=245$

Це рівняння моделює задачу з однією змінною. Вирішити для$x$.

$\begin{aligned} 0.08x+0.05(3,400-x)&=245 \\ \color{OliveGreen}{0.08x}\color{black}{+170}\color{OliveGreen}{-0.05x}&=245 \\ 0.03x+170\color{Cerulean}{-170} &=245\color{Cerulean}{-170} \\ 0.03x&=75 \\ \frac{0.03x}{\color{Cerulean}{0.03}}&=\frac{75}{\color{Cerulean}{0.03}} \\ x&=2,500 \end{aligned}$

Замінник назад.

$3,400-x=3,400-\color{OliveGreen}{2,500}\color{black}{=900}$

Відповідь:

Мері інвестувала $$2,500$ на$8$% в пайовий фонд і $$900$ при$5$% в компакт-диск.

Приклад$\PageIndex{13}$

Джо має кілька копійок і чвертей, що значення $$5.30$. У нього на одну менше, ніж в два рази більше копійки, ніж чверті. Скільки у нього кожної монети?

Рішення:

Почніть з ідентифікації змінних.

Нехай$q$ представляють кількість чвертей Джо тримає.

$2q-1$Дозволяти представляти кількість центів.

Щоб визначити загальну вартість ряду монет, помножте кількість монет на вартість кожної монети. Наприклад,$5$ квартали мають значення $$0.25 ⋅ 5 =$ $$1.25$.

$\color{Cerulean}{value\:in\:quarters\:+\:value\:in\:dimes\:=\:total\:value\:of\:coins}$

$0.25q+0.10(2q-1)=5.30$

Вирішити за кількістю чвертей,$q$.

$\begin{aligned} 0.25q+0.10(2q-1)&=5.30 \\ \color{OliveGreen}{0.25q+0.20q}\color{black}{-0.10}&=5.30 \\ 0.45q-0.10&=5.30 \\ 0.45q-0.10\color{Cerulean}{+0.10}&=5.30\color{Cerulean}{+0.10} \\ 0.45q&=5.40 \\ \frac{0.45q}{\color{Cerulean}{0.45}}&=\frac{5.40}{\color{Cerulean}{0.45}} \\ q&=12 \end{aligned}$

Назад підставляємо$2q − 1$ в, щоб знайти кількість копійок.

$2q-1=2(\color{OliveGreen}{12}\color{black}{)-1=24-1=23}$

Відповідь:

Джо має$12$ чверті і$23$ копійки. Перевірте, перемноживши$0.25 ⋅ 12 = $ $ $$3.00$ і $$0.10 ⋅ 23 = $ $$2.30$. Потім додайте для отримання правильної суми: $$3.00 + $ $$2.30 = $ $$5.30$.

Вправа$\PageIndex{3}$

Загальна сума $$5,900$ інвестується на два рахунки. Один рахунок заробляє$3.5$% відсотків, а інший заробляє$4.5$%. Якщо відсотки за$1$ рік складають $$229.50$, то скільки вкладається в кожен рахунок?

Відповідь: $$3,600$ інвестується в$3.5$% і $$2,300$ при$4.5$%.

Проблеми рівномірного руху (задачі відстані)

Рівномірний рух відноситься до руху зі швидкістю, або швидкістю, яка не змінюється. Ми можемо визначити пройдену відстань, помноживши середню швидкість на час, пройдений з цією швидкістю за допомогою формули$D=r⋅t$. Програми, що включають рівномірний рух, зазвичай мають багато даних, тому це допомагає спочатку організувати дані на діаграмі, а потім встановити алгебраїчне рівняння, яке моделює проблему.

Приклад$\PageIndex{14}$

Два поїзда відправляються зі станції одночасно, що рухаються в протилежних напрямках. Один подорожує зі швидкістю$70$ миль на годину, а інший -$60$ милями на годину. Скільки часу потрібно, щоб відстань між ними досягла$390$ миль?

Рішення:

Спочатку визначте невідому кількість і впорядкуйте дані.

$t$Дозволяти представляти час, необхідний для розділення$390$ миль.

$Знімок екрана (758) .png$

Малюнок$\PageIndex{6}$

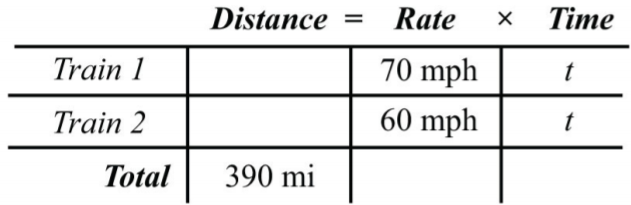
Наведена інформація заповнюється на наступному графіку. Час для кожного поїзда дорівнює.

$Знімок екрана (759) .png$

Малюнок$\PageIndex{7}$

Щоб уникнути введення ще двох змінних, використовуйте формулу$D=r⋅t$ для заповнення невідомих відстаней, пройдених кожним поїздом.

Відстань, пройдена поїздом 1:$D=r\cdot t=70\cdot t$

Відстань, пройдена поїздом 2:$D=r\cdot t=60\cdot t$

Тепер ми можемо повністю заповнити діаграму.

$Знімок екрана (760) .png$

Малюнок$\PageIndex{8}$

Алгебраїчне налаштування визначається стовпчиком відстані. Проблема запитує час, необхідний для того, щоб загальна відстань досягла$390$ миль.

$Знімок екрана (761) .png$

Малюнок$\PageIndex{9}$

Вирішити для$t$.

$\begin{aligned} 70t+60t&=390 \\ 130t&=390 \\ \frac{130t}{\color{Cerulean}{130}}&=\frac{390}{\color{Cerulean}{130}} \\ t&=3 \end{aligned}$

Відповідь:

Відстань між поїздами займає кілька$3$ годин, щоб досягти$390$ миль.

Приклад$\PageIndex{15}$

Поїзд, що прямує без зупинки до місця призначення, здатний здійснити поїздку із середньою швидкістю$72$ миль на годину. У зворотному напрямку поїзд робить кілька зупинок і здатний лише в середньому$48$ милі на годину. Якщо зворотна поїздка займає$2$ години довше, ніж початкова поїздка до пункту призначення, то який час у дорозі в кожну сторону?

Рішення:

Спочатку визначте невідому кількість і впорядкуйте дані.

$t$Дозволяти представляти час, необхідний для прибуття до пункту призначення.

$t+2$Дозволяти представляти час, необхідний для зворотної поїздки.

$Знімок екрана (762) .png$

Малюнок$\PageIndex{10}$

Наведена інформація заповнюється в наступному графіку:

$Знімок екрана (763) .png$

Малюнок$\PageIndex{11}$

Використовуйте формулу$D=r⋅t$, щоб заповнити невідомі відстані.

Відстань, пройдена за пунктом призначення:$D=r\cdot t=72\cdot t$

Відстань, пройдена в зворотній поїздці:$D=r\cdot t=48\cdot (t+2)$

Використовуйте ці вирази, щоб завершити діаграму.

$Знімок екрана (764) .png$

Малюнок$\PageIndex{12}$

Алгебраїчне налаштування знову визначається стовпчиком відстані. При цьому відстань до пункту призначення і назад однакове, а рівняння

$72t=48(t+2)$

Вирішити для$t$.

$\begin{aligned} 72t&=48(t+2) \\ 722&=48t+96 \\ 72t-48t&=48t+96-48t \\ 24t&=96 \\ \frac{24t}{24}&=\frac{96}{24} \\ t&=4 \end{aligned}$

Поїздка в зворотному напрямку займає$t+2=4+2=6$ години.

Відповідь:

Це займає$4$ години, щоб прибути до місця призначення і$6$ години, щоб повернутися.

Вправа$\PageIndex{4}$

Мері відправляється в школу на велосипеді з середньою швидкістю$6$ миль на годину. Її сестра Кейт, запізнюючись, йде$15$ хвилин пізніше і циклає з удвічі більшою швидкістю. Скільки часу знадобиться Кейт, щоб наздогнати Мері? Будьте обережні! Зверніть увагу на одиниці, наведені в задачі.

Відповідь: Це займе$15$ хвилини, щоб Кейт наздогнала згаяне.

Ключові виноси

Спростити процес вирішення реальних задач шляхом створення математичних моделей, що описують взаємозв'язок між невідомими. Використовуйте алгебру для вирішення отриманих рівнянь.
Ворожіння і перевірка рішень є поганою практикою. Цей метод іноді може дати правильні відповіді, але є ненадійним, особливо коли проблеми стають більш складними.
Прочитайте завдання кілька разів і шукайте ключові слова і фрази. Визначте невідомі і призначте змінні або вирази невідомим величинам. Шукайте відносини, які дозволяють використовувати тільки одну змінну. Налаштуйте математичну модель для ситуації та використовуйте алгебру для вирішення рівняння. Перевірте, чи має сенс рішення, і представити рішення у формі речення.
Не уникайте проблем зі словами: їх вирішення може бути веселим і корисним. З великою кількістю практики ви виявите, що вони насправді не такі вже й погані. Моделювання та рішення додатків є однією з основних причин вивчення алгебри.
Не відчувайте зневіри, коли перша спроба вирішити проблему слова не виходить. Це частина процесу. Спробуйте щось інше і вчіться на неправильних спробах.

Вправа$\PageIndex{5}$ Translate

Переведіть наступне в алгебраїчні рівняння.

Сума числа і$6$ дорівнює$37$.
Коли$12$ віднімається з двічі деяке число, результат є$6$.
У чотирнадцять$5$ разів менше, ніж число$1$.
Двічі віднімається деяке число,$30$ і результат є$50$.
П'ять разів сума$6$ і деяке число дорівнює$20$.
Сума$5$ разів деяке число і$6$ дорівнює$20$.
Коли сума числа і$3$ віднімається$10$ з результату$5$.
Сума триразового числа і п'ять разів це ж число$24$.
Десять віднімається з подвійного деякого числа і результатом є сума числа і$2$.
Шість менше деякого числа в десять разів перевищує суму цього числа і$5$.

Відповідь

1. $x+6=37$

3. $5x−14=1$

5. $5(x+6)=20$

7. $10−(x+3)=5$

9. $2x−10=x+2$

Вправа$\PageIndex{6}$ Number Problems

Встановіть алгебраїчне рівняння, а потім вирішіть.

Більше ціле число$1$ більше, ніж удвічі інше ціле число. Якщо сума цілих чисел дорівнює$25$, знайдіть цілі числа.
Якщо більше ціле число$2$ більше, ніж в$4$ рази інше ціле і їх різниця дорівнює$32$, знайдіть цілі числа.
Одне ціле число$30$ більше, ніж інше ціле число. Якщо різниця між більшим і подвійним меншим є$8$, знайдіть цілі числа.
Коефіцієнт деякого числа і$4$ є$22$. Знайдіть номер.
У вісім разів число зменшується в три рази стільки ж, що дає різницю$20$. Що таке число?
Одне ціле число на дві одиниці менше іншого. Якщо їх сума дорівнює$−22$, знайдіть два цілих числа.
Сума двох послідовних цілих чисел дорівнює$139$. Знайти цілі числа.
Сума трьох послідовних цілих чисел дорівнює$63$. Знайти цілі числа.
Сума трьох послідовних цілих чисел дорівнює$279$. Знайти цілі числа.
Різниця в два рази менша з двох послідовних цілих чисел і більша$39$. Знайти цілі числа.
Якщо менше з двох послідовних цілих чисел віднімається з двох разів більше, то результат буде$17$. Знайти цілі числа.
Сума двох послідовних парних чисел дорівнює$46$. Знайти цілі числа.
Сума двох послідовних парних чисел дорівнює$238$. Знайти цілі числа.
Сума трьох послідовних парних чисел дорівнює$96$. Знайти цілі числа.
Якщо менше з двох послідовних парних цілих чисел віднімається з$3$ разів, то більший результат$42$. Знайти цілі числа.
Сума трьох послідовних парних чисел дорівнює$90$. Знайти цілі числа.
Сума двох послідовних непарних цілих чисел дорівнює$68$. Знайти цілі числа.
Сума двох послідовних непарних цілих чисел дорівнює$180$. Знайти цілі числа.
Сума трьох послідовних непарних цілих чисел дорівнює$57$. Знайти цілі числа.
Якщо менше з двох послідовних непарних цілих чисел віднімається з двох, то більший результат буде$23$. Знайти цілі числа.
Двічі сума двох послідовних непарних цілих чисел дорівнює$32$. Знайти цілі числа.
Різниця між подвійним більшим з двох послідовних непарних цілих чисел і меншим$59$. Знайти цілі числа.

Відповідь

1. $8, 17$

3. $22, 52$

5. $4$

7. $69, 70$

9. $92, 93, 94$

11. $15, 16$

13. $118, 120$

15. $18, 20$

17. $33, 35$

19. $17, 19, 21$

21. $7, 9$

Вправа$\PageIndex{7}$ Geometry Problems

Встановіть алгебраїчне рівняння, а потім вирішіть.

Якщо периметр квадрата дорівнює$48$ дюймам, то знайдіть довжину кожної сторони.
Довжина прямокутника на$2$ дюйми більше його ширини. Якщо периметр дорівнює$36$ дюймам, знайдіть довжину і ширину.
Довжина прямокутника$2$ футів менше, ніж в два рази більше його ширини. Якщо периметр$26$ футів, знайдіть довжину і ширину.
Ширина прямокутника на$2$ сантиметри менше половини його довжини. Якщо периметр дорівнює$56$ сантиметрам, знайдіть довжину і ширину.
Довжина прямокутника$3$ футів менше, ніж в два рази більше його ширини. Якщо периметр$54$ футів, знайдіть розміри прямокутника.
Якщо довжина прямокутника вдвічі довша за ширину, а його периметр вимірює$72$ дюйми, знайдіть розміри прямокутника.
Периметр рівностороннього трикутника вимірює$63$ сантиметри. Знайдіть довжину кожної сторони.
Рівнобедрений трикутник, основа якого дорівнює половині довжини двох інших рівних сторін, має периметр$25$ сантиметрів. Знайдіть довжину кожної сторони.
Кожен з двох рівних ніжок рівнобедреного трикутника в два рази перевищує довжину підстави. Якщо периметр$105$ сантиметри, то якої довжини кожна ніжка?
Трикутник має сторони, міри яких є послідовними парними цілими числами. Якщо периметр дорівнює$42$ дюймам, знайдіть міру кожної сторони.
Трикутник має сторони, міри яких є послідовними непарними цілими числами. Якщо периметр дорівнює$21$ дюймам, знайдіть міру кожної сторони.
Трикутник має сторони, міри яких є послідовними цілими числами. Якщо периметр дорівнює$102$ дюймам, то знайдіть міру кожної сторони.
Окружність кола вимірює$50π$ одиниці виміру. Знайдіть радіус.
Окружність кола вимірює$10π$ одиниці виміру. Знайдіть радіус.
Окружність кола вимірює$100$ сантиметри. Визначте радіус до найближчої десятої.
Окружність кола вимірює$20$ сантиметри. Знайдіть діаметр, округлений до найближчої сотої.
Діаметр кола вимірює$5$ дюйми. Визначте окружність до найближчої десятої.
Діаметр кола -$13$ фути. Обчисліть точне значення окружності.

Відповідь

1. $12$дюймів

3. Ширина:$5$ стопи; довжина:$8$ фути

5. Ширина:$10$ стопи; довжина:$17$ фути

7. $21$сантиметри

9. $21$сантиметри,$42$ сантиметри,$42$ сантиметри

11. $5$дюйми,$7$ дюйми,$9$ дюйми

13. $25$одиниць

15. $15.9$сантиметри

17. $15.7$дюймів

Вправа$\PageIndex{8}$ Percent and Money Problems

Встановіть алгебраїчне рівняння, а потім вирішіть.

Обчисліть прості відсотки, зароблені на$2$ -річну інвестицію$1,550$ в $ під$8\frac{3}{4}$% річної процентної ставки.
Обчисліть прості відсотки, зароблені на$1$ -річну інвестицію$500$ в $ під$6$% річної процентної ставки.
За скільки років$10,000$ потрібно інвестувати $ під процентну ставку$8\frac{1}{2}$% річної, щоб отримати $$4,250$ в простих відсотках?
За скільки років$1,000$ потрібно інвестувати $ під процентну ставку$7.75$% річної, щоб отримати $$503.75$ в простих відсотках?
За якою річною процентною ставкою$2,500$ потрібно інвестувати $$3$ роками, щоб дати $$412.50$ в прості відсотки?
За якою річною процентною ставкою$500$ потрібно інвестувати $$2$ роками, щоб дати $$93.50$ в прості відсотки?
Якщо прості відсотки, зароблені за$1$ рік, становили $,$47.25$ а річна ставка дорівнювала$6.3$%, що було основним?
Якщо прості відсотки, зароблені$2$ роками, становили $,$369.60$ а річна ставка становила$5\frac{1}{4}$%, що було основним?
Джо інвестував минулорічну$2,500$ податкову декларацію $ у два різних рахунки. Він поклав більшу частину грошей на рахунок грошового ринку, заробляючи$5$% простих відсотків. Решту він вклав в компакт-диск, заробивши$8$% простих відсотків. Скільки він вклав на кожен рахунок, якщо загальний відсоток за рік склав $$138.50$?
Джеймс інвестував $$1,600$ на два рахунки. Один рахунок заробляє$4.25$% простих відсотків, а інший заробляє$8.5$%. Якщо відсотки за$1$ роком становили $$85$, скільки він вклав у кожен рахунок?
Джейн має свої$5,400$ заощадження $, інвестовані на два рахунки. Вона має частину його на компакт-диску під$3$% річних відсотків, а решта на ощадному рахунку, який заробляє$2$% річних відсотків. Якщо прості відсотки, зароблені з обох рахунків, складають $$140$ за рік, то скільки у неї на кожному рахунку?
Марті поклав торішній бонус у розмірі $$2,400$ на два рахунки. Він інвестував частину в компакт-диск з$2.5$% річних відсотків, а решту в фонд грошового ринку з$1.3$% річних відсотків. Його загальний відсоток за рік склав $$42.00$. Скільки він вклав в кожен рахунок?
Аліса вкладає гроші на два рахунки, один з$2$ відсотками річних відсотків, а інший з$3$% річних відсотків. Вона вкладає$3$ рази стільки ж в рахунок з вищою прибутковістю, як і в нижчий прибутковий рахунок. Якщо її загальний відсоток за рік становить $$27.50$, скільки вона вклала в кожен рахунок?
Джим вклав спадщину в двох окремих банках. Один банк запропонував$5.5$% річної процентної ставки, а інший$6\frac{1}{4}$%. Він вклав в більш прибутковий банківський рахунок вдвічі більше, ніж в інший. Якщо його сумарний простий відсоток за$1$ рік становив $$4,860$, то яка була сума його спадщини?
Якщо товар рекламується вартістю $$29.99$ плюс$9.25$% податку, яка загальна вартість?
Якщо товар рекламується вартістю $$32.98$ плюс$8\frac{3}{4}$% податку, яка загальна вартість?
Товар, включаючи податок$8.75$%, вартість $$46.49$. Яка початкова вартість товару до оподаткування?
Товар, включаючи податок$5.48$%, вартість $$17.82$. Яка початкова вартість товару до оподаткування?
Якщо їжа коштує $$32.75$, яка загальна сума після додавання чайового$15$%?
Скільки коштує$15$% чайових на рахунок ресторану, який становить $$33.33$?
У Рей є жменька копійок і нікелів, що оцінюють $$3.05$. У нього$5$ більше копійки, ніж у нього нікелів. Скільки у нього кожної монети?
У Джилл$3$ менше півдоларів, ніж у неї чверті. Значення всіх$27$ її монет додає до $$9.75$. Скільки кожної монети має Джилл?
Кеті повинна внести $ на$410$ суму п'ять- і десятидоларові купюри. У неї$1$ менше, ніж в три рази більше десятків, ніж у неї п'ятидоларові купюри. Скільки з кожного рахунку вона повинна внести?
Біллі має купу чвертей, копійок та нікелів, що значення $$3.75$. У нього$3$ більше копійок, ніж чверті і$5$ більше нікелів, ніж чвертей. Скільки кожної монети має Біллі?
Мері має банку з купюрами в один долар, півдоларовими монетами та кварталами вартістю $$14.00$. Вона має вдвічі більше чвертей, ніж вона робить півдоларові монети і стільки ж півдоларових монет, як однодоларові купюри. Скільки у неї кожного?
Чад має рахунки на один, п'ять- та десятидоларові купюри на загальну суму $$118$. У нього$2$ більше, ніж в$3$ рази більше, ніж він робить п'ятидоларові купюри і$1$ менше десяти-, ніж п'ятидоларові купюри. Скільки кожного законопроекту має Чад?

Відповідь

1. $$271.25$

3. $5$років

5. $5.5$%

7. $$750.00$

9. Джо інвестував $$2,050$ в рахунок грошового ринку і $$450$ в компакт-диск.

11. Джейн має $$3,200$ на компакт-диску та $$2,200$ в заощадженнях.

13. Аліса$250$ інвестувала $ в$2$% і $$750$ при$3$%.

15. $$32.76$

17. $$42.75$

19. $$37.66$

21. У нього є$17$ нікелі і$22$ копійки.

23. У Кеті$12$ п'ятірки і$35$ десятидоларові купюри.

25. Мері має купюри в$7$ один$7$ долар, півдоларові монети та$14$ чверті.

Вправа$\PageIndex{9}$ Uniform Motion (Distance Problems)

Налаштуйте алгебраїчне рівняння, а потім вирішіть.

Два автомобілі залишають локацію, що рухаються в протилежних напрямках. Якщо один автомобіль в середньому$55$ милі на годину, а інший$65$ середній милі на годину, то скільки часу знадобиться для них, щоб відокремити відстань$300$ миль?
Два літаки залишають аеропорт одночасно, подорожуючи в протилежних напрямках. Середні швидкості для літаків -$450$ милі на годину і$395$ милі на годину. Як довго це займе літаки, щоб бути відстань в$1,478.75$ милі один від одного?
Білл і Тед мчать по всій країні. Білл йде на$1$ годину раніше, ніж Тед і подорожує з середньою швидкістю$60$ миль на годину. Якщо Тед має намір наздогнати зі швидкістю$70$ миль на годину, то скільки часу це займе?
Двоє братів виїжджають з одного місця, один в машині, а інший на велосипеді, щоб зустрітися в будинку своєї бабусі на вечерю. Якщо один брат$30$ усереднює кілометри на годину в машині, а інший - в середньому$12$ милі на годину на велосипеді, то він займає у брата на велосипеді$1$ годину менше ніж в$3$ рази довше, ніж інший в машині. Скільки часу потрібно кожному з них, щоб здійснити поїздку?
Пілот комерційної авіакомпанії літав із середньою швидкістю$350$ миль на годину, перш ніж йому повідомили, що аеродром призначення може бути закритий через погані погодні умови. У спробі прибути перед штормом він збільшував швидкість$400$ миль на годину і летів ще$3$ годинами. Якщо загальна відстань, що пройшла, становила$2,950$ милі, то скільки часу зайняла поїздка?
Два брати проїхали$2,793$ кілометри від Лос-Анджелеса до Нью-Йорка. Один з братів, керуючи вдень, зміг скласти середні$70$ кілометри на годину, а інший, проїжджаючи вночі, зміг усереднити$53$ кілометри на годину. Якщо брат за кермом вночі проїхав$3$ годин менше, ніж брат за кермом вдень, то скільки годин вони проїхали кожен?
Джо і Еллен живуть$21$ милями один від одного. Відлітаючи при цьому, вони крутяться назустріч один одному. Якщо Джо в середньому$8$ милі на годину, а Еллен в середньому$6$ милі на годину, скільки часу знадобиться їм, щоб зустрітися?
Якщо їхати до автомайстерні з середньою швидкістю$30$ миль на годину потрібно$6$ хвилин, то скільки часу знадобиться, щоб повернутися назад із середньою швидкістю$4$ миль на годину?
Хайме і Алекс залишають ту ж локацію і подорожують в протилежних напрямках. Умови руху дозволили Алексу в середньому$14$ милі на годину швидше, ніж Хайме. Після$1\frac{1}{2}$ години вони знаходяться в$159$ милі один від одного. Знайдіть швидкість, з якою кожен зміг подорожувати.
Джейн і Холлі живуть$51$ милями один від одного і їдуть одночасно подорожуючи назустріч один одному, щоб зустрітися на обід. Джейн їздила по автостраді на вдвічі більшій середній швидкості, ніж Холлі. Вони змогли зустрітися за півгодини. З якою швидкістю здійснював кожен проїзд?

Відповідь

1. $2.5$годин

3. $6$годин

5. $8$годин

7. $1\frac{1}{2}$годин

9. Хайме:$46$ миль на годину; Алекс:$60$ миль на годину

Вправа$\PageIndex{10}$ Discussion Board Topics

Обговоріть ідеї розрахунку податків і поради подумки.
Дослідження історичних методів представлення невідомих.
Досліджуйте та порівняйте прості відсотки та складні відсотки. У чому різниця?
Обговоріть, чому алгебра є обов'язковим предметом.
Дослідження способів показати, що повторюване десяткове число є раціональним. Поділіться своїми висновками на дошці обговорень.

Відповідь

1. Відповіді можуть відрізнятися

3. Відповіді можуть відрізнятися

5. Відповіді можуть відрізнятися

Ключові слова	Переклад
Сума, збільшена на, більше, ніж, плюс, додана до, загальна	\(+\)
Різниця, зменшена на, віднімається від, менше, мінус	\(-\)
Продукт, помножений на, of, раз, в два рази	\(*\)
Коефіцієнт, розділений на, співвідношення, на	\(/\)
Є, підсумок, результат	\(=\)

Ключові фрази	Переклад
Сума числа і 7.	\(x+7\)
Сім більше, ніж число.	\(x+7\)
Різниця числа і 7.	\(x-7\)
Сім менше числа.
Сім віднімається з числа.
Твір 2 і число.	\(2x\)
Двічі число.	\(2x\)
Половина числа.	\(\frac{1}{2}x\)
Коефіцієнт числа і 7.	\(\frac{x}{7}\)

«3 рази сума числа і 12»	\(3(n+12)\)
«сума в 3 рази число і 12»	\(3n+12\)

Периметр прямокутника:	\(P=2l+2w\)
Периметр квадрата:	\(P=4s\)
Периметр трикутника:	\(P=a+b+c\)
Периметр кола (окружності):	\(C=2\pi r\)

Надані відсотки за часовий період:	\(I=\)$\(307.50\)
Дано принципал:	\(p=\)$\(1200\)
Задана ставка:	\(r=5\frac{1}{8}\)%\(=5.125\)%\(=0.05125\)

Відсотки, зароблені в ПІФ:	\(I=Prt=x⋅0.08⋅1=0.08x\)
Відсотки, зароблені на компакт-диску:	\(I=Prt=(3,400−x)⋅0.05⋅1=0.05(3,400−x)\)