2.8: Лінійні нерівності (одна змінна)

Цілі навчання

• Визначте лінійні нерівності та перевіряйте розв'язки.
• Розв'яжіть лінійні нерівності та виражайте розв'язки графічно на числовій лінії та в інтервальних позначеннях.
• Розв'яжіть складні лінійні нерівності та виражайте розв'язки графічно на числовій лінії та в інтервальних позначеннях.
• Розв'язуйте програми, що включають лінійні нерівності та інтерпретуйте результати.

Визначення лінійної нерівності

Лінійна нерівність - це математичне твердження, яке пов'язує лінійний вираз як менший або більший за інше. Нижче наведено кілька прикладів лінійних нерівностей, всі з яких вирішуються в цьому розділі:

$3x+7<16\quad -2x+1\geq 21\quad -7(2x+1)<1$

Розв'язок лінійної нерівності - це дійсне число, яке видасть справжнє твердження при заміні змінної. Лінійні нерівності мають або нескінченно багато розв'язків, або немає рішення. Якщо розв'язків нескінченно багато, графуйте розв'язку, встановлене на числовому рядку і/або висловіть рішення за допомогою інтервальних позначень.

Приклад$\PageIndex{1}$

Чи є$x=−2$ і$x=4$ рішення$3x+7<16$?

Рішення:

Підставляємо значення для$x$, спрощуємо і перевіряємо, чи отримаємо ми справжнє твердження.

$\begin{array}{c|c} {\underline{Check\:x=-2}}&{\underline{Check\:x=4}}\\{\begin{aligned} 3(\color{OliveGreen}{-2}\color{black}{)+7}&<16 \\ -6+7&<16 \\ 1&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{4}\color{black}{)+7}&<16 \\ 12+7&<16 \\ 19&<16\quad\color{red}{x} \end{aligned}} \end{array}$

Відповідь:

$x=-2$є рішенням і не$x=4$ є.

Алгебра лінійних нерівностей

Усі методи, крім однієї, вивчені для розв'язування лінійних рівнянь, застосовуються до розв'язання лінійних нерівностей. Ви можете додати або відняти будь-яке дійсне число до обох сторін нерівності, і ви можете помножити або розділити обидві сторони на будь-яке додатне дійсне число, щоб створити еквівалентні нерівності. Наприклад,

-5\ колір {Cerulean} {-7} &\ color {Cerulean} {Відняти\ :7\ :від\ :обидві\ :сторони.}\\ 3&>-12\ quad\ color {\ галочка} &\ колір {Cerulean} {True}\\ 10&>-5\\ frac {10} {\ color {Cerulean} {5}} &>\ розрив {-5} {\ color {Cerulean} {5}} &\ color {Cerulean} {Розділити\ :обидві\ :сторони\ :по\ :5.}\\ 2&>-1\ quad\ color { Cerulean} {\ галочка} &\ color {Cerulean} {True}\ end {вирівняний}\)

Як віднімання$7$ з кожної сторони, так і поділ кожної сторони на$+5$ призводить до еквівалентної нерівності, яка є істинною.

Приклад$\PageIndex{2}$

Розв'яжіть та графуйте набір рішень:

$3x+7<16$.

Рішення:

$\begin{aligned} 3x+7&<16 \\ 3x+7\color{Cerulean}{-7}&<16\color{Cerulean}{-7} \\ 3x&<9 \\ \frac{3x}{\color{Cerulean}{3}}&<\frac{9}{\color{Cerulean}{3}} \\ x&<3 \end{aligned}$

Малюнок$\PageIndex{1}$

Корисно взяти хвилину і вибрати кілька значень у наборі рішень і поза ним, замінити їх у вихідну нерівність, а потім перевірити результати. Як зазначено, слід$x=0$ розраховувати на вирішення початкової нерівності, але не$x=5$ слід.

$\begin{array}{c|c} {\underline{Check\:x=0}}&{\underline{Check\:x=5}}\\{\begin{aligned} 3(\color{OliveGreen}{0}\color{black}{)+7}&<16 \\ 7&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{5}\color{black}{)+7}&<16 \\ 15+7&<16 \\ 22&<16\quad\color{red}{x} \end{aligned}} \end{array}$

Перевірка таким чином дає хороший показник того, що нерівність вирішена правильно. Це можна зробити подумки.

Відповідь:

Інтервальні позначення:$(−∞, 3)$

При роботі з лінійними нерівностями застосовується інше правило при множенні або діленні на від'ємне число. Щоб проілюструвати проблему, розглянемо істинне твердження$10>−5$ і розділіть обидві сторони на$−5$.

\ frac {-5} {\ color {Cerulean} {-5}} &\ color {Cerulean} {Розділити\ :обидві\ :сторони\ :-5.}\\ -2&\ колір {червоний} {>}\ колір {чорний} {1}\ квадратний\ колір {x} &\ колір {Cerulean} {помилковий}\ кінець {вирівняний}\)

Поділ на$−5$ призводить до помилкового твердження. Щоб зберегти справжнє твердження, нерівність повинна бути зворотна.

$\begin{aligned} 10&\color{OliveGreen}{>}\color{black}{-5} \\ \frac{10}{\color{Cerulean}{-5}}&<\frac{-5}{\color{Cerulean}{-5}} &\color{Cerulean}{Reverse\:the\:inequality.} \\ -2&\color{OliveGreen}{<}\color{black}{1}\quad\color{Cerulean}{\checkmark}&\color{Cerulean}{True} \end{aligned}$

Така ж проблема виникає при множенні на від'ємне число. Це призводить до наступного нового правила: при множенні або діленні на від'ємне число зворотне нерівність. Це легко забути, тому особливо уважно стежте за негативними коефіцієнтами.

Загалом, задані алгебраїчні вирази$A$ і$B$, де$c$ додатне ненульове дійсне число, ми маємо такі властивості нерівностей:

$\begin{array}{ll}{\textbf{Addition property of inequalities:}}&{\text{If }A<B\text{ then, }A\color{Cerulean}{+c}\color{black}{<B}\color{Cerulean}{+c}}\\{\textbf{Subtraction property of inequalities:}}&{\text{If }A<B,\text{ then }A\color{Cerulean}{-c}\color{black}{<B}\color{Cerulean}{-c}}\\{\textbf{Multiplication property of inequalities:}}&{\text{If }A<B,\text{ then }\color{Cerulean}{c}\color{black}{A<}\color{Cerulean}{c}\color{black}{B}}\\{}&{\text{If }A<B,\text{ then }\color{Cerulean}{-c}\color{black}{A}\color{OliveGreen}{>}\color{Cerulean}{-c}\color{black}{B}}\\{\textbf{Division property of inequalities:}}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{c}}\color{black}{<\frac{B}{\color{Cerulean}{c}}}}\\{}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\color{black}{\frac{B}{\color{Cerulean}{-c}}}} \end{array}$

Ми використовуємо ці властивості для отримання еквівалентної нерівності, однієї з однаковим набором розв'язків, де змінна ізольована. Процес схожий на розв'язування лінійних рівнянь.

Приклад$\PageIndex{3}$

Вирішити:

$−2x+1≥21$.

Рішення:

Малюнок$\PageIndex{2}$

Відповідь:

Інтервальні позначення:$(−∞, −10]$

Приклад$\PageIndex{4}$

Вирішити:

$−7(2x+1)<1$.

Рішення:

$\begin{aligned} -7(2x+1)&<1 & & \color{Cerulean}{Distribute.} \\ -14x-7&<1 \\ -14x-7\color{Cerulean}{+7}&<1\color{Cerulean}{+7} \\ 14x&<8 \\ \frac{-14x}{\color{Cerulean}{-14}}&\color{OliveGreen}{>}\color{black}{\frac{8}{\color{Cerulean}{-14}}} & & \color{Cerulean}{Reverse\:the\:inequality.} \\ x&>-\color{black}{\frac{8\color{Cerulean}{\div 2}}{14\color{Cerulean}{\div 2}}} & & \color{Cerulean}{Reduce.} \\ x&>-\frac{4}{7} \end{aligned}$

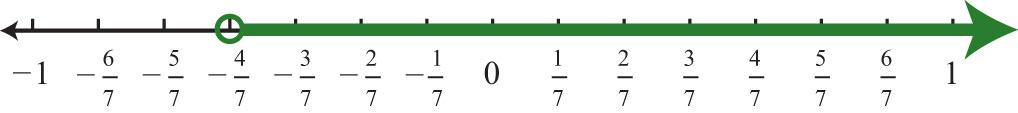
Малюнок$\PageIndex{3}$

Відповідь:

Інтервальні позначення:$(−\frac{4}{7}, ∞)$

Приклад$\PageIndex{5}$

Вирішити:

$5x−3(2x−1)≥2(x−3)$.

Рішення:

Малюнок$\PageIndex{4}$

Відповідь:

Інтервальні позначення:$(−∞, 3]$

Вправа$\PageIndex{1}$

Вирішити:

$3−5(x−1)≤28$.

Відповідь

$[−4, ∞)$

Складні нерівності

Нижче наведено кілька прикладів складних лінійних нерівностей:

$-3<2x+5<17$

$-1\leq\frac{1}{2}x-3<1$

$3x+1<10\quad or\quad 2x-1\geq 11$

Ці складні нерівності насправді є двома нерівностями в одному твердженні, з'єднаних словом «і» або словом «або». Наприклад,

$-3<2x+5<17$

це складна нерівність, оскільки вона може бути розкладена наступним чином:

$-3<2x+5\quad\text{and}\quad 2x+5<17$

Розв'яжіть кожну нерівність окремо, і перетин двох множин розв'язків вирішує вихідну складну нерівність. Хоча цей метод працює, є ще один метод, який зазвичай вимагає менше кроків. Застосовують властивості цього розділу до всіх трьох частин складної нерівності з метою виділення змінної в середині оператора для визначення меж множини розв'язку.

Приклад$\PageIndex{6}$

Вирішити:

$−3<2x+5<17$.

Рішення:

$\begin{array}{c} {-3<2x+5<17}\\{-3\color{Cerulean}{-5}\color{black}{<2x+5}\color{Cerulean}{-5}\color{black}{<17}\color{Cerulean}{-5}}\\{-8<2x<12}\\{\frac{-8}{\color{Cerulean}{2}}\color{black}{<\frac{2x}{\color{Cerulean}{2}}<\frac{12}{\color{Cerulean}{2}}}}\\{-4<x<6} \end{array}$

Малюнок$\PageIndex{5}$

Відповідь:

Інтервальні позначення:$(−4, 6)$

Приклад$\PageIndex{7}$

Вирішити:

$−1≤\frac{1}{2}x−3<1$.

Рішення:

$\begin{array}{c}{-1\leq\frac{1}{2}x-3<1}\\{-1\color{Cerulean}{+3}\color{black}{\leq\frac{1}{2}x-3}\color{Cerulean}{+3}\color{black}{<1}\color{Cerulean}{+3}}\\{2\leq\frac{1}{2}x<4}\\{\color{Cerulean}{2}\color{black}{\cdot 2\leq}\color{Cerulean}{2}\color{black}{\cdot\frac{1}{2}x<}\color{Cerulean}{2}\color{black}{\cdot 4}}\\{4\leq x<8} \end{array}$

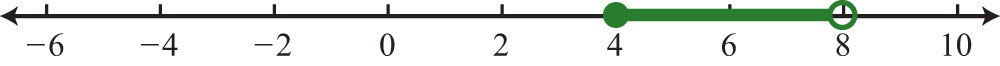
Малюнок$\PageIndex{6}$

Відповідь:

Інтервальні позначення:$[4, 8)$

Важливо відзначити, що при множенні або діленні всіх трьох частин складної нерівності на від'ємне число необхідно повернути назад всі нерівності в твердженні. Наприклад,

$\begin{array}{c}{-10<-2x<20}\\{\frac{-10}{\color{Cerulean}{-2}}\color{OliveGreen}{>}\color{black}{\frac{-2x}{\color{Cerulean}{-2}}}\color{OliveGreen}{>}\color{black}{\frac{20}{\color{Cerulean}{-2}}}}\\{5>x>-10} \end{array}$

Відповідь вище можна записати в еквівалентній формі, де менші числа лежать зліва, а більші числа лежать праворуч, так як вони з'являються на числовій лінії.

$-10<x<5$

Використовуючи інтервальне позначення, запишіть$(−10, 5)$.

Вправа$\PageIndex{2}$

Вирішити:

$−8≤2(−3x+5)<34$.

Відповідь

$(−4, 3]$

Для складних нерівностей зі словом «або» ви повинні працювати обидві нерівності окремо, а потім розглянути об'єднання множин рішень. Цінності в цьому союзі вирішують або нерівність.

Приклад$\PageIndex{8}$

Вирішити:

$3x+1<10$або$2x−1≥11$.

Рішення:

Вирішіть кожну нерівність і сформуйте об'єднання, об'єднавши множини рішень.

$\begin{array}{ccc}{3x+1<10}&{}&{2x-1\geq 11}\\{3x+1\color{Cerulean}{-1}\color{black}{<10}\color{Cerulean}{-1}}&{}&{2x-1\color{Cerulean}{+1}\color{black}{\geq 11}\color{Cerulean}{+1}}\\{3x<9}&{\text{or}}&{2x\geq 12}\\{\frac{3x}{\color{Cerulean}{3}}\color{black}{<\frac{9}{\color{Cerulean}{3}}}}&{}&{\frac{2x}{\color{Cerulean}{2}}\color{black}{\geq \frac{12}{\color{Cerulean}{2}}}}\\{x<3}&{}&{x\geq 6} \end{array}$

Малюнок$\PageIndex{7}$

Відповідь:

Інтервальні позначення:$(−∞, 3)∪[6, ∞)$

Вправа$\PageIndex{3}$

Вирішити:

$4x−1<-5$або$4x-1>5$.

Відповідь

$(−∞,−1)∪(\frac{3}{2}, ∞)$

Застосування лінійних нерівностей

Деякі ключові слова та фрази, які вказують на нерівності, узагальнені нижче:

Таблиця$\PageIndex{1}$

Ключові фрази	Переклад
Число - це як мінімум$5$.	$x\geq 5$
Число є$5$ або більше включно.
Число є не більше$3$.	$x\leq 3$
Число є$3$ або менш включно.
Число строго менше$4$.	$x<4$
Число менше$4$, не включно.
Число більше, ніж$7$.	$x>7$
Число більше$7$, ніж, не включено.
Число знаходиться між$2$ і$10$.	$2<x<10$
Число є принаймні$5$ і максимум$15$.	$5\leq x\leq 15$
Число може варіюватися від$5$ до$15$.

Як і у всіх додатках, уважно прочитайте проблему кілька разів і шукайте ключові слова і фрази. Визначте невідомі і призначте змінні. Далі перекладіть формулювання в математичну нерівність. Нарешті, використовуйте властивості, які ви навчилися вирішувати нерівність і висловити рішення графічно або в інтервальній нотації.

Приклад$\PageIndex{9}$

Перекласти:

П'ять менше, ніж удвічі більше числа$25$.

Рішення:

Спочатку виберіть змінну для невідомого числа і визначте ключові слова і фрази.

$\begin{array}{cccc}{\color{Cerulean}{twice\:a\:number}}&{\color{Cerulean}{five\:less\:than}}&{\color{Cerulean}{is\:at\:most}}&{}\\{\overbrace{\:\:2n\:\:}}&{\overbrace{\:\:-\:\:5\:\:}}&{\overbrace{\:\:\leq\:\:}}&{25} \end{array}$

Відповідь:

$2n−5≤25$.

Ключова фраза «є максимум» вказує на те, що величина має максимальне значення$25$ або менше.

Приклад$\PageIndex{10}$

Температура в пустелі може коливатися від$10°C$ до$45°C$ одного$24$ годинного періоду. Знайти еквівалентний діапазон в градусах Фаренгейта$F$, враховуючи це$C=\frac{5}{9}(F−32)$.

Рішення:

Встановіть складну нерівність, де температура в Цельсії включно між$10°C$ і$45°C$. Потім підставляємо вираз, еквівалентний температурі Цельсія, в нерівність і вирішуємо для$F$.

$\begin{array}{c}{10°C\leq\color{OliveGreen}{temperature\:in\:Celsius}\color{black}{\leq 45°C}}\\{10\leq\color{OliveGreen}{\frac{5}{9}(F-32)}\color{black}{\leq 45}}\\{\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{10\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{\frac{5}{9}(F-32)\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{45}}\\{18\leq F-32\leq 81}\\{18\color{Cerulean}{+32}\color{black}{\leq F-32}\color{Cerulean}{+32}\color{black}{\leq 81}\color{Cerulean}{+32}}\\{50\leq F\leq 113}\end{array}$

Відповідь:

Еквівалентний діапазон Фаренгейта - від$50°F$ до$113°F$.

Приклад$\PageIndex{11}$

У перших чотирьох подіях зустрічі гімнастка забиває$7.5, 8.2, 8.5$, і$9.0$. Що вона повинна забити на п'ятій події, щоб усереднити хоча б$8.5$?

Рішення:

Середній повинен бути не менше$8.5$; це означає, що середнє значення має бути більше або дорівнює$8.5$.

$\begin{aligned} average &\geq 5 \\ \frac{7.5+8.2+8.5+9.0+x}{5}&\geq 8.5 \\ \frac{33.2+x}{5}&\geq 8.5 \\ \color{Cerulean}{5\cdot}\color{black}{\frac{33.2+x}{5}}&\geq\color{Cerulean}{5\cdot}\color{black}{8.5} & & \color{Cerulean}{Multiply\:both\:sides\:by\:5.} \\ 33.2+x&\geq 42.5 \\ 33.2+x\color{Cerulean}{-33.2}&\geq 42.5\color{Cerulean}{-33.2} \\ x&\geq 9.3 \end{aligned}$

Відповідь:

Вона повинна забити хоча б$9.3$ на п'ятій події.

Ключові виноси

• Нерівності, як правило, мають нескінченно багато рішень. Розв'язки представлені графічно на числовому рядку або з використанням інтервальних позначень або обох.
• Все, крім одного з правил розв'язання лінійних нерівностей, такі ж, як і при розв'язанні лінійних рівнянь. Якщо розділити або помножити нерівність на від'ємне число, зворотне нерівність, щоб отримати еквівалентну нерівність.
• Складні нерівності за участю слова «або» вимагають від нас вирішити кожну нерівність і сформувати об'єднання кожного набору розв'язків. Це ті значення, які вирішують хоча б одну з заданих нерівностей.
• Складні нерівності за участю слова «і» вимагають перетину множин розв'язків для кожної нерівності. Це ті значення, які вирішують обидві або всі задані нерівності.
• Загальні рекомендації щодо вирішення проблем слів стосуються додатків, пов'язаних з нерівностями. Будьте в курсі нового списку ключових слів і фраз, які вказують на математичну установку, що включає нерівності.

Вправа$\PageIndex{4}$ Checking for Solutions

Визначте, чи є дане число розв'язком заданої нерівності.

1. $2x−3<6; x=-1$
2. $-3x+1\leq 0; x=-2$
3. $5x-20>0; x=3$
4. $\frac{1}{2}x+1>−\frac{3}{4}; x=−\frac{1}{4}$
5. $−5<7x+1<9; x=0$
6. $−20≤−3x−5≤−10; x=5$
7. $x<-3 \text{ or }x>3; x=−10$
8. $x<0\text{ or }x≥1; x=\frac{1}{2}$
9. $2x+1<−3\text{ or }2x+1≥5; x=2$
10. $4x−1<−17\text{ or }3x+2≥6; x=1$

Відповідь

1. Так

3. Ні

5. Так

7. Так

9. Так

Вправа$\PageIndex{5}$ Solving Linear Inequalities

Розв'яжіть та графуйте набір рішень. Крім того, представте рішення, встановлене в інтервальних позначеннях.

1. $x+5>1$
2. $x−3<−4$
3. $6x≤24$
4. $4x>−8$
5. $−7x≤14$
6. $−2x+5>9$
7. $7x−3≤25$
8. $12x+7>−53$
9. $−2x+5<-7$
10. $-2x+4\leq 4$
11. $-15x+10>20$
12. $−8x+1≤29$
13. $\frac{1}{7}x−3<1$
14. $\frac{1}{2}x−\frac{1}{3}>\frac{2}{3}$
15. $\frac{5}{3}x+\frac{1}{2}≤\frac{1}{3}$
16. $−\frac{3}{4}x−\frac{1}{2}≥\frac{5}{2}$
17. $−\frac{1}{5}x+\frac{3}{4}<−\frac{1}{5}$
18. $−\frac{2}{3}x+1<-3$
19. $2(-3x+1)<14$
20. $-7(x-2)+1<15$
21. $9x-3(3x+4)>−12$
22. $12x−4(3x+5)≤−2$
23. $5−3(2x−6)≥−1$
24. $9x−(10x−12)<22$
25. $2(x-7)-3(x+3)\leq -3$
26. $5x-3>3x+7$
27. $4(3x−2)≤−2(x+3)+12$
28. $5(x−3)≥15x−(10x+4)$
29. $12x+1>2(6x−3)−5$
30. $3(x−2)+5>2(3x+5)+2$
31. $−4(3x−1)+2x≤2(4x−1)−3$
32. $−2(x−2)+14x<7(2x+1)$

Відповідь

1. $x>−4; (−4, ∞)$

Малюнок$\PageIndex{8}$

3. $x≤4; (−∞, 4]$

Малюнок$\PageIndex{9}$

5. $x≥−2; [−2, ∞)$

Малюнок$\PageIndex{10}$

7. $x≤4; (−∞, 4]$

Малюнок$\PageIndex{11}$

9. $x>6; (6, ∞)$

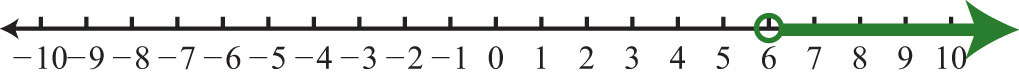
Малюнок$\PageIndex{12}$

11. $x<−\frac{2}{3}; (−∞, −\frac{2}{3})$

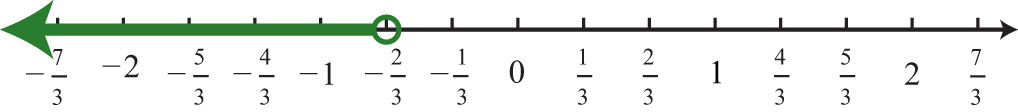
Малюнок$\PageIndex{13}$

13. $x<28; (−∞, 28)$

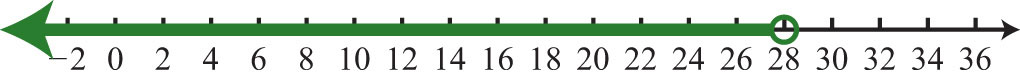
Малюнок$\PageIndex{14}$

15. $x≤−\frac{1}{10}; (−∞, −\frac{1}{10}]$

Малюнок$\PageIndex{15}$

17. $x>\frac{19}{4}; (\frac{19}{4}, ∞)$

Малюнок$\PageIndex{16}$

19. $x>−2; (−2, ∞)$

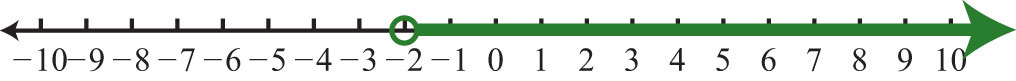
Малюнок$\PageIndex{17}$

21. $∅$

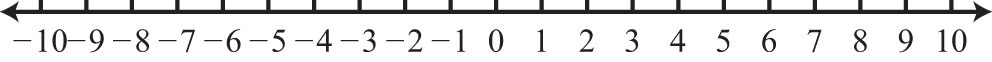
Малюнок$\PageIndex{18}$

23. $x≤4; (−∞, 4]$

Малюнок$\PageIndex{19}$

25. $x≥−20; [−20, ∞)$

Малюнок$\PageIndex{20}$

27. $x≤1; (−∞, 1]$

Малюнок$\PageIndex{21}$

29. $R$

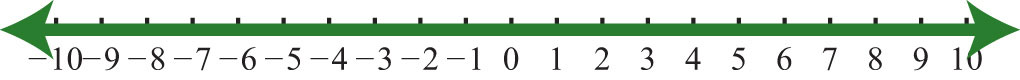
Малюнок$\PageIndex{22}$

31. $x≥\frac{1}{2}; [\frac{1}{2}, ∞)$

Малюнок$\PageIndex{23}$

Вправа$\PageIndex{6}$ Solving Linear Inequalities

Налаштуйте алгебраїчну нерівність, а потім вирішіть її.

1. Сума тричі більше числа і більше$4$ від'ємного$8$.
2. Сума$7$ і трикратного числа менше або дорівнює$1$.
3. Коли з числа віднімається$10$, результат - максимум$12$.
4. Коли$5$ раз віднімається число$6$, результат буде принаймні$26$.
5. Якщо п'ять додати до триразового числа, то в результаті виходить менше двадцяти.
6. Якщо з двох разів віднімається три числа, то результат більше або дорівнює дев'яти.
7. Білл заробляє $$12.00$ за день плюс $$0.25$ за кожну людину, яку він отримує, щоб зареєструватися, щоб проголосувати. Скільки людей він повинен зареєструватися, щоб заробити хоча б $$50.00$ за день?
8. З членство в гольф-клубі вартістю $$100$ на місяць, кожен раунд гольф коштує тільки $$25.00$. Скільки раундів гольф може член грати, якщо він хоче, щоб зберегти свої витрати до $$250$ на місяць щонайбільше?
9. Джо заробив$72, 85$ бали і$75$ на своїх перших трьох іспитах з алгебри. Що він повинен набрати на четвертому іспиті, щоб усереднити хоча б$80$?
10. Моріс заробив$4, 7$, і$9$ вказує$10$ на перші три вікторини. Що він повинен забити на четвертій вікторині, щоб усереднити хоча б$7$?
11. Комп'ютер налаштований на відключення, якщо температура перевищує$40°C$. Дайте еквівалентне твердження, використовуючи градуси за Фаренгейтом. (Підказка:$C=\frac{5}{9}(F−32)$.)
12. Певна марка макіяжу гарантовано не запускається, якщо температура буде менше$35°C$. Дайте еквівалентне твердження, використовуючи градуси за Фаренгейтом.

Відповідь

1. $n>−4$

3. $n≥−2$

5. $n<5$

7. Законопроект повинен реєструвати хоча б$152$ людей.

9. Джо повинен заробити хоча б$88$ на четвертому іспиті.

11. Комп'ютер вимкнеться, коли температура перевищить$104$° F.

Вправа$\PageIndex{7}$ Compound Inequalities

Розв'яжіть та графуйте набір рішень. Крім того, представте рішення, встановлене в інтервальних позначеннях.

1. $−1<x+3<5$
2. $−10≤5x<20$
3. $−2≤4x+6<10$
4. $−10≤3x−1≤−4$
5. $−15<3x−6≤6$
6. $−22<5x+3≤3$
7. $−1≤\frac{1}{2}x−5≤1$
8. $1<8x+5<5$
9. $−\frac{1}{5}≤\frac{2}{3}x−\frac{1}{5}<\frac{4}{5}$
10. $−\frac{1}{2}<\frac{3}{4}x−\frac{2}{3}≤\frac{1}{2}$
11. $−3≤3(x−1)≤3$
12. $−12<6(x−3)≤0$
13. $4<−2(x+3)<6$
14. $−5≤5(−x+1)<15$
15. $−\frac{3}{2}≤\frac{1}{4}(\frac{1}{2}x−1)+\frac{3}{4}<\frac{3}{2}$
16. $−4≤−\frac{1}{3}(3x+12)<4$
17. $−2≤12−2(x−3)≤20$
18. $−5<2(x-1)-3(x+2)<5$
19. $3x\leq -15\text{ or }2x>6$
20. $4x−1<-17\text{ or }3x+2\geq 8$
21. $-2x+1<-1\text{ or }-2x+1>1$
22. $7x+4≤4\text{ or }6x−5≥1$
23. $3x−7<14\text{ or }2x+3>7$
24. $−3x+1<-5\text{ or }-4x-3>−23$
25. $\frac{1}{2}x−2<-1\text{ or }\frac{1}{2}x-2>1$
26. $\frac{1}{3}x+3≥−2\text{ or }\frac{1}{3}x+3≤2$
27. $3x+7≤7\text{ or }−5x+6>6$
28. $−10x−3≤17\text{ or }20x−6>−26$
29. $2x−10<-2\text{ or }-3x+4>−5$
30. $5x+3<4\text{ or }5-10x>4$
31. $3x<18\text{ and }5x>-20$
32. $x+7\leq 5\text{ and } x−3≥−10$
33. $2x−1<5\text{ and }3x-1<10$
34. $5x+2<-13\text{ and }3x+4>13$

Відповідь

1. $−4<x<2; (-4,2)$

Малюнок$\PageIndex{24}$

3. $−2≤x<1; [−2, 1)$

Малюнок$\PageIndex{25}$

5. $-3<x\leq 4; (-3,4]$

Малюнок$\PageIndex{26}$

7. $8≤x≤12; [8, 12]$

Малюнок$\PageIndex{27}$

9. $0≤x<\frac{3}{2}; [0, \frac{3}{2})$

Малюнок$\PageIndex{28}$

11. $0≤x≤2; [0, 2]$

Малюнок$\PageIndex{29}$

13. $-6<x<-5; (-6,-5)$

Малюнок$\PageIndex{30}$

15. $−16≤x<8; [−16, 8)$

Малюнок$\PageIndex{31}$

17. $−1≤x≤10; [−1, 10]$

Малюнок$\PageIndex{32}$

19. $x≤−5\text{ or }x>3; (−∞, −5]∪(3, ∞)$

Малюнок$\PageIndex{33}$

21. $x>1\text{ or }x<0; (−∞, 0)∪(1, ∞)$

Малюнок$\PageIndex{34}$

23. $R$

Малюнок$\PageIndex{35}$

25. $x<2\text{ or }x>6; (−∞, 2)∪(6, ∞)$

Малюнок$\PageIndex{36}$

27. $x≤0; (−∞, 0]$

Малюнок$\PageIndex{37}$

29. $x<4; (−∞, 4)$

Малюнок$\PageIndex{38}$

31. $-4<x<6; (-4,6)$

Малюнок$\PageIndex{39}$

33. $x<3; (−∞, 3)$

Малюнок$\PageIndex{40}$

Вправа$\PageIndex{8}$ Compound Inequalities

Налаштуйте складну нерівність для наступного, а потім вирішуйте.

1. П'ять більше двох разів деяке число знаходиться між$15$ і$25$.
2. Чотири віднімається з трьох разів деяке число між$−4$ і$14$.
3. Клінт бажає заробити B, який принаймні,$80$ але менше, ніж$90$. Який діапазон він повинен набрати на четвертому іспиті, якщо перші три були$65, 75$, і$90$?
4. Певний антифриз ефективний для температурного діапазону від$−35°C$ до$120°C$. Знайти еквівалентний діапазон в градусах Фаренгейта.
5. Середня температура в Лондоні коливається від$23°C$$14°C$ влітку до взимку. Знайти еквівалентний діапазон в градусах Фаренгейта.
6. Якщо основа трикутника вимірює$5$ дюйми, то в якому діапазоні повинна бути висота, щоб площа була між$10$ квадратними дюймами і$20$ квадратними дюймами?
7. Прямокутник має довжину$7$ дюймів. Знайти всі можливі ширини, якщо площа повинна бути не менше$14$ квадратних дюймів і не більше$28$ квадратних дюймів.
8. Прямокутник має ширину$3$ сантиметрів. Знайдіть всі можливі довжини, якщо периметр повинен бути не менше$12$ сантиметрів і максимум$26$ сантиметрів.
9. Периметр квадрата повинен знаходитися між$40$ футами і$200$ стопами. Знайдіть довжину всіх можливих сторін, які задовольняють цій умові.
10. Якщо два рази кут знаходиться між$180$ градусами і$270$ градусами, то які межі початкового кута?
11. Якщо три рази кут між$270$ градусами і$360$ градусами, то які межі початкового кута?

Відповідь

1. $5<n<20$

3. Клінт повинен заробити рахунок в діапазоні від$90$ до$100$.

5. Середня температура в Лондоні коливається від$57.2°F$ до$73.4°F$.

7. Ширина повинна бути не менше$2$ дюймів і не більше$4$ дюймів.

9. Сторони повинні знаходитися між$10$ ступнями і$50$ стопами.

11. Кут знаходиться між$90$ градусами і$120$ градусами.

Вправа$\PageIndex{9}$ Discussion Board Topics

1. Досліджуйте та обговоріть використання множинних позначень з перехрестями та об'єднаннями.
2. Чи можемо ми об'єднати логічне «або» в одне твердження, як ми робимо для логічного «і»?

Відповідь

2. Відповіді можуть відрізнятися