2.2: Спрощення алгебраїчних виразів

Last updated
Save as PDF

Page ID: 58222

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Застосуйте властивість distributive для спрощення алгебраїчного виразу.
Визначте та комбінуйте подібні терміни.

Розподільна власність

Властивості дійсних чисел важливі в нашому вивченні алгебри, оскільки змінна - це просто буква, яка представляє дійсне число. Зокрема, розподільна власність стверджує, що дані будь-які дійсні числа$a, b,$ і$c$,

\[\color{Cerulean}{a}\color{black}{(b+c)=}\color{Cerulean}{a}\color{black}{b+}\color{Cerulean}{a}\color{black}{c}\]

Ця властивість застосовується при спрощенні алгебраїчних виразів. Щоб продемонструвати, як він використовується, спрощуємо двома$2(5−3)$ способами, і спостерігаємо такий же правильний результат.

Звичайно, якщо вміст дужок можна спростити, зробіть це спочатку. З іншого боку, коли вміст дужок не можна спростити, помножте кожен член у дужках на коефіцієнт поза дужками, використовуючи розподільну властивість. Застосування властивості distributive дозволяє множити і прибирати дужки.

Приклад$\PageIndex{1}$

Спростити:

$5(7y+2)$.

Рішення:

$5$Помножте на кожен член у дужках.

$\begin{aligned}\color{Cerulean}{5}\color{black}{(7y+2)}&=\color{Cerulean}{5}\color{black}{\cdot 7y+}\color{Cerulean}{5}\color{black}{\cdot 2} \\ &=35y+10 \end{aligned}$

Відповідь:

$35y+10$

Приклад$\PageIndex{2}$

Спростити:

$−3(2x^{2}+5x+1)$.

Рішення:

$−3$Помножте на кожен з коефіцієнтів членів всередині дужок.

Відповідь:

$-6x^{2}-15x-3$

Приклад$\PageIndex{3}$

Спростити:

$5(−2a+5b)−2c$.

Рішення:

Застосовуйте розподільну властивість, множивши лише терміни, згруповані в дужках на$5$.

$Знімок екрана (749) .png$

Малюнок$\PageIndex{1}$

Відповідь:

$-10a+25b-2c$

Оскільки множення є комутативним, ми також можемо записати розподільну властивість наступним чином:

\[(b+c)a=ba+ca\]

Приклад$\PageIndex{4}$

Спростити:

$(3x−4y+1)⋅3$.

Рішення:

Помножте кожен член в дужках на$3$.

$\begin{aligned} (3x-4y+1)\cdot 3&=3x\color{Cerulean}{\cdot 3}\color{black}{-4y}\color{Cerulean}{\cdot 3}\color{black}{+1}\color{Cerulean}{\cdot 3} \\ &=9x-12y+3 \end{aligned}$

Відповідь:

$9x-12y+3$

Ділення в алгебрі часто вказується за допомогою рядка дробу, а не символом ($÷$). А іноді корисно переписувати вирази, що передбачають поділ як продукти:

$\begin{array}{c}{\color{black}{\frac{x}{\color{Cerulean}{5}}=\frac{1x}{5}=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot x}}} \\{\color{black}{\frac{\color{Cerulean}{3}\color{black}{ab}}{\color{Cerulean}{7}}=\frac{3}{7}\cdot \frac{ab}{1}=\color{Cerulean}{\frac{3}{7}}\color{black}{\cdot ab}}}\\{\frac{x+y}{\color{Cerulean}{3}}=\frac{1}{3}\cdot \frac{(x+y)}{1}=\color{Cerulean}{\frac{1}{3}}\color{black}{\cdot (x+y)}} \end{array}$

Переписування алгебраїчних виразів як продуктів дозволяє застосовувати розподільну властивість.

Приклад$\PageIndex{5}$

Розділити:

\ (\ гідророзриву {25x^ {2} -5x+10} {5}.

Рішення:

Спочатку розглядайте це як$\frac{1}{5}$ раз вираз в чисельнику, а потім розподіліть.

$\begin{aligned} \frac{25x^{2}-5x+10}{\color{Cerulean}{5}}&=\frac{1}{5}\cdot\frac{(25x^{2}-5x+10)}{1} \\ &=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot (25x^{2}-5x+10)} &\color{Cerulean}{Multiply\:each\:term\:by\:\frac{1}{5}.} \\ &=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 25x^{2}-}\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 5x+}\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 10}&\color{Cerulean}{Simplify.} \\ &=5x^{2}-x+2 \end{aligned}$

Альтернативне рішення:

Думайте$5$ як спільний знаменник і розділіть кожен з членів в чисельнику на$5$:

$\begin{aligned} \frac{25x^{2}-5x+10}{5}&=\frac{25x^{2}}{5}-\frac{5x}{5}+\frac{10}{5} \\ &=5x^{2}-x+2 \end{aligned}$

Відповідь:

$5x^{2}-x+2$

Розподіл алгебраїчних виразів ми обговоримо більш детально в міру проходження курсу.

Вправа$\PageIndex{1}$

Спростити:

$\frac{1}{3}(−9x+27y−3)$.

Відповідь: $-3x+9y-1$

Поєднання подібних термінів

Терміни з однаковими змінними частинами називаються як терміни, або подібні терміни. Крім того, постійні терміни вважаються схожими на терміни. Якщо алгебраїчний вираз містить подібні терміни, застосуйте розподільну властивість наступним чином:

$\begin{array}{c}{2\color{Cerulean}{a}\color{black}{+3}\color{Cerulean}{a}\color{black}{=(2+3)}\color{Cerulean}{a}\color{black}{=5}\color{Cerulean}{a}}\\{7\color{Cerulean}{xy}\color{black}{-5}\color{Cerulean}{xy}\color{black}{=(7-5)}\color{Cerulean}{xy}\color{black}{=2}\color{Cerulean}{xy}}\\{10\color{Cerulean}{x^{2}}\color{black}{+4}\color{Cerulean}{x^{2}}\color{black}{-6}\color{Cerulean}{x^{2}}\color{black}{=(10+4-6)}\color{Cerulean}{x^{2}}\color{black}{=8}\color{Cerulean}{x^{2}}} \end{array}$

Іншими словами, якщо змінні частини членів точно такі ж, то ми можемо додати або відняти коефіцієнти, щоб отримати коефіцієнт одного члена з тією ж змінною частиною. Цей процес називається об'єднанням подібних термінів. Наприклад,

$3a^{2}b+2a^{2}b=5a^{2}b$

Зверніть увагу, що змінні фактори та їх показники не змінюються. Поєднання подібних термінів таким чином, щоб вираз не містило інших подібних термінів, називається спрощенням виразу. Скористайтеся цією ідеєю, щоб спростити алгебраїчні вирази з декількома подібними термінами.

Приклад$\PageIndex{6}$

Спростити:

$3a+2b−4a+9b$.

Рішення:

Визначте подібні терміни і об'єднайте їх.

$\begin{aligned} 3a+2b-4a+9b&=3\color{Cerulean}{a}\color{black}{-4}\color{Cerulean}{a}\color{black}{+2}\color{OliveGreen}{b}\color{black}{+9}\color{OliveGreen}{b}&\color{Cerulean}{Commutative\:property\:of\:addition} \\ &=-1a+11b &\color{Cerulean}{Combine\:like\:terms.} \\ &=-a+11b \end{aligned}$

Відповідь:

$-a+11b$

У попередньому прикладі перестановка термінів зазвичай виконується подумки і не відображається в поданні рішення.

Приклад$\PageIndex{7}$

Спростити:

$x^{2}+3x+2+4x^{2}−5x−7$.

Рішення:

Визначте подібні терміни і додайте відповідні коефіцієнти.

$\begin{array}{lc}{\color{Cerulean}{\underline{1x^{2}}}\color{black}{+}\color{OliveGreen}{\underline{\underline{3x}}}\color{black}{+\underline{\underline{\underline{2}}}+}\color{Cerulean}{\underline{4x^{2}}}\color{black}{-}\color{OliveGreen}{\underline{\underline{5x}}}\color{black}{-\underline{\underline{\underline{7}}}}}&{\color{Cerulean}{Identify\:like\:terms.}}\\{=5x^{2}-2x-5}&{\color{Cerulean}{Combine\:like\:terms.}}\end{array}$

Відповідь:

$5x^{2}-2x-5$

Приклад$\PageIndex{8}$

Спростити:

$5x^{2}y−3xy^{2}+4x^{2}y−2xy^{2}$.

Рішення:

Не забудьте залишити змінні фактори та їх показники незмінними в отриманому комбінованому терміні.

$\begin{array}{l}{\underline{5x^{2}y}-\underline{\underline{3xy^{2}}}+\underline{4x^{2}y}-\underline{\underline{2xy^{2}}}}\\{=9x^{2}y-5xy^{2}} \end{array}$

Відповідь:

$9x^{2}y-5xy^{2}$

Приклад$\PageIndex{9}$

Спростити:

$\frac{1}{2}a−\frac{1}{3}b+\frac{3}{4}a+b$.

Щоб скласти дробові коефіцієнти, використовуйте еквівалентні коефіцієнти зі спільними знаменниками для кожного подібного члена.

$\begin{aligned} \frac{1}{2}a-\frac{1}{3}b+\frac{3}{4}a+1b&=\frac{1}{2}a+\frac{3}{4}a-\frac{1}{3}b+1b \\ &=\frac{2}{4}a+\frac{3}{4}a-\frac{1}{3}b+\frac{3}{3}b \\&=\frac{5}{4}a+\frac{2}{3}b \end{aligned}$

Відповідь:

$\frac{5}{4}a+\frac{2}{3}b$

Приклад$\PageIndex{10}$

Спростити:

$−12x(x+y)^{3}+26x(x+y)^{3}$.

Рішення:

Розглянемо змінну частину бути$x(x+y)^{3}$. Тоді цей вираз має два подібних члени з коефіцієнтами$−12$ і$26$.

$\begin{aligned} &-12x(x+y)^{3}+26x(x+y)^{3} &\color{Cerulean}{Add\:the\:coefficients.} \\ &=14x(x+y)^{3} \end{aligned}$

Відповідь:

$14x(x+y)^{3}$

Вправа$\PageIndex{2}$

Спростити:

$−7x+8y−2x−3y$.

Відповідь: $−9x+5y$

Дистрибутивна власність та подібні терміни

При спрощенні нам часто доведеться поєднувати подібні терміни після того, як ми застосуємо розподільну властивість. Цей крок узгоджується з порядком операцій: множення перед додаванням.

Приклад$\PageIndex{11}$

Спростити:

$2(3a−b)$−$7(−2a+3b)$.

Рішення:

Розподіліть,$2$$−7$ а потім комбінуйте подібні терміни.

$Знімок екрана (750) .png$

Малюнок$\PageIndex{2}$

Відповідь:

$20a-23b$

У наведеному вище прикладі важливо зазначити, що ви можете видалити дужки та збирати подібні терміни, тому що ви множите другу кількість на$−7$, а не лише на$7$. Щоб правильно застосувати розподільну властивість, подумайте про це як додавання$−7$ разів заданої кількості,$2(3a−b)+(−7)(−2a+3b)$.

Вправа$\PageIndex{3}$

Спростити:

$−5(2x−3)+7x$.

Відповідь: $-3x+15$

Часто ми будемо стикатися з алгебраїчними виразами на кшталт$+(a+b)$ або$−(a+b)$. Як ми бачили, коефіцієнти насправді мають на увазі бути$+1$ і$−1$, відповідно, і тому розподільна властивість застосовується з використанням$+1$ або$–1$ як коефіцієнт. Помножте кожен член в дужках на такі фактори:

\[+(a+b)=+1(a+b)=(+1)a+(+1)b=a+b\]

\[-(a+b)=-1(a+b)=(-1)a+(-1)b=-a-b\]

Це призводить до двох корисних властивостей,

\[+(a+b)=a+b\]

\[-(a+b)=-a-b\]

Приклад$\PageIndex{12}$

Спростити:

$5x−(−2x^{2}+3x−1)$.

Рішення:

Помножте кожен член в дужках на,$−1$ а потім об'єднайте подібні терміни.

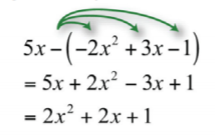$Знімок екрана (751) .png$

Малюнок$\PageIndex{3}$

Відповідь:

$2x^{2}+2x+1$

При розподілі негативного числа всі знаки в дужках будуть змінюватися. Зверніть увагу, що$5x$ в наведеному вище прикладі є окремим терміном; отже, розподільна властивість до нього не відноситься.

Приклад$\PageIndex{13}$

Спростити:

$5−2(x^{2}−4x−3)$.

Рішення:

Порядок операцій вимагає, щоб ми множилися перед відніманням. Тому розподіляйте,$−2$ а потім комбінуйте постійні терміни. Віднімання$5 − 2$ спочатку призводить до неправильного результату, як показано нижче:

$\begin{array}{c|c}{\underline{\color{red}{Incorrect!}}}&{\underline{\color{Cerulean}{Correct!}}}\\{\begin{aligned} &\color{red}{5-2}\color{black}{(x^{2}-4x-3)} \\ &=\color{red}{3}\color{black}{(x^{2}-4x-3)}\\&=3x^{2}-12x-9\quad\color{red}{x} \end{aligned}}&{\begin{aligned}&5\color{Cerulean}{-2}\color{black}{(x^{2}-4x-3)} \\ &=5\color{Cerulean}{-2}\color{black}{x^{2}}\color{Cerulean}{+8}\color{black}{x}\color{Cerulean}{+6} \\ &=-2x^{2}+8x+11\quad\color{Cerulean}{\checkmark} \end{aligned}} \end{array}$

Відповідь:

$-2x^{2}+8x+11$

Примітка

Варто повторити, що необхідно дотримуватися порядку операцій: множити і ділити перед складанням і відніманням!

Вправа$\PageIndex{4}$

Спростити:

$8−3(−x^{2}+2x−7)$.

Відповідь: $3x^{2}-6x+29$

Приклад$\PageIndex{14}$

Відніміть$3x−2$ з подвоєної кількості$−4x^{2}+2x−8$.

Рішення:

Спочатку згрупуйте кожен вираз і розглядайте кожне як кількість:

$(3x-2)\qquad\text{and}\qquad (-4x^{2}+2x-8)$

Далі визначте ключові слова і переведіть їх в математичний вираз.

$Знімок екрана (752) .png$

Малюнок$\PageIndex{4}$

Нарешті, спростіть отриманий вираз.

Відповідь:

$-8x^{2}+x-14$

Ключові винос

Властивості дійсних чисел застосовуються до алгебраїчних виразів, оскільки змінні - це просто уявлення невідомих дійсних чисел.
Поєднуйте подібні терміни або терміни з тією ж змінною частиною, щоб спростити вирази.
Використовувати розподільну властивість при множенні згрупованих алгебраїчних виразів,$a(b+c)=ab+ac$.
Найкраще застосовувати властивість розподілу лише тоді, коли вираз всередині групування повністю спрощено.
Після застосування розподільного властивості усуньте дужки, а потім об'єднайте будь-які подібні терміни.
Завжди використовуйте порядок операцій при спрощенні.

Вправа$\PageIndex{5}$ Distributive Property

Помножити.

$3(3x−2)$
$12(−5y+1)$
$−2(x+1)$
$5(a−b)$
$\frac{5}{8}(8x−16)$
$−\frac{3}{5}(10x−5)$
$(2x+3)⋅2$
$(5x−1)⋅5$
$(−x+7)(−3)$
$(−8x+1)(−2)$
$−(2a−3b)$
$−(x−1)$
$\frac{1}{3}(2x+5)$
$−\frac{3}{4}(y−2)$
$−3(2a+5b−c)$
$−(2y^{2}−5y+7)$
$5(y^{2}−6y−9)$
$−6(5x^{2}+2x−1)$
$7x^{2}−(3x−11)$
$−(2a−3b)+c$
$3(7x^{2}−2x)−3$
$\frac{1}{2}(4a^{2}−6a+4)$
$−\frac{1}{3}(9y^{2}−3y+27)$
$(5x^{2}−7x+9)(−5)$
$6(\frac{1}{3}x^{2}−\frac{1}{6}x+\frac{1}{2})$
$−2(3x^{3}−2x^{2}+x−3)$
$\frac{20x+30y−10z}{10}$
$\frac{−4a+20b−8c}{4}$
$\frac{3x^{2}−9x+81}{−3}$
$\frac{15y^{2}+20y−5}{5}$

Відповідь

1. $9x−6 $

3. $−2x−2 $

5. $5x−10 $

7. $4x+6 $

9. $3x−21 $

11. $−2a+3b$

13. $\frac{2}{3}x+\frac{5}{3}$

15. $−6a−15b+3c$

17. $5y^{2}−30y−45$

19. $7x^{2}−3x+11$

21. $21x^{2}−6x−3$

23. $−3y^{2}+y−9$

25. $2x^{2}−x+3$

27. $2x+3y−z$

29. $−x^{2}+3x−27$

Вправа$\PageIndex{6}$ Distributive Property

Перекладіть наступні пропозиції в алгебраїчні вирази, а потім спростіть.

Спростити два рази вираз$25x^{2}−9$.
Спростити протилежне виразу$6x^{2}+5x−1$.
Спростити продукт$5$ і$x^{2}−8$.
Спростити продукт$−3$ і$−2x^{2}+x−8$.

Відповідь

1. $50x^{2}−18$

3. $5x^{2}−40$

Вправа$\PageIndex{7}$ Combining Like Terms

Спростити.

$2x−3x$
$−2a+5a−12a$
$10y−30−15y$
$\frac{1}{3}x+\frac{5}{12}x$
$−\frac{1}{4}x+\frac{4}{5}+\frac{3}{8}x$
$2x−4x+7x−x$
$−3y−2y+10y−4y$
$5x−7x+8y+2y$
$−8α+2β−5α−6β$
$−6α+7β−2α+β$
$3x+5−2y+7−5x+3y$
$–y+8x−3+14x+1−y$
$4xy−6+2xy+8$
$−12ab−3+4ab−20$
$\frac{1}{3}x−\frac{2}{5}y+\frac{2}{3}x−\frac{3}{5}y$
$\frac{3}{8}a−\frac{2}{7}b−\frac{1}{4}a+\frac{3}{14}b$
$−4x^{2}−3xy+7+4x^{2}−5xy−3$
$x^{2}+y^{2}−2xy−x^{2}+5xy−y^{2}$
$x^{2}−y^{2}+2x^{2}−3y$
$\frac{1}{2}x^{2}−\frac{2}{3}y^{2}−\frac{1}{8}x^{2}+\frac{1}{5}y^{2}$
$\frac{3}{16}a^{2}−\frac{4}{5}+\frac{1}{4}a^{2}−\frac{1}{4}$
$\frac{1}{5}y^{2}−\frac{3}{4}+\frac{7}{10}y^{2}−\frac{1}{2}$
$6x^{2}y−3xy^{2}+2x^{2}y−5xy^{2}$
$12x^{2}y^{2}+3xy−13x^{2}y^{2}+10xy$
$−ab^{2}+a^{2}b−2ab^{2}+5a^{2}b$
$m^{2}n^{2}−mn+mn−3m^{2}n+4m^{2}n^{2}$
$2(x+y)^{2}+3(x+y)^{2}$
$\frac{1}{5}(x+2)^{3}−\frac{2}{3}(x+2)^{3}$
$−3x(x^{2}−1)+5x(x^{2}−1)$
$5(x−3)−8(x−3)$
$−14(2x+7)+6(2x+7)$
$4xy(x+2)^{2}−9xy(x+2)^{2}+xy(x+2)^{2}$

Відповідь

1. $−x$

3. $−5y−30$

5. $\frac{1}{8}x+\frac{4}{5}$

7. $y$

9. $−13α−4β$

11. $−2x+y+12$

13. $6xy+2$

15. $x−y$

17. $−8xy+4$

19. $3x^{2}−y^{2}−3y$

21. $\frac{7}{16}a^{2}−\frac{21}{20}$

23. $8x^{2}y−8xy^{2}$

25. $6a^{2}b−3ab^{2}$

27. $5(x+y)^{2}$

29. $2x(x^{2}−1)$

31. $−8(2x+7)$

Вправа$\PageIndex{8}$ Mixed Practice

Спростити.

$5(2x−3)+7$
$−2(4y+2)−3y$
$5x−2(4x−5)$
$3−(2x+7)$
$2x−(3x−4y−1)$
$(10y−8)−(40x+20y−7)$
$\frac{1}{2}y−\frac{3}{4}x−(\frac{2}{3}y−\frac{1}{5}x)$
$\frac{1}{5}a−\frac{3}{4}b+\frac{3}{15}a−\frac{1}{2}b$
$\frac{2}{3}(x−y)+x−2y$
$−\frac{1}{3}(6x−1)+\frac{1}{2}(4y−1)−(−2x+2y−\frac{1}{6})$
$(2x^{2}−7x+1)+(x^{2}+7x−5)$
$6(−2x^{2}+3x−1)+10x^{2}−5x$
$−(x^{2}−3x+8)+x^{2}−12$
$2(3a−4b)+4(−2a+3b)$
$−7(10x−7y)−6(8x+4y)$
$10(6x−9)−(80x−35)$
$10−5(x^{2}−3x−1)$
$4+6(y^{2}−9)$
$\frac{3}{4}x−(\frac{1}{2}x^{2}+\frac{2}{3}x−\frac{7}{5})$
$−\frac{7}{3}x^{2}+(−\frac{1}{6}x^{2}+7x−1)$
$(2y^{2}−3y+1)−(5y^{2}+10y−7)$
$(−10a^{2}−b^{2}+c)+(12a^{2}+b^{2}−4c)$
$−4(2x^{2}+3x−2)+5(x^{2}−4x−1)$
$2(3x^{2}−7x+1)−3(x^{2}+5x−1)$
$x^{2}y+3xy^{2}−(2x^{2}y−xy^{2})$
$3(x^{2}y^{2}−12xy)−(7x^{2}y^{2}−20xy+18)$
$3−5(ab−3)+2(ba−4)$
$−9−2(xy+7)−(yx−1)$
$−5(4α−2β+1)+10(α−3β+2)$
$\frac{1}{2}(100α^{2}−50αβ+2β^{2})−\frac{1}{5}(50α^{2}+10αβ−5β^{2})$

Відповідь

1. $10x−8$

3. $−3x+10$

5. $−x+4y+1$

7. $−\frac{11}{20}x−\frac{1}{6}y$

9. $\frac{5}{3}x−\frac{8}{3}y$

11. $3x^{2}−4$

13. $3x−20$

15. $−118x+25y$

17. $−5x^{2}+15x+15$

19. $−\frac{1}{2}x^{2}+\frac{1}{12}x+\frac{7}{5}$

21. $−3y^{2}−13y+8$

23. $−3x^{2}−32x+3$

25. $−x^{2}y+4xy^{2}$

27. $−3ab+10$

29. $−10α−20β+15$

Вправа$\PageIndex{9}$ Mixed Practice

Перекладіть наступні пропозиції в алгебраїчні вирази, а потім спростіть.

У чому різниця$3x−4$ і$−2x+5$?
Відняти$2x−3$ від$5x+7$.
Відніміть$4x+3$ з подвоєної кількості$x−2$.
Відніміть$−x+8$ з тричі кількість$10x−9$.

Відповідь

1. $5x-9$

3. $-2x-7$

Вправа$\PageIndex{10}$ Discussion Board Topics

Чи потрібно розподільне майно для поділу,$(a+b)÷c$? Поясніть.
Чи потрібна окрема розподільна властивість на три терміни,$a(b+c+d)$? Поясніть.
Поясніть, як відняти один вираз від іншого. Наведіть кілька прикладів і продемонструйте важливість того порядку, в якому виконується віднімання.
З огляду на алгебраїчний вираз$8−5(3x+4)$, поясніть, чому віднімання не$8−5$ є першим кроком.
Чи можете ви застосувати розподільну властивість до виразу$5(abc)$? Поясніть, чому чи чому ні, і наведіть кілька прикладів.
Як ви можете перевірити, чи правильно ви спростили вираз? Наведемо кілька прикладів.

Відповідь

1. Відповіді можуть відрізнятися

3. Відповіді можуть відрізнятися

5. Відповіді можуть відрізнятися