1.4: Алгебраїчні вирази та формули

Last updated
Save as PDF

Page ID: 58270

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте частини алгебраїчного виразу.
Застосовують розподільну властивість.
Оцінити алгебраїчні вирази.
Використовуйте формули, які моделюють загальні програми.

Алгебраїчні вирази та розподільна властивість

В алгебрі літери, звані змінними, використовуються для представлення чисел. Комбінації змінних і чисел поряд з математичними операціями утворюють алгебраїчні вирази ⁸⁷, або просто вирази. Нижче наведено кілька прикладів виразів з однією змінною$x$:

Таблиця$\PageIndex{1}$
$2x+3$	$x^{2}−9$	$\frac{1}{x}+\frac{x}{x+2}$	$3\sqrt{x}+x$

Терміни ⁸⁸ в алгебраїчному виразі відокремлені операторами додавання, а множники ⁸⁹ розділені операторами множення. Числовий коефіцієнт терміна називається коефіцієнтом ⁹⁰. Наприклад, алгебраїчний вираз$x^{2} y^{2} + 6xy − 3$ можна розглядати як$x^{2} y^{2} + 6xy + (−3)$ і має три терміни. Перший член представляє величину$x^{2} y^{2}$,$1x^{2} y^{2} = 1 ⋅ x ⋅ x ⋅ y ⋅ y$ де$1$ коефіцієнт, а x і y - змінні. Всі змінні фактори з їх показниками утворюють змінну частину члена ⁹¹. Якщо термін пишеться без змінного коефіцієнта, то його називають постійним терміном ⁹². Розглянемо складові$x^{2} y^{2} + 6xy − 3$,

Таблиця$\PageIndex{2}$
*Терміни*	*Коефіцієнт*	*Змінна частина*
$x^{2}y^{2}$	$1$	$x^{2}y^{2}$
$6xy$	$6$	$xy$
$−3$	$−3$

Третій член в цьому виразі$−3$, називається постійним терміном, оскільки він пишеться без змінного множника. Хоча змінна представляє невідому величину і може змінюватися, постійний термін не змінюється.

Приклад$\PageIndex{1}$:

Перерахуйте всі коефіцієнти і змінні частини кожного члена:$10a^{2}−5ab−b^{2}$.

Рішення

Третій термін ми хочемо думати в цьому прикладі$−b^{2}$ як$−1b^{2}$.

Таблиця$\PageIndex{3}$
*Терміни*	*Коефіцієнт*	*Змінна частина*
$10a^{2}$	$10$	$a^{2}$
$−5ab$	$−5$	$ab$
$−b^{2}$	$−1$	$b^{2}$

Відповідь: Коефіцієнти:$\{−5, −1, 10\}$; Змінні частини:$\{a^{2}, ab, b^{2}\}$

У нашому вивченні алгебри ми зіткнемося з найрізноманітнішими алгебраїчними виразами. Як правило, вирази використовують дві найпоширеніші змінні,$x$ і$y$. Однак вирази можуть використовувати будь-яку букву (або символ) для змінної, навіть грецькі літери, такі як alpha ($\alpha$) та beta ($\beta$). Деякі літери та символи зарезервовані для констант, таких як$π ≈ 3.14159$ і$e ≈ 2.71828$. Оскільки існує лише обмежена кількість букв, ви також будете використовувати індекси, для$x_{1} , x_{2} , x_{3} , x_{4} , …,$ позначення різних змінних.

Властивості дійсних чисел важливі в нашому вивченні алгебри, оскільки змінна - це просто буква, яка представляє дійсне число. Зокрема, розподільна властивість ⁹³ стверджує, що якщо дані будь-які дійсні числа$a, b$ і$c$, то,

$\color{Cerulean}{a}$$ ( b + c ) = \color{Cerulean}{a}$$b + \color{Cerulean}{a}$$c$

Ця властивість є такою, яку ми застосовуємо часто при спрощенні алгебраїчних виразів. Щоб продемонструвати, як він буде використовуватися, спрощуємо двома$2(5 − 3)$ способами, і спостерігаємо такий же правильний результат.

Таблиця$\PageIndex{4}$
*Спочатку робоча дужка.*	*Використання розподільного властивості.*
$ 2(\color{OliveGreen}{5−3}$$)=2(2)$ $=4$	$ 2(5−3)=$$\color{Cerulean}{2}$$⋅5−\color{Cerulean}{2}$$⋅3$ $=10−6$ $=4$

Звичайно, якщо вміст дужок можна спростити, ми повинні зробити це спочатку. З іншого боку, коли вміст дужок не можна спростити далі, ми множимо кожен член всередині нього на коефіцієнт поза ним, використовуючи розподільну властивість. Застосування властивості distributive дозволяє нам множити і прибирати дужки.

Приклад$\PageIndex{2}$:

Спростити:$5(−2a+5b)−2c$.

Рішення

Множимо лише ті терміни, згруповані в дужках, для яких ми застосовуємо розподільну властивість.

$=\color{Cerulean}{5}$$⋅(−2a)+\color{Cerulean}{5}$$⋅5b−2c$

$=−10a+25b−2c$

Відповідь:$−10a+25b−2c$

Нагадаємо, що множення є комутативним, і тому ми можемо записати розподільну властивість наступним чином,$(b + c) a = ba + ca$.

Приклад$\PageIndex{3}$:

Спростити:$(3x−4y+1)⋅3$.

Рішення

Помножте всі члени в дужках на$3$.

$(3x−4y+1)⋅3=3x\color{Cerulean}{⋅3}$$−4y\color{Cerulean}{⋅3}$$+1\color{Cerulean}{⋅3}$

$=9x−12y+3$

Відповідь:$9x−12y+3$

Терміни, змінні частини яких мають однакові змінні з однаковими показниками, називаються як терміни ⁹⁴, або подібні терміни ⁹⁵. Крім того, постійні терміни вважаються схожими на терміни. Якщо алгебраїчний вираз містить подібні терміни, застосуйте розподільну властивість наступним чином:

$5 \color{Cerulean}{x}$$ + 7 \color{Cerulean}{x}$$ = ( 5 + 7 ) \color{Cerulean}{x}$$ = 12 \color{Cerulean}{x}$

$4 \color{Cerulean}{x ^ { 2 }}$$ + 5 \color{Cerulean}{x ^ { 2 }}$$ - 7 \color{Cerulean}{x ^ { 2 }}$$ = ( 4 + 5 - 7 ) \color{Cerulean}{x ^ { 2 }}$$ = 2 \color{Cerulean}{x ^ { 2 }}$

Іншими словами, якщо змінні частини членів абсолютно однакові, то ми можемо скласти або відняти коефіцієнти, щоб отримати коефіцієнт одного члена з тією ж змінною частиною. Цей процес називається об'єднанням подібних термінів ⁹⁶. Наприклад,

$12 x ^ { 2 } y ^ { 3 } + 3 x ^ { 2 } y ^ { 3 } = 15 x ^ { 2 } y ^ { 3 }$

Зверніть увагу, що змінні фактори та їх показники не змінюються. Поєднання подібних термінів таким чином, щоб вираз не містило інших подібних термінів, називається спрощенням виразу ⁹⁷. Скористайтеся цією ідеєю, щоб спростити алгебраїчні вирази з декількома подібними термінами.

Приклад$\PageIndex{4}$:

Спростити:

$x ^ { 2 } - 10 x + 8 + 5 x ^ { 2 } - 6 x - 1$.

Рішення

Визначте подібні терміни і додайте відповідні коефіцієнти.

$\color{Cerulean}{\underline{1x^{2}}}$$ - \color{OliveGreen}{\underline{\underline{10x}}}$$ + \underline{\underline{\underline{8}}} + \color{Cerulean}{\underline{5 x ^ { 2 }}}$$ -\color{OliveGreen}{\underline{\underline{6x}}}$$ - \underline{\underline{\underline{1}}}$$\color{Cerulean}{Combine\: like\: terms.}$

$= 6 x ^ { 2 } - 16 x + 7$

Відповідь:$6 x ^ { 2 } - 16 x + 7$

Приклад$\PageIndex{5}$:

Спростити:$a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right)$.

Рішення

Розподіліть,$−2$ а потім комбінуйте подібні терміни.

$\begin{aligned} a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right) & = a ^ { 2 } b ^ { 2 } - a b - 4 a ^ { 2 } b ^ { 2 } + 10 a b - 2 \\ & = - 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2 \end{aligned}$

Відповідь:$- 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2$

Оцінювання алгебраїчних виразів

Алгебраїчний вираз можна розглядати як узагальнення окремих арифметичних операцій. Виконання цих операцій після підстановки заданих значень для змінних називається оцінкою ⁹⁸. В алгебрі змінна являє собою невідоме значення. Однак якщо проблема спеціально привласнює значення змінній, то ви можете замінити цю букву заданою цифрою і оцінити, використовуючи порядок операцій.

Приклад$\PageIndex{6}$:

Оцініть:

$5x − 2$де$x =\frac{2}{3}$
$y^{2} − y − 6$де$y = −4$

Рішення

Щоб уникнути поширених помилок, найкраще спочатку замінити всі змінні дужками, а потім замінити або замінити ⁹⁹ відповідне задане значення.

а.

$\begin{aligned} 5 x - 2 & = 5 (\:\: ) - 2 \\ & = 5 \left(\color{OliveGreen}{ \frac { 2 } { 3 }} \right) - 2 \\ & = \frac { 10 } { 3 } - \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 3 } { 3 }} \\ & = \frac { 10 - 6 } { 3 } \\ & = \frac { 4 } { 3 } \end{aligned}$

б.

$y ^ { 2 } - y - 6 = (\:\: ) ^ { 2 } - (\:\: ) - 6$

$= ( \color{OliveGreen}{- 4}$$ ) ^ { 2 } - ( \color{OliveGreen}{- 4}$$ ) - 6$

$\begin{array} { l } { = 16 + 4 - 6 } \\ { = 14 } \end{array}$

Відповідь:

а.$\frac{4}{3}$

б.$14$

Часто алгебраїчні вирази будуть включати більше однієї змінної.

Приклад$\PageIndex{7}$:

Оцініть$a ^ { 3 } - 8 b ^ { 3 }$, де$a = −1$ і$b = \frac{1}{2}$.

Рішення

Після підстановки у відповідних значеннях ми повинні подбати про спрощення, використовуючи правильний порядок операцій.

$a ^ { 3 } - 8 b ^ { 3 } = (\:\: ) ^ { 3 } - 8 (\:\: ) ^ { 3 } \color{Cerulean}{Replace\: variables\: with\: parentheses.}$

$= ( \color{OliveGreen}{- 1}$$ )^{3} -8(\color{OliveGreen}{\frac{1}{2}}$$)^{3} \color{Cerulean}{Substitute\: in\: the\: appropriate\: values.}$

$= - 1 - 8 \left( \frac { 1 } { 8 } \right) \color{Cerulean}{Simplify.}$

$\begin{array} { l } { = - 1 - 1 } \\ { = - 2 } \end{array}$

Відповідь:$-2$

Приклад$\PageIndex{8}$:

Оцініть$\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 }$, де$x = −\frac{3}{2}$ і$y = −3$.

Рішення

$\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 } = \frac { (\:\: ) ^ { 2 } - ( \:\:) ^ { 2 } } { 2 ( \:\:) - 1 }$

$= \frac { \left( \color{OliveGreen}{- \frac { 3 } { 2 }} \right) ^ { 2 } - ( \color{OliveGreen}{- 3} \color{Black}{) ^ { 2 } }} { 2 \left( - \color{OliveGreen}{\frac { 3 } { 2 }} \right) - 1 }$

$= \frac { \frac { 9 } { 4 } - 9 } { - 3 - 1 }$

На даний момент ми маємо складний дріб. Спростити чисельник, а потім помножити на зворотний знаменника.

$\begin{aligned} & = \frac { \frac { 9 } { 4 } - \frac { 9 } { 1 } \cdot \color{Cerulean}{\frac { 4 } { 4 } }} { - 4 } \\ & = \frac { \frac { - 27 } { 4 } } { { \frac { - 4 } { 1 } } } \\ & = \frac { - 27 } { 4 } \left( - \frac { 1 } { 4 } \right) \\ & = \frac { 27 } { 16 } \end{aligned}$

Відповідь:$\frac { 27 } { 16 }$

Відповідь на попередній приклад можна записати у вигляді змішаного числа,$\frac { 27 } { 16 } = 1 \frac { 11 } { 16 }$. Якщо початкова задача не містить мішаних чисел або не є відповіддю на реальну програму, розв'язки будуть виражені як зменшені неправильні дроби.

Приклад$\PageIndex{9}$:

Оцініть$\sqrt { b ^ { 2 } - 4 a c }$ де$a = −1, b = −7$, і$c = \frac{1}{4}$.

Рішення

Підставляємо відповідні значення, а потім спрощуємо.

$\sqrt { b ^ { 2 } - 4 a c } = \sqrt { ( \:\: ) ^ { 2 } - 4 ( \:\: ) \:\:(\:\:) }$

$ = \sqrt { ( \color{OliveGreen}{- 7}\color{Black}{ ) ^ { 2 } - 4 (}\color{OliveGreen}{ - 1}\color{Black}{ ) (}\color{OliveGreen}{ \frac { 1 } { 4 }}\color{Black}{)} } $

$\begin{aligned} & =\sqrt { 49 + 4(\frac{1}{4}) } \\ & = \sqrt { 49 + 1 } \\ & =\sqrt{50} \\& = \sqrt { 25 \cdot 2 } \\ & = 5 \sqrt { 2 } \end{aligned}$

Вирівняні:$5 \sqrt { 2 }$

Вправа$\PageIndex{1}$

Оцініть$\frac { \sqrt { 3 \pi V h } } { \pi h }$, де$V = 25\pi$ і$h = 3$.

Відповідь

$5$

www.youtube.com/В/Y4rcmCethu4

Використання формул

Основна відмінність алгебри від арифметики полягає в організованому використанні змінних. Ця ідея призводить до багаторазових формул ¹⁰⁰, які є математичними моделями, що використовують алгебраїчні вирази для опису поширених додатків. Наприклад, обсяг правого круглого конуса залежить від його радіуса$r$ і висоти$h$ і моделюється за формулою:

$V = \frac { 1 } { 3 } \pi r ^ { 2 } h$

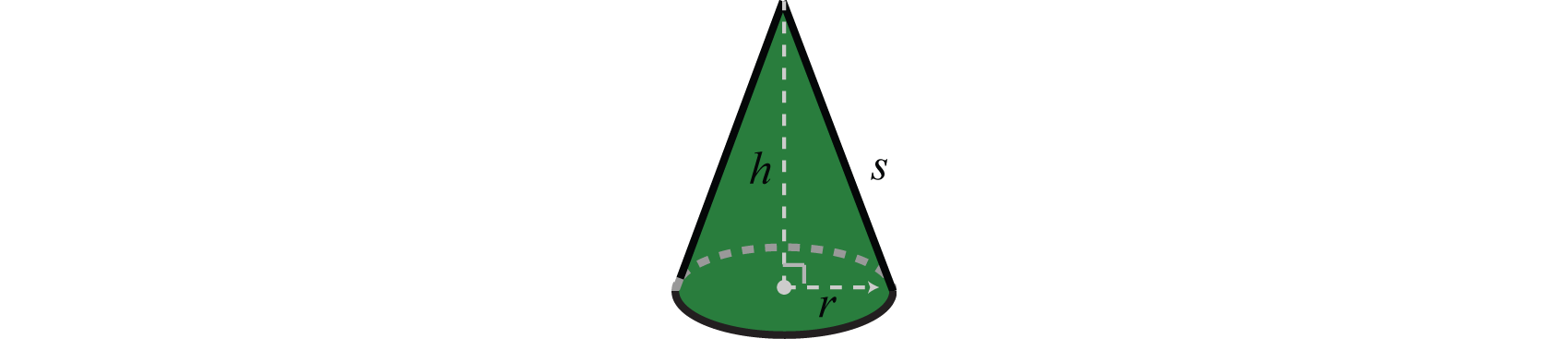
У цьому рівнянні змінні і константи використовуються для опису зв'язку між об'ємом і довжиною підстави і висотою. Якщо радіус підстави вимірює$3$ метри, а висота вимірює$5$ метри, то обсяг можна розрахувати за формулою наступним чином:

$\begin{aligned} V & = \frac { 1 } { 3 } \pi r ^ { 2 } h \\ & = \frac { 1 } { 3 } \pi ( 3 m ) ^ { 2 } ( 5 m ) \\ & = \frac { 1 } {\bcancel {3}} \pi \cdot \stackrel{\color{Cerulean}{3}}{\bcancel{9}} \cdot 5 m ^ { 3 } \\ & = 15 \pi \mathrm { m } ^ { 3 } \end{aligned}$

Використовуючи$π ≈ 3.14$, можна наблизити обсяг:$V ≈ 15 (3.14) = 47.1$ кубічні метри.

Далі наведено список формул, що описують площу і периметр спільних плоских фігур. Буква Р представляє периметр і вимірюється в лінійних одиницях. Буква А позначає площу і вимірюється в квадратних одиницях.

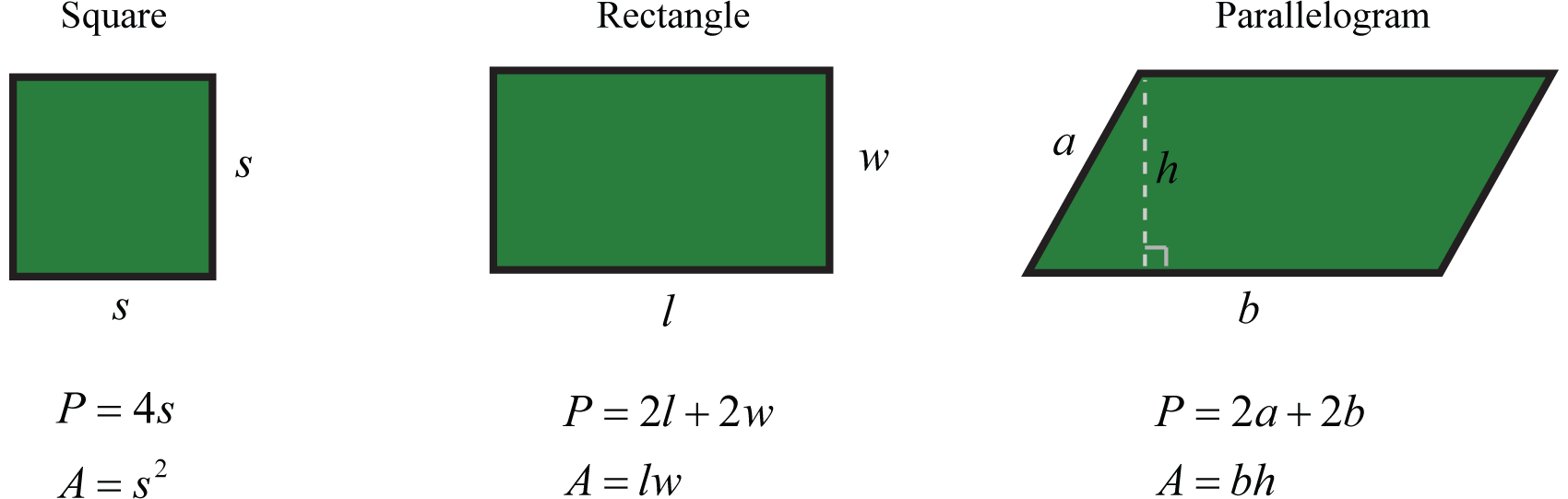
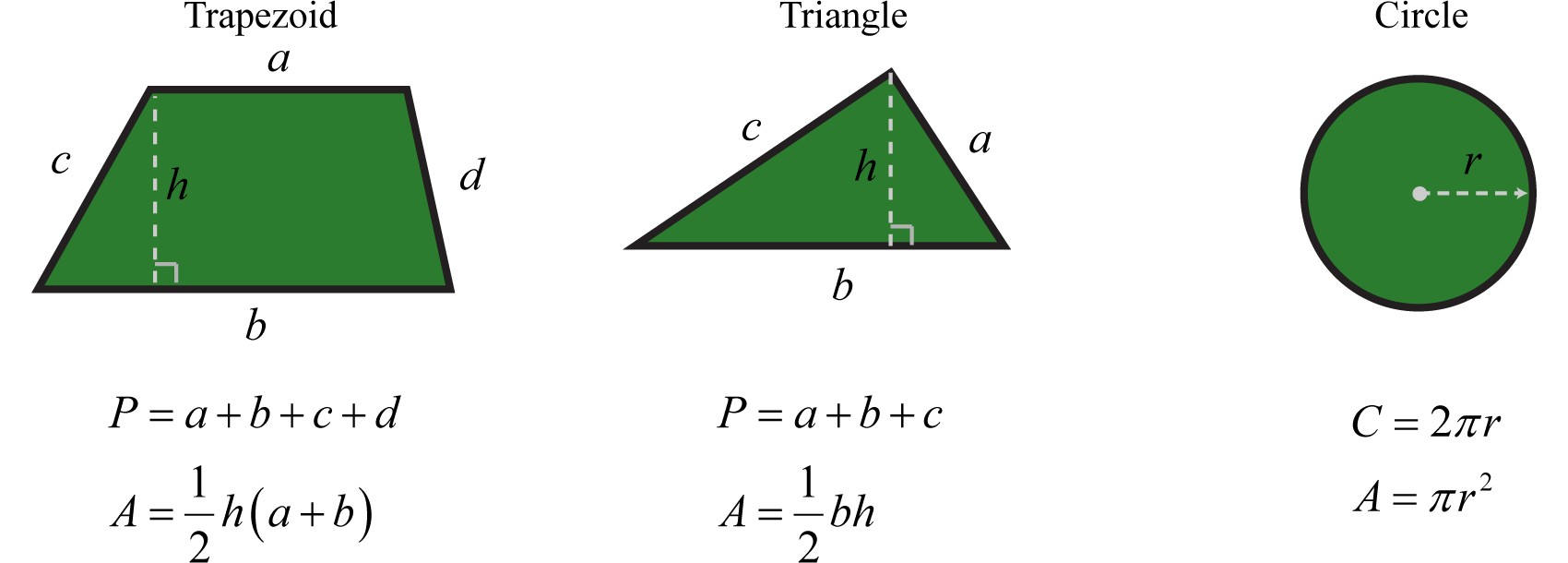
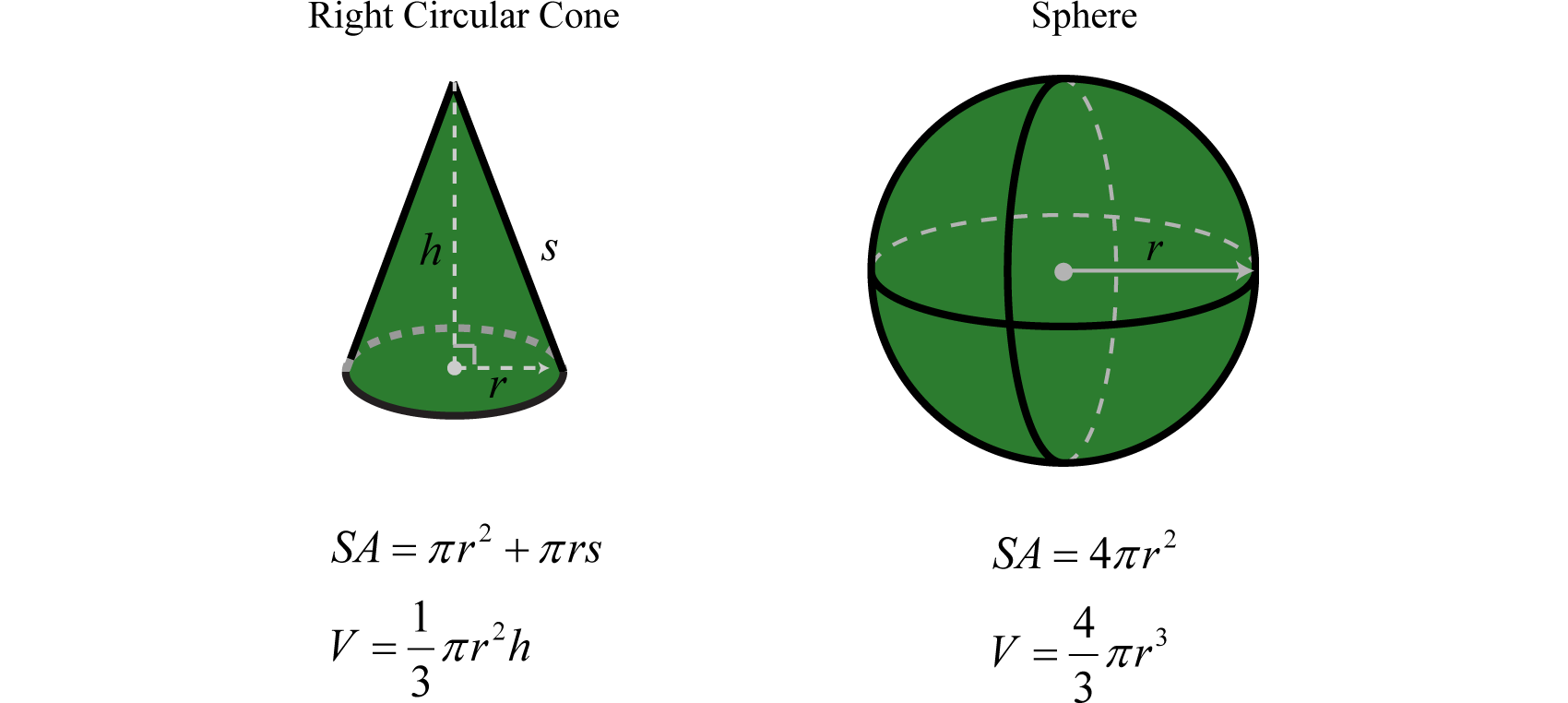
Далі наведено список формул, що описують площу поверхні і обсяг загальних фігур. Тут SA представляє площу поверхні і вимірюється в квадратних одиницях. Буква V позначає обсяг і вимірюється в кубічних одиницях.

Приклад$\PageIndex{10}$:

Діаметр сферичної кулі -$10$ дюйми. Визначте обсяг, округлений до найближчої сотої.

Рішення

Формула для обсягу сфери така

$V = \frac { 4 } { 3 } \pi r ^ { 3 }$

Ця формула дає обсяг через радіус,$r$. Тому ділимо діаметр на,$2$ а потім підставляємо в формулу. Ось$r = \frac{10}{2} = 5$ дюймів і у нас є

$\begin{aligned} V & = \frac { 4 } { 3 } \pi r ^ { 3 } \\ & = \frac { 4 } { 3 } \pi ( 5 \mathrm { in } ) ^ { 3 } \\ & = \frac { 4 } { 3 } \pi \cdot 125 \mathrm { in } ^ { 3 } \\ & = \frac { 500 \pi } { 3 } \mathrm { in } ^ { 3 } \approx 523.60 \mathrm { in } ^ { 3 } \end{aligned}$

Відповідь: Обсяг повітряної кулі становить приблизно$523.60$ кубічні дюйми.

Формули можна знайти в безлічі предметів. Наприклад, рівномірний рух ¹⁰¹ моделюється за формулою$D = rt$, яка виражає відстань$D$, в перерахунку на середню швидкість, або швидкість,$r$ і час, пройдений з цією швидкістю$t$. Ця формула використовується часто і читається: «Відстань дорівнює швидкості рази часу».$D = rt$

Приклад$\PageIndex{11}$:

Дорожня поїздка Джима зайняла$2\:\frac{1}{2}$ години із середньою швидкістю$66$ миль на годину. Як далеко він подорожував?

Рішення

Підставте відповідні значення в формулу, а потім спростіть.

$\begin{aligned} D & = r \cdot t \\ & = ( \color{Cerulean}{66 \frac { \mathrm { mi } } { \mathrm { hr } }}\color{Black}{ ) \cdot (}\color{Cerulean}{ 2 \frac { 1 } { 2 } \mathrm { hr }}\color{Black}{)} \\ & = \frac { 66 } { 1 } \cdot \frac { 5 } { 2 } \mathrm { mi } \\ & = 33 \cdot 5 \mathrm { mi } \\ & = 165 \mathrm { mi } \end{aligned}$

Відповідь: Джим пройшов$165$ милі.

Простий відсоток ¹⁰²$I$ дається за формулою$I = prt$, де$p$ представляє основну суму, вкладену за річною процентною ставкою$r$ за$t$ роки.

Приклад$\PageIndex{12}$:

Розрахуйте прості відсотки, зароблені на$2$ -річну$$1,250$ інвестицію за річною процентною ставкою$3\:\frac{3}{4} %$.

Рішення

$3\:\frac{3}{4}%$Перетворіть в десяткове число, перш ніж використовувати його у формулі.

$r = 3 \frac { 3 } { 4 } \% = 3.75 \% = 0.0375$

Скористайтеся цим і тим, що$p = $1,250$ і$t = 2$ роками для розрахунку простих відсотків.

$\begin{aligned} I & = p r t \\ & = ( \color{Cerulean}{1,250}\color{Black}{ ) (}\color{Cerulean}{ 0.0375}\color{Black}{ ) (}\color{Cerulean}{ 2}\color{Black}{ )} \\ & = 93.75 \end{aligned}$

Відповідь: Простий зароблений відсоток є$$93.75$.

Ключові винос

Подумайте про алгебраїчні вирази як узагальнення загальних арифметичних операцій, які утворюються шляхом об'єднання чисел, змінних та математичних операцій.
Дистрибутивне властивість$a (b + c) = ab + ac$, використовується при множенні згрупованих алгебраїчних виразів. Застосування властивості distributive дозволяє прибрати дужки.
Поєднуйте подібні терміни, або терміни, змінні частини яких мають однакові змінні з однаковими показниками, шляхом додавання або віднімання коефіцієнтів, щоб отримати коефіцієнт одного члена з тією ж змінною частиною. Пам'ятайте, що змінні фактори та їх показники не змінюються.
Щоб уникнути поширених помилок при оцінці, найкраще замінити всі змінні дужками, а потім підставити відповідні значення.
Використання алгебраїчних виразів дозволяє нам створювати корисні та багаторазові формули, які моделюють загальні програми.

Вправа$\PageIndex{2}$

Перерахуйте всі коефіцієнти і змінні частини кожного члена.

$−5x^{2} + x − 1$
$y^{2} − 9y + 3$
$5x^{2} − 3xy + y^{2}$
$a^{2}b^{2} + 2ab − 4$
$x^{2}y + xy^{2} − 3xy + 9$
$x^{4} − x^{3} + x^{2} − x + 2$

Відповідь

1. Коефіцієнти:$\{−5, 1, −1\}$; змінні частини:$\{x^{2} , x\}$

3. Коефіцієнти:$\{5, −3, 1\}$; змінні частини:$\{x^{2} , xy, y^{2} \}$

5. Коефіцієнти:$\{1, −3, 9\}$; змінні частини:$\{x^{2}y, xy^{2} , xy\}$

Вправа$\PageIndex{3}$

Помножити.

$5 (3x − 5) $
$3 (4x − 1) $
$−2 (2x^{2} − 5x + 1) $
$−5 (6x^{2} − 3x − 1)$
$\frac{2}{3} (9y^{2} + 12y − 3)$
$−\frac{3}{4} (8y^{2} + 20y + 4)$
$12(\frac{1}{3} a^{2} − \frac{5}{6} a + \frac{7}{12} )$
$−9 (\frac{1}{9} a^{2} − \frac{5}{3} a + 1 )$
$9 (a^{2} − 2b^{2} )$
$−5 (3x^{2} − y^{2} )$
$(5a^{2} − 3ab + b^{2} ) ⋅ 6$
$(a^{2}b^{2} − 9ab − 3) ⋅ 7$
$− (5x^{2} − xy + y^{2} )$
$− (x^{2}y^{2} − 6xy − 1)$

Відповідь

1. $15x − 25$

3. $−4x^{2} + 10x − 2$

5. $6y^{2} + 8y − 2$

7. $4a^{2} − 10a + 7$

9. $9a^{2} − 18b^{2}$

11. $30a^{2} − 18ab + 6b^{2}$

13. $−5x^{2} + xy − y^{2}$

Вправа$\PageIndex{4}$

Поєднуйте подібні терміни.

$18x − 5x + 3x$
$30x − 50x + 10x$
$3y − 4 + 2y − 12$
$12y + 7 − 15y − 6$
$2x^{2} − 3x + 2 + 5x^{2} − 6x + 1$
$9x^{2} + 7x − 5 − 10x^{2} − 8x + 6$
$\frac{3}{5} a^{2} − \frac{1}{2} + \frac{1}{3} a^{2} + \frac{4}{5}$
$\frac{1}{6} a^{2} + \frac{2}{3} − \frac{4}{3} a^{2} − \frac{1}{9}$
$\frac{1}{2} y^{2} + \frac{2}{3} y − 3 + \frac{3}{5} y^{2} + \frac{1}{3} y − \frac{7}{3}$
$\frac{5}{6} x^{2} + \frac{1}{8} x − 1 − \frac{1}{2} x^{2} + \frac{3}{4} x − \frac{4}{5}$
$a^{2}b^{2} + 5ab − 2 + 7a^{2}b^{2} − 6ab + 12$
$a^{2} − 12ab + 4b^{2} − 6a^{2} + 10ab − 5b^{2}$
$3x^{2}y + 12xy − 5xy^{2} + 5xy − 8x^{2}y + 2xy^{2}$
$10x^{2}y + 2xy − 4xy^{2} + 2x^{2}y − 8xy + 5xy^{2}$
$7m^{2}n − 9mn + mn^{2} − 6m^{2}n + mn − 2mn^{2}$
$m^{2}n − 5mn + 5mn^{2} − 3m^{2}n + 5mn + 2mn^{2}$
$x^{2n} − 3x^{n} + 5 + 2x^{2n} − 4x^{n} − 3$
$5y^{2n} − 3y^{n} + 1 − 3y^{2n} − 2y^{n} − 1$

Відповідь

1. $16x$

3. $5y − 16$

5. $7x^{2} − 9x + 3$

7. $\frac{14}{15}a^{2} + \frac{3}{10}$

9. $\frac{11}{10} y^{2} + y − \frac{16}{3}$

11. $8a^{2}b^{2} − ab + 10$

13. $−5x^{2}y + 17xy − 3xy^{2}$

15. $m^{2}n − 8mn − mn^{2}$

17. $3x^{2n} − 7x^{n} + 2$

Вправа$\PageIndex{5}$

Спростити.

$5 − 2 (4x + 8)$
$8 − 6 (2x − 1)$
$2 (x^{2} − 7x + 1) + 3x − 7$
$−5 (x^{2} + 4x − 1) + 8x^{2} − 5$
$5ab − 4 (ab + 5)$
$5 (7 − ab) + 2ab$
$2 − a^{2} + 3 (a^{2} + 4)$
$7 − 3y + 2 (y^{2} − 3y − 2)$
$8x^{2} − 3x − 5 (x^{2} + 4x − 1)$
$2 − 5y − 6 (y^{2} − y + 2)$
$a^{2}b^{2} − 5 + 3 (a^{2}b^{2} − 3ab + 2)$
$a^{2} − 3ab − 2 (a^{2} − ab + 1)$
$10y^{2} + 6 − (3y^{2} + 2y + 4)$
$4m^{2} − 3mn − (m^{2} − 3mn + n^{2} )$
$x^{2n} − 3x^{n} + 5 (x^{2n} − x^{n} + 1)$
$−3 (y^{2n} − 2y^{n} + 1) + 4y^{2n} − 5$

Відповідь

1. $−8x − 11$

3. $2x^{2} − 11x − 5$

5. $ab − 20$

7. $2a^{2} + 14$

9. $3x^{2} − 23x + 5$

11. $4a^{2}b^{2} − 9ab + 1$

13. $7y^{2} − 2y + 2$

15. $6x^{2n} − 8x^{n} + 5$

Вправа$\PageIndex{6}$

Оцінити.

$−2x + 3$де$x = −2$
$8x − 5$де$x = −1$
$x^{2} − x + 5$де$x = −5$
$2x^{2} − 8x + 1$де$x = 3$
$\frac { x ^ { 2 } - x + 2 } { 2 x - 1 }$де$x = -\frac{1}{2}$
$\frac { 9 x ^ { 2 } + x - 2 } { 3 x - 4 }$де$x = -\frac{2}{3}$
$( 3 y - 2 ) ( y + 5 )$де$y = \frac { 2 } { 3 }$
$(3x + 2) (5x + 1)$де$x = −\frac{1}{5}$
$(3x − 1) (x − 8)$де$x = −1$
$(7y + 5) (y + 1)$де$y = −2$
$y^{6} − y^{3} + 2$де$y = −1$
$y^{5} + y^{3} − 3$де$y = −2$
$a^{2} − 5b^{2}$де$a = −2$ і$b = −1$
$a^{3} − 2b^{3}$де$a = −3$ і$b = 2$
$(x − 2y) (x + 2y)$де$x = 2$ і$y = −5$
$(4x − 3y) (x − y)$де$x = −4$ і$y = −3$
$a^{2} − ab + b^{2}$де$a = −1$ і$b = −2$
$x^{2}y^{2} − xy + 2$де$x = −3$ і$y = −2$
$a^{4} − b^{4}$де$a = −2$ і$b = −3$
$a^{6} − 2a^{3}b^{3} − b^{6}$де$a = 2$ і$b = −1$

Відповідь

1. $7$

3. $35$

5. $−\frac{11}{8}$

7. $0$

9. $36$

11. $4$

13. $−1$

15. $−96$

17. $3$

19. $−65$

Вправа$\PageIndex{7}$

Оцінити$\sqrt { b ^ { 2 } - 4 a c }$ дані наступні значення.

$a = 6, b = 1$і$c = −1$
$a = 15, b = 4$і$c = −4$
$a = \frac{3}{4} , b = −2$і$c = −4$
$a = \frac{1}{2} , b = −2$і$c = −30$
$a = 1, b = 2$і$c = −1$
$a = 1, b = −4$і$c = −50$
$a = 1, b = −1$і$c = −\frac{1}{16}$
$a = −2, b = −\frac{1}{3}$і$c = 1$

Відповідь

1. $5$

3. $4$

5. $2\sqrt{2}$

7. $\frac { \sqrt { 5 } } { 2 }$

Вправа$\PageIndex{8}$

Перетворіть наступні температури в задані градуси Цельсія$C = \frac{5}{9} (F − 32)$, де F представляє градуси за Фаренгейтом.

$95°$F
$86°$F
$32°$F
$−40°$F

Відповідь

1. $35°$C

3. $0°$C

Вправа$\PageIndex{9}$

Обчисліть периметр і площу прямокутника з розмірами$12$ футів на$5$ фути.
Обчисліть периметр і площу прямокутника з розмірами$5$ метри на$1$ метр.
Обчисліть площу поверхні і обсяг сфери радіусом$6$ сантиметрів.
Радіус основи правого кругового циліндра вимірює$4$ дюйми, а висота вимірює$10$ дюйми. Розрахуйте площу поверхні і обсяг.
Обчисліть обсяг сфери діаметром$18$ сантиметрів.
Діаметр основи правого круглого конуса вимірює$6$ дюйми. Якщо висота$1\:\frac{1}{2}$ ступні, то розрахуйте її обсяг.
З огляду на, що висота правого кругового циліндра дорівнює радіусу підстави, виведіть формулу для площі поверхні через радіус підстави.
З огляду на, що площа підстави правого круглого циліндра дорівнює$25π$ квадратним дюймам, знайдіть обсяг, якщо висота -$1$ фут.
Хосе зміг проїхати з Тусона до Фенікса за$2$ години на середній швидкості$58$ миль/год. Як далеко Фенiкс від Туксона?
Якщо поїзд-куля може в середньому$152$ миль/год, то як далеко він може$\frac{3}{4}$ проїхати протягом години?
Маргарет їздила протягом$1\:\frac{3}{4}$ години з середньою швидкістю$68$ миль на годину. Як далеко вона подорожувала?
Поїздка з Флагстаффа, штат Аризона, до національного парку Гранд-Каньйон зайняла$1\:\frac{1}{2}$ години на середній швидкості$54$ миль/год. Як далеко Національний парк Гранд-Каньйон від Флагстаффа?
Розрахуйте прості відсотки, зароблені на$3$ -річну інвестицію$$2,500$ під річну процентну ставку$5\:\frac{1}{4} $%.
Розрахуйте прості відсотки, зароблені на$1$ -річну інвестицію$$5,750$ під річну процентну ставку$2\:\frac{5}{8} $%.
Що таке прості відсотки, зароблені на$5$ -річну інвестицію$$20,000$ при річній процентній ставці$6$%?
Що таке прості відсотки, зароблені на$1$ -річну інвестицію$$50,000$ при річній процентній ставці$4.5$%?
Час$t$ у секундах, коли об'єкт знаходиться у вільному падінні, задається формулою$t = \frac { \sqrt { s } } { 4 }$, де s представляє відстань у футах, на яку впав об'єкт. Скільки часу потрібно предмету, щоб впасти$32$ ногами? (Дайте точну відповідь і приблизну відповідь до найближчих сотих.)
Струм,$I$ виміряний в амперах, задається за формулою$I = \sqrt { \frac { P } { R } }$, де$P$ використовується потужність, виміряна в ватах, і$R$ - опір, виміряний в Омах. Якщо лампочка використовує$60$ ват потужності і має$240$ Ом опору, то скільки ампер струму потрібно?

Відповідь

1. $P = 34$фути;$A = 60$ квадратні фути

3. $SA = 144π$квадратні сантиметри;$V = 288π$ кубічні сантиметри

5. $972π$кубічні сантиметри

7. $SA = 4πr^{2}$

9. $116$миль

11. $119$миль

13. $$393.75$

15. $$6,000$

17. $\sqrt { 2 } \approx 1.41$секунд

Вправа$\PageIndex{10}$

Знайдіть і опублікуйте корисну математичну модель. Продемонструйте його використання деякими значеннями.
Досліджуйте та обговоріть історію змінної. Що ми можемо використовувати, якщо у нас закінчилися літери?
Знайдіть і розмістіть посилання на корисний ресурс з описом грецького алфавіту.
З огляду на алгебраїчний вираз$5 − 3 (9x − 1)$, поясніть, чому ми не віднімаємо$5$ і$3$ спочатку.
Чи потрібна окрема розподільна властивість більш ніж на два терміни? Наприклад,$a (b + c + d) = ab + ac + ad$. Поясніть.
Як ми можемо перевірити, чи правильно ми спростили вираз?

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

5. Відповідь може відрізнятися

Виноски

⁸⁷ Комбінації змінних і чисел поряд з математичними операціями, що використовуються для узагальнення конкретних арифметичних операцій.

⁸⁸ Компоненти алгебраїчного виразу, розділені операторами додавання.

⁸⁹ Складові терміна, розділені операторами множення.

⁹⁰ Числовий коефіцієнт терміна.

⁹¹ Всі змінні фактори з їх показниками.

⁹² Термін, написаний без змінного коефіцієнта.

^{93 Задано} будь-які дійсні числа$a, b,$$c, a (b + c) = ab + ac$ і/або$(b + c) a = ba + ca$.

⁹⁴ Постійні терміни або терміни, змінні частини яких мають однакові змінні з однаковими показниками.

⁹⁵ Використовується при зверненні до подібних термінів.

⁹⁶ Додавання або віднімання подібних термінів в алгебраїчному виразі для отримання одного члена з тією ж змінною частиною.

⁹⁷ Процес об'єднання подібних термінів, поки вираз не містить більше подібних термінів.

⁹⁸ Процес виконання операцій алгебраїчного виразу для заданих значень змінних.

⁹⁹ Акт заміни змінної на еквівалентну величину.

¹⁰⁰ Багаторазова математична модель, що використовує алгебраїчні вирази для опису загального застосування.

¹⁰¹ Відстань$D$ після подорожі за середнім курсом$r$ протягом деякого часу$t$ можна розрахувати за формулою$D = rt$.

¹⁰² Моделюється за формулою$I = prt$, де$p$ представлена основна сума, вкладена за річною процентною ставкою$r$ протягом$t$ багатьох років.

*Терміни*	*Коефіцієнт*	*Змінна частина*
\(x^{2}y^{2}\)	\(1\)	\(x^{2}y^{2}\)
\(6xy\)	\(6\)	\(xy\)
\(−3\)	\(−3\)

*Терміни*	*Коефіцієнт*	*Змінна частина*
\(10a^{2}\)	\(10\)	\(a^{2}\)
\(−5ab\)	\(−5\)	\(ab\)
\(−b^{2}\)	\(−1\)	\(b^{2}\)