5.6: Рішення радикальних рівнянь

Цілі навчання

• Розв'яжіть рівняння з квадратними коренями
• Вирішити рівняння за участю кубових

радикальні рівняння

Радикальне рівняння ²² - це будь-яке рівняння, яке містить один або кілька радикалів зі змінною в радиканді. Нижче наведено кілька прикладів радикальних рівнянь, всі з яких будуть розв'язані в цьому розділі:

Таблиця$\PageIndex{1}$

$\sqrt { 2 x - 1 } = 3$

$\sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 = 0$

$\sqrt { x + 2 } - \sqrt { x } = 1$

Починаємо з квадратного властивості рівності ²³; задані дійсні числа$a$ і$b$, маємо наступне:

$\text{If}\:\:\:a = b , \text { then } a ^ { 2 } = b ^ { 2 }$

Іншими словами, рівність зберігається, якщо ми квадратично обидві сторони рівняння.

$\begin{aligned} - 3 = - 3 \Rightarrow ( - 3 ) ^ { 2 } & = ( - 3 ) ^ { 2 } \\ 9 & = 9\:\:\color{Cerulean}{✓} \end{aligned}$

Зворотне, з іншого боку, не обов'язково вірно,

$\begin{aligned} 9 &= 9 \\ ( - 3 ) ^ { 2 } &= ( 3 ) ^ { 2 } \Rightarrow - 3 \neq 3\:\:\color{red}{✗} \end{aligned}$

Це важливо, тому що ми будемо використовувати цю властивість для вирішення радикальних рівнянь. Розглянемо дуже просте радикальне рівняння, яке можна вирішити оглядом,

$\sqrt { x } = 5$

Тут ми бачимо, що$x = 25$ це рішення. Щоб вирішити це рівняння алгебраїчно, використовують квадратичну властивість рівності і той факт, що$( \sqrt { a } ) ^ { 2 } = \sqrt { a ^ { 2 } } = a$ коли$a$ невід'ємний. Усуньте квадратний корінь, зрівнявши обидві сторони рівняння наступним чином:

$\begin{aligned} \color{Cerulean}{(}\color{black}{ \sqrt { x } }\color{Cerulean}{) ^ { 2 }} & \color{black}{=}\color{Cerulean}{ (}\color{black}{ 5}\color{Cerulean}{ ) ^ { 2 }} \\ x & = 25 \end{aligned}$

Як перевірка, ми можемо побачити це,$\sqrt{25}=5$ як очікувалося. Оскільки зворотне квадратичне властивість рівності не обов'язково вірно, рішення квадратного рівняння не можуть бути розв'язками оригіналу. Отже, квадратичне обох сторін рівняння вводить можливість сторонніх розв'язків ²⁴, які є розв'язками, які не вирішують вихідного рівняння. Наприклад,

$\sqrt { x } = - 5$

Це рівняння явно не має дійсного числового рішення. Однак квадратура обох сторін дає нам рішення:

$\begin{aligned} \color{Cerulean}{(}\color{black}{ \sqrt { x } }\color{Cerulean}{) ^ { 2 }} & \color{black}{=}\color{Cerulean}{ (}\color{black}{ -5}\color{Cerulean}{ ) ^ { 2 }} \\ x & = 25 \end{aligned}$

Як перевірка, ми можемо це побачити$\sqrt { 25 } \neq - 5$. З цієї причини ми повинні перевірити відповіді, які виникають в результаті квадратування обох сторін рівняння.

Приклад$\PageIndex{1}$:

Вирішити:$\sqrt { 3 x + 1 } = 4$.

Рішення

Ми можемо усунути квадратний корінь, застосувавши квадратне властивість рівності.

$\begin{aligned} \sqrt { 3 x + 1 } & = 4 \\ ( \sqrt { 3 x + 1 } ) ^ { 2 } & = ( 4 ) ^ { 2 }\quad\color{Cerulean}{Square \:both\:sides.} \\ 3 x + 1 & = 16 \quad\:\:\:\color{Cerulean}{Solve.}\\ 3 x & = 15 \\ x & = 5 \end{aligned}$

Далі ми повинні перевірити.

$\begin{aligned} \sqrt { 3 (\color{OliveGreen}{ 5}\color{black}{ )} + 1 } & = 4 \\ \sqrt { 15 + 1 } & = 4 \\ \sqrt { 16 } & = 4 \\ 4 & = 4\:\:\color{Cerulean}{✓} \end{aligned}$

Відповідь:

Рішення є$5$.

Існує геометрична інтерпретація до попереднього прикладу. Графік функції, визначеної$f ( x ) = \sqrt { 3 x + 1 }$ і визначити, де вона перетинає графік, заданий$g (x) = 4$.

Малюнок$\PageIndex{1}$

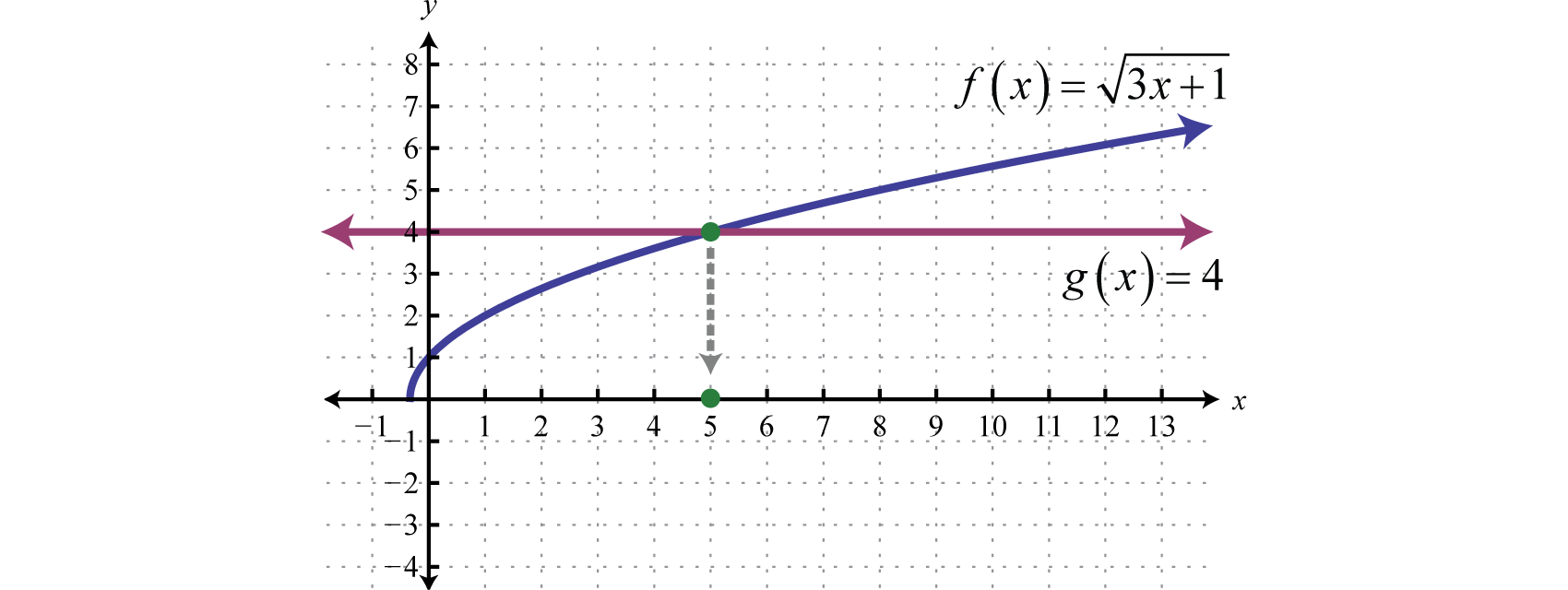
Як проілюстровано,$f ( x ) = g ( x )$ де$x=5$.

Приклад$\PageIndex{2}$:

Вирішити:$\sqrt { x - 3 } = x - 5$.

Рішення

Почніть зі зведення в квадрат обидві сторони рівняння.

$\begin{aligned} \sqrt { x - 3 } &= x - 5 \\ ( \sqrt { x - 3 } ) ^ { 2 } &= ( x - 5 ) ^ { 2 }\quad\quad\quad\color{Cerulean}{Square\:both\:sides.} \\ x - 3 &= x ^ { 2 } - 10 x + 25 \end{aligned}$

Отримане квадратне рівняння може бути вирішено факторингом.

$\begin{aligned} x - 3 & = x ^ { 2 } - 10 x + 25 \\ 0 & = x ^ { 2 } - 11 x + 28 \\ 0 & = ( x - 4 ) ( x - 7 ) \end{aligned}$

$\begin{array} { r l } { x - 4 = 0 } & { \text { or } \quad x - 7 = 0 } \\ { x = 4 } & \quad\quad\quad\quad\:{ x = 7 } \end{array}$

Перевірка розв'язків після зведення в квадрат обох сторін рівняння не є необов'язковою. Використовуйте вихідне рівняння при виконанні перевірки.

Таблиця$\PageIndex{2}$

$\color{Cerulean}{Check} \color{black}{x=4}$	$\color{Cerulean}{Check} \color{black}{x=7}$
$\begin{aligned} \sqrt { x - 3 } & = x - 5 \\ \sqrt { \color{Cerulean}{4}\color{black}{ -} 3 } & = \color{Cerulean}{4}\color{black}{ -} 5 \\ \sqrt { 1 } & = - 1 \\ 1 & = - 1 \quad \color{red}{✗} \end{aligned}$	$\begin{aligned} \sqrt { x - 3 } & = x - 5 \\ \sqrt { \color{Cerulean}{7}\color{black}{ -} 3 } & = \color{Cerulean}{7}\color{black}{ -} 5 \\ \sqrt { 4 } & = 2 \\ 2 & = 2\quad\color{Cerulean}{✓} \end{aligned}$

Після перевірки можна побачити, що$x = 4$ це стороннє рішення; воно не вирішує вихідного радикального рівняння. Нехтуйте цією відповіддю. Це залишає$x = 7$ єдиним рішенням.

Відповідь:

Рішення є$7$.

Геометрично ми бачимо, що$f ( x ) = \sqrt { x + 3 }$ дорівнює$g (x) = x − 5$ де$x = 7$.

Малюнок$\PageIndex{2}$

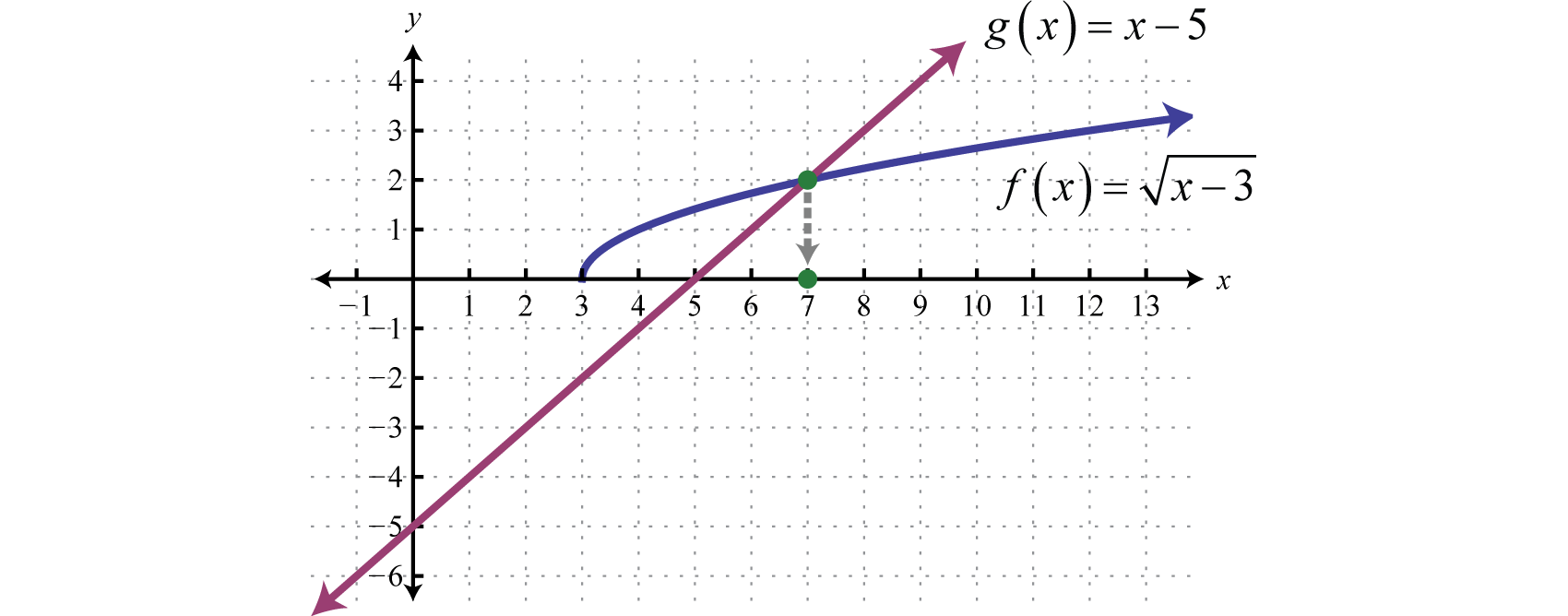
У попередніх двох прикладах зверніть увагу, що радикал ізольований на одній стороні рівняння. Як правило, це не так. Етапи розв'язання радикальних рівнянь за участю квадратних коренів викладені в наступному прикладі.

Приклад$\PageIndex{3}$:

Вирішити:$\sqrt { 2 x - 1 } + 2 = x$.

Рішення

Крок 1: Ізолюйте квадратний корінь. Почніть з віднімання 2 з обох сторін рівняння.

$\begin{aligned} \sqrt { 2 x - 1 } + 2 &= x \\ \sqrt { 2 x - 1 } &= x - 2 \end{aligned}$

Крок 2: Квадрат з обох сторін. Квадратування обох сторін усуває квадратний корінь.

$\begin{aligned} ( \sqrt { 2 x - 1 } ) ^ { 2 } &= ( x - 2 ) ^ { 2 } \\ 2 x - 1 &= x ^ { 2 } - 4 x + 4 \end{aligned}$

Крок 3: Розв'яжіть отримане рівняння. Тут нам залишається квадратне рівняння, яке можна вирішити факторингом.

$\begin{aligned} 2 x - 1 & = x ^ { 2 } - 4 x + 4 \\ 0 & = x ^ { 2 } - 6 x + 5 \\ 0 & = ( x - 1 ) ( x - 5 ) \end{aligned}$

$\begin{array} { r l } { x - 1 = 0 } & { \text { or } \quad x - 5 = 0 } \\ { x = 1 } & \quad\quad\quad\quad{ x = 5 } \end{array}$

Крок 4: Перевірте рішення у вихідному рівнянні. Квадратування обох сторін вводить можливість сторонніх рішень, отже, потрібна перевірка.

Таблиця$\PageIndex{3}$

$\color{Cerulean}{Check} \color{black}{x=1}$	$\color{Cerulean}{Check} \color{black}{x=5}$
$\begin{aligned} \sqrt { 2 x - 1 } + 2 & = x \\ \sqrt { 2 ( \color{Cerulean}{1}\color{black}{ )} - 1 } + 2 & = \color{Cerulean}{1} \\ \sqrt { 1 } + 2 & = 1 \\ 1 + 2 & = 1 \\ 3 & = 1 \:\:\color{red}{✗}\end{aligned}$	$\begin{aligned} \sqrt { 2 x - 1 } + 2 & = x \\ \sqrt { 2 ( \color{Cerulean}{5}\color{black}{ )} - 1 } + 2 & = \color{Cerulean}{5} \\ \sqrt { 9 } + 2 & = 5 \\ 3 + 2 & = 5 \\ 5 & = 5\:\:\color{Cerulean}{✓} \end{aligned}$

Після перевірки ми бачимо, що$x = 1$ це стороннє рішення; воно не вирішує вихідного радикального рівняння. Це залишає$x = 5$ єдиним рішенням.

Відповідь:

Рішення є$5$.

Іноді існує більше одного рішення радикального рівняння.

Приклад$\PageIndex{4}$:

Вирішити:$2 \sqrt { 2 x + 5 } - x = 4$.

Рішення

Почніть з виділення терміна з радикалом.

$\begin{aligned} 2 \sqrt { 2 x + 5 } - x &= 4 \quad\quad\color{Cerulean}{Add\:x\:to\:both\:sides.} \\ 2 \sqrt { 2 x + 5 } &= x + 4 \end{aligned}$

Незважаючи на те, що термін з лівого боку має коефіцієнт, ми все ж вважаємо його ізольованим. Нагадаємо, що терміни відокремлюються операторами додавання або віднімання.

$\begin{aligned} 2 \sqrt { 2 x + 5 } & = x + 4 \\ ( 2 \sqrt { 2 x + 5 } ) ^ { 2 } & = ( x + 4 ) ^ { 2 } \quad\quad\quad\color{Cerulean}{Square\:both\:sides.}\\ 4 ( 2 x + 5 ) & = x ^ { 2 } + 8 x + 16 \end{aligned}$

Розв'яжіть отримане квадратне рівняння.

$\begin{aligned} 4 ( 2 x + 5 ) & = x ^ { 2 } + 8 x + 16 \\ 8 x + 20 & = x ^ { 2 } + 8 x + 16 \\ 0 & = x ^ { 2 } - 4 \\ 0 & = ( x + 2 ) ( x - 2 ) \end{aligned}$

$\begin{array} { r l } { x + 2 = 0 } & { \text { or } x - 2 = 0 } \\ { x = - 2 } & \quad\quad\quad\:{ x = 2 } \end{array}$

Оскільки ми квадратично обидві сторони, ми повинні перевірити наші рішення.

Таблиця$\PageIndex{4}$

$\color{Cerulean}{Check} \color{black}{x=-2}$	$\color{Cerulean}{Check} \color{black}{x=2}$
$\begin{array} { r } { 2 \sqrt { 2 x + 5 } - x = 4 } \\ { 2 \sqrt { 2 ( \color{Cerulean}{- 2}\color{black}{ )} + 5 } - ( \color{Cerulean}{- 2}\color{black}{ )} = 4 } \\ { 2 \sqrt { - 4 + 5 } + 2 = 4 } \\ { 2 \sqrt { 1 } + 2 = 4 } \\ { 2 + 2 = 4 } \\ { 4 = 4 }\:\:\color{Cerulean}{✓} \end{array}$	$\begin{aligned} 2 \sqrt { 2 x + 5 } - x & = 4 \\ 2 \sqrt { 2 (\color{Cerulean}{ 2}\color{black}{ )} + 5 } - ( \color{Cerulean}{2}\color{black}{ )} & = 4 \\ 2 \sqrt { 4 + 5 } - 2 & = 4 \\ 2 \sqrt { 9 } - 2 & = 4 \\ 6 - 2 & = 4 \\ 4 & = 4 \:\:\color{Cerulean}{✓}\end{aligned}$

Після перевірки ми можемо побачити, що обидва є розв'язками вихідного рівняння.

Відповідь:

Рішення є$\pm 2$.

Іноді обидва можливі рішення є сторонніми.

Приклад$\PageIndex{5}$:

Вирішити:$\sqrt { 4 - 11 x } - x + 2 = 0$.

Рішення

Почніть з виділення радикала.

$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 & = 0\quad\quad\quad\quad\quad\color{Cerulean}{Isolate\:the\:radical.} \\ \sqrt { 4 - 11 x } & = x - 2 \\ ( \sqrt { 4 - 11 x } ) ^ { 2 } & = ( x - 2 ) ^ { 2 }\quad\quad\color{Cerulean}{Square\:both\:sides.} \\ 4 - 11 x & = x ^ { 2 } - 4 x + 4\:\:\color{Cerulean}{Solve.} \\ 0 & = x ^ { 2 } + 7 x \\ 0 & = x ( x + 7 ) \end{aligned}$

$\begin{aligned} x = 0 \text { or } x + 7 & = 0 \\ x & = - 7 \end{aligned}$

Оскільки ми квадратично обидві сторони, ми повинні перевірити наші рішення.

Таблиця$\PageIndex{5}$

$\color{Cerulean}{Check} \color{black}{x=0}$	$\color{Cerulean}{Check} \color{black}{x=-7}$
$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 & = 0 \\ \sqrt { 4 - 11 ( \color{Cerulean}{0}\color{black}{ )} } -\color{Cerulean}{ 0}\color{black}{ +} 2 & = 0 \\ \sqrt { 4 } + 2 & = 0 \\ 2 + 2 & = 0 \\ 4 & = 0 \:\:\color{red}{✗} \end{aligned}$	$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 &=0 \\ \sqrt { 4 - 11 ( \color{Cerulean}{- 7}\color{black}{ )} } - ( \color{Cerulean}{- 7}\color{black}{ )} + 2 &=0 \\ \sqrt { 4 + 77 } + 7 + 2 &=0 \\ \sqrt { 81 } + 9 &=0 \\ 9 + 9 &=0 \\ 18 &=0 \:\:\color{red}{✗} \end{aligned}$

Оскільки обидва можливі рішення є сторонніми, рівняння не має рішення.

Відповідь:

Немає рішення,$\emptyset$

Квадратне властивість рівності поширюється на будь-яку натуральну цілу силу$n$. З огляду на дійсні числа$a$ і$b$, ми маємо наступне:

$\text{If}\:\:\:a = b , \text { then } a ^ { n } = b ^ { n }$

Це часто називають властивістю влади рівності ²⁵. Використовують цю властивість поряд з тим$( \sqrt [ n ] { a } ) ^ { n } = \sqrt [ n ] { a ^ { n } } = a$, що, коли$a$ невід'ємний, для вирішення радикальних рівнянь з показниками більше$2$.

Приклад$\PageIndex{6}$:

Вирішити$\sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 = 0$.

Рішення

Виділіть радикал, а потім куб обидві сторони рівняння.

$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0\quad\quad\color{Cerulean}{Isolate\:the\:radical.} \\ \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } & = 2 \\ \left( \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } \right) ^ { 3 } & = ( 2 ) ^ { 3 }\quad\color{Cerulean}{Cube\:both\:sides.} \\ 4 x ^ { 2 } + 7 & = 8 \quad\quad\color{Cerulean}{Solve.}\\ 4 x ^ { 2 } - 1 & = 0 \\ ( 2 x + 1 ) ( 2 x - 1 ) & = 0 \end{aligned}$

$\begin{array} { r l } { 2 x + 1 = 0 } & { \text { or } \quad 2 x - 1 = 0 } \\ { 2 x = - 1 } &\quad\quad\quad\quad\: { 2 x = 1 } \\ { x = - \frac { 1 } { 2 } } &\quad\quad\quad\quad\:\:\; { x = \frac { 1 } { 2 } } \end{array}$

Перевірка.

Таблиця$\PageIndex{6}$

$\color{Cerulean}{Check} \color{black}{x=-\frac{1}{2}}$	$\color{Cerulean}{Check} \color{black}{x=\frac{1}{2}}$
$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \left( \color{Cerulean}{- \frac { 1 } { 2} } \right) ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \cdot \frac { 1 } { 4 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 8 } - 2 & = 0 \\ 2- 2 & = 0 \\ 0 & = 0\:\:\color{Cerulean}{✓} \end{aligned}$	$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \left( \color{Cerulean}{\frac { 1 } { 2} } \right) ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \cdot \frac { 1 } { 4 } + 7 } - 2 & = 0 \\ \sqrt[3]{1+7}-2 &=0 \\ \sqrt [ 3 ] { 8 } - 2 & = 0 \\ 2 - 2 & = 0 \\ 0 & = 0\:\:\color{Cerulean}{✓} \end{aligned}$

Відповідь:

Рішення є$\pm \frac { 1 } { 2 }$.

Вправа$\PageIndex{1}$

$x - 3 \sqrt { 3 x + 1 } = 3$

Відповідь

Рішення є$33$.

www.youtube.com/В/КР6х0КББТБС

Може бути так, що рівняння має більше одного члена, який складається з радикальних виразів.

Приклад$\PageIndex{7}$:

Вирішити:$\sqrt { 5 x - 3 } = \sqrt { 4 x - 1 }$.

Рішення

Обидва радикали вважаються ізольованими з окремих сторін рівняння.

$\begin{aligned} \sqrt { 5 x - 3 } & = \sqrt { 4 x - 1 } \\ ( \sqrt { 5 x - 3 } ) ^ { 2 } & = ( \sqrt { 4 x - 1 } ) ^ { 2 } \quad\color{Cerulean}{Square\:both\:sides.}\\ 5 x - 3 & = 4 x - 1 \quad\quad\quad\color{Cerulean}{Solve.}\\ x & = 2 \end{aligned}$

Перевірка$x=2$.

$\begin{aligned} \sqrt { 5 x - 3 } & = \sqrt { 4 x - 1 } \\ \sqrt { 5 ( \color{OliveGreen}{2}\color{black}{ )} - 3 } & = \sqrt { 4 ( \color{OliveGreen}{2}\color{black}{ )} - 1 } \\ \sqrt { 10 - 3 } & = \sqrt { 8 - 1 } \\ \sqrt { 7 } & = \sqrt { 7 }\:\:\color{Cerulean}{✓} \end{aligned}$

Відповідь:

Рішення є$2$.

Приклад$\PageIndex{8}$:

Вирішити:$\sqrt [ 3 ] { x ^ { 2 } + x - 14 } = \sqrt [ 3 ] { x + 50 }$.

Рішення

Усуньте радикали, кубіруючи обидві сторони.

$\begin{aligned} \sqrt [ 3 ] { x ^ { 2 } + x - 14 } & = \sqrt [ 3 ] { x + 50 } \\ \left( \sqrt [ 3 ] { x ^ { 2 } + x - 14 } \right) ^ { 3 } & = ( \sqrt [ 3 ] { x + 50 } ) ^ { 3 }\quad\color{Cerulean}{Cube\:both\:sides.} \\ x ^ { 2 } + x - 14 & = x + 50 \quad\quad\quad\color{Cerulean}{Solve.}\\ x ^ { 2 } - 64 & = 0 \\ ( x + 8 ) ( x - 8 ) & = 0 \end{aligned}$

$\begin{array} { r l } { x + 8 = 0 } & { \text { or } \quad x - 8 = 0 } \\ { x = - 8 } & \quad\quad\quad\quad{ x = 8 } \end{array}$

Перевірка.

Таблиця$\PageIndex{7}$

$\color{Cerulean}{Check} \color{black}{x=-8}$

$\color{Cerulean}{Check} \color{black}{x=8}$

$\begin{aligned} \sqrt [ 3 ] { x ^ { 2 } + x - 14 } & = \sqrt [ 3 ] { x + 50 } \\ \sqrt [ 3 ] { ( \color{Cerulean}{- 8}\color{black}{ )} ^ { 2 } + ( \color{Cerulean}{- 8}\color{black}{ )} - 14 } & = \sqrt [ 3 ] { ( \color{Cerulean}{- 8}\color{black}{ )} + 50 } \\ \sqrt [ 3 ] { 64 - 8 - 14 } & = \sqrt [ 3 ] { 42 } \\ \sqrt [ 3 ] { 42 } & = \sqrt [ 3 ] { 42 Table \(\PageIndex{7}$}\:\:\ color {Cerulean} {✓}\ кінець {вирівняний}\)

\ (\ почати {вирівняний}\ sqrt [3] {x ^ {2} + x - 14} & =\ sqrt [3] {x + 50}\\ sqrt [3] {(\ колір {зерулеан} {8}\ колір {чорний} {)} ^ {2} + (\ колір {зерулеан} {8}\ колір {чорний} {)} - 14} &\ sqrt [3] {(\ color {Cerulean} {8}\ колір {чорний} {)} + 50}\\ sqrt [3] {64 + 8 - 14} & =\ sqrt [3] ] {58}\\ sqrt [3] {58} & =\ sqrt [3] {58}\:\:\ color {Cerulean} {✓}\ кінець {вирівняний}\

Відповідь:

Рішення є$\pm 8$.

Виділити радикал з обох сторін рівняння може бути неможливим. Коли це так, ізолюйте радикали, по одному, і застосовуйте квадратну властивість рівності кілька разів, поки не залишиться лише многочлен.

Приклад$\PageIndex{9}$:

Вирішити:$\sqrt { x + 2 } - \sqrt { x } = 1$

Рішення

Почніть з виділення одного з радикалів. У цьому випадку додайте$\sqrt { x }$ до обох сторін рівняння.

$\begin{aligned} \sqrt { x + 2 } - \sqrt { x } & = 1 \\ \sqrt { x + 2 } & = \sqrt { x } + 1 \end{aligned}$

Далі квадрат з обох сторін. Подбайте про те, щоб застосувати розподільне властивість на праву сторону.

$\begin{aligned} ( \sqrt { x + 2 } ) ^ { 2 } & = ( \sqrt { x } + 1 ) ^ { 2 } \\ x + 2 & = ( \sqrt { x } + 1 ) ( \sqrt { x } + 1 ) \\ x + 2 & = \sqrt { x ^ { 2 } } + \sqrt { x } + \sqrt { x } + 1 \\ x + 2 & = x + 2 \sqrt { x } + 1 \end{aligned}$

На даний момент у нас є один термін, який містить радикал. Ізолюйте його і знову заквадратуйте обидві сторони.

$\begin{aligned} x + 2 & = x + 2 \sqrt { x } + 1 \\ 1 & = 2 \sqrt { x } \\ ( 1 ) ^ { 2 } & = ( 2 \sqrt { x } ) ^ { 2 } \\ 1 & = 4 x \\ \frac { 1 } { 4 } & = x \end{aligned}$

Перевірте, чи$x = \frac { 1 } { 4 }$ задовольняє вихідне рівняння$\sqrt { x + 2 } - \sqrt { x } = 1$

$\begin{array} { r } { \sqrt { \color{OliveGreen}{\frac { 1 } { 4 }}\color{black}{ +} 2 } - \sqrt { \color{OliveGreen}{\frac { 1 } { 4 }} } \color{black}{=} 1 } \\ { \sqrt { \frac { 9 } { 4 } } - \frac { 1 } { 2 } = 1 } \\ { \frac { 3 } { 2 } - \frac { 1 } { 2 } = 1 } \\ { \frac { 2 } { 2 } = 1 } \\ { 1 = 1 }\color{Cerulean}{✓} \end{array}$

Відповідь

Рішення є$\frac { 1 } { 4 }$.

$( A + B ) ^ { 2 } \neq A ^ { 2 } + B ^ { 2 }$Тому що ми не можемо просто квадратувати кожен термін. Наприклад, неправильно квадратувати кожен член наступним чином.

$\color{Cerulean}{(}\color{black}{ \sqrt { x + 2 }}\color{Cerulean}{ ) ^ { 2 } }\color{black}{-}\color{Cerulean}{ (}\color{black}{ \sqrt { x }}\color{Cerulean}{ ) ^ { 2 }}\color{black}{ =}\color{Cerulean}{ (}\color{black}{ 1}\color{Cerulean}{ ) ^ { 2 }}\\\color{red}{Incorrect!}$

Це поширена помилка і призводить до неправильного результату. При квадратизації обох сторін рівняння з декількома долями ми повинні подбати про застосування розподільної властивості.

Приклад$\PageIndex{10}$:

Вирішити:$\sqrt { 2 x + 10 } - \sqrt { x + 6 } = 1$

Рішення

Почніть з виділення одного з радикалів. У цьому випадку додайте$\sqrt{x+6}$ до обох сторін рівняння.

$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } &= 1 \\ \sqrt { 2 x + 10 } & = \sqrt { x + 6 } + 1 \end{aligned}$

Далі квадрат з обох сторін. Подбайте про те, щоб застосувати розподільне властивість на праву сторону.

$\begin{aligned} ( \sqrt { 2 x + 10 } ) ^ { 2 } & = ( \sqrt { x + 6 } + 1 ) ^ { 2 } \\ 2 x + 10 & = x + 6 + 2 \sqrt { x + 6 } + 1 \\ 2 x + 10 & = x + 7 + 2 \sqrt { x + 6 } \end{aligned}$

На даний момент у нас є один термін, який містить радикал. Ізолюйте його і знову заквадратуйте обидві сторони.

$\begin{aligned} 2 x + 10 & = x + 7 + 2 \sqrt { x + 6 } \\ x + 3 & = 2 \sqrt { x + 6 } \\ ( x + 3 ) ^ { 2 } & = ( 2 \sqrt { x + 6 } ) ^ { 2 } \\ x ^ { 2 } + 6 x + 9 & = 4 ( x + 6 ) \\ x ^ { 2 } + 6 x + 9 & = 4 x + 24 \\ x ^ { 2 } + 2 x - 15 & = 0 \\ (x - 3 ) ( x + 5 ) & = 0 \end{aligned}$

$\begin{array} { r l } { x - 3 = 0 } & { \text { or } \quad x + 5 = 0 } \\ { x = 3 } & \quad\quad\quad\quad\:{ x = - 5 } \end{array}$

Перевірка.

Таблиця$\PageIndex{8}$

$\color{Cerulean}{Check} \color{black}{x=3}$	$\color{Cerulean}{Check} \color{black}{x=-5}$
$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } & = 1 \\ \sqrt { 2 ( \color{Cerulean}{3}\color{black}{ )} + 10 } - \sqrt { \color{Cerulean}{3}\color{black}{ +} 6 } & = 1 \\ \sqrt { 16 } - \sqrt { 9 } & = 1 \\ 4 - 3 & = 1 \\ 1 & = 1\:\:\color{Cerulean}{✓} \end{aligned}$	$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } &= 1 \\ \sqrt { 2 (\color{Cerulean}{ - 5}\color{black}{ )} + 10 } - \sqrt { \color{Cerulean}{- 5}\color{black}{ +} 6 } &=1 \\ \sqrt { 0 } - \sqrt { 1 }& =1 \\ 0 - 1 &=1 \\ - 1 &=1\:\:\color{red}{✗} \end{aligned}$

Відповідь

Рішення є$3$.

Вправа$\PageIndex{2}$

Вирішити:$\sqrt { 4 x + 21 } - \sqrt { 2 x + 22 } = 1$

Відповідь

Рішення є$7$.

www.youtube.com/В/BTMEQWPSТравень

Ключові виноси

• Вирішіть рівняння, що включають квадратні корені, спочатку ізолюючи радикал, а потім квадратично обидві сторони. Квадратування квадратного кореня усуває радикал, залишаючи нам рівняння, яке можна вирішити за допомогою методів, вивчених раніше в нашому вивченні алгебри.
• Квадратування обох сторін рівняння вводить можливість сторонніх розв'язків. З цієї причини ви повинні перевірити свої рішення в оригінальному рівнянні.
• Вирішіть рівняння за участю$n$ коренів, спочатку виділивши радикал, а потім підніміть$n$ обидві сторони до степені. Це усуває радикал і призводить до рівняння, яке може бути вирішено за допомогою методів, які ви вже освоїли.
• Коли в рівнянні присутній більше одного радикального члена, ізолюйте їх по одному і застосуйте властивість влади рівності кілька разів, поки не залишиться лише многочлен.

Вправа$\PageIndex{3}$

Вирішити

1. $\sqrt { x } = 7$
2. $\sqrt { x } = 4$
3. $\sqrt { x } + 8 = 9$
4. $\sqrt { x } - 4 = 5$
5. $\sqrt { x } + 7 = 4$
6. $\sqrt { x } + 3 = 1$
7. $5 \sqrt { x } - 1 = 0$
8. $3 \sqrt { x } - 2 = 0$
9. $\sqrt { 3 x + 1 } = 2$
10. $\sqrt { 5 x - 4 } = 4$
11. $\sqrt { 7 x + 4 } + 6 = 11$
12. $\sqrt { 3 x - 5 } + 9 = 14$
13. $2 \sqrt { x - 1 } - 3 = 0$
14. $3 \sqrt { x + 1 } - 2 = 0$
15. $\sqrt { x + 1 } = \sqrt { x } + 1$
16. $\sqrt { 2 x - 1 } = \sqrt { 2 x } - 1$
17. $\sqrt { 4 x - 1 } = 2 \sqrt { x } - 1$
18. $\sqrt { 4 x - 11 } = 2 \sqrt { x } - 1$
19. $\sqrt { x + 8 } = \sqrt { x } - 4$
20. $\sqrt { 25 x - 1 } = 5 \sqrt { x } + 1$
21. $\sqrt [ 3 ] { x } = 3$
22. $\sqrt [ 3 ] { x } = - 4$
23. $\sqrt [ 3 ] { 2 x + 9 } = 3$
24. $\sqrt [ 3 ] { 4 x - 11 } = 1$
25. $\sqrt [ 3 ] { 5 x + 7 } + 3 = 1$
26. $\sqrt [ 3 ] { 3 x - 6 } + 5 = 2$
27. $4 - 2 \sqrt [ 3 ] { x + 2 } = 0$
28. $6 - 3 \sqrt [ 3 ] { 2 x - 3 } = 0$
29. $\sqrt [ 5 ] { 3 ( x + 10 ) } = 2$
30. $\sqrt [ 5 ] { 4 x + 3 } + 5 = 4$
31. $\sqrt { 8 x + 11 } = 3 \sqrt { x + 1 }$
32. $2 \sqrt { 3 x - 4 } = \sqrt { 2 ( 3 x + 1 ) }$
33. $\sqrt { 2 ( x + 10 ) } = \sqrt { 7 x - 15 }$
34. $\sqrt { 5 ( x - 4 ) } = \sqrt { x + 4 }$
35. $\sqrt [ 3 ] { 5 x - 2 } = \sqrt [ 3 ] { 4 x }$
36. $\sqrt [ 3 ] { 9 ( x - 1 ) } = \sqrt [ 3 ] { 3 ( x + 7 ) }$
37. $\sqrt [ 3 ] { 3 x + 1 } = \sqrt [ 3 ] { 2 ( x - 1 ) }$
38. $\sqrt [ 3 ] { 9 x } = \sqrt [ 3 ] { 3 ( x - 6 ) }$
39. $\sqrt [ 5 ] { 3 x - 5 } = \sqrt [ 5 ] { 2 x + 8 }$
40. $\sqrt [ 5 ] { x + 3 } = \sqrt [ 5 ] { 2 x + 5 }$
41. $\sqrt { 4 x + 21 } = x$
42. $\sqrt { 8 x + 9 } = x$
43. $\sqrt { 4 ( 2 x - 3 ) } = x$
44. $\sqrt { 3 ( 4 x - 9 ) } = x$
45. $2 \sqrt { x - 1 } = x$
46. $3 \sqrt { 2 x - 9 } = x$
47. $\sqrt { 9 x + 9 } = x + 1$
48. $\sqrt { 3 x + 10 } = x + 4$
49. $\sqrt { x - 1 } = x - 3$
50. $\sqrt { 2 x - 5 } = x - 4$
51. $\sqrt { 16 - 3 x } = x - 6$
52. $\sqrt { 7 - 3 x } = x - 3$
53. $3 \sqrt { 2 x + 10 } = x + 9$
54. $2 \sqrt { 2 x + 5 } = x + 4$
55. $3 \sqrt { x - 1 } - 1 = x$
56. $2 \sqrt { 2 x + 2 } - 1 = x$
57. $\sqrt { 10 x + 41 } - 5 = x$
58. $\sqrt { 6 ( x + 3 ) } - 3 = x$
59. $\sqrt { 8 x ^ { 2 } - 4 x + 1 } = 2 x$
60. $\sqrt { 18 x ^ { 2 } - 6 x + 1 } = 3 x$
61. $5 \sqrt { x + 2 } = x + 8$
62. $4 \sqrt { 2 ( x + 1 ) } = x + 7$
63. $\sqrt { x ^ { 2 } - 25 } = x$
64. $\sqrt { x ^ { 2 } + 9 } = x$
65. $3 + \sqrt { 6 x - 11 } = x$
66. $2 + \sqrt { 9 x - 8 } = x$
67. $\sqrt { 4 x + 25 } - x = 7$
68. $\sqrt { 8 x + 73 } - x = 10$
69. $2 \sqrt { 4 x + 3 } - 3 = 2 x$
70. $2 \sqrt { 6 x + 3 } - 3 = 3 x$
71. $2 x - 4 = \sqrt { 14 - 10 x }$
72. $3 x - 6 = \sqrt { 33 - 24 x }$
73. $\sqrt [ 3 ] { x ^ { 2 } - 24 } = 1$
74. $\sqrt [ 3 ] { x ^ { 2 } - 54 } = 3$
75. $\sqrt [ 3 ] { x ^ { 2 } + 6 x } + 1 = 4$
76. $\sqrt [ 3 ] { x ^ { 2 } + 2 x } + 5 = 7$
77. $\sqrt [ 3 ] { 25 x ^ { 2 } - 10 x - 7 } = - 2$
78. $\sqrt [ 3 ] { 9 x ^ { 2 } - 12 x - 23 } = - 3$
79. $\sqrt [ 3 ] { 4 x ^ { 2 } - 1 } - 2 = 0$
80. $4 \sqrt [ 3 ] { x ^ { 2 } } - 1 = 0$
81. $\sqrt [ 5 ] { x ( 2 x + 1 ) } - 1 = 0$
82. $\sqrt [ 5 ] { 3 x ^ { 2 } - 20 x } - 2 = 0$
83. $\sqrt { 2 x ^ { 2 } - 15 x + 25 } = \sqrt { ( x + 5 ) ( x - 5 ) }$
84. $\sqrt { x ^ { 2 } - 4 x + 4 } = \sqrt { x ( 5 - x ) }$
85. $\sqrt [ 3 ] { 2 \left( x ^ { 2 } + 3 x - 20 \right) } = \sqrt [ 3 ] { ( x + 3 ) ^ { 2 } }$
86. $\sqrt [ 3 ] { 3 x ^ { 2 } + 3 x + 40 } = \sqrt [ 3 ] { ( x - 5 ) ^ { 2 } }$
87. $\sqrt { 2 x - 5 } + \sqrt { 2 x } = 5$
88. $\sqrt { 4 x + 13 } - 2 \sqrt { x } = 3$
89. $\sqrt { 8 x + 17 } - 2 \sqrt { 2 - x } = 3$
90. $\sqrt { 3 x - 6 } - \sqrt { 2 x - 3 } = 1$
91. $\sqrt { 2 ( x - 2 ) } - \sqrt { x - 1 } = 1$
92. $\sqrt { 2 x + 5 } - \sqrt { x + 3 } = 2$
93. $\sqrt { 2 ( x + 1 ) } - \sqrt { 3 x + 4 } - 1 = 0$
94. $\sqrt { 6 - 5 x } + \sqrt { 3 - 3 x } - 1 = 0$
95. $\sqrt { x - 2 } - 1 = \sqrt { 2 ( x - 3 ) }$
96. $\sqrt { 14 - 11 x } + \sqrt { 7 - 9 x } = 1$
97. $\sqrt { x + 1 } = \sqrt { 3 } - \sqrt { 2 - x }$
98. $\sqrt { 2 x + 9 } - \sqrt { x + 1 } = 2$
99. $x ^ { 1 / 2 } - 10 = 0$
100. $x ^ { 1 / 2 } - 6 = 0$
101. $x ^ { 1 / 3 } + 2 = 0$
102. $x ^ { 1 / 3 } + 4 = 0$
103. $( x - 1 ) ^ { 1 / 2 } - 3 = 0$
104. $( x + 2 ) ^ { 1 / 2 } - 6 = 0$
105. $( 2 x - 1 ) ^ { 1 / 3 } + 3 = 0$
106. $( 3 x - 1 ) ^ { 1 / 3 } - 2 = 0$
107. $( 4 x + 15 ) ^ { 1 / 2 } - 2 x = 0$
108. $( 3 x + 2 ) ^ { 1 / 2 } - 3 x = 0$
109. $( 2 x + 12 ) ^ { 1 / 2 } - x = 6$
110. $( 4 x + 36 ) ^ { 1 / 2 } - x = 9$
111. $2 ( 5 x + 26 ) ^ { 1 / 2 } = x + 10$
112. $3 ( x - 1 ) ^ { 1 / 2 } = x + 1$
113. $x ^ { 1 / 2 } + ( 3 x - 2 ) ^ { 1 / 2 } = 2$
114. $( 6 x + 1 ) ^ { 1 / 2 } - ( 3 x ) ^ { 1 / 2 } = 1$
115. $( 3 x + 7 ) ^ { 1 / 2 } + ( x + 3 ) ^ { 1 / 2 } - 2 = 0$
116. $( 3 x ) ^ { 1 / 2 } + ( x + 1 ) ^ { 1 / 2 } - 5 = 0$

Відповідь

1. $49$

3. $1$

5. $Ø$

7. $\frac{1}{25}$

9. $1$

11. $3$

13. $\frac{13}{4}$

15. $0$

17. $\frac{1}{4}$

19. $Ø$

21. $27$

23. $9$

25. $−3$

27. $6$

29. $\frac{2}{3}$

31. $2$

33. $7$

35. $2$

37. $−3$

39. $13$

41. $7$

43. $2, 6$

45. $2$

47. $−1, 8$

49. $5$

51. $Ø$

53. $−3, 3$

55. $2, 5$

57. $−4, 4$

59. $\frac{1}{2}$

61. $2, 7$

63. $Ø$

65. $10$

67. $−6, −4$

69. $−\frac{1}{2}, \frac{3}{2}$

71. $Ø$

73. $−5, 5$

75. $−9, 3$

77. $\frac{1}{5}$

79. $− \frac{3}{2} ,\frac{ 3}{2}$

81. $−1, \frac{1}{2}$

83. $5, 10$

85. $−7, 7$

87. $\frac{9}{2}$

89. $1$

91. $10$

93. $Ø$

95. $3$

97. $1, 2$

99. $100$

101. $−8$

103. $10$

105. $−13$

107. $\frac{5}{2}$

109. $−6, −4$

111. $−2, 2$

113. $1$

115. $−2$

Вправа$\PageIndex{4}$

Визначте коріння заданих функцій. Нагадаємо, що корінь - це значення в домені, яке призводить до нуля. Іншими словами, знайдіть$x$ де$f (x) = 0$.

1. $f ( x ) = \sqrt { x + 5 } - 2$
2. $f ( x ) = \sqrt { 2 x - 3 } - 1$
3. $f ( x ) = 2 \sqrt { x + 2 } - 8$
4. $f ( x ) = 3 \sqrt { x - 7 } - 6$
5. $f ( x ) = \sqrt [ 3 ] { x + 1 } + 2$
6. $f ( x ) = 2 \sqrt [ 3 ] { x - 1 } + 6$

Відповідь

1. $−1$

3. $14$

5. $−9$

Вправа$\PageIndex{5}$

Вирішити для зазначеної змінної.

1. Вирішити для$\mathrm { P } : r = \sqrt { P } - 1$
2. Вирішити для$x : y = \sqrt { x - h } + k$
3. Вирішити для$s : t = \sqrt { \frac { 2 s } { g } }$
4. Вирішити для$\mathrm { L } : T = 2 \pi \sqrt { \frac { L } { 32 } }$
5. Вирішити для$\mathrm { R } : I = \sqrt { \frac { P } { R } }$
6. Вирішити для$h : r = \sqrt { \frac { 3 V } { \pi h } }$
7. Вирішити для$V : r = \sqrt [ 3 ] { \frac { 3 V } { 4 \pi } }$
8. Вирішити для$c : a = \sqrt [ 3 ] { \frac { b ^ { 2 } \pi } { 2 c } }$
9. Квадратний корінь$1$ менше дворазового числа дорівнює$2$ меншому числу. Знайдіть номер.
10. Квадратний корінь$4$ менше дворазового числа дорівнює$6$ меншому числу. Знайдіть номер.
11. Квадратний корінь з подвійного числа дорівнює половині цього числа. Знайдіть номер.
12. Квадратний корінь з подвійного числа дорівнює третині цього числа. Знайдіть номер.
13. Відстань$d$ в милі, яку людина може бачити об'єкт на горизонті, задається формулою,$d = \frac { \sqrt { 6 h } } { 2 }$ де$h$ представляє висоту в футах очей людини над рівнем моря. Наскільки високими повинні бути очі людини, щоб побачити об'єкт за$5$ милі?
14. Струм,$I$ виміряний в амперах, задається за формулою,$I = \sqrt { \frac { P } { R } }$ де$P$ використовується потужність, виміряна у ватах і опір,$R$ виміряний в Омах. Якщо лампочка вимагає$1/2$ ампер струму і використовує вати$60$ потужності, то яке опір через лампочку?

Відповідь

1. $P = ( r + 1 ) ^ { 2 }$

3. $s = \frac { g t ^ { 2 } } { 2 }$

5. $R = \frac { P } { I ^ { 2 } }$

7. $V = \frac { 4 \pi r ^ { 3 } } { 3 }$

9. $5$

11. $0,8$

13. $16 \frac { 2 } { 3 }$ноги

Вправа$\PageIndex{6}$

Період маятника$T$ в секундах задається за формулою

$T = 2 \pi \sqrt { \frac { L } { 32 } }$

де$L$ являє собою довжину в футах. Обчисліть довжину маятника з урахуванням періоду. Дайте точне значення і приблизне значення, округлене до найближчої десятої частини фута.

1. $1$другий
2. $2$секунд
3. $\frac{1}{2}$другий
4. $\frac{1}{3}$другий

Відповідь

1. $\frac { 8 } { \pi ^ { 2 } }$стопи;$0.8$ стопи

3. $\frac { 2 } { \pi ^ { 2 } }$стопи;$0.2$ стопи

Вправа$\PageIndex{7}$

Час$t$ у секундах, об'єкт знаходиться у вільному падінні, задається за формулою

$t = \frac { \sqrt { s } } { 4 }$

де$s$ представляє відстань, яку вона впала, в футах. Обчисліть відстань, на яку буде падати об'єкт, враховуючи кількість часу.

1. $1$другий
2. $2$секунд
3. $\frac{1}{2}$другий
4. $\frac{1}{4}$другий

Відповідь

1. $16$ноги

3. $4$ноги

Вправа$\PageIndex{9}$

1. Обговоріть причини, чому ми іноді отримуємо сторонні рішення при розв'язанні радикальних рівнянь. Чи є коли-небудь умови, коли нам не потрібно перевіряти сторонні рішення? Чому чи чому ні?
2. Якщо рівняння має кілька членів, поясніть, чому квадратування всіх з них є неправильним. Наведемо приклад.

Відповідь

1. Відповідь може відрізнятися

Виноски

²² Будь-яке рівняння, що містить один або кілька радикалів зі змінною в радиканді.

²³ Дано дійсні числа$a$ і$b$, де$a = b$, потім$a^{2} = b^{2}$.

²⁴ Правильно знайдене рішення, яке не вирішує вихідного рівняння. \

^{25 Задано} будь-яке натуральне ціле$n$ і дійсне число$a$ і$b$ де$a = b$, то$a ^ { n } = b ^ { n }$.