6.1: Додавання та віднімання поліномів
- Page ID
- 58998
До кінця цього розділу ви зможете:
- Визначте многочлени, мономи, біноми та тріноми
- Визначаємо ступінь многочленів
- Додавання та віднімання мономов
- Додавання та віднімання многочленів
- Оцінити многочлен для заданого значення
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\(8x+3x\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.37. - Відніміть:\((5n+8)−(2n−1)\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.10.52. - Пишіть в розгорнутому вигляді:\(a^{5}\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.7.
Визначте многочлени, мономи, біноми та триноми
Ви дізналися, що термін - це константа або добуток константи і однієї або декількох змінних. Коли вона має форму\(ax^{m}\), де\(a\) постійна і\(m\) є цілим числом, його називають мономіалом. Деякі приклади мономіальних є\(8,−2x^{2},4y^{3}\), і\(11z^{7}\).
Мономіал - це термін форми\(ax^{m}\), де\(a\) є постійною і\(m\) є позитивним цілим числом.
Мономіал, або два або більше мономи, об'єднані додаванням або відніманням, є поліном. Деякі многочлени мають спеціальні назви, засновані на кількості членів. Мономіал - це многочлен з рівно одним терміном. Біноміал має рівно два члени, а тріноміал має рівно три члени. Спеціальних назв для многочленів більше трьох членів немає.
- многочлен —мономіал, або два або більше мономи, об'єднані додаванням або відніманням, є поліном.
- мономіальний —многочлен з рівно одним членом називається мономіалом.
- біноміальний —многочлен з рівно двома членами називається біноміальним.
- trinomial —многочлен з рівно трьома членами називається тріноміалом.
Ось кілька прикладів многочленів.
\[\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber\]
Зверніть увагу, що кожен мономіальний, біноміальний і триноміальний також є поліномом. Вони просто особливі члени «сімейства» поліномів і тому мають особливі назви. Ми використовуємо слова мономіальний, біноміальний і триноміальний при зверненні до цих спеціальних поліномів і просто називаємо всі інші поліноми.
Визначте, чи є кожен многочлен мономіальним, біноміальним, триноміальним або іншим поліномом.
- \(4y^{2}−8y−6\)
- \(−5a^{4}b^{2}\)
- \(2x^{5}−5x^{3}−3x + 4\)
- \(13−5m^{3}\)
- q
- Відповідь
-
\(\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}\)
Визначте, чи є кожен многочлен мономіальним, біноміальним, триноміальним або іншим поліномом:
- 5б
- \(8 y^{3}-7 y^{2}-y-3\)
- \(-3 x^{2}-5 x+9\)
- \(81-4 a^{2}\)
- \(-5 x^{6}\)
- Відповідь
-
- мономіальний
- многочлен
- тріпомінал
- біноміальних
- мономіальний
Визначте, чи є кожен многочлен мономіальним, біноміальним, триноміальним або іншим поліномом:
- \(27 z^{3}-8\)
- \(12 m^{3}-5 m^{2}-2 m\)
- \(\frac{5}{6}\)
- \(8 x^{4}-7 x^{2}-6 x-5\)
- \(-n^{4}\)
- Відповідь
-
- біноміальних
- тріпомінал
- мономіальний
- многочлен
- мономіальний
Визначаємо ступінь многочленів
Ступінь многочлена і ступінь його членів визначаються показниками змінної. Мономіал, який не має змінної, просто константа, - це особливий випадок. Ступінь константи дорівнює 0, тобто вона не має змінної.
- Ступінь члена - це сума показників його змінних.
- Ступінь константи дорівнює 0.
- Ступінь многочлена - найвища ступінь з усіх його членів.
Давайте подивимося, як це працює, розглянувши кілька поліномів. Ми будемо приймати це крок за кроком, починаючи з мономов, а потім прогресуючи до поліномів з більшою кількістю термінів.

Многочлен знаходиться в стандартній формі, коли члени многочлена записуються в порядку спадання ступенів. Отримайте звичку спочатку писати термін з вищим ступенем.
Знайдіть ступінь наступних многочленів.
- 10г
- \(4 x^{3}-7 x+5\)
- −15
- \(-8 b^{2}+9 b-2\)
- \(8 x y^{2}+2 y\)
- Відповідь
-
- \(\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}\)
- \(\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
- \(\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}\)
- \(\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}\)
- \(\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
Знайдіть ступінь наступних многочленів:
- −15б
- \(10 z^{4}+4 z^{2}-5\)
- \(12 c^{5} d^{4}+9 c^{3} d^{9}-7\)
- \(3 x^{2} y-4 x\)
- −9
- Відповідь
-
- 1
- 4
- 12
- 3
- 0
Знайдіть ступінь наступних многочленів:
- 52
- \(a^{4} b-17 a^{4}\)
- \(5 x+6 y+2 z\)
- \(3 x^{2}-5 x+7\)
- \(-a^{3}\)
- Відповідь
-
- 0
- 5
- 1
- 2
- 3
Додавання та віднімання мономов
Ви навчилися спрощувати вирази, комбінуючи подібні терміни. Пам'ятайте, що подібні терміни повинні мати однакові змінні з однаковим показником. Оскільки мономи є термінами, додавання та віднімання мономов - це те саме, що і об'єднання подібних термінів. Якщо мономи схожі на терміни, ми просто об'єднаємо їх, додаючи або віднімаючи коефіцієнт.
Додати:\(25 y^{2}+15 y^{2}\)
- Відповідь
-
\(\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}\)
Додати:\(12 q^{2}+9 q^{2}\)
- Відповідь
-
21\(q^{2}\)
Додати:\(-15 c^{2}+8 c^{2}\)
- Відповідь
-
\(-7 c^{2}\)
Відніміть: 16p− (−7p)
- Відповідь
-
\(\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}\)
Відніміть: 8 м− (−5м).
- Відповідь
-
13м
Відніміть:\(-15 z^{3}-\left(-5 z^{3}\right)\)
- Відповідь
-
\(-10 z^{3}\)
Пам'ятайте, що подібні терміни повинні мати однакові змінні з однаковими показниками.
Спростити:\(c^{2}+7 d^{2}-6 c^{2}\)
- Відповідь
-
\(\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}\)
Додати:\(8 y^{2}+3 z^{2}-3 y^{2}\)
- Відповідь
-
\(5 y^{2}+3 z^{2}\)
Додати:\(3 m^{2}+n^{2}-7 m^{2}\)
- Відповідь
-
\(-4 m^{2}+n^{2}\)
Спростити:\(u^{2} v+5 u^{2}-3 v^{2}\)
- Відповідь
-
\ (\ begin {масив} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\\ text {Немає подібних термінів для об'єднання.} & u^ {2} v+5 u^ {2} -3 v^ {2}\ end {масив}\)
Спростити:\(m^{2} n^{2}-8 m^{2}+4 n^{2}\)
- Відповідь
-
Немає подібних термінів для комбінування.
Спростити:\(p q^{2}-6 p-5 q^{2}\)
- Відповідь
-
Немає подібних термінів для комбінування.
Додавання та віднімання многочленів
Ми можемо думати про додавання та віднімання поліномів як просто додавання та віднімання ряду мономов. Шукайте подібні терміни - ті, у яких однакові змінні та однаковий показник. Комутативна власність дозволяє нам змінювати умови, щоб скласти подібні терміни разом.
Знайдіть суму:\(\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)\)
- Відповідь
-
Визначте подібні терміни. 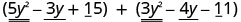
Переставляйте, щоб отримати подібні терміни разом. 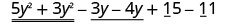
Поєднуйте подібні терміни. 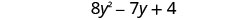
Знайдіть суму:\(\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)\)
- Відповідь
-
\(8 x^{2}-11 x+1\)
Знайдіть суму:\(\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)\)
- Відповідь
-
\(17 y^{2}+14 y+1\)
Знайдіть різницю:\(\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)\)
- Відповідь
-
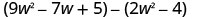
Поширюйте та ідентифікуйте подібні терміни. 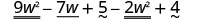
Перевпорядкувати умови. 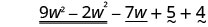
Поєднуйте подібні терміни. 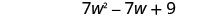
Знайдіть різницю:\(\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)\)
- Відповідь
-
\(15 x^{2}+3 x-5\)
Знайдіть різницю:\(\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)\)
- Відповідь
-
\(6 b^{2}+3\)
Відняти:\(\left(c^{2}-4 c+7\right)\) з\(\left(7 c^{2}-5 c+3\right)\)
- Відповідь
-
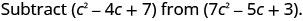
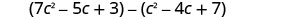
Поширюйте та ідентифікуйте подібні терміни. 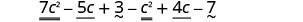
Перевпорядкувати умови. 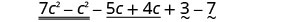
Поєднуйте подібні терміни. 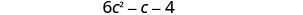
Відняти:\(\left(5 z^{2}-6 z-2\right)\) з\(\left(7 z^{2}+6 z-4\right)\)
- Відповідь
-
\(2 z^{2}+12 z-2\)
Відняти:\(\left(x^{2}-5 x-8\right)\) з\(\left(6 x^{2}+9 x-1\right)\)
- Відповідь
-
\(5 x^{2}+14 x+7\)
Знайдіть суму:\(\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)\)
- Відповідь
-
\(\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}\)
Знайдіть суму:\(\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)\)
- Відповідь
-
\(5 x^{2}-5 x y+5 y^{2}\)
Знайдіть суму:\(\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)\)
- Відповідь
-
\(7 x^{2}-6 x y-2 y^{2}\)
Знайдіть різницю:\(\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)\)
- Відповідь
-
\(\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}\)
Знайдіть різницю:\(\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)\)
- Відповідь
-
\(-5 a b-5 b^{2}\)
Знайдіть різницю:\(\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)\)
- Відповідь
-
\(4 n^{2}+7 m n\)
Спростити:\(\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)\)
- Відповідь
-
\(\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}\)
Спростити:\(\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)\)
- Відповідь
-
\(x^{3}-y^{3}\)
Спростити:\(\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)\)
- Відповідь
-
\(p^{3}-2 p^{2} q+q^{3}\)
Оцінити многочлен для заданого значення
Ми вже навчилися оцінювати вирази. Оскільки поліноми є вирази, ми будемо слідувати тим же процедурам, щоб оцінити многочлен. Ми підставимо задане значення для змінної, а потім спростимо, використовуючи порядок операцій.
Оцініть\(5x^{2}−8x+4\), коли
- х=4
- x=−2
- х=0
- Відповідь
-
1. x=4 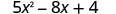

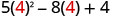
Спростіть показники. 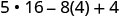
Помножити. 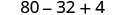
Спростити. 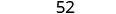
2. x=−2 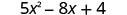

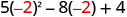
Спростіть показники. 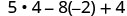
Помножити. 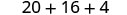
Спростити. 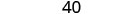
3. x=0 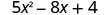

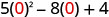
Спростіть показники. 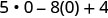
Помножити. 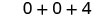
Спростити. 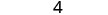
Оцініть:\(3x^{2}+2x−15\) коли
- х=3
- x=−5
- х=0
- Відповідь
-
- 18
- 50
- −15
Оцініть:\(5z^{2}−z−4\) коли
- z=−2
- з=0
- з=2
- Відповідь
-
- 18
- −4
- 14
Поліном\(−16t^{2}+250\) дає висоту м'яча tt секунд після того, як він скидається з будівлі висотою 250 футів. Знайдіть висоту через t = 2 секунди.
- Відповідь
-
\(\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}\)
Поліном\(−16t^{2}+250\) дає висоту м'яча tt секунд після того, як він скидається з будівлі висотою 250 футів. Знайти висоту через t = 0 секунд.
- Відповідь
-
250
Поліном\(−16t^{2}+250\) дає висоту кулі tt секунд після того, як він скидається з будівлі висотою 250 футів. Знайдіть висоту через t = 3 секунди.
- Відповідь
-
106
Поліном\(6x^{2}+15xy\) дає вартість, у доларах, виготовлення прямокутного контейнера, верх і низ якого є квадрати зі стороною х футів і сторонами висоти y футів. Знайдіть вартість виготовлення коробки з x = 4 футами і y=6y = 6 футів.
- Відповідь
-
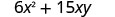
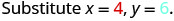
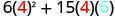
Спростити. 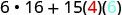
Спростити. 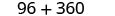
Спростити. 
Вартість виготовлення коробки становить 456 доларів.
Поліном\(6x^{2}+15xy\) дає вартість, у доларах, виготовлення прямокутного контейнера, верх і низ якого є квадрати зі стороною х футів і сторонами висоти y футів. Знайдіть вартість виготовлення коробки з x = 6 футів і y = 4 фути.
- Відповідь
-
$576
Поліном\(6x^{2}+15xy\) дає вартість, у доларах, виготовлення прямокутного контейнера, верх і низ якого є квадрати зі стороною х футів і сторонами висоти y футів. Знайдіть вартість виготовлення коробки з x = 5 футів і y = 8 футів.
- Відповідь
-
$750
Ключові концепції
- Мономи
- Мономіал - це термін виду\(ax^{m}\), де aa - постійна, а мм - ціле число
- Мономіал - це термін виду\(ax^{m}\), де aa - постійна, а мм - ціле число
- Поліноми
- многочлен —мономіал, або два або більше мономи, об'єднані додаванням або відніманням, є поліном.
- мономіальний —многочлен з рівно одним членом називається мономіалом.
- біноміальний —многочлен з рівно двома членами називається біноміальним.
- trinomial —многочлен з рівно трьома членами називається тріноміалом.
- Ступінь многочлена
- Ступінь члена - це сума показників його змінних.
- Ступінь константи дорівнює 0.
- Ступінь многочлена - найвища ступінь з усіх його членів.
Глосарій
- біноміальний
- Біноміал - це многочлен з рівно двома долями.
- ступінь постійної
- Ступінь будь-якої константи дорівнює 0.
- ступінь многочлена
- Ступінь многочлена - найвища ступінь з усіх його членів.
- ступінь терміну
- Ступінь терміна - це показник його змінної.
- мономіальний
- Мономіал - це термін виду\(ax^m\), де a - константа, а m - ціле число; мономіал має рівно один член.
- многочлен
- Многочлен - це моном, або два або більше мономи, об'єднані додаванням або відніманням.
- стандартна форма
- Многочлен знаходиться в стандартній формі, коли члени многочлена записуються в порядку спадання ступенів.
- тріпомінал
- Триноміал - це многочлен з рівно трьома долями.
