3.5: Вирішіть програми рівномірного руху
- Page ID
- 58899
До кінця цього розділу ви зможете:
- Вирішуйте програми рівномірного руху
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Знайдіть відстань, пройдену автомобілем, що йде 70 миль на годину протягом 3 годин.
Якщо ви пропустили цю проблему, перегляньте Вправа 2.6.1. - Вирішити\(x+1.2(x−10)=98\).
Якщо ви пропустили цю проблему, перегляньте Вправу 2.4.7. - Перетворіть 90 хвилин в години.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.11.1.
Вирішити рівномірні програми руху
Плануючи дорожню поїздку, часто допомагає знати, скільки часу знадобиться, щоб дістатися до пункту призначення або як далеко подорожувати щодня. Ми б використали формулу відстані, швидкості та часу, D = RT, яку ми вже бачили.
У цьому розділі ми будемо використовувати цю формулу в ситуаціях, які вимагають трохи більше алгебри для вирішення, ніж ті, які ми бачили раніше. Як правило, ми розглянемо порівняння двох сценаріїв, таких як два транспортні засоби, які подорожують за різними тарифами або в протилежних напрямках. Коли швидкість кожного транспортного засобу постійна, ми називаємо такі програми, як це проблеми рівномірного руху.
Наші стратегії вирішення проблем все ще будуть застосовуватися тут, але ми додамо до першого кроку. Перший крок буде включати в себе складання схеми, яка показує, що відбувається в прикладі. Малювання схеми допомагає нам зрозуміти, що відбувається так, що ми напишемо відповідне рівняння. Потім ми зробимо таблицю для організації інформації, як ми робили для грошових додатків.
Кроки наведені тут для зручності довідки:
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Намалюйте схему, щоб проілюструвати, що це відбувається.
- Створіть таблицю для організації інформації.
- Позначте стовпці швидкість, час, відстань.
- Перерахуйте два сценарії.
- Напишіть інформацію, яку ви знаєте.
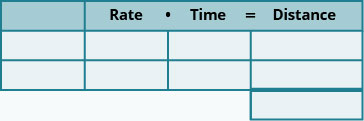
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Заповніть діаграму.
- Використовуйте змінні вирази, щоб представити цю величину в кожному рядку.
- Помножте ставку на час, щоб отримати відстань.
- Перевести в рівняння.
- Повторюйте проблему в одному реченні з усією важливою інформацією.
- Потім переведіть речення в рівняння.
- Вирішіть рівняння, використовуючи хороші методи алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
Експрес і місцевий поїзд виїжджають з Піттсбурга, щоб поїхати до Вашингтона, округ Колумбія Експрес може здійснити поїздку за 4 години, а місцевий поїзд займає 5 годин для поїздки. Швидкість експреса на 12 миль на годину швидше, ніж швидкість місцевого поїзда. Знайти швидкість обох поїздів.
- Відповідь
-
Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
Намалюйте схему, щоб проілюструвати, що це відбувається. Нижче наведено ескіз того, що відбувається в прикладі.
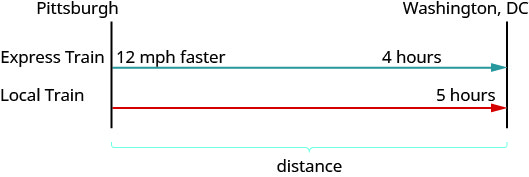
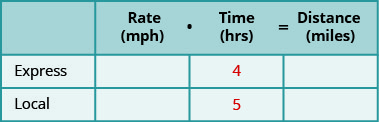
Створіть таблицю для організації інформації. Позначте стовпці «Оцінити», «Час» і «Відстань». Перерахуйте два сценарії. Напишіть інформацію, яку ви знаєте.
Крок 2. Визначте, що ми шукаємо.
Нас просять знайти швидкість обох поїздів. Зверніть увагу, що формула відстані використовує слово «швидкість», але частіше використовується «швидкість», коли ми говоримо про транспортні засоби повсякденною англійською мовою.
Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
Завершіть діаграму Використовуйте змінні вирази для представлення цієї кількості в кожному рядку. Шукаємо швидкість руху поїздів. Давайте r уявляємо швидкість місцевого поїзда. Оскільки швидкість експреса на 12 миль/год швидше, ми представляємо це як r+12.
\[\begin{aligned} r &=\text { speed of the local train } \\ r+12 &=\text { speed of the express train } \end{aligned}\]
Заповніть швидкості в діаграму.
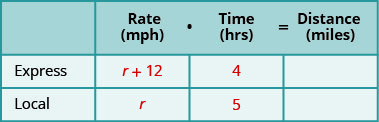
-
Помножте ставку на час, щоб отримати відстань.
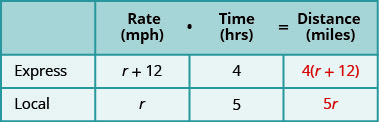
Крок 4. Перевести в рівняння.
Повторюйте проблему в одному реченні з усією важливою інформацією. Потім переведіть речення в рівняння. 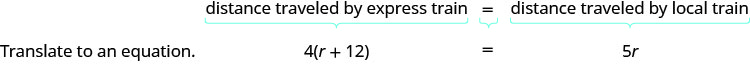
-
- Рівняння для моделювання цієї ситуації буде виходити з співвідношення між відстанями. Подивіться на схему, яку ми намалювали вище. Як відстань, пройдена експресом, пов'язана з відстанню, пройденого місцевим поїздом?
- Оскільки обидва поїзди відправляються з Піттсбурга і подорожують до Вашингтона, округ Колумбія, вони подорожують однакову відстань. Отже, пишемо:
Крок 5. Вирішіть рівняння, використовуючи хороші методи алгебри.
Крок 6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс. \[\begin{array}{ll}{\text { express train }} & {60 \mathrm{mph}(4 \text { hours })=240 \mathrm{miles}} \\ {\text { local train }} & {48 \mathrm{mph}(5 \text { hours })=240 \mathrm{miles} \checkmark \end{array}\]Тепер вирішіть це рівняння. 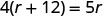
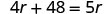
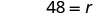
Так що швидкість місцевого поїзда становить 48 км/год.
Знайти швидкість експреса. 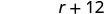


Швидкість експреса - 60 км/год.
Крок 7. Відповісти на питання повним реченням.
Швидкість місцевого поїзда становить 48 км/год, а швидкість експреса - 60 км/год.
Уейн і Денніс люблять їздити по велосипедній доріжці від Ріверсайд-парку до пляжу. Швидкість Денніса на сім миль на годину швидше, ніж швидкість Уейна, тому Вейн займає 2 години, щоб їхати до пляжу, тоді як Денніс займає 1,5 години для їзди. Знайдіть швидкість обох байкерів.
- Відповідь
-
Вейн 21 миль/год, Денніс 28 миль/год
Джеромі може проїхати від свого будинку в Клівленді до свого коледжу в Чикаго за 4,5 години. Його матері потрібно 6 годин, щоб зробити такий же диск. Джеромі проїжджає на 20 миль на годину швидше, ніж його мати. Знайдіть швидкість Джеромі і швидкість його матері.
- Відповідь
-
Джеромія 80 миль/год, мати 60 миль/год
У останньому прикладі вправ\(\PageIndex{4}\) у нас було два поїзди, які їхали однакову відстань. Діаграма та діаграма допомогли нам написати розв'язане нами рівняння. Давайте подивимося, як це працює в іншому випадку.
Крістофер і його батьки живуть на відстані 115 миль один від одного. Вони познайомилися в ресторані між будинками, щоб відсвяткувати день народження матері. Крістофер їхав 1,5 години, поки його батьки їхали 1 годину, щоб дістатися до ресторану. Середня швидкість Крістофера була на 10 миль на годину швидше, ніж середня швидкість його батьків. Якими були середні швидкості Крістофера та його батьків, коли вони їхали до ресторану?
- Відповідь
-
Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
Намалюйте схему, щоб проілюструвати, що це відбувається. Нижче показаний ескіз того, що відбувається на прикладі.
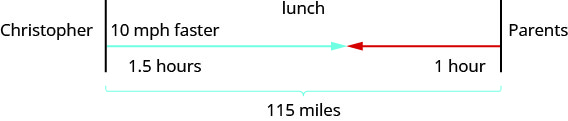
Створіть таблицю для організації інформації.
Позначте стовпці швидкість, час, відстань.
Перерахуйте два сценарії.
Напишіть інформацію, яку ви знаєте.
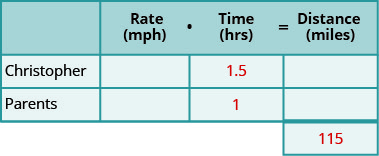
Крок 2. Визначте, що ми шукаємо.
Нас просять знайти середні швидкості Крістофера і його батьків.
Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
Заповніть діаграму. - Використовуйте змінні вирази, щоб представити цю величину в кожному рядку.
- Шукаємо їх середні швидкості. Давайте ж уявляємо середню швидкість батьків. Оскільки швидкість Крістофера на 10 миль/год швидше, ми представляємо це як r+10.
-
Заповніть швидкості в діаграму.
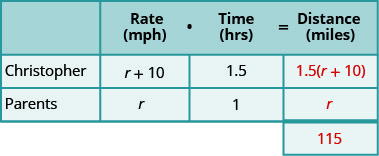
Помножте ставку на час, щоб отримати відстань.
Крок 4. Перевести в рівняння.
Повторюйте проблему в одному реченні з усією важливою інформацією. Потім переведіть речення в рівняння. Знову ж таки, нам потрібно визначити зв'язок між відстанями, щоб написати рівняння. Подивіться на схему, яку ми створили вище, і зверніть увагу на зв'язок між відстанню Крістофера і відстанню, яку пройшли його батьки.Відстань, яку пройшов Крістофер, плюс відстань, яку подорожують його батьки, повинні скласти до 115 миль. Отже, пишемо:

Крок 5. Вирішіть рівняння, використовуючи хороші методи алгебри.
\(\begin{array} {cc} {} &{1.5(r + 10) + r = 115} \\ {} &{1.5r + 15 + r = 115} \\ {\text{Now solve this equation.}} &{2.5r + 15 = 115} \\{} &{2.5r = 100} \\{} &{r = 40} \\ {} &{\text{so the parents' speed was 40 mph.}} \\ {} &{r + 10} \\ {\text{Christopher's speed is r + 10}} &{40 + 10} \\ {} &{50} \\ {} &{\text{Christopher's speed was 50 mph.}} \\ {} &{} \end{array}\)
Крок 6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
\(\begin{array}{llll} {\text{Christopher drove}} &{50\text{ mph (1.5 hours)}} &{=} &{75\text{ miles}}\\ {\text{His parents drove}} &{40\text{ mph (1 hour)}} &{=} &{\underline{40 \text{ miles}}}\\ {} &{} &{} &{115\text{ miles}} \end{array}\)
\(\begin{array}{ll} {\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{} \\{} &{\text{Christopher's speed was 50 mph.}}\\ {} &{\text{His parents' speed was 40 mph.}} \end{array}\)
Каріна їде зі свого будинку в Анахаймі до Берклі того ж дня, коли її брат їде з Берклі до Анахайму, тому вони вирішили зустрітися на обід по дорозі в Баттонвіллоу. Відстань від Анахайма до Берклі становить 410 миль. Карині потрібно 3 години, щоб дістатися до Buttonwillow, в той час як її брат їде 4 години, щоб дістатися туди. Середня швидкість, яку проїхав брат Карини, була на 15 миль на годину швидше, ніж середня швидкість Карини. Знайдіть середні швидкості Карини та її брата.
- Відповідь
-
Каріна 50 миль/год, брат 65 миль/год
Ешлі вступає до коледжу в Міннеаполісі, за 234 милі від свого будинку в Сіу-Фоллс. Вона хоче, щоб її батьки принесли їй більше зимового одягу, тому вони вирішили зустрітися в ресторані на дорозі між Міннеаполісом і Сіу-Фоллс. Ешлі та її батьки обидва проїхали 2 години до ресторану. Середня швидкість Ешлі була на сім миль на годину швидше, ніж середня швидкість її батьків. Знайдіть середню швидкість Ешлі та її батьків.
- Відповідь
-
батьки 55 миль/год, Ешлі 60 миль/год
Коли ви читаєте наступний приклад, подумайте про взаємозв'язок пройдених відстаней. Який з попередніх двох прикладів більше схожий на цю ситуацію?
Двоє водіїв вантажівок залишають зону відпочинку на міждержавній одночасно. Одна вантажівка їде на схід, а інша їде на захід. Вантажівка їде на захід їде зі швидкістю 70 миль/год, а вантажівка, що їде на схід, має середню швидкість 60 км/год. Як довго вони подорожуватимуть, перш ніж вони будуть 325 миль один від одного?
- Відповідь
-
Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
Намалюйте схему, щоб проілюструвати, що це відбувається.
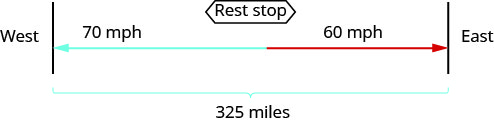
Створіть таблицю для організації інформації.

Крок 2. Визначте, що ми шукаємо.
Нас просять знайти кількість часу, який вантажівки проїдуть, поки вони не будуть 325 миль один від одного.
Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
Шукаємо пройдений час. Обидва вантажівки проїдуть однакову кількість часу. Назвемо час t. Оскільки їх швидкість різна, вони будуть їздити на різні відстані. Заповніть діаграму.
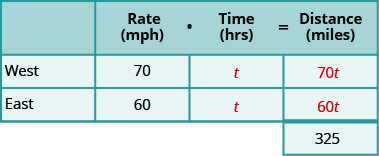
Крок 4. Перевести в рівняння.
Нам потрібно знайти співвідношення між відстанями, щоб написати рівняння. Дивлячись на діаграму, яка залежність між відстанню буде проїжджати кожен з вантажівок? Відстань, пройдену вантажівкою, що йде на захід, плюс відстань, пройдена вантажівкою, що йде на схід, повинна скласти до 325 миль. Отже, пишемо:

Крок 5. Вирішіть рівняння, використовуючи хороші методи алгебри.
\[\begin{array} {lrll} {\text{Now solve this equation. }} & {70 t+60 t} &{=} &{325} \\ {} &{130 t} &{=} &{325} \\ {} &{t} &{=} &{2.5} \end{array}\]
Крок 6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
\(\begin{array}{llll} {\text{Truck going West}} &{70\text{ mph (2.5 hours)}} &{=} &{175\text{ miles}}\\ {\text{Truck going East}} &{60\text{ mph (2.5 hour)}} &{=} &{\underline{150 \text{ miles}}}\\ {} &{} &{} &{325\text{ miles}} \end{array}\)
\(\begin{array}{ll} \\{\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{\text{It will take the truck 2.5 hours to be 325 miles apart.}} \end{array}\)
П'єр і Монік залишають свій будинок в Портленді одночасно. П'єр їде на північ на turnpike зі швидкістю 75 миль на годину, тоді як Моник їде на південь зі швидкістю 68 миль на годину. Скільки часу знадобиться їм, щоб бути 429 миль один від одного?
- Відповідь
-
3 години
Тхань і Нхат залишають свій офіс в Сакраменто одночасно. Тхань їде на північ по I-5 зі швидкістю 72 миль на годину. Нхат їде на південь на I-5 зі швидкістю 76 миль на годину. Скільки часу знадобиться їм, щоб бути на відстані 330 миль один від одного?
- Відповідь
-
2,2 години
Важливо переконатися, що одиниці збігаються, коли ми використовуємо швидкість відстані та формулу часу. Наприклад, якщо ставка вказана в милі на годину, то час повинен бути в годині.
Коли Кеті Мей ходить до школи, це займає у неї 30 хвилин. Якщо вона їде на своєму велосипеді, це займе у неї 15 хвилин. Її швидкість на три милі на годину швидше, коли вона їде на велосипеді, ніж коли вона ходить. Які її швидкість ходьби і її швидкість їзди на велосипеді?
- Відповідь
-
Спочатку ми малюємо діаграму, яка представляє ситуацію, щоб допомогти нам побачити, що відбувається.
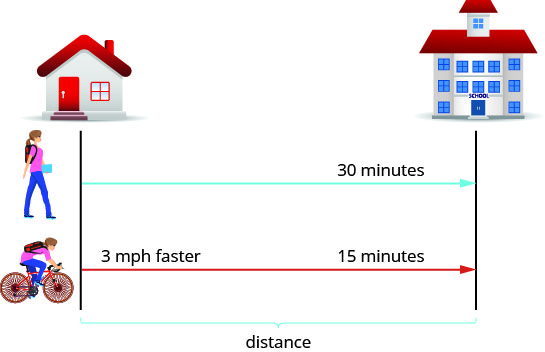
-
Нас просять знайти її швидкість ходьби і їзда на велосипеді. Назвемо її швидкість ходьби р. Оскільки її швидкість їзди на велосипеді на три милі на годину швидше, ми будемо називати цю швидкість r+3. Записуємо швидкості в графіку.
Швидкість у милі на годину, тому нам потрібно висловити час у годинами теж для того, щоб одиниці були однаковими. Пам'ятайте, одна година - це 60 хвилин. Отже:
\[\begin{array}{l}{30 \text { minutes is } \frac{30}{60} \text { or } \frac{1}{2} \text { hour }} \\ {15 \text { minutes is } \frac{15}{60} \text { or } \frac{1}{4} \text { hour }}\end{array}\]
Далі множимо ставку раз на час, щоб заповнити стовпець відстані.
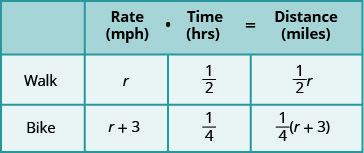
Рівняння буде виходити з того, що відстань від будинку Кеті Мей до її школи однакова, незалежно від того, ходить вона чи їздить на велосипеді.
Отже, ми говоримо:

Перевести в рівняння. 
Розв'яжіть це рівняння. 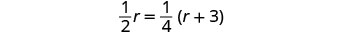
Очистити дроби, помноживши на РК всіх дробів у рівнянні. 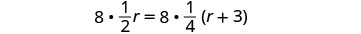
Спростити. 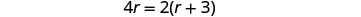
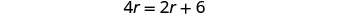


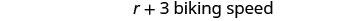

6 миль/год
(Каті) Мей на велосипеді швидкість)Давайте перевіримо, чи працює це.
Ходити 3 милі/год (0.5 година) = 1.5 милі
Велосипед 6 миль/год (0.25 година) = 1,5 миліТак, у будь-якому випадку Кеті Мей проїжджає 1,5 милі до школи. Швидкість ходьби Кеті Мей становить 3 милі/год.
Її швидкість їзди на велосипеді становить 6 миль/год.
Сюзі займає 50 хвилин, щоб піднятися в гору від стоянки до оглядової вежі. Їй потрібно 30 хвилин, щоб спуститися назад на стоянку. Її швидкість, що йде вниз, становить 2 милі на годину швидше, ніж її швидкість, що йде в гору. Знайдіть швидкісні підйоми та швидкісні спуску Сьюзі.
- Відповідь
-
в гору 1.8 миль/год, швидкісний спуск 3 миль/год
Llewyn займає 45 хвилин, щоб проїхати його човен вгору за течією від дока до його улюбленого місця риболовлі. Йому потрібно 30 хвилин, щоб проїхати човен назад за течією до причалу. Швидкість човна, що йде вниз за течією, на чотири милі на годину швидше, ніж його швидкість, що йде вгору за течією. Знайти човна 's вгору і вниз за течією швидкості.
- Відповідь
-
вгору за течією 8 миль/год, нижче за течією 12 км/
У формулі відстані, швидкості та часу час представляє фактичну кількість часу, що минув (у годині, хвилинах тощо). Якщо проблема дає нам початковий та кінцевий час як час годинника, ми повинні знайти минулий час, щоб використовувати формулу.
Гамільтон любить подорожувати до Лас-Вегаса, за 255 миль від свого будинку в окрузі Оранж. Під час своєї останньої поїздки він покинув свій будинок о 14:00. Перша частина його поїздки була на перевантажених міських автострадах. О 16:00 дорожній рух розчистився, і він зміг проїхати через пустелю зі швидкістю в 1,75 рази швидше, ніж коли він їхав у перевантаженій зоні. Він прибув до Лас-Вегаса о 6:30 вечора. Як швидко він їхав під час кожної частини своєї поїздки?
- Відповідь
-
Схема допоможе нам змоделювати цю поїздку.
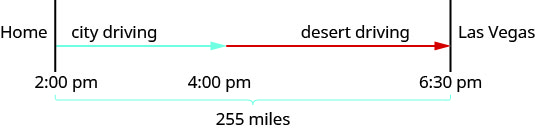
Далі створюємо таблицю для організації інформації.
Ми знаємо, що загальна відстань становить 255 миль. Шукаємо норму швидкості для кожної частини поїздки. Ставка в пустелі в 1,75 рази перевищує показник по місту. Якщо пустити r= ставка в місті, то ставка в пустелі дорівнює 1.75р.
Часи тут задаються як годинник часу. Гамільтон почав з дому о 14:00 і увійшов у пустелю о 16:30 вечора. Тож він провів дві години за кермом перевантажених автострад у місті. Потім він їхав швидше з 16:00 до 18:30 вечора в пустелі. Так він проїхав 2,5 години в пустелі.
Тепер множимо ставки на рази.
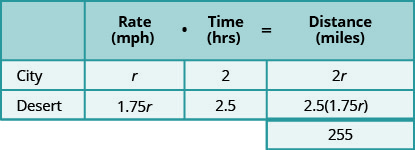
Дивлячись на діаграму нижче, ми можемо побачити, що сума відстані, пройденої в місті, і відстані, пройденої в пустелі, становить 255 миль.
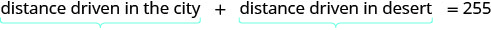
Перевести в рівняння. 
Розв'яжіть це рівняння. 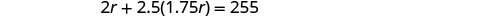
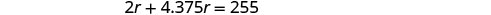
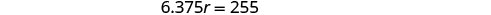
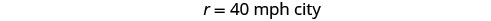
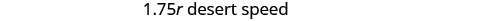
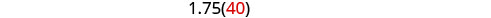
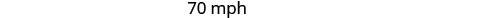
Перевірка.

Гамільтон проїхав 40 миль/год у місті та 70 миль/год у пустелі.
Круз тренується змагатися в триатлоні. Він покинув свій будинок о 6:00 і біг до 7:30. Потім він їхав на своєму велосипеді до 9:45. Він подолав загальну відстань 51 милю. Його швидкість при їзді на велосипеді була в 1,6 рази більше швидкості при бігу. Знайдіть швидкість їзди на велосипеді та бігу Круза.
- Відповідь
-
їзда на велосипеді 16 миль/год, біг 10 миль/год
Фуонг пішов з дому на своєму велосипеді о 10:00. Він їхав по рівній вулиці до 11:15, потім їхав в гору до 11:45. Він проїхав загалом 31 милю. Його швидкість їзди в гору була в 0,6 рази більше швидкості на рівній вулиці. Знайдіть свою швидкість на велосипеді в гору і по рівній вулиці.
- Відповідь
-
в гору 12 миль/год, плоска вулиця 20 миль/год
Ключові концепції
- Відстань, швидкість і час
- D = rt де D = відстань, r = швидкість, t = час
- Стратегія вирішення проблем - програми відстані, швидкості та часу
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
Намалюйте схему, щоб проілюструвати, що це відбувається.
Створіть таблицю для організації інформації: Позначте стовпці швидкість, час, відстань. Перерахуйте два сценарії. Напишіть інформацію, яку ви знаєте. - Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
Заповніть діаграму.
Використовуйте змінні вирази, щоб представити цю величину в кожному рядку.
Помножте ставку на час, щоб отримати відстань. - Перевести в рівняння.
Повторюйте проблему в одному реченні з усією важливою інформацією.
Потім переведіть речення в рівняння. - Вирішіть рівняння, використовуючи хороші методи алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
