3.2: Вирішити відсоток додатків
- Page ID
- 58891
До кінця цього розділу ви зможете:
- Перекласти та вирішити базові відсоткові рівняння
- Вирішити відсотки додатків
- Знайти відсоток збільшення і відсоток зниження
- Вирішуйте прості програми за інтересами
- Вирішуйте заявки зі знижкою або націнкою
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Перетворіть 4.5% до десяткового.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Перетворіть 0,6 до відсотка.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Округлення 0,875 до найближчої сотої.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Множимо (4,5) (2,38).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Вирішити 3.5=0.7n.
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Відніміть 50−37.45.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Перекласти та вирішити базові відсоткові рівняння
Ми будемо вирішувати відсоткові рівняння за допомогою методів, які ми використовували для розв'язання рівнянь з дробами або десятковими числами. Без інструментів алгебри найкращим методом, доступним для вирішення відсоткових проблем, було встановлення їх як пропорцій. Тепер, як студент алгебри, ви можете просто перевести англійські речення в алгебраїчні рівняння, а потім вирішити рівняння.
Ми можемо використовувати будь-яку вподобану букву як змінну, але непогано вибрати лист, який буде нагадувати нам про те, що ви шукаєте. Ми повинні бути впевнені, що змінимо заданий відсоток на десятковий, коли ми ставимо його в рівняння.
Перекладіть і вирішуйте: Яке число 35% від 90?
- Відповідь
-
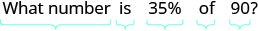
Перевести на алгебру. Нехай n = число. 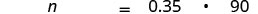
Пам'ятайте, що «з» означає множити, «є» означає дорівнює. Помножити. 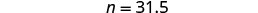
31.5 є 35% з 90
Перекладіть і вирішуйте:
Яке число 45% від 80?
- Відповідь
-
36
Перекладіть і вирішуйте:
Яке число 55% від 60?
- Відповідь
-
33
Ми повинні бути дуже обережними, коли перекладаємо слова в наступному прикладі. Невідома кількість спочатку не буде ізольована, як це було в прикладі. Ми знову будемо використовувати прямий переклад для написання рівняння.
Перекладіть і вирішуйте: 6,5% від якого числа становить 1,17$?
- Відповідь
-

Перекласти. Нехай n = число. 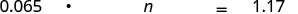
Помножити. 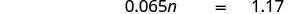
Розділіть обидві сторони на 0,065 і спростіть. 
6.5% від $18 є $1.17
Перекладіть і вирішуйте:
7,5% від якого числа є $1.95?
- Відповідь
-
$26
Перекладіть і вирішуйте:
8.5% від якого числа $3.06?
- Відповідь
-
$36
У наступному прикладі шукаємо відсотки.
Перекладіть і вирішуйте: 144 - це що відсоток з 96?
- Відповідь
-
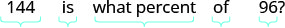
Перевести на алгебру. Нехай p = відсоток. 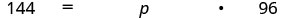
Помножити. 
Розділіть на 96 і спростіть. 
Перетворити на відсотки. 
144 є 150% з 96 Зауважте, що нас просять знайти відсотки, тому ми повинні мати свій кінцевий результат у відсотковій формі.
Перекладіть і вирішуйте:
110 - це який відсоток від 88?
- Відповідь
-
125%
Перекладіть і вирішуйте:
126 - це який відсоток від 72?
- Відповідь
-
175%
Вирішити додатки відсотків
Багато додатків відсотків - таких як поради, податок з продажів, знижки та відсотки - трапляються в нашому повсякденному житті. Щоб вирішити ці програми, ми переведемо на базове рівняння відсотків, подібно до тих, які ми вирішували в попередніх прикладах. Як тільки ми переводимо речення в рівняння відсотків, ми знаємо, як його вирішити.
Ми відновимо стратегію вирішення проблем, яку ми використовували раніше, для зручності ознайомлення.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в алгебраїчне рівняння.
- Вирішіть рівняння, використовуючи хороші методи алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
Тепер, коли ми маємо стратегію, на яку слід посилатися, і ми практикуємо рішення базових відсоткових рівнянь, ми готові вирішувати відсоткові додатки. Обов'язково запитайте себе, чи має сенс ваша остаточна відповідь - оскільки багато програм стосуватимуться повсякденних ситуацій, ви можете покластися на власний досвід.
Дезон і його подруга насолоджувалися приємною вечерею в ресторані, і його рахунок був $68.50. Він хоче залишити 18% чайових. Якщо чайові становитимуть 18% від загальної суми рахунку, скільки чайових він повинен залишити?
- Відповідь
-
Зверніть увагу, що ми використовували t для представлення невідомого наконечника.Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. кількість чайових повинен залишити Dezohn Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай t = кількість чайових. Крок 4. Перевести в рівняння. 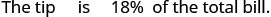
Напишіть речення, яке дає інформацію, щоб знайти її. 
Переведіть речення в рівняння. 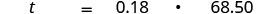
Крок 5. Вирішити рівняння. Помножити. 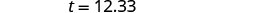
Крок 6. Перевірте. Чи має це сенс? Так, 20% від 70 доларів - це 14 доларів. Крок 7. Відповісти на питання повним реченням. Дезон повинен залишити чайові $12,33.
Сьєрра та її сестра насолоджувалися вечерею в ресторані, а рахунок становив $81,50. Якщо вона хоче залишити 18% від загального рахунку як свою чайову, скільки вона повинна залишити?
- Відповідь
-
$14.67
Kimngoc обідав у своєму улюбленому ресторані. Вона хоче залишити 15% від загального рахунку як її чайові. Якщо її рахунок становив 14,40 доларів, скільки вона залишить на чайові?
- Відповідь
-
$2.16
На етикетці на каші для сніданку Масао сказано, що одна порція крупи забезпечує 85 міліграмів (мг) калію, що становить 2% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість калію?
- Відповідь
-
Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. загальна кількість калію, яке рекомендується Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай a= загальна кількість калію. Крок 4. Перекласти. Напишіть речення, яке дає інформацію, щоб знайти її. 
Перевести в рівняння. 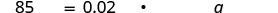
Крок 5. Вирішити рівняння. 
Крок 6. Перевірте. Чи має це сенс? Так, 2% - це невеликий відсоток, а 85 - невелика частина 4250. Крок 7. Відповісти на питання повним реченням. Кількість калію, яке рекомендується, становить 4250 мг.
Одна порція пшеничного квадратного злаку містить сім грамів клітковини, що становить 28% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість клітковини?
- Відповідь
-
25 грам
Одна порція рисової крупи містить 190 мг натрію, що становить 8% від рекомендованої добової кількості. Яка загальна рекомендована добова кількість натрію?
- Відповідь
-
2,375 мг
Mitzi отримав кілька вишуканих тістечок в подарунок. Обгортка сказала, що кожен будинковий має 480 калорій, і в ньому 240 калорій жиру. Який відсоток загальної кількості калорій в кожному брауні надходить від жиру?
- Відповідь
-
Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. відсоток від загальної кількості калорій з жиру Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай р = відсоток жиру. Крок 4. Перекласти. Напишіть речення, яке дає інформацію, щоб знайти її. 
Перевести в рівняння. 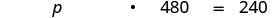
Крок 5. Вирішити рівняння. 
Розділити на 480. 
Викласти в процентну форму. 
Крок 6. Перевірте. Чи має це сенс? Так, 240 - це половина з 480, тому 50% має сенс. Крок 7. Відповісти на питання повним реченням. Із загальної кількості калорій в кожному будинковому 50% становить жир.
Вирішити. Округлити до найближчого цілого відсотка.
Вероніка планує приготувати кекси з міксу. На упаковці написано, що кожен кекс буде 230 калорій, а 60 калорій - з жиру. Який відсоток від загальної кількості калорій припадає на жир?
- Відповідь
-
26%
Вирішити. Округлити до найближчого цілого відсотка.
Суміш Рікардо планує використовувати для приготування тістечок, говорить про те, що кожен будинковий складе 190 калорій, а 76 калорій - з жиру. Який відсоток від загальної кількості калорій припадає на жир?
- Відповідь
-
40%
Знайти відсоток збільшення і відсоток зниження
Люди в засобах масової інформації часто говорять про те, наскільки сума збільшилася або зменшилася за певний проміжок часу. Зазвичай вони виражають це збільшення або зменшення у відсотках.
Щоб знайти процентне збільшення, спочатку знаходимо суму збільшення, різницю нової суми та початкової суми. Потім знаходимо, який відсоток становить сума збільшення від початкової суми.
- Знайти величину надбавки.
\(\text{new amount }−\text{ original amount }=\text{ increase}\) - Знайдіть відсоток збільшення.
Збільшення - це який відсоток від початкової суми?
У 2011 році губернатор Каліфорнії запропонував підвищити плату за коледж громади від 26 доларів за одиницю до 36 доларів за одиницю. Знайдіть відсоток збільшення. (Округлити до найближчої десятої частки відсотка.)
- Відповідь
-
Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. відсоток збільшення Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай p = p = відсоток. Крок 4. Перекласти. Напишіть речення, яке дає інформацію, щоб знайти її. Спочатку знайдіть величину надбавки. new amount − початкова сума = збільшення 36−26=10 Знайдіть відсоток. Збільшення - це який відсоток від початкової суми? 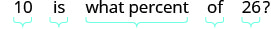
Перевести в рівняння. 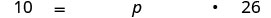
Крок 5. Вирішити рівняння. 
Розділити на 26. 
Змінити на відсоткову форму; округлити до найближчої десятої. 
Крок 6. Перевірте. Чи має це сенс? Так, 38,4% близький до\(\frac{1}{3}\), а 10 близький до\(\frac{1}{3}\) 26. Крок 7. Відповісти на питання повним реченням. Нові збори представляють собою збільшення на 38,4% порівняно зі старими комісіями.
Знайдіть відсоток збільшення. (Округлити до найближчої десятої частки відсотка.)
У 2011 році IRS збільшила франшизу вартість пробігу до 55,5 центів з 51 цента.
- Відповідь
-
8,8%
Знайдіть відсоток збільшення.
У 1995 році стандартна вартість проїзду на автобусі в Чикаго становила $1,50. У 2008 році стандартна вартість проїзду на автобусі становила $2,25.
- Відповідь
-
50%
Знаходження процентного зменшення дуже схоже на знаходження процентного збільшення, але тепер сума зменшення - це різниця початкової суми та нової суми. Потім знаходимо, який відсоток становить сума зменшення від початкової суми.
- Знайти величину зменшення.
\(\text{original amount }−\text{ new amount }=\text{ decrease}\) - Знайдіть відсоток зменшення.
Зниження - це який відсоток від початкової суми?
Середня ціна галона газу в одному місті в червні 2014 року становила $3,71. Середня ціна в цьому місті в липні становила $3.64. Знайдіть відсоток зменшення.
- Відповідь
-
Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. відсоток зниження Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості. Нехай p = відсоток зменшиться. Крок 4. Перекласти. Напишіть речення, яке дає інформацію, щоб знайти її. Спочатку знайдіть величину зменшення. 3.71−3.64=0.07 Знайдіть відсоток. Зниження - це який відсоток від початкової суми? 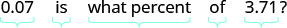
Перевести в рівняння. 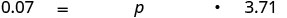
Крок 5. Вирішити рівняння. 
Розділити на 3,71. 
Змінити на відсоткову форму; округлити до найближчої десятої. 
Крок 6. Перевірте. Чи має це сенс? Так, якби початкова ціна становила 4 долари, зниження на 2% становило б 8 центів. Крок 7. Відповісти на питання повним реченням. Ціна на газ знизилася на 1,9%.
Знайдіть відсоток зменшення. (Округлити до найближчої десятої частки відсотка.)
Населення Північної Дакоти в 2010 році становило близько 672 000 осіб. За прогнозами, населення становитиме близько 630 000 у 2020 році.
- Відповідь
-
6,3%
Знайдіть відсоток зменшення.
У минулому році зарплата Шейли становила 42 000 доларів. Через відпущені дні цього року її зарплата становила 37 800 доларів.
- Відповідь
-
10%
Вирішіть прості програми для інтересів
Чи знаєте ви, що банки платять вам, щоб зберегти ваші гроші? Гроші, які клієнт вкладає в банк, називаються принципалом, П, а гроші, які банк платить клієнту, називаються відсотками. Відсотки обчислюються як певний відсоток від основної суми; називається процентною ставкою, р. Зазвичай ми виражаємо процентну ставку у відсотках на рік, і обчислюємо її, використовуючи десятковий еквівалент відсотків. Змінна t, (для часу) являє собою кількість років, в яких гроші знаходяться на рахунку.
Щоб знайти інтерес, ми використовуємо просту формулу відсотків, I=Prt.
Якщо сума грошей, П, звана основною, вкладається протягом t років за річною процентною ставкою r, сума відсотків, I, зароблених дорівнює
\[\begin{array}{lllll} {} &{} &{I} &{=} &{\text { interest }}\\ {I = Prt} &{\text{where}} &{P} &{=} &{\text { principle }}\\ {} &{} &{r} &{=} &{\text { rate }}\\ {} &{} &{t} &{=} &{\text { time }} \end{array}\]
Відсотки, зароблені за цією формулою, називають простими відсотками.
Відсотки можуть розраховуватися і іншим способом, званим складними відсотками. Цей тип інтересу буде висвітлений на наступних заняттях з математики.
Формула, яку ми використовуємо для обчислення простих відсотків, це I = Prt. Щоб скористатися формулою, підставляємо в значення, які нам дає задача, для змінних, а потім вирішуємо для невідомої змінної. Можливо, буде корисно впорядкувати інформацію в діаграмі.
Наталі внесла $12,500 на свій банківський рахунок, де вона заробить 4% відсотків. Скільки відсотків заробить Наталі за 5 років?
\[\begin{aligned} I &=? \\ P &=\$ 12,500 \\ r &=4 \% \\ t &=5 \text { years } \end{aligned}\]
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of interest earned}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for.}} &{\text{Let I = the amount of interest.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{I = (12500)(.04)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{I = 2500} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {\qquad \text{Is } $2,500 \text{ is a reasonable interest} } &{} \\ {\qquad \text{on }$12,500? \text{ Yes.}} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The interest is }$2500} \\ {\text{complete sentence.}} &{} \ \end{array}\)
Арелі інвестувала основний капітал у розмірі 950 доларів на свій банківський рахунок з процентною ставкою 3%. Скільки відсотків вона заробила за 5 років?
- Відповідь
-
$142,50
Сусана інвестувала основний капітал у розмірі 36 000 доларів на свій банківський рахунок з процентною ставкою 6,5%. Скільки відсотків вона заробила за 3 роки?
- Відповідь
-
$7020
Можуть бути випадки, коли ми знаємо суму відсотків, зароблених за певним принципалом протягом певного періоду часу, але ми не знаємо ставки. Щоб знайти ставку, використовуємо просту процентну формулу, підставляємо в задані значення принципала і часу, а потім вирішуємо для ставки.
Лорен позичив своєму братові 3000 доларів, щоб допомогти йому придбати машину. Через 4 роки його брат виплатив йому 3,000 доларів плюс 660 доларів у відсотках. Якою була процентна ставка?
\[\begin{array}{lll} {I} &{=} &{\$ 660} \\ {P} &{=} &{\$ 3000} \\ {r} &{=} &{?} \\ {t} &{=} &{4 \text { years } }\end{array}\]
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the rate of interest}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. Choose}} &{\text{Let r = the rate of interest.}} \\ {\text{ a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{660 = (3000)r(4)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{660 = (12000)r} \\ {\text{Divide.}} &{0.055 = r} \\ {\text{Change to percent form.}} &{5.5\% = r} \\\\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {I = Prt} &{} \\ {660 \stackrel{?}{=} (3000)(0.055)(4)} &{} \\ {660 = 660\checkmark} &{} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The rate of interest was }5.5%} \\ {\text{complete sentence.}} &{} \end{array}\)
Зверніть увагу, що в цьому прикладі брат Лорен заплатив відсотки Лорен, так само, як банк заплатив би відсотки, якби Лорен вклав туди свої гроші.
Джим позичив своїй сестрі 5000 доларів, щоб допомогти їй купити будинок. Через 3 роки вона заплатила йому 5000 доларів, плюс 900 доларів відсотків. Якою була процентна ставка?
- Відповідь
-
6%
Ханг позичив у батьків 7500 доларів, щоб оплатити навчання. За 5 років вона заплатила їм 1,500 відсотків на додаток до 7500 доларів, які вона позичила. Якою була процентна ставка?
- Відповідь
-
4%
Едуардо помітив, що в його нових документах про автокредит зазначено, що при процентній ставці 7,5% він заплатить 6 596,25 доларів відсотків протягом 5 років. Скільки він позичив, щоб заплатити за свою машину?
- Відповідь
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount borrowed (the principal)}} \\ {\text{a variable to represent that quantity.}} &{} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{Let P = principal borrowed.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{6596.25 = P(0.075)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{6596.25 = 0.375P} \\ {\text{Divide.}} &{17590 = P} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ {I = Prt} &{} \\ {6596.25 \stackrel{?}{=} (17590)(0.075)(5)} &{} \\ {6596.25 = 6596.25\checkmark} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The principal is }$17590} \\ {\text{complete sentence.}} &{} \ \end{array}\)
У новій заяві Шона про кредит на автомобіль говориться, що він заплатить 4,866,25 доларів у відсотках від процентної ставки 8,5% протягом 5 років. Скільки він позичив, щоб купити свою нову машину?
- Відповідь
-
$11,450
За 5 років банківський рахунок Глорії заробив 2400 доларів відсотків під 5%. Скільки вона внесли на рахунок?
- Відповідь
-
$9,600
Вирішуйте програми зі знижкою або націнкою
Додатки знижки дуже поширені в роздрібних налаштуваннях. Коли ви купуєте товар у продажу, початкова ціна була знижена на деяку суму в доларах. Ставка дисконтування, зазвичай дається у відсотках, використовується для визначення суми знижки. Для визначення суми знижки множимо ставку дисконту на початкову ціну.
Ми підсумовуємо модель знижки у вікні нижче.
\[\begin{array}{l}{\text { amount of discount }=\text { discount rate } \times \text { original price }} \\ {\text { sale price }=\text { original price - amount of discount }}\end{array}\]
Майте на увазі, що ціна продажу завжди повинна бути меншою за початкову ціну.
Еліза купила плаття, яке було знижено 35% від початкової ціни 140 доларів. Яка була ⓐ сума знижки та ⓑ ціна продажу сукні?
- Відповідь
-
1. \(\begin{array} {lll} {\text{Original price}} &{=} &{$140} \\ {\text{Discount rate}} &{=} &{35\%} \\ {\text{Discount?}} &{=} &{?} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{} \\ {\text{Translate into an equation}} &{d = 0.35(140)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 49} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is a }$49\text{ discount reasonable for a}} &{} \\ {$140\text{ dress? Yes.}} &{} \\\\ {\textbf{Step 7. Write} \text{ a complete sentence to answer}} &{\text{The amount of discount was }$49} \\ {\text{the question.}} &{} \ \end{array}\)2.
Прочитайте проблему ще раз.Крок 1. Визначте, що ми шукаємо. ціна продажу сукні Крок 2. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості. Нехай s= ціна продажу. Крок 3. Перевести в рівняння. Напишіть речення, яке дає інформацію, щоб знайти її. 
Перевести в рівняння. 
Крок 4. Вирішити рівняння. 
Крок 5. Перевірте. Чи має це сенс? Чи ціна продажу менша за початкову ціну? Так, 91 долар менше 140 доларів. Крок 6. Відповісти на питання повним реченням. Ціна продажу сукні становила 91 долар.
Знайдіть ⓐ суму знижки і ⓑ ціну продажу:
Серхіо купив ремінь, який був знижений 40% від початкової ціни 29 доларів.
- Відповідь
-
ⓐ $11.60 ⓑ $17.40
Знайдіть ⓐ суму знижки і ⓑ ціну продажу:
Оскар купив барбекю, який був знижений 65% від початкової ціни 395 доларів.
- Відповідь
-
ⓐ $256.75 ⓑ $138.25
Можуть бути випадки, коли ми знаємо початкову ціну та ціну продажу, і ми хочемо знати ставку дисконту. Щоб знайти ставку дисконтування, спочатку ми знайдемо суму знижки, а потім використаємо її для обчислення ставки у відсотках від початкової ціни. Вправа\(\PageIndex{37}\) покаже цей випадок.
Жаннет купила купальник за ціною продажу $13,95. Початкова ціна купальника становила 31 долар. Знайдіть ⓐ розмір знижки та ⓑ дисконтну ставку.
- Відповідь
-
ⓐ\(\begin{array} {lll} {\text{Original price}} &{=} &{$31} \\ {\text{Discount}} &{=} &{?} \\ {\text{Sale Price}} &{=} &{$ 13.95} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{\text{The discount is the difference between the original}} \\ {} &{\text{price and the sale price.}} \\{\text{Translate into an equation}} &{d = 31 - 13.95} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 17.05} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is }17.05\text{ less than 31? Yes.}} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a complete sentence.}} &{\text{The amount of discount was }$17.05} \end{array}\)ⓑ
1. Коли ми переведемо це в рівняння, ми отримуємо 17.05 дорівнює r раз 31. Нам кажуть вирішити рівняння 17.05 дорівнює 31р. Ми ділимо на 31, щоб отримати 0,55 дорівнює r Ми ставимо це у відсотках, щоб отримати r дорівнює 55%. Нам кажуть перевірити: чи є в цьому сенс? Чи дорівнює 7,05 55% від >1? Нижче цього, ми маємо 17.05 дорівнює зі знаком питання над ним 0.55 рази 31. Нижче цього у нас 17.05 дорівнює 17.05 з галочкою поруч з ним. Тоді нам кажуть відповісти на питання повним реченням: Ставка знижки склала 55%». >
Прочитайте проблему ще раз.Крок 1. Визначте, що ми шукаємо. облікова ставка Крок 2. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай r=r = ставка дисконтування. Крок 3. Перевести в рівняння. Напишіть речення, яке дає інформацію, щоб знайти її. 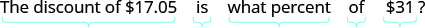
Перевести в рівняння. 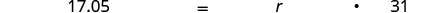
Крок 4. Вирішити рівняння. 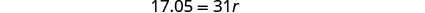
Розділіть обидві сторони на 31. 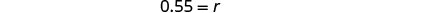
Змінити на відсоткову форму. 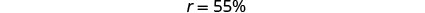
Крок 5. Перевірте. Чи має це сенс? Чи дорівнює $17.05 55% від $31? \(17.05\stackrel{?}{=}0.55(31)\) \(17.05=17.05\checkmark\) Крок 6. Відповісти на питання повним реченням. Ставка дисконту склала 55%.
Знайти
- розмір знижки та
- облікова ставка.
Лена купила кухонний стіл за ціною продажу 375,20$. Початкова ціна столу становила 560 доларів.
- Відповідь
-
- $184,80
- 33%
Знайти
- розмір знижки та
- облікова ставка.
Нік купив багатокімнатний кондиціонер за ціною продажу $340. Початкова ціна кондиціонера становила 400 доларів.
- Відповідь
-
- $60
- 15%
Додатки націнки дуже поширені в роздрібних налаштуваннях. Ціна, яку роздрібний продавець платить за товар, називається початковою вартістю. Потім роздрібний продавець додає націнку до початкової вартості, щоб отримати прейскурантну ціну, ціну, за яку він продає товар. Націнка зазвичай розраховується як відсоток від початкової вартості. Щоб визначити суму націнки, помножте ставку націнки на початкову вартість.
Підсумовуємо модель націнки в поле нижче.
\[\begin{array}{l}{\text { amount of mark-up }=\text { mark-up rate } \times \text { original cost }} \\ {\text { list price }=\text { original cost }+\text { amount of mark up }}\end{array}\]
Майте на увазі, що прейскурантна ціна завжди повинна бути більше, ніж початкова вартість.
Художня галерея Адама купила фотографію за оригінальною вартістю 250 доларів. Адам відзначив ціну вгору на 40%. Знайдіть
- сума націнки і
- прейскурант ціни фотографії.
- Відповідь
-
1.
2.Крок 1. Прочитайте проблему. Крок 2. Визначте, що ми шукаємо. сума націнки Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай m = сума націнки. Крок 4. Перевести в рівняння. Напишіть речення, яке дає інформацію, щоб знайти її. 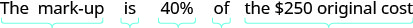
Перевести в рівняння. 
Крок 5. Вирішити рівняння. 
Крок 6. Перевірте. Чи має це сенс? Так, 40% менше половини і 100 менше половини з 250. Крок 7. Відповісти на питання повним реченням. Націнка на фотографії склала 100 доларів. Крок 1. Прочитайте проблему ще раз. Крок 2. Визначте, що ми шукаємо. прейскурант прайса Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для її представлення. Нехай p = прейскурантна ціна. Крок 4. Перевести в рівняння. Напишіть речення, яке дає інформацію, щоб знайти її. 
Перевести в рівняння. 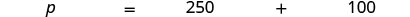
Крок 5. Вирішити рівняння. 
Крок 6. Перевірте. Чи має це сенс? Чи є прейскурантна ціна більше, ніж ціна нетто?
Це $350 більше, ніж $250? Так.Крок 7. Відповісти на питання повним реченням. Прайс-лист фотографії становив 350 доларів.
Знайти
- сума націнки і
- прейскурант прайс.
Музичний магазин Джима купив гітару за первісною вартістю 1200 доларів. Джим відзначив ціну вгору на 50%.
- Відповідь
-
- 600 дол. США
- $1,800
Знайти
- сума націнки і
- прейскурант прайс.
Магазин автоперепродажу купив Тойоту Пабло за 8500 доларів. Вони відзначили ціну вгору на 35%.
- Відповідь
-
- $2,975
- $11,475
Ключові концепції
- Відсоток Збільшення Щоб знайти відсоток збільшення:
- Знайти суму збільшення. increase=new amount−originalamountincrease=нова сумати−оригіналсума
- Знайдіть відсоток збільшення. Збільшення - це який відсоток від початкової суми?
- Відсоток Зменшення Щоб знайти відсоток зменшення:
- Знайти суму зменшення. decrease=початкова сума−newamountdecrease=початкова сума−newamount
- Знайдіть відсоток зменшення. Зниження - це який відсоток від початкової суми?
- Прості відсотки Якщо сума грошей, П, звана основною, вкладається протягом t років за річною процентною ставкою r, сума відсотків, I, зароблених дорівнює
\[\begin{aligned} I &=P r t \\ \text { where } I &=\text { interest } \\ P &=\text { principal } \\ r &=\text { rate } \\ t &=\text { time } \end{aligned}\]
- Знижка
- сума знижки - дисконтна ставка ·· початкова ціна
- ціна продажу - початкова ціна — знижка
- Націнка
- сума націнки - ставка націнки ·· первісна вартість
- прейскурант ціна первісна вартість +націнка
Глосарій
- сума знижки
- Сума знижки - це сума, отримана при множенні ставки дисконтування на початкову ціну товару.
- дисконтна ставка
- Ставка дисконтування - це відсоток, який використовується для визначення суми знижки, поширеної в роздрібних налаштуваннях.
- інтерес
- Відсотки - це гроші, які банк платить своїм клієнтам за зберігання їх грошей в банку.
- прайс-лист
- Ціна прейскуранта - це ціна, за яку продає товар роздрібний продавець.
- націнка
- Націнка - це відсоток від початкової вартості, який використовується для збільшення ціни товару.
- первісна вартість
- Початкова вартість у роздрібній торгівлі - це ціна, яку роздрібний продавець платить за товар.
- принципал
- Основний капітал - це початкова сума грошей, вкладених або позичених на певний період часу за певною процентною ставкою.
- процентна ставка
- Ставка відсотків становить відсоток від основної суми, зазвичай виражається у відсотках на рік.
- простий інтерес
- Простий відсоток - це відсотки, зароблені за формулою I = Prt.
