3.1: Використовуйте стратегію вирішення проблем

Last updated
Save as PDF

Page ID: 58883

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Підходьте до проблем слів з позитивним настроєм
Використовуйте стратегію вирішення проблем для проблем зі словами
Вирішити проблеми з числом

Примітка

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Переведіть «6 менше двох разів x» на алгебраїчний вираз.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.43.
Вирішити:$\frac{2}{3}x=24$.
Якщо ви пропустили цю проблему, перегляньте Вправа 2.2.10.
Вирішити:$3x+8=14$.
Якщо ви пропустили цю проблему, перегляньте Вправа 2.3.1.

Підійдіть до проблем слова з позитивним ставленням

«Якщо ти думаєш, що можеш... або думаєш, що не можеш... ти маєш рацію». —Генрі Форд

Світ сповнений проблем зі словами! Чи буде мій дохід кваліфікувати мене на оренду цієї квартири? Скільки перфоратора мені потрібно зробити для вечірки? Якого розміру діамант я можу дозволити собі купити своїй дівчині? Чи повинен я літати або їхати на возз'єднання сім'ї? Скільки потрібно грошей, щоб заправити машину газом? Скільки чайових я повинен залишити в ресторані? Скільки шкарпеток потрібно упакувати для відпустки? Якого розміру індичку мені потрібно купити на вечерю на День Подяки, а потім в який час мені потрібно поставити її в духовку? Якщо ми з сестрою купуємо мамі подарунок, скільки платить кожен з нас?

Тепер, коли ми можемо вирішувати рівняння, ми готові застосувати наші нові навички до проблем зі словами. Чи знаєте ви когось, хто мав негативний досвід у минулому зі словами проблем? У вас коли-небудь були думки, як у учня нижче (Рисунок$\PageIndex{1}$)?

Студент показаний з бульбашками думки кажучи: «Я не знаю, чи потрібно додавати, віднімати, множити або ділити! ,» «Я не розумію проблем зі словами! «Мої вчителі ніколи цього не пояснювали! ,» «Якщо я просто пропущу всі проблеми зі словами, я, ймовірно, все ще можу пройти клас», і «Я просто не можу цього зробити!» — Малюнок$\PageIndex{1}$: Негативні думки можуть бути перешкодами для успіху.

Коли ми відчуваємо, що не маємо контролю, і продовжуємо повторювати негативні думки, ми встановлюємо бар'єри на шляху до успіху. Нам потрібно заспокоїти свої страхи і змінити свої негативні почуття.

Почніть зі свіжого аркуша і починайте думати про позитивні думки. Якщо ми візьмемо під контроль і віримо, що можемо бути успішними, ми зможемо освоїти проблеми зі словами! Прочитайте позитивні думки на малюнку$\PageIndex{2}$ і скажіть їх вголос.

Студенту показують з бульбашками думки, кажучи: «Хоча проблеми зі словами були важкими в минулому, я думаю, що можу спробувати їх зараз», «Я краще підготовлений зараз. Думаю, я почну розбиратися в проблемах слів», «Я думаю, що зможу! Я думаю, що можу! ,» і «Це може зайняти час, але я можу почати вирішувати проблеми зі словами». — Малюнок$\PageIndex{2}$: Мислення позитивних думок - це перший крок до успіху.

Подумайте про щось поза школою, що ви можете зробити зараз, але не могли зробити 3 роки тому. Це за кермом автомобіля? Сноуборд? Готуєте вишукану страву? Розмовляєте новою мовою? Ваш минулий досвід зі словами проблеми трапився, коли ви були молодшими - тепер ви старші і готові досягти успіху!

Використовуйте стратегію вирішення проблем для проблем Word

Ми розглянули переклад англійських фраз на алгебраїчні вирази, використовуючи деякі основні математичні словники та символи. Ми також переклали англійські речення в алгебраїчні рівняння і вирішили деякі проблеми зі словами. Слово задачі застосовувало математику до повсякденних ситуацій. Ми переписали ситуацію в одному реченні, присвоїли змінну, а потім написали рівняння для вирішення задачі. Цей метод працює до тих пір, поки ситуація знайома і математика не надто складна.

Тепер ми розширимо нашу стратегію, щоб ми могли використовувати її для успішного вирішення будь-якої проблеми зі словами. Ми перерахуємо стратегію тут, а потім використаємо її для вирішення деяких проблем. Нижче ми підсумуємо ефективну стратегію вирішення проблем.

ВИКОРИСТОВУЙТЕ СТРАТЕГІЮ ВИРІШЕННЯ ПРОБЛЕМ ДЛЯ ВИРІШЕННЯ ЗАВДАНЬ ЗІ СЛОВАМИ.

Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
Визначте, що ми шукаємо.
Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в алгебраїчне рівняння.
Вирішіть рівняння, використовуючи хороші методи алгебри.
Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
Відповісти на питання повним реченням.

Вправа$\PageIndex{1}$

Пілар купила гаманець у продажу за$$18$, що становить половину від початкової ціни. Якою була початкова ціна гаманця?

Відповідь

Крок 1. Прочитайте проблему. Прочитайте проблему два або більше разів, якщо це необхідно. Шукайте будь-які незнайомі слова в словнику або в Інтернеті.

У цій проблемі зрозуміло, про що йде мова? Чи знайоме кожне слово?

Нехай р = початкова ціна гаманця.

Крок 2. Визначте, що ви шукаєте. Ви коли-небудь заходили у свою спальню, щоб щось отримати, а потім забули те, що шукали? Важко щось знайти, якщо ви не впевнені, що це таке! Прочитайте проблему ще раз і шукайте слова, які підкажуть вам, що ви шукаєте!

У цій задачі слова «яка була початкова ціна гаманця» розповідають нам, що нам потрібно знайти.

Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості. Ми можемо використовувати будь-яку букву для змінної, але виберіть ту, яка полегшує запам'ятовування того, що вона представляє.

Крок 4. Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Переведіть англійське речення в алгебраїчне рівняння.

Уважно перечитайте проблему, щоб побачити, як пов'язана дана інформація. Часто зустрічається одне речення, яке дає цю інформацію, або воно може допомогти написати одне речення з усією важливою інформацією. Шукайте підказкові слова, які допоможуть перевести речення на алгебру. Переведіть речення в рівняння.

Повторюйте проблему в одному реченні з усією важливою інформацією.	$\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}$
Перевести в рівняння.	$18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p$

Крок 5. Вирішіть рівняння, використовуючи хороші алгебраїчні методи. Навіть якщо ви знаєте рішення відразу, використання хороших алгебраїчних прийомів тут краще підготує вас до вирішення проблем, які не мають очевидних відповідей.

Розв'яжіть рівняння.	$18 = \frac{1}{2}p$
Помножте обидві сторони на 2.	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
Спростити.	$36 = p$

Крок 6. Перевірте відповідь у проблемі, щоб переконатися, що це має сенс. Ми вирішили рівняння і виявили$p=36$, що, що означає «початкова ціна» була$$36$.

Чи має сенс 36 доларів у проблемі? Та тому, що 18 - це половина з 36, а гаманець був у продажу за половину початкової ціни.

Якби це була домашня вправа, наша робота могла б виглядати так:

Пілар купила гаманець у продажу за$$18$, що в півтора рази менше початкової ціни. Якою була початкова ціна гаманця?

Крок 7. Відповісти на питання повним реченням. Проблема запитала «Яка була початкова ціна гаманця?»

Відповідь на питання: «Початкова ціна гаманця становила 36 доларів».

	Нехай$p =$ первісна ціна.
	$18$становить половину початкової ціни.
	$18 = \frac{1}{2}p$
Помножте обидві сторони на$2$.	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
Спростити.	$36 = p$
Перевірте. Чи$$36$ доступна ціна за гаманець?
Так.
$18$Одна половина$36$?
$18 \stackrel{?}{=} \frac{1}{2}\cdot 36$
$18 = 18\checkmark$
	Початкова ціна гаманця була$$36$.

Вправа$\PageIndex{2}$

Хоакін купив у продажу книжкову шафу$$120$, яка становила дві третини від початкової ціни. Якою була початкова ціна книжкової шафи?

Відповідь: $$180$

Вправа$\PageIndex{3}$

Дві п'яті пісні в плейлисті Маріель - кантрі. Якщо є пісні$16$ кантрі, яка загальна кількість пісень у плейлисті?

Відповідь: $40$

Спробуємо такий підхід на іншому прикладі.

Вправа$\PageIndex{4}$

Джіні та її однокласники сформували навчальну групу. Кількість дівчат у досліджуваній групі становила втричі більше, ніж в два рази більше, ніж у хлопчиків. У$11$ досліджуваній групі були дівчата. Скільки хлопчиків було в досліджуваній групі?

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.	Скільки хлопчиків було в досліджуваній групі?
Крок 3. Ім'я. Виберіть змінну, щоб представити кількість хлопчиків.	Нехай$n=$ кількість хлопчиків.
Крок 4. Перекласти. Повторюйте проблему в одному реченні з усією важливою інформацією.	$\color{cyan} \underbrace{\color{black}\textbf{The number}\\ \color{black}\textbf{of girls}(11)} \quad \underbrace{\strut \text{ } \\ \color{black}\textbf{was}} \quad \underbrace{\color{black}\textbf{three more than}\\ \color{black}\textbf{twice the number of boys}}$
Перевести в рівняння.	$\qquad 11 \qquad \quad = \qquad \qquad \quad 2b + 3$
Крок 5. Розв'яжіть рівняння.	$\quad 11 = 2b + 3 $
Відніміть по 3 з кожного боку.	$\quad 11 \,{\color{red}{- \,3}} = 2b + 3 \,{\color{red}{- \,3}} $
Спростити.	$\quad 8 = 2b $
Розділіть кожну сторону на 2.	$ \quad \dfrac{8}{\color{red}{2}}=\dfrac{2b}{\color{red}{2}} $
Спростити.	$\quad 4 = b$
Крок 6. Перевірте. По-перше, чи розумна наша відповідь? Так, мати$4$ хлопчиків у дослідницькій групі здається нормальним. Проблема говорить, що кількість дівчат була$3$ більш ніж удвічі більшою кількістю хлопчиків. Якщо є чотири хлопчики, це робить одинадцять дівчаток? Двічі$4$ хлопчики$8$. На три більше, ніж$8$ є$11$.
Крок 7. Дайте відповідь на питання.	У$4$ досліджуваній групі були хлопчики.

Вправа$\PageIndex{5}$

Гільєрмо купив підручники і зошити в книгарні. Кількість підручників була$3$ більш ніж в два рази більше зошитів. Він купив$7$ підручники. Скільки блокнотів він купив?

Відповідь: $2$

Вправа$\PageIndex{6}$

На цьому тижні Джеррі працював з головоломками судоку та кросвордами. Кількість загадок судоку, які він виконав, становить вісім більше, ніж в два рази перевищує кількість кросвордів. Він завершив головоломки$22$ судоку. Скільки кросвордів він зробив?

Відповідь: $7$

Вирішити проблеми з числом

Тепер, коли у нас є стратегія вирішення проблем, ми будемо використовувати її для декількох різних типів проблем слів. Перший тип, над яким ми будемо працювати, - це «проблеми з числом». Числові проблеми дають деякі підказки про одне або кілька чисел. Ми використовуємо ці підказки, щоб написати рівняння. Проблеми з числом зазвичай не виникають щодня, але вони забезпечують гарне введення в практику стратегії вирішення проблем, викладеної вище.

Вправа$\PageIndex{7}$

Різниця числа і шести є$13$. Знайдіть номер.

Відповідь

Крок 1. Прочитайте проблему. Чи всі слова знайомі?
Крок 2. Визначте, що ми шукаємо.	число
Крок 3. Ім'я. Виберіть змінну для представлення числа.	Нехай$n=$ число.
Крок 4. Перекласти. Не забудьте шукати підказкові слова на кшталт «різниця... з... і...»
Повторюйте проблему як одне речення.	$\color{cyan} \underbrace{\color{black}\textbf{The difference of the number and }\mathbf{6}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\strut \color{black}\mathbf{13}}$
Перевести в рівняння.	$\qquad \qquad \qquad n-6 \qquad \qquad \qquad \quad = \quad 13$
Крок 5. Розв'яжіть рівняння.	$\quad n - 6 = 13$
Спростити.	$\quad n =19$
Крок 6. Перевірте.
Різниця$19$ і$6$ є$13$. Це перевіряє!
Крок 7. Дайте відповідь на питання.	Число є$19$.

Вправа$\PageIndex{8}$

Різниця числа і вісімки є$17$. Знайдіть номер.

Відповідь: $25$

Вправа$\PageIndex{9}$

Різниця числа і одинадцяти є$−7$. Знайдіть номер.

Відповідь: $4$

Вправа$\PageIndex{10}$

Сума в два рази число і сім дорівнює$15$. Знайдіть номер.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.	число
Крок 3. Ім'я. Виберіть змінну для представлення числа.	Нехай$n =$ число.
Крок 4. Перекласти.
Повторюйте проблему як одне речення.	$.$
Перевести в рівняння.	$.$
Крок 5. Розв'яжіть рівняння.	$.$
Відніміть 7 з кожного боку і спростіть.	$.$
Розділіть кожну сторону на 2 і спростіть.	$.$
Крок 6. Перевірте.
Сума двох разів 4 і 7 дорівнює 15?
$\begin{array} {rrl} {2\cdot 4 + 7} &{\stackrel{?}{=}}& {15} \\ {15} &{=} &{15\checkmark} \end{array}$
Крок 7. Дайте відповідь на питання.	Число є$4$.

Ви помітили, що ми залишили деякі кроки, коли ми вирішили це рівняння? Якщо ви ще не готові залишити ці кроки, запишіть стільки, скільки вам потрібно.

Вправа$\PageIndex{11}$

Сума чотири рази число і два дорівнює$14$. Знайдіть номер.

Відповідь: $3$

Вправа$\PageIndex{12}$

Сума триразового числа і семи дорівнює$25$. Знайдіть номер.

Відповідь: $6$

Деякі проблеми з числовими словами просять нас знайти два або більше чисел. Можливо, буде спокусливо назвати їх усі різними змінними, але поки що ми розв'язували лише рівняння з однією змінною. Щоб уникнути використання більше однієї змінної, ми визначимо числа через одну і ту ж змінну. Обов'язково уважно прочитайте проблему, щоб дізнатися, як всі цифри співвідносяться один з одним.

Вправа$\PageIndex{13}$

Одне число на п'ять більше іншого. Сума чисел дорівнює 21. Знайдіть цифри.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.		Шукаємо два числа.
Крок 3. Ім'я. У нас є два числа, щоб назвати і потрібно ім'я для кожного.
Виберіть змінну для представлення першого числа.		Нехай$n=1^{st}$ номер.
Що ми знаємо про друге число?		Одне число на п'ять більше, ніж інше.
		$n+5=2^{nd}$число
Крок 4. Перекласти. Повторюйте проблему як одне речення з усією важливою інформацією.		Сума ^1-го числа і ^2-го числа дорівнює 21.
Перевести в рівняння.		$.$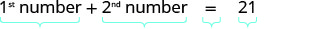
Підставляємо змінні вирази.		$.$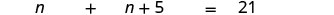
Крок 5. Розв'яжіть рівняння.		$.$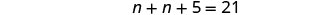
Поєднуйте подібні терміни.		$.$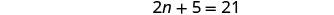
Відніміть 5 з обох сторін і спростіть.		$.$
Розділіть на 2 і спростіть.		$.$
Знайдіть і друге число.		$.$
		$.$
		$.$
Крок 6. Перевірте.
Чи перевіряють ці цифри в проблемі?
Одне число$5$ більше, ніж інше?	$13\stackrel{?}{=} 8 + 5$
Це тринадцять$5$ більше, ніж$8$? Так.	$13 = 13\checkmark$
Це сума двох чисел$21$?	$8 + 13 \stackrel{?}{=} 21$
	$21 = 21\checkmark$
Крок 7. Дайте відповідь на питання.		Цифри -$8$ і$13$.

Вправа$\PageIndex{14}$

Одне число на шість більше, ніж інше. Сума чисел - двадцять чотири. Знайдіть цифри.

Відповідь: 9, 15

Вправа$\PageIndex{15}$

Сума двох чисел - п'ятдесят вісім. Одне число на чотири більше іншого. Знайдіть цифри.

Відповідь: 27, 31

Вправа$\PageIndex{16}$

Сума двох чисел дорівнює від'ємним чотирнадцяти. Одне число на чотири менше іншого. Знайдіть цифри.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.		Шукаємо два числа.
Крок 3. Ім'я.
Виберіть змінну.		Нехай$n=1^{st}$ номер.
Одне число на 4 менше іншого.		$n−4=2^{nd}$число
Крок 4. Перекласти.
Напишіть як одне речення.		Сума 2 чисел від'ємна 14.
Перевести в рівняння.		$.$
Крок 5. Розв'яжіть рівняння.		$.$
Поєднуйте подібні терміни.		$.$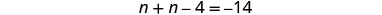
Додайте по 4 в кожну сторону і спростіть.		$.$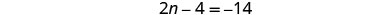
Спростити.		$.$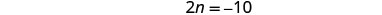
		$.$
		$.$
		$.$
		$.$
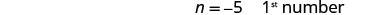
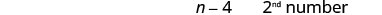
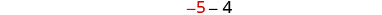
Крок 6. Перевірте.
Це −9 чотири менше −5?	$-5-4\stackrel{?}{=}-9$
	$-9 = -9 \checkmark$
Їх сума −14?	$-5+ (-9)\stackrel{?}{=}-14$
	$-14 = -14 \checkmark$
Крок 7. Дайте відповідь на питання.		Числа: −5 та −9.

Вправа$\PageIndex{17}$

Сума двох чисел від'ємна двадцять три. Одне число на сім менше іншого. Знайдіть цифри.

Відповідь: -15, -8

Вправа$\PageIndex{18}$

Сума двох чисел дорівнює$−18$. Одне число$40$ більше, ніж інше. Знайдіть цифри.

Відповідь: -29, 11

Вправа$\PageIndex{19}$

Одне число на десять більше, ніж в два рази інше. Їх сума одна. Знайдіть цифри.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ви шукаєте.		Шукаємо два числа.
Крок 3. Ім'я.
Виберіть змінну.		Нехай$x=1^{st}$ номер.
Одне число на 10 більше, ніж в два рази інше.		$2x+10=2^{nd}$число
Крок 4. Перекласти.
Повторюйте як одне речення.		Їх сума одна.
		Сума двох чисел дорівнює 1.
Перевести в рівняння.		$.$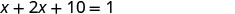
Крок 5. Розв'яжіть рівняння.
Поєднуйте подібні терміни.		$.$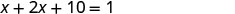
Відніміть 10 з кожного боку.		$.$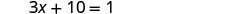
Розділіть кожну сторону на 3.		$.$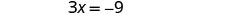
		$.$
		$.$
		$.$
		$.$
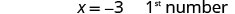
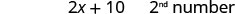
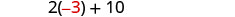
Крок 6. Перевірте.
Чи десять більше, ніж удвічі −3 дорівнює 4?	$2(-3) + 10 \stackrel{?}{=} 4$
	$-6 + 10 \stacktel{?}{=} 4$
	$4 = 4\checkmark$
Чи є їх сума 1?	$-3 + 4 \stackrel{?}{=} 1$
	$1 = 1\checkmark$
Крок 7. Дайте відповідь на питання.		Числа: −3 та −4.

Вправа$\PageIndex{20}$

Одне число на вісім більше, ніж в два рази інше. Їх сума - від'ємна четвірка. Знайдіть цифри.

Відповідь: $-4,\; 0$

Вправа$\PageIndex{21}$

Одне число в три більше, ніж в три рази інше. Їх сума є$−5$. Знайдіть цифри.

Відповідь: $-3,\; -2$

Деякі числові задачі включають послідовні цілі числа. Послідовні цілі числа - це цілі числа, які відразу слідують один за одним. Прикладами послідовних цілих чисел є:

\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]

Зверніть увагу, що кожне число на одне більше, ніж число, що передує йому. Так що, якщо ми визначимо перше число$n$, як, наступний послідовне ціле число є$n+1$. Той після цього на один більше$n+1$, ніж, так він і є$n+2$.$n+1+1$
\[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Вправа$\PageIndex{22}$

Сума двох послідовних цілих чисел дорівнює$47$. Знайдіть цифри.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ви шукаєте.	два послідовних цілих числа
Крок 3. Назвіть кожне число.	Нехай$n=1^{st}$ ціле число.
	$n+1=$наступне послідовне ціле число
Крок 4. Перекласти.
Повторюйте як одне речення.	Сума цілих чисел дорівнює$47$.
Перевести в рівняння.	$.$
Крок 5. Розв'яжіть рівняння.	$.$
Поєднуйте подібні терміни.	$.$
Відніміть по 1 з кожного боку.	$.$
Розділіть кожну сторону на 2.	$.$
	$.$
	$.$
	$.$
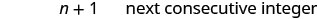
Крок 6. Перевірка.
$\begin{array} {lll} {23 + 24} &{\stackrel{?}{=}} &{47} \\ {47} &{=} &{47\checkmark} \end{array}$
Крок 7. Дайте відповідь на питання.	Два послідовних цілих числа - 23 та 24.

Вправа$\PageIndex{23}$

Сума двох послідовних цілих чисел дорівнює 95. Знайдіть цифри.

Відповідь: 47, 48

Вправа$\PageIndex{24}$

Сума двох послідовних цілих чисел дорівнює −31. Знайдіть цифри.

Відповідь: -16, -15

Вправа$\PageIndex{25}$

Знайти три послідовних цілих числа, сума яких дорівнює −42.

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.	три послідовних цілих числа
Крок 3. Назвіть кожне з трьох чисел.	Нехай$n=1^{st}$ ціле число.
	$n+1= 2^{nd}$послідовне ціле
	$n+2= 3^{rd}$послідовне ціле
Крок 4. Перекласти.
Повторюйте як одне речення.	Сума трьох цілих чисел дорівнює$−42$.
Перевести в рівняння.	$.$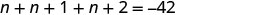
Крок 5. Розв'яжіть рівняння.	$.$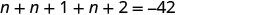
Поєднуйте подібні терміни.	$.$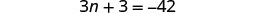
Відніміть по 3 з кожного боку.	$.$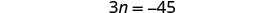
Розділіть кожну сторону на 3.	$.$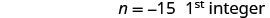
	$.$
	$.$
	$.$
	$.$
	$.$
	$.$
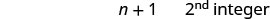
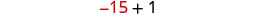
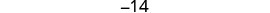
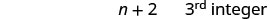
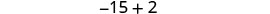
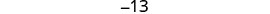
Крок 6. Перевірка.
$\begin{array}{lll} {-13 + (-14) + (-15)} &{\stackrel{?}{=}} &{-42} \\ {-42} &{=} &{-42\checkmark} \end{array}$
Крок 7. Дайте відповідь на питання.	Три послідовних цілих числа: −13, −14 та −15.

Вправа$\PageIndex{26}$

Знайти три послідовних цілих числа, сума яких дорівнює −96.

Відповідь: -33, -32, -31

Вправа$\PageIndex{27}$

Знайти три послідовних цілих числа, сума яких дорівнює −36.

Відповідь: -13, -12, -11

Тепер, коли ми працювали з послідовними цілими числами, ми будемо розширювати нашу роботу, щоб включити послідовні парні цілі числа і послідовні непарні цілі числа. Послідовні парні цілі числа - це парні цілі числа, які відразу слідують один за одним. Прикладами послідовних парних цілих чисел є:

\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]

Зверніть увагу, що кожне ціле число$2$ більше, ніж число, що передує йому. Якщо ми називаємо перший$n$, то наступний -$n+2$. Наступним буде$n+2+2$ або$n+4$.
\[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Послідовні непарні цілі числа - це непарні цілі числа, які відразу слідують один за одним. Розглянемо послідовні непарні цілі числа$77$$79$, і$81$.

\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]

\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

Чи здається дивним додати 2 (парне число), щоб отримати від одного непарного цілого числа до наступного? Ви отримуєте непарне число або парне число, коли ми додаємо 2 до 3? до 11? до 47?

Незалежно від того, чи запитує проблема послідовних парних чисел або непарних чисел, вам не потрібно робити нічого іншого. Візерунок залишається тим самим - щоб отримати від одного непарного або одного парного цілого числа до наступного, додайте 2.

Вправа$\PageIndex{28}$

Знайдіть три послідовних парних цілих числа, сума яких дорівнює 84.

Відповідь: \[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]

Вправа$\PageIndex{29}$

Знайдіть три послідовних парних цілих числа, сума яких дорівнює 102.

Відповідь: 32, 34, 36

Вправа$\PageIndex{30}$

Знайти три послідовних парних цілих числа, сума яких дорівнює −24.

Відповідь: −10, −8, −6

Вправа$\PageIndex{31}$

Сімейна пара разом заробляє 110 000 доларів на рік. Дружина заробляє на 16 000 доларів менше, ніж в два рази більше, ніж заробляє чоловік. На чому заробляє чоловік?

Відповідь

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.	Скільки заробляє чоловік?
Крок 3. Ім'я.
Виберіть змінну для представлення суми , яку заробляє чоловік.	Нехай$h=$ сума заробляє чоловік.
Дружина заробляє$$16,000$ менше, ніж в два рази більше.	$2h−16,000$суму, яку заробляє дружина.
Крок 4. Перекласти.	Разом чоловік і дружина заробляють$$110,000$.
Повторюйте проблему в одному реченні з усією важливою інформацією.	$.$
Перевести в рівняння.	$.$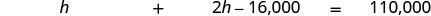
Крок 5. Розв'яжіть рівняння.	$h + 2h − 16,000 = 110,000$
Поєднуйте подібні терміни.	$3h − 16,000 = 110,000$
Додайте$16,000$ в обидві сторони і спростіть.	$3h = 126,000$
Розділіть кожну сторону на$3$.	$h = 42,000$
	$$42,000$сума чоловік заробляє
	$2h − 16,000$сума дружина заробляє
	$2(42,000) − 16,000$
	$84,000 − 16,000$
	$68,000$
Крок 6. Перевірка.
Якщо дружина заробляє,$$68,000$ а чоловік заробляє$$42,000$ - це загальна$$110,000$ (? Так!
Крок 7. Дайте відповідь на питання.	Чоловік$$42,000$ заробляє рік.

Вправа$\PageIndex{32}$

За даними Національної асоціації автомобільних дилерів, середня вартість автомобіля в 2014 році склала $28 500. Це було на 1500 доларів менше, ніж у 6 разів дорожче в 1975 році. Якою була середня вартість автомобіля в 1975 році?

Відповідь: $5000

Вправа$\PageIndex{33}$

Дані перепису населення США показують, що середня ціна нового будинку в Сполучених Штатах в листопаді 2014 року становила $280,900. Це було на 10 700 доларів більше, ніж у 14 разів більше ціни в листопаді 1964 року. Якою була середня ціна нового будинку в листопаді 1964 року?

Відповідь: $19300

Ключові концепції

Стратегія вирішення проблем
1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
2. Визначте, що ми шукаємо.
3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
4. Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в рівняння алгебри.
5. Вирішіть рівняння, використовуючи хороші методи алгебри.
6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
7. Відповісти на питання повним реченням.
Послідовні цілі числа
Послідовні цілі числа - це цілі числа, які відразу слідують один за одним.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Послідовні парні цілі числа - це парні цілі числа, які відразу слідують один за одним.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Послідовні непарні цілі числа - це непарні цілі числа, які відразу слідують один за одним.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

	Нехай\(p =\) первісна ціна.
	\(18\)становить половину початкової ціни.
	\(18 = \frac{1}{2}p\)
Помножте обидві сторони на\(2\).	\( {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p \)
Спростити.	\(36 = p\)
Перевірте. Чи\($36\) доступна ціна за гаманець?
Так.
\(18\)Одна половина\(36\)?
\(18 \stackrel{?}{=} \frac{1}{2}\cdot 36\)
\(18 = 18\checkmark\)
	Початкова ціна гаманця була\($36\).

Крок 1. Прочитайте проблему.
Крок 2. Визначте, що ми шукаємо.	Скільки заробляє чоловік?
Крок 3. Ім'я.
Виберіть змінну для представлення суми , яку заробляє чоловік.	Нехай\(h=\) сума заробляє чоловік.
Дружина заробляє\($16,000\) менше, ніж в два рази більше.	\(2h−16,000\)суму, яку заробляє дружина.
Крок 4. Перекласти.	Разом чоловік і дружина заробляють\($110,000\).
Повторюйте проблему в одному реченні з усією важливою інформацією.	$.$
Перевести в рівняння.	$.$
Крок 5. Розв'яжіть рівняння.	\(h + 2h − 16,000 = 110,000\)
Поєднуйте подібні терміни.	\(3h − 16,000 = 110,000\)
Додайте\(16,000\) в обидві сторони і спростіть.	\(3h = 126,000\)
Розділіть кожну сторону на\(3\).	\(h = 42,000\)
	\($42,000\)сума чоловік заробляє
	\(2h − 16,000\)сума дружина заробляє
	\(2(42,000) − 16,000\)
	\(84,000 − 16,000\)
	\(68,000\)
Крок 6. Перевірка.
Якщо дружина заробляє,\($68,000\) а чоловік заробляє\($42,000\) - це загальна\($110,000\) (? Так!
Крок 7. Дайте відповідь на питання.	Чоловік\($42,000\) заробляє рік.

ВИКОРИСТОВУЙТЕ СТРАТЕГІЮ ВИРІШЕННЯ ПРОБЛЕМ ДЛЯ ВИРІШЕННЯ ЗАВДАНЬ ЗІ СЛОВАМИ.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)

Вправа\(\PageIndex{6}\)

Вправа\(\PageIndex{7}\)

Вправа\(\PageIndex{8}\)

Вправа\(\PageIndex{9}\)

Вправа\(\PageIndex{10}\)

Вправа\(\PageIndex{11}\)

Вправа\(\PageIndex{12}\)

Вправа\(\PageIndex{13}\)

Вправа\(\PageIndex{14}\)

Вправа\(\PageIndex{15}\)

Вправа\(\PageIndex{16}\)

Вправа\(\PageIndex{17}\)

Вправа\(\PageIndex{18}\)

Вправа\(\PageIndex{19}\)

Вправа\(\PageIndex{20}\)

Вправа\(\PageIndex{21}\)

Вправа\(\PageIndex{22}\)

Вправа\(\PageIndex{23}\)

Вправа\(\PageIndex{24}\)

Вправа\(\PageIndex{25}\)

Вправа\(\PageIndex{26}\)

Вправа\(\PageIndex{27}\)

Вправа\(\PageIndex{28}\)

Вправа\(\PageIndex{29}\)

Вправа\(\PageIndex{30}\)

Вправа\(\PageIndex{31}\)

Вправа\(\PageIndex{32}\)

Вправа\(\PageIndex{33}\)

Повторюйте проблему в одному реченні з усією важливою інформацією.	\(\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}\)
Перевести в рівняння.	\(18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p\)