3.3: Вирішіть додатки для сумішей

Last updated
Save as PDF

Page ID: 58931

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Вирішіть проблеми з монетними словами
Вирішити проблеми з квитком та штампом
Вирішити проблеми зі змішаними словами
Використовуйте модель суміші для вирішення інвестиційних завдань, використовуючи прості відсотки

Примітка

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Помножити:$14(0.25)$.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.8.19.
Вирішити:$0.25x+0.10(x+4)=2.5$.
Якщо ви пропустили цю проблему, перегляньте Вправа 2.4.22.
Кількість копійок на три більше, ніж кількість чвертей. Нехай q являє собою кількість чвертей. Напишіть вираз для кількості копійок.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.43.

Вирішити проблеми з монетним словом

У задачах із сумішшю у нас буде два або більше елементів з різними значеннями для об'єднання разом. Модель суміші використовується бакалійниками та барменами, щоб переконатися, що вони встановлюють справедливі ціни на продукцію, яку вони продають. Багато інших професіоналів, як хіміки, інвестиційні банкіри та ландшафтні майстри також використовують модель суміші.

Примітка

Виконання маніпулятивної математичної діяльності Coin Lab допоможе вам краще зрозуміти проблеми зі змішаними словами.

Почнемо з розгляду знайомого всім додатка—гроші!

Уявімо, що ми беремо жменю монет з кишені або сумочки і кладемо їх на стіл. Як би ми визначили вартість цієї купи монет? Якщо ми зможемо сформувати покроковий план пошуку загальної вартості монет, це допоможе нам, коли ми почнемо вирішувати проблеми з монетними словами.

Отже, що б ми зробили? Щоб отримати деяке замовлення на безлад монет, ми могли б розділити монети на купи відповідно до їх вартості. Квартали б йшли з чвертями, копійки з копійками, нікелями з нікелем і так далі. Щоб отримати загальну вартість всіх монет, ми додамо загальну вартість кожної купи.

Купи копійок, нікелів, копійок і чвертей — Малюнок$\PageIndex{1}$

Як би ми визначили вартість кожної палі? Подумайте про купу копійок - скільки це коштує? Якщо ми порахуємо кількість копійок, ми будемо знати, скільки у нас є - кількість копійок.

Але це не говорить нам про значення всіх копійок. Скажімо, ми нарахували 17 копійок, скільки вони коштують? Кожен копійки коштує $0.10 - це значення одного копійки. Щоб знайти загальну вартість купи в 17 копійок, помножте 17 на $0.10, щоб отримати $1.70. Це загальна величина всіх 17 копійок. Цей метод призводить до наступної моделі.

ЗАГАЛЬНА ВАРТІСТЬ МОНЕТ

Для однотипних монет загальна вартість ряду монет знаходить за допомогою моделі

\[number\cdot value = total\space value\]

де
number - кількість монет

значення - це вартість кожної монети

загальна вартість - загальна вартість всіх монет

Кількість копійок, що перевищує значення кожного копійки, дорівнює загальному значенню копійок.

\[\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}\]

Ми могли б продовжити цей процес для кожного типу монет, і тоді ми б знали загальну вартість кожного типу монет. Щоб отримати загальну вартість всіх монет, додайте загальну вартість кожного типу монет.

Давайте розглянемо конкретний випадок. Припустимо, що є 14 чвертей, 17 копійок, 21 нікель і 39 копійок.

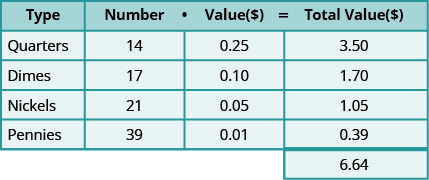
$Ця таблиця містить п'ять рядків і чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий ряд читає Чверті, 14, 0,25 і 3,50. Третій ряд читає Дайми, 17, 0,10 і 1,70. Четвертий ряд читає Нікельс, 21, 0,05 і 1,05. П'ятий ряд читає Пенні, 39, 0,01 і 0,39. Додаткова комірка читає 6.64.$

Таблиця$\PageIndex{1}$

Загальна вартість всіх монет становить $6.64.

Зверніть увагу, як діаграма допомагає організувати всю інформацію! Давайте подивимося, як ми використовуємо цей метод для вирішення проблеми з монетним словом.

Приклад$\PageIndex{1}$

Адальберто має $2,25 в копійках і нікелі в кишені. У нього на дев'ять більше нікелів, ніж копійок. Скільки у нього кожного типу монет?

Рішення

Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.

Визначте типи задіяних монет.
Подумайте про стратегію, яку ми використовували, щоб знайти значення жменьки монет. Перше, що нам потрібно, це помітити, які типи монет задіяні. Адальберто має копійки і нікельси. Створіть таблицю для упорядкування інформації. Див. Діаграму нижче.

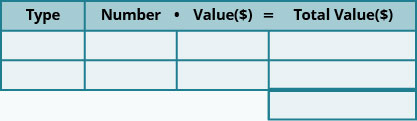
Позначте стовпці «тип», «число», «значення», «загальна вартість».
Перерахуйте види монет.
Впишіть в значення кожного виду монет.
Впишіть в загальну вартість всіх монет.

Ми можемо працювати з цією проблемою все в центах або в доларах. Тут ми зробимо це в доларах і поставимо в таблицю знак долара ($) як нагадування.
Значення копійки становить 0,10 долара, а значення нікелю - 0,05 долара. Загальна вартість всіх монет становить $2,25. У таблиці нижче наведена ця інформація.
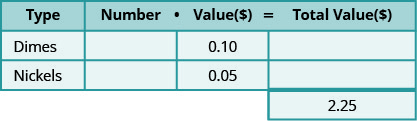
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий рядок читає Dimes, порожній, 0.10 і порожній. Третій рядок читає Нікельс, порожній, 0,05, і порожній. Додаткова комірка читає 2,25.$

Крок 2. Визначте, що ми шукаємо.

Нас просять знайти кількість копійок і нікелів Adalberto має.

Крок 3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.

Використовуйте змінні вирази, щоб представити кількість кожного типу монет і записати їх у таблицю.

Помножте кількість разів на значення, щоб отримати загальну вартість кожного типу монет.

Далі ми підрахували кількість кожного виду монет. У цій проблемі ми не можемо порахувати кожен тип монет - це те, що ви шукаєте, - але у нас є підказка. Нікелів на дев'ять більше, ніж копійок. Кількість нікелів на дев'ять більше, ніж кількість копійок.

\[\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}\]

Заповніть стовпець «число» в таблиці, щоб допомогти організувати все.

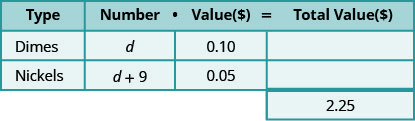
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий рядок читає Dimes, d, 0.10, і порожній. У третьому рядку читається Нікельс, d плюс 9, 0,05, і порожній. Додаткова комірка читає 2,25.$

Тепер у нас є вся необхідна нам інформація від проблеми!

Ми множимо число на значення, щоб отримати загальну вартість кожного типу монет. Хоча ми не знаємо фактичне число, у нас є вираз, щоб представити його.

І так тепер примножуємо$\text{number}\cdot\text{value}=\text{total value}$. Подивіться, як це робиться в таблиці нижче.

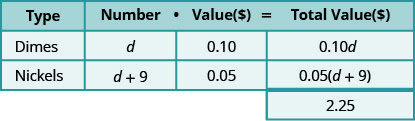
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий ряд читає Даймс, d, 0,10 і 0,10d. Третій ряд читає Нікельс, d плюс 9, 0,05, і в 0,05 рази більше кількості (d плюс 9). Додаткова комірка читає 2,25.$

Зверніть увагу, що ми зробили заголовок таблиці показати модель.

Крок 4. Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні. Переведіть англійське речення в алгебраїчне рівняння.

Напишіть рівняння, склавши загальні значення всіх типів монет.

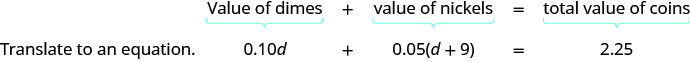
$Речення «значення копійок плюс значення нікелів дорівнює загальній вартості монет» можна перевести в рівняння. Переведіть «значення копійок» на 0,10d, перекладіть «значення ніклів» на 0,05d і перекладіть «загальна вартість монет» на 2,25. Повне рівняння становить 0,10d плюс 0,05 рази кількість d плюс 9 дорівнює 2,25.$

Крок 5. Вирішіть рівняння, використовуючи хороші методи алгебри.

Тепер вирішіть це рівняння.	$.$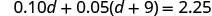
Розподілити.	$.$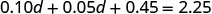
Поєднуйте подібні терміни.	$.$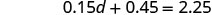
Відніміть 0,45 з кожного боку.	$.$
Розділити.	$.$
Так що є 12 копійок.
Кількість нікелів d+9d+9.	$.$
	$.$
	21

Крок 6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.

Чи перевіряє це?

\[\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}\]

Крок 7. Відповісти на питання повним реченням.

Адальберто має дванадцять копійок і двадцять один нікель.

Якби це була домашня вправа, наша робота могла б виглядати наступним чином.

$Домашнє завдання, написане на підкладці аркуш паперу. Завдання говорить: «У Адальберто в кишені 2 долари і 25 центів і нікелів. У нього на дев'ять більше нікелів, ніж копійок. Скільки у нього кожного типу?» Нижче це таблиця. Перший рядок таблиці є рядком заголовка, і кожна клітинка називає стовпець або стовпці під ним. Перша клітина зліва має назву «Тип». Друга комірка містить рівняння «Число» разів «Значення» дорівнює «Загальна вартість», один стовпець відповідає «Числу», один стовпець, відповідний «Значення», і один стовпець, відповідний загальному значенню. Отже, вміст стовпця «Число» збільшує вміст стовпця «Значення», що дорівнює вмісту стовпця «Загальна вартість». У другому рядку таблиці стовпець «Тип» містить «Копійки», стовпець «Число» містить d, стовпець «Значення» містить 0,10, а стовпець «Загальна вартість» містить 0,10d. У третьому рядку таблиці стовпець «Тип» містить «Нікельс», стовпець «Число» містить d плюс 9, стовпець «Значення містить 0.05, а стовпець «Загальна вартість» містить 0,05 рази більше кількості d плюс 9. Один рядок вниз, стовпець «Загальна вартість» містить ще одну комірку, яка містить 2,25. Нижче таблиці рівняння 0,10d плюс 0,05d плюс 0,45 дорівнює 2,25. Нижче це 0,15d плюс 0,45 дорівнює 2,25. Нижче це 0,15d дорівнює 1,80. Праворуч знаходиться d плюс 9, що перекладається на 12 плюс 9, або 21 нікель. Праворуч від цього є етап перевірки, де ми бачимо, якщо 12 копійок і 21 нікель складають 2 долари і 25 центів. 12 разів 0,10 дорівнює 1,20, а 21 раз (0,05) дорівнює 1,05. 1,20 плюс 1,05 дорівнює 2,25.$

Спробуйте$\PageIndex{1}$

Мікаела має $2,05 в копійках і нікельсах у її гаманці для змін. У неї на сім більше копійок, ніж нікелів. Скільки монет кожного типу у неї є?

Відповідь: 9 нікелів, 16 копійок

Спробуйте$\PageIndex{2}$

Ліліана має $2,10 в нікелі та чвертях у рюкзаку. У неї на 12 більше нікелів, ніж чвертей. Скільки монет кожного типу у неї є?

Відповідь: 17 нікелів, 5 чвертей

ВИРІШИТИ ПРОБЛЕМИ З МОНЕТНИМИ СЛОВАМИ.

Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте типи задіяних монет.
- Створіть таблицю для упорядкування інформації.
- Позначте стовпці «тип», «число», «значення», «загальна вартість».
- Перерахуйте види монет.
- Впишіть в значення кожного виду монет.
- Впишіть в загальну вартість всіх монет.
Визначте, що ми шукаємо.
Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Використовуйте змінні вирази, щоб представити кількість кожного типу монет і записати їх у таблицю.
- Помножте кількість разів на значення, щоб отримати загальну вартість кожного типу монет.
Перевести в рівняння.
Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім переведіть речення в рівняння.
Напишіть рівняння, склавши загальні значення всіх типів монет.
Вирішіть рівняння, використовуючи хороші методи алгебри.
Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
Відповісти на питання повним реченням.

Приклад$\PageIndex{2}$

Марія має $2,43 в кварталах і копійки в гаманці. У неї в два рази більше копійок, ніж чверті. Скільки монет кожного типу у неї є?

Рішення

Крок 1. Прочитайте проблему.

Визначте типи задіяних монет.

Ми знаємо, що у Марії є чверті і копійки.

Створіть таблицю для упорядкування інформації.

Крок 2. Визначте, що ви шукаєте.
- Шукаємо кількість чвертей і копійки.
Крок 3. Ім'я. Представляємо кількість чвертей і копійок за допомогою змінних.
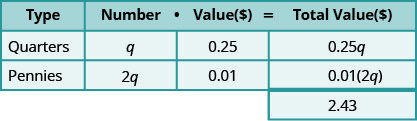
- Помножте «число» та «значення», щоб отримати «загальну вартість» кожного типу монет. $Без тексту Alt$
  Крок 4. Перекласти. Напишіть рівняння, додавши «загальну вартість» всіх типів монет.
  
  $\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}$
  $\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}$
  $\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}$

Спробуйте$\PageIndex{3}$

Суманта має 4,20 доларів у нікелі та копійки в скарбничці. У неї в два рази більше нікелів, ніж копійок. Скільки монет кожного типу у неї є?

Відповідь: 42 нікеля, 21 дайм

Спробуйте$\PageIndex{4}$

Елісон має в сумочці в три рази більше копійок, ніж чверті. Вона має $9.35 загалом. Скільки монет кожного типу у неї є?

Відповідь: 51 копійки, 17 кварталів

У наступному прикладі ми покажемо лише заповнену таблицю — запам'ятайте кроки, які ми вживаємо для заповнення таблиці.

Приклад$\PageIndex{3}$

Денні має $2,14 копійки і нікелі в його скарбничці. Кількість нікелів в два більше, ніж в десять разів перевищує кількість копійок. Скільки нікелів і скільки копійок у Денні?

Рішення

Крок 1. Прочитайте проблему.
Визначте типи задіяних монет.	копійки і нікельси
Створіть таблицю.
Впишіть в значення кожного виду монет.	Копійки коштують $0.01. Нікельси коштують $0,05.
Крок 2. Визначте, що ми шукаємо.	кількість копійок і нікелів
Крок 3. Ім'я. Представляють кількість кожного типу монет за допомогою змінних.
Кількість нікелів визначається з точки зору кількості копійок, тому почніть з копійок.	Нехай$p=$ кількість копійок.
Кількість нікелів в два більше, ніж в десять разів перевищує кількість копійок.	І нехай$10p+2=$ кількість нікелів.
Помножте число і значення, щоб отримати загальну вартість кожного типу монет.
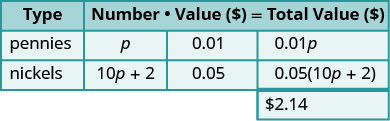$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий ряд читає копійки, р, 0,01, і 0,01п. Третій ряд читає нікелі, 10р плюс 2, 0,05 і 0,05 рази більше кількості (10р плюс 2). Додаткова комірка читає $2,14.$
Крок 4. Перекласти. Напишіть рівняння, склавши загальну вартість всіх типів монет.	$.$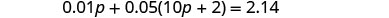
Крок 5. Розв'яжіть рівняння.	$.$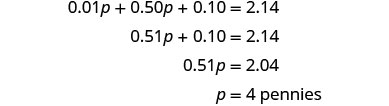
Скільки нікелів?	$.$
Крок 6. Перевірте відповідь в задачі і переконайтеся, що у Денні є сенс чотири копійки і 42 нікеля. Загальна вартість $2,14? $\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}$
Крок 7. Дайте відповідь на питання.	Денні має чотири копійки і 42 нікеля.

Спробуйте$\PageIndex{5}$

Джессі має $6,55 на чверть і нікелі в кишені. Кількість нікелів в п'ять більше ніж в два рази перевищує кількість чвертей. Скільки нікелів і скільки кварталів у Джессі?

Відповідь: 41 нікеля, 18 чвертей

Спробуйте$\PageIndex{6}$

Elane має $7,00 всього в копійках і нікельсах у своїй банку для монет. Кількість копійок, які має Елан, в сім менше, ніж втричі перевищує кількість нікелів. Скільки кожної монети має Елан?

Відповідь: 22 нікеля, 59 копійок

Вирішити проблеми з квитком і штампом Word

Проблеми, пов'язані з квитками або марками, дуже схожі на проблеми з монетами. Кожен тип квитка та штампа має значення, як і кожен тип монет. Отже, щоб вирішити ці проблеми, ми будемо слідувати тим самим крокам, які ми використовували для вирішення проблем з монетами.

Приклад$\PageIndex{4}$

На шкільному концерті загальна вартість проданих квитків становила 1 506 доларів. Студентські квитки продаються за $6 кожен, а дорослі квитки продаються по 9 доларів кожен. Кількість проданих квитків для дорослих була в п'ять менше, ніж втричі перевищує кількість проданих студентських квитків. Скільки студентських квитків і скільки було продано квитків для дорослих?

Рішення

Крок 1. Прочитайте проблему.

Визначте типи квитків, які беруть участь. Є студентські квитки і дорослі квитки.
Створіть таблицю для упорядкування інформації.

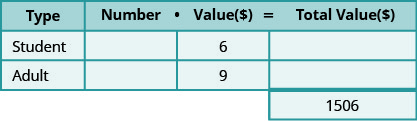
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий рядок читає Студент, порожній, 6, і порожній. Третій рядок читає Дорослий, порожній, 9 і порожній. Додаткова комірка читає 1506.$

Крок 2. Визначте, що ми шукаємо.

Шукаємо кількість студентських і дорослих квитків.

Крок 3. Ім'я. Представляють номер кожного типу квитка за допомогою змінних.

Ми знаємо, що кількість проданих квитків для дорослих була в п'ять менше, ніж втричі перевищує кількість проданих студентських квитків.

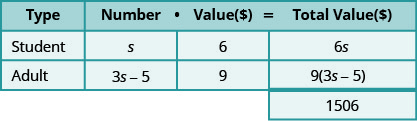
Помножте кількість на значення, щоб отримати загальну вартість кожного типу квитка. $Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий ряд читає Студент, s, 6 і 6s. Третій ряд читає Дорослий, 3s мінус 5, 9 і 9 разів більше кількості (3s мінус 5). Додаткова комірка читає 1506.$
Крок 4. Перекласти. Напишіть рівняння, додавши загальні значення кожного типу квитка.

\[6 s+9(3 s-5)=1506 \nonumber\]

Крок 5. Розв'яжіть рівняння.

\[\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber\]

Крок 6. Перевірте відповідь.

Було 47 студентських квитків по 6 доларів кожен і 136 дорослих квитків по 9 доларів кожен. Чи є загальним значенням $1,506? Ми знаходимо загальну вартість кожного типу квитків, множивши кількість квитків на його вартість, а потім додаємо, щоб отримати загальну вартість всіх проданих квитків.

\[\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber\]

Крок 7. Дайте відповідь на питання. Вони продали 47 студентських квитків та 136 квитків для дорослих.

Спробуйте$\PageIndex{7}$

У перший день турніру з водного поло загальна вартість проданих квитків становила $17 610. Одноденні абонементи продаються за 20 доларів, а турнірні абонементи продаються за 30 доларів. Кількість проданих турнірних пропусків склала на 37 більше, ніж кількість проданих денних пропусків. Скільки денних абонементів і скільки було продано турнірних абонементів?

Відповідь: 330 днів абонементів, 367 турнірних абонементів

Спробуйте$\PageIndex{8}$

У кінотеатрі загальна вартість проданих квитків становила 2 612,50 доларів. Дорослі квитки продаються за $10 кожен, а квитки для старшого/дитини продаються за $7.50 кожен. Кількість проданих квитків для літніх та дітей становила 25 менше, ніж удвічі більше проданих квитків для дорослих. Скільки квитків для старшого/дітей і скільки було продано квитків для дорослих?

Відповідь: 112 дорослих квитків, 199 квитків для літніх та дітей

Ми навчилися знаходити загальну кількість квитків, коли номер одного типу квитка базується на кількості іншого типу. Далі ми розглянемо приклад, де ми знаємо загальну кількість квитків і повинні з'ясувати, як пов'язані два типи квитків.

Припустимо, Бьянка продала всього 100 квитків. Кожен квиток був або дорослим, або дитячим квитком. Якщо вона продала 20 дитячих квитків, скільки квитків для дорослих вона продала?

Ви сказали «80»? Як ви це зрозуміли? Ви віднімали 20 від 100?

Якщо вона продала 45 дитячих квитків, скільки квитків для дорослих вона продала?

Ви сказали «55»? Як ви його знайшли? Віднімаючи 45 з 100?

Що робити, якщо вона продала 75 дитячих квитків? Скільки квитків для дорослих вона продала?

Кількість квитків для дорослих має бути 100−75. Вона продала 25 дорослих квитків.

Тепер, припустимо, Бьянка продала х дитячих квитків. Тоді скільки квитків для дорослих вона продала? Щоб це з'ясувати, ми б дотримувалися тієї ж логіки, яку ми використовували вище. У кожному конкретному випадку ми віднімали кількість дитячих квитків від 100, щоб отримати кількість дорослих квитків. Тепер ми робимо те ж саме з х.

Ми підсумували це нижче.

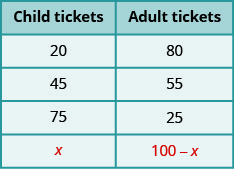
$Ця таблиця має п'ять рядків і два стовпці. Верхній рядок - це рядок заголовка, який читає зліва направо Дитячі квитки та квитки для дорослих. Другий ряд читається 20 і 80. Третій ряд читається 45 і 55. Четвертий ряд читає 75 і 25. П'ятий ряд читає х і 100 плюс х.$

Таблиця$\PageIndex{2}$

Ми можемо застосувати ці прийоми до інших прикладів

Приклад$\PageIndex{5}$

Гален продав 810 квитків на карнавал своєї церкви на загальну суму 2820 доларів. Дитячі квитки коштують 3 долари, а дорослі квитки коштують 5 доларів. Скільки дитячих квитків і скільки дорослих квитків він продав?

Рішення

Крок 1. Прочитайте проблему.

Визначте типи квитків, які беруть участь. Є дитячі квитки і дорослі квитки.
Створіть таблицю для упорядкування інформації.

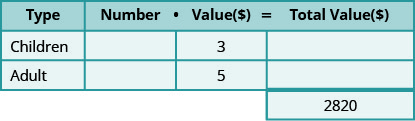
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий рядок читає Діти, порожній, 3, і порожній. Третій рядок читає Дорослий, порожній, 5 і порожній. Додаткова комірка читає 2820.$

Крок 2. Визначте, що ми шукаємо.

Шукаємо кількість дитячих та дорослих квитків.

Крок 3. Ім'я. Представляють номер кожного типу квитка за допомогою змінних.

Ми знаємо, що загальна кількість проданих квитків склала 810.
Це означає, що кількість дитячих квитків плюс кількість квитків для дорослих повинні складати до 810.
$c$Дозволяти кількість дитячих квитків.

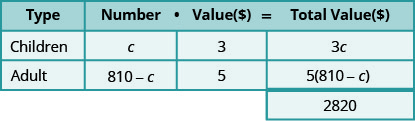
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий ряд читає Діти, c, 3, і 3c. Третій ряд читає Дорослий, 810 мінус c, 5, і 5 разів більше кількості (810 мінус с). Додаткова комірка читає 2820.$

Далі$810−c$ вказується кількість квитків для дорослих.
Помножте кількість на значення, щоб отримати загальну вартість кожного типу квитка.

Крок 4. Перекласти.

Напишіть рівняння, додавши загальні значення кожного типу квитка.

Крок 5. Розв'яжіть рівняння.

\[\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}\]

Скільки дорослих?

\[\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber\]

Крок 6. Перевірте відповідь. Було 615 дитячих квитків по 3 долари кожен і 195 дорослих квитків по 5 доларів кожен. Чи є загальною вартістю $2,820?

\[\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber\]

Крок 7. Дайте відповідь на питання. Гален продав 615 дитячих квитків і 195 дорослих квитків.

Спробуйте$\PageIndex{9}$

Під час своєї зміни в музейній касі Лія продала 115 квитків на загальну суму $1163. Дорослі квитки коштують 12 доларів, а студентські квитки коштують 5 доларів. Скільки квитків для дорослих і скільки студентських квитків продала Лія?

Відповідь: 84 дорослі квитки, 31 студентські квитки

Спробуйте$\PageIndex{10}$

Судно, що спостерігає за китами, мав 40 платних пасажирів на борту. Загальна кількість зібраних з квитків становила 1,196 доларів. Пасажири з повним тарифом заплатили по 32 долари, а пасажири зі зниженим тарифом - 26 доларів. Скільки пасажирів повного тарифу і скільки пасажирів зі зниженим тарифом було на кораблі?

Відповідь: 26 повних тарифів, 14 знижений тариф

Тепер ми зробимо один, де ми заповнюємо таблицю відразу.

Приклад$\PageIndex{6}$

Моніка заплатила $8,36 за марки. Кількість 41-центових марок становила чотири більше, ніж удвічі більше двоцентових марок. Скільки 41-центових марок і скільки двоцентових марок купила Моніка?

Рішення

Види штампів - 41-центові марки і двоцентові марки. Їх імена теж дають значення!

«Кількість 41-центових марок становила чотири більше, ніж удвічі більше двоцентових марок».

\[\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber\]

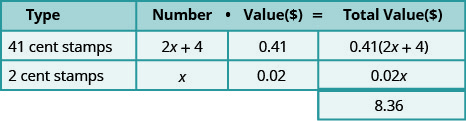
$Ця таблиця містить три рядки та чотири стовпці з додатковою коміркою внизу четвертого стовпця. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Число, Значення ($) та Загальна вартість ($). Другий рядок читає марки 41 цент, 2x плюс 4, 0.41 і 0.41 рази більше кількості (2x плюс 4). Третій ряд читає 2 центові марки, х, 0,02 і 0,02х. Додаткова комірка читає 8.36.$

\[\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber\]

Перевірка.

\[\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}\]
\[\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber\]

Спробуйте$\PageIndex{11}$

Ерік заплатив $13,36 за марки. Кількість 41-центових марок становила на вісім більше, ніж удвічі більше двоцентових марок. Скільки 41-центових марок і скільки двоцентових марок купив Ерік?

Відповідь: 32 в 0,41 долара, 12 в 0,02 долара

Спробуйте$\PageIndex{12}$

Кейлі заплатила $12,66 за марки. Кількість 41-центових марок була в чотири менше, ніж втричі перевищувала кількість 20-центових марок. Скільки 41-центових марок і скільки 20-центових марок купила Кейлі?

Відповідь: 26 в 0,41 долара, 10 в 0,20 долара

Вирішити проблеми зі змішаними словами

Тепер ми вирішимо ще кілька загальних застосувань моделі суміші. Бакалійники та бармени використовують модель суміші, щоб встановити справедливу ціну на продукт, виготовлений із змішування двох або більше інгредієнтів. Фінансові планувальники використовують модель суміші, коли вони вкладають гроші в різні рахунки і хочуть знайти загальну процентну ставку. Ландшафтні дизайнери використовують модель суміші, коли у них є асортимент рослин і фіксований бюджет, а координатори заходів роблять те ж саме при виборі закусок і страв для банкету.

Нашою першою проблемою слова суміші буде виготовлення слідової суміші з родзинок і горіхів.

Приклад$\PageIndex{7}$

Хеннінг змішує родзинки і горіхи, щоб зробити 10 фунтів стежки суміші. Ізюм коштує 2 долари за фунт, а горіхи коштують 6 доларів за фунт. Якщо Хеннінг хоче, щоб його вартість для стежки суміш була $5.20 за фунт, скільки фунтів родзинок і скільки фунтів горіхів він повинен використовувати?

Рішення

Як і раніше, ми заповнюємо діаграму, щоб упорядкувати нашу інформацію.

10 фунтів суміші слід буде надходити від змішування родзинок і горіхів.

\[\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber\]

Вводимо ціну за фунт за кожну позицію.

Множимо число на значення, щоб отримати загальну величину.

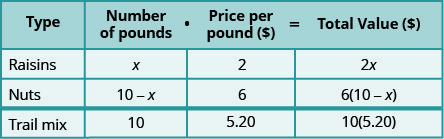
$Ця таблиця складається з чотирьох рядків і чотирьох стовпців. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Кількість фунтів, Ціна за фунт ($) та Загальна вартість ($). Другий ряд читає родзинки, х, 2 і 2х. Третій ряд читає горіхи, 10 мінус х, 6 і 6 разів більше кількості (10 мінус х). У четвертому ряду читається слідова суміш, 10, 5.20 і 10 разів 5.20.$

Зверніть увагу, що останній рядок в таблиці дає інформацію про загальну кількість суміші.

Ми знаємо, що значення родзинок плюс значення горіхів буде значенням слідової суміші.

Запишіть рівняння із загальних значень.	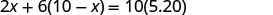$Приклад 3.32 JPG$
Розв'яжіть рівняння.	$.$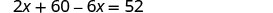
	$.$
	$.$
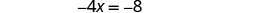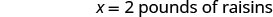Знайдіть кількість кілограмів горіхів.	$.$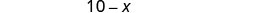
	$.$
	8 фунтів горіхів
Перевірка. $\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}$
	Хеннінг змішав два кілограми родзинок з вісьмома кілограмами горіхів.

Спробуйте$\PageIndex{13}$

Орландо змішує горіхи та зернові квадрати, щоб зробити партійний мікс. Горіхи продають за 7 доларів за фунт, а зернові квадрати продають за 4 долари за фунт. Орландо хоче зробити 30 фунтів партійної суміші вартістю $6.50 за фунт, скільки фунтів горіхів і скільки фунтів зернових квадратів він повинен використовувати?

Відповідь: 5 фунтів зернових квадратів, 25 фунтів горіхів

Спробуйте$\PageIndex{14}$

Бекка хоче змішати фруктовий сік і соду, щоб зробити пунш. Вона може купити фруктовий сік за 3 долари за галон і соду за 4 долари за галон. Якщо вона хоче зробити 28 галонів пуншу вартістю $3,25 за галон, скільки галонів фруктового соку і скільки галонів соди вона повинна купити?

Відповідь: 21 галони фруктового пуншу, 7 галонів соди

Ми також можемо використовувати модель суміші для вирішення інвестиційних проблем, використовуючи простий інтерес. Ми використовували просту формулу відсотків$I=Prt$, де$t$ представлено кількість років. Коли нам просто потрібно знайти інтерес на один рік, значить$t=1$, тоді$I=Pr$.

Приклад$\PageIndex{8}$

Стейсі має 20 000 доларів, щоб інвестувати в два різних банківських рахунки. Один рахунок виплачує відсотки в розмірі 3% на рік, а інший - відсотки 5% на рік. Скільки вона повинна інвестувати в кожен рахунок, якщо вона хоче заробляти 4,5% відсотків на рік від загальної суми?

Рішення

Ми заповнимо діаграму, щоб організувати нашу інформацію. Ми будемо використовувати просту формулу відсотків, щоб знайти відсотки, зароблені на різних рахунках.

Відсотки від змішаних інвестицій будуть надходити від додавання відсотків від рахунку, що заробляє 3%, і відсотки від рахунку, що заробляє 5%, щоб отримати загальний відсоток на $20,000.

\[\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}\]

Інвестована сума є основною для кожного рахунку.

Вводимо процентну ставку по кожному рахунку.

Множимо вкладену суму на ставку, щоб отримати відсотки.

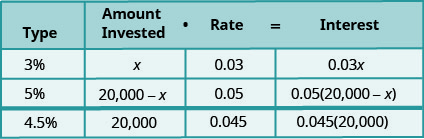
$Ця таблиця складається з чотирьох рядків і чотирьох стовпців. Верхній рядок - це рядок заголовка, який читає зліва направо Тип, Сума інвестування, Ставка та відсотки. Другий ряд читає 3%, х, 0,03 і 0,03х. Третій ряд читає 5%, 20 000 мінус х, 0,05 і 0,05 рази кількість (20 000 мінус х). Четвертий ряд читає 4,5%, 20 000, 0,045 і 0,045 разів 20 000.$

Зверніть увагу, що загальна сума інвестування, 20 000, - це сума вкладеної суми в 3%, а сума інвестування - 5%. А загальний відсоток - це сума відсотків$0.045(20,000)$, зароблених на 3% рахунку, і відсотків, зароблених на 5% рахунку.

Як і в інших додатках суміші, останній стовпець таблиці дає нам рівняння для вирішення.

Напишіть рівняння з зароблених відсотків. Розв'яжіть рівняння.	$\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}$
Знайти вкладену суму в 5%.	$.$ $.$ $.$
Перевірка. $\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}$
	Стейсі повинна інвестувати $5,000 на рахунок, який заробляє 3% і $15,000 на рахунку, який заробляє 5%.

Спробуйте$\PageIndex{15}$

Ремі має 14 000 доларів, щоб інвестувати в два пайові фонди. Один фонд виплачує відсотки під 4% на рік, а інший фонд виплачує відсотки під 7% на рік. Скільки вона повинна інвестувати в кожен фонд, якщо вона хоче заробити 6,1% відсотків від загальної суми?

Відповідь: $4200 при 4%, $9,800 при 7%

Спробуйте$\PageIndex{16}$

Марко має $8,000, щоб заощадити на освіті в коледжі своєї дочки. Він хоче розділити його між одним рахунком, який платить 3,2% відсотків на рік, та іншим рахунком, який платить 8% відсотків на рік. Скільки він повинен інвестувати в кожен рахунок, якщо хоче, щоб відсотки від загальної суми інвестицій становили 6,5%?

Відповідь: 2500 доларів на 3,2%, 5500 доларів при 8%

Ключові концепції

Загальна вартість монет Для одного типу монет загальна вартість ряду монет визначається за допомогою моделі.
number·value=загальна вартість, де число - кількість монет, а вартість - вартість кожної монети; загальна вартість - загальна вартість всіх монет
Стратегія вирішення проблем - Проблеми з монетним словом
1. Прочитайте проблему. Зробіть так, щоб всі слова і ідеї були зрозумілі. Визначте типи задіяних монет.
  - Створіть таблицю для упорядкування інформації.
  - Позначте стовпці тип, число, значення, загальне значення.
  - Перерахуйте види монет.
  - Впишіть в значення кожного виду монет.
  - Впишіть в загальну вартість всіх монет.
2. Визначте, що ми шукаємо.
3. Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
  Використовуйте змінні вирази, щоб представити кількість кожного типу монет і записати їх у таблицю.
  Помножте кількість разів на значення, щоб отримати загальну вартість кожного типу монет.
4. Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім переведіть речення в рівняння.
  Напишіть рівняння, склавши загальні значення всіх типів монет.
5. Вирішіть рівняння, використовуючи хороші методи алгебри.
6. Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
7. Відповісти на питання повним реченням.

Глосарій

проблеми з сумішшю: Проблеми суміші поєднують два або більше елементів з різними значеннями разом.

Примітка

ЗАГАЛЬНА ВАРТІСТЬ МОНЕТ

Приклад\(\PageIndex{1}\)

Спробуйте\(\PageIndex{1}\)

Спробуйте\(\PageIndex{2}\)

ВИРІШИТИ ПРОБЛЕМИ З МОНЕТНИМИ СЛОВАМИ.

Приклад\(\PageIndex{2}\)

Спробуйте\(\PageIndex{3}\)

Спробуйте\(\PageIndex{4}\)

Приклад\(\PageIndex{3}\)

Спробуйте\(\PageIndex{5}\)

Спробуйте\(\PageIndex{6}\)

Приклад\(\PageIndex{4}\)

Спробуйте\(\PageIndex{7}\)

Спробуйте\(\PageIndex{8}\)

Приклад\(\PageIndex{5}\)

Спробуйте\(\PageIndex{9}\)

Спробуйте\(\PageIndex{10}\)

Приклад\(\PageIndex{6}\)

Спробуйте\(\PageIndex{11}\)

Спробуйте\(\PageIndex{12}\)

Приклад\(\PageIndex{7}\)

Спробуйте\(\PageIndex{13}\)

Спробуйте\(\PageIndex{14}\)

Приклад\(\PageIndex{8}\)

Спробуйте\(\PageIndex{15}\)

Спробуйте\(\PageIndex{16}\)

Напишіть рівняння з зароблених відсотків. Розв'яжіть рівняння.	\(\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}\)
Знайти вкладену суму в 5%.	$.$ $.$ $.$
Перевірка. \(\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}\)
	Стейсі повинна інвестувати $5,000 на рахунок, який заробляє 3% і $15,000 на рахунку, який заробляє 5%.