1.7: Додавання та віднімання дробів
- Page ID
- 59089
До кінця цього розділу ви зможете:
- Додавання або віднімання дробів із загальним знаменником
- Додавання або віднімання дробів з різними знаменниками
- Використовуйте порядок операцій для спрощення складних дробів
- Оцінити змінні вирази з дробами
Більш ретельне ознайомлення з темами, розглянутими в цьому розділі, можна знайти в розділі Преалгебра, Дроби.
Додавання або віднімання дробів із загальним знаменником
Коли ми множили дроби, ми просто помножили чисельники і множили знаменники прямо поперек. Для додавання або віднімання дробів вони повинні мати спільний знаменник.
Якщо\(a,b\), і\(c\) є числами де\(c\neq 0\), то
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
Щоб додати або відняти дроби, додайте або відніміть чисельники і помістіть результат над спільним знаменником.
Виконання дій з маніпулятивної математики «Додавання моделі дробу» та «Віднімання модельного дробу» допоможе вам краще зрозуміти додавання та віднімання дробів.
Знайдіть суму:\(\dfrac{x}{3} + \dfrac{2}{3}\).
- Відповідь
-
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
Знайдіть суму:\(\dfrac{x}{4} + \dfrac{3}{4}\).
- Відповідь
-
\(\dfrac{x + 3}{4}\)
Знайдіть суму:\(\dfrac{y}{8} + \dfrac{5}{8}\).
- Відповідь
-
\(\dfrac{y + 5}{8}\)
Знайдіть різницю:\(-\dfrac{23}{24} - \dfrac{13}{24}\)
- Відповідь
-
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
Знайдіть різницю:\(-\dfrac{19}{28} - \dfrac{7}{28}\)
- Відповідь
-
\(-\dfrac{26}{28}\)
Знайдіть різницю:\(-\dfrac{27}{32} - \dfrac{1}{32}\)
- Відповідь
-
\(-\dfrac{7}{8}\)
Знайдіть різницю:\(-\dfrac{10}{x} - \dfrac{4}{x}\)
- Відповідь
-
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
Знайдіть різницю:\(-\dfrac{9}{x} - \dfrac{7}{x}\)
- Відповідь
-
\(-\dfrac{16}{x}\)
Знайдіть різницю:\(-\dfrac{17}{a} - \dfrac{5}{a}\)
- Відповідь
-
\(-\dfrac{22}{a}\)
Спростити:\(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
- Відповідь
-
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
Спростити:\(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Відповідь
-
\(-1\)
Спростити:\(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Відповідь
-
\(-\dfrac{2}{3}\)
Додавання або віднімання дробів з різними знаменниками
Як ми бачили, для додавання або віднімання дробів їх знаменники повинні бути однаковими. Найменший спільний знаменник (РК) двох дробів - це найменше число, яке можна використовувати як спільний знаменник дробів. РК-дисплей двох дробів є найменш загальним кратним (LCM) їх знаменників.
Найменш спільний знаменник (РК) двох дробів - найменш спільний кратний (НКМ) їх знаменників.
Виконання діяльності з маніпулятивної математики «Пошук найменш спільного знаменника» допоможе вам розвинути краще розуміння РК-дисплея.
Після того, як ми знайдемо найменш спільний знаменник двох дробів, перетворюємо дроби в еквівалентні дроби з РК. Складання цих кроків дозволяє нам додавати та віднімати дроби, оскільки їх знаменники будуть однаковими!
Додати:\(\dfrac{7}{12} + \dfrac{5}{18}\)
- Відповідь
-



Додати:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Відповідь
-
\(\dfrac{79}{60}\)
Додати:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Відповідь
-
\(\dfrac{103}{60}\)
- Чи мають вони спільний знаменник?
- Так—перейдіть до кроку 2.
- Ні - перепишіть кожен дріб з РК-дисплеєм (найменш спільний знаменник). Знайдіть РК-дисплей. Змініть кожен дріб на еквівалентний дріб з LCD як його знаменником.
- Додавання або віднімання дробів.
- Спрощуйте, якщо це можливо.
При знаходженні еквівалентних дробів, необхідних для створення спільних знаменників, існує швидкий спосіб знайти число, яке нам потрібно помножити як на чисельник, так і знаменник. Цей метод працює, якщо ми знайшли РК-дисплей шляхом факторингу в прості числа.
Подивіться на фактори РК-дисплея, а потім на кожен стовпець вище цих факторів. «Відсутні» фактори кожного знаменника - це потрібні нам числа.

У Вправи\(\PageIndex{13}\) РК, 36, має два фактори 2 і два фактори 3.
Чисельник 12 має два множники 2, але тільки один з 3 - тому він «відсутній» один 3 - ми множимо чисельник і знаменник на 3.
У чисельнику 18 відсутній один множник 2 - тому ми помножимо чисельник і знаменник на 2.
Ми будемо застосовувати цей метод, коли віднімаємо дроби у Вправі\(\PageIndex{16}\).
Відніміть:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Відповідь
-
Чи мають дроби спільний знаменник? Ні, тому нам потрібно знайти РК-дисплей.
Знайдіть РК-дисплей. 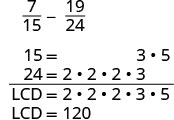
Зверніть увагу, 15 «відсутні» три фактори 2 і 24 «відсутні» 5 з факторів РК-дисплея. Таким чином, ми множимо 8 в першому дробі і 5 в другій дробі, щоб отримати РК-дисплей. Перепишіть як еквівалентні дроби з РК-дисплеєм. 
Спростити. 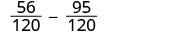
Відніміть. \(-\dfrac{39}{120}\) Перевірте, чи можна спростити відповідь. \(-\dfrac{13\cdot3}{40\cdot3}\) І 39, і 120 мають коефіцієнт 3. Спростити. \(-\dfrac{13}{40}\) Не спрощуйте еквівалентні дроби! Якщо ви це зробите, ви повернетеся до початкових дробів і втратите спільний знаменник!
Відніміть:\(\dfrac{13}{24} - \dfrac{17}{32}\)
- Відповідь
-
\(\dfrac{1}{96}\)
Відніміть:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Відповідь
-
\(\dfrac{75}{224}\)
У наступному прикладі один з дробів має змінну в своєму чисельнику. Зверніть увагу, що ми робимо ті ж кроки, що і коли обидва чисельники числа.
Додати:\(\dfrac{3}{5} + \dfrac{x}{8}\)
- Відповідь
-
Дроби мають різні знаменники.
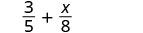
Знайдіть РК-дисплей. 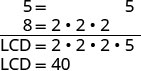
Перепишіть як еквівалентні дроби з РК-дисплеєм. 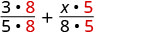
Спростити. 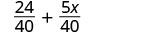
Додати. 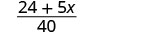
Пам'ятайте, що ми можемо додавати лише подібні терміни:\(24\) і не\(5x\) схожі на терміни.
Додати:\(\dfrac{y}{6} + \dfrac{7}{9}\)
- Відповідь
-
\(\dfrac{3y + 14}{18}\)
Додати:\(\dfrac{x}{6} + \dfrac{7}{15}\)
- Відповідь
-
\(\dfrac{15x + 42}{153}\)
Тепер у нас є всі чотири операції для дробів. Таблиця\(\PageIndex{1}\) підсумовує операції дробу.
| Множення дробу | Розділ дробу |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) Множимо чисельники і множимо знаменники |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) Помножте перший дріб на зворотний другий. |
| Додавання дробу | Віднімання дробу |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Додайте чисельники і помістіть суму над спільним знаменником. |
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Відніміть чисельники і помістіть різницю над спільним знаменником. |
| Для множення або поділу дробів, а РК-дисплей НЕ потрібен. Для додавання або віднімання дробів потрібен РК-дисплей. | |
Спростити:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
- Відповідь
-
Спочатку запитайте: «Що таке операція?» Одного разу ми виявимо операцію, яка визначить, чи потрібен нам спільний знаменник. Пам'ятайте, нам потрібен спільний знаменник, щоб скласти або відняти, але не множити або ділити.
1. Що таке операція? Операція - віднімання.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. Що таке операція? Множення.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
Спростити:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- Відповідь
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
Спростити:
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- Відповідь
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
Використовуйте порядок операцій для спрощення складних дробів
Ми бачили, що складний дріб - це дріб, в якому чисельник або знаменник містить дріб. Брусок дробу вказує на поділ. Ми спростили складний дріб\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)\(\dfrac{3}{4}\) діленням на\(\dfrac{5}{8}\).
Тепер ми розглянемо складні дроби, де чисельник або знаменник містить вираз, який можна спростити. Тому ми спочатку повинні повністю спростити чисельник і знаменник окремо, використовуючи порядок операцій. Потім чисельник ділимо на знаменник.
Спростити:\(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
- Відповідь
-



Спростити:\(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- Відповідь
-
\(\dfrac{1}{90}\)
Спростити:\(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- Відповідь
-
\(272\)
- Спростити чисельник.
- Спростити знаменник.
- Розділіть чисельник на знаменник. Спрощуйте, якщо це можливо.
Спростити:\(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
- Відповідь
-
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
Спростити:\(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- Відповідь
-
\(2\)
Спростити:\(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- Відповідь
-
\(\dfrac{2}{7}\)
Обчислення змінних виразів за допомогою дробів
Ми обчислювали вирази раніше, але тепер ми можемо оцінювати вирази з дробами. Пам'ятайте, щоб оцінити вираз, ми підставляємо значення змінної в вираз, а потім спрощуємо.
Оцініть\(x + \dfrac{1}{3}\), коли
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
- Відповідь
-
1. Щоб оцінити\(x + \dfrac{1}{3}\) коли\(x = -\dfrac{1}{3}\),\(-\dfrac{1}{3}\) підставляємо\(x\) в вираз.
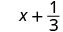
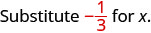
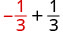
Спростити. \(0\)
2. Щоб оцінити\(x + \dfrac{1}{3}\) коли\(x = -\dfrac{3}{4}\),\(-\dfrac{3}{4}\) підставляємо\(x\) в вираз.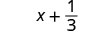

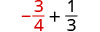
Перепишіть як еквівалентні дроби з LCD, 12. 
Спростити. 
Додати. \(-\dfrac{5}{12}\)
Оцініть\(x + \dfrac{3}{4}\), коли
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- Відповідь
-
- \(-1\)
- \(-\dfrac{1}{2}\)
Оцініть\(y + \dfrac{1}{2}\), коли
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- Відповідь
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
Оцініть\(-\dfrac{5}{6} - y\), коли\(y = -\dfrac{2}{3}\)
- Відповідь
-
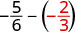
Перепишіть як еквівалентні дроби з РК-дисплеєм,\(6\). 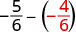
Відніміть. 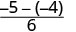
Спростити. \(-\dfrac{1}{6}\)
Оцініть\(y + \dfrac{1}{2}\), коли\(y = \dfrac{2}{3}\)
- Відповідь
-
\(-\dfrac{1}{4}\)
Оцініть\(y + \dfrac{1}{2}\), коли\(y = \dfrac{2}{3}\)
- Відповідь
-
\(-\dfrac{17}{8}\)
Оцініть\(2x^{2}y\), коли\(x = \dfrac{1}{4}\) і\(y = -\dfrac{2}{3}\).
- Відповідь
-
Підставляємо значення у вираз.
\(2x^{2}y\) 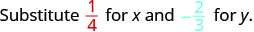
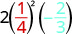
Спочатку спрощуйте показники. \(2(\frac{1}{16})(-\frac{2}{3})\) Помножити. Розділіть загальні фактори. Зверніть увагу, що\(16\) ми\(2\cdot2\cdot4\) пишемо, щоб було легко видалити \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) Спростити. \(-\frac{1}{12}\)
Оцініть\(3ab^{2}\), коли\(a = -\dfrac{2}{3}\) і\(b = -\dfrac{1}{2}\).
- Відповідь
-
\(-\dfrac{1}{2}\)
Оцініть\(4c^{3}d\), коли\(c = -\dfrac{1}{2}\) і\(d = -\dfrac{4}{3}\).
- Відповідь
-
\(\dfrac{2}{3}\)
У наступному прикладі будуть тільки змінні, ніяких констант.
Оцініть\(p = -4, q = -2\),\(\dfrac{p + q}{r}\) коли, і\(r = 8\).
- Відповідь
-
Щоб оцінити\(p = -4, q = -2\),\(\dfrac{p + q}{r}\) коли, і\(r = 8\), підставляємо значення у вираз.
\(\dfrac{p + q}{r}\) 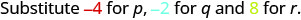
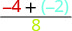
Додайте в чисельник першим. \(\dfrac{-6}{8}\) Спростити. \(-\dfrac{3}{4}\)
Оцініть\(a = -8, b = -7\),\(\dfrac{a+b}{c}\) коли, і\(c = 6\).
- Відповідь
-
\(-\dfrac{5}{2}\)
Оцініть\(x = 9, y = -18\),\(\dfrac{x+y}{z}\) коли, і\(z = -6\).
- Відповідь
-
\(\dfrac{3}{2}\)
Ключові концепції
- Додавання та віднімання дробів: Якщо\(a, b\) і\(c\) є числами де\(c\neq 0\), то
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) і\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
Для додавання або віднімання дробів додайте або відніміть чисельники і помістіть результат над спільним знаменником.
- Стратегія додавання або віднімання дробів
- Чи мають вони спільний знаменник?
Так—перейдіть до кроку 2.
Ні - перепишіть кожен дріб за допомогою РК-дисплея (Найменший спільний знаменник). Знайдіть РК-дисплей. Змініть кожен дріб на еквівалентний дріб з LCD як його знаменником. - Додавання або віднімання дробів.
- Спрощуйте, якщо це можливо. Для множення або поділу дробів РК-дисплей НЕ потрібен. Для додавання або віднімання дробів потрібен РК-дисплей.
- Чи мають вони спільний знаменник?
- Спрощення складних дробів
- Спростити чисельник.
- Спростити знаменник.
- Розділіть чисельник на знаменник. Спрощуйте, якщо це можливо.
