1.6: Візуалізація дробів
- Page ID
- 59058
До кінця цього розділу ви зможете:
- Знайти еквівалентні дроби
- Спрощення дробів
- Множення дробів
- Розділити дроби
- Спрощення виразів, написаних за допомогою рядка дробу
- Перекладіть фрази на вирази з дробами
Більш ретельне ознайомлення з темами, розглянутими в цьому розділі, можна знайти в розділі Преалгебра, Дроби.
Знайти еквівалентні дроби
Дроби - це спосіб представлення частин цілого. Дріб\(\dfrac{1}{3}\) означає, що одне ціле було розділене на 3 рівні частини і кожна частина - одна з трьох рівних частин. Див\(\PageIndex{1}\). Малюнок. Дріб\(\dfrac{2}{3}\) являє собою дві з трьох рівних частин. У\(\dfrac{2}{3}\) дробі 2 називається чисельником, а 3 - знаменником.
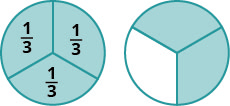
Пишуть дріб\(\dfrac{a}{b}\), де\(b\neq 0\) і
- \(a\)є чисельником і\(b\) є знаменником.
Дріб являє собою частини цілого. Знаменник\(b\) - це кількість рівних частин, на які було поділено ціле, а чисельник\(a\) вказує, скільки частин включено.
Якщо цілий пиріг був розрізаний на 6 частин і ми з'їдаємо всі 6 штук, ми з'їли\(\dfrac{6}{6}\) шматочки, або, іншими словами, один цілий пиріг.
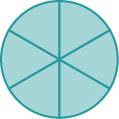
Отже\(\dfrac{6}{6}=1\). Це призводить нас до властивості одиниці, яка говорить нам, що будь-яке число, крім нуля, розділене саме по собі є\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
Будь-яке число, крім нуля, розділене саме по собі, дорівнює одиниці.
Виконання діяльності з маніпулятивної математики «Дроби, еквівалентні одиниці», допоможе вам розвинути краще розуміння дробів, еквівалентних одиниці.
Якщо пиріг розрізали на 6 частин і ми з'їли всіх 6, ми з'їли\(\dfrac{6}{6}\) шматочки, або, іншими словами, один цілий пиріг. Якщо пиріг розрізали на 8 частин і ми з'їли все 8, ми з'їли\(\dfrac{8}{8}\) шматочки, або один цілий пиріг. Ми з'їли однакову кількість—один цілий пиріг.
Дроби\(\dfrac{6}{6}\)\(\dfrac{8}{8}\) мають однакове значення, 1, і тому їх називають еквівалентними дробами. Еквівалентні дроби - це дроби, які мають однакове значення.
Давайте подумаємо про піцу цього разу. \(\PageIndex{3}\)На малюнку зображено два зображення: одна піца зліва, розрізана на два рівні частини, і друга піца такого ж розміру, розрізана на вісім частин справа. Це спосіб показати, що\(\dfrac{1}{2}\) еквівалентно\(\dfrac{4}{8}\). Іншими словами, вони є еквівалентними дробами.
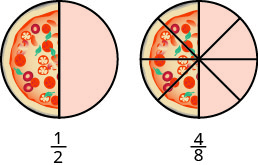
Еквівалентні дроби - це дроби, які мають однакове значення.
Як ми можемо використовувати математику, щоб\(\dfrac{1}{2}\) змінитися\(\dfrac{4}{8}\)? Як ми могли взяти піцу, яка розрізається на 2 частини і розрізати її на 8 частин? Ми могли б розрізати кожен з 2 великих шматочків на 4 менші шматочки! Вся піца потім буде розрізана на 88 частин, а не лише 2. Математично те, що ми описали, може бути написано так\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). Див\(\PageIndex{4}\). Малюнок.
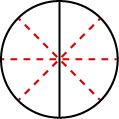
Дана модель призводить до наступної властивості:
\(a,b,c\)Якщо числа де\(b\neq 0, c\neq 0\), то
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
Якби ми розрізали піцу по-іншому, ми могли б отримати
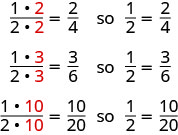
Отже, ми говоримо\(\dfrac{1}{2}\),\(\dfrac{2}{4}\),\(\dfrac{3}{6}\), і\(\dfrac{10}{20}\) еквівалентні дробу.
Виконання діяльності з маніпулятивної математики «Еквівалентні дроби» допоможе вам краще зрозуміти, що означає, коли два дроби еквівалентні.
Знайти три дроби, еквівалентні\(\dfrac{2}{5}\).
- Відповідь
-
Щоб знайти дріб, еквівалентний\(\dfrac{2}{5}\), множимо чисельник і знаменник на одне і те ж число. Ми можемо вибрати будь-яке число, крім нуля. Давайте помножимо їх на 2, 3, а потім на 5.
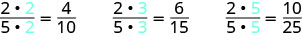
-
Отже,\(\dfrac{4}{10}\),\(\dfrac{6}{15}\), і\(\dfrac{10}{25}\) еквівалентні\(\dfrac{2}{5}\).
Знайти три дроби, еквівалентні\(\dfrac{3}{5}\).
- Відповідь
-
\(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\); відповіді можуть відрізнятися
Знайти три дроби, еквівалентні\(\dfrac{4}{5}\).
- Відповідь
-
\(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\); відповіді можуть відрізнятися
Спрощення дробів
Дріб вважається спрощеним, якщо в його чисельнику і знаменнику відсутні загальні множники, крім 1.
Наприклад,
- \(\dfrac{2}{3}\)спрощується, оскільки немає загальних факторів 2 і 3.
- \(\dfrac{10}{15}\)не спрощується, тому що 5 є загальним фактором 10 і 15.
Дріб вважається спрощеним, якщо в його чисельнику і знаменнику відсутні загальні множники.
Словосполучення зменшити дріб означає спростити дріб. Спрощуємо, або зменшуємо дріб, видаливши загальні множники чисельника і знаменника. Дріб не спрощується, поки не будуть видалені всі загальні фактори. Якщо вираз має дроби, воно не спрощується повністю, поки дроби не будуть спрощені.
У\(\PageIndex{4}\) Вправі ми використовували властивість еквівалентних дробів, щоб знайти еквівалентні дроби. Тепер ми будемо використовувати еквівалентну властивість fractions у зворотному напрямку для спрощення дробів. Ми можемо переписати властивість, щоб показати обидві форми разом.
\(a,b,c\)Якщо числа де\(b\neq 0,c\neq 0\),
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
Спростити:\(-\dfrac{32}{56}\)
- Відповідь
-
\(-\dfrac{32}{56}\) Перепишіть чисельник і знаменник із зазначенням загальних факторів. \(-\dfrac{4\cdot 8}{7\cdot 8}\) Спростіть використання властивості еквівалентних дробів. \(-\dfrac{4}{7}\) Зверніть увагу, що дріб\(-\dfrac{4}{7}\) спрощується, оскільки більше немає загальних факторів.
Спростити:\(-\dfrac{42}{54}\)
- Відповідь
-
\(-\dfrac{7}{9}\)
Спростити:\(-\dfrac{42}{54}\)
- Відповідь
-
\(-\dfrac{5}{9}\)
Іноді буває непросто знайти загальні чинники чисельника і знаменника. Коли це станеться, гарною ідеєю є множник чисельник і знаменник на просте число s, а потім розділити загальні фактори, використовуючи властивість еквівалентних дробів.
Спростити:\(-\dfrac{210}{385}\)
- Відповідь
-



Спростити:\(-\dfrac{69}{120}\)
- Відповідь
-
\(-\dfrac{23}{40}\)
Спростити:\(-\dfrac{120}{192}\)
- Відповідь
-
\(-\dfrac{5}{8}\)
Тепер ми підсумовуємо кроки, які слід виконати для спрощення дробів.
- Перепишіть чисельник і знаменник, щоб показати загальні фактори.
Якщо потрібно, спочатку перерахуйте чисельник і знаменник на прості числа. - Спростіть використання властивості еквівалентних дробів шляхом поділу загальних факторів.
- Помножте всі інші фактори, якщо це необхідно.
Спростити:\(\dfrac{5x}{5y}\)
- Відповідь
-
\(\dfrac{5x}{5y}\) Перепишіть, показуючи загальні фактори, потім розділіть загальні фактори. 
Спростити. \(\dfrac{x}{y}\)
Спростити:\(\dfrac{7x}{7y}\)
- Відповідь
-
\(\dfrac{x}{y}\)
Спростити:\(\dfrac{3a}{3b}\)
- Відповідь
-
\(\dfrac{a}{b}\)
Множення дробів
Багато людей вважають, що множення та ділення дробів простіше, ніж додавання та віднімання дробів. Отже, почнемо з множення дробу.
Виконання діяльності з маніпулятивної математики «Модельне множення дробів» допоможе вам краще зрозуміти множення дробів.Ми використаємо модель, щоб показати вам, як помножити два дроби і допомогти вам запам'ятати процедуру. Почнемо з\(\dfrac{3}{4}\).

Тепер ми візьмемо\(\dfrac{1}{2}\)\(\dfrac{3}{4}\).

Зверніть увагу, що тепер ціле ділиться на 8 рівних частин. Отже\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
Для множення дробів множимо чисельники і множимо знаменники.
Якщо\(a,b,c\) і\(d\) є числами де\(b\neq 0\) і\(d\neq 0\), то
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
Для множення дробів помножте чисельники і помножте знаменники.
При множенні дробів властивості позитивних і негативних чисел все ж застосовуються, звичайно. Це гарна ідея, щоб визначити знак продукту в якості першого кроку. У Вправи\(\PageIndex{13}\) ми помножимо негатив і позитив, тому продукт буде негативним.
Помножити:\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- Відповідь
-
Насамперед необхідно знайти ознаку вироби. Так як ознаки різні, продукт негативний.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
Помножити:\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- Відповідь
-
\(-\dfrac{4}{21}\)
Помножити:\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- Відповідь
-
\(-\dfrac{3}{16}\)
При множенні дробу на ціле число може бути корисним записати ціле число як дріб. Будь-яке ціле число, a, може бути записано як\(\dfrac{a}{1}\). Так, наприклад,\(3 = \dfrac{3}{1}\).
Помножити:\(-\dfrac{12}{5}(-20x)\)
- Відповідь
-
Визначте ознаку вироби. Ознаки однакові, тому продукт позитивний.
\(-\dfrac{12}{5}(-20x)\) Пишіть\(20x\) як дріб. \(\dfrac{12}{5}(\dfrac{20x}{1})\) Помножити. Перепишіть,\(20\) щоб показати загальний фактор\(5\) і розділити його. 
Спростити. \(48x\)
Помножити:\(\dfrac{11}{3}(-9a)\)
- Відповідь
-
\(-33a\)
Помножити:\(\dfrac{13}{7}(-14b)\)
- Відповідь
-
\(-26b\)
Розділити дроби
Тепер, коли ми знаємо, як множити дроби, ми майже готові ділити. Перш ніж ми зможемо це зробити, нам потрібен певний словниковий запас.
Зворотний дріб знаходять шляхом інвертування дробу, розміщення чисельника в знаменнику і знаменника в чисельнику. Відповідне\(\dfrac{2}{3}\) є\(\dfrac{3}{2}\).
Зауважте, що\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). Число і його зворотне множиться на\(1\).
Щоб отримати добуток\(1\) позитиву при множенні двох чисел, числа повинні мати однаковий знак. Так що взаємні повинні мати один і той же знак.
Відповідне\(-\dfrac{10}{7}\) є\(-\dfrac{7}{10}\), так як\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
Відповідне\(\dfrac{a}{b}\) є\(\dfrac{b}{a}\).
Число і його зворотне множення на одиницю\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
Виконання діяльності з маніпулятивної математики «Модельне поділ дробів» допоможе вам розвинути краще розуміння ділення дробів.
Для поділу дробів множимо перший дріб на зворотний другий.
Якщо\(a,b,c\) і\(d\) є числами де\(b\neq 0, c\neq 0\) і\(d\neq 0\), то
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
Для поділу дробів множимо перший дріб на зворотний другий.
Потрібно сказати\(b\neq 0, c\neq 0\) і\(d\neq 0\) бути впевненим, що ми не ділимо на нуль!
Розділити:\(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- Відповідь
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
Розділити:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- Відповідь
-
\(-\dfrac{21}{5p}\)
Розділити:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- Відповідь
-
\(-\dfrac{15}{8q}\)
Знайдіть частку:
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- Відповідь
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) Для поділу помножте перший дріб на зворотний другий. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) Визначте ознаку виробу, а потім помножте.. \(\dfrac{7\cdot 27}{18\cdot 14}\) Перепишіть, показуючи загальні фактори. 
Видаліть загальні фактори. \(\dfrac{3}{2\cdot 2}\) Спростити. \(\dfrac{3}{4}\)
Знайдіть частку:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Відповідь
-
\(\dfrac{4}{15}\)
Знайдіть частку:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Відповідь
-
\(\dfrac{2}{3}\)
Існує кілька способів запам'ятати, які кроки потрібно зробити для множення або поділу дробів. Один із способів - повторити виклик аутів до себе. Якщо ви робите це кожного разу, коли виконуєте вправу, ви будете запам'ятовувати кроки.
- «Щоб помножити дроби, помножте чисельники і помножте знаменники».
- «Щоб розділити дроби, помножте перший дріб на зворотний другий».
Інший спосіб - мати на увазі два приклади:
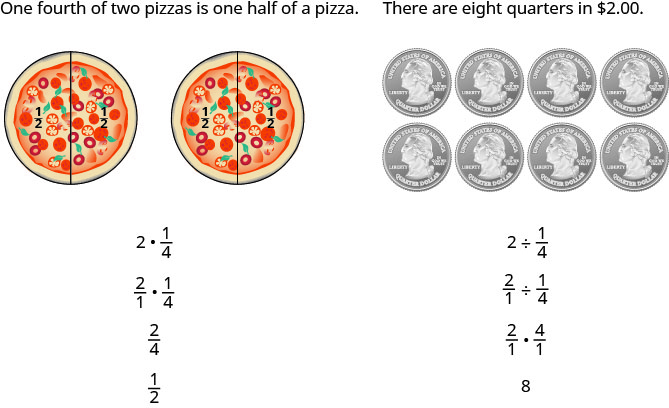
Чисельники або знаменники деяких дробів містять самі дроби. Дріб, в якому чисельником або знаменником є дріб, називається складним дробом.
Складний дріб - це дріб, в якому чисельник або знаменник містить дріб.
Деякі приклади складних дробів:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
Щоб спростити складний дріб, ми пам'ятаємо, що брусок дробу означає ділення. Наприклад, складна фракція\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) означає\(\dfrac{3}{4} \div \dfrac{5}{8}\).
Спростити:\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- Відповідь
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) Перепишіть як поділ. \(\dfrac{3}{4} \div \dfrac{5}{8}\) Помножте перший дріб на зворотний другий. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) Помножити. \(\dfrac{3\cdot 8}{4\cdot 5}\) Шукайте загальні фактори. 
Розділіть загальні фактори і спростіть. \(\dfrac{6}{5}\)
Спростити:\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- Відповідь
-
\(\dfrac{4}{5}\)
Спростити:\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- Відповідь
-
\(\dfrac{11}{14}\)
Спростити:\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- Відповідь
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) Перепишіть як поділ. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) Помножте перший дріб на зворотний другий. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) Помножити. \(\dfrac{x\cdot 6}{2\cdot xy}\) Шукайте загальні фактори. 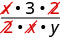
Розділіть загальні фактори і спростіть. \(\dfrac{3}{y}\)
Спростити:\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- Відповідь
-
\(\dfrac{3}{4b}\)
Спростити:\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- Відповідь
-
\(\dfrac{4}{q}\)
Спрощення виразів за допомогою смужки дробу
Рядок, який відокремлює чисельник від знаменника в дробі, називається брусом дробу. Рядок дробу діє як символ групування. Потім порядок операцій говорить нам, щоб спростити чисельник, а потім знаменник. Потім ділимо.
Щоб спростити вираз\(\dfrac{5 - 3}{7 + 1}\), спочатку спростимо чисельник і знаменник окремо. Потім ділимо.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- Спростити вираз в чисельнику. Спростити вираз в знаменнику.
- Спростити дріб.
Спростити:\(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- Відповідь
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
Спростити:\(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- Відповідь
-
\(-\dfrac{3}{4}\)
Спростити:\(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- Відповідь
-
\(-\dfrac{5}{3}\)
Куди йде негативний знак в дробі? Зазвичай негативний знак знаходиться перед дробом, але іноді ви побачите дріб з негативним чисельником, а іноді і з негативним знаменником. Пам'ятайте, що дроби являють собою поділ. Коли чисельник і знаменник мають різні знаки, частка негативна.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
Для будь-яких позитивних чисел\(a\) і\(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
Спростити:\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- Відповідь
-
Рядок дробу діє як символ групування. Так повністю спростите чисельник і знаменник окремо.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
Спростити:\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- Відповідь
-
\(4\)
Спростити:\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- Відповідь
-
\(2\)
Перекласти фрази на вирази з дробами
Тепер, коли ми виконали деяку роботу з дробами, ми готові перекладати фрази, які призвели б до виразів з дробами.
Англійські слова quotient і ratio часто використовуються для опису дробів. Пам'ятайте, що «частка» означає поділ. Частка aa і bb - результат, який ми отримуємо від ділення\(a\) на\(b\), або\(\dfrac{a}{b}\).
Переведіть англійську фразу в алгебраїчний вираз: частка різниці\( m\) і\(n\), і\(p\).
- Відповідь
-
Шукаємо частку різниці\(m\) і\(n\), і\(p\).. Це означає, що ми хочемо розділити різницю\(m\) і\(n\), і\(p\).
\[\dfrac{m - n}{p}\]
Переведіть англійську фразу в алгебраїчний вираз: частка різниці\(a\) і\(b\), і\(cd\).
- Відповідь
-
\(\dfrac{a - b}{cd}\)
Переведіть англійську фразу в алгебраїчний вираз: частка від суми\(p\) і\(q\), і\(r\).
- Відповідь
-
\(\dfrac{p + q}{r}\)
Ключові концепції
- Еквівалентні дроби властивість: Якщо\(a, b, c\) числа де\(b\neq 0, c\neq 0\), то
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) і\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - Ділення дробу: Якщо\(a, b, c\) і\(d\) є числами де\(b\neq 0, c\neq 0\) і\(d \neq 0\), то\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). Для поділу дробів помножте перший дріб на зворотний другий.
- Множення дробу: Якщо\(a,b,c\) і\(d\) є числами де\(b\neq 0, d\neq 0\), то\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). Для множення дробів помножте чисельники і помножте знаменники.
- Розміщення негативного знака у дробі: для будь-яких позитивних чисел\(a\) і\(b\),\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- Властивість One:\(\dfrac{a}{a} = 1\); Будь-яке число, крім нуля, розділене саме по собі - одне.
- Спрощення дробу
- Перепишіть чисельник і знаменник, щоб показати загальні фактори. Якщо потрібно, спочатку перерахуйте чисельник і знаменник на прості числа.
- Спростіть використання властивості еквівалентних дробів шляхом поділу загальних факторів.
- Помножте всі інші фактори.
- Спрощення виразу за допомогою смужки дробу
- Спростити вираз в чисельнику. Спростити вираз в знаменнику.
- Спростити дріб.
Глосарій
- складний дріб
- Складний дріб - це дріб, в якому чисельник або знаменник містить дріб.
- знаменник
- Знаменник - це величина на нижній частині дробу, яка вказує на кількість рівних частин, на які було поділено ціле.
- еквівалентні дроби
- Еквівалентні дроби - це дроби, які мають однакове значення.
- фракція
- Записується дріб\(\frac{a}{b}\)\(b\neq 0\), де, a - чисельник, а b - знаменник. Дріб являє собою частини цілого. Знаменник b - це кількість рівних частин, на які було поділено ціле, а чисельник aa вказує, скільки частин включено.
- чисельник
- Чисельник - це значення на верхній частині дробу, яке вказує, скільки частин цілого включено.
- взаємний
- Відповідне\(\frac{a}{b}\) є\(\frac{b}{a}\). Число і його зворотне множиться на одиницю:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- спрощений дріб
- Дріб вважається спрощеним, якщо в його чисельнику і знаменнику відсутні загальні множники.
