8.E: Квадратичні функції (вправи)

Last updated
Save as PDF

Page ID: 58264

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

8.1: Вступ до радикальних позначень

1) Перерахуйте всі реальні квадратні корені$-400$.

Відповідь: Справжніх квадратних коренів немає.

2) Перерахуйте всі реальні квадратні корені$64$.

3) Перерахуйте всі реальні квадратні корені$-25$.

Відповідь: Справжніх квадратних коренів немає.

4) Перерахуйте всі реальні квадратні корені$81$.

5) Перерахуйте всі реальні квадратні корені$49$.

Відповідь: $-7,7$

6) Перерахуйте всі реальні квадратні корені$-100$.

7) Перерахуйте всі реальні квадратні корені$324$.

Відповідь: $-18,18$

8) Перерахуйте всі реальні квадратні корені$36$.

9) Перерахуйте всі реальні квадратні корені$-225$.

Відповідь: Справжніх квадратних коренів немає.

10) Перерахуйте всі реальні квадратні корені$0$.

11) Перерахуйте всі реальні рішення$x^2 = -225$.

Відповідь: Реальних рішень немає.

12) Перерахуйте всі реальні рішення$x^2 = -25$.

13) Перерахуйте всі реальні рішення$x^2 = 361$.

Відповідь: $-19,19$

14) Перерахуйте всі реальні рішення$x^2 = 256$.

15) Перерахуйте всі реальні рішення$x^2 = -400$.

Відповідь: Реальних рішень немає.

16) Перерахуйте всі реальні рішення$x^2 = 0$.

17) Перерахуйте всі реальні рішення$x^2 = 169$.

Відповідь: $-13,13$

18) Перерахуйте всі реальні рішення$x^{2}=-100$.

19) Перерахуйте всі реальні рішення$x^{2}=625$.

Відповідь: $-25,25$

20) Перерахуйте всі реальні рішення$x^{2}=324$.

У вправах 21-30 спростіть кожне з заданих виразів.

21)$\sqrt{64}$

Відповідь: $8$

22)$-\sqrt{-529}$

23)$-\sqrt{-256}$

Відповідь: Вираз не є дійсним числом.

24)$\sqrt{-529}$

25)$-\sqrt{361}$

Відповідь: $-19$

26)$\sqrt{-361}$

27)$-\sqrt{100}$

Відповідь: $-10$

28)$-\sqrt{196}$

29)$\sqrt{441}$

Відповідь: $21$

30)$\sqrt{49}$

У вправах 31-38 спростіть кожне з заданих виразів.

31)$(-\sqrt{17})^{2}$

Відповідь: $17$

32)$(-\sqrt{31})^{2}$

33)$(\sqrt{59})^{2}$

Відповідь: $59$

34)$(\sqrt{43})^{2}$

35)$(-\sqrt{29})^{2}$

Відповідь: $29$

36)$(-\sqrt{89})^{2}$

37)$(\sqrt{79})^{2}$

Відповідь: $79$

38)$(\sqrt{3})^{2}$

У Вправи 39-42 для кожного з заданих рівнянь спочатку використовуйте утиліту 5:intersect в меню CALC графічного калькулятора для визначення розв'язків. Дотримуйтесь вказівок щодо подання калькулятора, як показано в прикладі 8.1.9 у звіті про рішення на домашньому папері. По-друге, вирішіть рівняння алгебраїчно, а потім скористайтеся калькулятором, щоб знайти наближення ваших відповідей та порівняти цей другий набір з першим набором відповідей.

39)$x^{2}=37$

Відповідь

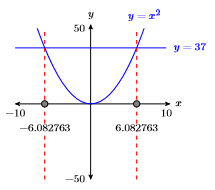
$Відповідь 8.1.39.png$

$\pm \sqrt{37} \approx \pm 6.082763$

40)$x^{2}=32$

41)$x^{2}=11$

Відповідь

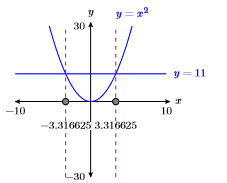
$Відповідь: 8.1.41.png$

$\pm \sqrt{11} \approx \pm 3.316625$

42)$x^{2}=42$

8.2: Спрощення радикальних виразів

У Вправи 1-6 спростіть заданий вираз, написавши свою відповідь, використовуючи символ одного квадратного кореня. Перевірте результат за допомогою графічного калькулятора.

1)$\sqrt{5} \sqrt{13}$

Відповідь: $\sqrt{65}$

2)$\sqrt{2} \sqrt{7}$

3)$\sqrt{17} \sqrt{2}$

Відповідь: $\sqrt{34}$

4)$\sqrt{5} \sqrt{11}$

5)$\sqrt{5} \sqrt{17}$

Відповідь: $\sqrt{85}$

6)$\sqrt{17} \sqrt{3}$

У вправах 7-26 перетворіть кожне з заданих виразів в просту радикальну форму.

7)$\sqrt{56}$

Відповідь: $2 \sqrt{14}$

8)$\sqrt{45}$

9)$\sqrt{99}$

Відповідь: $3 \sqrt{11}$

10)$\sqrt{75}$

11)$\sqrt{150}$

Відповідь: $5 \sqrt{6}$

12)$\sqrt{90}$

13)$\sqrt{40}$

Відповідь: $2 \sqrt{10}$

14)$\sqrt{171}$

15)$\sqrt{28}$

Відповідь: $2 \sqrt{7}$

16)$\sqrt{175}$

17)$\sqrt{153}$

Відповідь: $3 \sqrt{17}$

18)$\sqrt{125}$

19)$\sqrt{50}$

Відповідь: $5 \sqrt{2}$

20)$\sqrt{88}$

21)$\sqrt{18}$

Відповідь: $3 \sqrt{2}$

22)$\sqrt{117}$

23)$\sqrt{44}$

Відповідь: $2 \sqrt{11}$

24)$\sqrt{20}$

25)$\sqrt{104}$

Відповідь: $2 \sqrt{26}$

26)$\sqrt{27}$

У вправах 27-34 знайдіть довжину відсутньої сторони прямокутного трикутника. Ваша остаточна відповідь повинна бути в простій радикальній формі.

27)

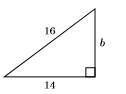
Відповідь: $2 \sqrt{15}$

28)

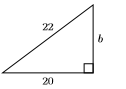
29)

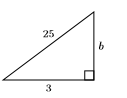
Відповідь: $2 \sqrt{154}$

30)

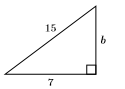
31)

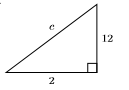
Відповідь: $2 \sqrt{37}$

32)

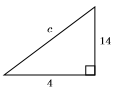
33)

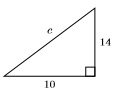
Відповідь: $2 \sqrt{74}$

34)

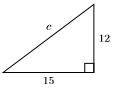
35) На малюнку нижче півколом вписаний прямокутний трикутник. Яка площа затіненої області?

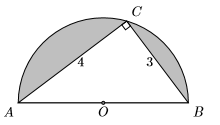
Відповідь: $\dfrac{25}{8} \pi-6$

36) На малюнку нижче півколом вписаний прямокутний трикутник. Яка площа затіненої області?

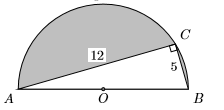
37) Найдовша ніжка прямокутного трикутника -$10$ стопи довші, ніж удвічі перевищує довжину його коротшої ноги. Гіпотенуза -$4$ стопи довше, ніж в три рази більше довжини коротшого катета. Знайдіть довжини всіх трьох сторін прямокутного трикутника.

Відповідь: $7,24,25$

38) Найдовша ніжка прямокутного трикутника -$2$ стопи довші, ніж удвічі перевищує довжину його коротшої ноги. Гіпотенуза -$3$ стопи довше, ніж удвічі більше довжини коротшого катета. Знайдіть довжини всіх трьох сторін прямокутного трикутника.

39) Сходи$19$ ноги довжиною спираються на стіну гаража. Якщо основа сходів знаходиться в$5$ футах від стіни гаража, наскільки високо до стіни гаража досягає сходи? Використовуйте калькулятор, щоб округлити відповідь до найближчої десятої частини фута.

Відповідь: $18.3$стопи

40) Сходи$19$ ноги довжиною спираються на стіну гаража. Якщо основа сходів знаходиться в$6$ футах від стіни гаража, наскільки високо до стіни гаража досягає сходи? Використовуйте калькулятор, щоб округлити відповідь до найближчої десятої частини фута.

8.3: Завершення площі

У Вправах 1-8 знайдіть всі дійсні розв'язки даного рівняння. Помістіть свої остаточні відповіді в простій радикальній формі.

1)$x^{2}=84$

Відповідь: $\pm 2 \sqrt{21}$

2)$x^{2}=88$

3)$x^{2}=68$

Відповідь: $\pm 2 \sqrt{17}$

4)$x^{2}=112$

5)$x^{2}=-16$

Відповідь: Немає реальних рішень

6)$x^{2}=-104$

7)$x^{2}=124$

Відповідь: $\pm 2 \sqrt{31}$

8)$x^{2}=148$

У вправах 9-12 знайдіть всі реальні розв'язки даного рівняння. Помістіть свої остаточні відповіді в простій радикальній формі.

9)$(x+19)^{2}=36$

Відповідь: $-25,-13$

10)$(x-4)^{2}=400$

11)$(x+14)^{2}=100$

Відповідь: $-24,-4$

12)$(x-15)^{2}=100$

У вправах 13-18 квадрат кожного з наступних біномів.

13)$(x+23)^{2}$

Відповідь: $x^{2}+46 x+529$

14)$(x-5)^{2}$

15)$(x+11)^{2}$

Відповідь: $x^{2}+22 x+121$

16)$(x-7)^{2}$

17)$(x-25)^{2}$

Відповідь: $x^{2}-50 x+625$

18)$(x+4)^{2}$

У вправах 19-24 враховуйте кожен з наступних триноміалів.

19)$x^{2}+24 x+144$

Відповідь:: $(x+12)^{2}$

20)$x^{2}-16 x+64$

21)$x^{2}-34 x+289$

Відповідь:: $(x-17)^{2}$

22)$x^{2}+8 x+16$

23)$x^{2}-20 x+100$

Відповідь:: $(x-10)^{2}$

24)$x^{2}+16 x+64$

У вправах 25-36 для кожного виразу заповніть квадрат, щоб сформувати ідеальний квадратний триноміал. Перевірте свою відповідь, враховуючи свій результат. Обов'язково перевірте свій середній термін.

25)$x^{2}-20 x$

Відповідь: $x^{2}-20 x+100$

26)$x^{2}-10 x$

27)$x^{2}-6 x$

Відповідь: $x^{2}-6 x+9$

28)$x^{2}-40 x$

29)$x^{2}+20 x$

Відповідь: $x^{2}+20 x+100$

30)$x^{2}+26 x$

31)$x^{2}+7 x$

Відповідь: $x^{2}+7 x+\frac {49}{4}$

32)$x^{2}+19 x$

33)$x^{2}+15 x$

Відповідь: $x^{2}+15 x+\frac {225}{4}$

34)$x^{2}+25 x$

35)$x^{2}-5 x$

Відповідь: $x^{2}-5 x+\frac {25}{4}$

36)$x^{2}-3 x$

У Вправах 37-52 знайдіть усі дійсні розв'язки заданого рівняння, якщо такі є. Помістіть свої остаточні відповіді в простій радикальній формі.

37)$x^{2}=18 x-18$

Відповідь: $9-3 \sqrt{7}, 9+3 \sqrt{7}$

38)$x^{2}=12 x-18$

39)$x^{2}=16 x-16$

Відповідь: $8-4 \sqrt{3}, 8+4 \sqrt{3}$

40)$x^{2}=12 x-4$

41)$x^{2}=-16 x-4$

Відповідь: $-8-2 \sqrt{15},-8+2 \sqrt{15}$

42)$x^{2}=-12 x-12$

43)$x^{2}=18 x-9$

Відповідь: $9-6 \sqrt{2}, 9+6 \sqrt{2}$

44)$x^{2}=16 x-10$

45)$x^{2}=16 x-8$

Відповідь: $8-2 \sqrt{14}, 8+2 \sqrt{14}$

46)$x^{2}=10 x-5$

47)$x^{2}=-18 x-18$

Відповідь: $-9-3 \sqrt{7},-9+3 \sqrt{7}$

48)$x^{2}=-10 x-17$

49)$x^{2}=-16 x-20$

Відповідь: $-8-2 \sqrt{11},-8+2 \sqrt{11}$

50)$x^{2}=-16 x-12$

51)$x^{2}=-18 x-1$

Відповідь: $-9-4 \sqrt{5},-9+4 \sqrt{5}$

52)$x^{2}=-12 x-8$

У вправах 53-56 розв'яжіть дане рівняння алгебраїчно, виклавши свої остаточні відповіді в простій радикальній формі. Далі скористайтеся графічним калькулятором для вирішення рівняння, дотримуючись техніки, викладеної в прикладі 8.3.8. Використовуйте Рекомендації щодо подання калькулятора, як показано в прикладі 8, під час звітування про рішення вашого домашнього завдання. Порівняйте рішення, визначені двома методами.

53)$x^{2}-2 x-17=0$

Відповідь: $1-3 \sqrt{2}, 1+3 \sqrt{2}$

54)$x^{2}-4 x-14=0$

55)$x^{2}-6 x-3=0$

Відповідь: $3-2 \sqrt{3}, 3+2 \sqrt{3}$

56)$x^{2}-4 x-16=0$

8.4: Квадратична формула

У вправах 1-8 розв'яжіть задане рівняння шляхом факторингу триноміала за допомогою$ac$ -методу, а потім застосувавши властивість нульового добутку. По-друге, створите друге рішення, використовуючи квадратичну формулу. Порівняйте свої відповіді.

1)$x^{2}-3 x-28=0$

Відповідь: $-4,7$

2)$x^{2}-4 x-12=0$

3)$x^{2}-8 x+15=0$

Відповідь: $3,5$

4)$x^{2}-6 x+8=0$

5)$x^{2}-2 x-48=0$

Відповідь: $-6,8$

6)$x^{2}+9 x+8=0$

7)$x^{2}+x-30=0$

Відповідь: $-6,5$

8)$x^{2}-17 x+72=0$

У вправах 9-16 використовуйте квадратичну формулу для вирішення заданого рівняння. Ваші остаточні відповіді повинні бути зведені до найнижчих термінів, а всі радикальні вирази повинні бути в простій радикальній формі.

9)$x^{2}-7 x-5=0$

Відповідь: $\dfrac{7 \pm \sqrt{69}}{2}$

10)$3 x^{2}-3 x-4=0$

11)$2 x^{2}+x-4=0$

Відповідь: $\dfrac{-1 \pm \sqrt{33}}{4}$

12)$2 x^{2}+7 x-3=0$

13)$x^{2}-7 x-4=0$

Відповідь: $\dfrac{7 \pm \sqrt{65}}{2}$

14)$x^{2}-5 x+1=0$

15)$4 x^{2}-x-2=0$

Відповідь: $\dfrac{1 \pm \sqrt{33}}{8}$

16)$5 x^{2}+x-2=0$

У вправах 17-24 використовуйте квадратичну формулу для вирішення заданого рівняння. Ваші остаточні відповіді повинні бути зведені до найнижчих термінів, а всі радикальні вирази повинні бути в простій радикальній формі.

17)$x^{2}-x-11=0$

Відповідь: $\dfrac{1 \pm 3 \sqrt{5}}{2}$

18)$x^{2}-11 x+19=0$

19)$x^{2}-9 x+9=0$

Відповідь: $\dfrac{9 \pm 3 \sqrt{5}}{2}$

20)$x^{2}+5 x-5=0$

21)$x^{2}-3 x-9=0$

Відповідь: $\dfrac{3 \pm 3 \sqrt{5}}{2}$

22)$x^{2}-5 x-5=0$

23)$x^{2}-7 x-19=0$

Відповідь: $\dfrac{7 \pm 5 \sqrt{5}}{2}$

24)$x^{2}+13 x+4=0$

У вправах 25-32 використовуйте квадратичну формулу для вирішення заданого рівняння. Ваші остаточні відповіді повинні бути зведені до найнижчих термінів, а всі радикальні вирази повинні бути в простій радикальній формі.

25)$12 x^{2}+10 x-1=0$

Відповідь: $\dfrac{-5 \pm \sqrt{37}}{12}$

26)$7 x^{2}+6 x-3=0$

27)$7 x^{2}-10 x+1=0$

Відповідь: $\dfrac{5 \pm 3 \sqrt{2}}{7}$

28)$7 x^{2}+4 x-1=0$

29)$2 x^{2}-12 x+3=0$

Відповідь: $\dfrac{6 \pm \sqrt{30}}{2}$

30)$2 x^{2}-6 x-13=0$

31)$13 x^{2}-2 x-2=0$

Відповідь: $\dfrac{1 \pm 3 \sqrt{3}}{13}$

32)$9 x^{2}-2 x-3=0$

33) Об'єкт запускається вертикально, а його висота$y$ (у футах) над рівнем землі задається рівнянням$y = 240 + 160t− 16t^2$, де$t$ - час (у секундах), який минув з моменту його запуску. Скільки часу має пройти після запуску, перш ніж об'єкт повернеться на рівень землі? Розмістивши відповідь в простій формі і зменшивши, скористайтеся вашим калькулятором, щоб округлити відповідь до найближчої десятої частки секунди.

Відповідь: $11.3$секунд

34) Об'єкт запускається вертикально, а його висота$y$ (у футах) над рівнем землі задається рівнянням$y = 192 + 288t− 16t^2$, де$t$ - час (у секундах), який минув з моменту його запуску. Скільки часу має пройти після запуску, перш ніж об'єкт повернеться на рівень землі? Розмістивши відповідь в простій формі і зменшивши, скористайтеся вашим калькулятором, щоб округлити відповідь до найближчої десятої частки секунди.

35) Виручка виробника,$R$ нарахована від продажу$x$ віджетів, задається рівнянням$R = 6000x − 5x^2$. Витрати виробника на побудову$x$ віджетів задаються рівнянням$C = 500000 + 5.25x$. Точка беззбитковості для виробника визначається як кількість вбудованих та проданих віджетів, тому дохід та витрати виробника ідентичні. Знайдіть кількість віджетів, необхідних для побудови і продажу, щоб виробник «зламав рівність». Округляйте відповіді до найближчого віджету.

Відповідь: $90$віджети,$1109$ віджети

36) Виручка виробника,$R$ нарахована від продажу$x$ віджетів, задається рівнянням$R = 4500x−15.25x^2$. Скільки віджетів потрібно продати, щоб виручка виробника була$\$125,000$? Округляйте відповіді до найближчого віджету.

37) Майк сідає на свій велосипед опівдні і починає їздити через північ з постійною швидкістю$6$ миль на годину. О 14:00 Тодд сідає на свій велосипед в тій же відправній точці і починає їздити на схід з постійною швидкістю$8$ миль на годину. В який час доби вони будуть один від$60$ одного (як ворона летить)? Не турбуйтеся про просту форму, просто повідомте час доби, виправте до найближчої хвилини.

Відповідь: 19:12 вечора

38) Мікаела сідає на свій велосипед опівдні і починає їздити через північ з постійною швидкістю$4$ миль на годину. О 13:00 Розмарі сідає на свій велосипед в тій же вихідній точці і починає їздити на схід з постійною швидкістю$6$ миль на годину. В який час доби вони будуть один від$20$ одного (як ворона летить)? Не турбуйтеся про просту форму, просто повідомте час доби, виправте до найближчої хвилини.

39) Площа прямокутного поля -$76$ квадратні фути. Довжина поля на$7$ ноги більше його ширини. Знайдіть розміри поля, виправте до найближчої десятої частини фута.

Відповідь: $5.9$по$12.9$ ногам

40) Площа прямокутного поля$50$ квадратних футів. Довжина поля на$8$ ноги більше його ширини. Знайдіть розміри поля, виправте до найближчої десятої частини фута.

41) Середні концентрації вуглекислого газу над Мауна-Лоа, Гаваї, збираються дослідницькою лабораторією земної системи (ESRL) спільно з Національним управлінням океанічних та атмосферних впливів (NOAA). Середні річні концентрації в частках на мільйон за роки 1962, 1982 і 2002 наведені в наступній таблиці.

Рік	1962	1982	2002
Концентрація (проміле)	318	341	373

Квадратична модель підходить до цих даних, що дає,\[C =0 .01125t^2 +0 .925t+ 318 \nonumber \] де$t$ кількість років з 1962 року і$C$ є середньорічною концентрацією (частинами на мільйон) вуглекислого газу над Мауна-Лоа. Використовуйте модель, щоб знайти рік, коли середня концентрація вуглекислого газу становила$330$ частини на мільйон. Округлите відповідь до найближчого року.

Відповідь: 1973

42) Бюро перепису населення США надає історичні дані про кількість американців старше віку$85$.

Рік	1970	1990	2010
Населення понад 85 (мільйони)	1.4	3.0	5.7

Квадратична модель підходить до цих даних,$t$ що дає,\[P =0 .01375t^2 +0 .0525t+1 .4 \nonumber \] де кількість років з 1970 року і$P$ кількість американців (у мільйоні) у віці$85$. Використовуйте модель, щоб знайти рік, коли число американців старше віку$85$ було$2,200,000$. Округлите відповідь до найближчого року.