7.4: Рішення раціональних рівнянь

Last updated
Save as PDF

Page ID: 58257

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У розділі 3 глави 2 ми показали, що найбільш ефективним способом розв'язання рівняння, що містить дроби, було спочатку очистити дроби шляхом множення обох сторін рівняння на найменш спільний знаменник. Наприклад, з урахуванням рівняння

\[\dfrac{1}{2}x+\dfrac{1}{3}=\dfrac{1}{4} \nonumber \]

ми спочатку очистили дроби, помноживши обидві сторони на$12$.

\[\begin{align*} 12\left [ \dfrac{1}{2}x + \dfrac{1}{3}\right ] &= \left [ \dfrac{1}{4} \right ]12\\ 6x+4 &= 3 \end{align*} \nonumber \]

Ця процедура працює однаково добре, коли знаменники містять змінну.

Приклад$\PageIndex{1}$

Вирішити для$x$:$1-\dfrac{2}{x} = \dfrac{3}{x^2}$

Рішення

Спільним знаменником є$x^2$. Починаємо з очищення дробів, множивши обидві сторони рівняння на$x^2$.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [1- \dfrac{2}{x} \right] &= \left [ \dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2. \end{align*} \nonumber \]

Тепер використовуємо розподільне властивість.

\[{\color {Red} x^2}[1]-{\color {Red} x^2}\left [\dfrac{2}{x} \right ] = \left [\dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2. \nonumber \]

Тепер скасуємо загальні фактори і спростимо.

\[x^2 - 2x =3 \quad \color {Red} \text {Cancel. Simplify. } \nonumber \]

Отримане рівняння$x$ нелінійне (піднімається на ступінь більше$1$). Зробіть одну сторону нуль, потім коефіцієнт.

\[\begin{align*} x^2-2x-3 &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero.}\\ (x-3)(x+1) &= 0 \quad \color {Red} \text {Factor.} \end{align*} \nonumber \]

Використовуйте властивість нульового продукту, щоб завершити рішення. Або перший коефіцієнт дорівнює нулю, або другий множник дорівнює нулю.

\[\begin{align*} x-3 &= 0 \\ x &= 3 \end{align*} \nonumber\]

або

\[\begin{align*} x+1 &= 0 \\ x &= -1 \end{align*} \nonumber\]

Значить, рішення є$x = −1$ і$x = 3$.

Перевірте. $−1$Замініть$x$, потім$3$ на$x$ вихідне рівняння і спростити.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} -1})^2} &= \dfrac{3}{({\color {Red} -1})^2} \\ 1+2 &= 3\\ 3 &= 3 \end{align*} \nonumber\]

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} 3})} &= \dfrac{3}{({\color {Red} 3})^2} \\ 1-\dfrac{2}{3} &= \dfrac{3}{9}\\ \dfrac{1}{3} &= \dfrac{1}{3} \end{align*} \nonumber\]

Зверніть увагу, що обидва призводять до істинних тверджень, показуючи, що обидва$x =−1$ і$x =3$ перевіряють у вихідному рівнянні.

Вправа$\PageIndex{1}$

Вирішити для$x$:$1-\dfrac{6}{x} = -\dfrac{8}{x^2}$

Відповідь: $2,4$

Приклад$\PageIndex{2}$

Вирішити для$x$:$6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Рішення

Спільним знаменником є$x^2$.

\[\begin{align*} 6-\dfrac{22}{x^2} &= \dfrac{29}{x} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [6-\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[6]-{\color {Red} x^2}\left [\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 6x^2-22 &= 29x \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber \]

Це останнє рівняння нелінійне. Зробіть одну сторону нулем.

\[6x^2 −29x−22 = 0 \nonumber \]

Пара цілих чисел$4$ і$−33$ має добуток$ac = −132$ і суму$b = −29$. Розбийте середній термін на суму, використовуючи цю пару, а потім коефіцієнт шляхом групування.

\[\begin{align*} 6x^2 +4x-33x-22 &= 0 \\ 2x(3x + 2)-11(3x + 2) &= 0 \\ (2x - 11)(3x + 2) &= 0 \end{align*} \nonumber \]

Нарешті, використовуйте властивість нульового продукту для запису:

\[\begin{align*} 2x - 11 &= 0 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \end{align*} \nonumber \]

або

\[\begin{align*} 3x + 2 &= 0 \\ 3x &= -2 \\ x &= -\dfrac{2}{3} \end{align*}\]

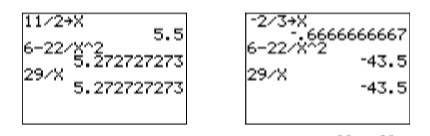
Перевірте: Давайте перевіримо ці рішення за допомогою наших калькуляторів. Введіть$11/2$, натискаємо кнопку STO►, натискаємо$\mathrm{X,T,\theta,n}$ кнопку і клавішу ENTER (див. екран калькулятора зліва на малюнку$\PageIndex{1}$). Далі введіть ліву частину рівняння як$6-22/X^2$ і натисніть клавішу ENTER. Введіть праву частину рівняння як$29/X$ і натисніть клавішу ENTER. Результати однакові (див. Екран калькулятора зліва на малюнку$\PageIndex{1}$). Це підтверджує, що$11/2$ це рішення$6−22/x^2 = 29/x$.

На екрані калькулятора праворуч на малюнку$\PageIndex{1}$ показана аналогічна перевірка рішення$x = −2/3$.

рис. 7.4.1.png — Малюнок$\PageIndex{1}$: Перевірка рішень$6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Вправа$\PageIndex{2}$

Вирішити для$x$:$\dfrac{7}{x^2}+8=-\dfrac{30}{x}$

Відповідь: $−1/4, −7/2$

Розв'язування раціональних рівнянь за допомогою графічного калькулятора

Давайте скористаємося графічним калькулятором для вирішення рівняння, що містить раціональні вирази.

Приклад$\PageIndex{3}$

Розглянемо наступне рівняння:\[2-\dfrac{9}{x}=\dfrac{5}{x^2} \nonumber \] Вирішіть рівняння алгебраїчно, а потім розв'яжіть рівняння графічно за допомогою графічного калькулятора. Порівняйте свої рішення.

Рішення

Алгебраїчне рішення: По-перше, алгебраїчний підхід. Помножте обидві сторони рівняння на загальний знаменник$x^2$.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [2-\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[2]-{\color {Red} x^2}\left [\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 2x^2-9x &= 5 \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber\]

Останнє рівняння нелінійне. Зробіть одну сторону нулем.

\[2x^2 −9x−5=0 \quad \color {Red} \text {Make one side zero.} \nonumber \]

Пара цілих чисел$−10$ і$1$ мають добуток, що дорівнює$ac = −10$ і дорівнює сумі$b = −9$. Розбийте середній термін за допомогою цієї пари, а потім коефіцієнт шляхом групування.

\[\begin{align*} 2x^2-10x+x-5 &= 0 \quad \color {Red} -10x+x=-9x\\ 2x(x-5) + 1(x-5) &= 0 \quad \color {Red} \text {Factor by grouping.} \\ (2x + 1)(x-5) &= 0 \quad \color {Red} \text {Factor out } x-5 \end{align*} \nonumber\]

Тепер використовуйте властивість нульового продукту, щоб записати:

\[\begin{align*} 2x+1 &= 0\\ 2x &= -1\\ x &= -\dfrac{1}{2} \end{align*} \nonumber \]

або

\[\begin{align*} x-5 &= 0\\ x &= 5 \end{align*} \nonumber\]

Значить, рішення є$x = −1/2$ і$x = 5$.

Графічне рішення: Ми можемо завантажувати кожну сторону рівняння окремо, а потім використовувати утиліту intersect, щоб знайти, де графіки перетинаються. Однак у цьому випадку трохи простіше зробити одну сторону рівняння нуль, намалювати єдиний графік, а потім відзначити, де графік перетинає$x$ вісь -.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.} \\ 2-\dfrac{9}{x} - \dfrac{5}{x^2} &= 0 \quad \color {Red} \text {Make one side zero.} \nonumber \end{align*} \nonumber\]

Завантажте ліву частину рівняння в$\mathrm{Y1}$ як$\mathrm{2-9/X-5/X}\land 2$ (див. Зображення зліва на малюнку$\PageIndex{2}$), потім виберіть 6:ZStandard з меню ZOOM, щоб створити зображення праворуч на малюнку$\PageIndex{2}$.

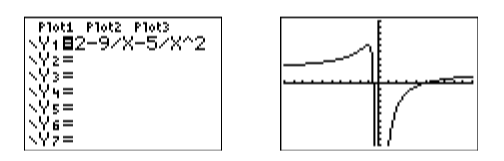
рис. 7.4.2.png — Малюнок$\PageIndex{2}$: Намалюйте графік$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

Далі, рішення

\[2-\dfrac{9}{x}-\dfrac{5}{x^2} = 0 \nonumber \]

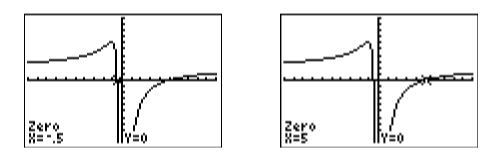
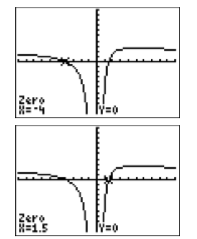
знаходять, зазначивши, де граф$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$ перетинає$x$ -вісь. Виберіть 2: нуль у меню CALC. За допомогою клавіш зі стрілками перемістіть курсор ліворуч від першого$x$ -перехоплення, а потім натисніть ENTER, щоб встановити «Ліва межа». Далі наведіть курсор праворуч від першого$x$ -перехоплення, а потім натисніть ENTER, щоб встановити «Right bound». Нарешті, залиште курсор там, де він є, і натисніть ENTER, щоб встановити «Вгадати». Калькулятор відповідає результатом, показаним на малюнку зліва на малюнку$\PageIndex{3}$.

Повторіть процедуру пошуку нуля, щоб захопити координати другого$x$ -перехоплення (див. Зображення праворуч на малюнку$\PageIndex{3}$).

рис. 7.4.3.png — Малюнок$\PageIndex{3}$: Розташування нулів$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

Повідомлення про рішення домашнього завдання: Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див. Рис.$\PageIndex{4}$).
Розмістіть параметри WINDOW в кінці кожної осі (див. Рисунок$\PageIndex{4}$).
Позначте графік його рівнянням (див. Малюнок$\PageIndex{4}$).
Пропустіть пунктирні вертикальні лінії через кожну$x$ -перехоплення. Затіньте та позначте$x$ -значення точок, де пунктирна вертикальна лінія перетинає$x$ вісь -. Це розв'язки рівняння$2− 9/x− 5/x^2 = 0$ (див. Малюнок$\PageIndex{4}$).

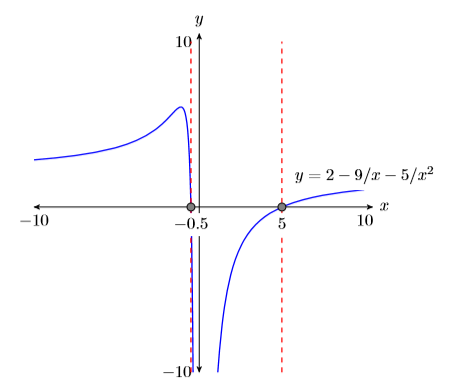
рис. 7.4.4.png — Малюнок$\PageIndex{4}$: Повідомлення про графічне рішення на домашнє завдання.

Таким чином, калькулятор повідомляє, що розв'язки$2−9/x −5/x^2 = 0$ є$x =−0.5$ і$x = 5$, які відповідають алгебраїчним розв'язкам$x = −1/2$ і$x = 5$.

Вправа$\PageIndex{3}$

Вирішіть рівняння$2+\dfrac{5}{x}=\dfrac{12}{x^2}$ як алгебраїчно, так і графічно, а потім порівняйте свої рішення.

Відповідь

$−4, 3/2$

$Ех 7.4.3.png$

Чисельні програми

Давайте застосуємо те, що ми навчилися, до програми.

Приклад$\PageIndex{4}$

Сума числа і його зворотна дорівнює$41/20$. Знайдіть номер.

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштувати словник змінних:$x$ Дозволяти представляти невідоме число.
Налаштуйте рівняння: Якщо невідоме число є$x$, то його зворотне дорівнює$1/x$. Таким чином, «сума числа і його зворотне є$41/20$» стає:\[x+\dfrac{1}{x}=\dfrac{41}{20} \nonumber \]
Вирішити рівняння: Очистіть дроби, помноживши обидві сторони на$20x$, найменш спільний знаменник. \[\begin{align*} x+\dfrac{1}{x} &= \dfrac{41}{20} \quad \color {Red} \text {Model equation.}\\ {\color {Red}20x}\left [x+\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Multiply both sides by }20x\\ {\color {Red}20x}[x]+{\color {Red}20x}\left [\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Distribute }20x.\\ 20x^2+20 &= 41x \quad \color {Red} \text {Cancel and simplify.} \end{align*} \nonumber \]Рівняння нелінійне. Зробіть одну сторону нулем. \[20x^2 −41x + 20 = 0 \quad \color {Red} \text {Make one side zero.}\nonumber \]Пара цілих чисел$−16$ і$−25$ має добуток$ac = 400$ і суму$b = −41$. Розбийте середній член останнього рівняння на суму подібних термінів за допомогою цієї пари, а потім множник шляхом групування. \[\begin{align*} 20x^2 - 16x-25x + 20 &= 0 \quad \color {Red} -16x-25x=-41x\\ 4x(5x-4)-5(5x-4) &= 0 \quad \color {Red} \text {Factor by grouping.}\\ (4x-5)(5x-4) &= 0 \quad \color {Red} \text {Factor out }5x-4.\\ \end{align*} \nonumber \]Тепер ми можемо використовувати властивість нульового продукту для запису:\[\begin{align*} 4x-5 &= 0 \\ 4x &= 5 \\ x &= \dfrac{5}{4} \end{align*} \nonumber\] або\[\begin{align*} 5x-4 &= 0 \\ 5x &= 4 \\ x &= \dfrac{4}{5} \end{align*} \nonumber\]
Дайте відповідь на питання: Можливі два числа,$5/4$ і$4/5$.
Озирніться назад: Сума невідомого числа та його взаємного числа повинна дорівнювати$41/20$. Відповідь$5/4$ має зворотний$4/5$. Їх сума:\[\begin{align*} \dfrac{5}{4} + \dfrac{4}{5} &= \dfrac{16}{20} + \dfrac{25}{20}\\ &= \dfrac{41}{20} \end{align*} \nonumber\] Таким чином,$5/4$ є дійсним рішенням. Друга відповідь$4/5$ має зворотний$5/4$, тому зрозуміло, що їх сума теж є$41/20$. Отже,$4/5$ це також дійсне рішення.

Вправа$\PageIndex{4}$

Сума числа і його зворотна дорівнює$53/14$. Знайдіть номер.

Відповідь: $2/7, 7/2$