7.2: Наукові позначення

Починаємо цей розділ з вивчення повноважень десяти.

\[\begin{align*} 10^1 &= 10\\ 10^2 &= 10\cdot 10 = 100\\ 10^3 &= 10\cdot 10\cdot 10 = 1,000\\ 10^4 &= 10\cdot 10\cdot 10\cdot 10 = 10,000 \end{align*} \nonumber \]

Зауважте, що відповідь для\(10^3\) є одиницею, за якою слідують три нулі. Відповіддю для\(10^4\) є одиниця, за якою слідують чотири нулі. Ви бачите візерунок?

Ненегативні сили десяти

У\(10^n\) виразі показник відповідає кількості нулів у відповіді. Отже,\(1\) за ним\(10^n\) слідуватимуть\(n\) нулі.

Приклад\(\PageIndex{1}\)

Спростити:\(10^9\).

Рішення

\(10^9\)має бути а\(1\) потім\(9\) нулі. \[10^9 =1 ,000,000,000 \nonumber \]

Вправа\(\PageIndex{1}\)

Спростити:\(10^6\).

Відповідь

\(1,000,000\)

Далі розберемо негативні сили десяти.

\[\begin{align*} 10^{-1} &= \dfrac{1}{10} = 0.1\\ 10^{-2} &= \dfrac{1}{100} = 0.01\\ 10^{-3} &= \dfrac{1}{1000} = 0.001\\ 10^{-4} &= \dfrac{1}{10000} = 0.0001 \end{align*} \nonumber \]

Зауважте, що відповідь для\(10^{−3}\) має три знака після коми, а відповідь\(10^{−4}\) містить чотири знака після коми.

Негативні сили десяти

У\(10^{−n}\) виразі показник відповідає кількості десяткових знаків у відповіді. Отже,\(10^{−n}\) буде мати n знаків після коми, перший\(n−1\) з яких - нулі, а цифра в n-му знаку після коми - a\(1\).

Приклад\(\PageIndex{2}\)

Спростити:\(10^{−7}\).

Рішення

\(10^{−7}\)має мати сім знаків після коми, перші шість з яких - нулі, а цифра в сьомому знаку після коми - a\(1\). \[10^{−7} = 0 .0000001 \nonumber \]

Вправа\(\PageIndex{2}\)

Спростити:\(10^{−5}\).

Відповідь

\(0.00001\)

Множення десяткових чисел на ступені десяти

Давайте\(1.234567\) помножимо на\(10^3\), або еквівалентно, на\(1,000\).

\[\begin{array}{ccc} 1.234567 \\ \;\;\times 1000\\ \hline 1234.567000 \end{array} \nonumber \]

Сума цифр праворуч від десяткової крапки в\(1.234567\) і\(1000\) є\(6\). Тому ставимо десяткову крапку в добутку так, щоб праворуч від десяткової крапки було шість цифр.

Однак кінцеві нулі можуть бути видалені без зміни вартості товару. Тобто\(1.234567\) часи\(1000\) є\(1234.567\). Зверніть увагу, що десяткова крапка у добутку знаходиться на три розряди далі праворуч, ніж у вихідному коефіцієнті. Це спостереження призводить до наступного результату.

Множення на невід'ємне степеня десять

Множення десяткового числа на\(10^n\), куди\(n = 0, 1, 2, 3, \ldots ,\) буде переміщено\(n\) десяткові розряди вправо.

Приклад\(\PageIndex{3}\)

Спростити:\(325.6783×10^2\).

Рішення

Множення на\(10^2\) призведе до переміщення десяткової крапки на два розряди вправо. Таким чином:\[325.6783×10^2 = 32,567.83 \nonumber \]

Вправа\(\PageIndex{3}\)

Спростити:\(23.57889×10^3\)

Відповідь

\(23,578.89\)

Приклад\(\PageIndex{4}\)

Спростити:\(1.25×10^5\).

Рішення

Множення на\(10^5\) призведе до переміщення десяткової крапки на два розряди вправо. У цьому випадку нам потрібно додати нулі в кінці числа, щоб виконати переміщення\(5\) знаків після коми вправо. \[1.25×105 = 125,000 \nonumber \]

Вправа\(\PageIndex{14}\)

Спростити:\(2.35×10^4\)

Відповідь

\(23,500\)

Давайте\(453.9\) помножимо на\(10^{−2}\), або еквівалентно, на\(0.01\).

\[\begin{array}{ccc} 453.9 \\ \times 0.01\\ \hline 4.539 \end{array} \nonumber \]

Сума цифр праворуч від десяткової крапки в\(453.9\) і\(0.01\) є\(3\). Тому ставимо десяткову крапку в твір так, щоб праворуч від десяткової крапки були\(3\) цифри. Тобто,\(453.9×10^{−2} = 4.539\). Зверніть увагу, що десяткова крапка у добутку знаходиться на два розряди далі лівіше, ніж у вихідному коефіцієнті. Це спостереження призводить до наступного результату.

Помноження на негативну силу в десять

Множення десяткового числа на\(10^{−n}\), куди\(n = 1, 2, 3, \ldots ,\) буде переміщено\(n\) десяткові розряди вліво.

Приклад\(\PageIndex{5}\)

Спростити:\(14,567.8×10^{−3}\).

Рішення

Множення на\(10^{−3}\) призведе до переміщення десяткової крапки на три розряди вліво. Таким чином:\[14,567.8×10^{−3} = 14 .5678 \nonumber \]

Вправа\(\PageIndex{5}\)

Спростити:\(3,854.2×10^{−1}\)

Відповідь

\(385 .42\)

Приклад\(\PageIndex{6}\)

Спростити:\(4.3×10^{−4}\).

Рішення

Множення на\(10^{−4}\) призведе до переміщення десяткової крапки на чотири розряди вліво. У цьому випадку нам потрібно додати кілька провідних нулів на початку числа, щоб виконати переміщення\(4\) знаків після коми вліво. \[4.3×10^{−4} =0.00043\nonumber \]. Зверніть увагу також на початковий нуль перед десятковою крапкою. Хоча\(.00043\) це еквівалентне число, форма\(0.00043\) є кращою в математиці та науці.

Вправа\(\PageIndex{6}\)

Спростити:\(2.2×10^{−2}\)

Відповідь

\(0.022\)

Форма наукового позначення

Почнемо з визначення форми числа, яке називається науковим позначенням.

Наукові позначення

Число, що має форму,\[a×10^b \nonumber \] де\(b\) є цілим числом і\(1 ≤| a| < 10\), як кажуть, є в науковому позначенні.

Вимога\(1 ≤| a| < 10\) говорить про те, що величина а повинна бути мінімум\(1\) і менше\(10\).

• Число\(12.34×10^{−4}\) не в науковому позначенні, тому\(|12.34| = 12.34\) що більше, ніж\(10\).
• Число\(−0.95×10^3\) не в науковому позначенні,\(|−0.95|= 0.95\) тому що менше\(1\).
• Число\(7.58×10^{−12}\) знаходиться в науковому позначенні\(|7.58|=7.58\), тому що більше або дорівнює\(1\) і менше\(10\).
• Число\(−1.0×10^{15}\) знаходиться в науковому позначенні\(|−1.0|=1.0\), тому що більше або дорівнює\(1\) і менше\(10\).

Після розгляду цих прикладів випливає, що число в науковому позначенні має мати рівно одну з цифр\(1, 2, 3, \ldots , 9\) перед десятковою крапкою. Рівно один, не більше, не менше. Таким чином, кожне з наступних чисел знаходиться в науковому позначенні.

\[4.7×10^8, \quad −3.764×10^{−1}, \quad 3.2×10^0, \quad \text {and} \quad −1.25×10^{−22} \nonumber \]

Розміщення числа в науковому позначенні

Щоб помістити число в наукові позначення, нам потрібно перемістити десяткову крапку так, щоб рівно одна з цифр\(1, 2, 3, \ldots , 9\) залишилася ліворуч від десяткової крапки, а потім помножити на відповідну потужність\(10\) так, щоб результат був еквівалентний вихідному числу.

Приклад\(\PageIndex{7}\)

Помістіть число\(1,234\) в наукові позначення.

Рішення

Перемістіть десяткову крапку на три розряди вліво так, щоб вона розташовувалася відразу після\(1\). Щоб зробити це нове число рівним\(1,234\), помножте на\(10^3\). Таким чином:\[1,234 = 1.234×10^3 \nonumber \]

Перевірка: Множення на\(10^3\) переміщує десяткові три розряди вправо, отже:\[1.234×10^3 =1,234 \nonumber \] Це початкове число, тому наша форма наукового позначення є правильною.

Вправа\(\PageIndex{7}\)

Помістіть число\(54,321\) в наукові позначення.

Відповідь

\(5 .4321×10^4\)

Приклад\(\PageIndex{8}\)

Помістіть число\(0.000025\) в наукові позначення.

Рішення

Перемістіть десяткову крапку на п'ять знаків вправо так, щоб вона розташовувалася відразу після\(2\). Щоб зробити це нове число рівним\(0.000025\), помножте на\(10^{−5}\). Таким чином:\[0.000025 = 2.5×10^{−5} \nonumber \]

Перевірка: Множення на\(10^{−5}\) пересуває десяткові п'ять знаків ліворуч, отже:\[2.5×10^{−5} = 0 .000025 \nonumber \] Це початкове число, тому наша форма наукового позначення є правильною.

Вправа\(\PageIndex{8}\)

Помістіть число\(0.0175\) в наукові позначення.

Відповідь

\(1.75×10^{−2}\)

Приклад\(\PageIndex{9}\)

Помістіть число\(34.5×10^{−11}\) в наукові позначення.

Рішення

Спочатку перемістіть десяткову крапку на одне місце вліво, щоб вона розташовувалася відразу після трьох. Щоб зробити цю нову форму рівною\(34.5\), помножте на\(10^1\). \[34.5×10^{−11} = 3.45×10^1×10^{−11} \nonumber \]Тепер повторіть базу\(10\) і додайте експоненти.

\[=3 .45×10^{−10} \nonumber \]

Вправа\(\PageIndex{9}\)

Помістіть число\(756.98×10^{−5}\) в наукові позначення.

Відповідь

\(7.5698×10^{−3}\)

Приклад\(\PageIndex{10}\)

Помістіть число\(0.00093×10^{12}\) в наукові позначення.

Рішення

Спочатку перемістіть десяткову крапку на чотири розряди вправо, щоб вона розташовувалася відразу після дев'ятки. Щоб зробити цю нову форму рівною\(0.00093\), помножте на\(10^{−4}\). \[0.00093×10^{12} = 9.3×10^{−4} ×10^{12} \nonumber \]

Тепер повторіть базу\(10\) і додайте експоненти. \[=9.3×10^8 \nonumber \]

Вправа\(\PageIndex{10}\)

Помістіть число\(0.00824×10^8\) в наукові позначення.

Відповідь

\(8.24×10^5\)

Наукові позначення та графічний калькулятор

Графічний калькулятор TI-84 має спеціальну кнопку для введення чисел в наукові позначення. Знайдіть клавішу «кома» приблизно цифрову клавішу на\(7\) клавіатурі калькулятора (див. Малюнок\(\PageIndex{1}\)). Трохи вище клавіші «кома», надрукованої на корпусі калькулятора, знаходиться символ EE. Він у тому ж кольорі, що ^{і 2-й} ключ, тому вам доведеться використовувати ^2-ю клавішу, щоб отримати доступ до цього символу.

Малюнок\(\PageIndex{1}\): Знайдіть мітку EE над клавішею «кома» на клавіатурі.

Ми це знаємо\(2.3 × 10^2 = 230\). Давайте подивимося, чи дає калькулятор таку ж інтерпретацію.

1. Введіть\(2.3\).
2. Натискаємо ^2-ю клавішу, потім клавішу коми. Це поставить E на екран перегляду калькулятора.
3. Введіть a\(2\).
4. Натисніть клавішу ENTER.

Малюнок\(\PageIndex{2}\): Введення чисел у наукові позначення.

Результат цих кроків показаний на першому зображенні на малюнку\(\PageIndex{2}\). Зверніть увагу, що калькулятор інтерпретує\(2.3\mathbf{E}2\) як\(2.3×10^2\) і дає правильну відповідь,\(230\). Ви можете продовжувати вводити цифри в наукові позначення (див. середнє зображення на малюнку\(\PageIndex{2}\)). Однак в якийсь момент числа стають занадто великими, і калькулятор реагує, виводячи цифри в науковому позначенні. Ви також можете змусити калькулятор відображати цифри у наукових позначеннях у всіх ситуаціях, спочатку натиснувши клавішу MODE, потім вибравши SCI у першому рядку та натиснувши клавішу ENTER (див. третє зображення на малюнку\(\PageIndex{2}\)). Ви можете повернути калькулятор в «звичайний» режим, вибравши NORMAL і натиснувши клавішу ENTER.

Приклад\(\PageIndex{11}\)

Скористайтеся калькулятором графіків, щоб спростити:\[(2.35×10^{−12})(3.25×10^{−4}) \nonumber \]

Рішення

По-перше, зауважте, що ми можемо\((2.35×10^{−12})(3.25×10^{−4})\) наблизити, взявши добуток\(2\)\(3\) і і додаючи повноваження десяти.

\[\begin{align*} &(2.35\times 10^{-12})(3.25\times 10^{-4}) \\ &\approx (2\times 10^{-12})(3\times 10^{-4}) \quad \color {Red} \text {Approximate: } 2.35\approx 2 \text { and } 3.25\approx 3 \\ &\approx 6\times 10^{-16} \quad \color {Red} 2\cdot 3 = 6 \text { and } 10^{-12}\cdot 10^{-4} = 10^{-16} \end{align*} \nonumber \]

Графічний калькулятор дасть точну відповідь. Введіть\(2.35\mathbf{E}-12\), натисніть кнопку «раз», потім введіть 3.25E-4 і натисніть кнопку ENTER. Обов'язково використовуйте кнопку «заперечувати», а не кнопку «відняти» для отримання знака мінус. Результат показаний на малюнку\(\PageIndex{3}\).

Малюнок\(\PageIndex{3}\): Обчислення\((2.35×10^{−12})(3.25×10^{−4})\).

Таким чином,\((2.35×10^{−12})(3.25×10^{−4})=7 .6375×10^{−16}\). Зверніть увагу, що це досить близько до нашої оцінки\(6 ×10^{−16}\).

Вправа\(\PageIndex{11}\)

Скористайтеся калькулятором графіків, щоб спростити:\[(3.42×10^6)(5.86×10^{−9}) \nonumber \]

Відповідь

\(2.00412×10^{−2}\)

Повідомлення про вашу відповідь на домашнє завдання

Обчисливши відповідь на приклад\(\PageIndex{11}\) на вашому калькуляторі, напишіть на домашнє завдання наступне:\[(2.35×10^{−12})(3.25×10^{−4})=7.6375×10^{−16} \nonumber \] Не пишіть\(7.6375\mathbf{E}-16\).

Приклад\(\PageIndex{12}\)

Скористайтеся калькулятором графіків, щоб спростити:\[\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \nonumber \]

Рішення

Знову ж таки, зробити приблизну відповідь нескладно.

\[\begin{align*} &\dfrac{6.1\times 10^{-3}}{(2.7\times 10^4)(1.1\times 10^8)} \\ &\approx \dfrac{6\times 10^{-3}}{(3\times 10^4)(1\times 10^8)} \quad \color {Red} 6.1\approx 6, 2.7\approx 3, \text { and } 1.1\approx 1 \\ &\approx \dfrac{6\times 10^{-3}}{3\times 10^{12}} \quad \color {Red} 3\cdot 1=3 \text { and } 10^{4}\cdot 10^{8} = 10^{12}\\ &\approx \dfrac{6}{3}\cdot \dfrac{10^{-3}}{10^{12}} \quad \color {Red} \dfrac{ac}{bd}=\dfrac{a}{b}\cdot \dfrac{c}{d}\\ &\approx 2\times 10^{-15} \quad \color {Red} \dfrac{6}{3}=2 \text { and } \dfrac{10^{-3}}{10^{12}}=10^{-15} \end{align*} \nonumber\]

Давайте отримаємо точну відповідь за допомогою нашого калькулятора. Введіть чисельник як\(6.1\mathbf{E}3\), потім натисніть кнопку «ділення». Пам'ятайте, що ми повинні оточити знаменник дужками. Отже, натисніть клавішу відкритих дужок, а потім введіть\(2.7\mathbf{E}4\). Натисніть клавішу «раз», потім введіть\(1.1\mathbf{E}8\). Натисніть клавішу закриття дужок і натисніть кнопку ENTER. Результат показаний на малюнку\(\PageIndex{4}\).

Малюнок\(\PageIndex{4}\): Обчислення\(6.1×10^{−3}/(2.7×10^4 ×1.1×10^8)\).

Таким чином,\(6.1×10^{−3}/(2.7×10^4 ×1.1×10^8)=2 .05387205×10^{−15}\). Зверніть увагу, що це досить близько до нашої оцінки\(2×10^{−15}\).

Вправа\(\PageIndex{12}\)

Скористайтеся калькулятором графіків, щоб спростити:\[\dfrac{2.6\times 10^{4}}{(7.1\times 10^{-2})(6.3\times 10^7)} \nonumber \]

Відповідь

\(5.8126537×10^{−3}\)

Приклад\(\PageIndex{13}\)

Загальний закон гравітації Ісаака Ньютона визначається формулою,\[F = \dfrac{GmM}{r^2} \nonumber \] де\(F\) сила тяжіння між двома об'єктами, що мають масу\(M\),\(m\)\(r\) і відстань між двома об'єктами, і\(G\) є гравітаційною константою Ньютона, яка визначається:\[G =6 .67428\times 10^{-11} \text {N(m/kg)}^2 \nonumber\] З огляду на, що маса Місяця дорівнює\(7.3477×10^{22}\) кілограмам (кг), маса землі -\(5.9736×10^{24}\) кілограми (кг), а середня відстань між місяцем і землею -\(3.84403×10^8\) метри (м), знайдіть силу тяжіння між землею і місяцем (в ньютонах (N)).

Рішення

Підключіть задані числа до універсального закону тяжіння Ньютона.

\[F=\dfrac{GmM}{r^2} \nonumber \]

\[F=\dfrac{(6.673\times 10^{-11})(7.3477\times 10^{22})(5.9736\times 10^{24})}{(3.84403\times 10^8)^2} \nonumber \]

Введіть вираз до калькулятора (див. Рис.\(\PageIndex{5}\)):

\[(6.673\mathbf{E}-11*7.3477\mathbf{E}22*5.9736\mathbf{E}24)/(3.84403\mathbf{E}8)\wedge 2 \nonumber\]

Малюнок\(\PageIndex{5}\): Обчислювальна сила тяжіння між землею і місяцем.

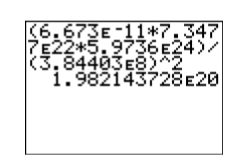
Значить, сила тяжіння між землею і місяцем приблизно дорівнює\(1.98×10^{20}\) ньютонам (N).

Вправа\(\PageIndex{13}\)

Маса Міжнародної космічної станції становить\(450,000\) кг, а її середня відстань до центру землі -\(387,000\) м Знайдіть силу тяжіння між землею і станцією (в ньютонах (N)).

Відповідь

\(≈ 1.20×109 N\)

Приклад\(\PageIndex{14}\)

Найближча зірка до землі - Альфа Центавра,\(4.37\) світлових років від землі. Світловий рік - це відстань, яку світло проїде за один рік. Швидкість світла -\(186,000\) милі в секунду. У скільки миль від землі знаходиться Альфа Центавра?

Рішення

Оскільки швидкість світла вимірюється в милі в секунду, давайте спочатку обчислимо кількість секунд у\(4.37\) роках. Оскільки є\(365\) дні в році,\(24\) години в день,\(60\) хвилини в годину і\(60\) секунди в хвилині, ми можемо написати:

\[\begin{aligned} 4.37 \text {yr} &= 4.37\text {yr}\times 365\dfrac{\text {day}}{\text {yr}}\times 24\dfrac{\text {hr}}{\text {day}}\times 60\dfrac{\text {min}}{\text {hr}}\times 60\dfrac{\text {s}}{\text {min}}\\ &= 4.37{\color {Red}\not {\color {Black}\text {yr}}}\times 365\dfrac{\color {Red}\not {\color {Black}\text {day}}}{\color {Red}\not {\color {Black}\text {yr}}}\times 24\dfrac{\color {Red}\not {\color {Black}\text {hr}}}{\color {Red} \not {\color {Black}\text {day}}}\times 60\dfrac{\color {Red}\not {\color {Black}\text {min}}}{\color {Red}\not {\color {Black}\text {hr}}}\times 60\dfrac{\text {s}}{\color {Red}\not {\color {Black}\text {min}}} \end {aligned} \nonumber \]

Зверніть увагу, як одиниці скасовуються, вказуючи, що кінцева відповідь вказана в секундах. З нашим режимом калькулятора встановлено наукові позначення (див. Зображення праворуч на малюнку\(\PageIndex{2}\)), ми множимо числа, щоб отримати результат, показаний на малюнку\(\PageIndex{6}\). Округлення, кількість секунд в\(4.37\) роках приблизно дорівнює\(1.38 × 10^8\) секундам.

Далі ми обчислюємо відстань, яку проїжджає світло в\(4.37\) роках. Використовуючи той факт, що пройдена відстань дорівнює швидкості, помноженої на пройдений час, ми маємо:

\[\begin{aligned} \text {Distance} &= \text {Speed}\times \text {Time}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\text {s}}\cdot 1.38\times 10^8\text {s}\\ &= 1.86\times 10^5\dfrac{\text {mi}}{\color {Red}\not {\color {Black}\text {s}}}\cdot 1.38\times 10^8 {\color {Red}\not {\color {Black}\text {s}}} \end {aligned} \nonumber\]

Зверніть увагу, як одиниці скасовуються, вказуючи, що наша відповідь вказана в милі. Знову ж таки, з нашим калькулятором, встановленим в режимі наукових позначень, ми обчислюємо добуток\(1.86×10^5\) і\(1.38×10^8\). Результат показаний на зображенні праворуч на малюнку\(\PageIndex{6}\).

Малюнок\(\PageIndex{6}\): Обчислення відстані до Альфи Центавра в милі.

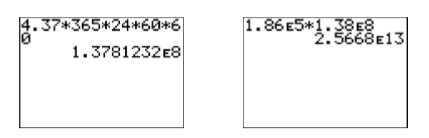
Таким чином, зірка Альфа Центавра знаходиться приблизно в\(2.5668×10^{13}\) милі від землі, або\[2.5668×10^{13} \text {miles} ≈ 25,668,000,000,000 \text {miles} \nonumber \] вимовляється «двадцять п'ять квадрильйонів, шістсот шістдесят вісім трильйонів миль».

Вправа\(\PageIndex{14}\)

Зірка Сіріус знаходиться в\(8.58\) світлових роках від землі. У скільки миль від землі знаходиться Сіріус?

Відповідь

\(≈ 5.2425×10^{13}\)миль