7.3: Спрощення раціональних виразів

Last updated
Save as PDF

Page ID: 58258

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Кожного разу, коли ви ділите многочлен на другий многочлен, ви формуєте те, що є, Ви знайдете цей матеріал дуже корисним для цього розділу. Відомий як раціональний вираз.

Примітка

Читачам настійно рекомендується переглянути матеріал про фракції, представлений у розділі 3 глави 1.

Раціональне вираження

Вираз\[\dfrac{p(x)}{q(x)} \nonumber\] де$p(x)$ і$q(x)$ є поліномами, називається раціональним виразом.

Наприклад, кожне з наступних є раціональним виразом.

$\dfrac{x+2}{3x}$
$\dfrac{x+3}{x^2-2x-4}$
$\dfrac{2x}{3y^2}$

У прикладі а) раціональний вираз складається з біноміального над мономіалом. Приклад б) будується шляхом ділення біноміала на триноміал. Приклад c) складається з мономії над мономіалом, типу раціонального виразу, який приверне найбільшу увагу в цьому розділі.

Множення та ділення раціональних виразів

Ми зосередимося на раціональних виразах з мономіальними чисельниками і знаменниками. Нагадаємо, що для формування добутку двох раціональних чисел ми просто множимо чисельники і знаменники. Цей же прийом використовується для множення будь-яких двох раціональних виразів.

Множення раціональних виразів

З огляду на$a/b$ і$c/d$, їх продукт визначається як:\[\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{ac}{bd} \nonumber \]

Пам'ятайте, потрібно лише множити чисельники і знаменники. Наприклад:

$\dfrac{x}{3}\cdot \dfrac{2}{y} = \dfrac{2x}{3y}$
$\dfrac{2a}{3b^2}\cdot \dfrac{5a}{9b^3} = \dfrac{10a^2}{27b^5}$
$\dfrac{x}{2y}\cdot \left (-\dfrac{3x}{4y^2} \right ) = -\dfrac{3x^2}{8y^3}$

Звичайно, як показує наступний приклад, іноді вам також потрібно зменшити свою відповідь до найнижчих термінів.

Приклад$\PageIndex{1}$

Спростити:$\dfrac{2}{x}\cdot \dfrac{x^2}{4}$.

Рішення

Множимо чисельники і знаменники.

\[\dfrac{2}{x}\cdot \dfrac{x^2}{4} = \dfrac{2x^5}{4x^3} \nonumber \]

Тепер існує кілька різних способів звести цю відповідь до найнижчих термінів, два з яких наведені нижче.

Можна перерахувати чисельник і знаменник, а потім скасувати загальні множники. \[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2\cdot x\cdot x\cdot x\cdot x\cdot x}{2\cdot 2\cdot x\cdot x\cdot x}\\ &= \dfrac{\not{2}\cdot \not {x}\cdot \not{x}\cdot \not{x}\cdot x\cdot x}{\not{2}\cdot 2\cdot \not{x}\cdot \not{x}\cdot \not{x}}\\ &= \dfrac{x^2}{2} \end{align*} \nonumber\]

Або ви можете написати відповідь як добуток, повторити базу і відняти показники. \[\begin{align*} \dfrac{2x^5}{4x^3}&= \dfrac{2}{4}\cdot \dfrac{x^5}{x^3} \\ &= \dfrac{1}{2}\cdot x^{5-3} \\ &= \dfrac{1}{2}x^2 \end{align*} \nonumber \]

Оскільки ділення на те$2$ саме, що і множення на$1/2$, ці відповіді рівнозначні. Також врахуйте, що правосторонній метод більш ефективний

Вправа$\PageIndex{1}$

Просто:$\dfrac{9}{x^2}\cdot \dfrac{x}{6}$.

Відповідь: $\dfrac{3}{2x}$

Нагадаємо, що при діленні дробів інвертуємо другий дріб і множимо.

Розподіл раціональних виразів

Враховуючи a/b і c/d, їх частка визначається як:\[\begin{align*} \dfrac{a}{b}\div \dfrac{c}{d} &= \dfrac{a}{b}\cdot \dfrac{d}{c}\\ &= \dfrac{ad}{bc} \end{align*}\nonumber\]

Приклад$\PageIndex{2}$

Спростити:$\dfrac{x^2}{y}\div \dfrac{x^4}{2y^2}$.

Рішення

Інвертувати, потім помножити.

\[\begin{align*} \dfrac{x^2}{y}\div \dfrac{x^4}{2y^2} &= \dfrac{x^2}{y}\cdot \dfrac{2y^2}{x^4}\\ &= \dfrac{2x^2y^2}{x^4y} \end{align*} \nonumber \]

Тепер існує кілька різних способів звести цю відповідь до найнижчих термінів, два з яких наведені нижче.

Можна перерахувати чисельник і знаменник, а потім скасувати загальні множники. \[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= \dfrac{2\cdot x\cdot x\cdot y\cdot y}{x\cdot x\cdot x\cdot x\cdot y}\\ &= \dfrac{2\cdot \not{x}\cdot \not{x}\cdot \not{y}\cdot y}{\not{x}\cdot \not{x}\cdot x\cdot x\cdot \not{y}}\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]

Або ви можете написати відповідь як добуток, повторити базу і відняти показники. \[\begin{align*} \dfrac{2x^2y^2}{x^4y}&= 2\cdot \dfrac{x^2}{x^4}\cdot \dfrac{y^2}{y^1}\\ &= 2x^{-2}y^1\\ &= \dfrac{2y}{x^2} \end{align*} \nonumber\]На останньому кроці,$x^{−2}$ це те ж саме$1/x^2$, що, потім множимо чисельники і знаменники.

Відзначимо, що правосторонній метод більш ефективний.

Вправа$\PageIndex{2}$

Спростити:$\dfrac{3y}{x^3}\div \dfrac{y^2}{4x}$.

Відповідь: $\dfrac{12}{x^2y}$

Додавання та віднімання раціональних виразів

Спочатку нагадаємо правила додавання або віднімання дробів, які мають «загальний» знаменник.

Додавання раціональних виразів

Задано$a/c$ і$b/c$, їх сума визначається так:\[\dfrac{a}{c} + \dfrac{b}{c}=\dfrac{a+b}{c} \nonumber\] Тобто додайте чисельники і помістіть результат над спільним знаменником.

Наступні приклади мають спільний знаменник. Складаємо чисельники, потім поміщаємо результат над загальним знаменником.

\[\dfrac{5}{7}+\dfrac{1}{7}=\dfrac{6}{7},\quad \dfrac{2}{x}+\dfrac{3}{x}=\dfrac{5}{x}, \quad \text {and} \quad \dfrac{x}{y}+\dfrac{3y}{y}=\dfrac{x+3y}{y} \nonumber\]

Приклад$\PageIndex{3}$

Спростити:$\dfrac{3x}{xy}+\dfrac{2y}{xy} \nonumber$.

Рішення

Додайте чисельники, розмістивши результат над спільним знаменником.

\[\dfrac{3x}{xy}+\dfrac{2y}{xy} = \dfrac{3x+2y}{xy} \nonumber\]

Вправа$\PageIndex{3}$

Спростити:$\dfrac{4x}{x^2y}+\dfrac{5y^2}{x^2y}$

Відповідь: $\dfrac{4x+5y^2}{x^2y}$

Віднімання раціональних виразів

Задано$a/c$ і$b/c$, їх відмінність визначається так:\[\dfrac{a}{c} - \dfrac{b}{c}=\dfrac{a-b}{c} \nonumber\] Тобто відніміть чисельники і помістіть результат над спільним знаменником.

Наступні приклади мають спільний знаменник. Віднімаємо чисельники, потім поміщаємо результат над загальним знаменником.

\[\dfrac{7}{9}-\dfrac{2}{9}=\dfrac{2}{9},\quad \dfrac{5a}{b}-\dfrac{3a}{b}=\dfrac{2a}{b}, \quad \text {and} \quad \dfrac{3x}{xy}-\dfrac{5y}{xy}=\dfrac{3x-5y}{xy} \nonumber\]

Як показує наступний приклад, іноді вам, можливо, доведеться зменшити свою відповідь до найнижчих термінів.

Приклад$\PageIndex{4}$

Спростити:$\dfrac{5xy}{2z}-\dfrac{3xy}{2z}$.

Рішення

Відніміть чисельники, помістивши результат над спільним знаменником.

\[\begin{align*} \dfrac{5xy}{2z}-\dfrac{3xy}{2z} &= \dfrac{5xy-3xy}{2z}\\ &= \dfrac{2xy}{2z} \end{align*} \nonumber \]

Щоб звести до найнижчих членів, розділіть і чисельник, і знаменник на$2$.

\[\dfrac{xy}{z} \nonumber \]

Вправа$\PageIndex{4}$

Спростити:$\dfrac{8x}{3yz^2}-\dfrac{2x}{3yz^2}$.

Відповідь: $\dfrac{2x}{yz^2}$

Найменший спільний знаменник

При додаванні або відніманні, якщо раціональні вирази не мають спільного знаменника, спочатку потрібно зробити еквівалентні дроби із загальним знаменником.

Найменш спільний знаменник

Якщо дроби$a/b$ і$c/d$ не мають спільного знаменника, то найменше спільний знаменник для$b$ і$d$ визначається як найменше число (або вираз), що ділиться на обидва$b$ і$d$. У символах,$\mathrm{LCD}(b,d)$ являє собою найменш спільний знаменник$b$ і$d$.

Приклад$\PageIndex{5}$

Спростити:$\dfrac{x}{6}+\dfrac{2x}{9}$.

Рішення

Найменше число ділиться на обидва$6$ і$9$ є$18$; т$\mathrm{LCD}(6,9) = 18$. Е. Спочатку ми повинні зробити еквівалентні дроби із загальним знаменником$18$.

\[\begin{align*} \dfrac{x}{6}+\dfrac{2x}{9} &= \dfrac{x}{6}\cdot {\color {Red}\dfrac{3}{3}}+\dfrac{2x}{9}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3x}{18}+\dfrac{4x}{18} \end{align*} \nonumber \]

\[=\dfrac{7x}{18} \nonumber \]

Вправа$\PageIndex{5}$

Спростити:$\dfrac{3x}{8}+\dfrac{5x}{6}$.

Відповідь: $\dfrac{29x}{24}$

Приклад$\PageIndex{6}$

Спростити:$\dfrac{y}{8x}-\dfrac{y}{12x}$.

Рішення

Найменший вираз ділиться на обидва$8x$ і$12x$ є$24x$; т$\mathrm{LCD}(8x,12x) = 24x$. Е. Спочатку ми повинні зробити еквівалентні дроби із загальним знаменником$24x$, а потім помістити різницю чисельників над спільним знаменником.

\[\begin{align*} \dfrac{y}{8x}-\dfrac{y}{12x} &= \dfrac{y}{8x}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{12x}\cdot {\color {Red}\dfrac{2}{2}}\\ &= \dfrac{3y}{24x}-\dfrac{2y}{24x}\\ &= \dfrac{y}{24x} \end{align*} \nonumber\]

Вправа$\PageIndex{6}$

Спростити:$\dfrac{x}{8y}-\dfrac{x}{10y}$.

Відповідь: $\dfrac{x}{40y}$

У$\PageIndex{5}$ прикладі було нескладно уявити собі найменшу кількість, ділиться на обидва$6$ і$9$. Аналогічне твердження може застосовуватися і до Example$\PageIndex{6}$. Це не так у всіх ситуаціях.

Приклад$\PageIndex{7}$

Спростити:$\dfrac{5y}{72}-\dfrac{y}{108}$.

Рішення

У цьому прикладі непросто викликати найменшу кількість, що ділиться на обидва$72$ і$108$. Як ми побачимо, на допомогу прийде просте факторизація.

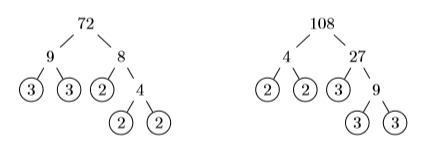
$рис. 7.3.a.png$

Таким чином,$72 = 2^3\cdot 3^2$ і$108 = 2^2\cdot 3^3$.

Примітка: Порядок пошуку найменш спільного знаменника (LCD)

Щоб знайти найменш спільний знаменник для двох і більше дробів, дійте наступним чином:

Простий коефіцієнт кожного знаменника, ставлячи свої відповіді в експоненціальній формі.
Щоб визначити$\mathrm{LCD}$, запишіть кожен фактор, який з'являється у ваших простих факторизаціях до найвищої сили, що він з'являється.

Слідуючи вищеописаній процедурі, ми перерахуємо просту факторизацію кожного знаменника в експоненціальній формі. Найвища сила$2$, що з'являється, є$2^3$. Найвища сила$3$, що з'являється, є$3^3$.

\[\begin{align*} 72 &= 2^3\cdot 3^2 \quad \color {Red} \text {Prime factor } 72.\\ 108 &= 2^2\cdot 3^3 \quad \color {Red} \text {Prime factor } 108.\\ \mathrm{LCD} &= 2^3\cdot 3^3 \quad \color {Red} \text {Highest power of } 2 \text { is } 2^3. \text { Highest power of } 3 \text { is } 3^3. \end{align*} \nonumber\]

Тому$\mathrm{LCD}$ є$2^3\cdot 3^3 = 8\cdot 27$ або$216$. Звідси:

\[\begin{align*} \dfrac{5y}{72}-\dfrac{y}{108} &= \dfrac{5y}{72}\cdot {\color {Red}\dfrac{3}{3}}-\dfrac{y}{108}\cdot {\color {Red}\dfrac{2}{2}} \quad \color {Red} \text {Make equivalent fractions.} \\ &= \dfrac{15y}{216}-\dfrac{2y}{216} \quad \color {Red} \text {Simplify.} \\ &= \dfrac{13y}{216} \quad \color {Red} \text {Subtract numerators.} \end{align*} \nonumber\]

Вправа$\PageIndex{7}$

Спростити:$\dfrac{7x}{36}-\dfrac{3x}{40}$.

Відповідь: $\dfrac{43x}{360}$

Приклад$\PageIndex{8}$

Спростити:$\dfrac{7}{15xy^2}-\dfrac{11}{20x^2}$

Рішення

Простий множник кожного знаменника, розміщуючи результати в експоненціальній формі.

\[\begin{align*} 15xy^2 &= 3\cdot 5\cdot x\cdot y^2 \\ 20x^2 &= 2^2 \cdot 5\cdot x^2 \end{align*} \nonumber \]

Щоб знайти$\mathrm{LCD} $, перерахуйте кожен фактор, який виявляється найвищою силою, що він з'являється.

\[\mathrm{LCD} = 2^2\cdot 3\cdot 5\cdot x^2 \cdot y^2 \nonumber \]

Спростити.

\[\mathrm{LCD} = 60 x^2 y^2 \nonumber \]

Зробивши еквівалентні дроби, помістіть різницю чисельників над цим спільним знаменником.

\[\begin{align*} \dfrac{7}{15xy^2}-\dfrac{11}{20x^2} &= \dfrac{7}{15xy^2}\cdot {\color {Red}\dfrac{4x}{4x}}-\dfrac{11}{20x^2}\cdot {\color {Red}\dfrac{3y^2}{3y^2}}\\ &= \dfrac{28x}{60x^2y^2}-\dfrac{33y^2}{60x^2y^2}\\ &= \dfrac{28x-33y^2}{60x^2y^2} \end{align*} \nonumber \]

Вправа$\PageIndex{8}$

Спростити:$\dfrac{11}{18xy^2}+\dfrac{7x}{30xy}$

Відповідь: $\dfrac{55+21x^2}{90x^2y}$

Ділення многочлена на мономіал

Ми знаємо, що множення є розподільним щодо додавання; тобто$a(b + c)=ab + ac$. Ми використовуємо цю властивість для виконання множень, таких як:\[x^2(2x^2 −3x−8) = 2x^4 −3x^3 −8x^2 \nonumber \] Однак вірно також, що поділ є розподільним щодо додавання.

Розподільне майно для поділу

Якщо$a$,$b$, і$c$ є будь-якими числами, то:\[\dfrac{a+b}{c} = \dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

Наприклад, зверніть увагу, що\[\dfrac{4+6}{2} = \dfrac{4}{2}+\dfrac{6}{2} \nonumber \]

Ця форма розподільного властивості може бути використана для поділу многочлена на моном.

Приклад$\PageIndex{9}$

Розділити$x^2 −2x−3$ на$x^2$.

Рішення

Використовуємо розподільну властивість, діливши кожен член на$x^2$.

\[\dfrac{x^2-2x-3}{x^2} = \dfrac{x^2}{x^2}-\dfrac{2x}{x^2}-\dfrac{3}{x^2} \nonumber \]

Тепер ми скорочуємо кожен термін останнього результату до найнижчих, скасовуючи загальні фактори.

\[= 1-\dfrac{2}{x}-\dfrac{3}{x^2} \nonumber \]

Вправа$\PageIndex{9}$

Розділити$9x^3+8x^2−6x$ на$3x^2$.

Відповідь: $3x+\dfrac{8}{3}-\dfrac{2}{x}$

Приклад$\PageIndex{10}$

Розділити$2x^3 −3x + 12$ на$6x^3$.

Рішення

Використовуємо розподільну властивість, діливши кожен член на$6x^3$.

\[\dfrac{2x^3-3x+12}{6x^3} = \dfrac{2x^3}{6x^3}-\dfrac{3x}{6x^3}+\dfrac{12}{6x^3} \nonumber\]

Тепер ми скорочуємо кожен термін останнього результату до найнижчих, скасовуючи загальні фактори.

\[= \dfrac{1}{3}-\dfrac{1}{2x^2}+\dfrac{2}{x^3} \nonumber\]

Вправа$\PageIndex{10}$

Розділити$−4x^2 +6x−9$ на$2x^4$.

Відповідь: $-\dfrac{2}{x^2}+\dfrac{3}{x^3}-\dfrac{9}{x^4}$