7.1: Негативні показники

Last updated
Save as PDF

Page ID: 58272

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми починаємо з, здавалося б, дурного, але потужного визначення того, що означає підняти число до сили$−1$.

Підняття до влади$−1$

Щоб підняти об'єкт до сили$−1$, просто інвертуйте об'єкт (переверніть його догори дном).

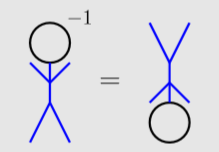
$рис. 7.1.a.png$

Більш формально інвертування числа відоме як прийняття його взаємно.

Приклад$\PageIndex{1}$

Спростіть кожне з наведених нижче виразів:

$4^{-1}$
$\left ( \dfrac{2}{3} \right )^{-1}$
$-\left ( \dfrac{3}{5} \right )^{-1}$

Рішення

У кожному конкретному випадку ми просто інвертуємо задане число.

$\left ( \dfrac{2}{3} \right )^{-1} = \dfrac{3}{2}$
$-\left ( \dfrac{3}{5} \right )^{-1} = -\dfrac{5}{3}$

Вправа$\PageIndex{1}$

Спростити:$\left ( \dfrac{7}{4} \right )^{-1}$

Відповідь: $\dfrac{4}{7}$

Можливо, ви запитаєте «Чому підвищення до потужності мінус один інвертує число?» Щоб відповісти на це питання, згадайте добуток числа і його взаємне одне. Наприклад,

\[4\cdot \dfrac{1}{4} = 1 \label{Eq7.1.1}\]

Далі розглянемо, що відбувається, коли ми множимо$4^1$ і$4^{−1}$. Якщо ми застосуємо звичайний закон експонентів (якщо припустити, що вони працюють як для позитивних, так і для негативних показників), ми додамо експоненти ($1 + (−1) = 0$).

\[4^1\cdot 4^{-1} = 4^0 \label{Eq7.1.2}\]

Однак, тому що$4^1 = 4$ і$4^0 = 1$, це останнє рівняння еквівалентно:

\[4\cdot 4^{-1} = 1 \label{Eq7.1.3}\]

Коли ви порівнюєте рівняння\ ref {Eq7.1.1} і\ ref {Eq7.1.3}, зрозуміло, що$4^{−1}$ і$1/4$ є обома зворотними числом$4$. Тому що взаємні унікальні,$4^{-1} = \dfrac{1}{4}$.

Подібним чином можна відкрити для себе сенс$a^{−n}$. Почніть з того, що множення взаємних дає відповідь одного.

\[a^n\cdot \dfrac{1}{a^n} = 1 \label{Eq7.1.4}\]

Якщо ми помножимо$a^n$ і$a^{−n}$, ми додаємо показники наступним чином.

\[a^n\cdot a^{−n} = a^0 \nonumber \]

$a\neq = 0$Забезпечуючи$a^0 = 1$, то, щоб ми могли написати

\[a^n\cdot a^{-n} = 1 \label{Eq7.1.5}\]

Порівнюючи рівняння\ ref {Eq7.1.4} і\ ref {Eq7.1.5}, ми зауважимо, що обидва$1/a^n$ і$a^{−n}$ є зворотними$a^n$. Тому що кожне число має унікальні$1/a^n$ взаємні,$a^{−n}$ і рівні.

Підвищення до від'ємного цілого

За умови\ neq= 0,

\[a^{-n} = \dfrac{1}{a^n} \nonumber \]

Приклад$\PageIndex{2}$

Спростіть кожне з наведених нижче виразів:

$2^{-3}$
$(-5)^{-2}$
$(-4)^{-3}$

Рішення

У кожному прикладі ми використовуємо властивість$a^{−n} =1/a^n$ для спрощення даного виразу.

$\begin{align*} 2^{-3} &= \dfrac{1}{2^3}\\ &= \dfrac{1}{8} \end{align*}$
$\begin{align*} (-5)^{-2} &= \dfrac{1}{(-5)^2}\\ &= \dfrac{1}{25} \end{align*}$
$\begin{align*} (-4)^{-3} &= \dfrac{1}{(-4)^3}\\ &= -\dfrac{1}{64} \end{align*}$

У Підняття до негативного цілого числа, ми розглянемо, як ви можете виконати кожне з перерахованих вище обчислень подумки.

Вправа$\PageIndex{2}$

Спростити:$3^{-2}$

Відповідь: $\dfrac{1}{9}$

Закони експонентів

У аргументах, що демонструють це$4^{−1} =1 /4$ і$a^{−n} =1/a^n$, ми звернулися до одного із законів експонентів, засвоєних у розділі 5 глави 5. На щастя, закони показників працюють точно так само, незалежно від того, чи є експоненти позитивними чи негативними цілими числами.

Закони експонентів

Якщо$m$ і$n$ є цілими числами, то:

$a^ma^n = a^{m+n}$
$\dfrac{a^m}{a^n} = a^{m-n}$
$(a^m)^n = a^{mn}$
$(ab)^n = a^nb^n$
$\left (\dfrac{a}{b} \right )^n = \dfrac{a^n}{a^n}$

Приклад$\PageIndex{3}$

Спростіть кожне з наведених нижче виразів:

$y^5y^{−7} $
$2^{−2}\cdot 2^{−3}$
$x^{−4}x^6$

Рішення

У кожному конкретному випадку ми використовуємо перший закон експонентів ($a^ma^n = a^{m+n}$). Оскільки ми множимо як основи, ми повторюємо базу і додаємо експоненти.

$\begin{align*} y^5y^{-7} &= y^{5+(-7)}\\ &= y^{-2} \end{align*}$
$\begin{align*} 2^{-2}\cdot 2^{-3} &= 2^{-2+(-3)}\\ &= 2^{-5} \end{align*}$
$\begin{align*} x^{-4}x^{6} &= x^{-4+6}\\ &= x^2 \end{align*}$

Вправа$\PageIndex{3}$

Спростити:$t^8\cdot t^{−4}$

Відповідь: $t^4$

Приклад$\PageIndex{4}$

Спростіть кожне з наведених нижче виразів:

$\dfrac{x^4}{x^7}$
$\dfrac{3^{-4}}{3^5}$
$\dfrac{z^{-3}}{z^{-5}}$

Рішення

У кожному конкретному випадку ми використовуємо другий закон експонентів ($a^m/a^n = a^{m−n}$). Оскільки ми ділимося як основи, ми повторюємо базу і віднімаємо показники. Нагадаємо, що віднімання означає «додати протилежне».

$\begin{align*} \dfrac{x^4}{x^7} &= x^{4-7}\\ &= x^{4+(-7)}\\ &= x^{-3} \end{align*}$
$\begin{align*} \dfrac{3^{-4}}{3^5} &= 3^{-4-5}\\ &= 3^{-4+(-5)}\\ &= 3^{-9} \end{align*}$
$\begin{align*} \dfrac{z^{-3}}{z^{-5}} &= z^{-3-(-5)}\\ &= z^{-3+5}\\ &= z^{2} \end{align*}$

Вправа$\PageIndex{4}$

Спростити:$\dfrac{y^{-6}}{y^{-2}}$

Відповідь: $y^{-4}$

Приклад$\PageIndex{5}$

Спростіть кожне з наведених нижче виразів:

$(5^{−2})^3$
$(a^{−3})^{−4}$
$(w^2)^{−7}$

Рішення

У кожному конкретному випадку ми використовуємо третій закон експонентів ($(a^m)^n = a^{mn}$). Оскільки ми піднімаємо силу до іншої сили, ми повторюємо базу і множимо показники.

$\begin{align*} (5^{-2})^3 &= 5^{(-2)(3)}\\ &= 5^{-6} \end{align*}$
$\begin{align*} (a^{-3})^{-4} &= a^{(-3)(-4)}\\ &= a^{12} \end{align*}$
$\begin{align*} (w^2)^{-7} &= w^{(2)(-7)}\\ &= w^{-14} \end{align*}$

Вправа$\PageIndex{5}$

Спростити:$(z^5)^{−2}$

Відповідь: $z^{-10)$

Підвищення до від'ємного цілого

Ми знаємо, що відбувається, коли ви піднімаєте число до$−1$, ви інвертуєте число або перевертаєте його догори дном. Але що відбувається, коли ви піднімаєте число до від'ємного цілого числа, відмінного від негативного?

Як приклад розглянемо вираз$3^{−2}$. Використовуючи третій закон експонентів ($(a^m)^n = a^{mn}$), ми можемо записати цей вираз у двох еквівалентних формах.

Зверніть увагу,$3^{−2}$ що еквівалентно$(3^2)^{−1}$. Вони еквівалентні тому, що третій закон експонентів наказує нам множити показники при підвищенні сили до іншої сили. Нарешті, зауважте$(3^2)^{−1}$, що для оцінки ми спочатку квадратично, потім інвертуємо результат. \[\begin{align*} 3^{-2} &= (3^2)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 9^{-1} \quad \color {Red} \text {Simplify: } 3^2=9\\ &= \dfrac{1}{9} \quad \color {Red} \text {Simplify: } 9^{-1}=1/9 \end{align*} \nonumber \]
Зверніть увагу,$3^{−2}$ що також еквівалентно$(3^{−1})^2$. Вони еквівалентні тому, що третій закон експонентів наказує нам множити показники при підвищенні сили до іншої сили. Нарешті, зауважте$(3^{−1})^2$, що для оцінки ми спочатку інвертуємо, потім квадратично результат. \[\begin{align*} 3^{-2} &= (3^{-1})^2 \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (\dfrac{1}{3} \right )^2 \quad \color {Red} \text {Simplify: } 3^{-1}=1/3\\ &= \dfrac{1}{9} \quad \color {Red} \text {Simplify: } (1/3)^{2}=1/9 \end{align*} \nonumber \]

Використовуючи будь-яку техніку,$3^{−2} =1/9$. Ви можете або квадрат і інвертувати, або ви можете інвертувати і квадрат. У кожному випадку$2$ означає «квадрат», а знак мінус означає «інвертувати», і цей приклад показує, що не має значення, що ви робите першим.

Приклад$\PageIndex{6}$

Спростіть кожне з наведених нижче виразів:

$5^{−3}$
$(−4)^{−2}$
$\left (\dfrac{3}{5} \right )^{-2}$
$\left (-\dfrac{2}{3} \right )^{-3}$

Рішення

Ми будемо куб потім інвертувати. \[\begin{align*} 5^{-3} &= (5^3)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 125^{-1} \quad \color {Red} \text {Simplify: } 5^{3}=125\\ &= \dfrac{1}{125} \quad \color {Red} \text {Invert: } 125^{-1}=1/125 \end{align*} \nonumber \]Зверніть увагу, що три означають «куб», а знак мінус означає «інвертувати», тому можна виконати всю цю роботу подумки:$5$ кубик дістати$125$, потім інвертувати, щоб отримати$1/125$.
Ми будемо квадрат потім інвертувати. \[\begin{align*} (-4)^{-2} &= ((-4)^2)^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= 16^{-1} \quad \color {Red} \text {Simplify: } (-4)^{2}=16\\ &= \dfrac{1}{16} \quad \color {Red} \text {Invert: } 16^{-1}=1/16 \end{align*} \nonumber \]Зверніть увагу, що два означають «квадрат», а знак мінус означає «інвертувати», тому можна виконати всю цю роботу подумки: квадрат$−4$ отримати$16$, потім інвертувати, щоб отримати$1/16$.
Знову ж таки, ми будемо квадрат потім інвертувати. \[\begin{align*} \left (\dfrac{3}{5} \right )^{-2} &= \left ( \left (\dfrac{3}{5} \right )^{2} \right )^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (\dfrac{9}{25} \right )^{-1} \quad \color {Red} \text {Simplify: } (3/5)^{2}=9/25\\ &= \dfrac{25}{9} \quad \color {Red} \text {Invert: } (9/25)^{-1}=25/9 \end{align*} \nonumber \]Зверніть увагу, що два означають «квадрат», а знак мінус означає «інвертувати», тому можна виконати всю цю роботу подумки: квадрат$3/5$ отримати$9/25$, потім інвертувати, щоб отримати$25/9$.
Цього разу ми будемо куб потім інвертувати. \[\begin{align*} \left (-\dfrac{2}{3} \right )^{-3} &= \left ( \left (-\dfrac{2}{3} \right )^{3} \right )^{-1} \quad \color {Red} \text {Repeat base and multiply exponents.}\\ &= \left (-\dfrac{8}{27} \right )^{-1} \quad \color {Red} \text {Simplify: } (-2/3)^{2}=-8/27\\ &= -\dfrac{27}{8} \quad \color {Red} \text {Invert: } (-8/27)^{-1}=-27/8 \end{align*} \nonumber \]Зверніть увагу, що три означають «куб», а знак мінус означає «інвертувати», тому можна виконати всю цю роботу подумки:$−2/3$ кубик дістати$−8/27$, потім інвертувати, щоб отримати$−27/8$.

Вправа$\PageIndex{6}$

Спростити:$\left (\dfrac{5}{4} \right )^{-3}$

Відповідь: $\dfrac{64}{125}$

Застосування законів експонентів

У цьому розділі ми спростимо кілька більш складних виразів, використовуючи закони експонентів.

Приклад$\PageIndex{7}$

Спростити:$(2x^{−2}y^3)(−3x^5y^{−6})$

Рішення

Всі задіяні оператори - множення, тому комутативні і асоціативні властивості множення дозволяють змінювати порядок і угруповання. Ми покажемо це перегрупування тут, але цей крок можна зробити подумки. \[(2x−2y^3)(−3x^5y^{−6}) = [(2)(−3)](x^{−2}x^5)(y^3y^{−6}) \nonumber \]При множенні повторюємо базу і додаємо показники. \[\begin{align*} &= -6x^{-2+5}y^{3+(-6)} \\ &= -6x^3y^{-3} \end{align*} \nonumber \]У вирішенні вище, ми, мабуть, показали занадто багато роботи. Набагато простіше виконати всі ці кроки подумки, множивши на$2$ і$−3$, потім повторюючи основи і додаючи показники, як у:\[(2x^{−2}y^3)(−3x^5y^{−6})=−6x^3y^{−3} \nonumber \]

Вправа$\PageIndex{7}$

Спростити:$(−5x^8y^{−2})(−2x^{−6}y^{−1})$

Відповідь: $10x^2y^{−3}$

Приклад$\PageIndex{8}$

Спростити:$\dfrac{6x^{-2}y^5}{9x^3y^{-2}}$

Рішення

Найпростіший підхід - спочатку написати вираз як твір.

\[\dfrac{6x^{-2}y^5}{9x^3y^{-2}} = \dfrac{6}{9}\cdot \dfrac{x^{-2}}{x^3}\cdot \dfrac{y^5}{y^{-2}} \nonumber \]

Знизити$6/9$ до найнижчих термінів. Оскільки ми ділимося як основи, ми повторюємо базу і віднімаємо показники.

\[\begin{align*} &= \dfrac{2}{3}x^{-2-3}y^{5-(-2)}\\ &= \dfrac{2}{3}x^{-2+(-3)}y^{5+2}\\ &= \dfrac{2}{3}x^{-5}y^{7} \end{align*} \nonumber\]У вирішенні вище, ми, мабуть, показали занадто багато роботи. Набагато простіше уявити собі написання виразу як твір, зменшуючи 6/9, потім повторюючи основи та віднімаючи показники, як у:

\[\dfrac{6x^{-2}y^5}{9x^3y^{-2}} = \dfrac{2}{3}x^{-5}y^{7} \nonumber \]

Вправа$\PageIndex{8}$

Спростити:$\dfrac{10x^{3}y^{-1}}{4x^{-2}y^{5}}$

Відповідь: $\dfrac{5}{2}x^{5}y^{-6}$

Приклад$\PageIndex{9}$

Спростити:$(2x^{−2}y^4)^{−3}$

Рішення

Четвертий закон експонентів ($(ab)^n = a^nb^n$) говорить, що коли ви піднімаєте продукт до влади, ви повинні підняти кожен фактор до цієї сили. Отже, ми починаємо з підвищення кожного фактора до мінус три потужності.

\[(2x^{−2}y^3)^{−3} =2^{−3}(x^{−2})^{−3}(y^4)^{−3} \nonumber \]

Щоб підняти два на мінус три, ми повинні куб два і інвертувати:$2^{−3} =1 /8$. По-друге, підвищення сили до влади вимагає, щоб ми повторювали базу і множили показники.

\[\begin{align*} &= \dfrac{1}{8}x^{(-2)(-3)}y^{(4)(-3)}\\ &= \dfrac{1}{8}x^{6}y^{-12} \end{align*} \nonumber \]

У вирішенні вище, ми, мабуть, показали занадто багато роботи. Набагато простіше підняти кожен коефіцієнт до мінус трьох подумки:$2^{−3} =1 /8$, потім помножити кожен показник на інші фактори на$−3$, як в

\[(2x^{-2}y^4)^{-3} = \dfrac{1}{8}x^{6}y^{-12} \nonumber \]

Вправа$\PageIndex{9}$

Спростити:$(3x^4y^{−3})^{−2}$

Відповідь: $\dfrac{1}{9}x^{-8}y^{6}$

Очищення негативних показників

Часто нас просять надати остаточну відповідь, яка не містить негативних показників. Зазвичай можна почути інструкцію «немає негативних показників у остаточній відповіді». Давайте вивчимо пару прийомів, які дозволяють нам очистити нашу відповідь від негативних показників.

Приклад$\PageIndex{10}$

Розглянемо вираз:\[\dfrac{x^2}{y^{-3}} \nonumber \]

Спростіть так, щоб отриманий еквівалентний вираз не містив негативних показників.

Рішення

Піднявши y до$−3$ засобів, ми повинні куб і інвертувати, так$y^{−3} = 1/y^3$.

\[\dfrac{x^2}{y^{-3}} = \dfrac{x^2}{\tfrac{1}{y^3}} \nonumber \]

Щоб розділити$x^2$ на$1/y^3$, інвертуємо і множимо.

\[\begin{align*} &= x^2 \div \dfrac{1}{y^{3}}\\ &= \dfrac{x^2}{1}\cdot \dfrac{y^{3}}{1}\\ &= x^2y^3 \end{align*} \nonumber \]

Альтернативний підхід: альтернативний підхід використовує закони експонентів. Починаємо з множення чисельника і знаменника на$y^3$.

\[\begin{align*} \dfrac{x^2}{y^{-3}} &= \dfrac{x^2}{y^{-3}} \cdot \dfrac{y^3}{y^{3}}\\ &= \dfrac{x^2y^3}{y^0}\\ &= x^2y^3 \end{align*} \nonumber \]

На останньому кроці зверніть увагу, як ми використовували той факт, що$y^0 = 1$

Вправа$\PageIndex{10}$

Спростіть вираз\[\dfrac{y^5}{x^{-2}} \nonumber \] так, щоб отриманий еквівалентний вираз не містив негативних показників.

Відповідь: $y^5x^2$

Приклад$\PageIndex{11}$

Розглянемо вираз:\[\dfrac{2x^2y^{-2}}{z^{3}} \nonumber \] Спростити так, щоб отриманий еквівалентний вираз не містив негативних показників.

Рішення

Знову ж таки, ми можемо видалити всі негативні показники, приймаючи взаємні. В даному випадку$y^{−2} =1/y^2$ (квадратний і інвертний).

\[\begin{align*} \dfrac{2x^2y^{-2}}{z^{3}} &= \dfrac{2x^2\cdot \tfrac{1}{y ^2}}{z^{3}} \\ &= \dfrac{\tfrac{2x^2}{y^2}}{z^3} \end{align*} \nonumber \]

Щоб розділити$2x^2/y^2$ на$z^3$, інвертуємо і множимо.

\[\begin{align*} &= \dfrac{2x^2}{y^2}\div {z^{3}} \\ &= \dfrac{2x^2}{y^2}\cdot \dfrac{1}{z^3}\\ &= \dfrac{2x^2}{y^2z^3} \end{align*} \nonumber \]

Альтернативний підхід: альтернативний підхід знову використовує закони експонентів. Починаємо з множення чисельника і знаменника на$y^2$.

\[\begin{align*} \dfrac{2x^2y^{-2}}{z^{3}} &= \dfrac{2x^2y^{-2}}{z^3}\cdot \dfrac{y^2}{y^2} \\ &= \dfrac{2x^2y^0}{y^2z^3}\\ &= \dfrac{2x^2}{y^2z^3} \end{align*} \nonumber \]

На останньому кроці зверніть увагу, як ми використовували той факт, що$y^0 = 1$.

Вправа$\PageIndex{11}$

Спростіть вираз\[\dfrac{x^{-3}y^2}{3z^{-4}} \nonumber \] так, щоб отриманий еквівалентний вираз не містив негативних показників.

Відповідь: $\dfrac{y^2z^4}{3x^3}$