4.4: Застосування лінійних систем

Last updated
Save as PDF

Page ID: 58224

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми створюємо і вирішуємо додатки, які ведуть до систем лінійних рівнянь. Коли ми створюємо та вирішуємо наші моделі, ми будемо дотримуватися вимог до вирішення проблем Word з розділу 2, розділ 5. Однак замість того, щоб встановлювати єдине рівняння, ми створили систему рівнянь для кожного додатка.

Приклад$\PageIndex{1}$

У геометрії два кути, які підсумовуються,$90^{\circ}$ називаються взаємодоповнюючими кутами. Якщо другий з двох взаємодоповнюючих кутів більше, ніж удвічі$30^{\circ}$ більший перший кут, знайдіть ступінь міри обох кутів.

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштуйте словник змінних. Наш змінний словник буде мати форму діаграми, називаючи два взаємодоповнюючих кути$\alpha$ і$β$.

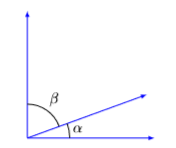
$рис 4.4.a.png$

Налаштуйте системи рівнянь. «Другий кут на$30$ градуси більше, ніж удвічі перший кут» стає\[\beta=30+2 \alpha \label{Eq4.4.1}\] По-друге, кути взаємодоповнюють, що означає, що сума кутів є$90^{\circ}$. \[\alpha+\beta=90 \label{Eq4.4.2}\]Таким чином, ми маємо систему з двох рівнянь в двох невідомих$\alpha$ і$β$.
Вирішити систему. Оскільки рівняння\ ref {Eq4.4.1} вже вирішено$β$, давайте скористаємося методом підстановки та заміною$30 + 2α$$β$ в Equation\ ref {Eq4.4.2}. \[\begin{aligned} \alpha+\beta &= 90 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.2} \\ \alpha+(30+2 \alpha) &= 90 \quad \color {Red} \text { Substitute } 30+2 \alpha \text { for } \beta \\ 3 \alpha+30 &= 90 \quad \color {Red} \text { Combine like terms. } \\ 3 \alpha &= 60 \quad \color {Red} \text { Subtract } 30 \text { from both sides. } \\ \alpha &= 20 \quad \color {Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]
Дайте відповідь на питання. Перший кут -$α = 20$ градуси. Другий кут - це:\[\begin{aligned} \beta &= 30+2 \alpha \quad {\color {Red} \text { Equation }}\ref{Eq4.4.1} \\ \beta &= 30+2(20) \quad \color {Red} \text { Substitute } 20 \text { for } \alpha \\ \beta &=70 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
Озирніться назад. Безумовно$70^{\circ}$,$30^{\circ}$ більше, ніж в два рази$20^{\circ}$. Також зверніть увагу на те$20^{\circ}+70^{\circ}=90^{\circ}$, що, таким чином, кути доповнюють один одного. У нас є правильне рішення.

Вправа$\PageIndex{1}$

Якщо другий з двох взаємодоповнюючих кутів$6^{\circ}$$3$ times the більший за перший кут, знайдіть ступінь міри обох кутів.

Відповідь: $21$і$69$

Приклад$\PageIndex{2}$

Периметр прямокутника -$280$ фути. Довжина прямокутника$10$ футів менше, ніж в два рази більше ширини. Знайдіть ширину і довжину прямокутника.

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштуйте словник змінних. Наш змінний словник буде мати форму діаграми, називаючи ширину і довжину$W$ і$L$, відповідно.

$рис. 4.4.b.png$

Налаштуйте систему рівнянь. Периметр знаходять шляхом підсумовування чотирьох сторін прямокутника. \[\begin{array}{l}{P=L+W+L+W} \\ {P=2 L+2 W}\end{array} \nonumber\]Нам сказали периметр$280$ футів, так що ми можемо замінити$280$$P$ в останньому рівнянні. \[280=2 L+2 W \nonumber \]Ми можемо спростити це рівняння, розділивши обидві сторони на$2$, даючи наступний результат:\[L+W=140 \nonumber \] По-друге, нам кажуть, що «довжина$10$ футів менше ніж удвічі більше ширини». Це означає:\[L=2 W-10 \nonumber \] Таким чином, система, яку нам потрібно вирішити, є:\[L+W=140 \label{Eq4.4.3} \]\[L=2 W-10 \label{Eq4.4.4} \]
Вирішити систему. Оскільки рівняння\ ref {Eq4.4.4} вже вирішено$L$, давайте скористаємося методом підстановки та заміною$2W −10$$L$ в Equation\ ref {Eq4.4.3}. \[\begin{aligned} W+L &= 140 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.3} \\ W+(2 W-10) &= 140 \quad \color {Red} \text { Substitute } 2 W-10 \text { for } L \\ 3 W-10 &= 140 \quad \color {Red} \text { Combine like terms. } \\ 3 W &= 150 \quad \color {Red} \text { Add } 10 \text { to both sides. } \\ W &= 50 \quad \color {Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]
Дайте відповідь на питання. Ширина -$W = 50$ ноги. Довжина така:\[\begin{aligned} L &= 2W-10 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.4} \\ L &= 2(50)-10 \quad \color {Red} \text { Substitute } 50 \text { for } W. \\ L &= 90 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \] Таким чином, довжина -$L = 90$ стопи.
Озирніться назад. Можливо, зображення, позначене нашими відповідями, найкраще може продемонструвати, що ми маємо правильне рішення. Пам'ятайте, ми виявили, що ширина була$50$ футами, а довжина -$90$ ногами.

$рис 4.4.c.png$

Зверніть увагу, що периметр -$P = 90 + 50 + 90 + 50 = 280$ фути. По-друге, врахуйте, що довжина$90$$10$ ніг менше ніж в два рази більше ширини. Отже, ми маємо правильне рішення.

Вправа$\PageIndex{2}$

Периметр прямокутника дорівнює$368$ meters. The length of the rectangle is $34$ meters more than twice the width. Find the width and length of the rectangle.

Відповідь: довжина$=134$, ширина$=50$

Приклад$\PageIndex{3}$

Паскаль має зміни$\$3.25$ в кишені, все в копійки і чверті. У нього є$22$ монети у всіх. Скільки у нього копійок?

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштуйте словник змінних. $D$Дозволяти представляють кількість копійок і нехай$Q$ представляють кількість чвертей.

Налаштуйте систему рівнянь. Використання таблиці для узагальнення інформації - хороша стратегія. У першій колонці ми перерахуємо тип монети. Другий стовпець дає номер кожного виду монет, а третій стовпець містить значення (у центах) кількості монет в кишені Паскаля.

	Кількість монет	Значення (в центах)
Даймс	$D$	$10D$
Квартали	$Q$	$25Q$
Підсумки	$22$	$325$

Зверніть увагу, що$D$ рази, оцінені в$10$ центах за штуку, коштують$10D$ центів. Точно так само$Q$ квартали, оцінені в$25$ центах за штуку, коштують$25Q$ центів. Зверніть увагу також, як ми змінилися$\$3.25$ на$325$ центи. Другий стовпець таблиці дає нам перше рівняння. \[D+Q=22 \label{Eq4.4.5}\]Третій стовпець таблиці дає нам наше друге рівняння. \[10 D+25 Q=325 \label{Eq4.4.6}\]

Вирішити систему. Оскільки рівняння\ ref {Eq4.4.5} і\ ref {Eq4.4.6} обидва знаходяться в стандартній формі$Ax + By = C$, ми будемо використовувати метод усунення, щоб знайти рішення. Оскільки питання просить нас знайти кількість копійок у кишені Паскаля, ми зосередимося на усуненні$Q$ -термінів та збереженні$D$ термінів. \[\begin{aligned} -25 D-25 Q &=-550 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.5} \color {Red} \text { by } -25\\ 10 D+25 Q &=325 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.6}\\ \hline-15 D\quad\qquad &=-225 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Розділення обох сторін останнього рівняння на$−15$ дає нам$D = 15$.
Дайте відповідь на питання. Попереднє рішення говорить нам, що Паскаль має$15$ копійки в кишені.

Озирніться назад. Знову ж таки, підведення результатів у таблиці може допомогти нам зрозуміти, чи є у нас правильне рішення. По-перше, тому що нам сказали, що у Паскаля є$22$ монети, і ми виявили, що у нього є$15$ копійки, це означає, що він повинен мати$7$ чверті.

	Кількість монет	Значення (в центах)
Даймс	$15$	$150$
Квартали	$7$	$175$
Підсумки	$22$	$325$

П'ятнадцять$150$ копійок коштують центів, а$7$ чверті коштують$175$ центів. Це загальна кількість$22$ монет і$325$ центів, або$\$3.25$. Таким чином, ми маємо правильне рішення.

Вправа$\PageIndex{3}$

Елоїза має$\$7.10$ in change in her pocket, all in nickels and quarters. she has $46$ coins in all. How many quarters does she have?

Відповідь: $24$

Приклад$\PageIndex{4}$

Роза успадковує$\$10,000$ і вирішує вкласти гроші на два рахунки, одну частину в сертифікат депозиту, який виплачує$4\%$ відсотки на рік, а решту в пайовий фонд, який платить$5\%$ за рік. Наприкінці першого року інвестиції Рози заробляють$\$420$ в цілому відсотки. Знайдіть суму, вкладену в кожен рахунок.

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштуйте словник змінних. $C$Дозволяти представляти суму, вкладену в депозитний сертифікат і$M$ представляти суму, вкладену в ПІФ.

Налаштуйте систему рівнянь. Ми знову будемо використовувати таблицю для узагальнення інформації.

	Оцінити	Сума інвестування	Інтерес
Депозитний сертифікат	$4\%$	$C$	$0.04C$
пайовий фонд	$5\%$	$M$	$0.05M$
Підсумки		$10,000$	$420$

На$4\%$, відсотки, зароблені на інвестиції в$C$ доларах, знаходять шляхом$4\%$ взяття$C$ (тобто,$0.04C$). Аналогічним чином і відсотки, зароблені на ПІФ, є$0.05M$. Третій стовпець таблиці дає нам перше рівняння. Загальний обсяг інвестицій становить$\$10,000$. \[C+M=10000 \nonumber \]Четвертий стовпець таблиці дає нам наше друге рівняння. Загальні зароблені відсотки - це сума відсотків, зароблених на кожному рахунку. \[0.04 C+0.05 M=420 \nonumber \]Давайте очистимо десяткові числа з останнього рівняння, помноживши обидві сторони рівняння на$100$. \[4 C+5 M=42000 \nonumber \]Таким чином, система, яку нам потрібно вирішити, це:\[C+M=10000 \label{Eq4.4.7}\]\[4 C+5 M=42000 \label{Eq4.4.8}\]

Вирішити систему. Оскільки рівняння\ ref {Eq4.4.7} і\ ref {Eq4.4.8} обидва знаходяться в стандартній формі$Ax + By = C$, ми будемо використовувати метод усунення, щоб знайти рішення. Ми зосередимося на усуненні$C$ -термінів. \[\begin{aligned} -4C-4M &=-40000 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.7} \color {Red} \text { by } -4\\ 4C+5M &=\;\;\;42000 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.8}\\ \hline-15 M &=\;\quad2000 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Таким чином, сума вкладається в ПІФ в$M = \$2 ,000$.
Дайте відповідь на питання. Питання просить нас знайти суму, вкладену в кожен рахунок. Отже, підставляємо$M = 2000$ в Equation\ ref {Eq4.4.7} і вирішуємо для$C$. \[\begin{aligned} C+M &=10000 \quad {\color {Red} \text {Equation }} \ref{Eq4.4.7}\\ C+2000 &=10000 \quad \color {Red} \text { Substitute 2000 for M }\\ C &=\;\;8000 \quad \color {Red} \text {Subtract 2000 from both sides.} \end{aligned} \nonumber \]Таким чином$C = \$8 ,000$ було інвестовано в депозитне свідоцтво.

Озирніться назад. По-перше, відзначимо, що вкладення в депозитний сертифікат і ПІФу,$\$8,000$ а$\$2,000$ відповідно, загальні$\$10,000$. Давайте розрахуємо відсотки по кожній інвестиції:$4\%$ of$\$8,000$ is$\$320$ and$5\%$ of$\$2,000$ is$\$100$.

	Оцінити	Сума інвестування	Інтерес
Депозитний сертифікат	$4\%$	$8,000$	$320$
пайовий фонд	$5\%$	$2,000$	$100$
Підсумки		$10,000$	$420$

Зверніть увагу, що загальний відсоток становить$\$420$, як це вимагається в постановці проблеми. Таким чином, наше рішення є правильним.

Вправа$\PageIndex{4}$

Айлін успадковує$\$40,000$ and decides to invest the money in two accounts, part in a сертифікат депозиту, який сплачує$3\%$ interest per year, and the rest in a mutual fund that pays $6\%$ per year. At the end of the перший рік, її інвестиції заробляють загалом$\$2,010$ in interest. Find the amount invested in each account.

Відповідь: $\$13,000$в депозитному сертифікаті,$\$27,000$ в пайовому фонді.

Приклад$\PageIndex{5}$

$\$0.50$Роздрібна торгівля арахісом за фунт і вартість кешью$\$1.25$ за фунт. Якби ви були власником магазину, скільки фунтів арахісу та кешью ви повинні змішати, щоб зробити$50$ фунти арахісово-кешью суміші вартістю$\$0.95$ за фунт?

Рішення

У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

Налаштуйте словник змінних. $P$Дозволяти кількість фунтів арахісу, використовуваних і нехай$C$ буде кількість фунтів кешью, використовуваних.

Налаштуйте систему рівнянь. Ми знову будемо використовувати таблицю для узагальнення інформації.

	Вартість за фунт	Сума (фунти)	Вартість
Арахіс	$\$0.50$	$P$	$0.50P$
Кешью	$\$1.25$	$C$	$1.25C$
Підсумки	$\$0.95$	$50$	$0.95(50)=47.50$

$\$0.50$За фунт,$P$ фунти арахісу коштують$0.50P$. $\$1.25$За фунт,$C$ фунти кешью коштують$1.25C$. Нарешті,$\$0.95$ за фунт,$50$ фунти суміші арахісу та кешью коштуватимуть$0.95(50)$, або$\$47.50$. Третій стовпець таблиці дає нам перше рівняння. Загальна кількість фунтів суміші задається наступним рівнянням:\[P+C=50 \nonumber \] Четвертий стовпець таблиці дає нам наше друге рівняння. Загальна вартість становить суму витрат на придбання арахісу та кешью. \[0.50 P+1.25 C=47.50 \nonumber \]Давайте очистимо десяткові числа з останнього рівняння, помноживши обидві сторони рівняння на$100$. \[50 P+125 C=4750 \nonumber \]Таким чином, система, яку нам потрібно вирішити, це:\[P+C=50 \label{Eq4.4.9}\]\[50 P+125 C=4750 \label{Eq4.4.10}\]

Вирішити систему. Оскільки рівняння\ ref {Eq4.4.9} і\ ref {Eq4.4.10} обидва знаходяться в стандартній формі$Ax + By = C$, ми будемо використовувати метод усунення, щоб знайти рішення. Ми зосередимося на усуненні$P$ -термінів. \[\begin{aligned} -50P-50C &=-2500 \quad {\color {Red} \text {Multiply equation }} \ref{Eq4.4.9} \color {Red} \text { by } -50\\ 50P+125C &=\;\;\;4750 \quad {\color {Red} \text { Equation }} \ref{Eq4.4.10}\\ \hline 75C &=\quad2250 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]Розділіть обидві сторони$75$, щоб отримати$C = 30$ кілограми кешью знаходяться в суміші.
Дайте відповідь на питання. Питання задається як кількостями, арахісом, так і кешью. $C = 30$Замініть рівняння\ ref {Eq4.4.9} для визначення$P$. \[\begin{aligned} P+C &=50 \quad {\color {Red} \text {Equation }} \ref{Eq4.4.9}\\ C+30 &=50 \quad \color {Red} \text { Substitute 30 for C }\\ P &=20 \quad \color {Red} \text {Subtract 30 from both sides.} \end{aligned} \nonumber\]Таким чином, в суміші є$P = 20$ кілограми арахісу.

Озирніться назад. По-перше, зверніть увагу, що кількість арахісу та кешью в суміші становить$20$ і$30$ фунти відповідно, тому загальна суміш важить$50$ кілограми, як потрібно. Давайте розрахуємо витрати: на арахіс$0.50(20)$, або$\$10$, для кешью,$1.25(30) = 37.50$.

	Вартість за фунт	Сума (фунти)	Вартість
Арахіс	$\$0.50$	$20$	$\$10.00$
Кешью	$\$1.25$	$30$	$\$37.50$
Підсумки	$\$0.95$	$50$	$\$47.50$

Зверніть увагу, що загальна вартість є$\$47.50$, як це вимагається в постановці проблеми. Таким чином, наше рішення є правильним.

Вправа$\PageIndex{5}$

Магазин продає арахіс для$\$4.00$ per pound and pecans for $\$7.00$ per pound. How many pounds of peanuts and how many pounds of pecans should you mix to make a $25$-lb mixture costing $\$5.80$ per pound?

Відповідь: $10$фунти арахісу,$15$ фунти пекан

	Кількість монет	Значення (в центах)
Даймс	\(D\)	\(10D\)
Квартали	\(Q\)	\(25Q\)
Підсумки	\(22\)	\(325\)

	Кількість монет	Значення (в центах)
Даймс	\(15\)	\(150\)
Квартали	\(7\)	\(175\)
Підсумки	\(22\)	\(325\)

	Оцінити	Сума інвестування	Інтерес
Депозитний сертифікат	\(4\%\)	\(C\)	\(0.04C\)
пайовий фонд	\(5\%\)	\(M\)	\(0.05M\)
Підсумки		\(10,000\)	\(420\)

	Оцінити	Сума інвестування	Інтерес
Депозитний сертифікат	\(4\%\)	\(8,000\)	\(320\)
пайовий фонд	\(5\%\)	\(2,000\)	\(100\)
Підсумки		\(10,000\)	\(420\)

	Вартість за фунт	Сума (фунти)	Вартість
Арахіс	\(\$0.50\)	\(P\)	\(0.50P\)
Кешью	\(\$1.25\)	\(C\)	\(1.25C\)
Підсумки	\(\$0.95\)	\(50\)	\(0.95(50)=47.50\)

	Вартість за фунт	Сума (фунти)	Вартість
Арахіс	\(\$0.50\)	\(20\)	\(\$10.00\)
Кешью	\(\$1.25\)	\(30\)	\(\$37.50\)
Підсумки	\(\$0.95\)	\(50\)	\(\$47.50\)