2.3: Моделювання лінійних функцій
- Page ID
- 58338
Цілі навчання
- Визначте рівняння прямої, заданої двома точками.
- Визначте рівняння прямої, заданої нахилом і\(y\) -перехопленням.
- Знайдіть лінійні функції, які моделюють загальні програми.
Рівняння ліній
З огляду на алгебраїчне рівняння прямої, ми можемо зробити графік його кількома способами. У цьому розділі нам буде дано геометричний опис прямої та знайдемо алгебраїчне рівняння. Знаходження рівняння прямої може бути здійснено кількома способами. У наступному прикладі використовується форма перехоплення нахилу\(y = mx + b\), або використання позначення функції,\(f (x) = mx + b\). Якщо ми можемо визначити нахил\(m\), і\(y\) -перехоплення\((0, b)\), то ми можемо побудувати рівняння.
Приклад\(\PageIndex{1}\):
Знайти рівняння лінії, що проходить через\((−3, 6)\) і\((5, −4)\).
Рішення
Починаємо з знаходження ухилу. З огляду на дві точки, ми можемо знайти нахил, використовуючи формулу нахилу.
\(\begin{array} { l l } { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( - 3,6 ) } & { ( 5 , - 4 ) } \end{array}\)
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { - 4 - ( 6 ) } { 5 - ( - 3 ) } \\ & = \frac { - 4 - 6 } { 5 + 3 } \\ & = \frac { - 10 } { 8 } \\ & = - \frac { 5 } { 4 } \end{aligned}\)
Ось\(m = −\frac{5}{4}\) і у нас
\(\begin{array} { l } { f ( x ) = m x + b } \\ { f ( x ) = - \frac { 5 } { 4 } x + b } \end{array}\)
Щоб знайти\(b\), підставляємо або одну з заданих точок, через яку проходить лінія. Тут ми будемо використовувати\((−3, 6)\), але\((5, −4)\) працювали б так само добре:
\(\begin{aligned} f ( x ) & = - \frac { 5 } { 4 } x + b \quad\quad\color{Cerulean} {Use (x, f(x))=(-3,6)} \\ \color{OliveGreen}{6} & \color{Black}{=} - \frac { 5 } { 4 } ( \color{OliveGreen}{- 3}\color{Black}{ )} + b \\ 6 & = \frac { 15 } { 4 } + b \\ \frac { 6 \cdot \color{Cerulean}{4} } { \color{Black}{1} \cdot \color{Cerulean}{4} } - \frac { 15 } { 4 } & = b \\ \frac { 24-15 } { 4 } - 15 \\ \frac { 9 } { 4 } & = b \end{aligned}\)
Тому рівняння прямої, що проходить через дві задані точки, таке:
\(\begin{array} { l } { f ( x ) = m x \:\:+\:\: b } \\ \quad\quad\quad\quad\color{Cerulean}{\downarrow\quad\:\:\:\:\:\downarrow} \\ { f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 } } \end{array}\)
Відповідь
\[f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 }\]
Далі намітимо альтернативний метод знаходження рівнянь ліній. Почніть з застосування формули нахилу із заданою точкою\((x_{1} , y_{1})\) та змінною точкою\((x, y)\).
\(\begin{aligned} m & = \frac { y - y _ { 1 } } { x - x _ { 1 } } \\ \frac { m } { 1 } & = \frac { y - y _ { 1 } } { x - x _ { 1 } } \quad\quad\color{Cerulean}{Cross \:multiply}\\ m \left( x - x _ { 1 } \right) & = y - y _ { 1 } \quad\quad\color{Cerulean}{Apply \:the \:symmetric\: property}\\ \left( y - y _ { 1 } \right) & = m \left( x - x _ { 1 } \right) \end{aligned}\)
Тому рівняння невертикальної прямої можна записати в точково-похилій формі 30:
\(y - y _ { 1 } = m \left( x - x _ { 1 } \right) \quad\color{Cerulean}{Point-slope\: form.}\)
Точка-нахил форми особливо корисна для пошуку рівняння прямої з урахуванням нахилу та будь-якого впорядкованого парного рішення. Після знаходження нахилу,\(−\frac{5}{4}\) в попередньому прикладі, ми могли б використовувати цю форму, щоб знайти рівняння.
\(\begin{array} { l } { \color{Cerulean} { Point \quad\quad Slope } } \\ { \left( x _ { 1 } , y _ { 1 } \right) } \\ { ( - 3,6 ) \quad m = - \frac { 5 } { 4 } } \end{array}\)
Підставляємо наступним чином.
\(\begin{aligned} y - y _ { 1 } & = \color{Cerulean}{m} \color{Black}{\left( x - x _ { 1 } \right)} \\ y - ( \color{OliveGreen}{6}\color{Black}{ )} & = \color{Cerulean}{- \frac { 5 } { 4 } }\color{Black}{(} x - (\color{OliveGreen}{ - 3}\color{Black}{ )} ) \quad \color {Cerulean} { Solve\:for\: y } \\ y - 6 & = - \frac { 5 } { 4 } ( x + 3 ) \quad\quad\color{Cerulean} { Distribute } \\ y - 6 & = - \frac { 5 } { 4 } x - \frac { 15 } { 4 } \\ y & = - \frac { 5 } { 4 } x - \frac { 15 } { 4 } +6 \\ y & = - \frac { 5 } { 4 } x + \frac { 9 } { 4 } \end{aligned}\)
Зверніть увагу, що ми отримуємо ту ж лінійну функцію\(f ( x ) = - \frac { 5 } { 4 } x + \frac { 9 } { 4 }\).
Іноді змінна не виражається явно з точки зору іншого; однак все ж передбачається, що одна змінна залежить від іншої. Наприклад, рівняння\(2x + 3y = 6\) неявно представляє функцію.\(f (x) = −\frac{2}{3}x + 2\) Вам повинно стати комфортно працювати з функціями в будь-якій формі.
Приклад\(\PageIndex{2}\)
Знайдіть рівняння наступної лінійної функції:
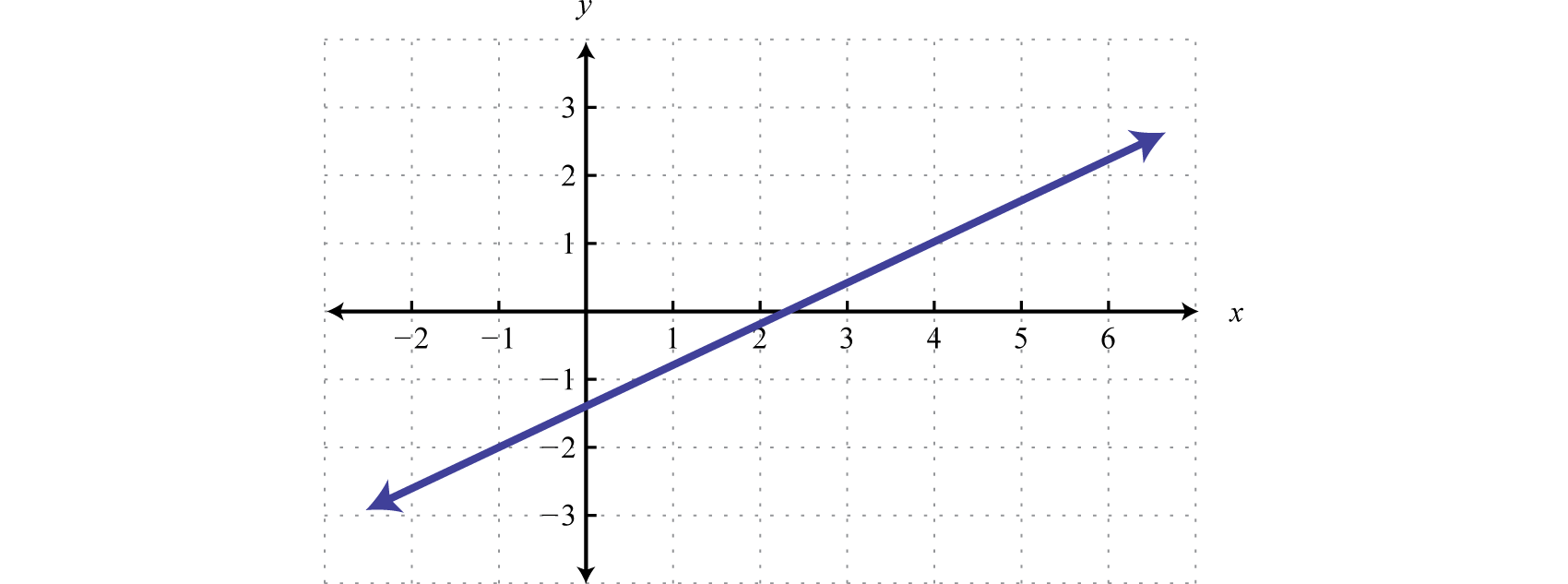
Рішення
З графіка можна визначити дві точки\((−1, −2)\) і\((4, 1)\). Використовуйте ці точки, щоб зчитувати нахил з графіка. Підйом - це\(3\) одиниці, а біг -\(5\) одиниці.
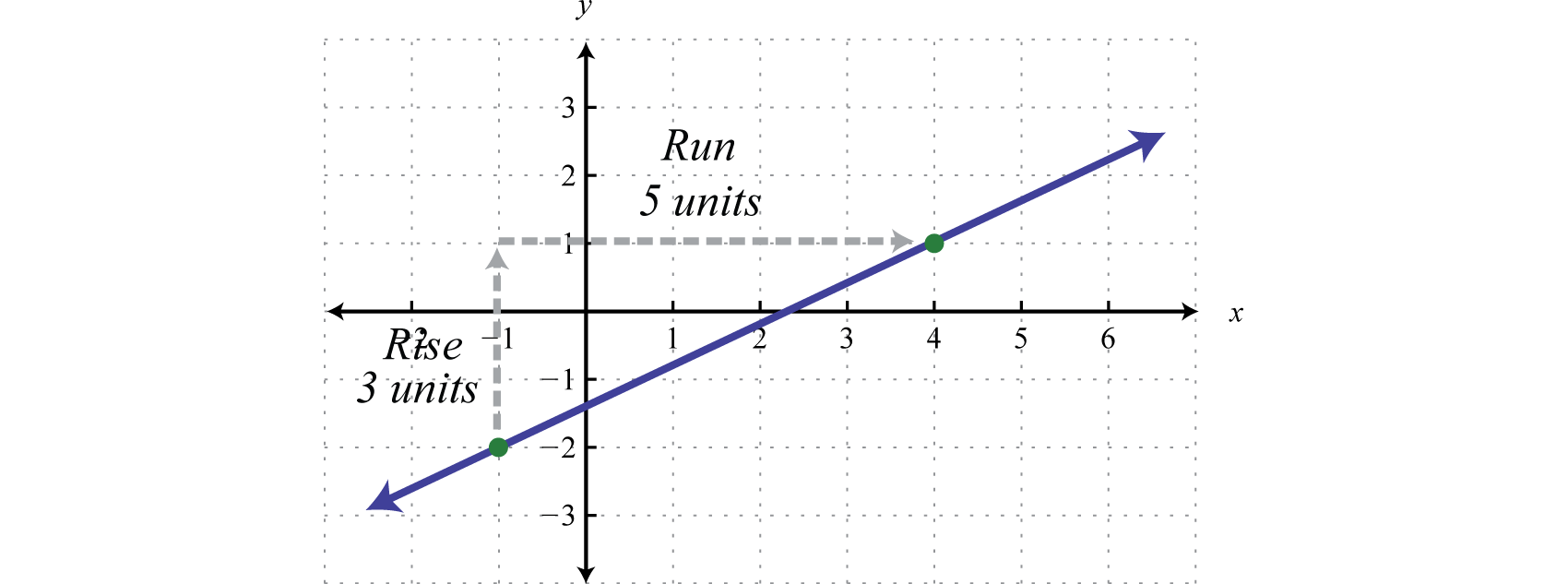
Тому у нас є ухил і точка. (Неважливо, який із заданих пунктів ми використовуємо, результат буде однаковим.)
\(\begin{array} { l } { \color{Cerulean} { Point } }\quad\quad\:\:\color{Cerulean}{Slope} \\ { ( - 1 , - 2 ) \quad m = \frac { 3 } { 5 } } \end{array}\)
Використовуйте точку-нахил форми для визначення рівняння прямої.
\(\begin{aligned} y - y _ { 1 } & = \color{Cerulean}{m} \color{Black}{\left( x - x _ { 1 } \right)} \\ y - ( \color{OliveGreen}{- 2}\color{Black}{ )} & = \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{(} x - ( \color{OliveGreen}{- 1}\color{Black}{ )} ) \quad \color {Cerulean} { Solve\: for\: y. } \\ y + 2 & = \frac { 3 } { 5 } ( x + 1 ) \\ y + 2 & = \frac { 3 } { 5 } x + \frac { 3 } { 5 } \\ y & = \frac { 3 } { 5 } x + \frac { 3 } { 5 } - 2 \\ y & = \frac { 3 } { 5 } x - \frac { 7 } { 5 } \end{aligned}\)
Відповідь
\[f(x)=\frac{3}{5}x−\frac{7}{5}\]
Нагадаємо, що паралельні лінії 31 - це лінії в одній площині, які ніколи не перетинаються. Дві невертикальні лінії в одній площині з ухилами\(m_{1}\) і\(m_{2}\) паралельні, якщо їх нахили однакові,\(m_{1} = m_{2}\).
Приклад\(\PageIndex{3}\)
Знайти рівняння прямої, що проходить через\((3, −2)\) і паралельно\(x − 2y = −2\).
Рішення
Щоб знайти нахил заданої лінії, вирішуйте для\(y\).
\(\begin{aligned} x - 2 y & = - 2 \\ - 2 y & = - x - 2 \\ y & = \frac { - x - 2 } { - 2 } \\ y & = \frac { - x } { - 2 } - \frac { 2 } { - 2 } \\ y & = \frac { 1 } { 2 } x + 1 \end{aligned}\)
Тут дана лінія має нахил\(m = \frac{1}{2}\) і, отже, нахил паралельної\(m_{∥} = \frac{1}{2}\) лінії.Позначення\(m_{∥}\) читається «\(m\)паралельно». Оскільки нам дано точку, і ми тепер маємо нахил, ми вирішимо використовувати точку-нахил форми прямої для визначення рівняння.
\(\begin{array} { l l } { \color{Cerulean}{ Point } } & { \color{Cerulean}{ Slope } } \\ { ( 3 , - 2 ) } & { m _ { \| } = \frac { 1 } { 2 } } \end{array}\)
\(\begin{aligned} y - y _ { 1 } & = m \left( x - x _ { 1 } \right) \color{Cerulean}{Point-Slope\: form}\\ y - ( - 2 ) & = \frac { 1 } { 2 } ( x - 3 ) \\ y + 2 & = \frac { 1 } { 2 } x - \frac { 3 } { 2 } \\ y + 2 \color{Cerulean}{- 2} & = \frac { 1 } { 2 } x - \frac { 3 } { 2 } \color{Cerulean}{- 2} \\ y & = \frac { 1 } { 2 } x - \frac { 7 } { 2 } \end{aligned}\)
Відповідь
\[f ( x ) = \frac { 1 } { 2 } x - \frac { 7 } { 2 }\]
Важливо мати геометричне розуміння цього питання. Нас попросили знайти рівняння прямої, паралельної іншій лінії, що проходить через певну точку.
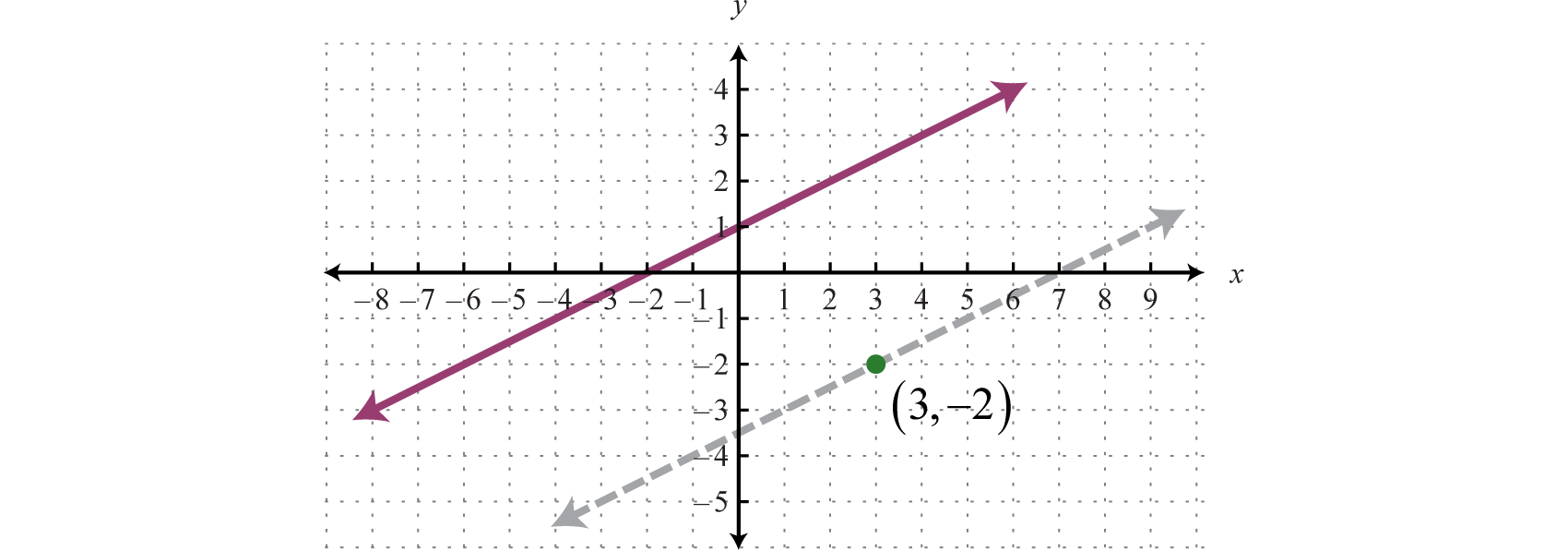
Через точку\((3, −2)\) ми знайшли паралельну лінію\(y = \frac{1}{2} x − \frac{7}{2}\), показану у вигляді пунктирної лінії. Зверніть увагу, що нахил такий же, як і дана лінія\(y = \frac{1}{2} x + 1\), але\(y\) -перехоплення відрізняється.
Нагадаємо, що перпендикулярні лінії 32 - це лінії в одній площині, які перетинаються під прямим кутом (\(90\)градуси). Дві невертикальні лінії, в одній площині з ухилами\(m_{1}\) і\(m_{2}\), перпендикулярні, якщо добуток їх нахилів є\(−1\),\(m_{1} ⋅ m_{2} = −1\). Ми можемо вирішити\(m_{1}\) і отримати\(m_{1} = −\frac{1}{m_{2}}\). У такому вигляді ми бачимо, що перпендикулярні лінії мають нахили, які є негативними зворотними 33, або протилежними зворотними 34. Загалом, задані дійсні числа a та b,
\(\text{If}\: m = \frac { a } { b } \text { then } m _ { \perp } = - \frac { b } { a }\)
Математичне позначення\(m_{⊥}\) читається «\(m\)перпендикулярно». Наприклад, протилежне\(m = −\frac{3}{5}\) взаємне є\(m⊥ = \frac{5}{3}\). Ми можемо переконатися, що два укоси виробляють перпендикулярні лінії, якщо їх продукт є\(−1\).
\(m \cdot m _ { \perp } = - \frac { 3 } { 5 } \cdot \frac { 5 } { 3 } = - \frac { 15 } { 15 } = - 1\color{Cerulean}{✓}\)
Приклад\(\PageIndex{4}\):
Знайти рівняння прямої, що проходить через\((−5, −2)\) і перпендикулярно до\(x + 4y = 4\).
Рішення
Щоб знайти нахил заданої лінії, вирішуйте для\(y\).
\(\begin{aligned} x + 4 y & = 4 \\ 4 y & = - x + 4 \\ y & = \frac { - x + 4 } { 4 } \\ y & = \frac { - x } { 4 } + \frac { 4 } { 4 } \\ y & = - \frac { 1 } { 4 } x + 1 \end{aligned}\)
Дана лінія має нахил\(m = −\frac{1}{4}\), і, таким чином,\(m⊥ = +\frac{4}{1} = 4\). Заставте цей нахил і задану точку в точку-нахил форми.
\(\begin{array} { l l } { \color{Cerulean} { Point } } & { \color{Cerulean} { Slope } } \\ { ( - 5 , - 2 ) } & { m _ { \perp } = 4 } \end{array}\)
\(\begin{aligned} y - y _ { 1 } & = m \left( x - x _ { 1 } \right) \\ y - ( - 2 ) & = 4 ( x - ( - 5 ) ) \\ y + 2 & = 4 ( x + 5 ) \\ y + 5 & = 4 x + 20 \\ y & = 4 x + 18 \end{aligned}\)
Відповідь
\[f(x)=4x+18\]
Геометрично ми бачимо, що лінія\(y=4x+18\), показана у вигляді пунктирної лінії на графіку, проходить наскрізь\((-5, -2)\) і перпендикулярна заданій прямій\(y=\frac{1}{4}x+1\).
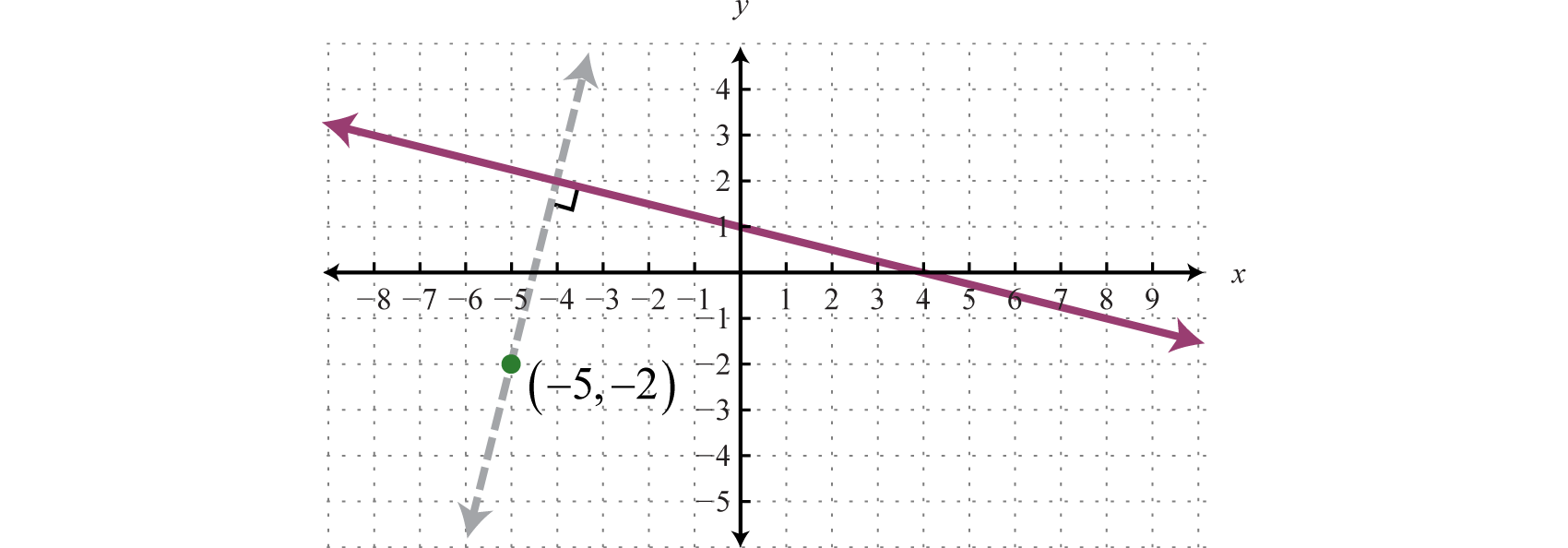
Вправа\(\PageIndex{1}\)
Знайти рівняння прямої, що проходить через\((−5, −2)\) і перпендикулярно до\(\frac{1}{3} x − \frac{1}{2} y = −2\).
- Відповідь
-
\(y = - \frac { 3 } { 2 } x - \frac { 19 } { 2 }\)
www.youtube.com/В/NCNJW7JD2SK
Моделювання лінійних додатків
Дані можуть бути використані для побудови функцій, які моделюють реальні програми. Після визначення рівняння, яке відповідає заданим даними, ми можемо використовувати рівняння для створення певних прогнозів; це називається математичним моделюванням 35.
Приклад\(\PageIndex{5}\):
Вартість щоденної оренди вантажівки\($48.00\), плюс додаткова\($0.45\) за кожну пройдену милю. Напишіть функцію, яка дає вартість добової оренди вантажного автомобіля і використовуйте її для визначення загальної вартості оренди вантажівки на добу і проїзду його\(60\) миль.
Рішення
Загальна вартість оренди вантажного автомобіля залежить від кількості пройдених миль. Якщо ми дозволимо\(x\) представляти кількість пройдених миль, то\(0.45x\) представляє змінну вартість оренди вантажівки. Використовуйте цю та фіксовану вартість\($48.00\), щоб написати функцію, яка моделює загальну вартість,
\(C ( x ) = 0.45 x + 48\)
Скористайтеся цією функцією, щоб розрахувати вартість прокату при\(x = 60\) милі.
\(\begin{aligned} C ( 60 ) & = 0.45 ( 60 ) + 48 \\ & = 27 + 48 \\ & = 75 \end{aligned}\)
Відповідь:
Загальна вартість оренди вантажівки на день і за кермом його\(60\) миль буде\($75\).
Ми можемо використовувати модель,\(C (x) = 0.45x + 48\) щоб відповісти на багато інших питань. Наприклад, скільки миль можна проїхати, щоб зберегти вартість оренди максимум\($66\)? Щоб відповісти на це питання, встановіть нерівність, яка виражає вартість менше або дорівнює\($66\).
\(\begin{aligned} C ( x ) & \leq \$ 66 \\ 0.45 x + 48 & \leq 66 \end{aligned}\)
Вирішіть\(x\) для визначення кількості миль, які можна проїхати.
\(\begin{aligned} 0.45 x + 48 & \leq 66 \\ 0.45 x & \leq 18 \\ x & \leq 40 \end{aligned}\)
Щоб обмежити вартість оренди\($66\), вантажівка може проїхати\(40\) милі або менше.
Приклад\(\PageIndex{6}\):
Компанія придбала нову одиницю обладнання для\($12,000\). Через чотири роки його оцінили в\($9,000\) доларах. Використовуйте ці дані для побудови лінійної функції, яка моделює значення одиниці обладнання з плином часу.
Рішення
Вартість товару залежить від кількості років після її придбання. Тому вік одиниці обладнання є незалежною змінною. Використовуйте впорядковані пари, де\(x\) -значення представляють вік, а\(y\) -значення представляють відповідне значення.
\((age, value)\)
З задачі можна визначити дві впорядковані пари. Придбано новий\((age = 0)\), предмет вартості\($12,000\), а через\(4\) роки товар був оцінений в\($9,000\). Тому ми можемо записати наступні дві\((age, value)\) впорядковані пари:
\(( 0,\:12,000 ) \quad \text { and } \quad ( 4,\: 9,000 )\)
Використовуйте ці дві впорядковані пари для побудови лінійної моделі. Почніть з знаходження ухилу\(m\).
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { 9,000 - 12,000 } { 4 - 0 } \\ & = \frac { - 3,000 } { 4 } \\ & = - 750 \end{aligned}\)
Ось у нас\(m = −750\). Впорядкована пара\((0, 12,000)\) дає\(y\) -перехоплення; отже,\(b = 12,000\).
\(\begin{array} { l } { y = m x + b } \\ { y = - 750 x + 12,000 } \end{array}\)
Нарешті, напишіть цю модель як функцію, яка дає значення одиниці обладнання з часом. Виберіть назву функції\(V\), значення та змінну\(t\) замість того, щоб\(x\) відображати час у роках.
\(V ( t ) = - 750 t + 12,000\)
Відповідь:
\(V ( t ) = - 750 t + 12,000\)
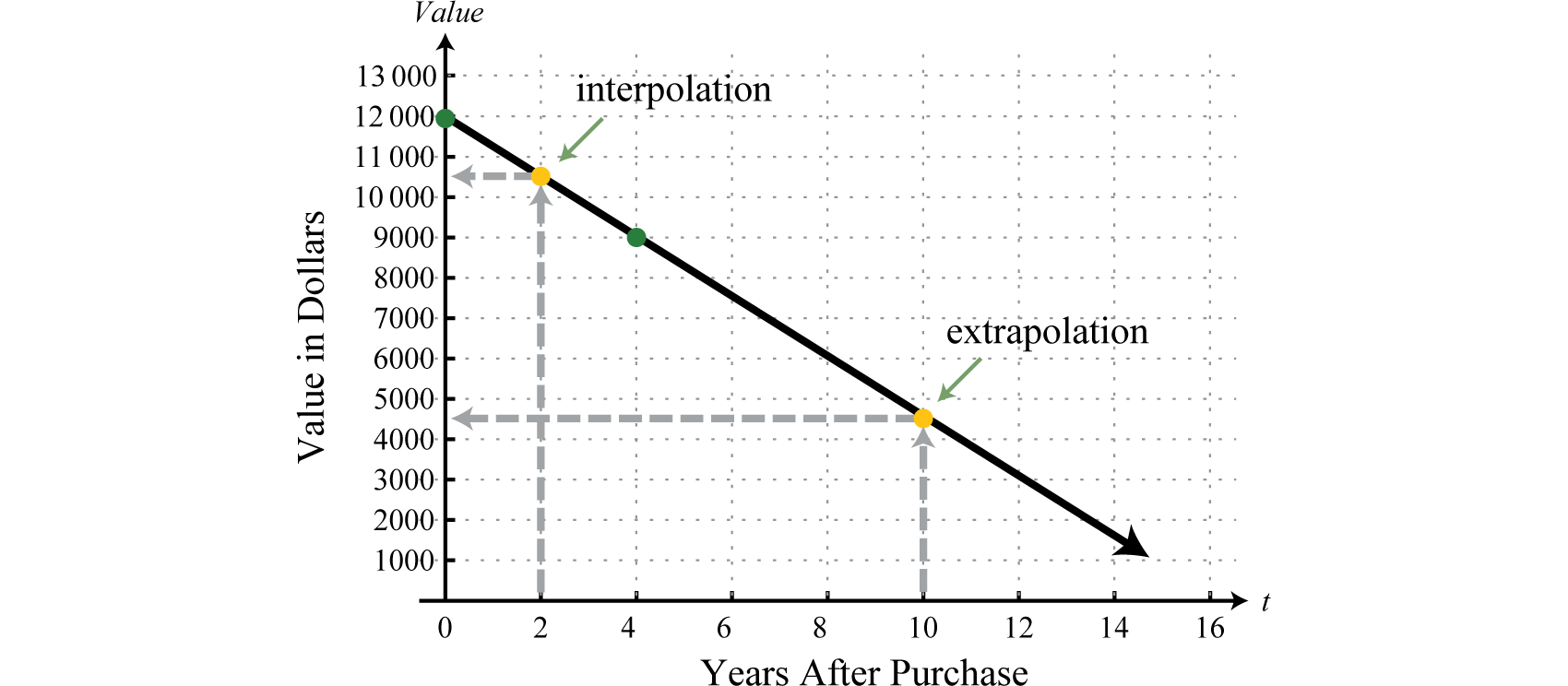
Функція\(V (t) = −750t + 12,000\) називається лінійною моделлю амортизації 36. Він використовує лінійне рівняння для вираження зменшення значення елемента з плином часу. Використання цієї функції для визначення значення елемента між заданими точками даних називається інтерполяцією 37. Наприклад, ми можемо використовувати функцію для визначення значення елемента\(t = 2\), де,
\(\begin{aligned} V ( 2 ) & = - 750 ( 2 ) + 12,000 \\ & = 10,500 \end{aligned}\)
Функція показує, що товар коштував\($10,500\) два роки після того, як він був придбаний. Використання цієї моделі для прогнозування значення поза заданих точок даних називається екстраполяцією 38. Наприклад, ми можемо використовувати функцію для визначення значення елемента, коли\(t = 10\):
\(\begin{aligned} V ( 10 ) & = - 750 ( 10 ) + 12,000 \\ & = - 7,500 + 12,000 \\ & = 4,500 \end{aligned}\)
Модель прогнозує, що одиниця обладнання буде коштувати\($4,500\) десять років після її придбання.
У бізнес-додатку дохід виходить від продажу ряду предметів. Наприклад, якщо товар можна продати,\($150\) і ми дозволяємо\(n\) представляти кількість проданих одиниць, то ми можемо сформувати таку функцію доходу 39:
\(R(n)=150n\)
Використовуйте цю функцію для визначення доходу, отриманого від продажу\(n=100\) одиниць,
\(R ( 100 ) = 150 ( 100 ) = 15,000\)
Функція показує, що дохід, отриманий від продажу\(100\) предметів, є\($15,000\). Як правило, продають предмети не представляють собою всю історію. Існує ряд витрат, пов'язаних з отриманням доходу. Наприклад, якщо існує одноразова плата за встановлення\($5,280\) та вартість\($62\) кожного товару, ми можемо сформувати наступну функцію витрат 40:
\(C ( n ) = 62 n + 5,280\)
Тут\(n\) відображається кількість вироблених предметів. Скористайтеся цією функцією для визначення вартості, пов'язаної з виробничими\(n = 100\) одиницями:
\(C ( 100 ) = 62 ( 100 ) + 5,280 = 11,480\)
Функція показує, що вартість, пов'язана з виробництвом 100 найменувань, становить $11 480. Прибуток це виручка за вирахуванням витрат:
\(\begin{aligned} \color{Cerulean} { Profit } & = \color {Cerulean} { Revenue -Cost } \\ & = 15,000 - 11,480 \\ & = 3,520 \end{aligned}\)
Тому прибуток, отриманий від виробництва та продажу\(100\) предметів, є\($3,520\). Загалом, враховуючи функцію доходу\(R\) та функцію витрат\(C\), ми можемо сформувати функцію прибутку 41 шляхом віднімання наступним чином:
\(P ( n ) = R ( n ) - C ( n )\)
Приклад\(\PageIndex{7}\):
Вартість в доларах виробництва n найменувань задається за формулою\(C (n) = 62n + 5,280\). Виручка в доларах дається\(R (n) = 150n\), де\(n\) являє собою кількість проданих предметів. Напишіть функцію, яка дає прибуток, отриманий шляхом виробництва та продажу n предметів. Використовуйте функцію, щоб визначити, скільки предметів необхідно виробити і продати, щоб заробити мінімум прибуток\($7,000\).
Рішення
Отримати функцію прибутку, віднімаючи функцію витрат з функції доходу.
\(\begin{aligned} P ( n ) & = R ( n ) - C ( n ) \\ & = 150 n - ( 62 n + 5,280 ) \\ & = 150 n - 62 n - 5,280 \\ & = 88 n - 5,280 \end{aligned}\)
Тому\(P (n) = 88n + 5,280\) моделює прибуток. Щоб визначити кількість предметів, які повинні бути виготовлені і продані для отримання прибутку хоча б\($7,000\), вирішують наступне:
\(\begin{aligned} P ( n ) & \geq 7,000 \\ 88 n - 5,280 & \geq 7,000 \\ 88 n & \geq 12,280 \\ n & \geq 139.5 \end{aligned}\)
Округлення, тому що кількість вироблених і проданих одиниць має бути цілим числом. Щоб переконатися в цьому, підрахуйте прибуток де\(n\) є\(139\) і\(140\) одиниці.
\(\begin{array} { l } { P ( 139 ) = 88 ( 139 ) - 5,280 = 6,952 } \\ { P ( 140 ) = 88 ( 140 ) - 5,280 = 7,040 } \end{array}\)
Відповідь:
\(140\)або більше предметів повинні бути вироблені і продані, щоб заробити принаймні прибуток\($7,000\).
Іноді витрати перевищують виручку, в такому випадку прибуток буде негативною. Наприклад, використовуйте функцію прибутку попереднього прикладу, щоб обчислити прибуток\(P (n) = 88n − 5,280\), що генерується де\(n = 50\).
\(P ( 50 ) = 88 ( 50 ) - 5,280 = - 880\)
Це вказує на те, що коли\(50\) одиниці виробляються та продаються, відповідний прибуток є збитком\($880\).
Часто важливо визначити, скільки предметів потрібно виготовити і продати, щоб беззбитковість. Беззбитковість означає не мати ні виграшу, ні збитку; в цьому випадку прибуток буде дорівнює нулю. Щоб визначити точку беззбитковості 42, встановіть функцію прибутку рівну нулю і вирішіть:
\(\begin{aligned} P ( n ) & = 88 n - 5,280 \\ 0 & = 88 n - 5,280 \\ 5,280 & = 88 n \\ 60 & = n \end{aligned}\)
Тому\(60\) предмети необхідно виробляти і продавати, щоб беззбитковість.

Вправа\(\PageIndex{2}\)
Нестандартні футболки можна продавати для\($6.50\) кожного. На додаток до початкової плати за встановлення\($120\), кожна футболка коштує\($3.50\) виробляти.
- Напишіть функцію, яка моделює дохід і функцію, яка моделює вартість.
- Визначте функцію, яка моделює прибуток, і використовуйте її для визначення прибутку від виробництва та продажу\(150\) футболок.
- Розрахуйте кількість футболок, які повинні бути продані для беззбитковості.
- Відповідь
-
а. дохід:\(R (x) = 6.50x\); вартість:\(C (x) = 3.50x + 120\);
b. прибуток:\(P (x) = 3x + 120\);\($330\)
c.\(40\)
Ключові виноси
- За двома точками ми можемо знайти рівняння прямої.
- Паралельні лінії мають однаковий нахил.
- Перпендикулярні лінії мають нахили, протилежні взаємно. Іншими словами, якщо\(m = \frac{a}{b}\), то\(m_{⊥} = −\frac{b}{a}\).
- Щоб знайти рівняння прямої, спочатку використовуйте задану інформацію для визначення нахилу. Потім використовуйте нахил і точку на лінії, щоб знайти рівняння, використовуючи форму точка-нахил.
- Для побудови лінійної функції, яка моделює реальну програму, спочатку ідентифікуйте залежні та незалежні змінні. Далі знайдіть дві впорядковані пари, які описують дану ситуацію. Використовуйте ці дві впорядковані пари для побудови лінійної функції шляхом знаходження нахилу та\(y\) -перехоплення.
Вправа\(\PageIndex{3}\)
Знайти лінійну функцію,\(f\) що проходить через задані точки.
- \((−1, 2)\)і\((3, −4)\)
- \((3, −2)\)і\((−1, −4)\)
- \((−5, −6)\)і\((−4, 2)\)
- \((2, −7)\)і\((3, −5)\)
- \((10, −15)\)і\((7, −6)\)
- \((−9, 13)\)і\((−8, 12)\)
- \((−12, 22)\)і\((6, −20)\)
- \((6, −12)\)і\((−4, 13)\)
- \((\frac{1}{3}, \frac{4}{5})\)і\((\frac{1}{2} ,1)\)
- \((−\frac{3}{2}, −\frac{5}{2})\)і\((1, \frac{5}{6})\)
- \((−5, 10)\)і\((−1, 10)\)
- \((4, 0)\)і\((−7, 0)\)
- Відповідь
-
1. \(f (x) = −\frac{3}{2} x + \frac{1}{2}\)
3. \(f (x) = 8x + 34\)
5. \(f (x) = −3x + 15\)
7. \(f (x) = −\frac{7}{3} x − 6\)
9. \(f (x) = \frac{6}{5} x + \frac{2}{5}\)
11. \(f (x) = 10\)
Вправа\(\PageIndex{4}\)
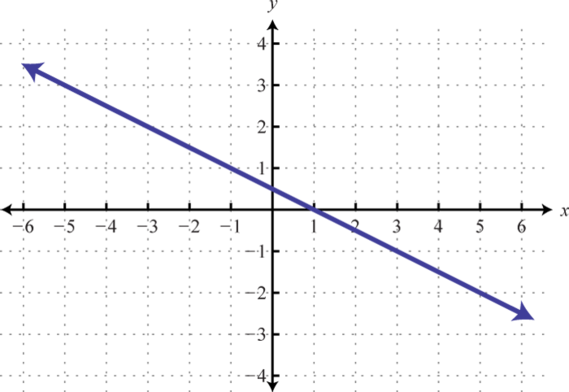
Знайдіть рівняння заданої лінійної функції.
1.
2.
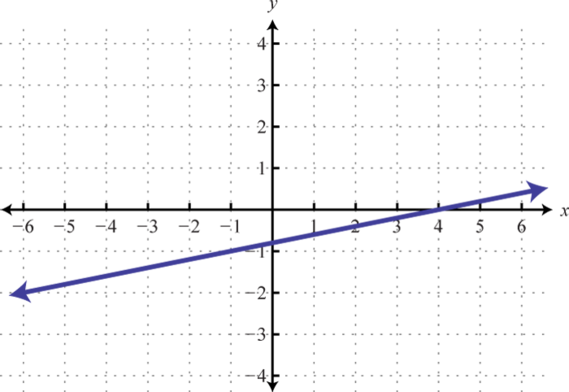
3.
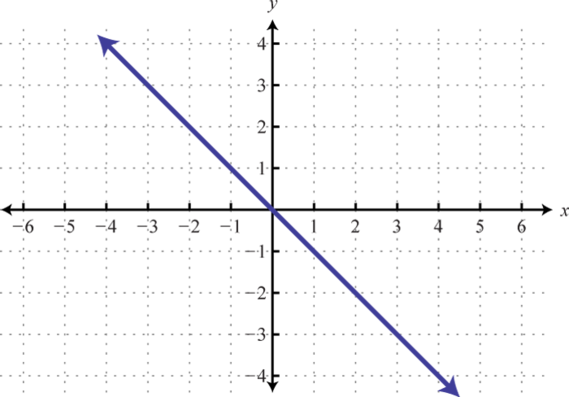
4.
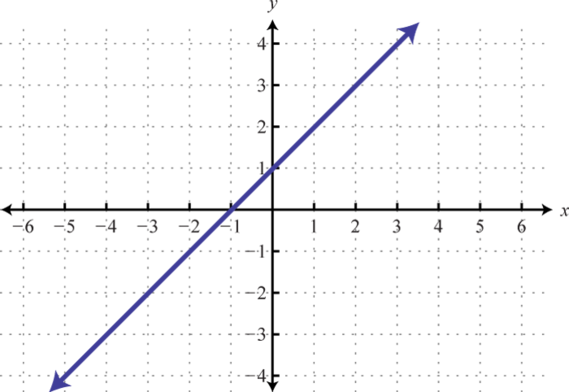
5.
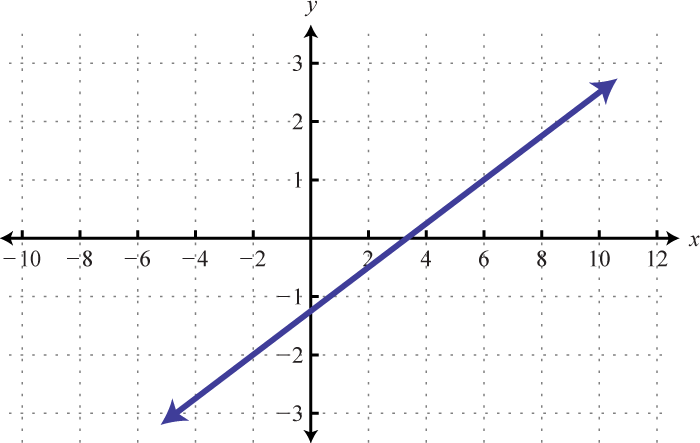
6.
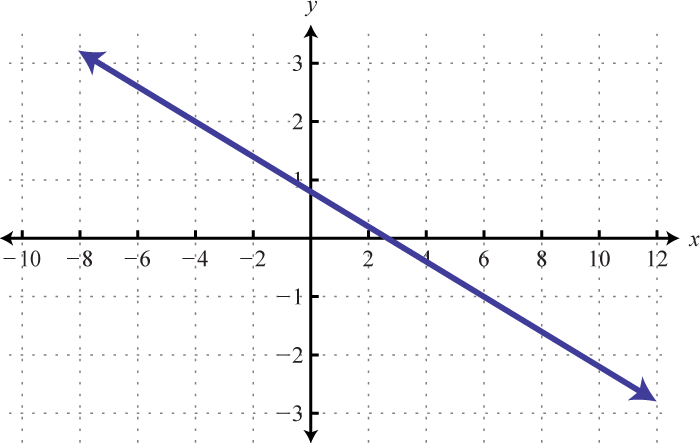
7.
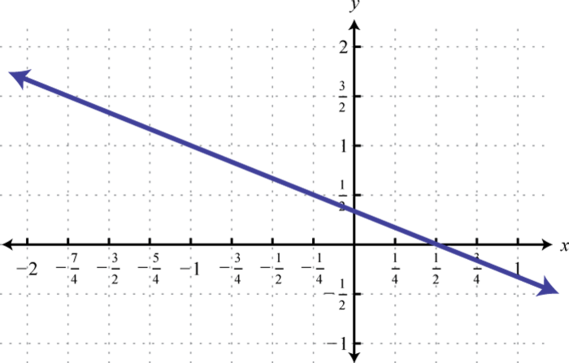
8.
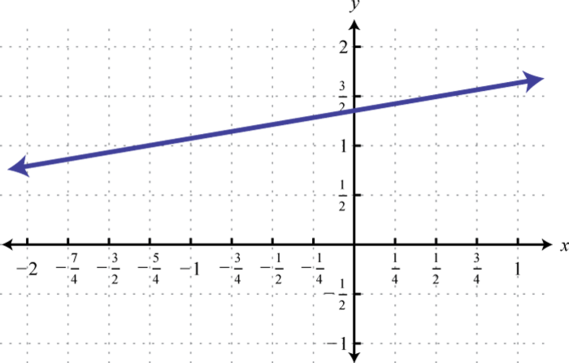
9.
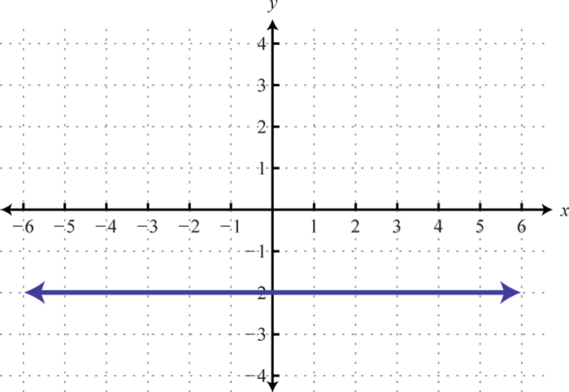
10.
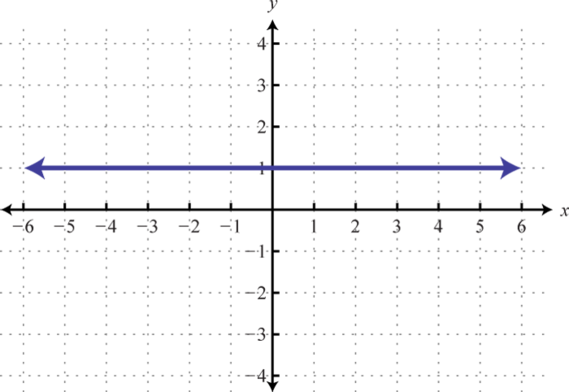
- Відповідь
-
1. \(f (x) = − \frac{1}{2} x + \frac{1}{2}\)
3. \(f (x) = −x\)
5. \(f (x) = \frac{3}{8} x − \frac{5}{4}\)
7. \(f (x) = −\frac{2}{3} x + \frac{1}{3}\)
9. \(f (x) = −2\)
Вправа\(\PageIndex{5}\)
Знайдіть рівняння прямої:
- Паралельно\(y = −\frac{5}{3}x +\frac{1}{2}\) і проходячи наскрізь\((−3, 4)\).
- Паралельно\(y = −\frac{3}{4}x −\frac{7}{3}\) і проходячи наскрізь\((−8, −1)\).
- Паралельно\(y = \frac{1}{3}x + 6\) і проходячи наскрізь\((2, −5)\).
- Паралельно\(y = \frac{1}{4}x + \frac{5}{3}\) і проходячи наскрізь\((5, 6)\).
- Паралельно\(4x − 5y = 15\) і проходячи наскрізь\((−1, −2)\).
- Паралельно\(3x − 4y = 2\) і проходячи наскрізь\((−6, 8)\).
- Паралельно\(2x + 12y = 9\) і проходячи наскрізь\((10, −9)\).
- Паралельно\(9x + 24y = 2\) і проходячи наскрізь\((−12, −4)\).
- Паралельно\(\frac{2}{15}x + \frac{1}{3}y = \frac{1}{10}\) і проходячи наскрізь\((−15, 4)\).
- Паралельно\(\frac{1}{3}x + \frac{2}{7}y = 1\) і проходячи наскрізь\((12, −11)\).
- Перпендикулярно\(y = 5x + 2\) і проходить наскрізь\((10, −5)\).
- Перпендикулярно\(y = −2x + 1\) і проходить наскрізь\((−8, −11)\).
- Перпендикулярно\(y = \frac{3}{2}x − 5\) і проходить наскрізь\((5, −3)\).
- Перпендикулярно\(y = \frac{3}{4}x − \frac{1}{2}\) і проходить наскрізь\((−6, −4)\).
- Перпендикулярно\(12x + 15y = 3\) і проходить наскрізь\((12, 15)\).
- Перпендикулярно\(24x + 15y = 12\) і проходить наскрізь\((2, −1)\).
- Перпендикулярно\(14x − y = 3\) і проходить наскрізь\((7, 3)\).
- Перпендикулярно\(x − y = 4\) і проходить наскрізь\((6, −2)\).
- Перпендикулярно\(\frac{2}{15}x − \frac{3}{5}y = −1\) і проходить наскрізь\((1, −1)\).
- Перпендикулярно\(\frac{3}{4}x − \frac{2}{3}y = \frac{1}{2}\) і проходить наскрізь\((−3, 6)\).
- Дайте рівняння прямої, яка збігається з\(x\) -віссю.
- Дайте рівняння прямої, яка збігається з\(y\) -віссю.
- З огляду на будь-яку лінію в стандартному вигляді\(ax + by = c\), визначте нахил будь-якої перпендикулярної лінії.
- З огляду на будь-яку лінію в стандартному вигляді\(ax + by = c\), визначте нахил будь-якої паралельної лінії.
- Відповідь
-
1. \(y = −\frac{5}{3}x − 1\)
3. \(y = \frac{1}{3}x − \frac{17}{3}\)
5. \(y = \frac{4}{5}x − \frac{6}{5}\)
7. \(y = −\frac{1}{6}x − \frac{22}{3}\)
9. \(y = −\frac{2}{5}x − 2\)
11. \(y = −\frac{1}{5}x − 3\)
13. \(y = −\frac{2}{3}x + \frac{1}{3}\)
15. \(y = \frac{5}{4}x\)
17. \(y = −\frac{1}{14}x + \frac{7}{2}\)
19. \(y = −\frac{9}{2}x + \frac{7}{2}\)
21. \(y = 0\)
23. \(m_{⊥} = \frac{b}{a}\)
Вправа\(\PageIndex{6}\)
Використовуйте алгебру, щоб вирішити наступне.
- Компанія бажає придбати ручки з печаткою логотипу компанії. На додаток до початкової плати за встановлення\($90\), кожна ручка коштує\($1.35\) виробляти. Напишіть функцію, яка дає вартість в перерахунку на кількість вироблених ручок. Використовуйте функцію для визначення вартості виготовлення\(500\) ручок з нанесеним на неї логотипом компанії.
- Компанія з прокату автомобілів стягує щоденну норму\($42.00\) плюс\($0.51\) за милю. Напишіть функцію, яка дає вартість оренди автомобіля на добу в перерахунку на кількість пройдених миль. Скористайтеся функцією визначення вартості оренди автомобіля на добу і проїзду його\(76\) миль.
- Певний план стільникового телефону\($16\) заряджає щомісяця і\($0.15\) за хвилину використання. Напишіть функцію, яка дає вартість телефону в місяць виходячи з кількості хвилин використання. Використовуйте функцію, щоб визначити кількість хвилин використання, якщо рахунок за перший місяць був\($46\).
- Компанія веб-сервісів стягує\($2.50\) місяць плюс\($0.14\) за гігабайт пам'яті у своїй системі. Напишіть функцію, яка дає вартість зберігання в місяць в перерахунку на кількість збережених гігабайт. Скільки гігабайт зберігається, якщо рахунок за цей місяць був\($6.00\)?
- Мері відстежує свої рахунки за стільниковий телефон протягом останніх двох місяців. Рахунок за перший місяць був\($45.00\) розрахований на\(150\) хвилини використання. Рахунок за другий місяць був\($25.00\) розрахований на\(50\) хвилини використання. Знайдіть лінійну функцію, яка дає загальний щомісячний рахунок на основі хвилин використання.
- Компанія в перший рік свого бізнесу випустила\(1,200\) брошури на загальну вартість\($5,050\). У наступному році компанія випустила\(500\) більше брошур за вартістю\($2,250\). Використовуйте цю інформацію, щоб знайти лінійну функцію, яка дає загальну вартість виготовлення брошур з кількості випущених брошур.
- Вебмайстер помітив, що кількість зареєстрованих користувачів неухильно зростає з початку рекламної кампанії. Перш ніж почати рекламувати, у нього були\(2,200\) зареєстровані користувачі, а після\(4\) місяців реклами у нього тепер\(5,480\) зареєстровані користувачі. Використовуйте ці дані для написання лінійної функції, яка дає загальну кількість зареєстрованих користувачів, враховуючи кількість місяців після початку реклами. Використовуйте функцію прогнозування кількості\(8\) місяців користувачів в рекламній кампанії.
- Фермер кукурудзи в Каліфорнії зміг виробляти\(154\) бушелі кукурудзи на акр через\(2\) роки після початку своєї діяльності. В даний час, після\(7\) багатьох років експлуатації, він збільшив свою врожайність до\(164\) бушелів на акр. Використовуйте цю інформацію для написання лінійної функції, яка дає загальну врожайність на акр на основі кількості років експлуатації, і використовуйте її для прогнозування врожайності на наступний рік.
- Комерційний фургон був придбаний новий для\($22,500\) і, як очікується, буде нікчемний через\(12\) роки. Використовуйте цю інформацію, щоб записати лінійну функцію амортизації для вартості фургона. Використовуйте функцію для визначення вартості фургона після\(8\) багатьох років використання.
- Середня тривалість життя промислового зварювального робота становить\(10\) роки, після чого вважається, що він не має значення. Якщо промисловий зварювальний робот був придбаний новий для\($58,000\), напишіть функцію, яка дає значення робота з точки зору кількості років експлуатації. Використовуйте функцію для оцінки робота після\(3\) багатьох років роботи.
- Бізнес придбав одиницю обладнання нове для\($2,400\). Після\(5\) багатьох років використання обладнання цінується в\($1,650\). Знайдіть лінійну функцію, яка дає значення обладнання з точки зору років використання. Використовуйте функцію для визначення кількості років, після яких одиниця обладнання не матиме ніякого значення.
- Продавець заробляє базову зарплату\($2,400\) в місяць плюс\(5\)% комісії з усіх продажів. Напишіть функцію, яка дає щомісячну зарплату продавця в плані продажів. Використовуйте функцію для визначення щомісячних продажів, необхідних для заробітку хоча б за\($3,600\) місяць.
- Коли певний професор був найнятий\(2005\), зарахування до коледжу було\(8,500\) студентами. Через п'ять років, в\(2010\), зарахування зросло до\(11,200\) студентів. Визначте лінійну функцію зростання, яка моделює студентське населення в роках з тих пір\(2005\). Використовуйте модель для прогнозування року, в якому зарахування перевищить\(13,000\) учнів.
- В\(1980\), населення Каліфорнії становило близько\(24\) мільйона чоловік. Через двадцять років, в рік\(2000\), населення становило близько\(34\) мільйона. Використовуйте ці дані для побудови лінійної функції для моделювання зростання чисельності населення за роки з тих пір\(1980\). Використовуйте функцію, щоб передбачити рік, в якому населення досягне\(40\) мільйона.
- Класичний автомобіль купується для\($24,500\) і, як очікується, буде збільшуватися в вартості з кожним роком\($672\). Напишіть лінійну функцію, яка моделює оцінку автомобіля за кількістю років після покупки. Використовуйте функцію для прогнозування вартості автомобіля в\(7\) роках.
- Компанія повідомила про продажі першого\($52,000\) та другого\($64,500\) кварталів відповідно.
- Напишіть лінійну функцію, яка моделює продажі за рік в перерахунку на квартал\(n\).
- Використовуйте модель для прогнозування продажів в третьому і четвертому кварталах.
- Конкретна пошукова система призначає рейтинг веб-сторінці на основі кількості посилань, які спрямовують користувачів на веб-сторінку. Якщо посилання не знайдено, веб-сторінці присвоюється рейтинг\(1\). Якщо знайдені\(20\) посилання, що направляють користувачів на веб-сторінку, пошукова система призначає рейтинг сторінки\(3.5\).
- Знайдіть лінійну функцію, яка дає рейтинг веб-сторінки на основі кількості посилань, які спрямовують на неї користувачів.
- Скільки посилань знадобиться для отримання рейтингу сторінок\(5\)?
- Онлайн-продажі того чи іншого товару пов'язані з кількістю кліків по його рекламі. Виявлено, що\(1,520\) кліки за місяць\($2,748\) призводять до онлайн-продажів, а\(1,840\) кліки — онлайн-продажі.\($2,956\) Напишіть лінійну функцію, яка моделює онлайн-продажі товару на основі кількості кліків по його рекламі. Скільки кліків нам потрібно очікувати\($3,385\) в щомісячних онлайн-продажах від цього конкретного продукту?
- Бізнес з виробництва велосипедів може виробляти\(x\) велосипеди за вартістю, в доларах, заданої формулою\(C (x) = 85x + 2,400\). Компанія реалізує кожен велосипед за оптовою ціною\($145\). Дохід, в доларах, дається\(R (x) = 145x\), де\(x\) представляє кількість проданих велосипедів. Напишіть функцію, яка дає прибуток в перерахунку на кількість вироблених і проданих велосипедів. Використовуйте функцію для визначення кількості велосипедів, які потрібно виготовити і продати, щоб беззбитковість.
- Вартість, в доларах, виготовлення\(n\) нестандартних ламп дається за формулою\(C (n) = 28n + 360\). Кожна лампа може продаватися в Інтернеті для\($79\). Виручка в доларах, дається за рахунок\(R (n) = 79n\), де\(n\) представляє кількість проданих ламп. Напишіть функцію, яка дає прибуток від виробництва та продажу\(n\) нестандартних ламп. Використовуйте функцію, щоб визначити, скільки ламп потрібно випустити і продати, щоб заробити хоча б\($1,000\) на прибуток.
- Виробник може виробляти настільну гру\($12\) за ціною за одиницю після початкових інвестицій фіксованого переоснащення\($12,500\). Ігри можуть продаватися для\($22\) кожного роздрібним торговцям.
- Напишіть функцію, яка дає виробничі витрати, коли виробляються\(n\) ігри.
- Напишіть функцію, яка дає дохід від продажу\(n\) ігор роздрібним торговцям.
- Напишіть функцію, яка дає прибуток від виробництва і продажу\(n\) одиниць.
- Скільки одиниць потрібно продати, щоб отримати принаймні прибуток\($37,500\)?
- Торговий автомат можна здати в оренду за вартістю\($90\) в місяць. Предмети, що використовуються для запасів машини, можна придбати для\($0.50\) кожного і продати для\($1.25\) кожного.
- Напишіть функцію, яка дає щомісячні витрати на лізинг і запас торгового автомата\(n\) предметами.
- Напишіть функцію, яка дає дохід, отриманий від продажу\(n\) предметів.
- Напишіть функцію, яка дає прибуток від запасів і продажу\(n\) предметів в місяць.
- Скільки предметів потрібно продати щомісяця, щоб беззбитковість?
- Відповідь
-
1. \(C ( x ) = 1.35 x + 90 ; \$ 765\)
3. \(C ( x ) = 0.15 x + 16 ;\: 200 \:\text{minutes}\)
5. \(C ( x ) = 0.20 x + 15\)
7. \(U ( x ) = 820 x + 2,200 \:; 8,760 \: \text{users}\)
9. \(V ( t ) = - 1,875 t + 22,500 ;\: \$ 7,500\)
11. \(V ( t ) = - 150 t + 2,400\: ; 16\: \text{years}\)
13. \(P ( x ) = 540 x + 8,500 ;\: 2013\)
15. \(V ( t ) = 672 t + 24,500 ;\: \$ 29,204\)
17. (1)\(r ( n ) = 0.125 n + 1\); (2)\(32\) посилання
19. \(P ( x ) = 60 x - 2,400\: ; 40\:\text{bicycles}\)
21. (1)\(C ( n ) = 12 n + 12,500\); (2)\(R ( n ) = 22 n\); (3)\(P ( n ) = 10 n - 12,500\); (4) принаймні\(5,000\) одиниць
Вправа\(\PageIndex{1}\)
- Досліджуйте та обговоріть лінійну амортизацію. У лінійній моделі амортизації що представляють ухил і\(y\) -перехоплення?
- Запишіть власні кроки для пошуку рівняння прямої. Опублікуйте свої кроки на дошці обговорень.
- Відповідь
-
1. Відповідь може відрізнятися
Виноски
30 Будь-яка невертикальна лінія може бути записана у вигляді\(y − y_{1} = m (x − x_{1} )\), де\(m\) нахил і\((x_{1} , y_{1} )\) є будь-якою точкою на лінії.
31 Лінії в одній площині, які не перетинаються; їх нахили однакові.
32 Лінії в одній площині, які перетинаються під прямим кутом; їх нахили протилежні взаємно.
33 Використовується при зверненні до протилежних взаємних.
34 Два дійсних числа, добуток яких є\(−1\). З огляду на дійсне число\(\frac{a}{b}\), протилежне зворотне є\(−\frac{b}{a}\).
35 Використання даних для пошуку математичних рівнянь, які описують або моделюють реальні програми.
36 Лінійна функція, яка використовується для опису зменшується значення елемента з плином часу.
37 Використання лінійної функції для оцінки значення між заданими точками даних.
38 Використання лінійної функції для оцінки значень, що виходять за межі заданих точок даних.
39 Функція, яка моделює дохід на основі кількості проданих одиниць.
40 Функція, яка моделює вартість виробництва ряду одиниць.
41 Функція, яка моделює прибуток як дохід за вирахуванням витрат.
42 Точка, при якій прибуток не є ні негативним, ні позитивним; прибуток дорівнює нулю.
