1.3: Раціональні числа

Last updated
Save as PDF

Page ID: 58141

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Починаємо з визначення раціонального числа.

Раціональні числа

Будь-яке число, яке може бути виражено у вигляді$p/q$, де$p$ і$q$ є цілими числами$q \neq 0$, називається раціональним числом. Буква$\mathbb{Q}$ використовується для представлення множини раціональних чисел. Тобто:

\[\mathbb{Q}=\left\{\dfrac{p}{q} : p \text { and } q \text { are integers, } q \neq 0\right\} \nonumber \]

Тому що$-2/3$$4/5$, і$123/(-12)$ мають вигляд$p/q$, де$p$ і$q$ є цілими числами, кожен є прикладом раціонального числа. Якщо ви думаєте, що чуєте слово «дріб», коли ми говоримо «раціональне число», ви маєте рацію у своєму мисленні. Будь-яке число, яке можна виразити у вигляді дробу, де чисельник і знаменник є цілими числами, є раціональним числом. Кожне ціле число також є раціональним числом. Візьмемо, наприклад, ціле число$-12$. Є кілька способів, які ми можемо висловити$-12$ як дріб з цілим числом чисельником і знаменником$-12/1$,$24/(-2)$,, і$-36/3$ будучи кілька.

Зменшення дробів до найнижчих термінів

Спочатку ми визначаємо, що мається на увазі під найбільшим спільним дільником двох цілих чисел.

Найбільший спільний дільник

Задано два цілих числа$a$ і$b$, найбільший спільний дільник$a$ і$b$ є найбільшим цілим числом, яке ділиться рівномірно (без залишку) на обидва$a$ і$b$. Позначення$\operatorname{GCD}(a, b)$ використовується для представлення найбільшого спільного дільника$a$ і$b$.

Наприклад,$\operatorname{GCD}(12,18)=6, \operatorname{GCD}(32,40)=8,$ і$\operatorname{GCD}(18,27)=9$.

Тепер ми можемо констатувати, коли дріб скорочується до найнижчих показників.

Найнижчі терміни

$a/b$Фракція, як кажуть, зменшується до найнижчих показників, якщо і тільки тоді$\operatorname{GCD}(a, b)=1$.

Загальною методикою, яка використовується для зведення дробу до найнижчих членів, є поділ чисельника та знаменника на їх найбільший спільний дільник.

Приклад$\PageIndex{1}$

Знизити$8/12$ до найнижчих термінів.

Рішення

Зауважте, що$\operatorname{GCD}(8,12)=4$. Розділіть і чисельник, і знаменник на$4$.

\[\begin{aligned} \dfrac{8}{12} &=\dfrac{8 \div 4}{12 \div 4} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(8,12)=4 \\ &=\dfrac{2}{3} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 8/12 &= 2/3 \end{aligned} \nonumber\]

Вправа$\PageIndex{1}$

Зменшити:$-48 / 60$.

Відповідь: $-4 / 5$

Згадайте визначення простого числа.

Просте число

Натуральне число більше одиниці є простим тоді і тільки тоді, коли його єдиними дільниками є один і сам.

Наприклад,$7$ є простим (його єдиними дільниками є$1$ і$7$), але не$14$ є (його дільники є$1$,$2$,$7$, і$14$). У подібній моді$2$,$3$,, і$5$ є простими, але$6$,$15$, і не$21$ є простими.

Приклад$\PageIndex{2}$

Знизити$10/40$ до найнижчих термінів.

Рішення

Зауважте, що$\operatorname{GCD}(10,40)=10$. Ділимо чисельник і знаменник на$10$.

\[\begin{aligned} \dfrac{10}{40} &=\dfrac{10 \div 10}{40 \div 10} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(10,40)=10 \\ &=\dfrac{1}{4} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 10/40 &= 1/4 \end{aligned} \nonumber\]

Альтернативне рішення

Використовуйте множникові дерева для вираження чисельника та знаменника як добутку простих множників.

$рис. 1.3.1a.png$

Малюнок$\PageIndex{1}$

Значить,$10=2 \cdot 5$ і$40=2 \cdot 2 \cdot 2 \cdot 5$. Тепер, щоб звести$10/40$ до найнижчих членів, замініть чисельник і знаменник на їх прості множники, а потім скасувати множники, які є загальними як для чисельника, так і знаменника.

\ [\ почати {вирівняний}
\ dfrac {10} {40} &=\ dfrac {2\ cdot 5} {2\ cdot 2\ cdot 2\ cdot 5}\ quad\ color {Червоний}\ текст {Простий множник чисельник і знаменник.} \\
&=\ dfrac {\ колір {\ колір {червоний}\ не} 2\ cdot {\ колір {червоний}\ не} 5} {\ колір {червоний}\ не} 2\ cdot 2\ cdot {\ колір {червоний}\ не} 5}\ квадратний\ колір {червоний}\ текст {Скасувати загальні фактори.} \\
&=\ dfrac {1} {4}\ quad\ color {Червоний}\ text {Спрощення чисельника і знаменника.}
\ end {вирівняний}\]

Коли ми скасуємо$2$ з обох чисельника і знаменника, ми насправді ділимо як чисельник і знаменник на$2$. Аналогічну заяву можна зробити і про скасування$5$. Скасування обох$2$ і a$5$ еквівалентно діленню чисельника і знаменника на$10$. Це пояснює$1$ в чисельнику, коли всі фактори скасовуються.

Вправа$\PageIndex{2}$

$18/ 24$Знизити до найнижчих термінів.

Відповідь: $3/ 4$

Приклад $\PageIndex{2}$демонструє важливий момент.

Коли всі фактори скасовуються

Коли всі множники скасовуються або чисельником, або знаменником, отриманий чисельник або знаменник дорівнює одиниці.

Множення дробів

По-перше, визначення.

Множення дробів

Якщо$a/b$ і$c/d$ є двома фракціями, то їх продукт визначається наступним чином:

\[\dfrac{a}{b} \cdot \dfrac{c}{d}=\dfrac{a c}{b d} \nonumber \]

Таким чином, щоб знайти добуток$a/b$ і$c/d$, досить просто помножити чисельники і помножити знаменники. Наприклад:

\[\dfrac{1}{2} \cdot \dfrac{3}{4}=\dfrac{3}{8} \quad \text { and } \quad -\dfrac{2}{5} \cdot \dfrac{7}{3}= -\dfrac{14}{15} \quad \text { and } \quad -\dfrac{5}{8} \cdot \left(-\dfrac{1}{6} \right)=\dfrac{5}{48} \nonumber \]

Як і цілочисельне множення, подібні знаки дають позитивну відповідь, на відміну від знаків дають негативну відповідь. Звичайно, коли це необхідно, не забудьте зменшити свою відповідь до найнижчих термінів.

Приклад$\PageIndex{3}$

Спростити:$-\dfrac{14}{20} \cdot \dfrac{10}{21}$.

Рішення

Множимо чисельники і знаменники, потім зменшуємо до найнижчих.

\ [\ почати {вирівняний}
-\ dfrac {14} {20}\ cdot\ dfrac {10} {21} &=-\ dfrac {140} {420}\ квадратний\ колір {Червоний}\ текст {Множення чисельників і знаменників}\\
&=-\ dfrac {2\ cdot 2\ cdot 2\ cdot 5\ cdot 7} {2\ cdot 2\ cdot 7} точка 3\ cdot 5\ cdot 7}\ квадратний\ колір {червоний}\ текст {Простий фактор.} \\
&=-\ dfrac {\ колір {\ колір {червоний}\ не} 2\ cdot {\ колір {червоний}\ не} 2\ cdot {\ колір {червоний}\ не} 7} {\ колір {червоний}\ ні} 2\ точка {колір {колір {колір {колір {червоний}\ не} 2\ cdot {колір {червоний}\ не} 2\ dot 3\ dot {{Червоний}\ not} 5\ cdot {\ color {Red}\ not} 7}\ quad\ color {Red}\ text {Скасувати загальні фактори.} \\
&=-\ dfrac {1} {3}\ квадратний\ колір {червоний}\ текст {спростити.}
\ end {вирівняний}\ nonumber\]

Зверніть увагу, що коли всі множники скасовуються з чисельника, ви залишитеся з$1$. Таким чином,$(-14/20)\cdot (10/21) = -1/3$.

Вправа$\PageIndex{3}$

Спростити:$-\dfrac{8}{9} \cdot\left(-\dfrac{27}{20}\right)$.

Відповідь: $6/5$

Правило скасування

При множенні дробів скасуйте загальні множники за таким правилом: «Скасувати множник в чисельнику для ідентичного множника в знаменнику».

Правило - «скасувати щось зверху для чогось внизу». Таким чином, альтернативним підходом до множення дробів є множник чисельників і знаменників на місці, а потім скасування множника в чисельнику для ідентичного множника в знаменнику.

Приклад$\PageIndex{4}$

Спростити:$\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right)$.

Рішення

Факторні чисельники та знаменники на місці, а потім скасовують загальні множники в чисельниках для загальних факторів у знаменниках.

\ [\ почати {вирівняний}
\ drac {15} {8}\ ddot\ ліворуч (-\ dfrac {14} {9}\ праворуч) &=\ drac {3\ dot 5} {2\ dot 2\ dot 2}\ dot\ ліворуч (-\ drac {2\ dot 7} {3\ dot 3}\ праворуч)\ квадрат\ {колір Червоний}\ text {Факторні чисельники та знаменники.} \\
&=\ dfrac {\ колір {\ колір {червоний}\ не} 3\ cdot 5} {\ колір {червоний}\ не} 2\ крапка 2}\ крапка\ ліворуч (-\ dfrac {\ колір {\ колір {червоний}\ not} 2\ dot 7} {\ колір {червоний}\ ні} 3\ dot 3}\ праворуч)\ квадратний\ {Red}\ text {Скасувати множник в чисельнику для загального множника в знаменнику.} \\
&=-\ dfrac {35} {12}\ quad\ color {Червоний}\ text {Множення чисельників і знаменників.}
\ end {вирівняний}\ nonumber\]

Відзначимо, що на відміну від ознак виходить негативний продукт. Таким чином,$(15/8)\cdot (-14/9) = -35/12$.

Вправа$\PageIndex{4}$

Спростити:$-\dfrac{6}{45} \cdot\left(-\dfrac{35}{14}\right)$

Відповідь: $1/3$

Ділення дробів

Кожне ненульове раціональне число має мультиплікативне обернене або зворотне.

Взаємний

Якщо$a$ є будь-яким ненульовим раціональним числом, то$1/a$ називається мультиплікативним оберненим або зворотним$a$, і:

\[a \cdot \dfrac{1}{a}=1 \nonumber \]

Зверніть увагу, що:

\[2 \cdot \dfrac{1}{2}=1 \quad \text { and } \quad \dfrac{3}{5} \cdot \dfrac{5}{3}=1 \quad \text { and } \quad -\dfrac{4}{7} \cdot\left(-\dfrac{7}{4}\right)=1 \nonumber \]

Таким чином,$2$ взаємне є$1/2$,$3/5$ взаємне є$5/3$, і$-4/7$ взаємне є$-7/4$. Зауважте, що щоб знайти зворотне число, просто інвертуйте число (переверніть його догори дном). Тепер ми можемо визначити частку двох дробів.

Розподіл дробів

Якщо$a/b$ і$c/d$ є двома дробами, то їх частка визначається наступним чином:

\[\dfrac{a}{b} \div \dfrac{c}{d}=\dfrac{a}{b} \cdot \dfrac{d}{c} \nonumber \]

Наведене вище визначення ділення підсумовується фразою «інвертувати і помножити».

Приклад$\PageIndex{5}$

Спростити:$-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right)$.

Рішення

Інвертувати і помножити, потім коефіцієнт на місце і скасувати загальні множники в чисельнику для загальних факторів у знаменнику.

\ [\ почати {вирівняний}
-\ dfrac {35} {21}\ div\ ліворуч (-\ dfrac {10} {12}\ праворуч) &=-\ dfrac {35} {21}\ cdot\ ліворуч (-\ dfrac {12} {10}\ праворуч)\ quad\ колір {червоний}\ текст {Інвертувати і помножити.} \\
&=-\ drac {5\ cdot 7} {3\ cdot 7}\ cdot\ ліворуч (-\ dfrac {2\ cdot 2\ dot 3} {2\ cdot 5}\ праворуч)\ квадратний\ колір {червоний}\ текст {Простий фактор.} \\
&=-\ dfrac {\ колір {\ колір {червоний}\ не} 5\ cdot {\ колір {червоний}\ не} 7} {\ колір {червоний}\ not} 3\ cdot {червоний}\ not} 7}\ ddot\ left (-\ dfrac {\ колір {червоний}\ ні} 2\ cdot 2\ dot {\ колір {червоний}\ not} 3} {{\ color {Red}\ not} 2\ cdot {\ color {Red}\ not} 5}\ праворуч)\ quad\ color {Червоний}\ text {Скасувати загальні фактори.} \\
&=\ dfrac {2} {1}\ quad\ color {Червоний}\ text {Множення чисельників і знаменників.}\\ &=2\ quad\ color {Red}\ text {Simplify.} \ end {вирівняний}\ nonumber\]

Зверніть увагу, що коли всі фактори в знаменнику скасовуються, а$1$ залишається. Таким чином,$(-35/21)÷(-10/12) = 2$. Відзначимо також, що подібні ознаки дають позитивний результат.

Вправа$\PageIndex{5}$

Спростити:$-\dfrac{4}{9} \div \dfrac{27}{81}$.

Відповідь: $-4/3$

Додавання дробів

Спочатку визначення.

Додавання дробів

Якщо два дроби мають спільний знаменник, додайте чисельники і помістіть результат над спільним знаменником. В символах:

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \nonumber \]

Наприклад:

\[-\dfrac{3}{5}+\dfrac{7}{5}=\dfrac{4}{5} \quad \text { and } \quad-\dfrac{4}{3}+\left(-\dfrac{7}{3}\right)=-\dfrac{11}{3} \quad \text { and } \quad \dfrac{4}{7}+\left(-\dfrac{5}{7}\right)=-\dfrac{1}{7} \nonumber \]

Якщо дроби не мають спільного знаменника, спочатку створіть еквівалентні дроби з найменшим спільним знаменником, а потім додайте відповідно до наведеного вище правила.

Найменш спільний знаменник

Якщо дроби$a/b$ і$c/d$ не мають спільного знаменника, то найменш спільний знаменник для$b$ і$d$, написаний$\mathrm{LCD}(b, d)$, визначається як найменше число, що ділиться на обидва$b$ і$d$.

Приклад$\PageIndex{6}$

Спростити:$-\dfrac{3}{8}+\dfrac{5}{12}$.

Рішення

Найменшим спільним знаменником в даному випадку є найменше число, що ділиться на обидва$8$ і$12$. В даному випадку,$\mathrm{LCD}(8,12)=24$. Спочатку нам потрібно зробити еквівалентні дроби зі спільним знаменником$24$.

\[\begin{aligned} -\dfrac{3}{8}+\dfrac{5}{12} &=-\dfrac{3}{8} \cdot \dfrac{\color{Red}3}{\color{Red}3}+\dfrac{5}{12} \cdot \dfrac{\color{Red}2}{\color{Red}2} \quad \color{Red} \text{Make equivalent fraction with a common denominator of } 24 \\ &=-\dfrac{9}{24}+\dfrac{10}{24} \quad \color{Red} \text{Multiply numerators and denominators.}\\ &=\dfrac{1}{24} \quad \color{Red} \text{Add: } -9+10=1 \end{aligned} \nonumber\]

Зверніть увагу, як ми додаємо чисельники на останньому кроці, розміщуючи результат над спільним знаменником. Таким чином,$-3/8+5/12 = 1/24$.

Вправа$\PageIndex{6}$

Спростити:$-\dfrac{5}{6}+\dfrac{1}{9}$.

Відповідь: $-13/18$

Порядок операцій

Раціональні числа підпорядковуються тим самим Правилам, що і цілі числа.

Правила, що керують порядком операцій

При оцінці виразів дійте в наступному порядку.

Спочатку оцініть вирази, що містяться в символах групування. Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.
Оцінити всі експоненти, які з'являються у виразі.
Виконуйте всі множення і ділення в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.
Виконуйте всі додавання і віднімання в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.

Приклад$\PageIndex{7}$

З огляду на$x =2 /3$$y = -3/5$, і$z = 10 /9$, оцінити$xy + yz$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінних у виразі$xy + yz$ відкритими дужками. Далі підставляємо задані значення змінних ($2/3$$-3/5$for$x$$y$, for і$10 /9$ for$z$) у відкриті дужки.

\[\begin{aligned} x y+y z &=( )(\;\;)+(\;\;)(\;\;) \quad \color{Red} \text{Replace variables with parentheses}\\ &=\left(\dfrac{2}{3}\right)\left(-\dfrac{3}{5}\right)+\left(-\dfrac{3}{5}\right)\left(\dfrac{10}{9}\right) \quad \color{Red} \text{Substitute: } 2/3 \text{ for } x,-3/5 \text{ for } y, \text{ and } 10/9 \text{ for } z \end{aligned} \nonumber \]

Скористайтеся Правилами, що керують порядком операцій, щоб спростити.

\ [\ почати {вирівняний}
&=-\ dfrac {6} {15} +\ лівий (-\ dfrac {30} {45}\ праворуч)\ квадратний\ колір {Червоний}\ текст {Множення}\\
&=-\ dfrac {2} {2}\ dfrac {2}\ праворуч)\ quad\ колір {червоний}\ текст {Зменшити}\\
&=-\ drac {2} {5}\ ddot\ dfrac {3} {3} +\ лівий (-\ dfrac {2} {3}\ ddot\ dfrac {5} {5}\ праворуч )\ quad\ color {Red}\ text {Зробити еквівалентні дроби з}\\
&=-\ dfrac {6} {15} +\ left (-\ dfrac {10} {15}\ праворуч)\ quad\ color {Red}\ text {\
&=-\ dfrac {16} {15}\ quad\ color {Червоний}\ text {{Додати}
кінець {вирівняний}\ nonumber\]

Таким чином, якщо$x=2 / 3, y=-3 / 5,$ і$z=10 / 9,$ тоді$x y+y z=-16 / 15$

Вправа$\PageIndex{7}$

Дано$a=-1 / 2, b=2 / 3$ і$c=-3 / 4$, оцінити вираз$a+bc$ і спростити результат.

Відповідь: $-1$

Приклад$\PageIndex{8}$

Дано$x=-3/5$, оцініть$-x^{3}$.

Рішення

Спочатку замініть кожне входження змінної$x$ відкритими дужками, потім підставляємо$-3/5$ на$x$.

\ [\ begin {вирівняний}
-x^ {3} &=- () ^ {3}\ quad\ color {Red}\ text {Замінити x відкритими дужками.} \\
&=-\ ліворуч (-\ dfrac {3} {5}\ праворуч) ^ {3}\ квадратний\ колір {Червоний}\ текст {Заміна -3/5 для x}\\
&=-\ ліворуч (-\ dfrac {3} {5}\ праворуч)\ лівий (-\ dfrac {3} {3} {5}\ праворуч)\ лівий (-\ dfrac {3} {3} 5}\ праворуч)\ quad\ color {Червоний}\ text {Напишіть -3/5 як множник тричі}\\
&=-\ left (-\ dfrac {27} {125}\ праворуч)\ quad\ color {Red}\ text {Добуток трьох від'ємних дробів від'ємний. Множення чисельників і знаменників.} \\
&=\ dfrac {27} {125}\ quad\ color {Червоний}\ текст {Протилежність -27/125}
\ кінець {вирівняний}\ nonumber\]

Значить$-x^{3}=27 / 125$, дано$x=-3/5$.

Вправа$\PageIndex{8}$

Спростити:$(-1 / 3)^{4}$.

Відповідь: $1/81$

Приклад$\PageIndex{9}$

Дано$a=-4/3$ і$b=-3 / 2$, оцініть$a^{2}+2 a b-3 b^{2}$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінних у виразі$a^{2}+2 a b-3 b^{2}$ відкритими дужками.

Далі підставляємо задані значення змінних ($-4/3$$-3/2$for$a$ і$b$ for) у відкриті дужки.

\[\begin{aligned} a^{2}+2 a b-3 b^{2} &=(\;\; )^{2}+2(\;\; )( \;\;)-3(\; ) ^{2} \\ &=\left(-\dfrac{4}{3}\right)^{2}+2\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-3\left(-\dfrac{3}{2}\right)^{2} \end{aligned} \nonumber \]

Далі оцінюємо показники:$(-4 / 3)^{2}=16 / 9$ і$(-3 / 2)^{2}=9 / 4$
\[=\dfrac{16}{9}+\dfrac{2}{1}\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-\dfrac{3}{1}\left(\dfrac{9}{4}\right) \nonumber \]

Далі виконуємо множення і зменшуємо.

\[\begin{array}{l}{=\dfrac{16}{9}+\dfrac{24}{6}-\dfrac{27}{4}} \\ {=\dfrac{16}{9}+4-\dfrac{27}{4}}\end{array} \nonumber \]

Зробіть еквівалентні дроби із загальним знаменником, потім додайте.

\[\begin{array}{l}{=\dfrac{16}{9} \cdot {\color{Red} \dfrac{4}{4}}+4 \cdot {\color{Red} \dfrac{36}{36}}-\dfrac{27}{4} \cdot {\color{Red} \dfrac{9}{9}}} \\ {=\dfrac{64}{36}+\dfrac{144}{36}-\dfrac{243}{36}} \\ {=-\dfrac{35}{36}}\end{array} \nonumber \]

Таким чином, якщо$a=-4 / 3$ і$b=-3 / 2$, то$a^{2}+2 a b-3 b^{2}=-35 / 36$

Вправа$\PageIndex{9}$

Дано$x=-3 / 4$ і$y=-4 / 5$, оцініть$x^{2}-y^{2}$.

Відповідь: $-31/400$

Дроби на графічному калькуляторі

Ми завжди повинні пам'ятати, що графічний калькулятор - це «апроксимуюча машина». У невеликій кількості ситуацій він здатний дати точну відповідь, але для більшості розрахунків найкраще, на яке ми можемо сподіватися, - це приблизна відповідь.

Однак калькулятор дає точні результати для операцій за участю дробів, якщо ми не використовуємо дроби зі знаменниками, які занадто великі, щоб калькулятор відповідав точною відповіддю.

Приклад$\PageIndex{10}$

Скористайтеся калькулятором графіків, щоб спростити кожне з наведенихСпрощення за допомогою графічного калькулятора:

$\dfrac{2}{3}+\dfrac{1}{2}$
$\dfrac{2}{3} \cdot \dfrac{5}{7}$
$\dfrac{3}{5} \div \dfrac{1}{3}$

Рішення

Вводимо кожен вираз по черзі.

Правила, що керують порядком операцій, говорять нам, що ми повинні виконувати поділи перед доповненнями. Таким чином, вираз$2/3+1/2$ еквівалентно:
\[\begin{aligned} 2 / 3+1 / 2 &=\dfrac{2}{3}+\dfrac{1}{2} \quad \color{Red} \text{Divide first.}\\ &=\dfrac{4}{6}+\dfrac{3}{6} \quad \color{Red} \text{Equivalent fractions with LCD.}\\ &=\dfrac{7}{6} \quad \color{Red} \text{Add.} \end{aligned} \nonumber \] Введіть вираз$2/3+1/2$ на калькуляторі, а потім натисніть клавішу ENTER. Результат показаний на першому зображенні на малюнку$\PageIndex{2}$. Далі натисніть кнопку MATH, потім виберіть 1:Frac (див. Друге зображення на малюнку$\PageIndex{2}$) і знову натисніть клавішу ENTER. Зверніть увагу, що результат, показаний на третьому зображенні на малюнку,$\PageIndex{2}$ відповідає правильній відповіді$7/6$ знайденої вище.

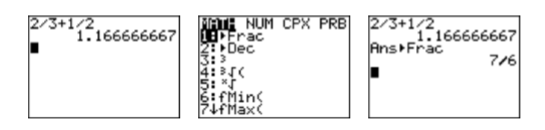
$рис. 1.3.2.png$

Малюнок$\PageIndex{2}$: Розрахунок$2/3+1/2$.

Правила, що керують порядком операцій, говорять нам, що немає переваги ділення над множенням, або навпаки. Ми повинні виконувати ділення і множення в міру їх виникнення, рухаючись зліва направо. Звідси:\ [\ почати {вирівняний}
2/3\ раз 5/7 &=\ dfrac {2} {3}\ раз 5/7\ квадратний\ колір {Червоний}\ текст {Розділити:} 2/3=\ dfrac {2} {3}\\
&=\ dfrac {10} {3}/7\ quad\ колір {червоний}\ текст {Множення:}\ dfrac {2} {3}\ раз 5=\ dfrac {10} {3}\
&=\ dfrac {10} {3}\ раз\ dfrac {1} {7}\ quad\ color {Червоний}\ текст {Інвертувати і помножити.} \\
&=\ dfrac {10} {21}\ quad\ color {Червоний}\ text {Множення:}\ dfrac {10} {3}\ times\ dfrac {1} {7} =\ dfrac {10} {21}
\ end {вирівняний}\ nonumber\] Це саме той самий результат, який ми отримуємо, коли виконуємо наступний розрахунок. \[\dfrac{2}{3} \times \dfrac{5}{7}=\dfrac{10}{21} \quad \color{Red} \text{Multiply numerators and denominators.} \nonumber \]Звідси:\[2 / 3 \times 5 / 7 \quad \text { is equivalent to } \quad \dfrac{2}{3} \times \dfrac{5}{7} \nonumber \] Введіть вираз$2/3×5/7$ на калькуляторі, а потім натисніть клавішу ENTER. Результат показаний на першому зображенні на малюнку$\PageIndex{3}$. Далі натисніть кнопку MATH, потім виберіть 1:Frac (див. Друге зображення на малюнку$\PageIndex{3}$) і знову натисніть клавішу ENTER. Зверніть увагу, що результат, показаний на третьому зображенні на малюнку,$\PageIndex{3}$ відповідає правильній відповіді$10/21$ знайденої вище.

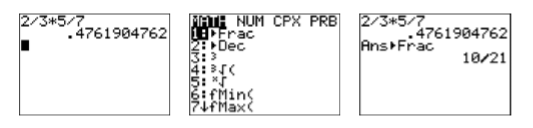
$рис. 1.3.3.png$

Малюнок$\PageIndex{3}$: Розрахунок$2/3×1/2$.

Цей приклад демонструє, що нам потрібно постійне нагадування про Правила, що керують порядком операцій. Ми знаємо, що в цій ситуації нам потрібно інвертувати і множити. \[\begin{aligned} \dfrac{3}{5} \div \dfrac{1}{3}&= \dfrac{3}{5} \times \dfrac{3}{1} \quad \color{Red} \text { Invert and multiply. } \\ &=\dfrac{9}{5} \quad \color{Red} \text { Multiply numerators and denominators. } \end{aligned} \nonumber \]
Отже, правильна відповідь - 9/5. Введіть вираз$3/5/1/3$ на калькуляторі, а потім натисніть клавішу ENTER. Виберіть 1: Frac з меню MATH і натисніть клавішу ENTER ще раз. Зауважте, що результат на першому зображенні$\PageIndex{4}$ на малюнку не відповідає правильній відповіді,$9/5$ знайденій вище. Що ми зробили не так? Якщо точно дотримуватися Правил Керівного Порядку операцій, то:\ [\ begin {вирівняний}
3/5/1/3 & =\ dfrac {3} {5}/1/3\ quad\ color {Red}\ text {3}\ quad\
color {3}\ dfrac {3}\ dfrac {3} {5} {Розділити:}\ dfrac {3} {5}/1=\ dfrac {3} {5}\\
& =\ dfrac {3} {5}\ times\ dfrac {1} {3}\ quad\ color {Червоний}\ текст {Інвертувати і помножити.} \\
& =\ dfrac {1} {5}\ quad\ color {Червоний}\ текст {Множення:}\ dfrac {3} {5}\ times\ dfrac {1} {3} =\ dfrac {1} {5}
\ end {вирівняний}\ nonumber\] Це пояснює відповідь, знайдену на першому зображенні на малюнку$\PageIndex{4}$. Однак це також показує, що:\[ 3 / 5 / 1 / 3 \quad \text { is not equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] Ми можемо вилікувати проблему, використовуючи символи групування. \[\begin{aligned} (3 / 5) /(1 / 3) &=\dfrac{3}{5} / \dfrac{1}{3} \quad \color{Red} \text { Parentheses first. } \\ &=\dfrac{3}{5} \div \dfrac{1}{3} \quad \color{Red} \text { is equivalent to } \div \end{aligned} \nonumber \]Звідси:\[(3 / 5) /(1 / 3) \quad \text { is equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] Введіть вираз$(3/5)/(1/3)$ на калькуляторі, а потім натисніть клавішу ENTER. Виберіть 1: Frac з меню MATH і натисніть клавішу ENTER ще раз. Зверніть увагу, що результат на другому зображенні на малюнку$\PageIndex{4}$ відповідає правильній відповіді$9/5$.

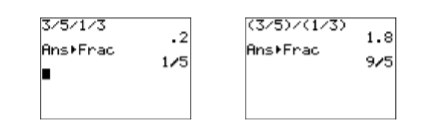
$рис. 1.3.4.png$

Малюнок$\PageIndex{4}$: Розрахунок$(3/5)/(1/3)$.

Вправа$\PageIndex{10}$

Спростіть за допомогою графічного калькулятора:$-\dfrac{4}{5}+\dfrac{8}{3}$.

Відповідь: $28/15$

Дописувачі

Template:ContribElemAlgebraArnold