1.1: Вступ до цілих чисел

Last updated
Save as PDF

Page ID: 58139

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Починаємо з набору підрахунку чисел, формально званих набором натуральних чисел.

Натуральні числа

\[\mathbb{N}=\{1,2,3,4,5, \ldots \} \nonumber \]Множиною називається множина натуральних чисел.

Якщо додати число нуль до набору натуральних чисел, то у нас є набір чисел, які називаються цілими числами.

Цілі числа

Безліч\[W=\{0,1,2,3,4,5, \ldots\} \nonumber \] називається сукупністю цілих чисел.

Число$0$ особливе, оскільки щоразу, коли ви додаєте його до іншого цілого числа, ви отримуєте однакове число як відповідь.

Властивість адитивної ідентичності

Якщо a - будь-яке ціле число, то з цієї\[a +0=a \nonumber \] причини все число$0$ називається адитивної ідентичністю.

Таким чином, наприклад,$3 + 0 = 3$,$15 + 0 = 15$, і$123 + 0 = 123$. Це все приклади властивості адитивної ідентичності. Кожне натуральне число має протилежне, так що при складанні їх разом їх сума дорівнює нулю.

Адитивна зворотна властивість

Якщо$a$ є будь-яке натуральне число, то визначте протилежне$a$, символізується$-a$, так що\[a +(-a)=0 \nonumber \] Число$-a$ називається «протилежним»$a$, або більш формально, адитивним оберненим$a$.

Наприклад, протилежне (добавка обернена)$3$ is$−3$, і$3+(−3) = 0$. Протилежне (добавка обернена)$12$ is$−12$, і$12 + (−12) = 0$. Протилежність$254$ є$−254$, і$254+(−254) = 0$. Це все приклади адитивних інверсів і адитивного зворотного властивості.

Тому що$7+(−7) = 0$, ми сказали,$−7$ що протилежне (добавка обернена)$7$. Однак ми також можемо це повернути і сказати,$7$ що протилежне$−7$. Якщо перевести словосполучення «$−7$протилежне є$7$» в математичні символи, отримаємо$−(−7) = 7$.

Протилежність протилежному

Тому що можна$a+(-a)=0,$ сказати,$a$ що протилежне$-a$. В символах пишемо:\[-(-a)=a \nonumber \]

Таким чином, наприклад,$-(-11)=11$,$-(-103)=103$, і$-(-1255)=1255$.

Цілі числа

Якщо ми збираємо всі натуральні числа і їх адитивні зворотні, то включаємо число нуль, у нас буде колекція чисел, званих цілими числами.

Цілі числа

\[\mathbb{Z}=\{\ldots,-5,-4,-3,-2,-1,0,1,2,3,4,5, \ldots\} \nonumber \]Множиною називається множина цілих чисел.

Цілі числа можна зробити так, щоб відповідати точкам на прямій дуже природним чином. Спочатку намалюйте лінію, а потім знайдіть нуль в будь-якому місці. По-друге, поставте цифру один праворуч від нуля. Це визначає довжину однієї одиниці. Нарешті, знайдіть числа$1,2,3,4,5, \dots$ праворуч від нуля, потім їх протилежності (адитивні інверси)$-1,-2,-3,-4,-5, \dots$ зліва від нуля (див. Рис.$\PageIndex{1}$).

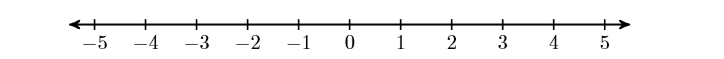
$рис. 1.1.png$

Малюнок$\PageIndex{1}$: Кожне ціле число відповідає унікальній позиції на числовому рядку.

Зверніть увагу, що коли ми рухаємося вправо на числовому рядку, цілі числа стають більшими. З іншого боку, коли ми рухаємося вліво на числовому рядку, цілі числа стають меншими.

Позитивні та від'ємні цілі числа

У числовому рядку деякі цілі числа лежать праворуч від нуля, а деякі лежать ліворуч від нуля.

Якщо$a$ є цілим числом, яке лежить праворуч від нуля, то$a$ називається натуральним числом.
Якщо$a$ є цілим числом, яке лежить зліва від нуля, то$a$ називається від'ємним цілим числом.

Таким чином,,$4$$25$, і$142$ є додатними цілими числами, while$-7$,$-53,$ і$-435$ є від'ємними цілими числами.

Абсолютне значення

Абсолютне значення (або величина) цілого числа визначається наступним чином.

Абсолютне значення цілого числа

Якщо$a$ є цілим числом, то абсолютне значення$a$$|a|$, записане, визначається як відстань між цілим і нулем у числовому рядку.

Приклад$\PageIndex{1}$

Спростити$|-4|$.

Рішення

Розглянемо положення$-4$ на числовому рядку. Зверніть увагу, що$-4$ лежить на відстані чотирьох одиниць від нуля.

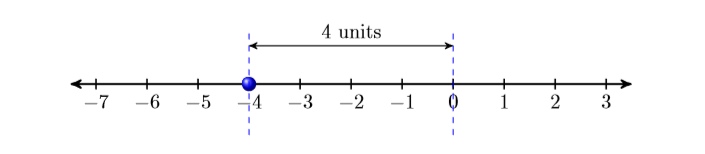
$рис. 1.1.2.png$

Малюнок$\PageIndex{2}$

Тому що абсолютне значення (величина) цілого числа дорівнює його відстані від нуля,$|-4|=4$.

Вправа$\PageIndex{1}$

Спростити:$|-23|$

Відповідь: $|-23|=23$

Подібним чином:

Ціле число$5$ лежить на відстані п'яти одиниць від нуля. Отже,$|5|= 5$.
Ціле число$0$ лежить нуль одиниць від нуля, отже,$|0|= 0$. Зверніть увагу, що абсолютне значення будь-якого числа є або додатним, або нулем. Тобто абсолютне значення числа є невід'ємним (не від'ємним).

Додавання цілих чисел

Цей розділ призначений для швидкого перегляду додавання цілих чисел. Розглянемо перший з двох випадків.

Додавання цілих чисел з подібними знаками

Щоб додати два цілих числа з подібними знаками (обидва додатні або обидва негативні), додайте їх величини (абсолютні значення), а потім префіксі їх загальний знак.

Приклад$\PageIndex{2}$

Спростити$7+12$.

Рішення

У нас є подібні знаки. Величини (абсолютні значення)$7$ і$12$ є$7$ і$12$, відповідно. Якщо додати величини, то отримаємо$19$. Якщо префіксити загальний знак, то отримаємо$19$. Тобто:\[7+12=19 \nonumber \]

Вправа$\PageIndex{2}$

Спростити:$13+28$.

Відповідь: $41$

Приклад$\PageIndex{3}$

Спростити$-8+(-9)$.

Рішення

У нас є подібні знаки. Величини (абсолютні значення)$-8$ і$-9$ є$8$ і$9$, відповідно. Якщо додати величини, то отримаємо$17$. Якщо префіксити загальний знак, то отримаємо$-17$. Тобто:\[-8+(-9)=-17 \nonumber \]

Вправа$\PageIndex{3}$

Спростити:$-12+(-21)$.

Відповідь: $-33$

Далі розглянемо випадок, коли у нас є несхожі ознаки.

Додавання цілих чисел з несхожими знаками

Щоб додати два цілих числа зі знаками відмінності (один позитивний і один від'ємний), відніміть ціле число з меншою величиною (абсолютне значення) від числа з більшою величиною, а потім префікс знак цілого числа з більшою величиною.

Приклад$\PageIndex{4}$

Спростити$-14+11$.

Рішення

У нас несхожі ознаки. Величини (абсолютні значення)$-14$ і$11$ є$14$ і$11$, відповідно. Якщо відняти меншу величину від більшої, то отримаємо$3$. Число$-14$ має більшу величину, тому ми префікуємо нашу відповідь його негативним знаком. Тобто:\[-14+11=-3 \nonumber \]

Вправа$\PageIndex{4}$

Спростити:$12+(-29)$.

Відповідь: $-17$

Приклад$\PageIndex{5}$

Спростити$40+(-25)$.

Рішення

У нас несхожі ознаки. Величини (абсолютні значення)$40$ і$-25$ є$40$ і$25$, відповідно. Якщо відняти меншу величину від більшої, то отримаємо$15$. Число$40$ має більшу величину, тому ми префікуємо нашу відповідь його позитивним знаком. Тобто:\[40+(-25)=15 \nonumber \]

Вправа$\PageIndex{5}$

Спростити:$32+(-90)$.

Відповідь: $-58$

Математичні властивості додавання

Порядок, в якому ми додаємо цілі числа, значення не має. Тобто$-20 + 34$ дає відповідь, ідентичну сумі$34 + (−20)$. В обох випадках відповідь є$14$. Цей факт називають комутативним властивістю додавання.

Комутативна властивість додавання

Якщо$a$ і$b$ є будь-якими двома цілими числами, то:\[a+b=b+a \nonumber \]

Далі, коли ми додаємо три цілих числа, не має значення, які два ми додаємо першим. Наприклад, якщо спочатку скласти друге і третє з трьох чисел, то отримаємо:

\[\begin{aligned}-11+(-2+5) &=-11+3 \quad {\color{Red} \text { Parentheses first: }-2+5=3} \\ &=-8 \quad {\color{Red} \text { Add: }-11+3=-8} \end{aligned} \nonumber \]

З іншого боку, якщо спочатку додати перше і друге з трьох чисел, ми отримаємо:

\[\begin{aligned}(-11+(-2))+5 &=-13+5 \quad {\color{Red} \text { Parentheses first: }-11+(-2)=-13} \\ &=-8 \quad {\color{Red} \text { Add: }-13+5=-8} \end{aligned} \nonumber \]

Таким чином,$-11 + (−2 + 5) = (−11 + (−2)) + 5$. Цей факт називають асоціативним властивістю додавання.

Асоціативна властивість додавання

Якщо$a$$b$, і$c$ є будь-якими трьома цілими числами, то:\[a +( b + c)=( a + b)+c \nonumber \]

Цілочисельне віднімання

Віднімання - це зворотне, або протилежне, додавання.

Віднімання цілих чисел

Якщо$a$ і$b$ є будь-якими двома цілими числами, то:\[a-b = a +(-b) \nonumber \] Віднімання$b$ ідентично додаванню протилежного (адитивного оберненого)$b$.

Приклад$\PageIndex{6}$

Спростити:$-13-27$.

Рішення

«Протилежність» (добавка обернена)$27$ є$-27$. Отже, віднімання$27$ - це те ж саме, що і додавання$-27$.

$\begin{aligned}-13-27&=-13+(-27) \quad {\color{Red} \text { Subtracting 27 is the same as adding −27.}} \\ &=-50 \quad {\color{Red} \text { Add the magnitudes, then prefix the common negative sign.}} \end{aligned}$

Вправа$\PageIndex{6}$

Спростити:$-11-15$.

Відповідь: $-26$

Приклад$\PageIndex{7}$

Спростити:$-27-(-50)$.

Рішення

«Протилежність» (добавка обернена)$-50$ is$-(-50)$, або$50$. Отже, віднімання$-50$ - це те ж саме, що і додавання$50$.

$\begin{aligned}-27-(-50)&=-27+50 \quad {\color{Red} \text { Subtracting -50 is the same as adding 50.}} \\&=23 \quad {\color{Red} \text { Subtract the smaller magnitude from the larger magnitude, then prefix the sign of the larger magnitude.}} \end{aligned}$

Вправа$\PageIndex{7}$

Спростити:$-18-(-54)$.

Відповідь: $36$

Числочисельне множення

Цей розділ призначений для швидкого перегляду множення та ділення цілих чисел.

Як Знаки

Якщо$a$ і$b$ є цілими числами з подібними знаками (як додатними, так і негативними), то добуток$ab$ і частка$a/b$ є додатними.

\[\begin{array}{ll}{(+)(+)=+} \quad {\text { or }} & {(+) /(+)=+} \\ {(-)(-)=+\quad \text { or }} & {(-) /(-)=+}\end{array} \nonumber \]

Приклад$\PageIndex{8}$

Спростіть кожне з наступних виразів:

$(2)(3)$
$(-12)(-8)$
$-14 /(-2)$

Рішення

При множенні або діленні подібні знаки дають позитивний результат.

$(2)(3)=6$
$(-12)(-8)=96$
$-14 /(-2)=7$

Вправа$\PageIndex{8}$

Спростити:$(-18)(-5)$.

Відповідь: $90$

На відміну від знаків

Якщо$a$ і$b$ є цілими числами з несхожими знаками (один позитивний і один негативний), то добуток$ab$ і частка$a/b$ негативні.

\[\begin{array}{ll}{(+)(-)=-} & {\text { or }}& {(+) /(-)=-} \\ {(-)(+)=-} & {\text { or }} & {(-) /(+)=-}\end{array} \nonumber \]

Приклад$\PageIndex{9}$

Спростіть кожне з наступних виразів:

$(2)(-12)$
$(-9)(12)$
$24/(-8)$

Рішення

При множенні або діленні, на відміну від знаків, дають негативний результат.

$(2)(-12)=-24$
$(-9)(12)=-108$
$24 /(-8)=-3$

Вправа$\PageIndex{9}$

Спростити:$(-19)(3)$.

Відповідь: $-57$

Математичні властивості множення

Порядок, в якому ми множимо цілі числа, значення не має. Тобто$(-8)(5)$ дає відповідь ідентичний$(5)(-8)$. В обох випадках відповідь є$-40$. Цей факт називається комутативним властивістю множення.

Комутативна властивість множення

Якщо$a$ і$b$ є будь-якими двома цілими числами, то:\[a \cdot b=b+a \nonumber \]

Далі, коли ми множимо три цілих числа, не має значення, які два ми помножимо спочатку. Якщо спочатку помножити друге і третє з трьох чисел, то отримаємо:

\[\begin{aligned}(-3)[(-4)(-5)] &=(-3)(20) & {\color{Red} \text { Brackets first: }(-4)(-5)=20} \\ &=-60 & {\color{Red} \text { Multiply: }(-3)(20)=-60} \end{aligned} \nonumber \]

З іншого боку, якщо спочатку помножити перше і друге з трьох чисел, то отримаємо:

\[\begin{aligned}[(-3)(-4)](-5)&=(12)(-5) & {\color{Red} \text { Brackets first: }(-3)(-4)=12} \\ & =-60 & {\color{Red} \text { Multiply: }(12)(-5)=-60}\end{aligned} \nonumber \]

Таким чином,$(-3)[(-4)(-5)]=[(-3)(-4)](-5)$. Цей факт називається асоціативним властивістю множення.

Асоціативна властивість множення

Якщо$a$$b$, і$c$ є будь-якими трьома цілими числами, то:\[a \cdot(b \cdot c)=(a \cdot b) \cdot c \nonumber \]

Коли ви множите ціле число на$1$, ви отримаєте однакове число назад як добуток. Наприклад,$(1)(5) = 5$ і$(-11)(1) = -11$. Цей факт відомий як мультиплікативна властивість ідентичності.

Властивість мультиплікативної ідентичності

Якщо a - будь-яке ціле число, то: З цієї\[1 \cdot a=a \quad \text { and } \quad a \cdot 1=a \nonumber \] причини ціле число$1$ називається «мультиплікативною ідентичністю».

Нарешті, зауважте, що$(-1)(5) = -5$. Таким чином,$5$ множення на$-1$ ідентично прийнятню «протилежного»$5$ або заперечення$5$.

Мультиплікативна властивість$−1$

Множення на мінус одне ідентично запереченню. Тобто:\[(-1) a=-a \nonumber \]

Показники

У$a^n$ експоненціальному$a$ виразі число називається базовим, тоді як число$n$ називається показником. Тепер ми визначаємо, що мається на увазі під показником.

Показники

$a$Дозволяти ціле число і нехай$n$ бути будь-яке ціле число. Якщо$n \neq 0$, то:\[a^{n}=\underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_{n \text { times }} \nonumber \]

Тобто обчислити$a^n$, записувати$a$ як множник$n$ раз.

Приклад$\PageIndex{10}$

Спростити$(-2)^{3}$.

Рішення

У експоненціальному виразі зверніть увагу$(-2)^3$, що$-2$ є основою,$3$ while - експонентою. Показник підказує нам написати базу як коефіцієнт три рази. Спростіть результат, виконуючи множення по порядку, рухаючись зліва направо.

\[\begin{aligned}(-2)^{3} & =(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, three times.}} \\ & =(4)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =-8 \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ \text{Thus } (-2)^{3} &=-8\end{aligned} \nonumber \]

Вправа$\PageIndex{10}$

Спростити:$(-2)^{2}$.

Відповідь: $4$

У прикладі відзначимо $\PageIndex{10}$, що твір трьох негативних чинників є негативним. Спробуємо інший приклад.

Приклад$\PageIndex{11}$

Спростити$(-2)^{4}$.

Рішення

У експоненціальному виразі зверніть увагу$(-2)4$, що$-2$ є основою,$4$ while - експонентою. Експонента говорить нам написати базу як коефіцієнт чотири рази. Спростіть результат, виконуючи множення по порядку, рухаючись зліва направо.

\[\begin{aligned}(-2)^{4} & =(-2)(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, four times.}} \\ & =(4)(-2)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =(-8)(-2) \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ & = 16 \quad {\color{Red}\text { Multiply: (-8)(-2)=-8}}\\ \text{Thus } (-2)^{4} &=16\end{aligned} \nonumber \]

Вправа$\PageIndex{11}$

Спростити:$(-2)^{5}$.

Відповідь: $-32$

У прикладі відзначимо $\PageIndex{11}$, що добуток чотирьох негативних чинників є позитивним. Приклади $\PageIndex{10}$і $\PageIndex{11}$розкриваємо наступну закономірність.

Непарні або парні показники

Коли від'ємне ціле число піднімається до парного показника, результат позитивний.
Коли від'ємне ціле число піднімається до непарного показника, результат буде від'ємним.

Графічний калькулятор: заперечення проти віднімання

$рис. 1.1.3.png$

Малюнок$\PageIndex{3}$: Нижня половина ТІ-84.

Розглянемо вигляд нижньої половини графічного калькулятора TI-84 на рис$\PageIndex{3}$. Зверніть увагу, що є дві клавіші, які містять якийсь негативний знак, один у нижньому рядку клавіш, а інший в останньому стовпці клавіш праворуч, розташований трохи вище символу плюс.

$рис. 1.1.4.png$

Малюнок$\PageIndex{4}$

Перша з цих кнопок є унарним оператором «заперечення». Якщо ви хочете звести нанівець єдине (таким чином слово «унарне») число, то це ключ до використання. Наприклад, введіть,$-3$ натиснувши наступну послідовність кнопок. Результат показаний на малюнку$\PageIndex{7}$.

$рис. 1.1.5.png$

Малюнок$\PageIndex{5}$

Друга кнопка - двійковий оператор «віднімання». Якщо ви хочете відняти одне число з іншого числа (таким чином слово «двійковий»), то це ключ для використання. Наприклад, введіть,$7-15$ натиснувши наступну послідовність кнопок. Результат показаний на малюнку$\PageIndex{8}$.

$рис. 1.1.6.png$

Малюнок$\PageIndex{6}$

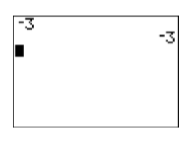
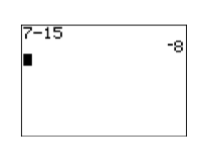
$рис. 1.1.7.png$ $рис. 1.1.8.png$

Малюнок$\PageIndex{7}$: Заперечення числа. Малюнок$\PageIndex{8}$: Відніміть два числа.

Примітка

Не міняйте між собою ролі оператора унарного заперечення та оператора двійкового віднімання.

Щоб звести нанівець число, використовуйте: (-)
Щоб відняти одне число від іншого, використовуйте: -

Якщо ви поміняєте ролі цих операторів, калькулятор відповість, що ви зробили «синтаксичну помилку» (див. Рисунки$\PageIndex{9}$ та$\PageIndex{10}$).

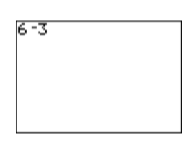
$рис. 1.1.9.png$ $рис. 1.1.10.png$

Малюнок$\PageIndex{9}$: Використання неправильного символу для віднімання. Малюнок$\PageIndex{10}$: Результуюча синтаксична помилка.

Приклад$\PageIndex{12}$

Скористайтеся калькулятором графіків TI-84, щоб спростити кожне з наступних виразів:

$-717-432$
$(232)(-313)$
$(-17)^{3}$

Рішення

Знак мінус в кожному з цих прикладів виглядає точно так само, але іноді його використовують як «негативний» знак і іноді його використовують як знак «віднімання».

Вираз$-717-432$ просить нас відняти$432$ від «негативного»$717$. Введіть наступну послідовність натискань клавіш, щоб отримати результат, показаний на першому зображенні на малюнку$\PageIndex{11}$.

$рис. 1.1.11a.png$

Отже,$-717-432=-1149$.

Вираз$(232)(-313)$ просить нас знайти твір$232$ і «негативний»$313$. Введіть наступну послідовність натискань клавіш, щоб отримати результат, показаний на другому зображенні на малюнку.$\PageIndex{11}$.

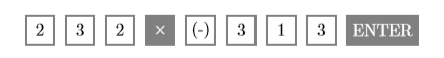
$рис. 1.1.11b.png$

Отже,$(232)(-313)=-72616$.

Вираз$(-17)^3$ просить нас підняти «негатив» до третьої влади. Введіть наступну послідовність натискань клавіш, щоб отримати результат, показаний на третьому зображенні на малюнку$\PageIndex{11}$. Символ «каретка» ^ розташований трохи над клавішею поділу в крайньому правому стовпці графічного калькулятора TI-84.

$рис. 1.1.11c.png$

Отже,$(-17)^{3}=-4913$.

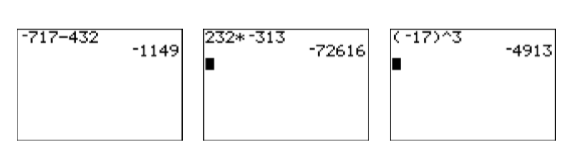
$рис. 1.1.11.png$

Малюнок$\PageIndex{11}$: Розрахунки, зроблені на графічному калькуляторі.

Вправа$\PageIndex{12}$

Використовуйте графічний калькулятор для оцінки$(-225)^3$.

Відповідь: $(-225)^3 = -11390625$

Дописувачі

Template:ContribElemAlgebraArnold